Kapitel 7 Konfidenzintervalle
Lernziele
- Punkt- und Intervallschätzer voneinander abgrenzen und charakterisieren können
- Herleitung von Intervallschätzern aus dem Zentralen Grenzwertsatz erklären können
- Konfidenzfaktoren aus der Normalverteilungstabelle ablesen und interpretieren können
- Korrekte (präzise) Formulierung zur Interpretation von Konfidenzintervallen kennen.
Im ersten Kapitel haben wir Lage- und Streuungsmaße kennengelernt. Im Normalfall kennen wir die wahren Werte der Grundgesamtheit nicht, sondern schätzen diese aus einer Stichprobe:
| Wahrer Wert der Grundgesamtheit | Schätzer aus der Stichprobe | |
|---|---|---|
| Mittelwert | \(\mu\) | \(\overline{x}\) |
| Varianz | \(\sigma^2\) | \(s^2\) |
| Standardabweichung | \(\sigma\) | \(s\) |
Beispielsweise ist \(\overline{x}\) ein Schätzer für \(\mu\). Dabei stellt sich die Frage, wie zuverlässig dieser Schätzer den wahren Wert trifft. Wenn wir nur den einen Wert für \(\overline{x}\) angeben, können wir nicht ablesen oder erkennen, wie treffsicher dieser Schätzer ist. Da er nur einen Wert beinhaltet, nennen wir ihn auch „Punktschätzer“, im Gegensatz zu „Intervallschätzern“, die wir in diesem Kapitel behandeln.
Aus dem Abschnitt 4.2 wissen wir, dass das arithmetische Mittel unabhängiger identisch-verteilter Zufallsbeobachtungen \(\overline{X}\) eine Zufallsvariable ist, die einer statistischen Verteilung folgt, und wir kennen diese Verteilung zumindest approximativ:
\[\overline{X} \sim N\left(\mu,\frac{\sigma^2}{n}\right)\]
Auf dieser Grundlage ermitteln wir im Folgenden einen Intervallschätzer für \(\mu\).
Um Wahrscheinlichkeiten ablesen zu können, müssen wir die Verteilung standardisieren, d. h. so verschieben und stauchen oder strecken, dass es eine Standardnormalverteilung wird: \(\overline{X} \sim N(\mu,\frac{\sigma^2}{n}) \to N(0,1)\). Am Rande sei erwähnt, dass wir bei bekannter Varianz die Normalverteilung anwenden dürfen; falls die Varianz aus der Stichprobe geschätzt wird, ist die t-Verteilung exakter. Diese Verteilung lernen wir im 8. Kapitel kennen. Für unsere Zwecke genügt die Näherung durch die Normalverteilung.
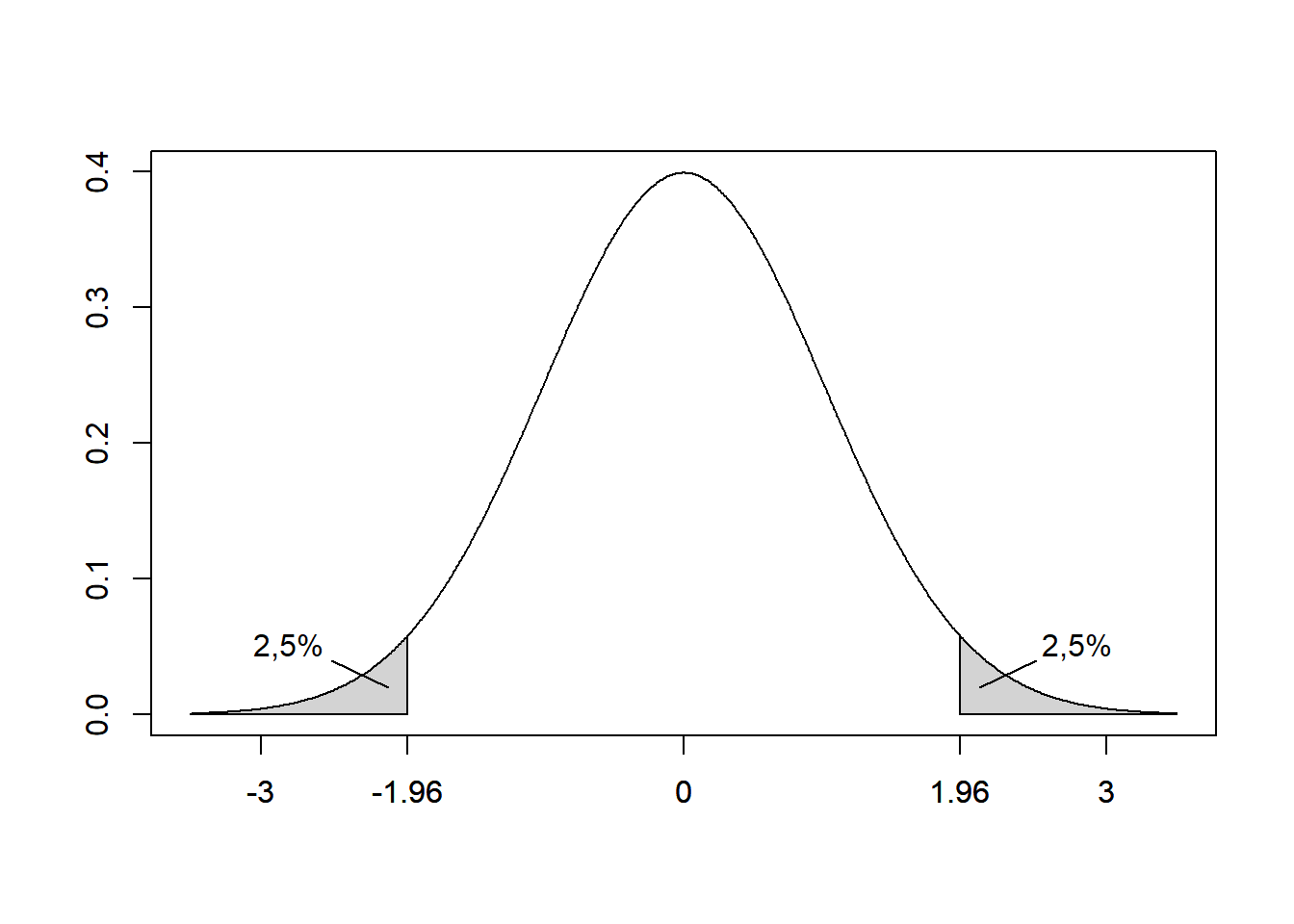
Abbildung 7.1: Standardnormalverteilung mit jeweils 2,5 Prozent der Fläche unter dem Funktionsgraphen in den beiden Flanken hervorgehoben
Wir sehen die uns vertraute Glockenkurve. Da es eine Standardnormalverteilung ist, liegt sie symmetrisch um Null. Nun möchten wir in der Mitte der Kurve 95 % der Fläche eingrenzen, d. h. rechts und links jeweils 2,5 % wegschneiden. An welchen Stellen muss geschnitten werden? Den gesuchten Wert finden Sie z.B. mithilfe der Tabelle 8.1 für die Standardnormalverteilung, indem Sie im Körper der Tabelle den Wert 1-0,025 = 0,975 suchen. (Antwort: 1,96)
Diese Werte setzen wir nun in unsere Formel für \(z\) (siehe Abschnitt 3.2.1) ein und lösen nach \(\mu\) auf, denn wir suchen einen Intervallschätzer für \(\mu\):
\[Z=\frac{\overline{X}-μ}{\sqrt{\sigma^2⁄n}}\]
Für die linke Grenze ergibt sich \(\overline{X}-1,96\sqrt{\sigma^2⁄n} ≤ μ\)
und für die rechte Grenze entsprechend \(\overline{X}+1,96\sqrt{\sigma^2⁄n} ≥ μ\). Für empirische Beobachtungen schreiben wir also entsprechend
\(\overline{x}-1,96\sqrt{s^2⁄n} ≤ μ ≤ \overline{x}+1,96\sqrt{s^2⁄n}\).
Dieses Intervall heißt Konfidenzintervall und wird mit 95 %-iger Wahrscheinlichkeit den wahren Wert \(\mu\) überdecken. Sie sollten auf diese Formulierung achten: Die Aussage „Der wahre Wert liegt mit 95 % Wahrscheinlichkeit innerhalb des Intervalls“ ist falsch, weil der wahre Wert feststeht. Vielmehr ist das Intervall die Zufallsvariable, denn für mehrere Stichproben, aus denen Sie das Intervall schätzen, wird jedes Mal ein geringfügig anderes Intervall herauskommen.
Wenn der Stichprobenumfang steigt, wird die Schätzung von \(\overline{x}\) aus der Stichprobe verlässlicher, so dass das Intervall unter sonst gleichen Bedingungen schmaler wird. Umgekehrt wird das Intervall breiter, wenn die Zufallsvariable \(X\) stärker streut. Dies schlägt sich in einer größeren Varianz (\(s^2\)) nieder. Mit der Größe der Grundgesamtheit haben die Intervallgrenzen nichts zu tun. Dies wird oftmals verwechselt.
Aus der Formel ist unmittelbar ersichtlich, dass das hier besprochene Konfidenzintervall immer symmetrisch um den Punktschätzer liegt.
Wir haben uns ein Sicherheitsniveau von 95 % vorgegeben, weil dies gebräuchlich ist. Diese Wahrscheinlichkeit, mit der wir im Durchschnitt mit unserem Intervall richtig liegen, heißt Konfidenzniveau. Die Stellen, an denen wir in der Grafik die 95 % in der Mitte eingegrenzt haben, sind Konfidenzfaktoren (bei 95 %: 1,96).
Aufgabe 7.1 (Bestimmen der Konfidenzfaktoren) Zu Übungszwecken sollten Sie die Konfidenzfaktoren für die beiden anderen recht gebräuchlichen Konfidenzniveaus aus der Tabelle der Standardnormalverteilung ablesen und untenstehend ergänzen:
| Konfidenzniveau | Konfidenzfaktor |
|---|---|
| 90 % | |
| 95 % | 1,96 |
| 99 % |
Die richtigen Werte sind intuitiv einleuchtend: Wenn wir die Sicherheit erhöhen, mit der wir mit unserem Intervallschätzer richtig liegen, dann muss das Intervall breiter werden, d. h., der Konfidenzfaktor steigt mit Erhöhung des Konfidenzniveaus und unter sonst gleichen Bedingungen an.
Wir wollen die Berechnung eines 95 %-Konfidenzintervalls am Beispiel der Vermögensverteilung in Großbritannien im Jahr 1979 veranschaulichen.
Beispiel 7.1 (Konfidenzintervall für die mittlere Vermögensverteilung) Die folgenden Werte kennen wir bereits. Wir gehen hier davon aus, dass dies die Werte für die Grundgesamtheit sind (da knapp 20 Mio Befragte):
| \(µ\) | 16.399 |
| \(σ^2\) | 652.915.569 |
| \(σ\) | 25.552 |
Daraus ziehen wir eine Stichprobe vom Umfang \(n=100\) und ermitteln einen Stichprobenmittelwert von 15.000. Die Varianz in der Stichprobe sei \(s^2= 550.000.000\). Wir rechnen in Tausend, d. h. \(\overline{x} = 15\) und \(s^2 = 550\).
Das 95 %-Konfidenzintervall lautet \[\overline{x}-1{,}96\sqrt{s^2⁄n} ≤ μ ≤ \overline{x}+1{,}96\sqrt{s^2⁄n}\] \[15-1{,}96\sqrt{550⁄100} ≤ μ ≤ 15+1{,}96\sqrt{550⁄100}=[10{,}4 ;19{,}6]\] Diese beiden Intervallgrenzen entsprechen -1,96 bzw. + 1,96 in der Standardnormalverteilung.
Wird das Experiment viele Male wiederholt, so werden wir in etwa 95 % der Fälle einen Intervallschätzer erhalten, der den wahren Wert überdeckt.
Mit den Konfidenzintervallen haben wir eine Möglichkeit kennengelernt, die Unsicherheit beim Schlussfolgern von der Stichprobe auf die Grundgesamtheit zu erfassen. Mit Intervallschätzern besteht eine gewisse Unsicherheit, ob wir mit der Schätzung den wahren Wert treffen bzw. ihn einschließen. Im Gegensatz zu Punktschätzern können wir aber mit den Intervallschätzern die Unsicherheit der Schätzung quantifizieren (z. B.: 10 %, 5 %, 1 %) und diese zusätzlich zum Schätzergebnis angeben. Dies ist ein wesentlicher Zuwachs an Informationen im Vergleich zum Punktschätzer.
Aufgabe 7.2 (Konfidenzintervalle für die mittlere Vermögensverteilung) Berechnen Sie das Konfidenzintervall aus Beispiel 7.1 für die Konfidenzniveaus 90 % und 99 % und diskutieren Sie Ihre Ergebnisse: Wie aussagekräftig sind die Intervalle?
Aufgabe 7.3 (Konfidenzintervall für Sichteinlagen) 50 Bankkunden haben im Durchschnitt einen Kontostand von 2.000 Euro bei einer Standardabweichung von 350 Euro. Berechnen Sie das 90 %-Konfidenzintervall für den Kontostand der Bankkunden.
Hintergrund: Diese Sichteinlagen stehen der Bank relativ zuverlässig zur Verfügung; sie werden deshalb in den Liquiditätsanforderungen nach Basel III günstig behandelt.
Aufgabe 7.4 (Konfidenzintervall für Schadenquoten) Wir betrachten nun die Schadenquoten (Schadenhöhe / Prämieneinnnahmen) aus Aufgabe 1.8:
| Jahr i | Prämien \(x_i\) in Mio. € | Schäden \(y_i\) in Mio. € | Schadenquoten |
|---|---|---|---|
| 1 | 4,903 | 2,200 | 0,449 |
| 2 | 4,754 | 2,095 | 0,441 |
| 3 | 4,618 | 3,377 | 0,731 |
| 4 | 4,479 | 2,455 | 0,548 |
| 5 | 4,388 | 2,121 | 0,529 |
| 6 | 4,435 | 2,100 | 0,473 |
| 7 | 4,638 | 2,336 | 0,504 |
| 8 | 4,790 | 2,816 | 0,588 |
| 9 | 5,011 | 2,418 | 0,483 |
| 10 | 5,250 | 2,855 | 0,544 |
| 11 | 5,349 | 2,901 | 0,542 |
| 12 | 5,805 | 2,715 | 0,468 |
| 13 | 5,929 | 2,634 | 0,444 |
| 14 | 6,122 | 2,822 | 0,461 |
| 15 | 6,542 | 3,270 | 0,500 |
Ermitteln Sie das 90 %-Konfindenzintervall für die durchschnittliche Schadenquote.
Bisher haben wir Konfidenzintervalle für den Mittelwert berechnet. Wir wenden uns nun den Intervallschätzern für Anteile zu und erarbeiten uns diese anhand eines Beispiels.
Beispiel 7.2 (Konfidenzintervall für die Arbeitslosenquote) Wir betrachten eine Stichprobe mit 200 Männern, von denen 15 arbeitslos sind. Formal bedeutet dies:
\(n=200\), \(p=15/200 = 0{,}075\), d. h., die Arbeitslosenquote in der Stichprobe beträgt 7,5 %. \(\pi\) bezeichnet die Arbeitslosenquote in der Grundgesamtheit. Der Schätzer p ist normalverteilt:
\[p \sim N\left(\pi ,\frac{\pi(1-\pi)}{n}\right)\]
Das 95 %-Konfidenzintervall für die Arbeitslosenrate in der Grundgesamtheit lautet
\[p-1{,}96 \sqrt{p(1-p)⁄n} ≤ \pi ≤ p+1{,}96\sqrt{(p(1-p)⁄n}\] \[=0{,}075-1{,}96\sqrt{0{,}075(1-0{,}075)⁄200} ≤ \pi ≤ 0{,}075+1{,}96\sqrt{0{,}075(1-0{,}075)⁄200}\] \[= [0{,}038 ; 0{,}112]\]
Also mit 95 % Wahrscheinlichkeit überdecken wir mit dem Intervall von 3,8 % bis 11,2 % die wahre Arbeitslosenrate in der Grundgesamtheit. Mit dem hohen 95 %-Konfidenzniveau bekommen wir für die vorliegende Stichprobenzahl ein recht breites Konfidenzintervall. Dass die Arbeitslosenrate zwischen 4 % und 11 % liegt, wussten Sie wahrscheinlich auch ohne Intervallschätzer!
Aufgabe 7.5 (Konfidenzintervall für Anteil an Auszahlungen in der Gebäudeversicherung) Ein Versicherer zieht eine Stichprobe der Größe 200 aus seinem Bestand an 1.000 Gebäudeversicherungen. In dieser Stichprobe waren 25 Policen, für die der Versicherer auszahlen musste. Berechnen Sie ein 90 %-Konfidenzintervall für den Anteil an Gebäudeversicherungsverträgen, für die ausgezahlt werden muss.
Abschließend sei erwähnt, dass es auch Konfidenzintervalle für die Varianz gibt. Der Konfidenzfaktor muss dann aus einer Chi-Quadrat-Verteilung kommen. Diese Verteilung lernen wir im 8. Kapitel kennen.
Mit diesen Überlegungen zu Konfidenzintervallen für Anteile schließen wir unsere Betrachtung von Intervallschätzern ab. Wir haben uns erarbeitet, wie wir auf der Grundlage des Zentralen Grenzwertsatzes ein Intervall angeben können, das mit einer bestimmten Wahrscheinlichkeit (meist 90 %, 95 % oder 99 %) den wahren Wert aus der Grundgesamtheit überdeckt. Dies ist wesentlich informativer als die Angabe eines Punktschätzers. Wir können Intervallschätzer für den Mittelwert und für einen Anteil berechnen.
Schlüsselbegriffe:
Punkt- und Intervallschätzer; Herleitung von Intervallschätzern aus dem Zentralen Grenzwertsatz; Konfidenzfaktoren; Interpretation von Konfidenzintervallen
Literatur: