5.1 Introduction

As we saw, the most popular method for estimating survival, when there is censoring, is the well-known product-limit estimator also known as Kaplan-Meier estimator (Kaplan and Meier 1958). The popularity of the product-limit estimator is explained by its simplicity and intuitive appeal while requiring very week assumptions. It simply takes into account with the empirical probability of surviving over certain time.

The method does not take into account of covariates, so it is mainly descriptive. Discrete covariates can be included by splitting the sample for each level of the covariate and applying the product-limit estimator for each subsample. This approach is not recommended for continuous covariates.

To account to this extra difficulty several generalizations to the Kaplan-Meier estimator have been proposed throughout the last decades. Beran (1981) was the first one who proposed an estimator of the conditional distribution (survival) function with censored data in a fully nonparametric way. His estimator was further studied among others by Dabrowska (1987), Akritas (1994), Gonzalez-Manteiga and Cadarso-Suárez (1994) and Van Keilegom, Akritas, and Veraverbeke (2001). All these estimators can be used to estimate the distribution (or survival) function conditional to a continuous covariable in a regression model, when data are subject to censoring. However, none of the above methods can be used to estimate the conditional survival when the covariate is censored.

In many longitudinal medical studies, patients may experience several events through a follow-up period. In these studies, the analysis of sequentially ordered events are often of interest. The events of concern can be of the same nature (e.g., recurrent disease episodes in cancer studies) or represent different states in the disease process (e.g., ‘alive and disease-free’, ‘alive with recurrence’ and ‘dead’). If the events are of the same nature, this is usually referred as recurrent events (Cook and Lawless 2007). One example of this scheme can be see at Figure 5.1.

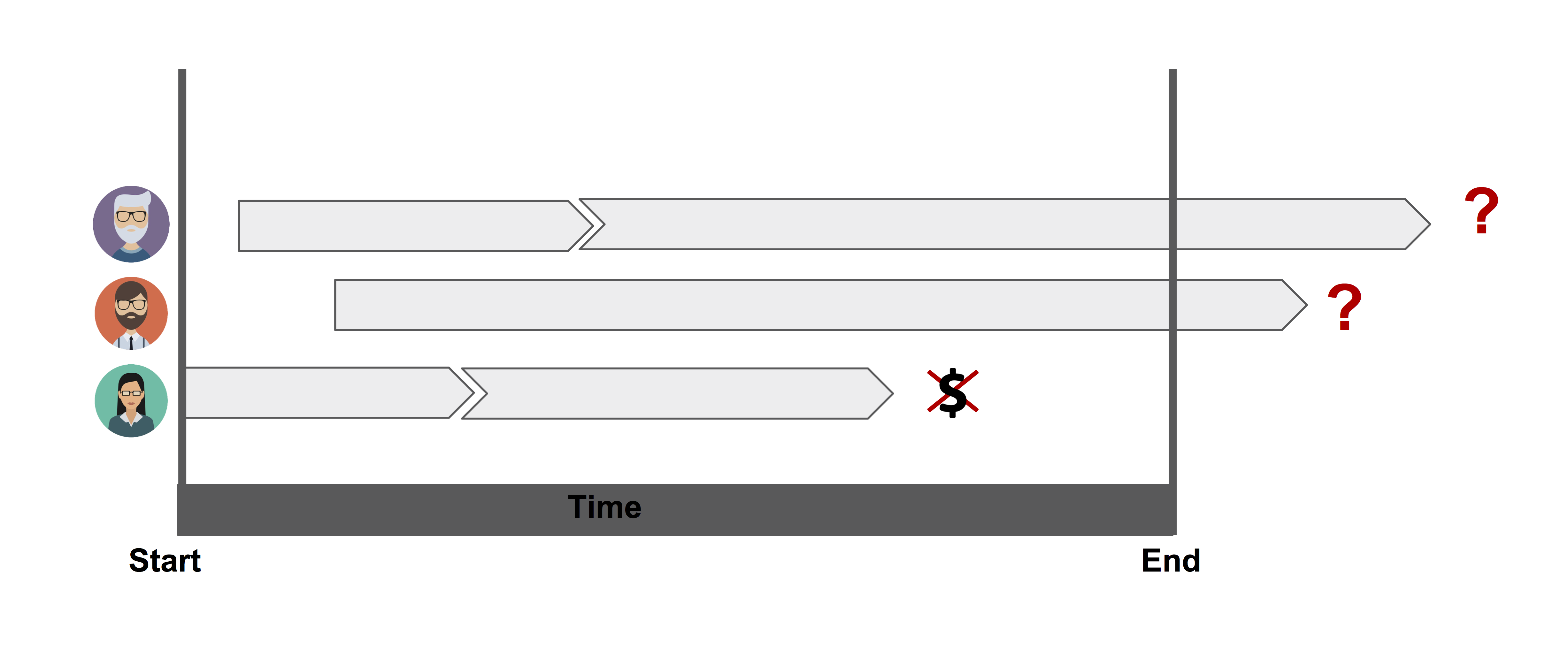
Figure 5.1: Illustration of censoring.

In the above situation maybe we want to obtain estimates for some conditional survival. Let’s do it now!

References

Kaplan, E.L., and P. Meier. 1958. “Nonparametric Estimation from Incomplete Observations.” Journal of the American Statistical Association 53: 457–81.

Beran, R. 1981. Nonparametric Regression with Randomly Censored Survival Data. University of California, Berkeley: Technical report.

Dabrowska, D. 1987. “Non-Parametric Regression with Censored Survival Data.” Scandinavian Journal of Statistics 14: 181–97.

Akritas, M.G. 1994. “Nearest Neighbor Estimation of a Bivariate Distribution Under Random Censoring.” The Annals of Statistics 22: 1299–1327.

Gonzalez-Manteiga, W., and C. Cadarso-Suárez. 1994. “Asymptotic Properties of a Generalized Kaplan-Meier Estimator with Some Applications.” Communications in Statistics-Theory and Methods 4(1): 65–78.

Van Keilegom, I., Akritas M., and N. Veraverbeke. 2001. “Estimation of the Conditional Distribution in Regression with Censored Data: A Comparative Study.” Computational Statistics and Data Analysis 35: 487–500.

Cook, R.J., and J.F. Lawless. 2007. The Analysis of Recurrent Event Data. New York: Springer.