1.2 Censoring

The distinguishing feature of survival analysis is that it incorporates a phenomen called censoring. Censoring occurs when we have some information about individual survival time, but we don’t know the time exactly.

There are generally several reasons why censoring may occur:

• a person does not experience the event before the study ends
• a person is lost to follow-up during the study period
• a person withdraws from the study because of death (if death is not the event of interest) or some other reason

There are three types:

• Right censoring: Random right censoring arise often in medical, biological and financial applications. In this studies, patients may enter the study at different times and the real event time is greater than the observed time. We know that the person’s true survival time becomes incomplete at the right side of the follow-up period, occurring when the study ends or when the person is lost to follow-up or is withdrawn. For these data, the complete survival time interval, which we don’t really know, has been cut off (i.e., censored) at the right side of the observed survival time interval. This is the assumed censoring in the case of credit scoring.

• Left censoring: The survival time of some subject is considered to be left censored if it is less than the value observed. That is, the event of interest has already occurred for the individual before the observed time (not easy to deal with). For example, if we are following persons until they become HIV positive, we may record a failure when a subject first tests positive for the virus. However, we may not know the exact time of first exposure to the virus, and therefore do not know exactly when the failure occurred. Thus, the survival time is censored on the left side since the true survival time, which ends at exposure, is shorter than the follow-up time, which ends when the subject’s test is positive.

• Interval censoring: When the survival time is only known to occur within an interval. Such interval censoring occurs when patients in a clinical trial or longitudinal study have periodic follow-up and the patient’s event time is only known to fall in some interval. As an example, again considering HIV, a subject may have had two HIV tests, where he/she was HIV negative at the time (say, \(t_1\)) of the first test and HIV positive at the time (\(t_2\)) of the second test. In such a case, the subject’s true survival time occurred after time \(t_1\) and before time \(t_2\), i.e., the subject is interval-censored in the time interval (\(t_1\), \(t_2\)).

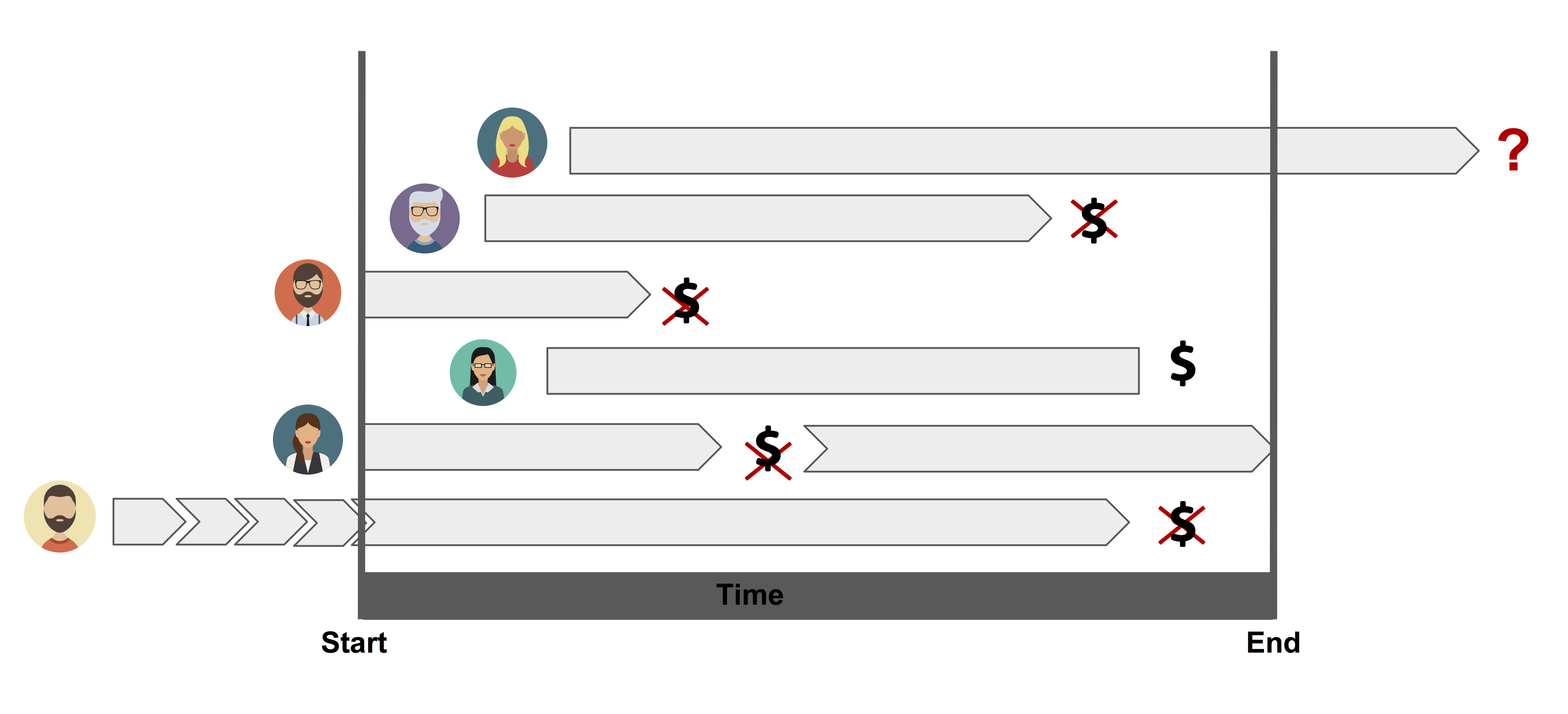
Figure 1.1: Illustration of censoring.

It is important to highlight in this context (time-to-default) which situations we are going to considered as censoring. The bank has special characteristics that are not seen in other applications. Censored cases are considered to be loans that did not experience default by the moment of data gathering. Additionally, early repayment and mature cases (or complete, those ones who reach their predefined end date before the moment of data gathering) are also marked censored.

Another classification:

• Random type I censoring: Also known as Generalized Type I Censoring. When individuals enter the study at different times and the terminal point of the study is predetermined by the investigator, so that the censoring times are known when an individual is entered into the study.

• Type II censoring: The study continues until the failure of the first \(r\) individuals, where \(r\) is some predetermined integer (\(r<n\)). All subjects are put on test at the same time, and the test is terminated when \(r\) of the \(n\) subjects have “failed”.