Classical statistics vs. machine learning

Learning outcomes/objective:

• Understand difference between classic statistics and machine learning.

1 Cultures and goals

• Two cultures of statistical analysis (Breiman 2001; Molina and Garip 2019, 29)
  • Data modeling vs. algorithmic modeling (Breiman 2001)
    • $\approx$ generative modelling vs. algorithmic modeling (Donoho 2017)
• Generative modeling (classical statistics, Objective: Inference/explanation)
  • Goal: understand how an outcome is related to inputs
  • Analyst proposes a stochastic model that could have generated the data, and estimates the parameters of the model from the data
  • Leads to simple and interpretable models BUT often ignores model uncertainty and out-of-sample performance
• Predictive modeling (Objective: Prediction)
  • Goal: prediction, i.e., forecast the outcome for unseen (Q: ?) or future observations
  • Analyst treats underlying generative model for data as unknown and primarily considers the predictive accuracy of alternative models on new data
  • Leads to complex models that perform well out of sample BUT can produce black-box results that offer little insight on the mechanism linking the inputs to the output (but Interpretable ML)
• Example: Predicting/explaining unemployment with a linear regression model
• See also James et al. (2013, Ch. 2.1.1)

1.1 Machine learning as programming (!) paradigm

• ML reflects a different programming paradigm (Chollet and Allaire 2018, chap. 1.1.2)
• Machine learning arises from this question: could a computer […] learn on its own how to perform a specified task? […] Rather than programmers crafting data-processing rules by hand, could a computer automatically learn these rules by looking at data?

Source: , Chap. 1.1.2

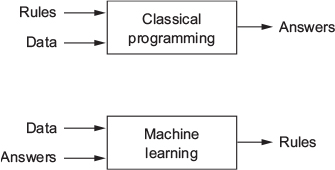
• Classical programming (paradigm of symbolic AI)
  • Humans input rules (a program) and data to be processed according to these rules, and out come answers
• Machine learning paradigm
  • Humans input data + answers expected from the data, and out come the rules [these rules can then be applied to new data]
• ML system is trained rather than explicitly programmed
  • Trained: Presented with many examples relevant to a task → finds statistical structure in these examples &rarr allows system to come up with rules for automating the task (remember Alpha Go)
• Role of math
  • While related to math. statistics, ML tends to deal with large, complex datasets (e.g., millions of images, each consisting of thousands of pixels)
  • As a result ML (especially deep learning) exhibits comparatively little mathematical theory and is engineering oriented (ideas proven more often empirically than mathematically) (Chollet and Allaire 2018, chap. 1.1.2)

1.2 Terminological differences (1)

• Terminology is a source of confusion (Athey and Imbens 2019, 689)

• Q: Do you know any machine learning terminology?

• Statistical learning vs. machine learning (ML) (James et al. 2013, 1)

  • Terms reflect disciplinary origin (statistics vs. computer science)
  • We will use the two as synonyms (as well as AI)

• Regression problem: Prediction of a continuous or quantitative output values (James et al. 2013, 2)

  • e.g., predict wage using age, education and year

• Classification problem: Prediction of a non-numerical value—that is, a categorical or qualitative output

  • e.g., predict increase/decrease of stock market on a given day using previous movements

• Q: What does the “inference” in statistical inference stand for? (Population vs. sample)

1.3 Terminological differences (2)

• Terminology: Well-established older labels vs. “new” terminology
  • Sample used to estimate the parameters vs. training sample
  • Model is estimated vs. Model is trained
  • Regressors, covariates, predictors vs. features (or inputs)
  • Dependent variable/outcome vs. output
  • Regression parameters (coefficients) vs. weights

1.4 Supervised vs. unsupervised learning

• Supervised statistical learning: involves building a statistical model for predicting, or estimating, an output based on one or more inputs
  • We observe both features $x_i$ and the outcome $y_i$
• Unsupervised statistical learning: There are inputs but no supervising output; we can still learn about relationships and structure from such data
  • Only observe $X_i$ and try to group them into clusters
• Good analogy: Child in Kindergarden sorts toys (with or without teacher’s input) (James et al. 2013, 1; Athey and Imbens 2019, 689)

References

Athey, Susan, and Guido W Imbens. 2019. “Machine Learning Methods That Economists Should Know About.” Annu. Rev. Econom. 11 (1): 685–725.

Breiman, Leo. 2001. “Statistical Modeling: The Two Cultures (with Comments and a Rejoinder by the Author).” SSO Schweiz. Monatsschr. Zahnheilkd. 16 (3): 199–231.

Chollet, Francois, and J J Allaire. 2018. Deep Learning with R. 1st ed. Manning Publications.

Donoho, David. 2017. “50 Years of Data Science.” J. Comput. Graph. Stat. 26 (4): 745–66.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning: With Applications in R. Springer Texts in Statistics. Springer.

Molina, Mario, and Filiz Garip. 2019. “Machine Learning for Sociology.” Annu. Rev. Sociol., July.