8 Standard Error of the Mean

Let’s consider once again what we learned about sample means and proportions.

We can sample from any number of distributions: Bernoulli, binomial, uniform, normal, and (starting this week) we can sample from distributions where we don’t know the shape before we start sampling. Our ultimate goal is to describe the distribution we are sampling from – right now in terms of central tendency (mean) – but eventually also about relationships in the population.

In thinking through the process of making inferences there are three distributions of data that we care about. It is imperative that you understand the differences between these three things.

First is the population that we are sampling from. Let’s consider this Chi-squared distribution to be the population (you don’t have to know what this is) that looks like this:

eval <- seq(-5,60,.001)
plot(eval,dchisq(eval,10,ncp=12), type="l", main="Population",
     xlab="Values",ylab="Density", ylim=c(0,0.06), xlim=c(0,65))

So this is what is generating the values when we take a sample. We are unlikely to get anything less than (say) 5. We are most likely to get values around 20. We are unlikely to get values greater than 50. This is s non-symmetrical distribution so we aren’t likely to have a sample where the mean and median are equal. Again, we can think of this as the population or the “data generating process”.

Alright, now we will take a sample of 50 from this population:

set.seed(19104)
x <- rchisq(50,10,ncp=12)
head(x)
#> [1] 17.17206 15.50880 29.22219 18.31710 31.47061 20.98213

What does that sample look like?

plot(density(x), main="Sample", xlab="Value", ylim=c(0,0.06), xlim=c(0,65))

We can think of each sample as being a rough approximation of the population it was generated from. The larger the sample size, the more the sample will look like the population. (However, critically, this is NOT what the Central Limit Theorem is.)

Let’s plot the population beside the density of our sample to see how close of approximation we got:

plot(density(x), main="Sample", xlab="Value", ylim=c(0,0.06), xlim=c(0,65))
points(eval,dchisq(eval,10,ncp=12),col="firebrick", type="l")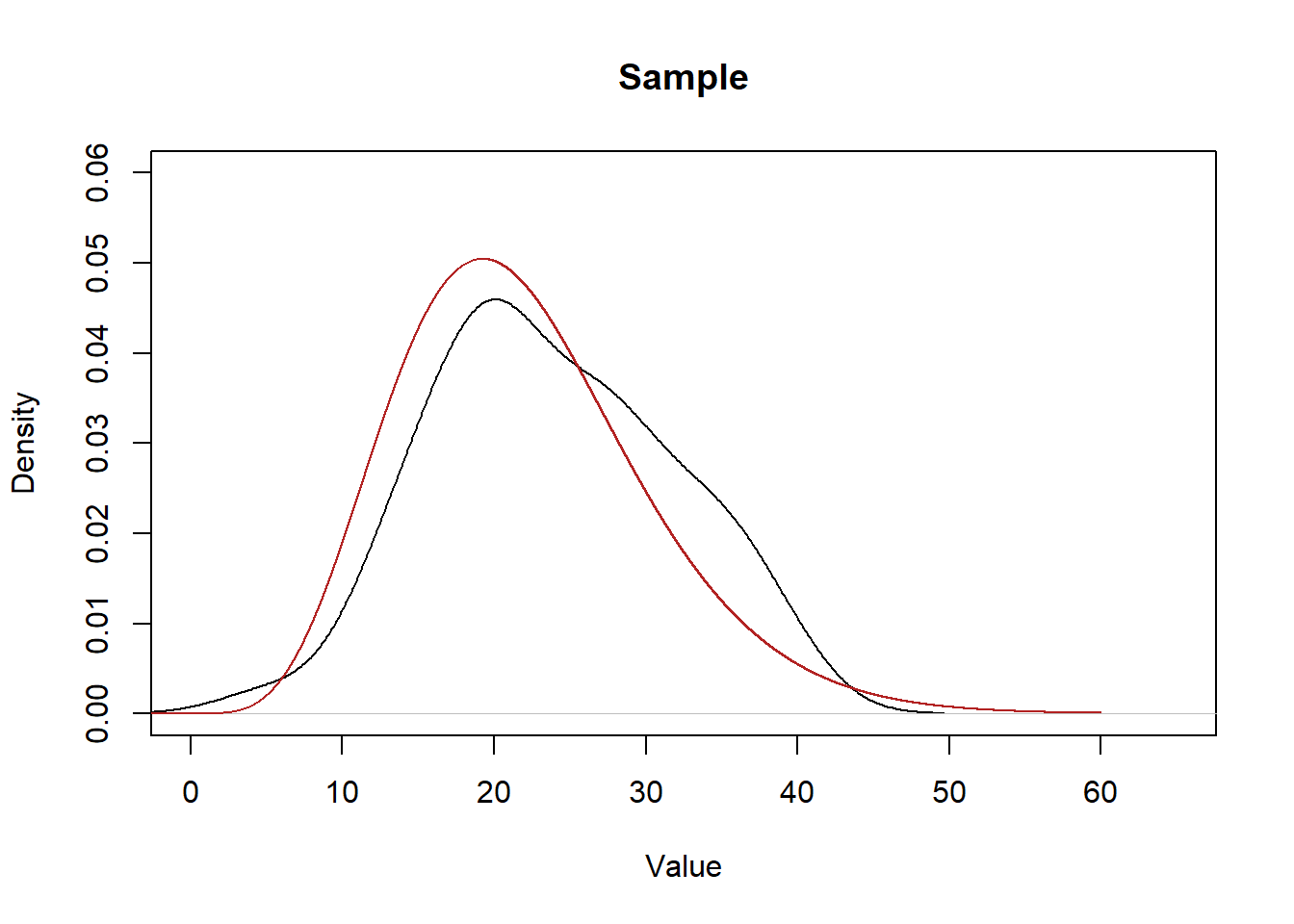

It’s definitely…. in the ballpark?

Every time we take a sample we will get a distribution of data that will be a rough approximation of the population. Here’s 9 more samples:

par(mfrow=c(3,3))
for(i in 1:9){
samp <- rchisq(50,10,ncp=12)
plot(density(samp), main="Sample", xlab="Value", ylim=c(0,0.06), xlim=c(0,65))
points(eval,dchisq(eval,10,ncp=12),col="firebrick", type="l")
}

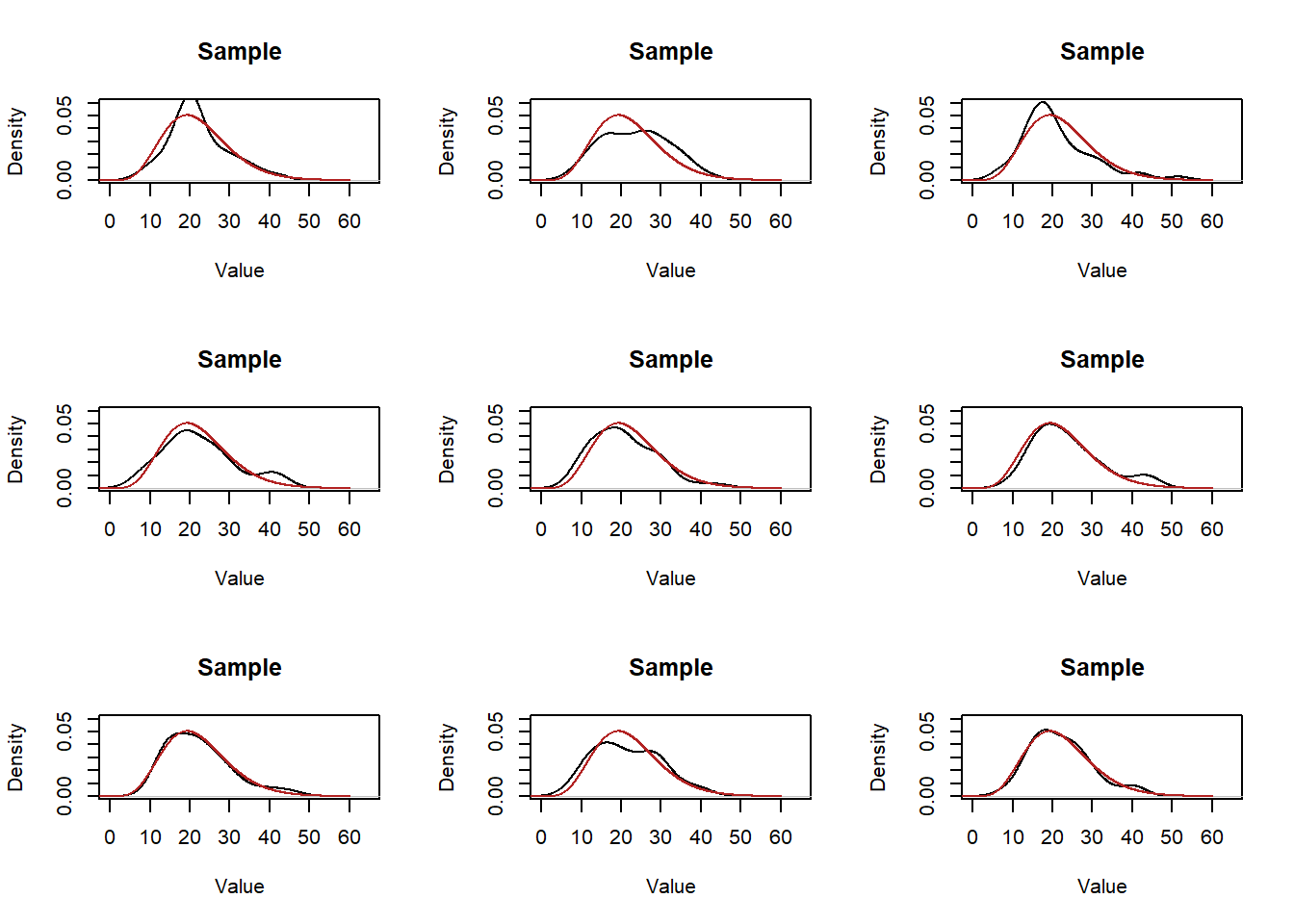
So all of these “roughly” approximate the population….. but how good a job do they do? We can eyeball it but that’s not a great answer…. We intuitively also know that if we up the sample size we will do a “better” job of estimating the distribution in the population:

par(mfrow=c(3,3))
for(i in 1:9){
samp <- rchisq(1000,10,ncp=12)
plot(density(samp), main="Sample", xlab="Value", ylim=c(0,0.06), xlim=c(0,65))
points(eval,dchisq(eval,10,ncp=12),col="firebrick", type="l")
}

But again, we can’t put numbers onto this.

What the key thing we have learned is that, while it’s somewhat futile to ask “How much will my sample distribution look like the population for a sample size of \(n\)?”, we can predict how much the sample mean will look like the true population expected value.

To reiterate this: statistics does not have a good way of estimating how close the distribution of the sample will be to the distribution of the population. We know that as the sample size increases they will look increasingly the same, but “how much will the distribution of my sample deviate from the distribution of the population for an \(n\) of 50” is not an answerable question.

But! We know that the sample mean is itself a random variable, with this distribution \(\bar{X_n} \sim N(\mu=E[X], \sigma^2 = V[X]/n)\).

So, we can’t answer “how much deviation is there in the distribution of our sample compared to the population for an n of 50?”, but we can answer: “how much deviation in the sample mean will there be for an n of 50”.

Specifically, each sample mean for an n of 50 will be drawn from this normal distribution, based on my knowledge that the \(E[X]=22\) and \(V[X]=68\).

mean.eval <- seq(15,29,.001)
plot(mean.eval, dnorm(mean.eval, mean=22, sd=sqrt(68/50)), type="l",
     main="Sampling Distribution of the Sample Mean", 
     xlab="Value of Sample Mean",
     ylab="Density")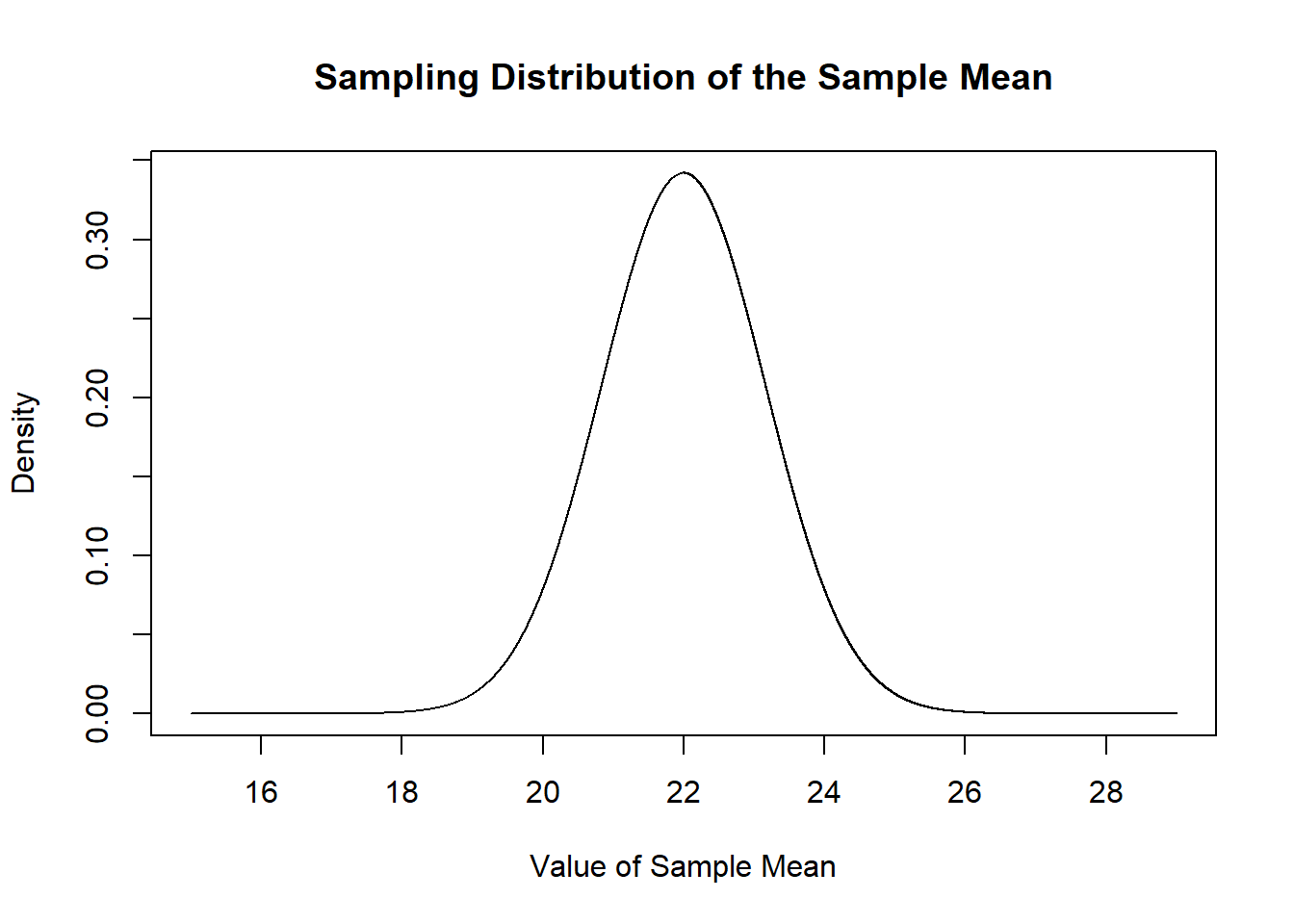

We can prove this to ourselves by repeatedly sampling and taking a bunch of sample means and plotting their density compared to this sampling distribution.

sample.means <- rep(NA, 10000)

for(i in 1:10000){
  sample.means[i] <- mean(rchisq(50,10,ncp=12))
}

plot(mean.eval, dnorm(mean.eval, mean=22, sd=sqrt(68/50)), type="l",
     main="Sampling Distribution of the Sample Mean", 
     xlab="Value of Sample Mean",
     ylab="Density")
points(density(sample.means), type="l", col="darkblue")

They are the same distribution.

The third distribution we care about is the sampling distribution of an estimate that we form using our sample. Here we are looking at the sampling distribution of the sample mean, but many estimates and accompanying sampling distributions are possible.

While we cannot determine “how much will the distribution of our sample vary from the population distribution?” we Can determine, “how much will the sample mean vary from sample to sample?”

Because the random variable that generates sample means is known, we can ask: what proportion of sample means will be within 2 of the true population mean. In other words, what is the probability mass that is between the two lines below:

plot(mean.eval, dnorm(mean.eval, mean=22, sd=sqrt(68/50)), type="l",
     main="Sampling Distribution of the Sample Mean", 
     xlab="Value of Sample Mean",
     ylab="Density")
abline(v=c(20,24), lty=2)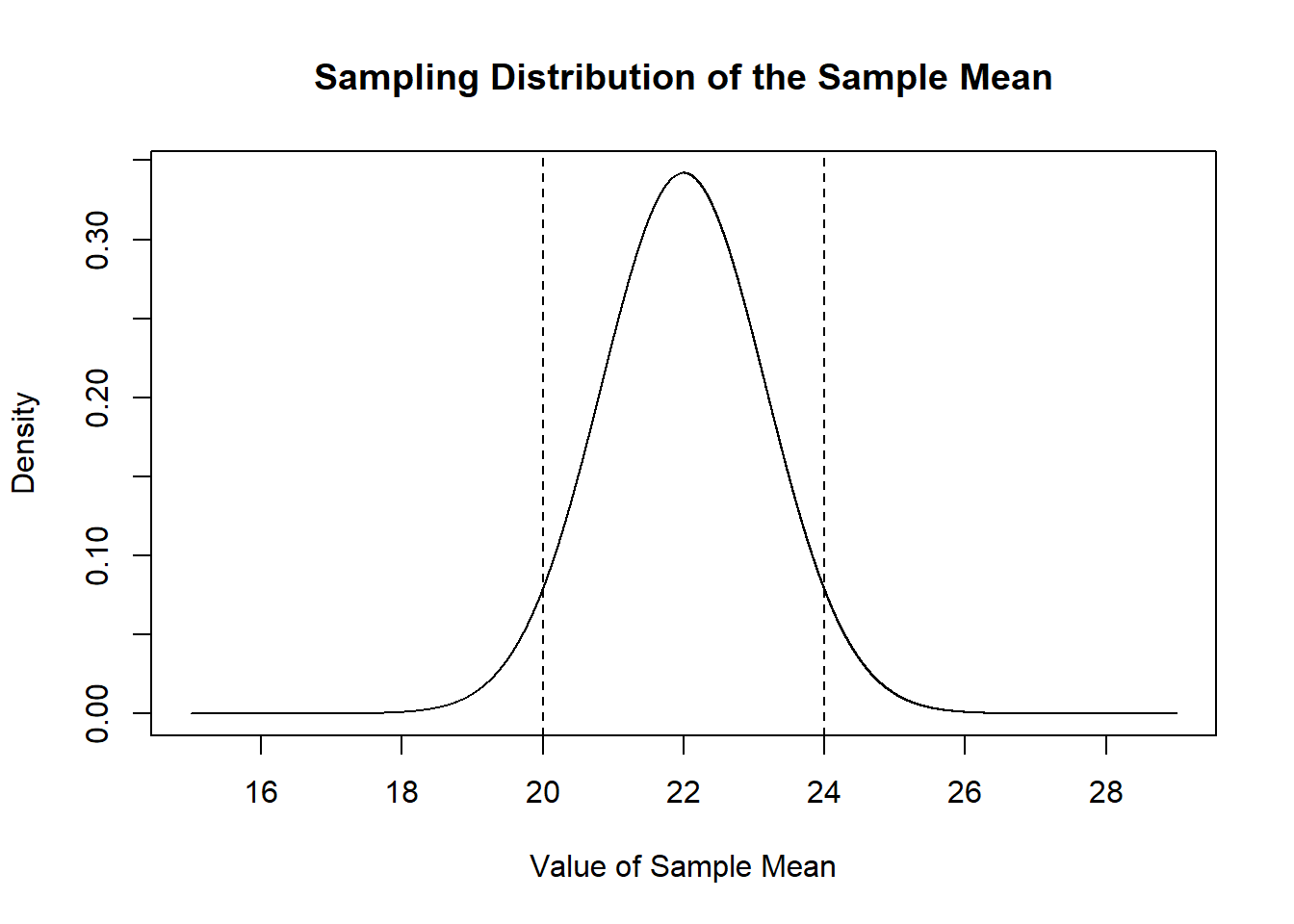

Because we know exactly what shape that sampling distribution is, we can answer this question preceisely using the normal distribution:

pnorm(24,22,sqrt(68/50)) - pnorm(20,22,sqrt(68/50))
#> [1] 0.9136522

There is a 91% chance a sample mean drawn from this distribution will be between 20 and 24.

Is that true?

mean(sample.means>=20 & sample.means<=24)
#> [1] 0.9194

Yes!

What is the range in which 70% of all estimates will lie?

Well that’s leaving 15% in the left tail so:

qnorm(.15, 22, sqrt(68/50))
#> [1] 20.79132

#How much above and below the mean
val <- 22 - qnorm(.15, 22, sqrt(68/50))

22 + val
#> [1] 23.20868
22 - val
#> [1] 20.79132

That range contains 70% of all estimates.

What are the relationships between the population, estimate, and the sampling distribution of the mean?

The population and sample distributions are clearly related. The distribution of the sample is generated by the population so it is a rough (but not perfect) approximation. We have seen that the mean of a sample is equal to the expected value of the population, in expectation (the law of large numbers). However it is also true that the variance of a sample is a rough approximation of the population level variance:

sample.vars <- rep(NA, 10000)

for(i in 1:10000){
  sample.vars[i] <- var(rchisq(50,10,ncp=12))
}
summary(sample.vars)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   24.91   57.05   66.47   68.03   77.44  145.34

The sampling distribution of sample mean is related to the sample because each sample produces a sample mean. The sampling distribution of the sample mean is intricately related to the population, because the shape of the normal distribution is driven by the expected value and variance of the population.

Let’s do another (familiar??) example. In the population the true probability of supporting Joe Biden over Donald Trump in Pennsylvania in 2020 was 50.59%. If we run a sample of 1500 people, what is the probability that survey will be within 1 percentage point of the truth?

First, what will the sampling distribution of the sample mean look like?

The population is a Bernoulli RV with probability of success of .5059. Which means that the sample mean will be: \(\bar{X_n} \sim N(\mu=.5059, \sigma^2=\frac{.5059*(1-.5059)}{1500}= .000167)\).

So this is what the sampling distribution of the mean will look like, and we want to know how much probability is in between the two lines.

eval.bern <- seq(.45,.55,.0001)
plot(eval.bern, dnorm(eval.bern, .5059, sqrt(.000167)), type="l", main="Sampling Distribution")
abline(v=c(.5059-.01, .5059+.01), lty=2)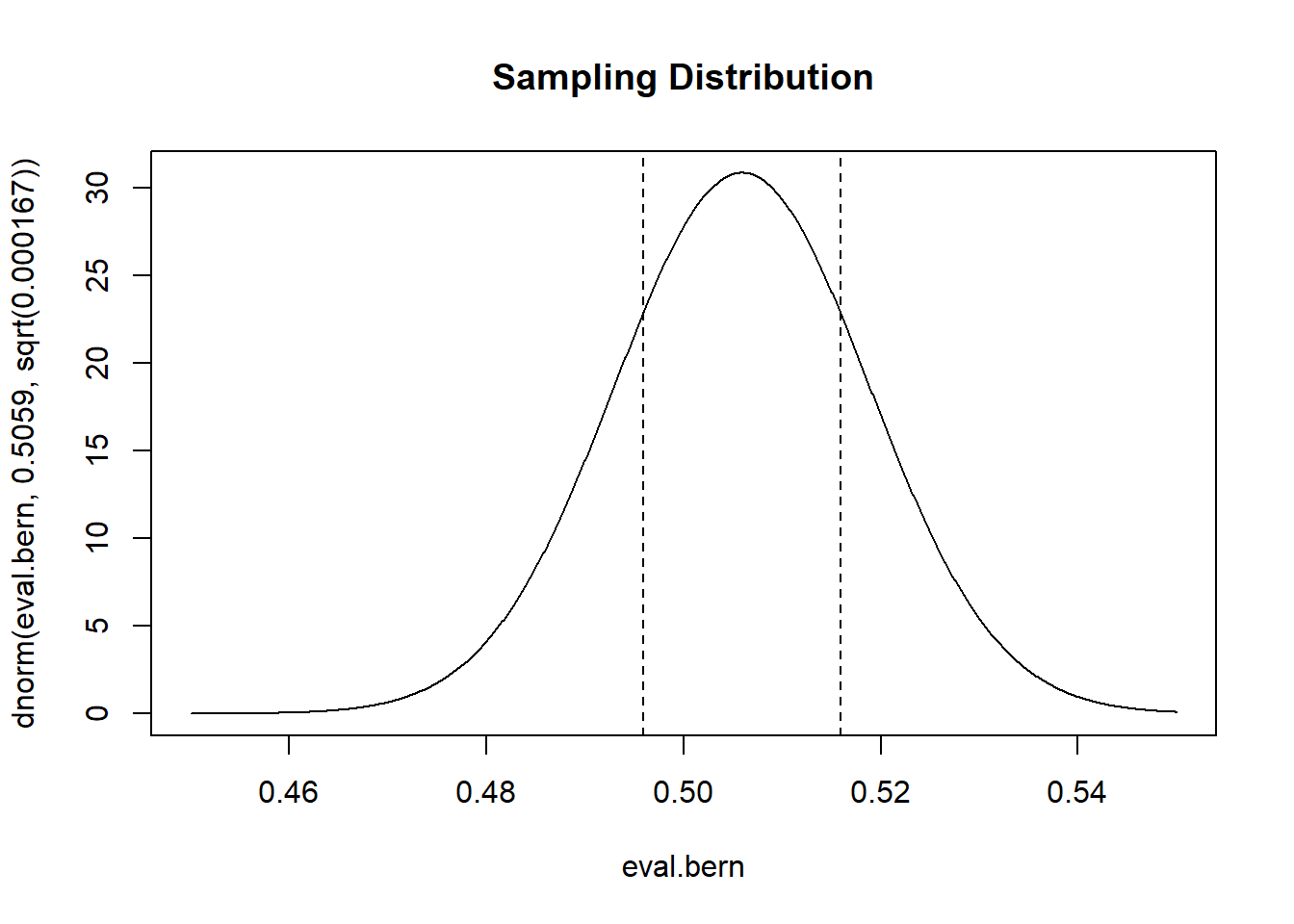

To get this answer:

pnorm(.5059+.01,  .5059, sqrt(.000167)) - pnorm(.5059-.01,  .5059, sqrt(.000167))
#> [1] 0.5609647

There is an approximately 56% chance of the sample mean being between these two points.

In this case: can we use the binomial distribution to get the same answer? Yes…. but it’s not the cleanest option.

We can surmise that many draws from this Bernoulli will be a binomial RV with a probability of success of \(\pi =.5059\) and an \(n=1500\), that would look like this:

plot(650:850,dbinom(650:850, 1500,.5059))

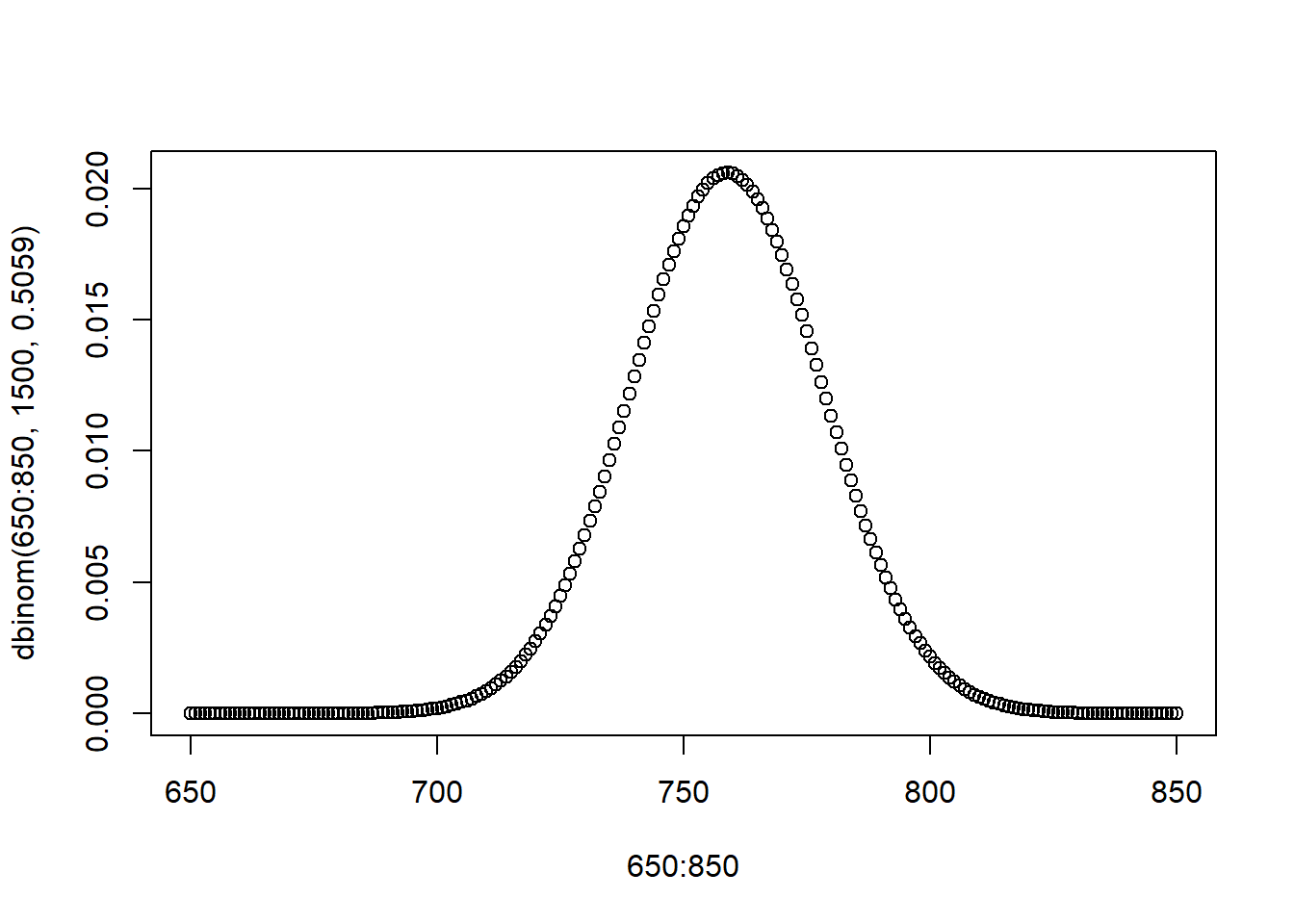
And we could then think about the range from \(.4959*1500\approx 744\) \(.5159*1500\approx 774\)…. But, I have to do some weird rounding to get whole numbers here, and I have to worry about the whole binomial thing of whether the exact probability of 744 should be included or not…. It’s just a mess. And this method only applies to when the population variable is a Bernoulli. It’s way better and cleaner to just think about the sample mean being normally distributed. No rounding! No worries about the probability of exact numbers!

Plus, If I asked: what \(n\) do I need to be 95% confident my mean will be within 1 percentage point of the true mean… I don’t have a good way to answer that mathematically with the binomial distribution, when that answer is pretty easy when thinking about the normally distributed sample mean.

8.1 But we don’t know the population

So far we have seen that we can predict what the distribution of sample means will look like if we know the expected value and variance of the population we are pulling from… But…. the whole point is that we don’t know the population!

Consider, again, me running a poll of PA voters in late October 2022. I get the following data on the proportion that support Fetterman:

x <- rbinom(500,1, .525)
head(x)
#> [1] 1 1 0 1 1 1
mean(x)
#> [1] 0.532
var(x)
#> [1] 0.2494749

What if I want to answer the question: How likely is it for me to get this data if the truth is that the race is tied?

How can I assess that?

Up to this point we have known the distribution of the population are pulling from and therefore we could assess what the range of means are. But what about now where we don’t know what the population looks like.

We want to draw a sampling distribution here. As such we need a \(\mu\) and a \(\sigma\). Remembering that our question is: “How likely is it for me to get this data if the truth is that the race is tied?” do we need to know the true population expected value? No! We are explicitly saying: what if the sampling distribution was centered on 50%? So we don’t need to worry about what the true population mean is to draw the sampling distribution we want to draw.

OK, but here’s the harder part: we need a \(\sigma\). Up to this point we have said that the sampling distribution of the sample mean is \(\sim N(\mu=E[X], \sigma^2 = V[X]/n\). But we don’t have the variance of the population level random variable.

What can we use instead?

Well we really only have one option. We know that the distribution of our sample is a rough approximation of the distribution of the population, so what happens if we use the variance of our sample as a stand-in for the variance of the population.

To be clear, the variance of the population is a fixed known thing. Because we are “god” here and know the truth I know that the variance of the population is \(\pi(1-\pi)= .525*.475=.249\). What is the variance of our actual sample?

var(x)
#> [1] 0.2494749

It’s close! What would the two sampling distributions look like, once with the true variance, once with the sample variance:

eval <- seq(.4,.6,.001)
plot(eval, dnorm(eval, mean=.5, sd=sqrt(.249/500)), type="l", col="firebrick")
points(eval, dnorm(eval, mean=.5, sd=sqrt(var(x)/500)), type="l", col="darkblue")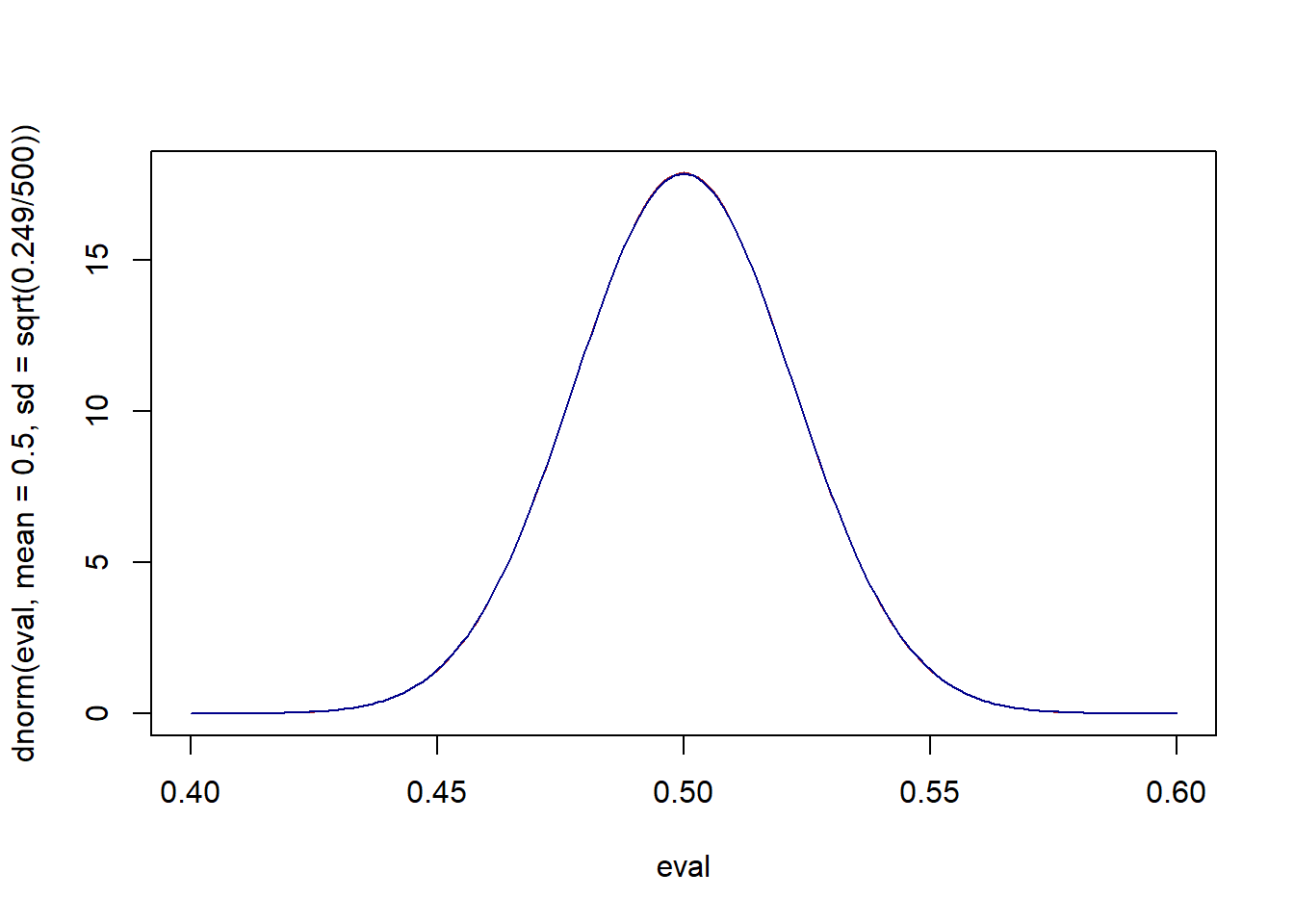

Effectively the same.

Let’s take a bunch of samples, calculate the variance of each, and plot the sampling distribution generated from each of them on top of each other to see generally how well we do:

plot(eval, dnorm(eval, mean=.5, sd=sqrt(.249/500)), type="l", col="firebrick")

for(i in 1:1000){
  samp.var <- var(rbinom(500,1, .525))
  points(eval, dnorm(eval, mean=.5, sd=sqrt(samp.var/500)), type="l", col="gray80")
}
points(eval, dnorm(eval, mean=.5, sd=sqrt(.249/500)), type="l", col="firebrick")

That looks pretty good! Again, here we are comparing the “true” sampling distributrion that is generated using the population level variance to many sampling distributions that are generating from subbing in the sample variance to represent the population variance.

One thing to note is that the equation to calculate the sample variance (which we denote as \(S^2\)) is:

\[ S^2 = \frac{1}{n-1}*\sum_{i=1}^{n}(X_i- \bar{X_n})^2 \]

This is, effectively, the average deviation from the average. However, instead of dividing by \(n\) we divide by \(n-1\).

Why? Because. That’s why! But for real if we went through and did the math then:

\[ E[\frac{1}{n-1}*\sum_{i=1}^{n}(X_i- \bar{X_n})^2] = \sigma^2\\ And..\\ E[\frac{1}{n}*\sum_{i=1}^{n}(X_i- \bar{X_n})^2] \neq \sigma^2\\ \]

Helpfully, the var() and sd() commands automatically makes this adjustment.

So in the “real” world all we do to figure out a sampling distribution for the sample mean is to sub in the sample variance for the population variance. (With one additional complication, that we will get to).

So that’s pretty straight forward, but at the same time so many of the questions we have answered about sampling rely also on knowing the true population expected value. For example on the midterm you calculated sampling distributions around a true level of support for Biden and calculated, for example, what percentage of polls will be withing 2 percentage points of the truth.

But if we are entering a world in which we don’t know the truth, those kinds of questions really do us no good.

So let’s consider what sort of question we might want to answer in the world where we don’t know the population.

Let’s take a sample mean of a small sample from the normal distribution (100 people) and look at the mean and variance:

set.seed(19104)
x <- rnorm(100,64,3)
mean(x)
#> [1] 63.92013
var(x)
#> [1] 7.876416

Now again, In this case we know that the truth is 64, but in the real world we would not.

What we want to effectively know is where the true value might plausibly lie in relation to this value.

Is it plausible that the truth is 70? or 50? Could the truth be 0?

There are (roughly) two ways to answer this question: confidence intervals and hypothesis tests. We will cover CIs today and spend next week covering hypothesis tests.

8.2 Confidence Intervals

A confidence interval is a zone that we are some percent certain contains the true population paramater. So if a 70% confidence interval ranged from \([5,10]\) that would mean that we are 70% confident the population paramater is within those bounds.

How do we put a such a confidence interval around our sample above?

We define a confidence level as \((1-\alpha)*100\), such that a 70% confidence interval implies an \(\alpha\) of .3.

For a given \(\alpha\) a confidence interval around any given sample mean is:

\[CI(\alpha) = [\bar{X_n}-z_{\alpha/2}*SE,\bar{X_n}+z_{\alpha/2}*SE]\]

Where \(z\) is the standard normal distribution.

Ok that’s a lot so let’s walk through this. This claims that to form a confidence interval we have to evaluate the standard normal distribution at \(-\alpha/2\) and \(\alpha/2\). We can take those two values and multiply them by the standard error. The resulting amount above and below the mean will be a zone that contains the true population parameter \((1-\alpha)*100\) percent of the time.

In previous weeks we used the standard normal proactively. If we wanted to say: what range will 70% of all sample means lie, we could say: how many standard errors contain 70% of the probability mass? To get that we would look at this zone:

eval <- seq(-3,3,.001)
plot(eval, dnorm(eval), main="Standard Normal", type="l")
abline(v=qnorm(.15))
abline(v=qnorm(.15)*-1)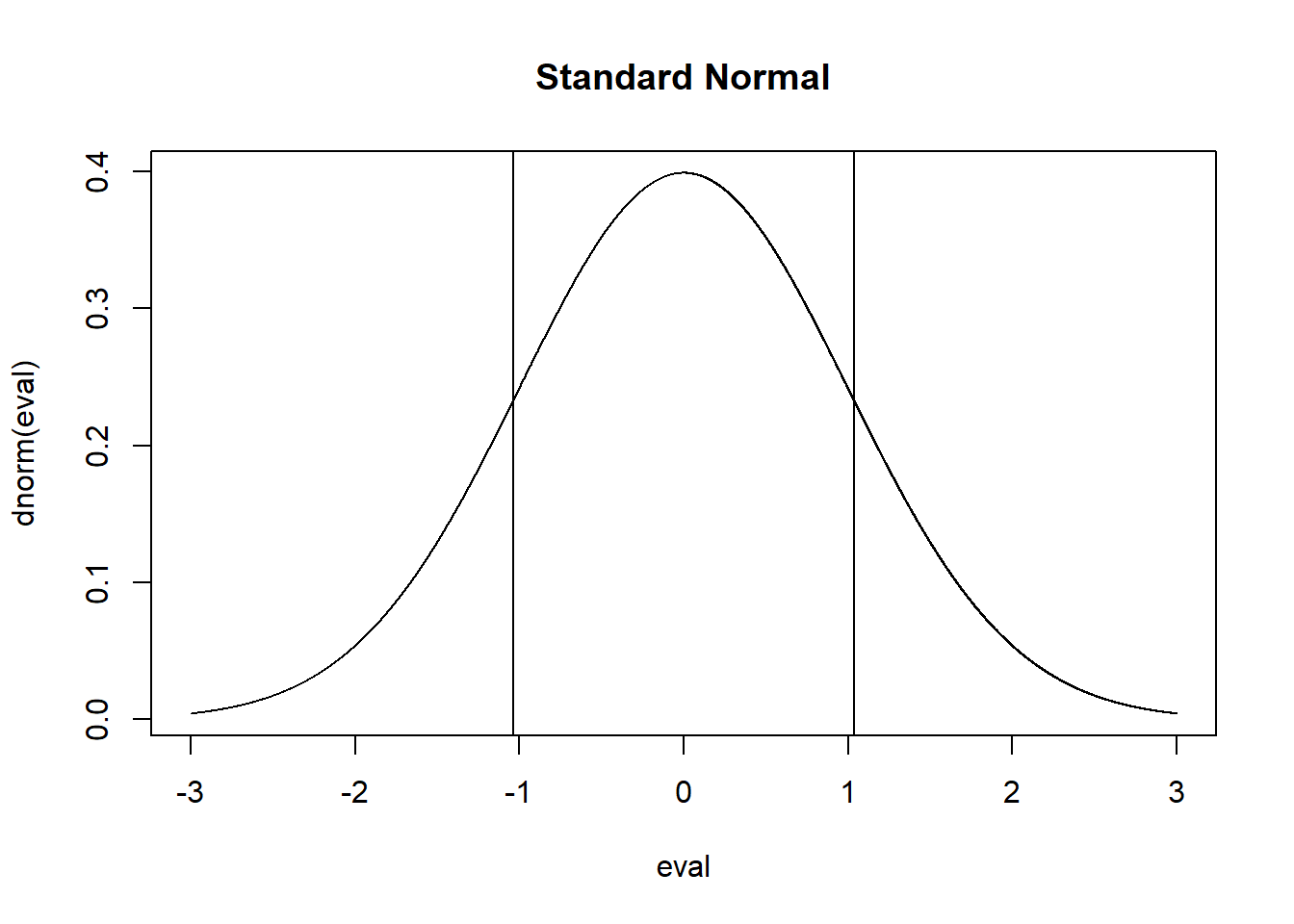

qnorm(.15)
#> [1] -1.036433

And we could say that the zone \(\pm 1.04\) standard errors from the true population expected value will contain 70% of all sample means. However it is also true that \(\pm 1.04\) standard errors around any sample mean will contain the true population parameter 70% of the time.

This is a confusing, and somewhat wild fact. I’m about to show you that this is true, but it’s hard to actually explain this intuitively. I will try, but I also want you to know that you can just know this is true and not try to work out in your head why it makes theoretical sense.

So using that logic, the confidence interval for our sample which had a \(\bar{X_n}=63.92\) and \(s^2=7.88\) would be:

\[ se = \sqrt{7.88/100} = .28\\ \alpha = .3\\ z_{\alpha/2}=1.04\\ CI(\alpha) = [\bar{X_n}-z_{\alpha/2}*SE,\bar{X_n}+z_{\alpha/2}*SE]\\ CI(\alpha) = [63.92-1.04*.28,63.92+1.04*.28]\\ CI(\alpha) = [63.62,64.21]\\ \]

There is a 70% chance that the true population parameter is contained within that interval.

OK: so let’s prove that this is true. Let’s repeatedly sample from the same population, and using information wholly contained within that sample let’s calculate the confidence interval and test to see whether it contains the true population parameter. First let’s visualize doing this 10 times:

lower <- rep(NA,10)
upper <- rep(NA,10)

for(i in 1:10){
samp <- rnorm(100,64,3)
xbar <- mean(samp)
s2 <- var(samp)
se <- sqrt(s2/100)
lower[i] <- xbar - 1.04*se
upper[i] <- xbar + 1.04*se
}

plot( seq(63.2,65,.2),seq(1,10), type="n", xlim=c(63,65))
abline(v=64, lty=2, col="firebrick")
segments(lower, 1:10, upper, 1:10)

Our expectation is that 7 out of these 10 confidence intervals will contain the true population paramater. In reality 8 out of the 10 do, which is very close. To see if this is true though we can repeat this process 10,000 times:

ci.contains <- rep(NA,10000)

for(i in 1:10000){
samp <- rnorm(100,64,3)
xbar <- mean(samp)
s2 <- var(samp)
se <- sqrt(s2/100)
lower <- xbar - 1.04*se
upper<- xbar + 1.04*se
ci.contains[i] <- lower<=64 & upper>=64
}
mean(ci.contains)
#> [1] 0.6976

Yes! 70% of similarly constructed confidence intervals contain the true population parameter.

A note on language here. Technically speaking the definition that I’ve given you: “a confidence interval has a X% probability of containing the true population parameter” is incorrect. Any given confidence interval is a real zone with 2 fixed numbers. The population parameter is also a fixed, real number. So a confidence interval either does, or does not, contain the true population paramater. There is nothing about chance to it, and some people will absolutely jump down your throat if you claim that there is a 70% chance this confidence interval contains the truth. The correct thing to say is “70% of similarly constructed confidence intervals contain the true population paramater” which jeeeeeeeeeesus this is why people hate statistics.

I’m not a professional statistician and to me it makes sense that if 70% of confidence intervals contain the truth, the probability that the one that I have contains the truth is 70%. That is technically wrong but it makes intuitive sense and I’m fine with it.

Looking at the equation for the confidence interval we can think through what makes wider or narrower confidence intervals:

\[CI(\alpha) = [\bar{X_n}-z_{\alpha/2}*SE,\bar{X_n}+z_{\alpha/2}*SE]\]

Our sample mean is a fixed number so that’s not going to affect things. What about \(\alpha\)? This is the probability in the tails of the standard normal distribution that leaves our stated amount of confidence in the middle. The smaller this number the larger the number of standard errors away from 0 we need to go to leave that much in the tail. So smaller \(\alpha\) means a wider confidence interval. This makes intuitive sense! If we want to be more confident that an interval contains the truth then that interval needs to be wider.

So if we wanted to be 95% confident that our interval contains the true population paramater, we would need to find a new value in the standard normal:

qnorm(.025)
#> [1] -1.959964

1.96! Our old friend. Let’s use that and draw 10 new samples and confidence intervals:

lower <- rep(NA,10)
upper <- rep(NA,10)

for(i in 1:10){
samp <- rnorm(100,64,3)
xbar <- mean(samp)
s <- sd(samp)
se <- s/10
lower[i] <- xbar - 1.96*se
upper[i] <- xbar + 1.96*se
}

plot( seq(63.2,65,.2),seq(1,10), type="n", xlim=c(63,65))
abline(v=64, lty=2, col="firebrick")
segments(lower, 1:10, upper, 1:10)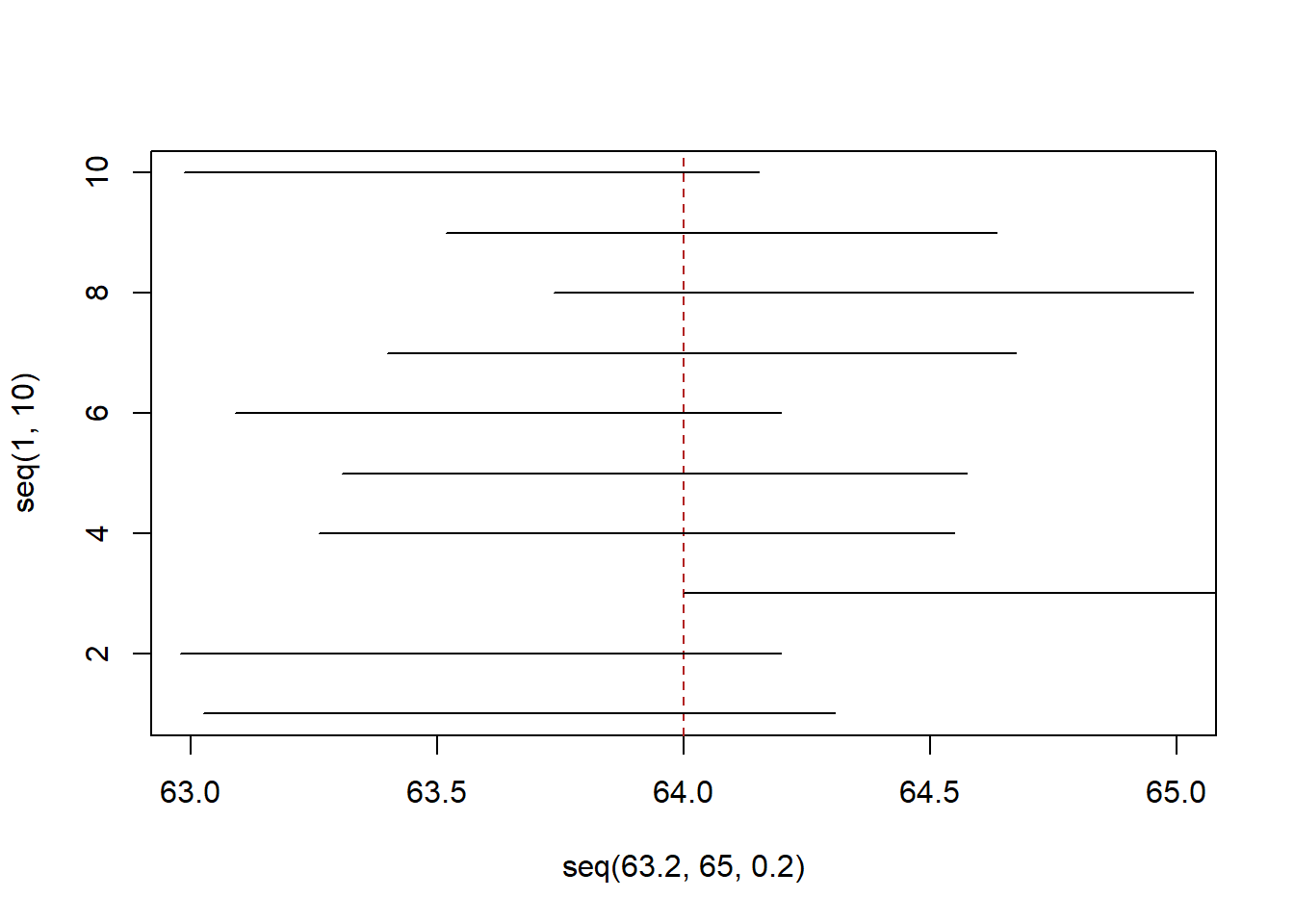

We expected that 0 or 1 of these confidence intervals would miss the true value, and indeed, one does.

Finally the standard error \(s/\sqrt{n}\) affects the width of the confidence interval. All else equal a larger \(s\) means a wider confidence interval. This makes sense! If your sample is more random, it is way harder to make a conclusion about where the true population paramater might be. For a larger \(n\) your confidence interval decreases. This is the law of large numbers! As the sample size increases the sample mean converges on the true population mean. As such, it makes sense that the confidence interval around any given sample mean will be smaller when \(n\) gets larger.

In all honesty I find confidence intervals minimally helpful, as they are more confusing than what is generally thought. Still: I got to teach them to you.

There is one additional (and very important) complication to what we have done so far. I have used thus far used the standard normal distribution to define the number of standard errors necessary to set a confidence interval. Let’s see what happens, however, if I use this method on a very small sample.

Let’s draw from the same distribution, but instead take a sample of 10 people. Again we are going to use the fact that 70% of the standard normal distributino is \(\pm1.04\) to define the bounds of a 70% confidence interval.

lower <- rep(NA,10)
upper <- rep(NA,10)

for(i in 1:10){
samp <- rnorm(10,64,3)
xbar <- mean(samp)
s <- sd(samp)
se <- s/sqrt(10)
lower[i] <- xbar - 1.04*se
upper[i] <- xbar + 1.04*se
}

plot( seq(63.2,65,.2),seq(1,10), type="n", xlim=c(63,65))
abline(v=64, lty=2, col="firebrick")
segments(lower, 1:10, upper, 1:10)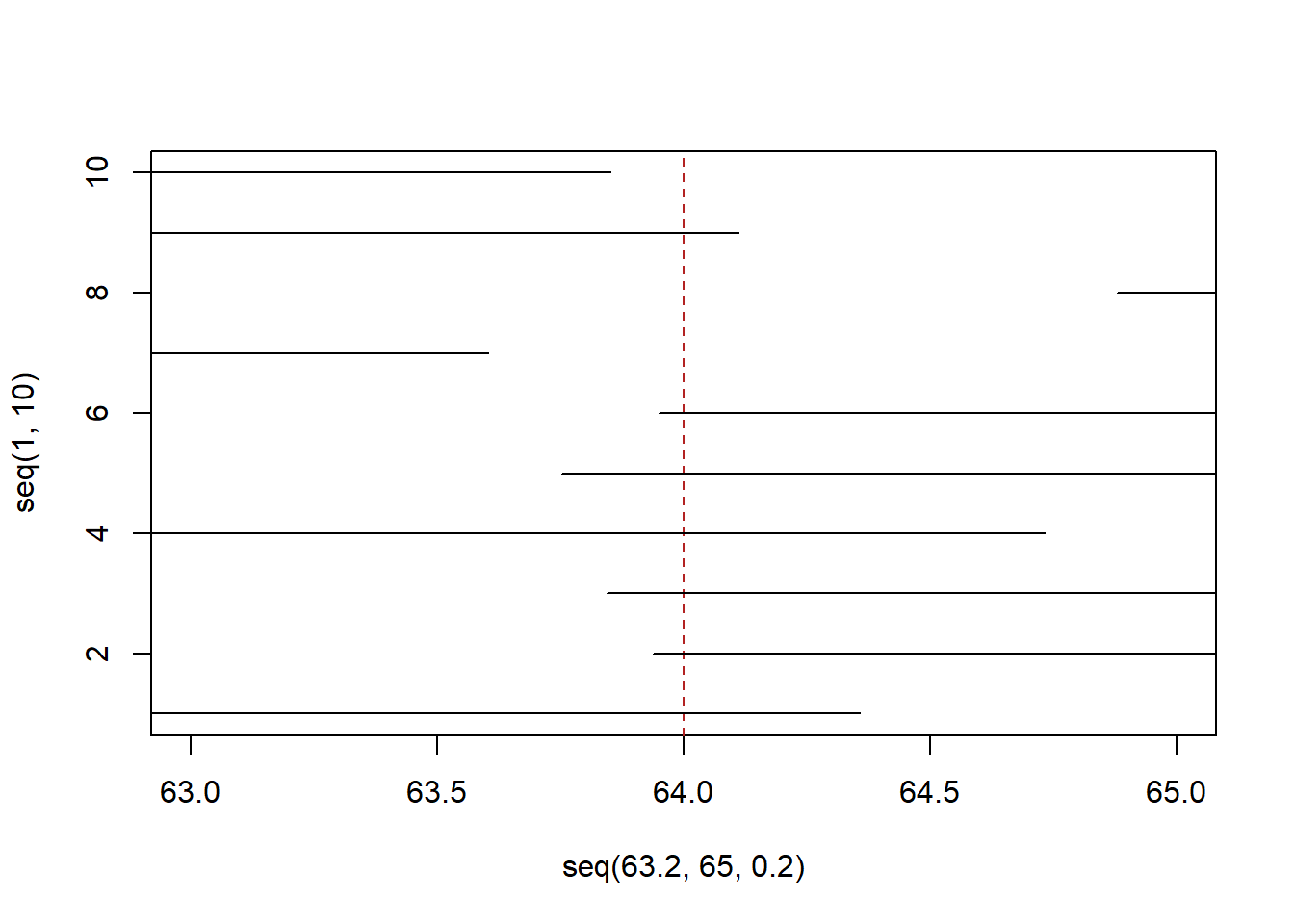

So far so good. As expected our confidence intervals are wider and 2 of them don’t contain the truth (we expect 3).

But! Let’s do this 10,000 times to see if it is true that 70% of constructed CIs contain the truth:

ci.contains <- rep(NA,10000)

for(i in 1:10000){
samp <- rnorm(10,64,3)
xbar <- mean(samp)
s <- sd(samp)
se <- s/sqrt(10)
lower <- xbar - 1.04*se
upper<- xbar + 1.04*se
ci.contains[i] <- lower<=64 & upper>=64
}
mean(ci.contains)
#> [1] 0.6801

Whoops! Only 68% contain the truth. It’s close, but actually systematically wrong.

The very important reason is that when we are using the sample variance as a stand in for the population variance then the sampling distribution is not normally distributed.

When we were defining the sampling distribution before we found that the central limit theorem dictated that:

\[ \frac{\bar{X_n}-E[X]}{\sqrt{V[X]/n}} \sim N(0,1) \]

That if we took the sampling distribution of the sample means, subtracted off the truth and divided by the standard error we would be left with the standard normal distribution. This is equivalent to saying: the sampling distribution of the sample mean is normally distributed with mean \(\mu=E[X]\) and variance \(\sigma^2=V[X]/n\).

When we are using the sample standard deviation as a stand in for the population variance in the calculation of the standard error, however, the sampling distribution of the sample mean is:

\[ \frac{\bar{X_n}-E[X]}{s/\sqrt{n}} \sim t_{n-1} \]

Instead of collapsing to a standard normal, the sampling distribution is now \(t\) distributed with \(n-1\) degrees of freedom. The t distribution looks a lot like the normal distribution, but critically, it subtlety changes is shape as \(n\) grows larger. Critically, at very low \(n\) the \(t\) distribution is shorter with fatter tails than the standard normal distribution.

Here is the t distribution with \(n-1=10-1=9\) degrees of freedom vs. the standard normal:

eval <- seq(-3,3,.001)
plot(eval, dnorm(eval), type="l")
points(eval, dt(eval,9), type="l", col="firebrick")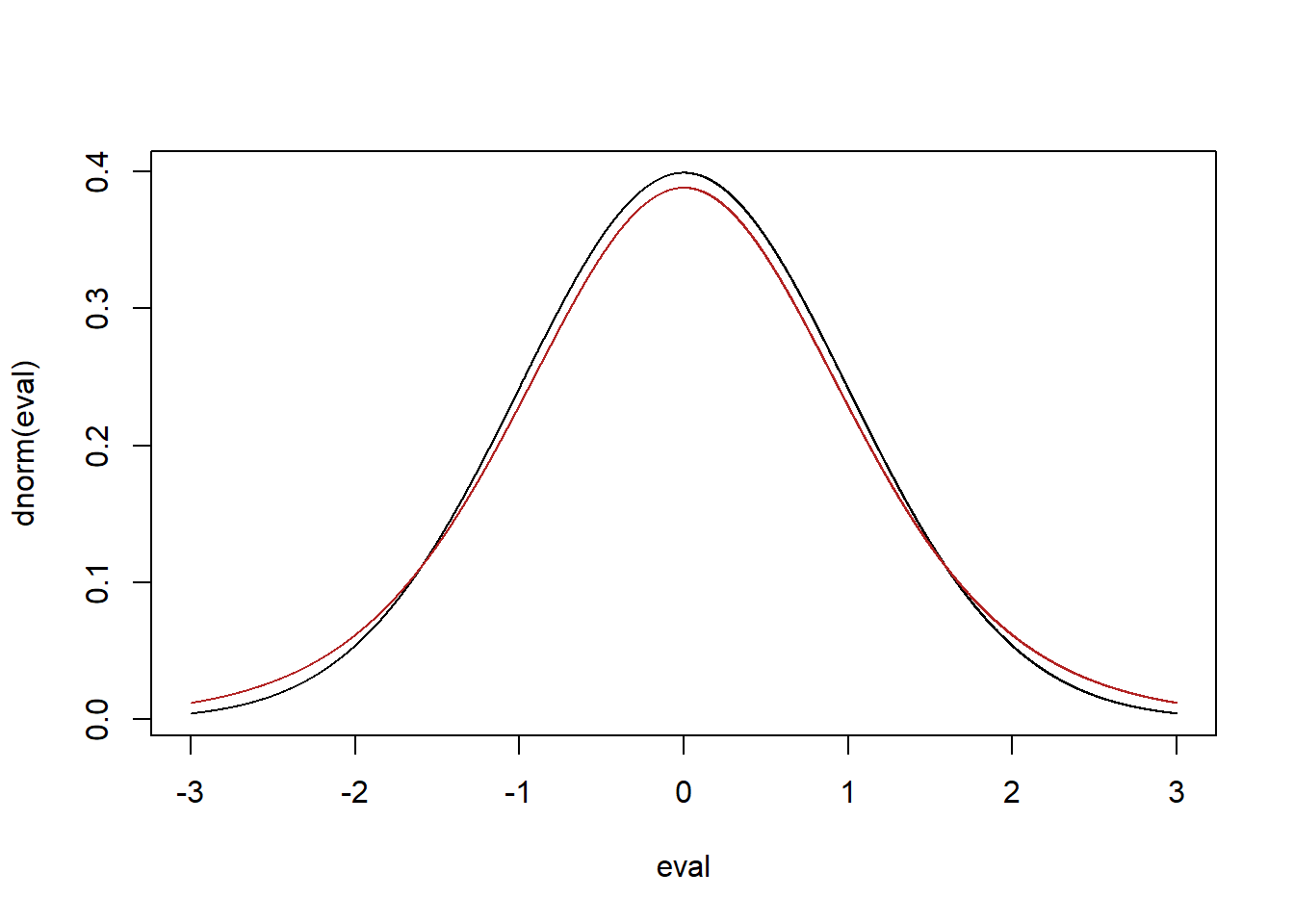

Because this t distribution is a different shape than the standard normal it means that when we are constructing a confidence interval using the sample variation as a stand in for the population variance we will get a different set of bounds based on the sample size.

To get the bounds for a 70% confidence interval:

#From the standard normal
qnorm(.15)
#> [1] -1.036433

#Using the t distirbution
qt(.15, df=9)
#> [1] -1.099716

And now let’s use that to define our bounds and see if 70% of confidence intervals contain the truth:

ci.contains <- rep(NA,10000)

for(i in 1:10000){
samp <- rnorm(10,64,3)
xbar <- mean(samp)
s <- sd(samp)
se <- s/sqrt(10)
lower <- xbar - 1.10*se
upper<- xbar + 1.10*se
ci.contains[i] <- lower<=64 & upper>=64
}
mean(ci.contains)
#> [1] 0.6974

Yes! So the T distribution is what you must use to define a confidence interval if you are using the sample variance as a stand in for the population variance.

OK: but why did using the standard normal work when we had a sample size of 100? This is because the \(T\) distribution converges on the standard normal distirbution as n gets larger than, like, 30:

eval <- seq(-3,3,.001)
plot(eval, dnorm(eval), type="l")
points(eval, dt(eval,29), type="l", col="firebrick")

So the \(t\) distribution only gives you a different answer than the standard normal for \(n\)’s that are under 30.

THAT BEING SAID YOU HAVE TO USE THE T DISTRIBUTION IF YOU ARE DERIVING THE SAMPLING DISTRIBUTION USING THE SAMPLE VARIANCE. Even though it “doesn’t matter” that is the distribution of the sampling distribution under these conditions.