13 Regression Functional Form
13.1 Regression with categorical variables.
Let’s load in data from the American Community Survey about various features of US counties:
rm(list=ls())
library(rio)
acs <- import("https://github.com/marctrussler/IIS-Data/raw/main/ACSCountyData.csv")I want to know how population density relates to transit ridership in the US. The variable population.density is the number of people per square mile in these counties and percent.transit.commute is exactly what it sounds like. At a baseline, what is the correlation between these things?
cor(acs$population.density, acs$percent.transit.commute, use="pairwise.complete")
#> [1] 0.8230231Very high!
Having population density is great, but what if instead of this very continuous measure we simply had a classification of whether a county was rural urban or suburban, split in this way:
acs$density[acs$population.density<50] <- 1
acs$density[acs$population.density>=50 & acs$population.density<1000] <- 2
acs$density[acs$population.density>=1000] <- 3
table(acs$density)
#>
#> 1 2 3
#> 1689 1304 149How can we find the effect of this three-category population density variable on the percent of people commuting by transit?
First, let’s take a look at this relationship:
plot(acs$density, acs$percent.transit.commute)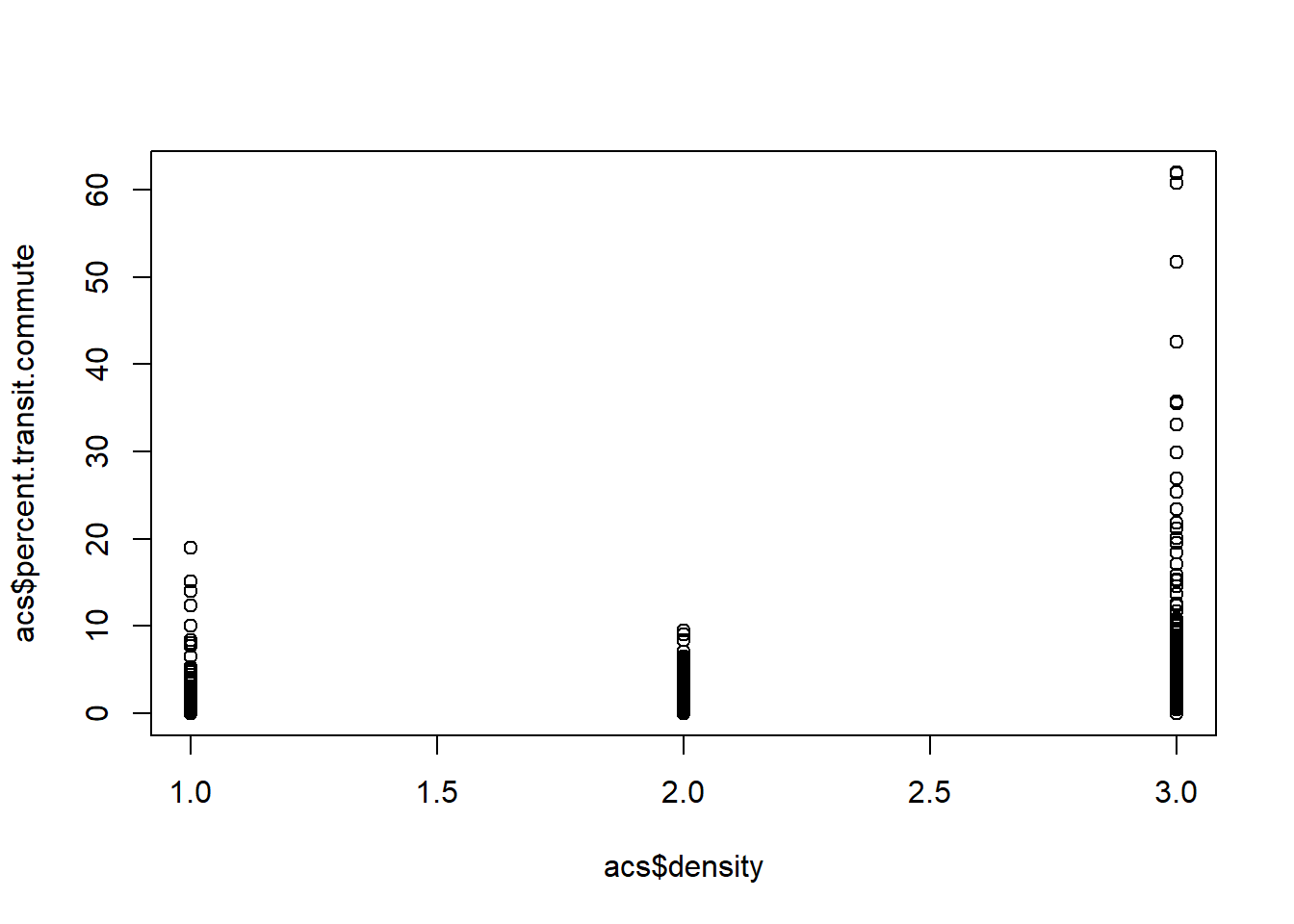
It’s pretty hard to determine what’s going on here, but it looks positive to me…
A slightly better way to visualize would be:
boxplot(acs$percent.transit.commute ~ acs$density)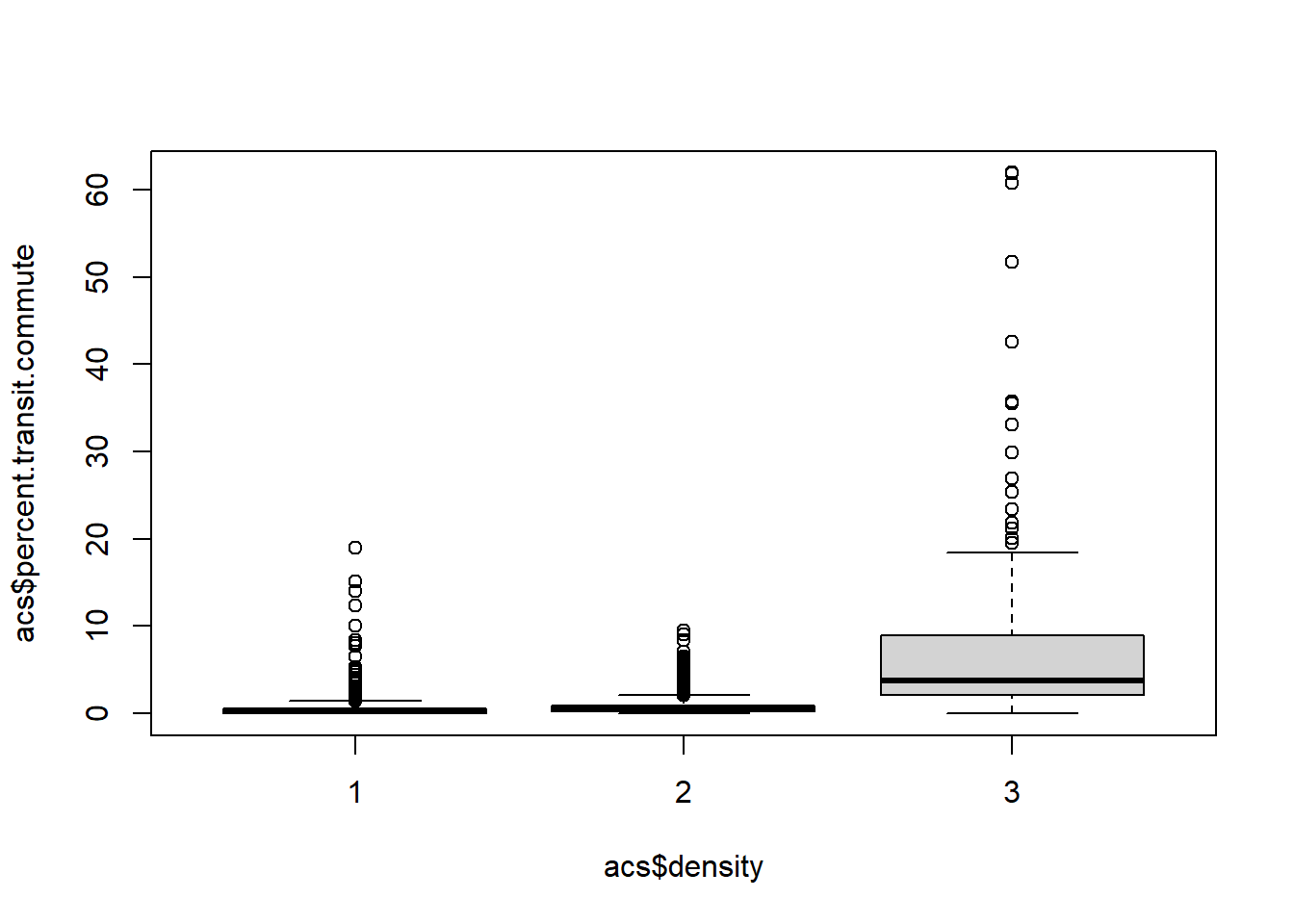
boxplot(acs$percent.transit.commute ~ acs$density, outline=F)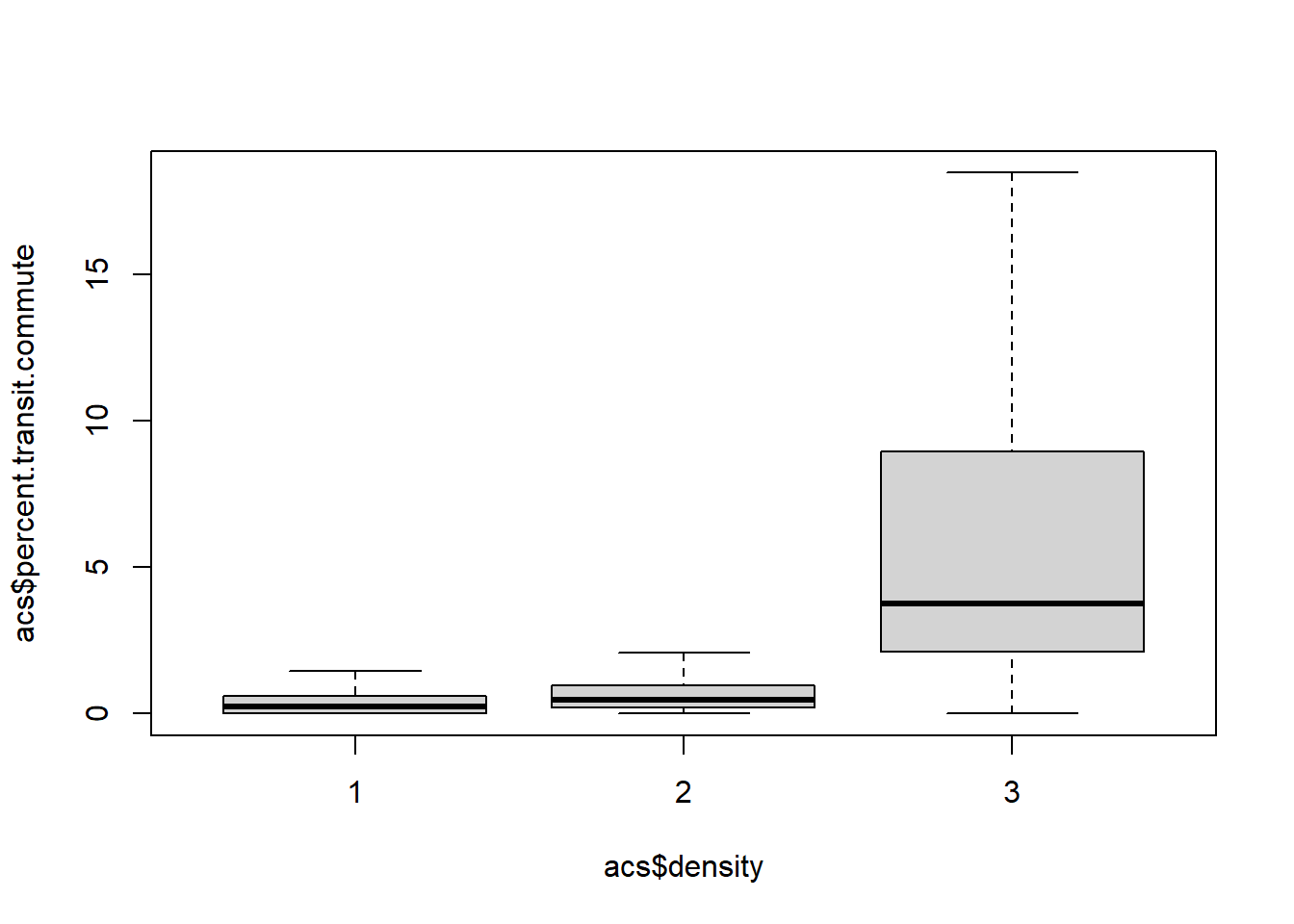
Can we summarize this with a regression?
Yes! Regression only needs numeric inputs, so this will totally work fine mechanically.
m <- lm(percent.transit.commute ~ density, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = percent.transit.commute ~ density, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.606 -1.296 -0.083 0.307 58.319
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.67845 0.14583 -11.51 <2e-16 ***
#> density 1.76132 0.09001 19.57 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.962 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1087, Adjusted R-squared: 0.1084
#> F-statistic: 382.9 on 1 and 3139 DF, p-value: < 2.2e-16But we have to be careful about how we interpret this. The coefficient on density is 1.76. Every one unit increase in density leads to an additional 1.76 percentage point of the population commuting by transit. What is 1 unit for this variable? It is moving from rural to suburban, or from suburban to urban.
So what is the effect of moving from rural to urban? \(1.76+1.76=3.52\).
What does the intercept represent here? We know the intercept is the average value of percent.transit.commute when all variables are 0. What does that mean here? It’s gibberish! density can’t take on the value of 0 so this is not a helpful number.
Are we happy with this regression? Let’s look at the scatterplot:
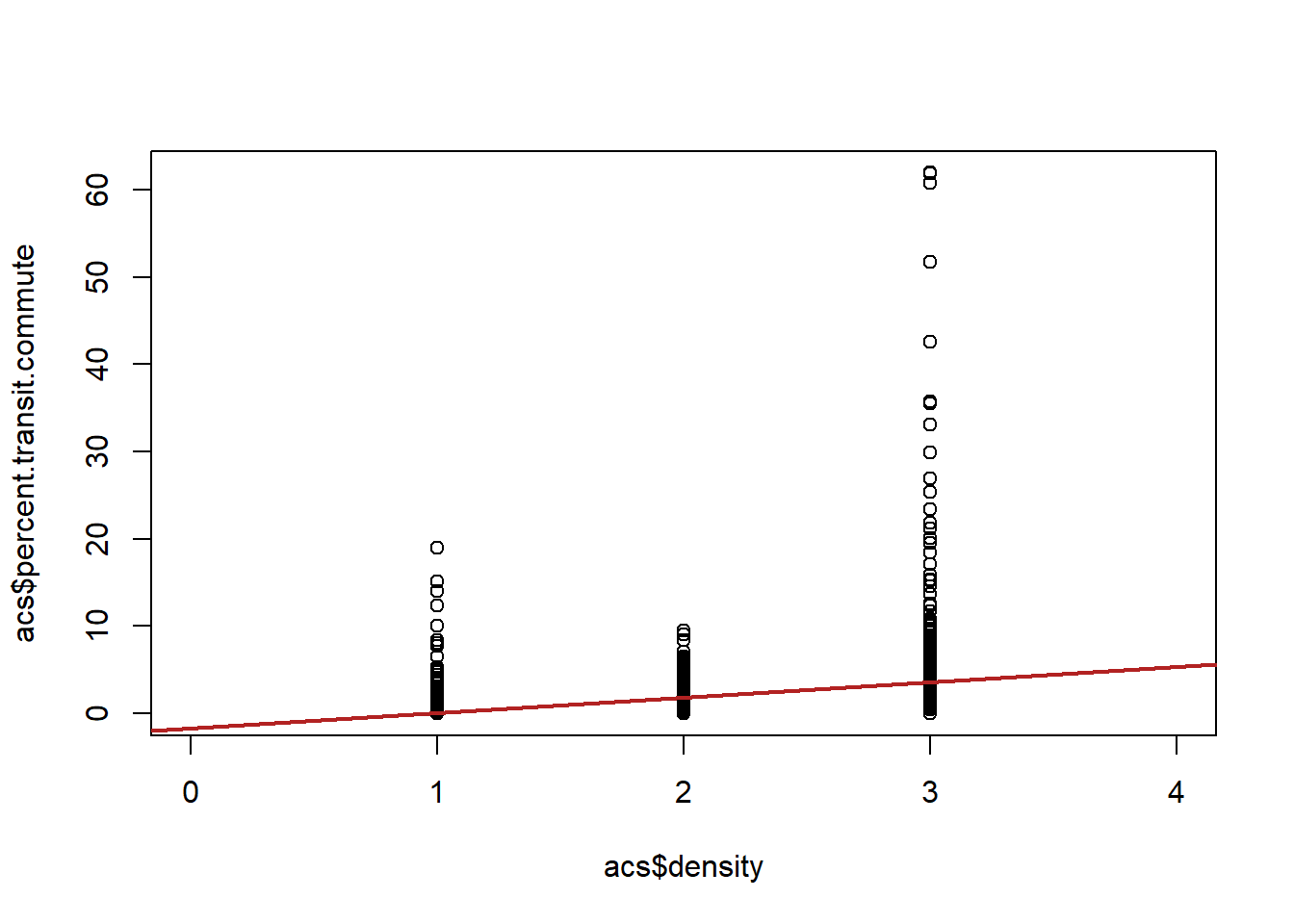
If we are willing to assume that the jumps from one level (rural to suburban, suburban to urban) are all equal then this regression is fine. We just treat the variable as-if it was a continuous variable. But in this case this doesn’t seem to be the case. Here the junmp from suburban to urban matters a lot more and we are smoothing over it in a way that is problematic. We need a method that allows us to understand those two jumps are of different sizes.
Plus, applying this method (just convert a categorical variable to a continuous variable) breaks down when we have an un-ordered categorical variable.
Consider we want to run a regression where the dependent variable is median income and the independent variable is the percent of individuals commuting by public transit
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
plot(acs$percent.transit.commute, acs$median.income)
abline(lm(median.income ~ percent.transit.commute, data=acs), lwd=2, col="firebrick")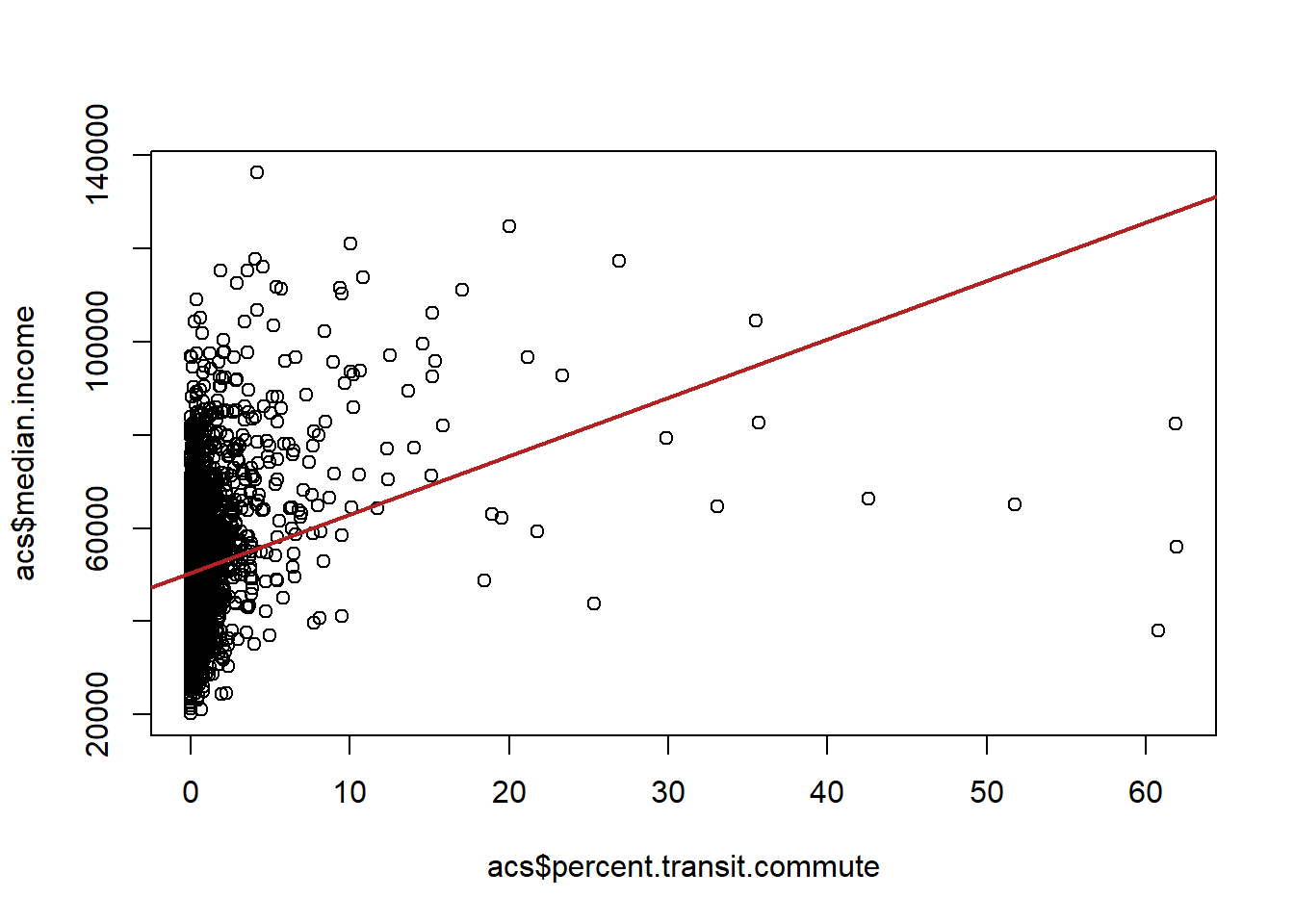
We find that there is a positive relationship, the higher percentage of a county that commutes by transit, the higher the median income of that county.
However, we might think that one reason that county may both have a higher percentage of transit commutes in it and have a higher median income is because of the region it is in. For example, places in the north-east have a well developed transit system and also are generally more well off. Alternatively, the south has poorly developed mass transit and also has several regions which have deep poverty. So it might not be that that transit commuting is related to wealth. Instead we’re just picking up the differences between regions.
So we’d like to “control” for region here. But region is not a numeric variable! It has no order. It would make no sense to do Northeast=1, South=2….
The solution to this problem is to change this categorical variable into a series of “dummy” variables which indicates whether a case is in this category, or not.
table(acs$census.region)
#>
#> midwest northeast south west
#> 1055 217 1422 448We need to create 4 dummy variables, one for each region:
Here’s a hard way to do it:
acs$midwest[acs$census.region=="midwest"]<- 1
acs$midwest[acs$census.region!="midwest"]<- 0
acs$northeast[acs$census.region=="northeast"]<- 1
acs$northeast[acs$census.region!="northeast"]<- 0
acs$south[acs$census.region=="south"]<- 1
acs$south[acs$census.region!="south"]<- 0
acs$west[acs$census.region=="west"]<- 1
acs$west[acs$census.region!="west"]<- 0
#Check if this worked:
table(acs$census.region, acs$midwest)
#>
#> 0 1
#> midwest 0 1055
#> northeast 217 0
#> south 1422 0
#> west 448 0
table(acs$census.region, acs$northeast)
#>
#> 0 1
#> midwest 1055 0
#> northeast 0 217
#> south 1422 0
#> west 448 0
table(acs$census.region, acs$south)
#>
#> 0 1
#> midwest 1055 0
#> northeast 217 0
#> south 0 1422
#> west 448 0
table(acs$census.region, acs$west)
#>
#> 0 1
#> midwest 1055 0
#> northeast 217 0
#> south 1422 0
#> west 0 448Thankfully, there is a package that does this in a more automated way:
#acs[,29:32] <- NULL
#
##install.packages("fastDummies")
#library(fastDummies)
#acs <- dummy_cols(acs, select_columns = "census.region")
#
##Doesn't give them great names, but that's easy to fix:
#names(acs)[29:32] <- c("west","midwest", "northeast","south")Ok! Now we have 4 numeric indicator for which census region each county is in.
Let’s throw these into a regression, just forgetting about the transit variable for now:
m <- lm(median.income ~ midwest + northeast + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ midwest + northeast + south + west,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients: (1 not defined because of singularities)
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 55590.7 614.4 90.481 < 2e-16 ***
#> midwest -2104.2 733.1 -2.870 0.00413 **
#> northeast 6403.3 1074.7 5.958 2.84e-09 ***
#> south -8268.1 704.4 -11.738 < 2e-16 ***
#> west NA NA NA NA
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Ok, so what happened here? We got three coefficients but are getting NA for west…
But let’s think, in particular, about how we defined the intercept and what it means relative to these 4 indicator variables.
These variables are equal to 1 if the county is in the region, and 0 otherwise. All counties are in at least one of the regions. Remember that the intercept is the average value of Y when all of the variables are equal to zero. So: what counties are identified when all the variables are equal to zero? There are no counties in that category! Each county is 1 for at least one of the regions! There cannot be an intercept if all these variables are included.
To make this clear, here are 4 counties from 4 different regions. Notice that you have to be 1 for exactly one of the regions.
counties <- c(1055,4007,9001,17173)
c <- acs[acs$county.fips %in% counties,]
keep <- c("county.name","state.full","census.region","midwest","northeast","south","west")
c <- c[keep]
c
#> county.name state.full census.region midwest
#> 1 Etowah County Alabama south 0
#> 102 Gila County Arizona west 0
#> 312 Fairfield County Connecticut northeast 0
#> 604 Shelby County Illinois midwest 1
#> northeast south west
#> 1 0 1 0
#> 102 0 0 1
#> 312 1 0 0
#> 604 0 0 0Here’s the important point: If we have a set of indicators that are exhaustive (i.e. each case is 1 on at least one of them) We have to omit exactly one for the regression to run.
We refer to this omitted category as the “reference” category. There’s no guideline for which one to omit, but you should make clear which one you’ve omitted.
So for example, we could omit the midwest:
m <- lm(median.income ~ northeast + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ northeast + south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 53486.5 399.9 133.743 < 2e-16 ***
#> northeast 8507.4 968.2 8.786 < 2e-16 ***
#> south -6163.9 527.8 -11.678 < 2e-16 ***
#> west 2104.2 733.1 2.870 0.00413 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Let’s think through what these numbers mean now. The intercept is the average income when all the other variables are equal to zero. What are we talking about when northeast, south, and west, are equal to zero? The midwest! The intercept here is the average median income of counties in the midwest.
mean(acs$median.income[acs$census.region=="midwest"])
#> [1] 53486.52What do each of these coefficients represent? They represent the the change in the average median income in each of these regions, compared to the midwest, so the average median income in the northeast is:
coef(m)["(Intercept)"] + coef(m)["northeast"]
#> (Intercept)
#> 61993.96
mean(acs$median.income[acs$census.region=="northeast"])
#> [1] 61993.96Note that you get the same “answer” when you omit a different category, but the numbers will change:
m <- lm(median.income ~ midwest + south + west, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ midwest + south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -31506 -8314 -2055 5236 88945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 61994.0 881.8 70.304 < 2e-16 ***
#> midwest -8507.4 968.2 -8.786 < 2e-16 ***
#> south -14671.4 946.7 -15.497 < 2e-16 ***
#> west -6403.3 1074.7 -5.958 2.84e-09 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12990 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1023, Adjusted R-squared: 0.1015
#> F-statistic: 119.2 on 3 and 3137 DF, p-value: < 2.2e-16Now our intercept is the average median income in the northeast, which is the same as we saw above and the coefficient for midwest is just the inverse from what we had above.
So let’s use this knowledge to control for region when estimating the effect of transit ridership on household income
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
m2 <- lm(median.income ~ percent.transit.commute + northeast + south + west, data=acs)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + northeast +
#> south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> northeast 4995.19 971.66 5.141
#> south -6208.27 511.96 -12.126
#> west 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> northeast 2.9e-07 ***
#> south < 2e-16 ***
#> west 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16Indeed, controlling for region did slightly attenuate (make smaller) the effect of transit commuting. The intercept now is the average median income in the midwest for a county with 0 transit ridership (which may not exist) The coefficients on each of the region dummies is the change in the average level of median income in each of these regions relative to the midwest, controlling for transit ridership.
There is a slightly easier (but less intuitive) way to do this same thing, by treating census.region as a factor variable
acs$census.region <- as.factor(acs$census.region)When something is a factor variable and we put it in a regression, R will automatically do the work to turn it into dummies:
m <- lm(median.income ~ percent.transit.commute + census.region, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + census.region,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> census.regionnortheast 4995.19 971.66 5.141
#> census.regionsouth -6208.27 511.96 -12.126
#> census.regionwest 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> census.regionnortheast 2.9e-07 ***
#> census.regionsouth < 2e-16 ***
#> census.regionwest 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16R will automatically choose the reference category for you in this case. We can use the relevel() command to force R to consider one of the categories to be the reference
acs$census.region <- relevel(acs$census.region, ref="northeast")
m <- lm(median.income ~ percent.transit.commute + census.region, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + census.region,
#> data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 57840.62 904.67 63.936
#> percent.transit.commute 1050.00 74.53 14.089
#> census.regionmidwest -4995.19 971.66 -5.141
#> census.regionsouth -11203.47 950.65 -11.785
#> census.regionwest -3779.47 1058.92 -3.569
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> census.regionmidwest 2.9e-07 ***
#> census.regionsouth < 2e-16 ***
#> census.regionwest 0.000363 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-1613.2 Presenting regression results
Generate some regressions:
m1 <- lm(median.income ~ percent.transit.commute, data=acs)
summary(m1)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -88643 -8532 -1280 6198 80684
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 50350.26 245.41 205.17
#> percent.transit.commute 1256.54 74.68 16.83
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> percent.transit.commute <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13130 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.08273, Adjusted R-squared: 0.08244
#> F-statistic: 283.1 on 1 and 3139 DF, p-value: < 2.2e-16
m2 <- lm(median.income ~ percent.transit.commute + northeast + south + west, data=acs)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.transit.commute + northeast +
#> south + west, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -83579 -7773 -1899 5279 85257
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52845.43 390.56 135.308
#> percent.transit.commute 1050.00 74.53 14.089
#> northeast 4995.19 971.66 5.141
#> south -6208.27 511.96 -12.126
#> west 1215.72 713.84 1.703
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> percent.transit.commute < 2e-16 ***
#> northeast 2.9e-07 ***
#> south < 2e-16 ***
#> west 0.0887 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12600 on 3136 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.1558, Adjusted R-squared: 0.1547
#> F-statistic: 144.6 on 4 and 3136 DF, p-value: < 2.2e-16If you want to run a regression and output the results in a way that looks nice, you have a couple of options. If you want to visualize, one option is to use a coefplot
#install.packages("coefplot")
library(coefplot)
#> Warning: package 'coefplot' was built under R version 4.1.3
#> Loading required package: ggplot2
#> Warning: package 'ggplot2' was built under R version 4.1.3
coefplot(m2)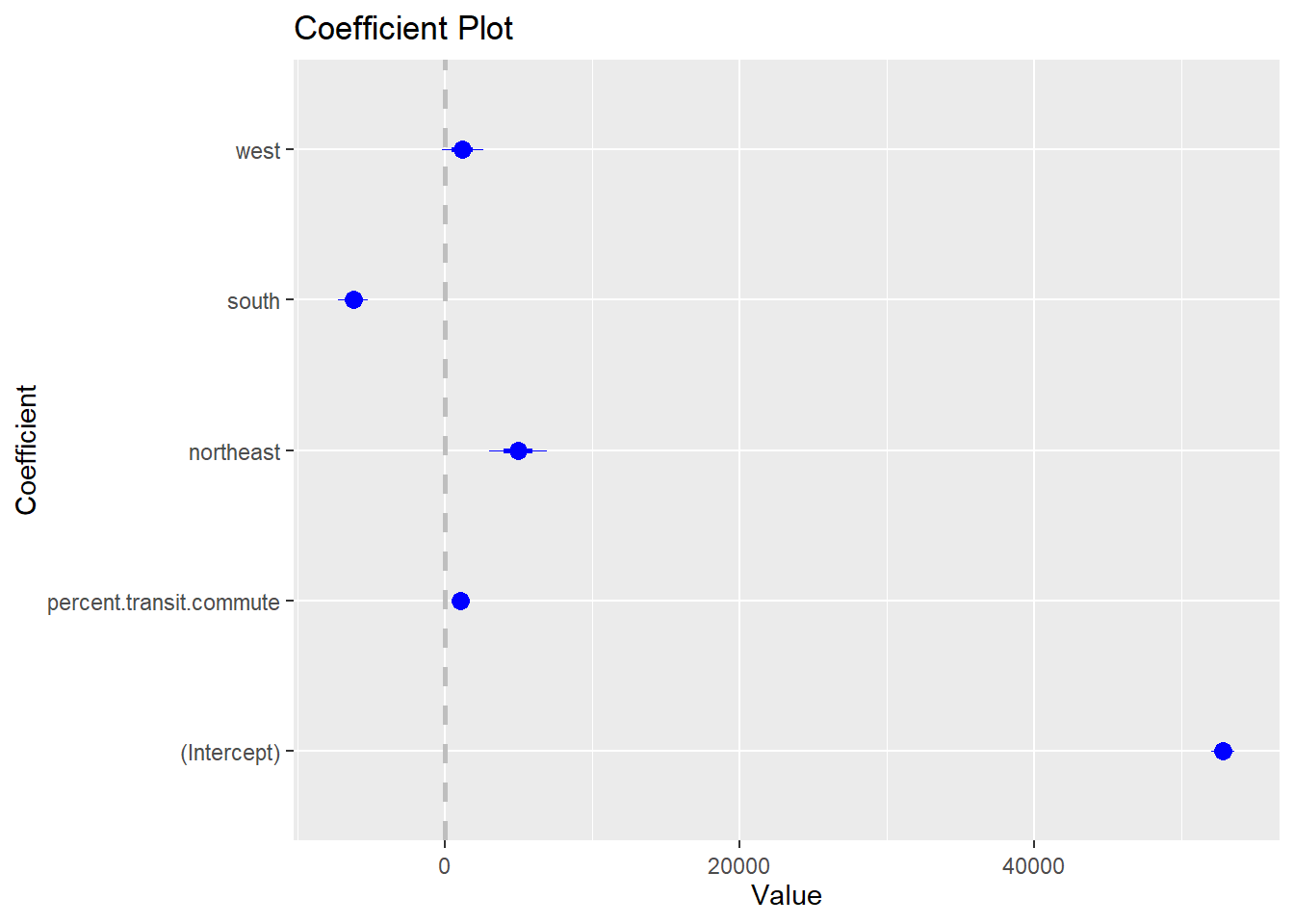
This isn’t particularly nice, and you can do this nicer in ggplot. I’ll leave you to google how to do that.
(Honestly, when I make coefficient plots I do them “by hand” extracting coefficients and confidence intervals and plotting just using the grid system):
Generating tables can be done using the “stargazer” package. One nice thing about this is that you can output multiple models with the same DV together:
library(stargazer)
#>
#> Please cite as:
#> Hlavac, Marek (2018). stargazer: Well-Formatted Regression and Summary Statistics Tables.
#> R package version 5.2.2. https://CRAN.R-project.org/package=stargazer
#The "text" type will output into R in a nice looking format:
stargazer(m1, m2, type="text")
#>
#> ===========================================================================
#> Dependent variable:
#> ---------------------------------------------------
#> median.income
#> (1) (2)
#> ---------------------------------------------------------------------------
#> percent.transit.commute 1,256.536*** 1,049.999***
#> (74.676) (74.528)
#>
#> northeast 4,995.192***
#> (971.664)
#>
#> south -6,208.274***
#> (511.962)
#>
#> west 1,215.719*
#> (713.836)
#>
#> Constant 50,350.260*** 52,845.430***
#> (245.409) (390.557)
#>
#> ---------------------------------------------------------------------------
#> Observations 3,141 3,141
#> R2 0.083 0.156
#> Adjusted R2 0.082 0.155
#> Residual Std. Error 13,126.480 (df = 3139) 12,599.180 (df = 3136)
#> F Statistic 283.129*** (df = 1; 3139) 144.642*** (df = 4; 3136)
#> ===========================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01To output into an html rmarkdown just omit the out and add results='asis' to your code chunk options
stargazer(m1, m2, type="html", style="apsr",
dep.var.labels = "Median Income",
covariate.labels = c("% Transit Commuters",
"Region: NorthEast",
"Region: South",
"Region: West"))| Median Income | ||
| (1) | (2) | |
| % Transit Commuters | 1,256.536*** | 1,049.999*** |
| (74.676) | (74.528) | |
| Region: NorthEast | 4,995.192*** | |
| (971.664) | ||
| Region: South | -6,208.274*** | |
| (511.962) | ||
| Region: West | 1,215.719* | |
| (713.836) | ||
| Constant | 50,350.260*** | 52,845.430*** |
| (245.409) | (390.557) | |
| N | 3,141 | 3,141 |
| R2 | 0.083 | 0.156 |
| Adjusted R2 | 0.082 | 0.155 |
| Residual Std. Error | 13,126.480 (df = 3139) | 12,599.180 (df = 3136) |
| F Statistic | 283.129*** (df = 1; 3139) | 144.642*** (df = 4; 3136) |
| p < .1; p < .05; p < .01 | ||
Can get wild with this.. https://www.jakeruss.com/cheatsheets/stargazer/
13.3 Regression assumptions
You can run regression on any set of numerical variables, but that does not mean that your regression is giving you the “right” answer, or the true relationship between the independent and dependent variables in the population.
In order for your regression to be outputting the “right” answers the regression must satisfy 5 criteria called the “Gauss-Markov Assumptions”.
Before getting there, I want to talk about one twist to the regression equation, which we have defined as:
\[ \hat{y} = \hat{\alpha} + \hat{\beta} X_i \]
As we have discussed, this equation defines the regression line. You can input an x and it will output a the y-level of the regression line at that point.
We can also write the following equation
\[ y_i = \hat{\alpha} + \hat{\beta} x_i + \hat{u}_i \]
The middle bit \(\alpha + \beta x_i\) is the same, and we know this produces the regression line. But notice that the left hand side is no longer set equal to \(\hat{y}\) but instead to \(y_i\). In other words, this is the equation which tells you, for a given x, what does the actual y value equal? To get from the regression line to the actual y value, we need to add back on the residual which in the sample is \(u_i\). So this equation says, for our sample, this is the relationship between x’s and y’s.
We can also think about this same equation existing in the population:
\[ Y_i = \alpha + \beta X_i + \epsilon_i \]
When we talk about the population we get rid of the hats (which denote that something is an estimate) and also change \(u\) to \(\epsilon\). What we are effectively defining here is the data generating process. How do y’s get produced by x’s? Well there is some sort of population level intercept and slope, but those aren’t purely deterministic. To each point is added some amount of error, \(\epsilon\), which generates our final data. We could literally generate data using a similar equation (and this is similar to your problem set):
set.seed(19104)
#X exists:
x <- rnorm(100, mean=50, sd=3)
#Y data generating process:
y <- 4 + 3*x + rnorm(100,mean=0, sd=2)
plot(x,y)
#Everytime we runw we get something newThinking this way about the regression equation as a “data generating process”, we can think about the GM assumptions.
The Gauss-Markov Assumptions are:
- X has full rank
- The true model that generates the data is \(Y = \alpha + \beta X_1 + \beta X_2 \ldots + \beta X_k + \epsilon_i\)
- \(E[\epsilon^2|X] =\sigma^2\)
- \(E[\epsilon_i \epsilon_j|X] = 0\) if \(i\neq j\)
- \(E[\epsilon_i|X] = 0\)
We are going to talk about these a bit out of order.
13.3.1 GM1: Full Rank
The first, that X has full rank, is saying that one variable cannot be a linear combination of others. We actually just saw an example of this when we were making categorical variables. There we saw that if we had an exhaustive set of categories OLS must drop one in order to actually compute. The only other situation that this will happen is if you try to regress a variable that has no variation. A variable with no variation is a linear transformation of the intercept, so that won’t work!
The first assumption is not really one you have to think about because R will literally not run a regression that violates this, as we saw above.
Similarly, if you try to run a regression with an independent variable that has no variation:
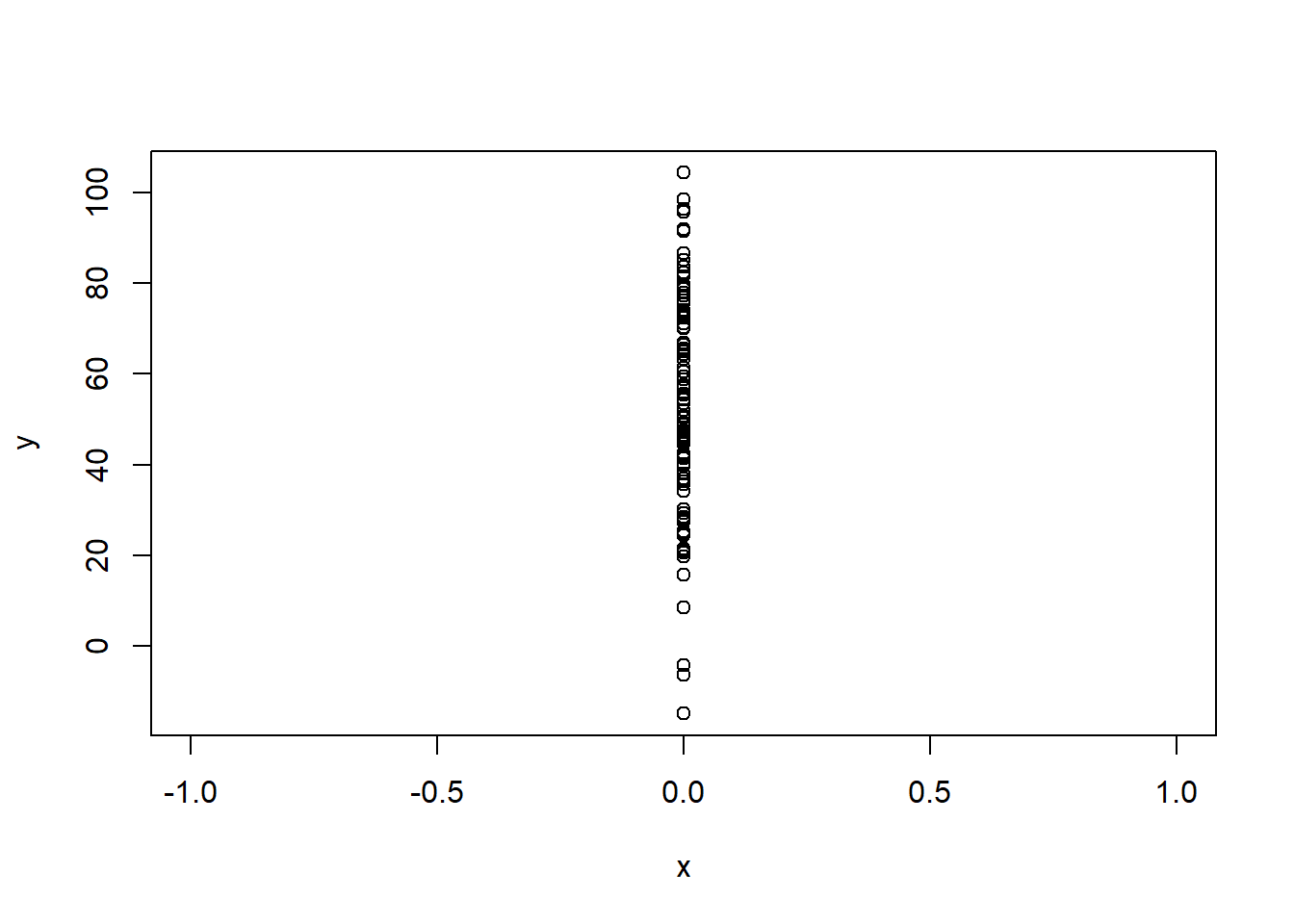
lm(y ~ x)
#>
#> Call:
#> lm(formula = y ~ x)
#>
#> Coefficients:
#> (Intercept) x
#> 53.46 NA13.3.2 GM 5 Causality
Jumping around, the 5th OLS assumption that \(E[\epsilon_i|X] = 0\) is talking about causality. This is sometimes thought of as an extra or “bonus” assumption that \(\beta\) actually represents the true effect of X on Y. One way we think about that is saying that the errors \(\epsilon\) are uncorrelated with other factors. You can just think of this as: there are no confounding variables.
m <- lm(percent.transit.commute ~ median.income, data=acs)13.3.3 GM 3 No Heteroskedasticity
Assumptions 3 and 4 are a bit more important, as they talk about whether we can trust the standard errors being produced. Both of these assumptions are about each point being independent from all other points. If each point is independent from all other points then it must also be the case that each points error term \(\epsilon\) is independent from all other points. A couple of things break this.
Assumption 3 says that, conditional on x, the squared error term must be equal to \(\sigma^2\). Less important here is what sigma squared is, and more important is that this is saying that the error must be constant across levels of X.
Have a look at these two graphs:
#Homoskedastic Errors
x <- runif(100, min=0, max=100)
y <- 2 + 3*x + rnorm(100, mean=0, sd=15)
plot(x,y)
abline(lm(y~x), col="firebrick" ,lwd=2)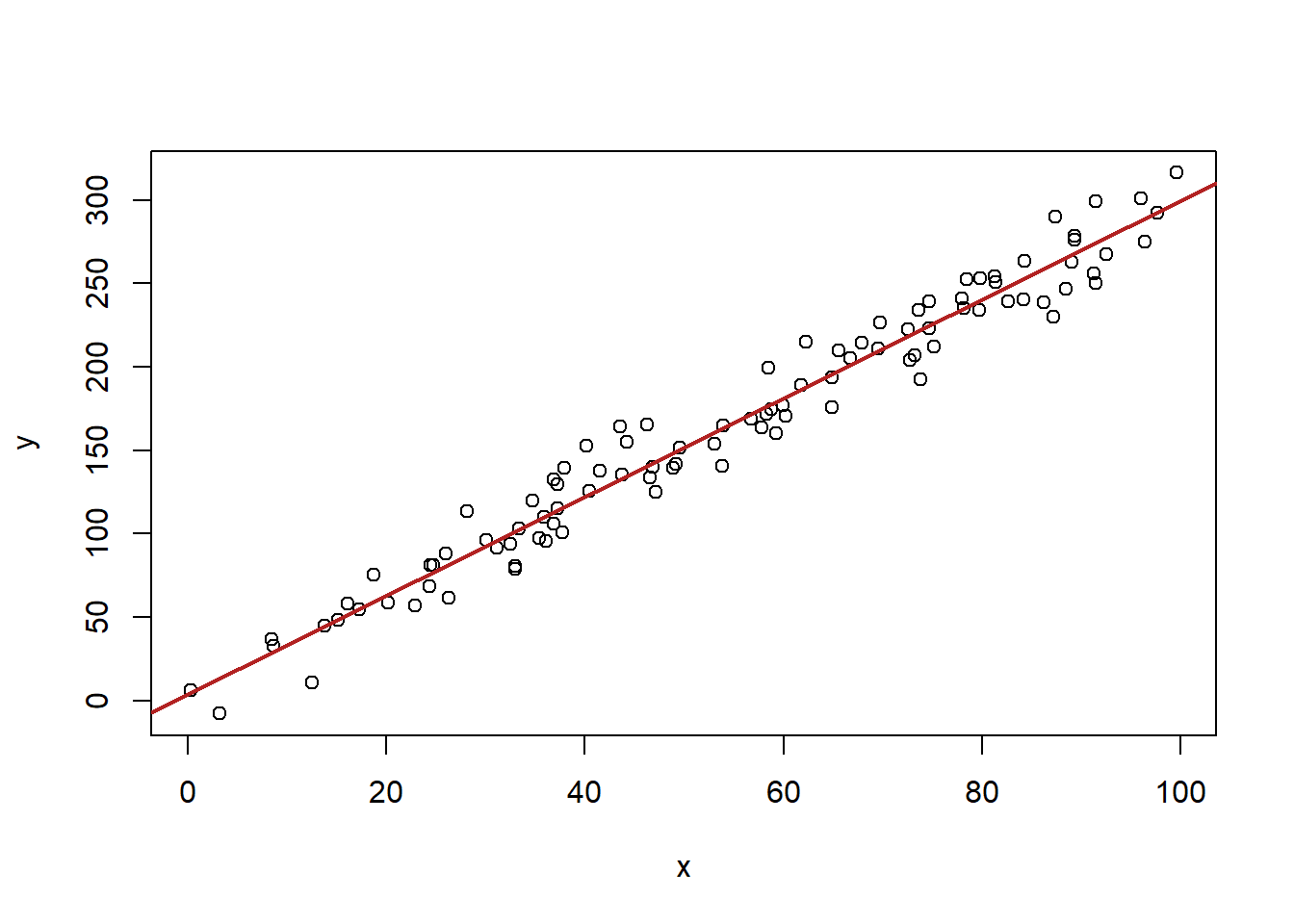
#Heteroskedastic Errors
x <- runif(100, min=0, max=100)
y <- 2 + 3*x + rnorm(100, mean=0, sd=x*2)
plot(x,y)
abline(lm(y~x), col="firebrick" ,lwd=2)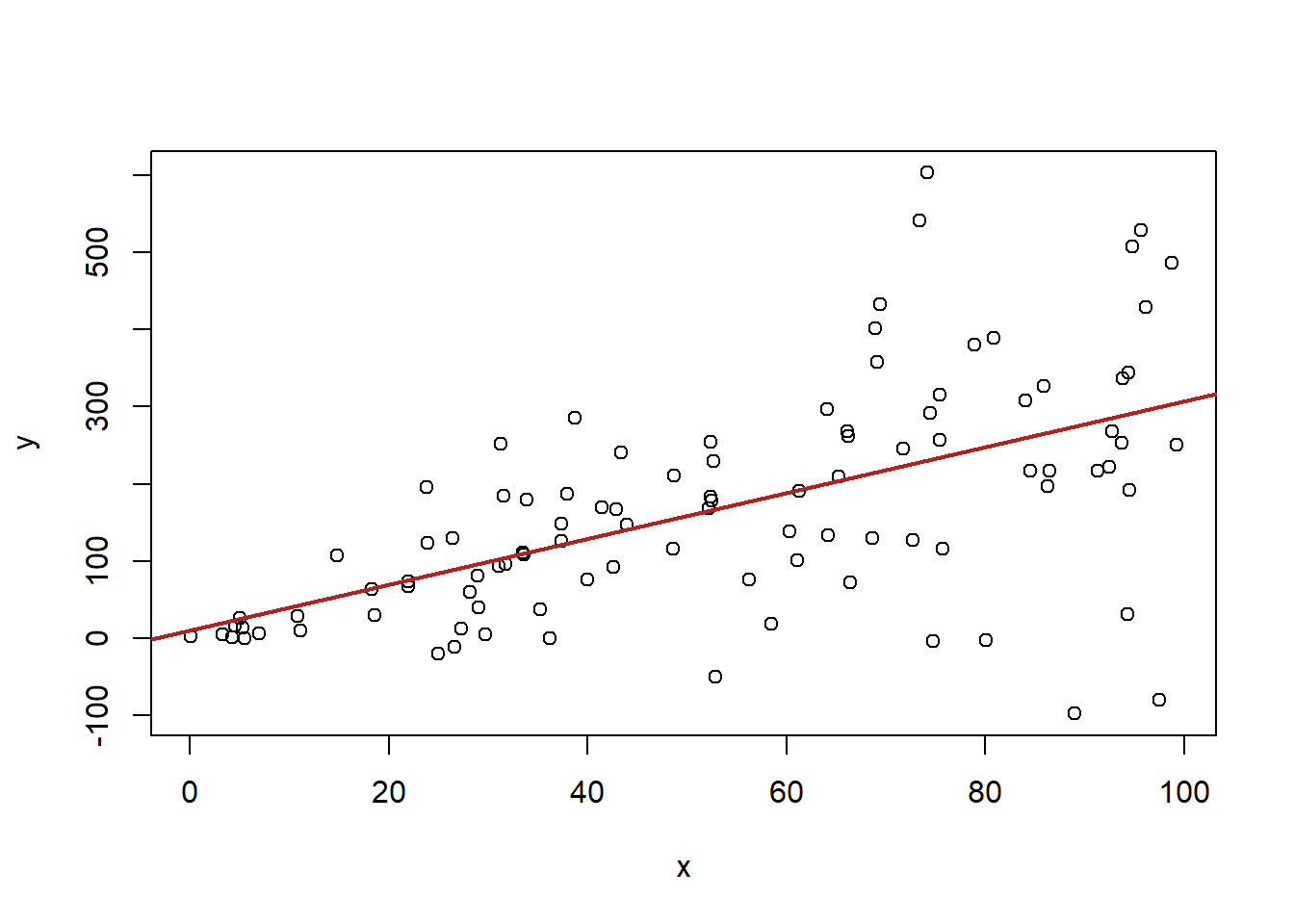
In the second graph the errors are not constant across levels of X. These are heteroskedastic errors. The consequence of these is that the estimated standard error on beta will be wrong.
We can show that via simulation
betas <- rep(NA,10000)
ses <- rep(NA,10000)
for(i in 1:10000){
x <- runif(100, min=0, max=100)
y <- 2 + 3*x + rnorm(100, mean=0, sd=x*2)
m <- lm(y ~ x)
betas[i] <- coef(m)["x"]
ses[i] <- sqrt(vcov(m)["x","x"])
}
#Empirical standard error
sd(betas)
#> [1] 0.4423603
#Average calculated standard errors in samples
mean(ses)
#> [1] 0.399791How to do we diagnose and address heteroskedasticity?
library(AER)
data("CASchools")
head(CASchools)
#> district school county grades
#> 1 75119 Sunol Glen Unified Alameda KK-08
#> 2 61499 Manzanita Elementary Butte KK-08
#> 3 61549 Thermalito Union Elementary Butte KK-08
#> 4 61457 Golden Feather Union Elementary Butte KK-08
#> 5 61523 Palermo Union Elementary Butte KK-08
#> 6 62042 Burrel Union Elementary Fresno KK-08
#> students teachers calworks lunch computer expenditure
#> 1 195 10.90 0.5102 2.0408 67 6384.911
#> 2 240 11.15 15.4167 47.9167 101 5099.381
#> 3 1550 82.90 55.0323 76.3226 169 5501.955
#> 4 243 14.00 36.4754 77.0492 85 7101.831
#> 5 1335 71.50 33.1086 78.4270 171 5235.988
#> 6 137 6.40 12.3188 86.9565 25 5580.147
#> income english read math
#> 1 22.690001 0.000000 691.6 690.0
#> 2 9.824000 4.583333 660.5 661.9
#> 3 8.978000 30.000002 636.3 650.9
#> 4 8.978000 0.000000 651.9 643.5
#> 5 9.080333 13.857677 641.8 639.9
#> 6 10.415000 12.408759 605.7 605.4
#Creating Variables
CASchools$STR <- CASchools$students/CASchools$teachers
summary(CASchools$STR)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 14.00 18.58 19.72 19.64 20.87 25.80
CASchools$score <- (CASchools$read + CASchools$math)/2
summary(CASchools$score)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 605.5 640.0 654.5 654.2 666.7 706.8
dat <- CASchools
dat$esl <- dat$english
#lm(math ~ esl)Before we plot this to assess hetero/homoskedasticity let’s think through what is likely to be the case. Do we expect more variation in math scores when esl is high/low?
Probably, yes. My expectation is that schools with a low number of esl kids will be in all sorts of neighborhoods with all sorts of different levels of funding, family income etc.
So I expect a lot of variation in math scores in these types of schools. Schools with a high number of esl kids will all be in similar types of neighborhoods so I expect a bit less variation in math scores in these schools.
Note that we’re not talking about the relationship between esl and math scores, but how the random variance in math changes across levels of esl.
Further, while we have tools to diagnose heteroskedasticity, part of what you do will be using your theoretical knowledge of cases to determine whether it is likely to be a problem. This is what I did here with my deep knowledge of the California school system (kidding! I cheated and looked at the data first…)
Let’s take a look at what we see.
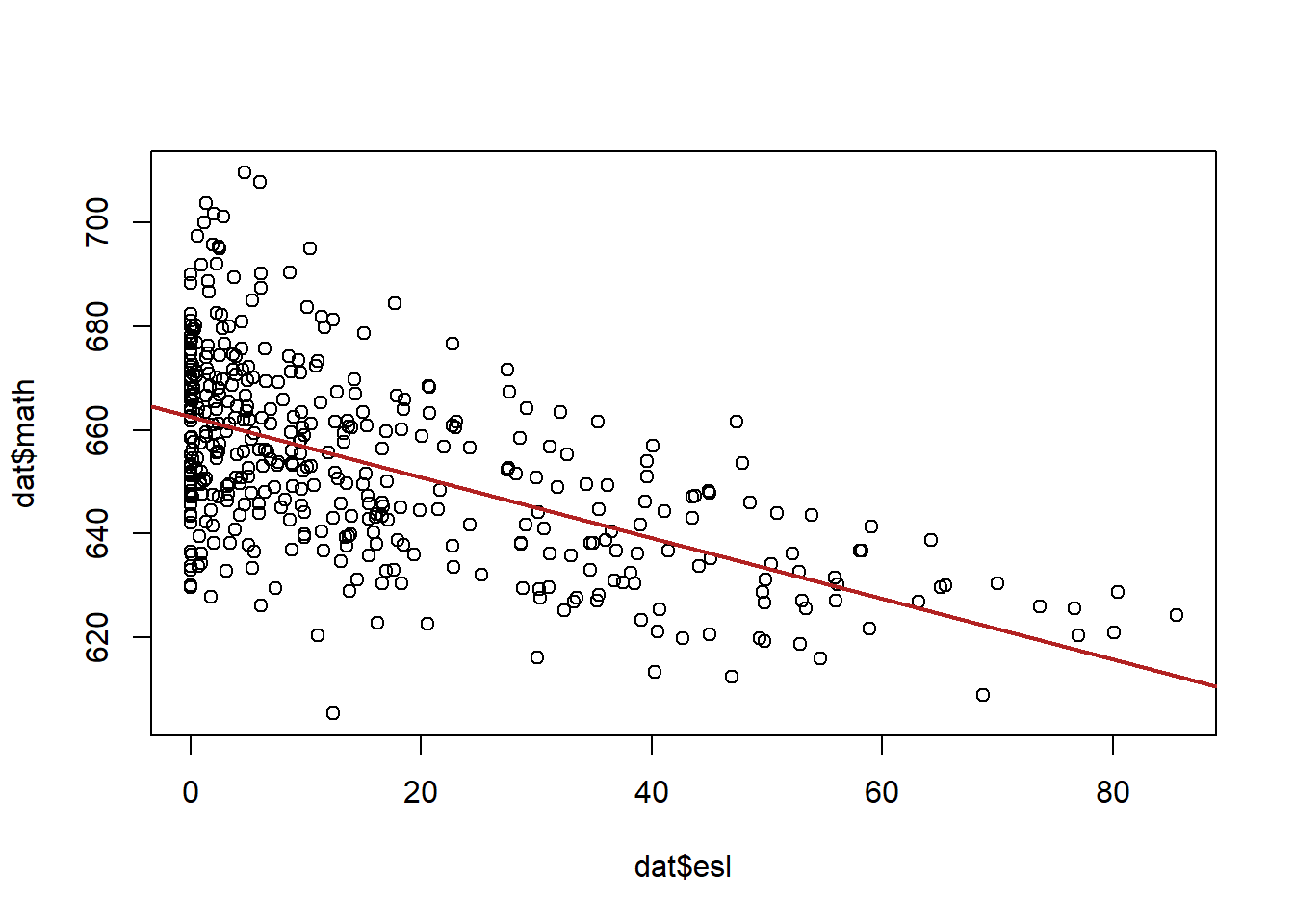
This seems to reflect our prediction, in general there seems to be a lot more variation in math scores when esl is lower, and less when esl is higher.
There is a specific test for heteroskedasticity beyond what we can see with our eyes:
library(lmtest)
m <- lm(math ~ esl, data=dat)
bptest(m)
#>
#> studentized Breusch-Pagan test
#>
#> data: m
#> BP = 12.084, df = 1, p-value = 0.0005085This test will be statistically significant if heteroskedasticity is present. Here we reject the null hypothesis of homoskedasticity.
How can we fix this?
Well, one way to fix heteroskedasticity is to better model the reasons for higher variance in some cases.
We think that there is more unmodeled variance at the low end of esl. In other words schools without a lot of english as a second language children come from all different types of places. If we add variables that explain math scores among that group better heteroskedasticity will be reduced.
So, for example, if we add to our regression other variables which help us determine what sort of schools these are…
m <- lm(math ~ esl + lunch + calworks + income, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = math ~ esl + lunch + calworks + income, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -30.8808 -6.6403 -0.0207 5.8995 30.0311
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 660.25387 2.47171 267.124 < 2e-16 ***
#> esl -0.14893 0.03831 -3.887 0.000118 ***
#> lunch -0.32979 0.04215 -7.825 4.26e-14 ***
#> calworks -0.11171 0.06657 -1.678 0.094090 .
#> income 0.76129 0.09542 7.979 1.46e-14 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 9.928 on 415 degrees of freedom
#> Multiple R-squared: 0.7224, Adjusted R-squared: 0.7198
#> F-statistic: 270 on 4 and 415 DF, p-value: < 2.2e-16
bptest(m)
#>
#> studentized Breusch-Pagan test
#>
#> data: m
#> BP = 7.4826, df = 4, p-value = 0.1125We no longer have a heteroskedastic regression.
The other way to deal with heteroskedasticity is to employ Hubert-White (or simply “robust”) standard errors.
For this we need the sandwich package
library(sandwich)
library(lmtest)
m <- lm(math ~ esl, data=dat)
robust.vcov <- vcovHC(m, type="HC1")
coeftest(m, vcov=robust.vcov)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 662.539315 1.046782 632.929 < 2.2e-16 ***
#> esl -0.583245 0.033671 -17.322 < 2.2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 113.3.4 GM 4 No Auto-Correlation
Assumption 4 talks about “auto-correlation”. This has the same problem of breaking the assumption that the errors of one data point are independent from others, but here it is because that points are related to one another in some un-modeled way. This is almost always due to time or to clusters.
First let’s think about time:
Here is quarterly American GDP since the year 2000:
gdp <- import("https://github.com/marctrussler/IIS-Data/raw/main/GDP.csv")
gdp <- gdp[213:307,]
plot(gdp$DATE, gdp$GDP)
abline(lm(gdp$GDP ~ gdp$DATE), col="firebrick", lwd=2)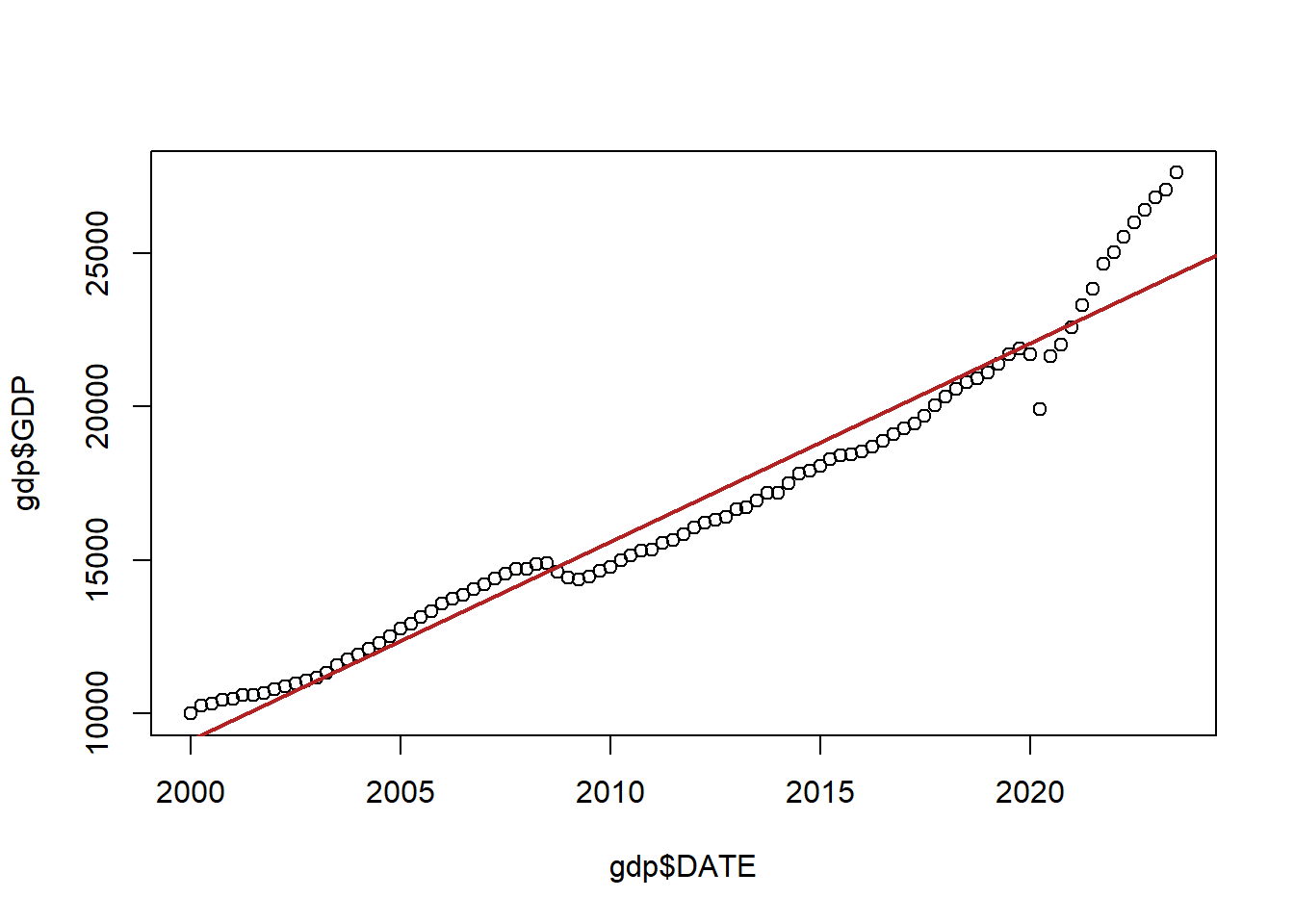
Now, ignoring the fact there that this red line doesn’t do a great job of fitting the data, the problem here is that the errors being made from point to point are not independent from one another.
Let’s look at the relationships between the date and the residuals from that regression:
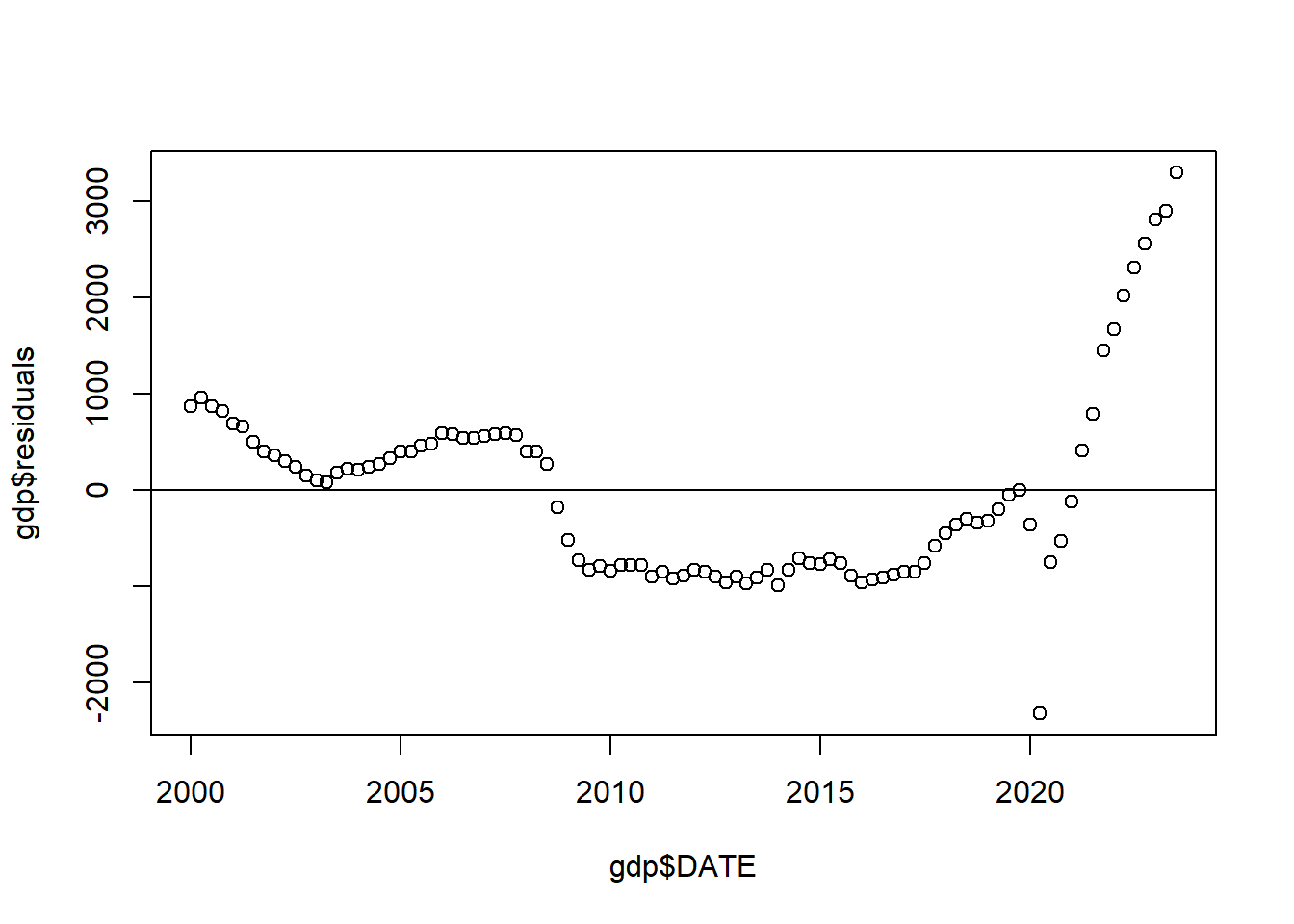
What we want to think about is that if there are two adjacent points than a lot of the time knowing the residual of one point will tell you what the residual of the neighboring point is. There are some exceptions here (like the 2nd quarter of 2020!), but in general if you tell me the error of one point I can make a good guess at the error of it’s neighbor.
For comparison, here is what this same plot looks like when things are fine (from the data we created abo:
x <- runif(100, min=0, max=100)
y <- 2 + 3*x + rnorm(100, mean=0, sd=15)
resid <- residuals(lm(y~x))
plot(x,resid)
abline(h=0)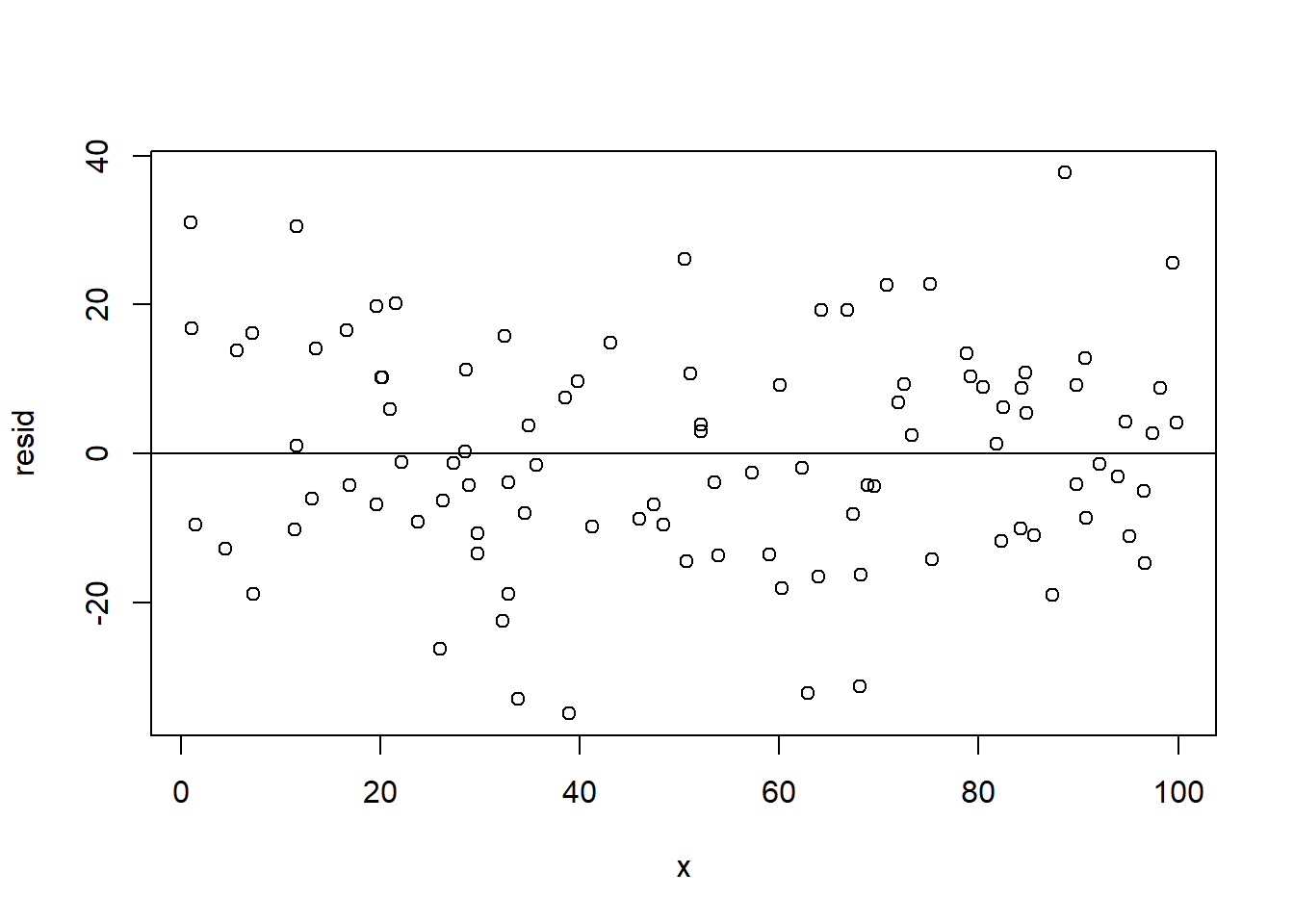
Here the error on one point doesn’t really tell you anything about its neighbors.
How do we deal with time-based autocorrelation? Run! It’s very hard to deal with and is the focus of full courses. For right now it’s enough to know that this sort of pattern runs counter to the assumption of OLS.
The other situation that breaks the assumptions of OLS is when your data comes from clusters.
Using the ACS data, let’s look at the relationship between the percent of people with a college degree and median income, but only for counties in either NY and MS. (These states chosen to be the most different possible.)
Here is the relationship at the baseline:
head(acs)
#> V1 county.fips county.name state.full state.abbr
#> 1 1 1055 Etowah County Alabama AL
#> 2 2 1133 Winston County Alabama AL
#> 3 3 1053 Escambia County Alabama AL
#> 4 4 1001 Autauga County Alabama AL
#> 5 5 1003 Baldwin County Alabama AL
#> 6 6 1005 Barbour County Alabama AL
#> state.alpha state.icpsr census.region population
#> 1 1 41 south 102939
#> 2 1 41 south 23875
#> 3 1 41 south 37328
#> 4 1 41 south 55200
#> 5 1 41 south 208107
#> 6 1 41 south 25782
#> population.density percent.senior percent.white
#> 1 192.30800 18.33804 80.34856
#> 2 38.94912 21.05550 96.33927
#> 3 39.49123 17.34891 61.87045
#> 4 92.85992 14.58333 76.87862
#> 5 130.90190 19.54043 86.26620
#> 6 29.13214 17.97378 47.38189
#> percent.black percent.asian percent.amerindian
#> 1 15.7491330 0.7179009 0.7295583
#> 2 0.3769634 0.1298429 0.3895288
#> 3 31.9331333 0.3616588 3.8496571
#> 4 19.1394928 1.0289855 0.2880435
#> 5 9.4970376 0.8072770 0.7313545
#> 6 47.5758281 0.3723528 0.2792646
#> percent.less.hs percent.college unemployment.rate
#> 1 15.483020 17.73318 6.499382
#> 2 21.851723 13.53585 7.597536
#> 3 18.455613 12.65935 13.461675
#> 4 11.311414 27.68929 4.228036
#> 5 9.735422 31.34588 4.444240
#> 6 26.968580 12.21592 9.524798
#> median.income gini median.rent percent.child.poverty
#> 1 44023 0.4483 669 30.00183
#> 2 38504 0.4517 525 23.91744
#> 3 35000 0.4823 587 33.89582
#> 4 58786 0.4602 966 22.71976
#> 5 55962 0.4609 958 13.38019
#> 6 34186 0.4731 590 47.59704
#> percent.adult.poverty percent.car.commute
#> 1 15.42045 94.28592
#> 2 15.83042 94.63996
#> 3 23.50816 98.54988
#> 4 14.03953 95.15310
#> 5 10.37312 91.71079
#> 6 25.40757 94.22581
#> percent.transit.commute percent.bicycle.commute
#> 1 0.20813669 0.08470679
#> 2 0.38203288 0.00000000
#> 3 0.00000000 0.06667222
#> 4 0.10643524 0.05731128
#> 5 0.08969591 0.05797419
#> 6 0.25767159 0.00000000
#> percent.walk.commute average.commute.time
#> 1 0.8373872 24
#> 2 0.3473026 29
#> 3 0.4250354 23
#> 4 0.6263304 26
#> 5 0.6956902 27
#> 6 2.1316468 23
#> percent.no.insurance density midwest northeast south west
#> 1 10.357590 2 0 0 1 0
#> 2 12.150785 1 0 0 1 0
#> 3 14.308294 1 0 0 1 0
#> 4 7.019928 2 0 0 1 0
#> 5 10.025612 2 0 0 1 0
#> 6 9.921651 1 0 0 1 0
acs.reduc <- acs[acs$state.abbr %in% c("MS","NY"),]
m <- lm(median.income ~ percent.college, data=acs.reduc)
plot(acs.reduc$percent.college, acs.reduc$median.income, pch=16)
abline(m, col="black")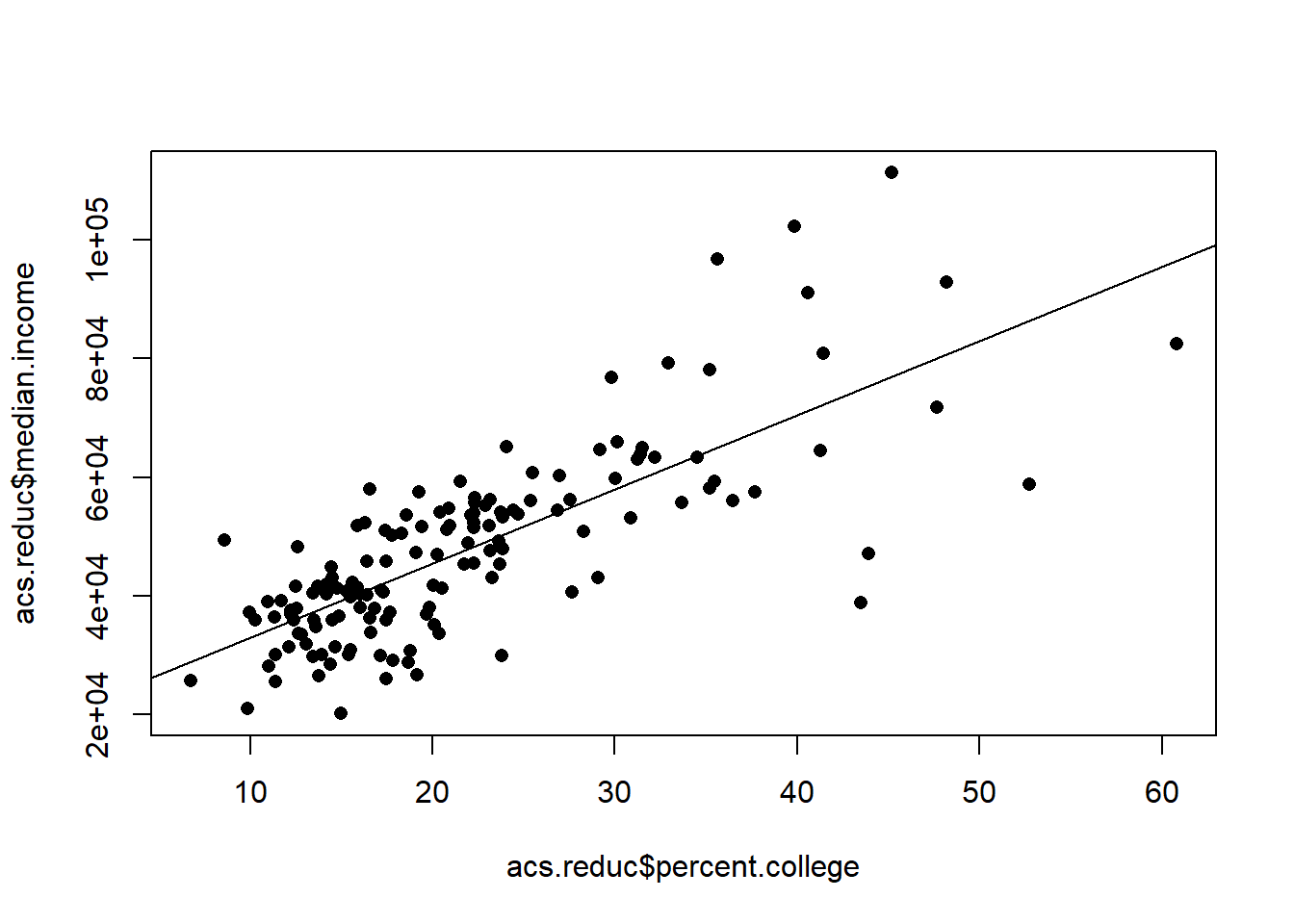
It looks pretty reasonable, but let’s reveal which points belong to what states.
plot(acs.reduc$percent.college[acs.reduc$state.abbr=="MS"], acs.reduc$median.income[acs.reduc$state.abbr=="MS"], col="firebrick", pch=16)
points(acs.reduc$percent.college[acs.reduc$state.abbr=="NY"], acs.reduc$median.income[acs.reduc$state.abbr=="NY"], col="darkblue", pch=16)
abline(m, col="black")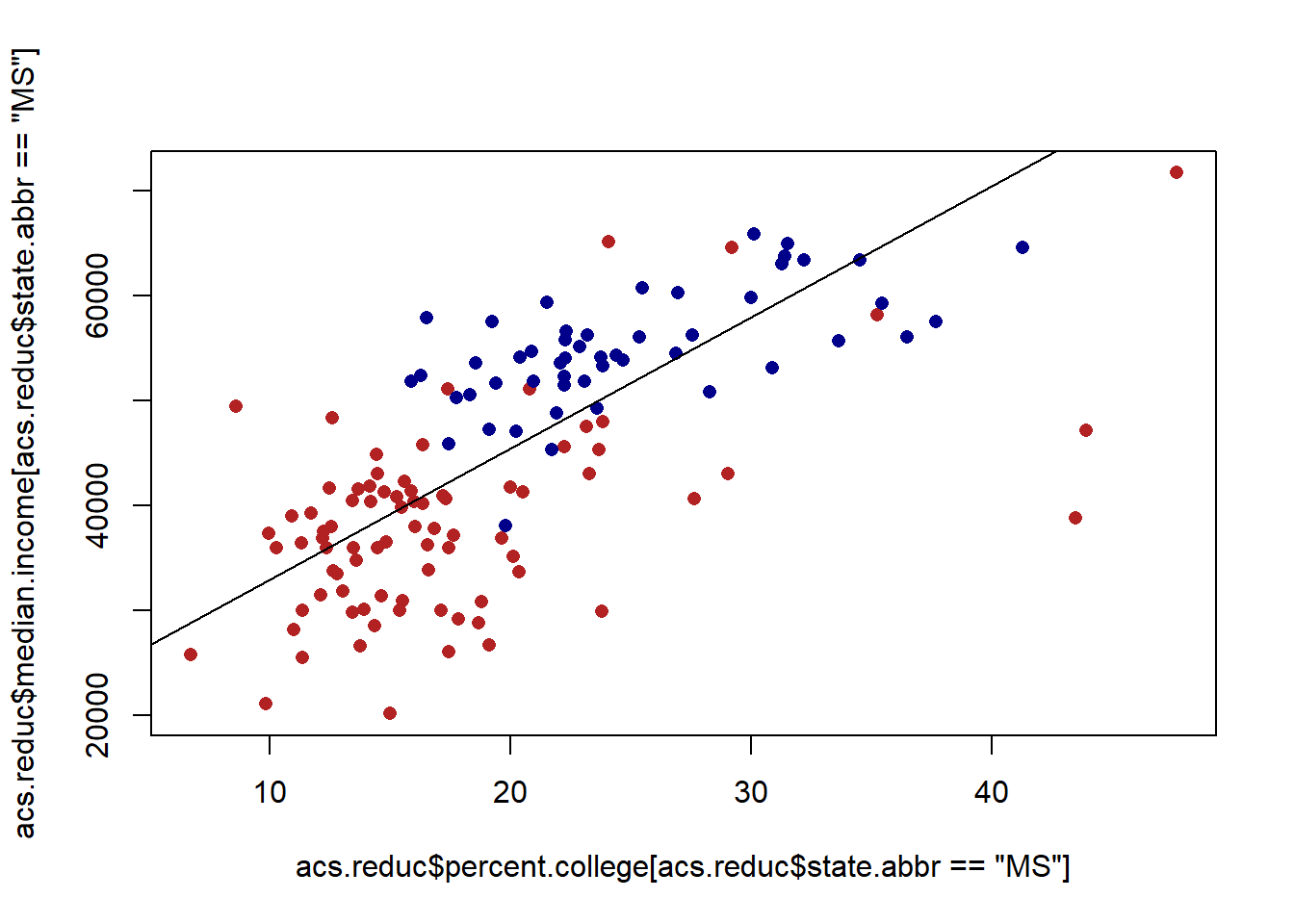
When we reveal that we start to see the problem of auto-correlation. The points for Mississippi are, on average, below the line. The points for New York are, on average, above the line. This means that for points within those clusters the errors are correlated.
Again, we can see this in a residual plot:
acs.reduc$resid <- residuals(m)
plot(acs.reduc$percent.college[acs.reduc$state.abbr=="MS"], acs.reduc$resid[acs.reduc$state.abbr=="MS"], col="firebrick", pch=16)
points(acs.reduc$percent.college[acs.reduc$state.abbr=="NY"], acs.reduc$resid[acs.reduc$state.abbr=="NY"], col="darkblue", pch=16)
abline(h=0)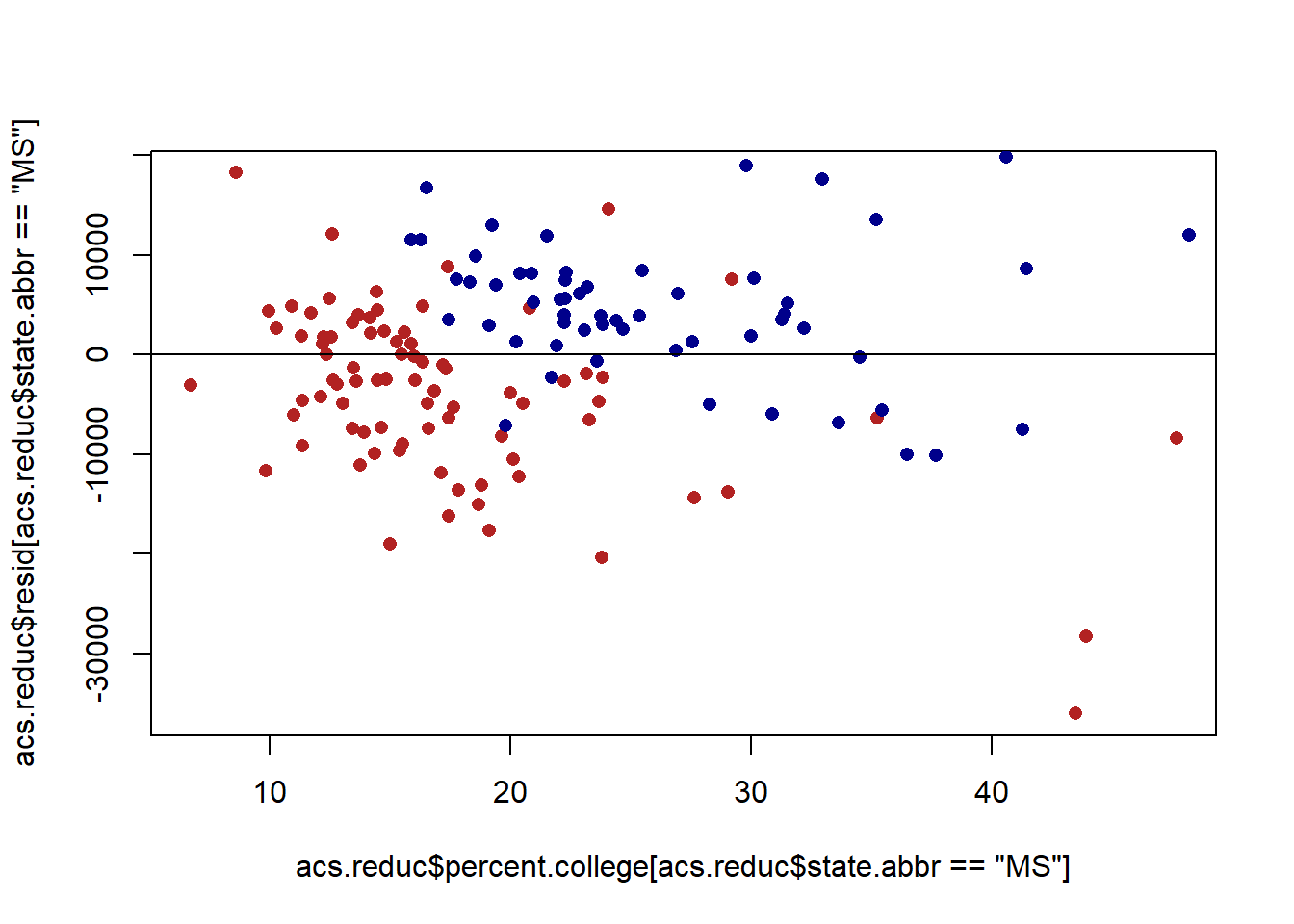
How do we fix this problem?
The first, and, simplest method is to simply use a method of calculating standard errors that takes into account the clustered structure of your data.
Above, we used the sandwhich package to generate heteroskedastic-robust standard errors. We can use the same package to generate clustered standard errors. In the vcovCL() function we can specify what variable our data are clustered on. Here it is state, so I’ve put that variable into the command. I’ve also included type="HC1" into this. This is actually the default so I didn’t have to put it in, but I wanted to point out that cluster standard errors are also heteroskedastic robust as well! A bonus!
m <- lm(median.income ~ percent.college, data=acs.reduc)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.college, data = acs.reduc)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -36050 -6140 1073 5270 34248
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 20468.08 2133.36 9.594 <2e-16 ***
#> percent.college 1250.74 89.04 14.047 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 10380 on 142 degrees of freedom
#> Multiple R-squared: 0.5815, Adjusted R-squared: 0.5786
#> F-statistic: 197.3 on 1 and 142 DF, p-value: < 2.2e-16
library(sandwich)
cluster.vcov <- vcovCL(m, cluster= ~ state.abbr, type="HC1")
cluster.vcov2 <- vcovCL(m, cluster= ~ state.abbr)
#Compare to original var-covar matrix
vcov(m)
#> (Intercept) percent.college
#> (Intercept) 4551246.2 -173642.147
#> percent.college -173642.1 7927.854
#New hypothesis test
coeftest(m, vcov = cluster.vcov )
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 20468.08 1048.71 19.517 < 2.2e-16 ***
#> percent.college 1250.74 154.34 8.104 2.223e-13 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#You can also put the new variance covariance matrix into stargazer:
#Extract standard errors from new vcov matrix:
cluster.se <- sqrt(diag(cluster.vcov))
#(I just have to copy and paster that list(NULL) part of it as I always forget how to do it.)
stargazer(m, type="text", se=list(NULL,cluster.se))
#>
#> ===============================================
#> Dependent variable:
#> ---------------------------
#> median.income
#> -----------------------------------------------
#> percent.college 1,250.737***
#> (89.038)
#>
#> Constant 20,468.080***
#> (2,133.365)
#>
#> -----------------------------------------------
#> Observations 144
#> R2 0.582
#> Adjusted R2 0.579
#> Residual Std. Error 10,378.420 (df = 142)
#> F Statistic 197.322*** (df = 1; 142)
#> ===============================================
#> Note: *p<0.1; **p<0.05; ***p<0.01While “fixing the standard errors” works in this situation, a more blatant problem here is that this simply isn’t a great model for what we are seeing in the data. To properly understand the relationship between schooling and income there are clearly a large numebr of confounding factors that can make counties in New York have both a large percentage of people with a college degree and a high median income.
A more fair comparison might simply be to look at the relationship within the two states.
We’ve already seen how to do this! We can use an indicator variable to set a different intercept for NY. (Here we just need the one because counties are either in NY or MS).
acs.reduc$ny <- acs.reduc$state.abbr=="NY"
m2<- lm(median.income ~ percent.college + ny, data=acs.reduc)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.college + ny, data = acs.reduc)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -24236 -5145 -412 3957 35078
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 22573.20 1863.06 12.116 < 2e-16 ***
#> percent.college 906.70 90.86 9.979 < 2e-16 ***
#> nyTRUE 12612.24 1782.45 7.076 6.39e-11 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8947 on 141 degrees of freedom
#> Multiple R-squared: 0.6912, Adjusted R-squared: 0.6868
#> F-statistic: 157.8 on 2 and 141 DF, p-value: < 2.2e-16The coefficient on nyTRUE indicates that the average median income in NY is around $12000 higher than in MS, holding constant the effect of education. If we use these numbers to graph this out:
plot(acs.reduc$percent.college[acs.reduc$state.abbr=="MS"], acs.reduc$median.income[acs.reduc$state.abbr=="MS"], col="firebrick", pch=16)
abline(a=coef(m2)["(Intercept)"], b=coef(m2)["percent.college"], col="firebrick")
points(acs.reduc$percent.college[acs.reduc$state.abbr=="NY"], acs.reduc$median.income[acs.reduc$state.abbr=="NY"], col="darkblue", pch=16)
abline(a=coef(m2)["(Intercept)"] + coef(m2)["nyTRUE"], b=coef(m2)["percent.college"], col="darkblue")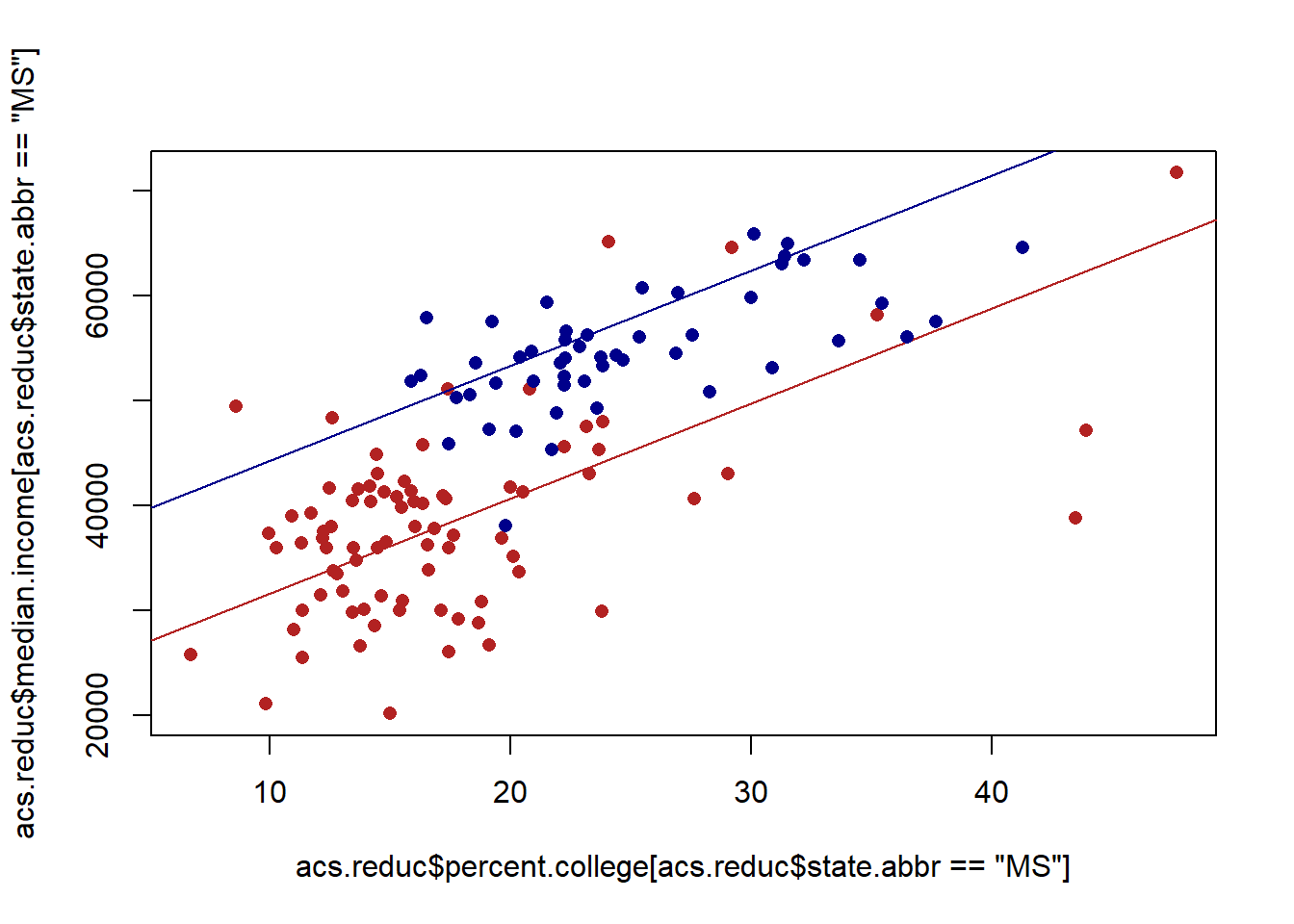
Let’s look at a residual plot of this graph:
acs.reduc$resid <- residuals(m2)
plot(acs.reduc$percent.college[acs.reduc$state.abbr=="MS"], acs.reduc$resid[acs.reduc$state.abbr=="MS"], col="firebrick", pch=16)
points(acs.reduc$percent.college[acs.reduc$state.abbr=="NY"], acs.reduc$resid[acs.reduc$state.abbr=="NY"], col="darkblue", pch=16)
abline(h=0)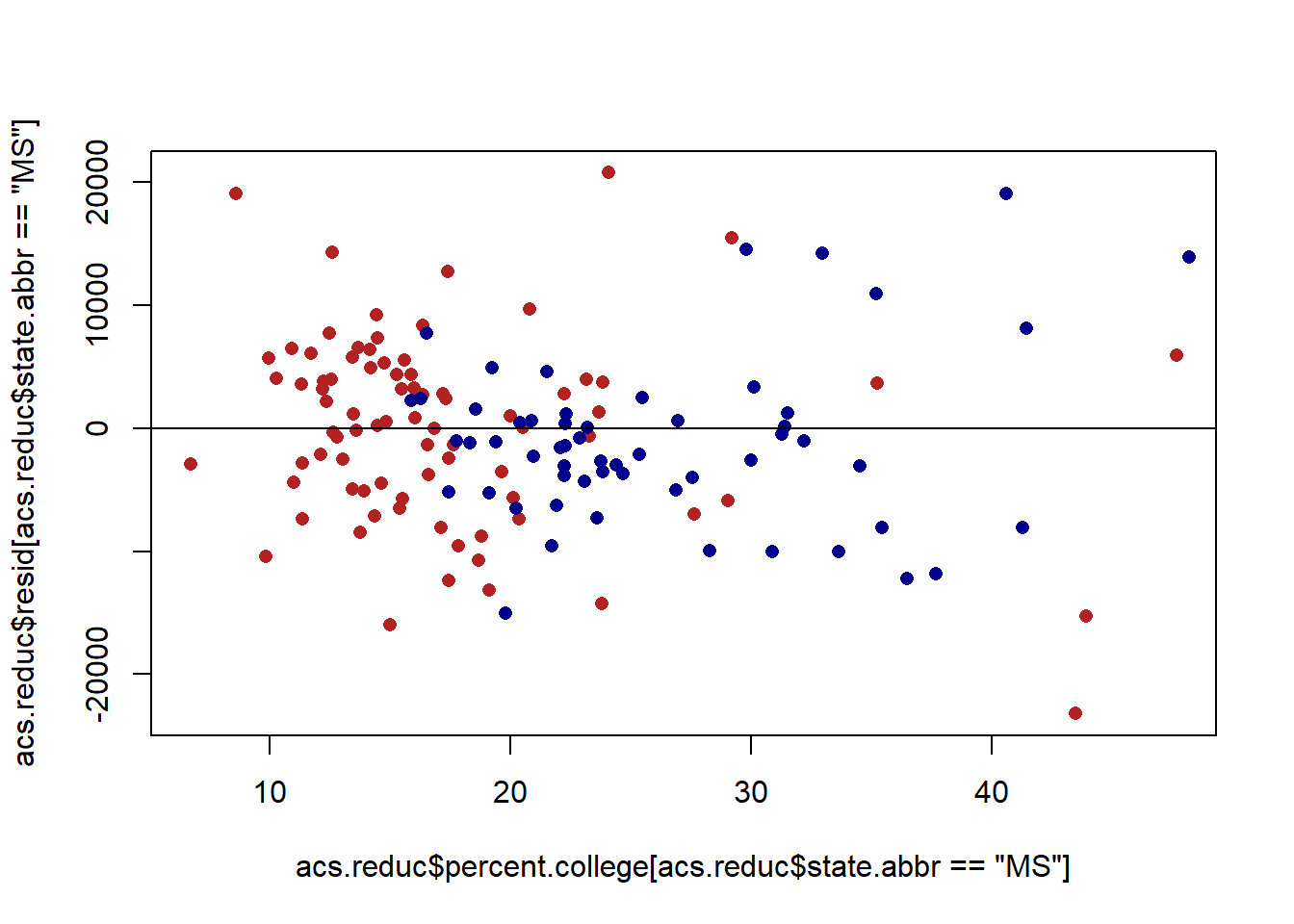
The residuals are now much more random! So an additional way of dealing with this auto-correlation is to model the data in a way that takes away that problem. There will be one caveat to this below, however.
We could imagine applying this same logic to this relationship to the entire dataset:
plot(acs$percent.college, acs$median.income, col="black", pch=16)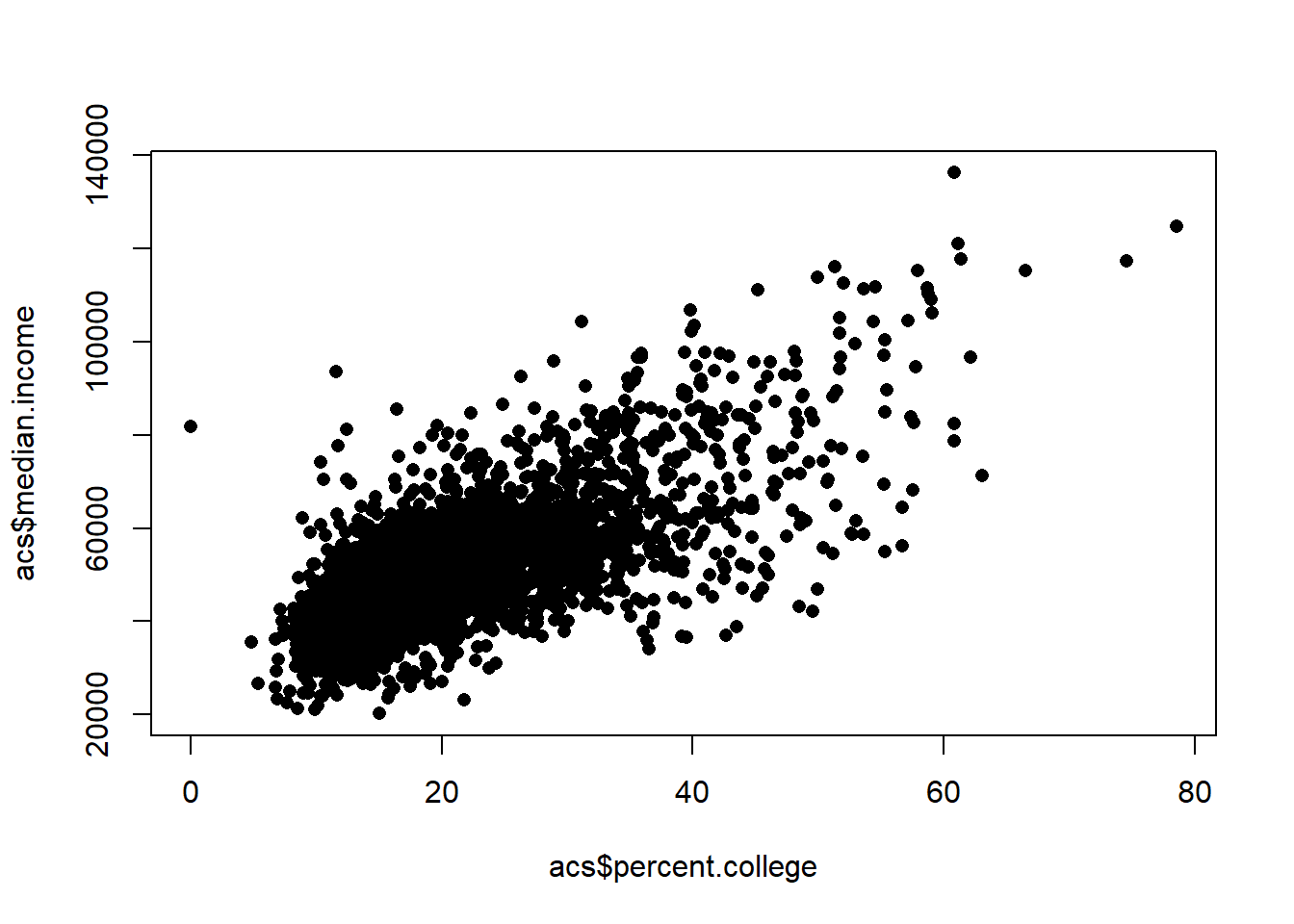
We might think the same problem exists in all the data. These are not a “random sample” but are actually observations from states, and there are unobserved things that will make the errors in CA correlate, and the erros in CT correlate, and the errors in DE correlate etc….
So in this case we may want to do something similar and fix our standard errors to account for this:
#Standard OLS
m <- lm(median.income ~ percent.college, data=acs)
summary(m)
#>
#> Call:
#> lm(formula = median.income ~ percent.college, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -37849 -6044 -623 5696 52223
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 29651.55 435.98 68.01 <2e-16 ***
#> percent.college 1016.55 18.52 54.90 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 9789 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.4899, Adjusted R-squared: 0.4897
#> F-statistic: 3014 on 1 and 3139 DF, p-value: < 2.2e-16
#Cluster standard errors
cluster.vcov <- vcovCL(m, cluster = ~ state.abbr)
coeftest(m, cluster.vcov)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 29651.551 1337.982 22.161 < 2.2e-16 ***
#> percent.college 1016.547 55.331 18.372 < 2.2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Or we could take the more extreme step and only look at the variation within states by including an indicators for each state. We can do that manually using a factor variable, but it’s going to be super unwieldy:
acs$state <- as.factor(acs$state.abbr)
m2 <- lm(median.income ~ percent.college + state, data=acs)
summary(m2)
#>
#> Call:
#> lm(formula = median.income ~ percent.college + state, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -35915 -4858 -449 4544 47495
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 46755.66 1655.59 28.241 < 2e-16 ***
#> percent.college 912.97 18.32 49.824 < 2e-16 ***
#> stateAL -21096.75 1918.67 -10.996 < 2e-16 ***
#> stateAR -20750.19 1889.23 -10.983 < 2e-16 ***
#> stateAZ -17529.52 2742.22 -6.392 1.88e-10 ***
#> stateCA -6873.33 1961.78 -3.504 0.000466 ***
#> stateCO -19116.50 1935.97 -9.874 < 2e-16 ***
#> stateCT -3381.02 3451.98 -0.979 0.327437
#> stateDC -16710.50 8790.68 -1.901 0.057404 .
#> stateDE -9369.81 5229.17 -1.792 0.073257 .
#> stateFL -17783.53 1916.27 -9.280 < 2e-16 ***
#> stateGA -18150.37 1742.94 -10.414 < 2e-16 ***
#> stateHI -1214.25 4175.73 -0.291 0.771234
#> stateIA -11435.15 1820.37 -6.282 3.82e-10 ***
#> stateID -17750.20 2062.17 -8.608 < 2e-16 ***
#> stateIL -11181.58 1814.49 -6.162 8.09e-10 ***
#> stateIN -10598.85 1837.02 -5.770 8.73e-09 ***
#> stateKS -16431.21 1808.40 -9.086 < 2e-16 ***
#> stateKY -18396.02 1788.30 -10.287 < 2e-16 ***
#> stateLA -18904.43 1932.92 -9.780 < 2e-16 ***
#> stateMA -9705.59 2824.94 -3.436 0.000599 ***
#> stateMD -1083.99 2384.50 -0.455 0.649429
#> stateME -20002.21 2685.66 -7.448 1.22e-13 ***
#> stateMI -16938.75 1859.65 -9.109 < 2e-16 ***
#> stateMN -8668.97 1848.46 -4.690 2.85e-06 ***
#> stateMO -17424.47 1793.33 -9.716 < 2e-16 ***
#> stateMS -24291.55 1865.37 -13.022 < 2e-16 ***
#> stateMT -19839.68 1972.35 -10.059 < 2e-16 ***
#> stateNC -20201.99 1818.31 -11.110 < 2e-16 ***
#> stateND -6023.26 1991.17 -3.025 0.002507 **
#> stateNE -13895.60 1833.55 -7.579 4.59e-14 ***
#> stateNH -9737.95 3166.90 -3.075 0.002124 **
#> stateNJ -307.58 2482.49 -0.124 0.901404
#> stateNM -23962.35 2210.37 -10.841 < 2e-16 ***
#> stateNV -3712.33 2634.60 -1.409 0.158915
#> stateNY -11745.19 1941.38 -6.050 1.62e-09 ***
#> stateOH -11413.25 1846.57 -6.181 7.21e-10 ***
#> stateOK -16927.43 1879.44 -9.007 < 2e-16 ***
#> stateOR -17363.56 2151.04 -8.072 9.79e-16 ***
#> statePA -12768.99 1916.17 -6.664 3.15e-11 ***
#> stateRI -11403.91 4185.96 -2.724 0.006480 **
#> stateSC -21428.18 2044.63 -10.480 < 2e-16 ***
#> stateSD -15480.07 1920.55 -8.060 1.08e-15 ***
#> stateTN -17363.67 1832.16 -9.477 < 2e-16 ***
#> stateTX -12375.51 1691.58 -7.316 3.24e-13 ***
#> stateUT -9294.74 2264.41 -4.105 4.15e-05 ***
#> stateVA -12398.06 1767.81 -7.013 2.85e-12 ***
#> stateVT -19288.06 2811.61 -6.860 8.28e-12 ***
#> stateWA -13907.04 2114.63 -6.577 5.63e-11 ***
#> stateWI -11671.03 1895.96 -6.156 8.44e-10 ***
#> stateWV -18803.79 1982.07 -9.487 < 2e-16 ***
#> stateWY -10009.15 2407.35 -4.158 3.30e-05 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8621 on 3089 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.6107, Adjusted R-squared: 0.6043
#> F-statistic: 95.01 on 51 and 3089 DF, p-value: < 2.2e-16Super hard to read!
Instead, we can recognize this as a broader “type” of regression; one where the data are clusters and we want to estimate our relationships within those clusters. To do so we use a “fixed effects” regression. A fixed effects regression is simply a regression where we include indicator variables for each of the clusters, less one. There are functions that will do this in a more straightforward way for us, however. There are actually a few packages that do this but I like felm() (“fixed-effects linear model”) from the lfe package
#install.packages("lfe")
library(lfe)
#> Loading required package: Matrix
#> Warning: package 'Matrix' was built under R version 4.1.3
#>
#> Attaching package: 'lfe'
#> The following object is masked from 'package:lmtest':
#>
#> waldtest
m.fe <- felm(median.income ~ percent.college | state.abbr, data=acs)
summary(m.fe)
#>
#> Call:
#> felm(formula = median.income ~ percent.college | state.abbr, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -35915 -4858 -449 4544 47495
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> percent.college 912.97 18.32 49.82 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8621 on 3089 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared(full model): 0.6107 Adjusted R-squared: 0.6043
#> Multiple R-squared(proj model): 0.4456 Adjusted R-squared: 0.4364
#> F-statistic(full model):95.01 on 51 and 3089 DF, p-value: < 2.2e-16
#> F-statistic(proj model): 2482 on 1 and 3089 DF, p-value: < 2.2e-16We can see this gives us exactly the same answer as the regression above, we just are supressing all of the dummy variables. We can see all them if we do:
getfe(m.fe)
#> effect obs comp fe idx
#> state.abbr.AK 46755.66 29 1 state.abbr AK
#> state.abbr.AL 25658.91 67 1 state.abbr AL
#> state.abbr.AR 26005.47 75 1 state.abbr AR
#> state.abbr.AZ 29226.14 15 1 state.abbr AZ
#> state.abbr.CA 39882.33 58 1 state.abbr CA
#> state.abbr.CO 27639.16 64 1 state.abbr CO
#> state.abbr.CT 43374.63 8 1 state.abbr CT
#> state.abbr.DC 30045.16 1 1 state.abbr DC
#> state.abbr.DE 37385.85 3 1 state.abbr DE
#> state.abbr.FL 28972.12 67 1 state.abbr FL
#> state.abbr.GA 28605.29 159 1 state.abbr GA
#> state.abbr.HI 45541.41 5 1 state.abbr HI
#> state.abbr.IA 35320.51 99 1 state.abbr IA
#> state.abbr.ID 29005.46 44 1 state.abbr ID
#> state.abbr.IL 35574.08 102 1 state.abbr IL
#> state.abbr.IN 36156.81 92 1 state.abbr IN
#> state.abbr.KS 30324.44 105 1 state.abbr KS
#> state.abbr.KY 28359.63 120 1 state.abbr KY
#> state.abbr.LA 27851.23 64 1 state.abbr LA
#> state.abbr.MA 37050.07 14 1 state.abbr MA
#> state.abbr.MD 45671.66 24 1 state.abbr MD
#> state.abbr.ME 26753.44 16 1 state.abbr ME
#> state.abbr.MI 29816.90 83 1 state.abbr MI
#> state.abbr.MN 38086.68 87 1 state.abbr MN
#> state.abbr.MO 29331.18 115 1 state.abbr MO
#> state.abbr.MS 22464.10 82 1 state.abbr MS
#> state.abbr.MT 26915.97 56 1 state.abbr MT
#> state.abbr.NC 26553.67 100 1 state.abbr NC
#> state.abbr.ND 40732.40 53 1 state.abbr ND
#> state.abbr.NE 32860.05 93 1 state.abbr NE
#> state.abbr.NH 37017.70 10 1 state.abbr NH
#> state.abbr.NJ 46448.08 21 1 state.abbr NJ
#> state.abbr.NM 22793.31 32 1 state.abbr NM
#> state.abbr.NV 43043.32 17 1 state.abbr NV
#> state.abbr.NY 35010.46 62 1 state.abbr NY
#> state.abbr.OH 35342.41 88 1 state.abbr OH
#> state.abbr.OK 29828.23 77 1 state.abbr OK
#> state.abbr.OR 29392.09 36 1 state.abbr OR
#> state.abbr.PA 33986.67 67 1 state.abbr PA
#> state.abbr.RI 35351.75 5 1 state.abbr RI
#> state.abbr.SC 25327.48 46 1 state.abbr SC
#> state.abbr.SD 31275.59 66 1 state.abbr SD
#> state.abbr.TN 29391.99 95 1 state.abbr TN
#> state.abbr.TX 34380.15 254 1 state.abbr TX
#> state.abbr.UT 37460.91 29 1 state.abbr UT
#> state.abbr.VA 34357.59 133 1 state.abbr VA
#> state.abbr.VT 27467.59 14 1 state.abbr VT
#> state.abbr.WA 32848.61 39 1 state.abbr WA
#> state.abbr.WI 35084.62 72 1 state.abbr WI
#> state.abbr.WV 27951.87 55 1 state.abbr WV
#> state.abbr.WY 36746.51 23 1 state.abbr WYThe only complication to the idea of “hey, let’s just model the clusters and then the errors will be uncorrelated” is that best practices is to still use clustered standard errors in a fixed effect model. Why this is the case is actually beyond my stats ability, I just know that is best practice. The felm command actually makes this super simple, however. The command works as felm(model | fixed effect variable | instrumental variable| cluster variable, data). We won’t be using instrumental variables here, so we can just enter that as 0:
m.fe.cl <- felm(median.income ~ percent.college | state.abbr | 0 | state.abbr, data=acs)
summary(m.fe.cl)
#>
#> Call:
#> felm(formula = median.income ~ percent.college | state.abbr | 0 | state.abbr, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -35915 -4858 -449 4544 47495
#>
#> Coefficients:
#> Estimate Cluster s.e. t value Pr(>|t|)
#> percent.college 912.97 47.85 19.08 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8621 on 3089 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared(full model): 0.6107 Adjusted R-squared: 0.6043
#> Multiple R-squared(proj model): 0.4456 Adjusted R-squared: 0.4364
#> F-statistic(full model, *iid*):95.01 on 51 and 3089 DF, p-value: < 2.2e-16
#> F-statistic(proj model): 364 on 1 and 50 DF, p-value: < 2.2e-16
#Much higher standard error!13.3.5 GM 2 Correct Functional Form
Assumption 2 is the “functional form” assumption, which says that your data was generated by the model that you have specified. The two violations of this are generally: non-linear relationships and interactions.
Let me give an example:
library(AER)
data("CASchools")
head(CASchools)
#> district school county grades
#> 1 75119 Sunol Glen Unified Alameda KK-08
#> 2 61499 Manzanita Elementary Butte KK-08
#> 3 61549 Thermalito Union Elementary Butte KK-08
#> 4 61457 Golden Feather Union Elementary Butte KK-08
#> 5 61523 Palermo Union Elementary Butte KK-08
#> 6 62042 Burrel Union Elementary Fresno KK-08
#> students teachers calworks lunch computer expenditure
#> 1 195 10.90 0.5102 2.0408 67 6384.911
#> 2 240 11.15 15.4167 47.9167 101 5099.381
#> 3 1550 82.90 55.0323 76.3226 169 5501.955
#> 4 243 14.00 36.4754 77.0492 85 7101.831
#> 5 1335 71.50 33.1086 78.4270 171 5235.988
#> 6 137 6.40 12.3188 86.9565 25 5580.147
#> income english read math
#> 1 22.690001 0.000000 691.6 690.0
#> 2 9.824000 4.583333 660.5 661.9
#> 3 8.978000 30.000002 636.3 650.9
#> 4 8.978000 0.000000 651.9 643.5
#> 5 9.080333 13.857677 641.8 639.9
#> 6 10.415000 12.408759 605.7 605.4
#Creating Variables
CASchools$STR <- CASchools$students/CASchools$teachers
summary(CASchools$STR)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 14.00 18.58 19.72 19.64 20.87 25.80
CASchools$score <- (CASchools$read + CASchools$math)/2
summary(CASchools$score)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 605.5 640.0 654.5 654.2 666.7 706.8
#Changing names
dat <- CASchools
library(ggplot2)
p <- ggplot(dat, aes(x=income, y=score)) + geom_point() +
labs(x="Avereage Household Income", y = "School Test Scores") +
geom_smooth(method = lm, formula = y ~ poly(x, 1), se = FALSE)
p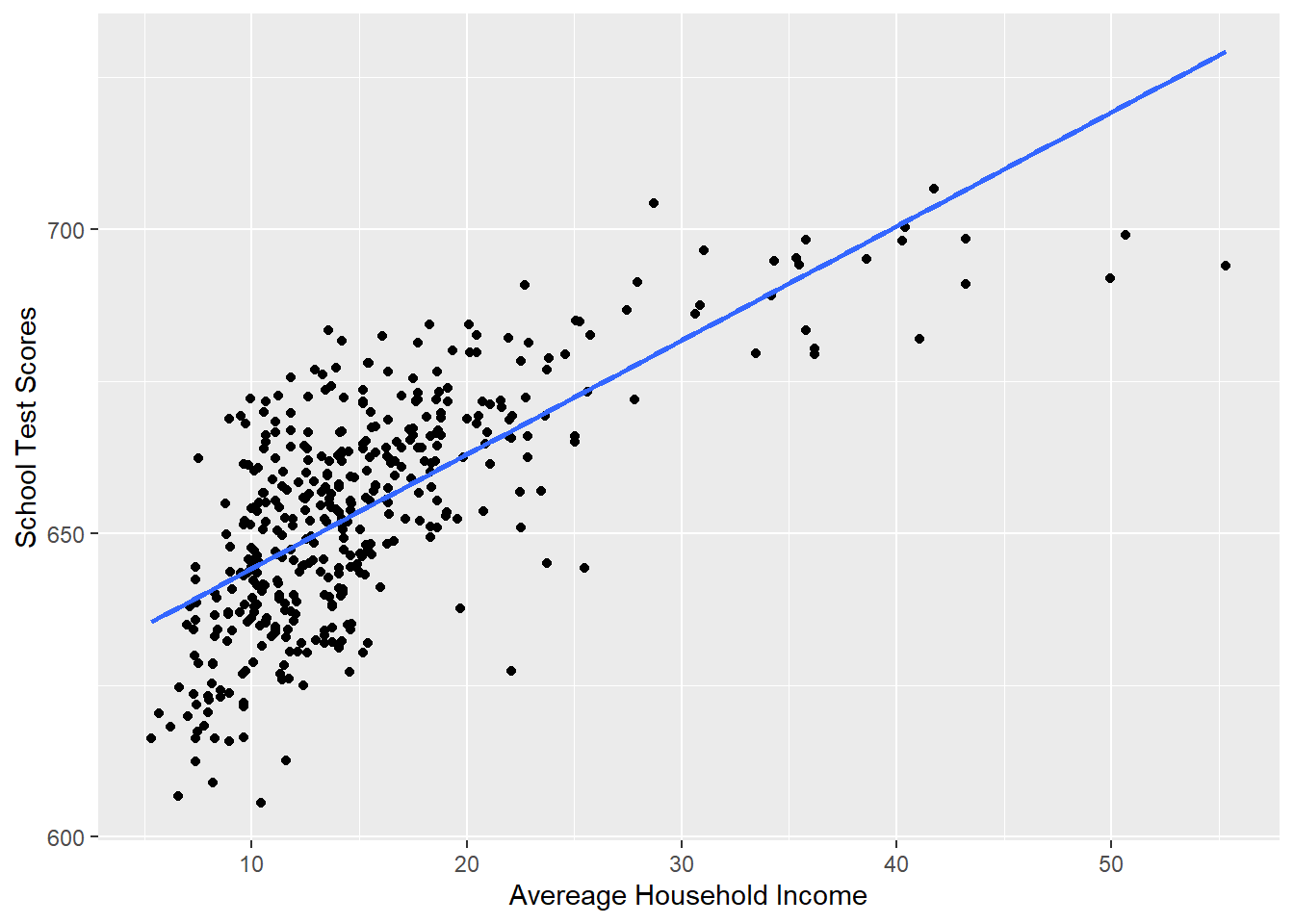
summary(lm(score ~ income, data=dat))
#>
#> Call:
#> lm(formula = score ~ income, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -39.574 -8.803 0.603 9.032 32.530
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 625.3836 1.5324 408.11 <2e-16 ***
#> income 1.8785 0.0905 20.76 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13.39 on 418 degrees of freedom
#> Multiple R-squared: 0.5076, Adjusted R-squared: 0.5064
#> F-statistic: 430.8 on 1 and 418 DF, p-value: < 2.2e-16Just looking at this visually, does this line well represent this relationship? Not really, no.
If I was to describe this relationship, I would say that test scores improve a lot when household income goes from 5 to 25, and then the effect levels off
The way we deal with this is adding polynomial terms to our regression. The easy way to think about polynomials is: it let’s the line curve.
A slightly better way to think about it is: we want to the relationship between income and test scores to change across the levels of income. When income is low the relationship is more steep, when income is high the relationship is more shallow
To do this we modify the simple bivariate regression by adding an additional variable income squared:
\[ y = a + bx + e\\ y = a + b_1 x + b_2 x^2 + e \]
To implement this we can use the poly() function:
#YOU MUST USE THE RAW=T OPTION WHEN YOU USE THE POLY FUNCTION
#OR IT WILL NOT WORK
m <- lm(score ~ poly(income, 2, raw=T), data=dat )
summary(m)
#>
#> Call:
#> lm(formula = score ~ poly(income, 2, raw = T), data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -44.416 -9.048 0.440 8.347 31.639
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 607.30174 3.04622 199.362
#> poly(income, 2, raw = T)1 3.85099 0.30426 12.657
#> poly(income, 2, raw = T)2 -0.04231 0.00626 -6.758
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> poly(income, 2, raw = T)1 < 2e-16 ***
#> poly(income, 2, raw = T)2 4.71e-11 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12.72 on 417 degrees of freedom
#> Multiple R-squared: 0.5562, Adjusted R-squared: 0.554
#> F-statistic: 261.3 on 2 and 417 DF, p-value: < 2.2e-16
#This is equivalent to:
dat$income2 <- dat$income^2
m <- lm(score ~ income + income2, data=dat )
summary(m)
#>
#> Call:
#> lm(formula = score ~ income + income2, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -44.416 -9.048 0.440 8.347 31.639
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 607.30174 3.04622 199.362 < 2e-16 ***
#> income 3.85099 0.30426 12.657 < 2e-16 ***
#> income2 -0.04231 0.00626 -6.758 4.71e-11 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 12.72 on 417 degrees of freedom
#> Multiple R-squared: 0.5562, Adjusted R-squared: 0.554
#> F-statistic: 261.3 on 2 and 417 DF, p-value: < 2.2e-16
#Plotting this relationship:
library(ggplot2)
p <- ggplot(dat, aes(x=income, y=score)) + geom_point() +
labs(x="Avereage Household Income", y = "School Test Scores") +
geom_smooth(method = lm, formula = y ~ poly(x, 2), se = FALSE)
p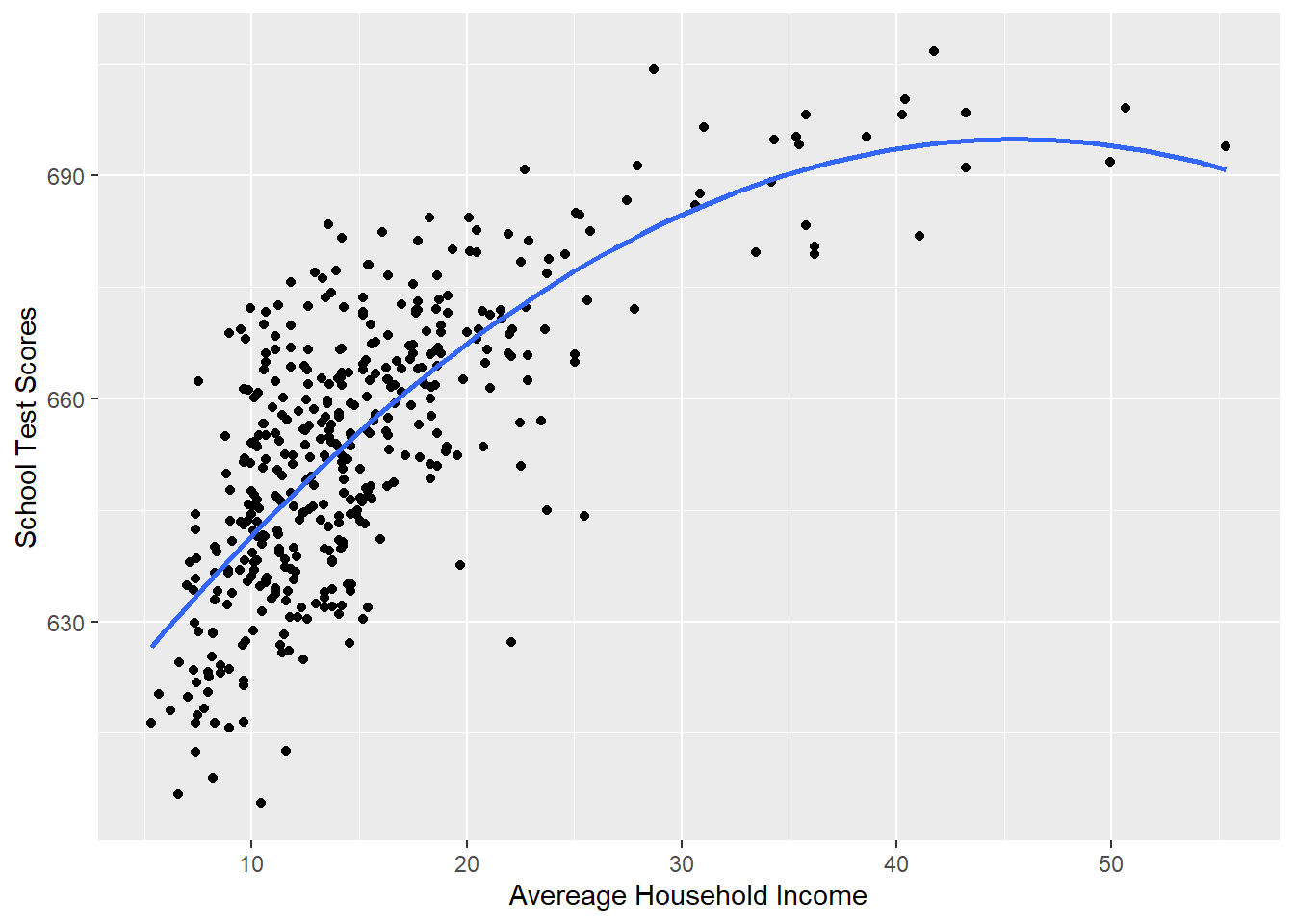
Visually fits much better.
Why does this work, and how can we describe the effect of x on y?
It’s now more complicated because the effect of income depends on what value of income we are talking about. As in, the steepness of the line varies across the level of income.
The tool that we use to calculate the slope of a line is a partial derivative from calculus.
In particular we are going to use the power rule, which states that:
\[ \frac{\partial y}{\partial x}(X^k) =k*X^{k-1} \\ \frac{\partial y}{\partial x}(aX^k) =k*aX^{k-1} \\ \frac{\partial y}{\partial x}(a) =0 \\ \frac{\partial y}{\partial x}(Z) =0 \\ \]
How does this apply to our standard regression equation?
\[ \hat{y} = \hat{\alpha} + \hat{\beta}*x + \hat{\beta}*Z \\ \frac{\partial y}{\partial x} = 1*\beta*x^0\\ \frac{\partial y}{\partial x} = \beta\\ \]
Which makes a lot of sense!
What is the effect of x when we add a polynomial term?
\[ \hat{y} = \hat{\alpha} + \hat{\beta_1}*x + \hat{\beta_2}*x^2 \\ \frac{\partial y}{\partial x} = \hat{\beta}_1 + 2*\hat{\beta_2}*x \]
So here, if we wanted to know the effect of income when income is at 20
coef(m)
#> (Intercept) income income2
#> 607.30174351 3.85099392 -0.04230845
coef(m)[2] + 2*coef(m)[3]*20
#> income
#> 2.158656
#2.15
#and at 30
coef(m)[2] + 2*coef(m)[3]*30
#> income
#> 1.312487
#and at 50
coef(m)[2] + 2*coef(m)[3]*50
#> income
#> -0.3798508The effect of x changes as x itself increases.
We could continue to add polynomial terms:
#Plotting this relationship:
library(ggplot2)
p <- ggplot(dat, aes(x=income, y=score)) + geom_point() +
labs(x="Avereage Household Income", y = "School Test Scores") +
geom_smooth(method = lm, formula = y ~ poly(x, 4), se = FALSE)
p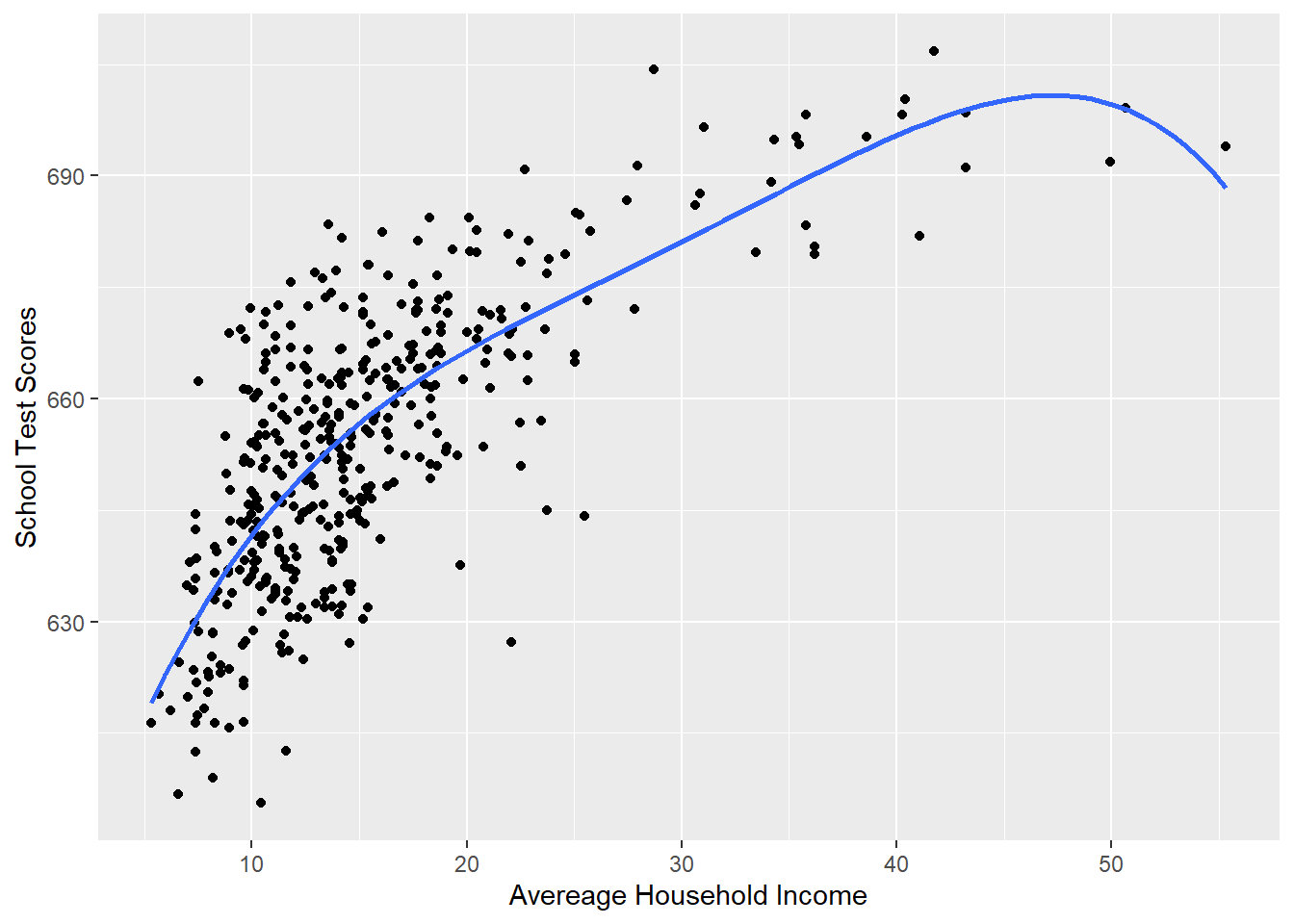
And we could use differentiations to determine the slope of that line:
\[ \hat{y} = \alpha + \beta_1*x + \beta_2*x^2 + \beta_3 * x^3 + \beta_4 *x^4\\ \frac{\partial y}{\partial x} = \beta_1 + 2*\beta_2*x + 3*\beta_3*x^2 + 4*\beta_4*x^3\\ \]
At all these points:
m <- lm(score ~ poly(income, 4, raw=T), data=dat )
coef(m)
#> (Intercept) poly(income, 4, raw = T)1
#> 5.773402e+02 9.876232e+00
#> poly(income, 4, raw = T)2 poly(income, 4, raw = T)3
#> -4.342116e-01 9.791736e-03
#> poly(income, 4, raw = T)4
#> -8.159040e-05
#20
coef(m)[2] + 2*coef(m)[3]*20 + 3*coef(m)[4]*20^2 + 4*coef(m)[5]*20^3
#> poly(income, 4, raw = T)1
#> 1.646959
#and at 30
coef(m)[2] + 2*coef(m)[3]*30 + 3*coef(m)[4]*30^2 + 4*coef(m)[5]*30^3
#> poly(income, 4, raw = T)1
#> 1.44946
#and at 50
coef(m)[2] + 2*coef(m)[3]*50 + 3*coef(m)[4]*50^2 + 4*coef(m)[5]*50^3
#> poly(income, 4, raw = T)1
#> -0.9021091Isn’t this better? Aren’t we getting a more exact fit? The \(r^2\) is almost certainly higher! That’s good, right?
Why might we not like doing this? Let’s remember the overall goal of describing the population-level data generating process. We think this is one of many samples of data. At the extreme we could fly around and capture every single bit of random variation in these data, but we don’t think that this is a good way to summarize what this relationship is in a way that might be generalizable to other samples of data. In the parlance of regression, we have to balance describing a plausible functional form for the data with not over-fitting our regression to this specific dataset. I would say the 4th-order polynomial is absolutely over-fitting.