10 Covariance
Let’s say we work in a psychology lab and we run an experiment where we give some sort of treatment (say, exposing students to some sort of video prime or not), and then measure some sort of outcome \(y\). The data that we get might look something like this:
set.seed(19104)
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
y <- c(y0,y1)
x <- c(rep(0,50), rep(1,50))
dat <- cbind.data.frame(x,y)
head(dat)
#> x y
#> 1 0 17.85445
#> 2 0 25.55715
#> 3 0 29.99189
#> 4 0 28.97014
#> 5 0 22.22095
#> 6 0 10.75801The variable x is what we call the “treatment” variable and indicates if someone received the treatment (1), or not (0). The variable y gives the individuals’ measurement for the outcome variable. We can now think about there being two means that we care about:
table(dat$x)
#>
#> 0 1
#> 50 50
mean(dat$y[x==1])
#> [1] 27.93583
sd(dat$y[x==1])
#> [1] 6.202173
mean(dat$y[x==0])
#> [1] 22.44682
sd(dat$y[x==0])
#> [1] 10.86982We are particularly interested in the difference between these means. In the context of an experiment what we are primarily interested in is whether being exposed to treatment increased or decreased individuals value on the outcome variable. Because, in an experiment, assignment to the treatment variable x is randomly assigned, any difference between the groups on the outcome variable must be due to treatment.
Like everything we’ve talked about so far here, we think that these data are being drawn from some hypothetical population (or in this case, not hypothetical because we generated these data). Everytime we take a new sample of 100 people we will get a different distribution of responses. Once we have our tests, our goal is to determine what is plausible in the population.
In particular, we want to test the following null and alternative hypotheses:
\[ H_o: \bar{X_c} = \bar{X_t}\\ H_a: \bar{X_c} \neq \bar{X_t}\\ \]
But we could also re-arrange these null and alternative hypotheses into the following:
\[ H_o: \bar{X_c} - \bar{X_t} = 0\\ H_a: \bar{X_c} - \bar{X_t} \neq 0 \]
Before when we set the test statistic it was simply a mean. In this case, however, our test statistic is going to be the difference in the two means. This is made clear from the actual hypothesis we are trying to test.
#Test statistic
diff.means <- mean(dat$y[dat$x==1]) - mean(dat$y[dat$x==0])
diff.means
#> [1] 5.489011In this particular sample the difference in means is 5.48.
But just as before, we know that every time we take a sample we are going to get a slightly different difference in means. Our goal is to determine whether it is zero, or not. When we just have one sample, we want to be able to answer the question: if the truth was that the difference in the population is 0, how likely is it to get something more extreme than 5.48? Clearly: we need a sampling distribution. We need to understand the plausible range of values that might occur if we were to sample, again, and again, and again. Is that distribution normally distributed? How wide is it?
In this case we are god and created this sample from a known population. As such, we can literally sample many, many, times to generate a sampling distribution:
diff.means <- rep(NA, 10000)
for(i in 1:10000){
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
diff.means[i] <- mean(y1) - mean(y0)
}
mean(diff.means)
#> [1] 5.007569
sd(diff.means)
#> [1] 2.032258
plot(density(diff.means), main="Sampling Distribution of the Difference in Means")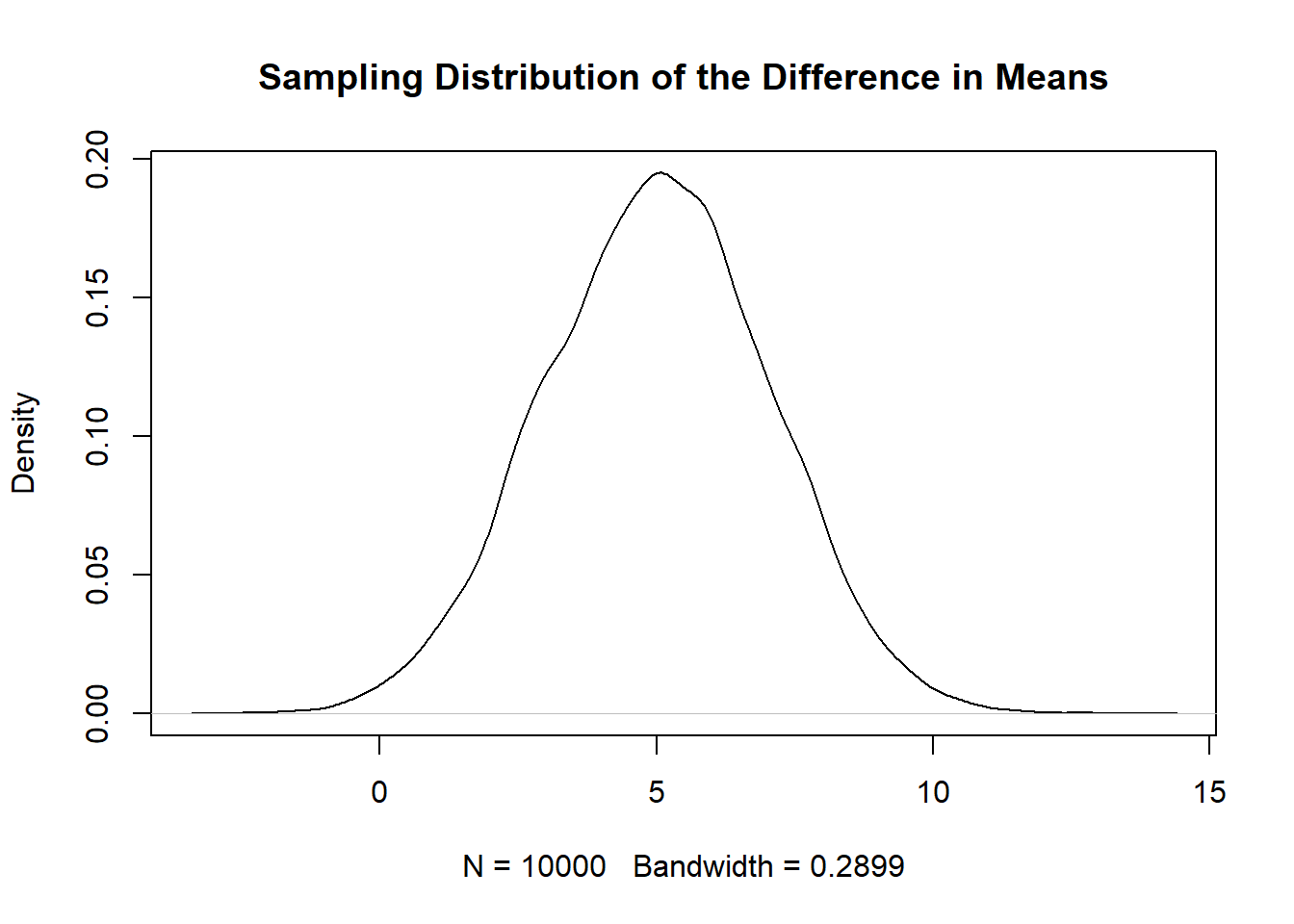
To be clear, this is 10,000 difference in means drawn from the same population from which we drew the first sample. Quite helpfully, this distribution appears to be normally distributed. But just because something is bell shaped and symmetrical doesn’t mean that it is normal. It might have a peak that’s too high or tails that are too thick. But we can check that.
First: What does the standard deviation of these 10,000 means represent?The standard error! The standard deviation of sampling distribution is the standard error.
sd(diff.means)
#> [1] 2.032258Further, we can see that this distribution is centered on 5 (which if we look above is the true difference between the two groups). If we plot a normal distribution with \(\mu=10\) and \(\sigma=2\), is it the same as this simulation?
plot(density(diff.means), main="Sampling Distribution of the Difference in Means")
eval <- seq(0,20,.001)
points(eval, dnorm(eval, mean=5, sd=sd(diff.means)), type="l", col="firebrick")
I feel pretty good in saying that, yes, this sampling distribution is normally distributed with a \(\sigma \approx 2\).
So the difference between two means is normally distributed. If that’s the case, all we need to know is the standard error, and we will be able to perform the exact same hypothesis tests that we have been doing already.
So I won’t leave you in suspense, the standard error of a difference in means is:
\[ se = \sqrt{\frac{\sigma_0^2}{n_0} + \frac{\sigma_1^2}{n_1} } \]
Just as before, the standard error of the difference in means is a function of both the underlying variance in the population and the sample size. The difference here is that we have two population distributions we are sampling from, and two different \(n\), representing group size.
So if we use the fact that we generated these populations we get:
se <- sqrt( (13^2/50) + (6^2/50))
se
#> [1] 2.024846
#Confirmed to be 2ishWith that information in hand we can perform a hypothesis test on our original result of 5.48.
We have already determined the null and alternative hypothesis (above). And our test statistic of 5.48. We will go with an \(\alpha=.05\).
The sampling distribution we believe to be normally distributed with \(\sigma=2.02\).
To calculate the z-score we want to know how many standard error’s our test statistic is from the null hypothesis.
(5.48-0)/2.02
#> [1] 2.712871And then to find the two-sided p-value we can evaluate this under the standard normal distribution:
pnorm(2.71, lower.tail=F)*2
#> [1] 0.006728321The probability of seeing a result this extreme if the truth was that the difference between the means of the two groups was 0 is a bit less than 1%.
Of course, in setting things up this way we have returned to the ridiculousness of using features of the population to determine the probable location of the population.
Similar to what we did with one mean, we can sub in the sample standard deviations for the population level standard deviations and calculate that way. So we can calculate the standard error via:
\[ se = \sqrt{\frac{s_0^2}{n_0} + \frac{s_1^2}{n_1} } \]
and similar to the one sample t-test, the sampling distribution when using the sample variance in place of the population variance is t distributed.
Specifically:
\[ \frac{(\bar{X_1} - \bar{X_0}) - (\mu_1 - \mu_0)}{ \sqrt{\frac{s_0^2}{n_0} + \frac{s_1^2}{n_1} }} \sim t_v \] The distribution of all possible differences in means, subtract the true difference in means, and divide by the standard error, we are left with a t distribution with \(v\) degrees of freedom.
However, for the t distribution we know that we must supply the degrees of freedom. What is the degrees of freedom for a two-sample t-test? It’s terrible!
\[ v= \frac{(\frac{s_0^2}{n_0} + \frac{s_0^2}{n_0})^2 }{ \frac{(\frac{s_0^2}{n_0})^2}{n_0-1} +\frac{(\frac{s_1^2}{n_1})^2}{n_1-1}} \]
num <- ((var(dat$y[dat$x==0])/50) + (var(dat$y[dat$x==1])/50))^2
denom1 <- ((var(dat$y[dat$x==0])/50)^2)/49
denom2 <- ((var(dat$y[dat$x==1])/50)^2)/49
df <- num/(denom1 +denom2)
df
#> [1] 77.84799OK: that gives us the ingredients we need to perform a hypothesis test. Just as above we can determine how many standard errors our test statistic (5.48) is from the null hypothesis:
5.48/se
#> [1] 3.096292And then determine the probability more extreme than that in both directions under the t distribution with \(v\) degrees of freedom:
pt(3.1, df=df, lower.tail=F)*2
#> [1] 0.002693752Very low, less than 1% probability.
So here is where I’m going to give up on doing this math myself and lean on R. R knows all of the equations, and has all the qt tools built in, and so simply using the t.test function is a much more straight-forward way of assessing things for a two-sample t.test.
We briefly saw last week that the t.test function can easily do a one-sample t-test. We can feed it a vector and a null hypothesis and it will do the appropriate test:
t.test(dat$y, mu=25)
#>
#> One Sample t-test
#>
#> data: dat$y
#> t = 0.20737, df = 99, p-value = 0.8361
#> alternative hypothesis: true mean is not equal to 25
#> 95 percent confidence interval:
#> 23.36060 27.02205
#> sample estimates:
#> mean of x
#> 25.19133We can easily adapt this for a two-sample t-test by having one continuous variable, and a second variable which splits that variable into exactly two groups/ This is what we have here:
head(dat)
#> x y
#> 1 0 17.85445
#> 2 0 25.55715
#> 3 0 29.99189
#> 4 0 28.97014
#> 5 0 22.22095
#> 6 0 10.75801
x <- t.test(dat$y ~ dat$x)
x
#>
#> Welch Two Sample t-test
#>
#> data: dat$y by dat$x
#> t = -3.1014, df = 77.848, p-value = 0.002683
#> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
#> 95 percent confidence interval:
#> -9.012638 -1.965384
#> sample estimates:
#> mean in group 0 mean in group 1
#> 22.44682 27.93583Let’s look at what this has given us here. It has reported back what the mean in group 0 and group 1 is. It has listed what the alternative hypothesis is: that the true difference in means between group 0 and group 1 is not equal to 0. Unstated here is that the null hypothesis is that the true difference between the group means is 0.
It skips some steps and tells us the t score, which we know is the difference in means expressed in standard error units.
If we look into what is inside a saved result of a t function:
names(x)
#> [1] "statistic" "parameter" "p.value" "conf.int"
#> [5] "estimate" "null.value" "stderr" "alternative"
#> [9] "method" "data.name"
x$stderr
#> [1] 1.769859We see that the calculated standard error is the same as we calculated ourselves above. The degrees of freedom is also more or less the same then what we calculated using the ugly math above. As all those things are the same, the p-value calculated by this function is also approximately the same.
So that saves some time!
The more important thing here is this: yes it is slightly more complicated to derive the standard error and degrees of freedom for a difference in means test…. but, once we have those things there is nothing different about the hypothesis testing then when we were doing a simple mean.
In other words: for any statistic I calculate, if you give me the standard error and the shape of the sampling distribution (is it the standard normal? Do I need to know the degrees of freedom for a t distribution?) then I can easily calculate a hypothesis test for any null hypothesis.
This also means that the power calculations we were doing last class still apply to a difference in means test.
In this case the true difference in means is 5, and the sampling distribution is approximately normal with a \(\sigma=2.02\).
As such, we can determine the false positive rate visually by showing what the true difference in mean generating distribution is:
eval <- seq(-5,15,.001)
plot(eval, dnorm(eval, mean=5, sd=2.02), type="l", col="firebrick", lwd=2, main="Power Analysis")
legend("topleft", c("True Sampling Distribution","Null Sampling Distribution"), lty=c(1,1), col=c("firebrick","darkblue"))
And then look at where the null hypothesis sampling distribution would be, and which means under that distribution would lead us to (falsely) conclude that we should not reject the null hypothesis of no difference between these means:
eval <- seq(-5,15,.001)
plot(eval, dnorm(eval, mean=5, sd=2.02), type="l", col="firebrick", lwd=2, main="Power Analysis")
points(eval, dnorm(eval, mean=0, sd=2.02), type="l", lwd=2, col="darkblue")
abline(v=1.96*2.02, lty=2, col="darkblue")
abline(v=-1.96*2.02, lty=2, col="darkblue")
legend("topleft", c("True Sampling Distribution","Null Sampling Distribution"), lty=c(1,1), col=c("firebrick","darkblue"))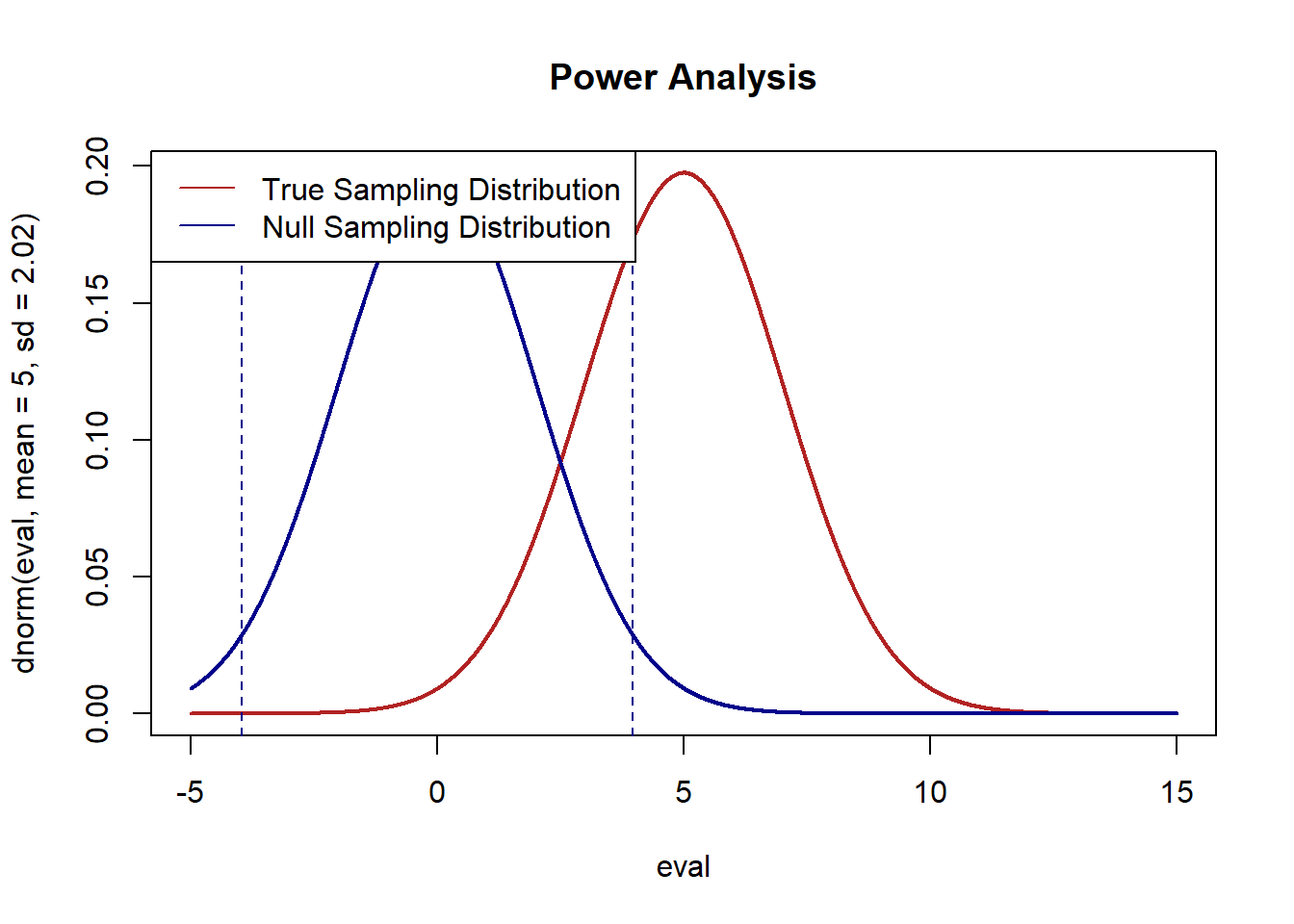
And then determine the area under the red curve that is between the two blue lines:
Approximately 30% false negative rate with this data generating process.
Let’s simulate that to confirm:
false.negative <- rep(NA, 10000)
for(i in 1:10000){
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
y <- c(y0,y1)
x <- c(rep(0,50), rep(1,50))
dat.sim <- cbind.data.frame(x,y)
test <- t.test(dat.sim$y ~ dat.sim$x)
false.negative[i] <- test$p.value>.05
}
mean(false.negative)
#> [1] 0.3205Approximately the same 30% ish false negative rate.
When we think about power in the context of a difference in means test, it really gets to the level of driving research decisions.
Imagine if we were running a psychology lab and we wanted to test to see whether this intervention had an impact on people, and so we recruited 100 undergrads and gave 50 of them the treatment and 50 of them the control. If we had done that and this was the paramaters, there is a 30% likelihood we will get a false negative. Those are terrible odds!
That is why doing a power-analysis before an experiment is so critical. What would we need to know before running an experiment to conduct a power analysis.
We need two pieces of information: a guess at the truth (how far away from 0 will this be?), and a guess at the standard error.
Recall that the standard error for a difference in means is:
\[ se = \sqrt{\frac{\sigma_0^2}{n_0} + \frac{\sigma_1^2}{n_1} } \]
So to calculate that before the fact we have to have group sizes \(n\) and group variances \(\sigma\). The \(n\) is something that we can control but \(\sigma\) is not. That being said: you are usually not the first person to measure anything. If you are doing a study your measure of interest has probably been measured before by someone, and you can use that previous study to determine what the variance of your variable is likely to be. You could also set it as artificially high to give a “worse case scenario”.
Let’s say we look up a previous study that has used our same outcome variable and found that the variance of their measure was 10. We could then make a guess at what our standard error might be:
n <- 50
se <- sqrt( ((10^2)/n) + ((10^2)/n) )In a similar way we could make a guess at the likely difference between the two means from previous studies and see what our statistical power would be. Let’s say it’s 3, then we could calculate:
Terrible statistical power!
Alternatively, we could take what we have right now and say: if we have a sample size of 100 (50 in each group), what is the false positive rate for various true differences between the two means?
true.diff <- seq(0,15,.01)
false.negative <- pnorm(1.96*se, mean=true.diff, sd=se) - pnorm(-1*1.96*se, mean=true.diff, sd=se)
plot(true.diff, false.negative, xlab="True difference between groups", ylab="False negative rate", type="l")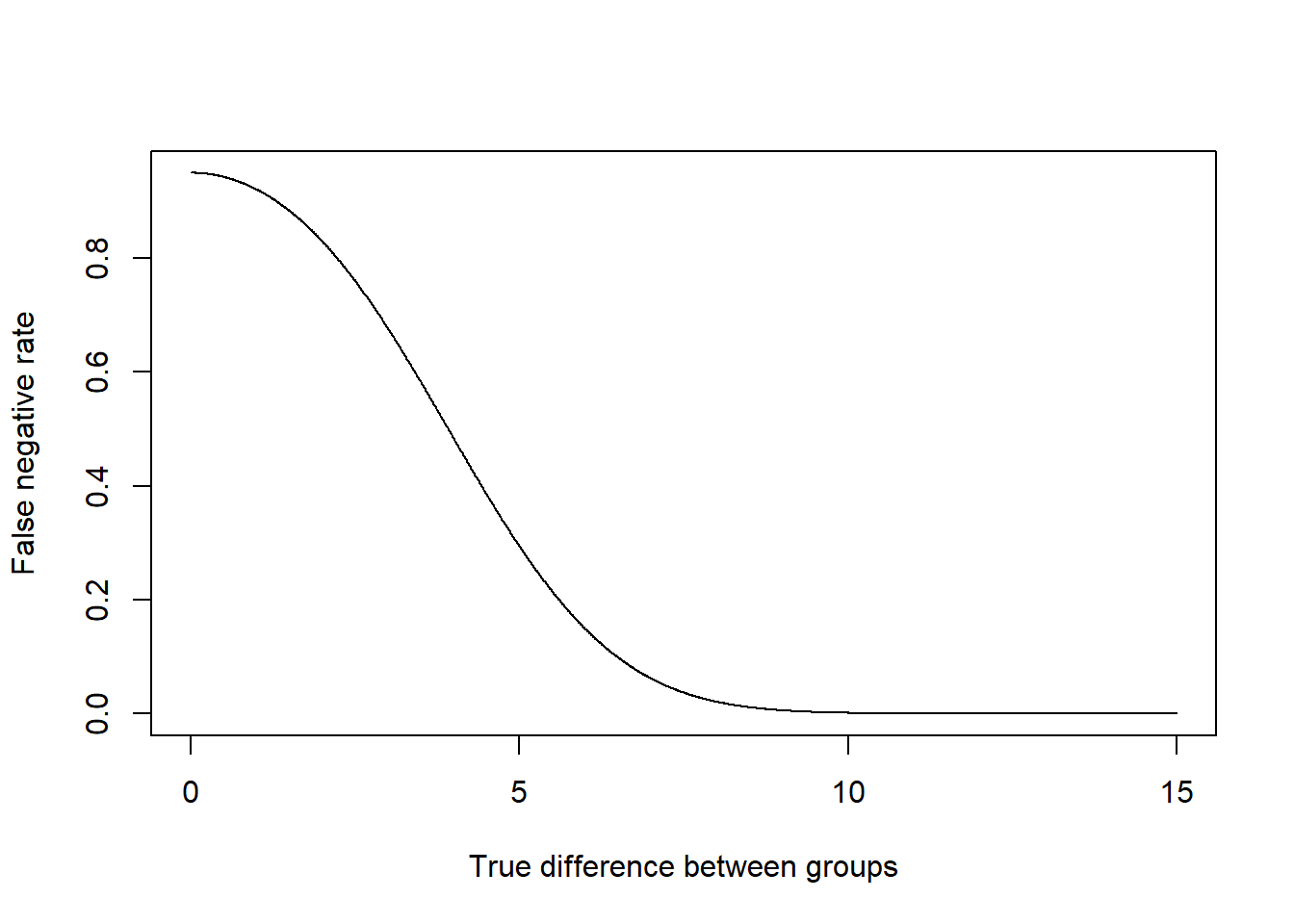
We could also imagine doing the same thing by holding constant a true difference between the groups and seeing what size \(n\) we would need to reliably detect that effect.
Difference in means tests are super powerful and very helpful for analyzing experiments in particular. But it’s pretty clear where there drawbacks are. If we have just one more group we can’t do a difference in means test. More problematically, this method is completely useless if we have two continuous variables and want to see if they are related to one another. That’s where we will need covariance, correlation, and regression.
The last thing we will talk about with difference in means is the relationship between confidence intervals and a difference in means test.
Consider our original data, which had two samples of 50. Thinking of these two samples seperately, let’s put confidence intervals around each of them.
ctrl <- t.test(dat$y[dat$x==0])
treat <- t.test(dat$y[dat$x==1])
plot(ctrl$conf.int, c(0,0), ylim=c(-0.5,1.5), xlim=c(20,35),
type="n", axes=F, xlab="Y",ylab="")
segments(ctrl$conf.int[1], 0,ctrl$conf.int[2],0)
segments(treat$conf.int[1], 1, treat$conf.int[2],1)
axis(side=2, at=c(0,1), labels=c("Control","Treatment"))
axis(side=1)
Looking at these two means separately, we would say that for each of these groups, 95% of similarly constructed confidence intervals will contain the true group mean. If our goal here is to say if treatment is significantly different in the treatment and the control group, at this time do you think that we can rule out that y is actually equal in these two groups?
My inclination here is to say yes. If the confidence intervals are giving us plausible ranges that these means will fall in, and those two plausible ranges do not overlap, then I am fairly confident that we will reject the null hypothesis that they are equal (and we did above).
OK, but what about this:
set.seed(19146)
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
y <- c(y0,y1)
x <- c(rep(0,50), rep(1,50))
dat.sim <- cbind.data.frame(x,y)
ctrl <- t.test(dat.sim$y[dat.sim$x==0])
treat <- t.test(dat.sim$y[dat.sim$x==1])
plot(ctrl$conf.int, c(0,0), ylim=c(-0.5,1.5), xlim=c(20,35),
type="n", axes=F, xlab="Y",ylab="")
segments(ctrl$conf.int[1], 0,ctrl$conf.int[2],0)
segments(treat$conf.int[1], 1, treat$conf.int[2],1)
axis(side=2, at=c(0,1), labels=c("Control","Treatment"))
axis(side=1)
In this case, the plausible ranges where the true means might lie overlap each other. Above, we concluded that if those two lines didn’t overlap it was likely that there was a true difference between the means. Should we do the same here? Should we fail to reject the null hypothesis of no difference between these two means based on the fact that there individual confidence intervals are overlapping?
Let’s run a t.test on these data to find out:
t.test(dat.sim$y ~ dat.sim$x)
#>
#> Welch Two Sample t-test
#>
#> data: dat.sim$y by dat.sim$x
#> t = -2.2236, df = 62.89, p-value = 0.02978
#> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
#> 95 percent confidence interval:
#> -9.4306515 -0.5029804
#> sample estimates:
#> mean in group 0 mean in group 1
#> 22.67512 27.64194Uh oh! The p-value on the difference in means test is less than 5% even though the two 95% confidence intervals overlap. This leads us to a really critical thing: Overlapping confidence intervals is not a valid statistical test. You see this mistake being made all the time. You will see it soon and you will get to feel smug about knowing that people seeing that confidence intervals are overlapping and concluding that the two means are not different is wrong.
Let’s simulate a bunch of times and see if this is always the case!
reject.null.cis <- rep(NA)
reject.null.p <- rep(NA)
for(i in 1:10000){
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
y <- c(y0,y1)
x <- c(rep(0,50), rep(1,50))
dat.sim <- cbind.data.frame(x,y)
ctrl <- t.test(dat.sim$y[dat.sim$x==0])
treat <- t.test(dat.sim$y[dat.sim$x==1])
#Reject Null with CIs
reject.null.cis[i] <- treat$conf.int[1] > ctrl$conf.int[2]
#Reject Null with real test
p <- t.test(dat.sim$y ~ dat.sim$x)$p.value
reject.null.p[i] <- p<.05
}
table(reject.null.cis, reject.null.p)
#> reject.null.p
#> reject.null.cis FALSE TRUE
#> FALSE 3163 2574
#> TRUE 0 4263Of the 10,000 simulations, approximately 6700 times the data resulted in us truly rejecting the null hypothesis of no difference between the two means. In 4200 the confidence intervals were not overlapping, but in 2500 of those cases the confidence intervals were overlapping. So in 2500 cases we would mistakenly fail to reject the null hypothesis when the correct statistical test says that we should.
On the other hand, in 3100 cases the simulated data would not cause us to reject the null hypothesis. In all of those cases, the confidence intervals were not overlapping.
This leads to the following conclusion: If two 95% confidence intervals on two means are not overlapping, then a hypothesis test on whether the difference can be distinguished from zero will reject the null hypothesis of no difference. If two 95% confidence intervals are overlapping, then it is unknown whether a hypothesis test on the difference will be able to distinguish the result from zero, or not.
10.1 Review
Last class we discussed the following data, which would be common when we are running an experiment:
set.seed(19104)
y0 <- rnorm(50,23, 13)
y1 <- rnorm(50, 28, 6)
y <- c(y0,y1)
x <- c(rep(0,50), rep(1,50))
dat <- cbind.data.frame(x,y)
head(dat)
#> x y
#> 1 0 17.85445
#> 2 0 25.55715
#> 3 0 29.99189
#> 4 0 28.97014
#> 5 0 22.22095
#> 6 0 10.75801We have two variables, x and y. x takes on two possible values: 0 and 1. y takes on many values. To describe the relationship between these variables we performed a difference in means test. Specifically we calculated the mean of y when x was equal to 0 and when x was equal to 1. We found that y was higher (5.48) when x was equal to 1. We further determined that this result was unlikely to occur if the truth was that the difference in means was 0.
We can think of a difference in means as just that: we have two groups and the difference between them is statistically significant, or not. But we can also think about this describing the relationship between x and y. If we think about this in a scatterplot:
plot(dat$x, dat$y)
points(c(0,1), c(mean(dat$y[dat$x==0]), mean(dat$y[dat$x==1])), col="firebrick", pch=16)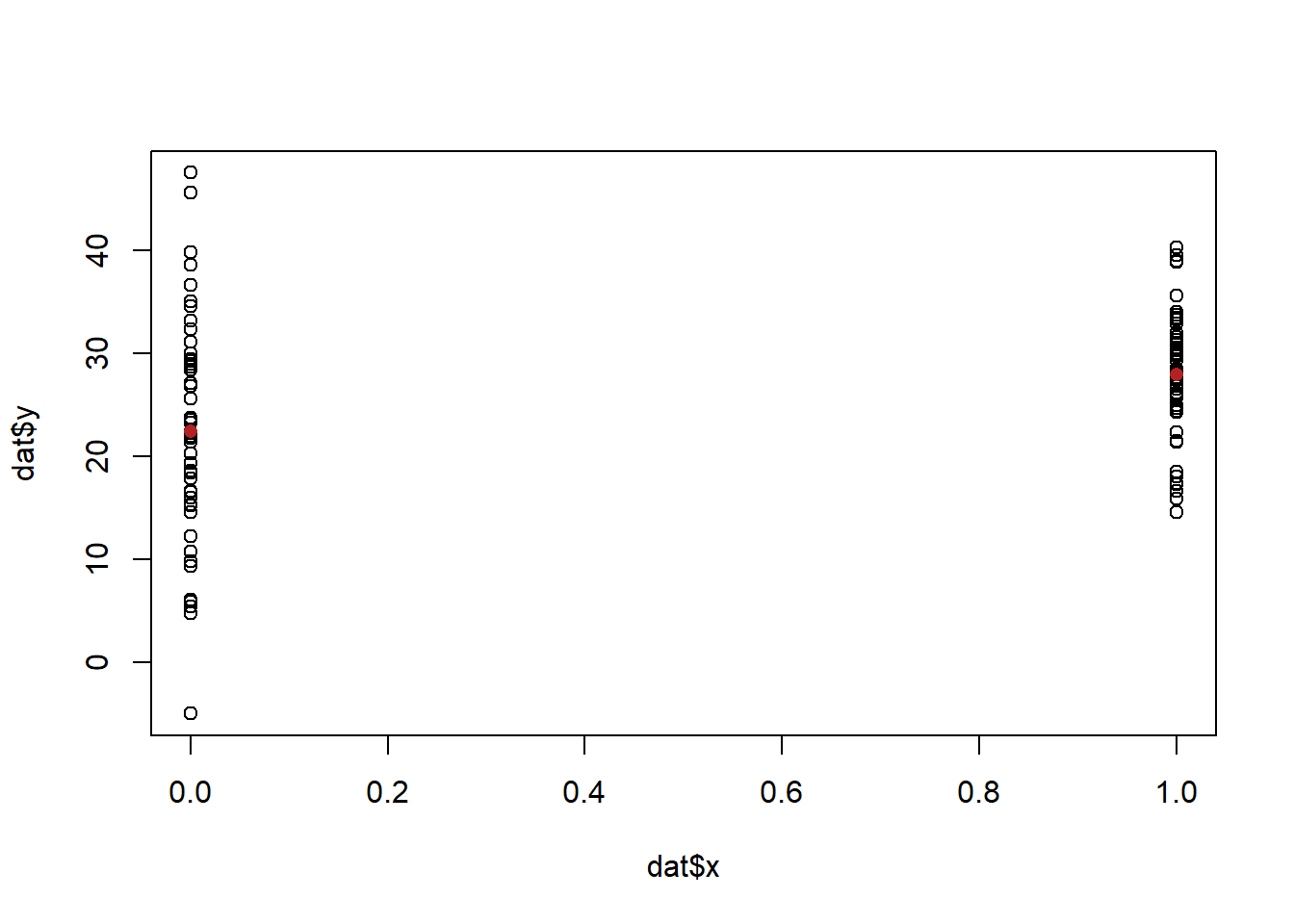
We might think about descibing that relationship in terms of what happens to y when x increases. I’ve marked in the two averages here, and it’s pretty clear that we can say that when x increases the average of y goes up.
10.2 Covariance
That relationship is fairly easy to describe, but what if we have these data instead:
set.seed(19103)
x <- rnorm(10,mean=0, sd=5)
y <- x*6*rnorm(10)
a <- cbind.data.frame(x,y)
plot(a$x, a$y, pch=16)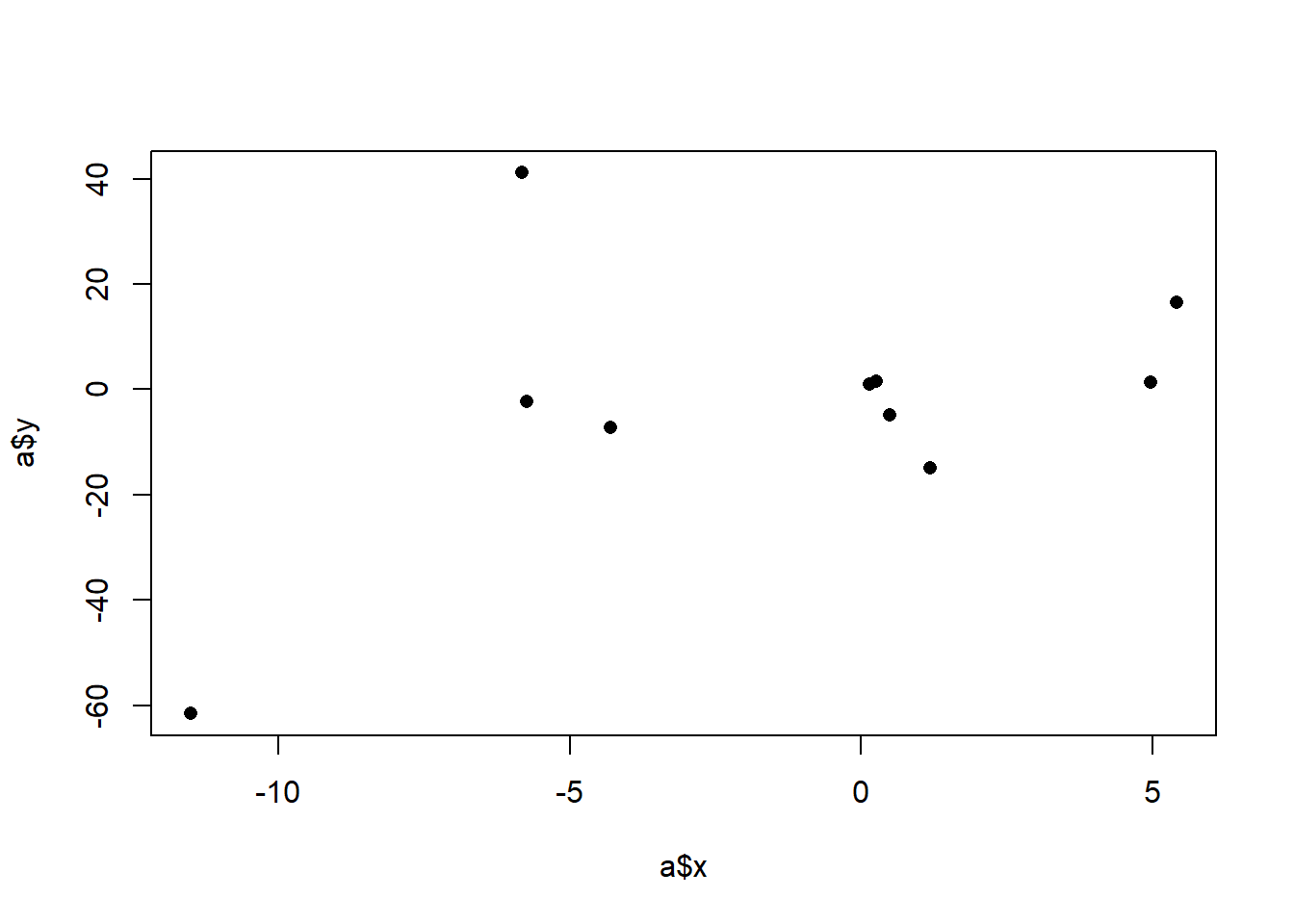
Before we get fancy with math, how would we generally describe what we are seeing here? We might say that there is a “positive relationship”, but why? What mechanically is happening here that is causing us to say that. More specifically, it seems that when x increases across it’s range y increases as well. In the above it was easy to see that x has two levels and when we went from level 0 to level 1, the average value of y increases. Here x has many levels, so it’s harder to say what the right way is to numerically describe what’s happening here. We might for example, think about splitting this x into two groups and calcualting the mean level in each group. For example we might consider the points lower than 0 and higher than 0 as two groups and calcualting their two means:
plot(a$x[a$x<0], a$y[a$x<0], pch=16, xlim=c(-12,7), col="darkblue")
points(a$x[a$x>0], a$y[a$x>0], pch=16, col="darkgreen")
segments(-20,mean(a$x[a$x<0]),0, mean(a$x[a$x<0]), col="darkblue")
segments(0,mean(a$x[a$x>0]),20, mean(a$x[a$x>0]), col="darkgreen")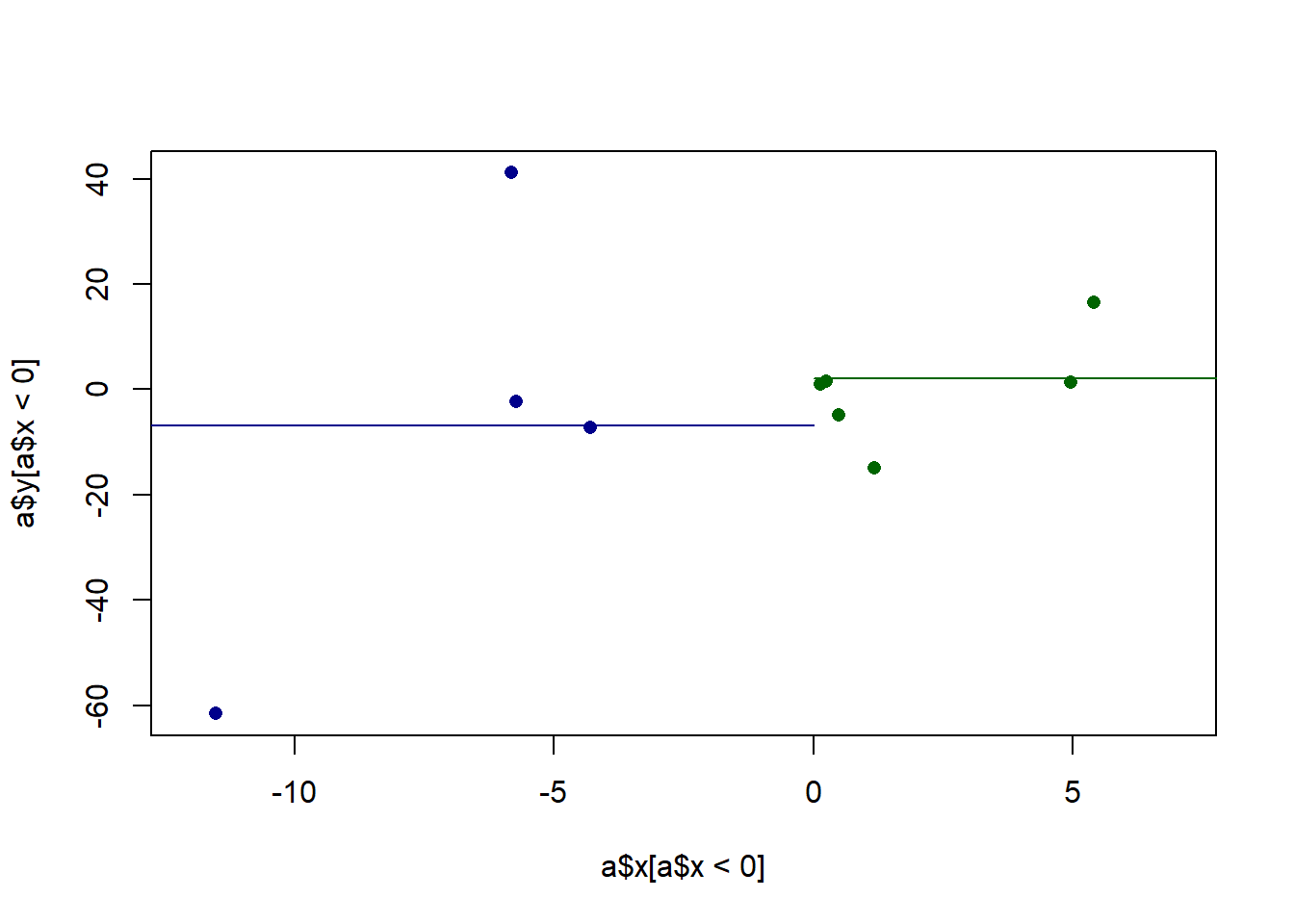
There is a difference in 9 between those two groups, and that does a reasonable job of describing the fact that as x increases y increases. Yet at the same time we are throwing away a lot of information. It would be nice if we took into account that there are many levels to x, not just two.
Furthermore, we also know that this is just a sample of data. In particular, given that there are not many points here, each point is having a high effect on the overall measure. That point at (-11.5, -61.5) is doing a lot of work to give us this relationship. We also want a method that is going to be sensitive to the fact that outliers might create a “false positive” of a relationship. We want to make sure that we are able to test the plausibability of there being a relationship in the population based on the variance we see in our data. In other words, we want a method that sees the above as being different from:
set.seed(19103)
x <- rnorm(10,mean=0, sd=5)
y <- x*3 + rnorm(10, mean=0, sd=1)
b <- cbind.data.frame(x,y)
plot(b$x, b$y, pch=16, xlim=c(-12,7), col="darkblue")
points(b$x[b$x<0], b$y[b$x<0], pch=16, col="darkblue")
points(b$x[b$x>0], b$y[b$x>0], pch=16, col="darkgreen")
segments(-20,mean(b$x[b$x<0]),0, mean(b$x[b$x<0]), col="darkblue")
segments(0,mean(b$x[b$x>0]),20, mean(b$x[b$x>0]), col="darkgreen")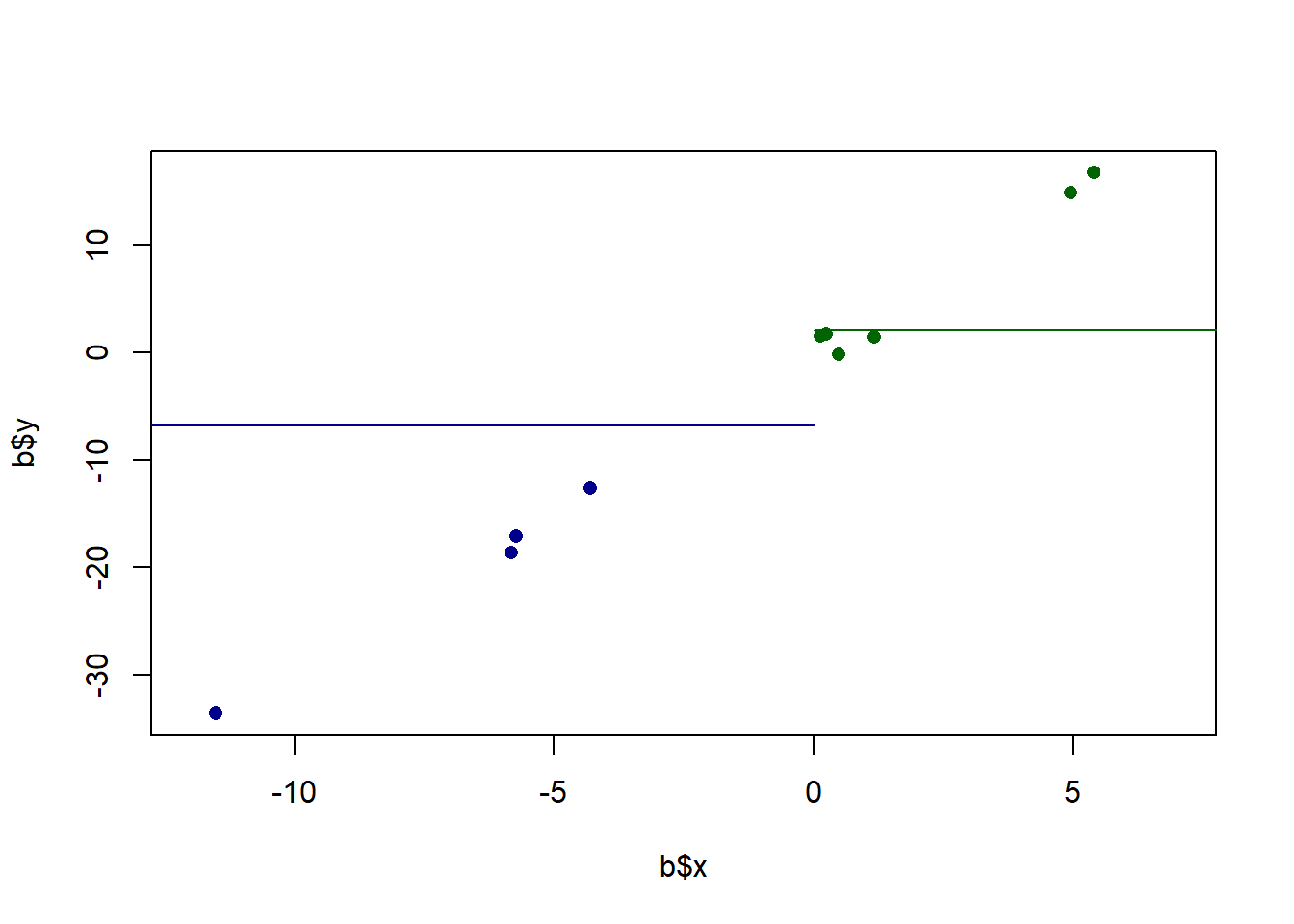
Here the difference between the means is very similar to what is above, and yet we would say that the relationship is much more consistently positive. My feeling is that if we repeatedly re-sampled this second relationship we will see a positive slope more reliably then in the first example. Ideally a method of describing the relationship between two variables would take into account the strength or reliability of that relationship.
The first method we will use to describe a relationship between two variables is their covariance. We represent covariance as: \(\hat{\sigma_{x,y}}\). The “hat” signifies that this is an estimate of the population level covariance. Like everything else we do, each covariance we observe in a sample is a realization of a random variable that is centered on the one true population covariance.
Covariance is defined as:
\[ \hat{\sigma_{x,y}} = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})(y_i - \bar{y}) \]
Breaking this down, we are effectively taking the deviations of x from their average, and the deviations of the ys from their average, and multiplying them together. We then divide by the sample size to get the average product of the deviations from the average. Note that, crucially, nothing here is squared. We have become very accustomed to variance being squared because variance can only be positive. In this case there is no squares so covariance can be positive or negative. Let’s go through the process a bit at a time with our small datasets to determine the covariance
a
#> x y
#> 1 -5.7353680 -2.3584497
#> 2 -5.8232989 41.1500563
#> 3 -4.2947444 -7.1439237
#> 4 0.4840690 -4.8086427
#> 5 0.1415545 0.9169479
#> 6 4.9638353 1.3479493
#> 7 0.2564384 1.5103761
#> 8 1.1786314 -14.8501926
#> 9 5.4112385 16.5743911
#> 10 -11.5068133 -61.5758292
#Determine deviations from the column averages
a$x.dev <- a$x - mean(a$x)
a$y.dev <- a$y - mean(a$y)
a$product <- a$x.dev*a$y.dev
a
#> x y x.dev y.dev
#> 1 -5.7353680 -2.3584497 -4.242922 0.565282
#> 2 -5.8232989 41.1500563 -4.330853 44.073788
#> 3 -4.2947444 -7.1439237 -2.802299 -4.220192
#> 4 0.4840690 -4.8086427 1.976515 -1.884911
#> 5 0.1415545 0.9169479 1.634000 3.840680
#> 6 4.9638353 1.3479493 6.456281 4.271681
#> 7 0.2564384 1.5103761 1.748884 4.434108
#> 8 1.1786314 -14.8501926 2.671077 -11.926461
#> 9 5.4112385 16.5743911 6.903684 19.498123
#> 10 -11.5068133 -61.5758292 -10.014368 -58.652098
#> product
#> 1 -2.398447
#> 2 -190.877105
#> 3 11.826238
#> 4 -3.725554
#> 5 6.275672
#> 6 27.579173
#> 7 7.754741
#> 8 -31.856497
#> 9 134.608884
#> 10 587.363663
sum(a$product)/9
#> [1] 60.72786We can see that, ultimately, the covariance is 60, but let’s think through how we got there. The covariance is generated by summing up the products and dividing by \(n-1\). So large, positive, products will lead to a higher positive covariance. Large, negative, products will lead to a highly negative covariance. What creates a large positive product? These are rows where the x and y values both vary in the same direction, whether that direction be positive or negative. To think about this visually, we can think about splitting a scatterplot into 4 quadrants based on the mean of x and y:
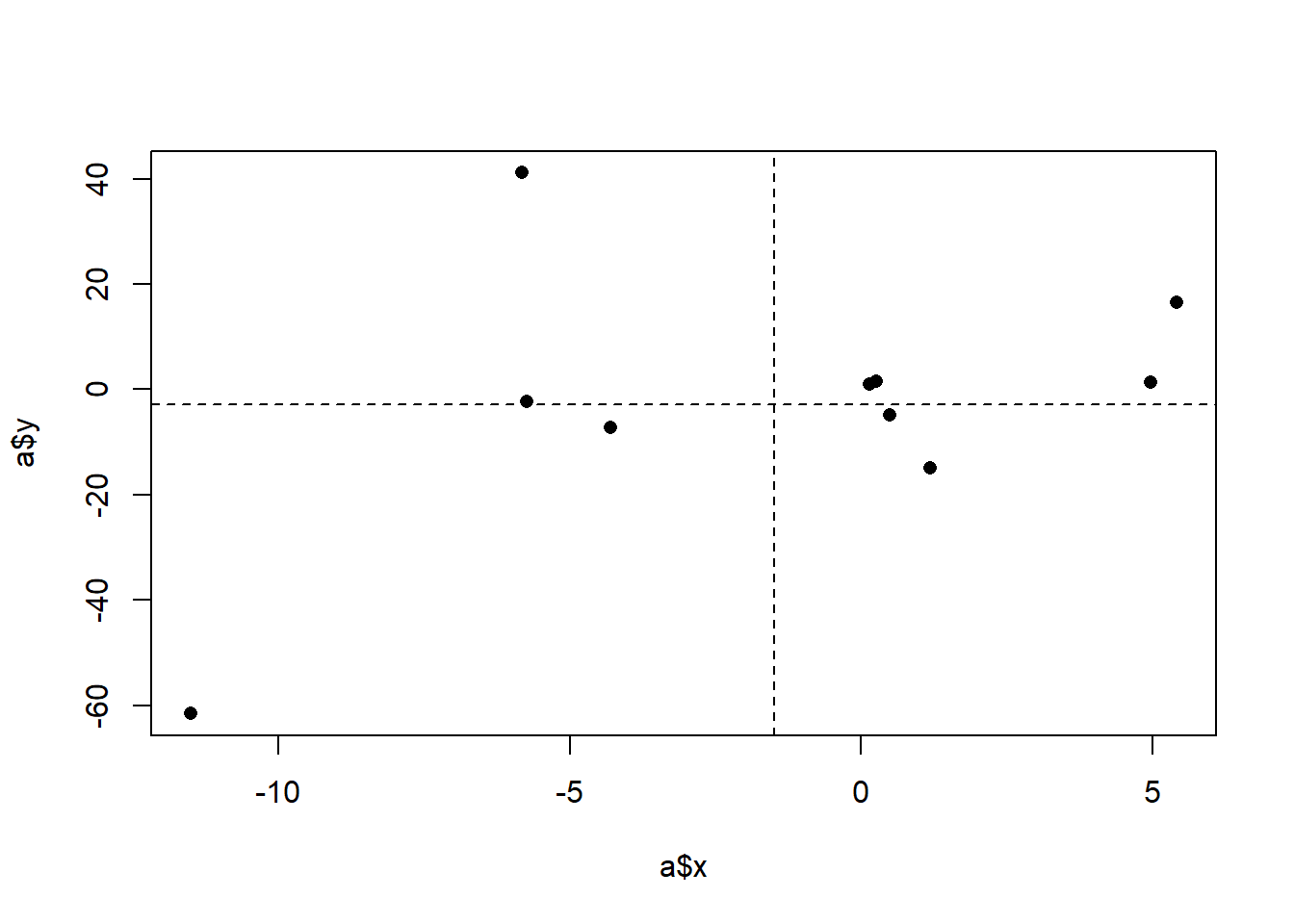
The thing that generates positive products are those data points that are in the lower left and upper right quadrants. The ``deeper’’ into a quadrant (the more the data point varies from both the x and y means), the higher the positive product will be.
Large negative products will be generated when x and y values both vary in opposite directions. That’s the only way to generate a negative product (as a pos times a negative is how you get a negative product). Visually, this means points that are in the upper left, and lower right quadrants.
Ultimately one covariance number describes the relative frequency and size of the products in the 4 different quadrants. This covariance came out to 60 which indicates that there are more data points in the bottom left and top right quadrants.
Consider, this alternative where the scatterplot looks like this:
set.seed(19103)
x <- rnorm(10,mean=0, sd=5)
y <- x*-6*rnorm(10)
c <- cbind.data.frame(x,y)
plot(a$x, a$y, pch=16)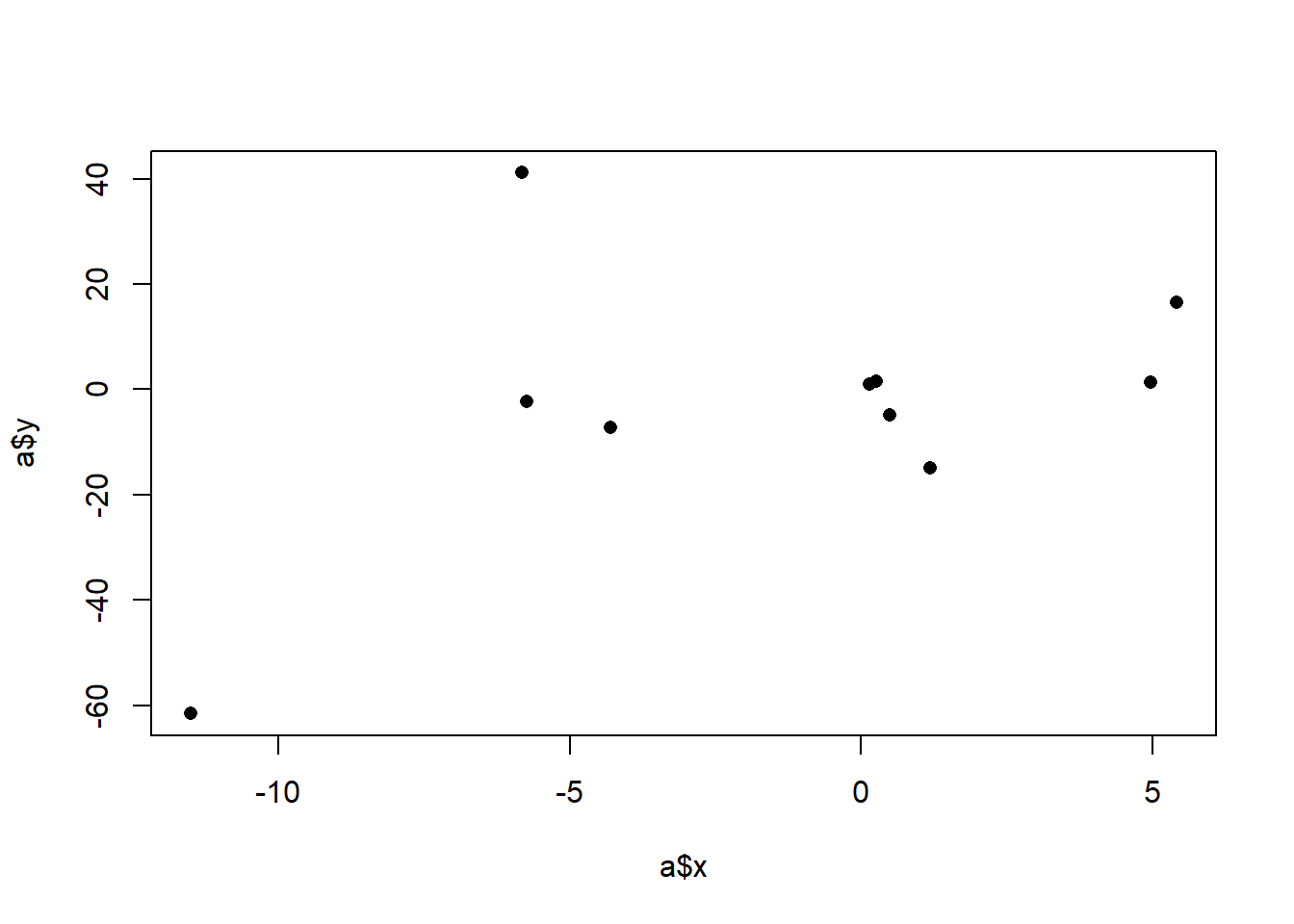
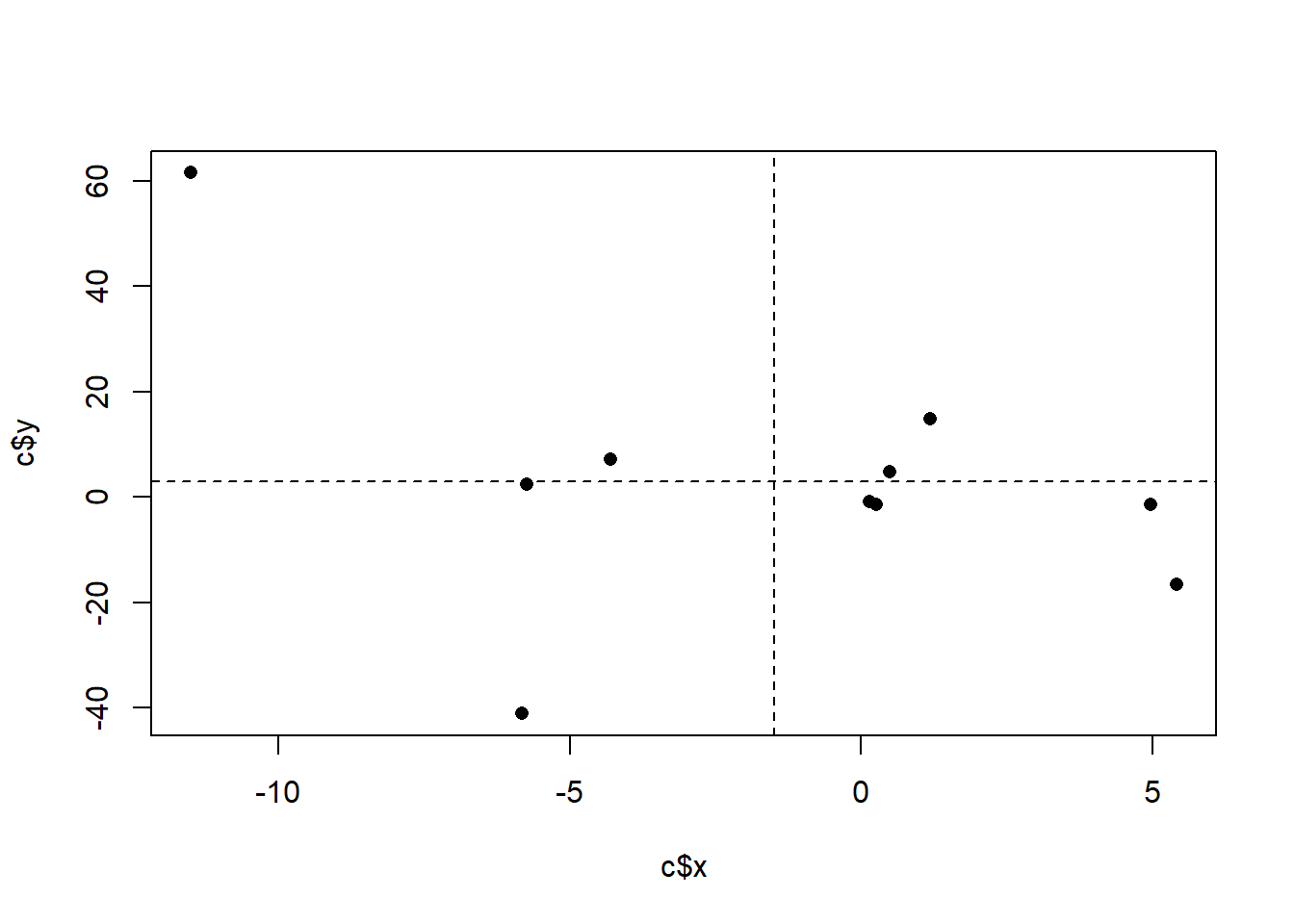
Here we have more of the points in the upper left/bottom right (this is actually just the other graph flipped), and as such we see that:
c$x.dev <- c$x - mean(c$x)
c$y.dev <- c$y - mean(c$y)
c$product <- c$x.dev*c$y.dev
c
#> x y x.dev y.dev
#> 1 -5.7353680 2.3584497 -4.242922 -0.565282
#> 2 -5.8232989 -41.1500563 -4.330853 -44.073788
#> 3 -4.2947444 7.1439237 -2.802299 4.220192
#> 4 0.4840690 4.8086427 1.976515 1.884911
#> 5 0.1415545 -0.9169479 1.634000 -3.840680
#> 6 4.9638353 -1.3479493 6.456281 -4.271681
#> 7 0.2564384 -1.5103761 1.748884 -4.434108
#> 8 1.1786314 14.8501926 2.671077 11.926461
#> 9 5.4112385 -16.5743911 6.903684 -19.498123
#> 10 -11.5068133 61.5758292 -10.014368 58.652098
#> product
#> 1 2.398447
#> 2 190.877105
#> 3 -11.826238
#> 4 3.725554
#> 5 -6.275672
#> 6 -27.579173
#> 7 -7.754741
#> 8 31.856497
#> 9 -134.608884
#> 10 -587.363663
sum(c$product)/9
#> [1] -60.72786The covariance is negative.
Consider a couple more datasets and what that will mean for the covariance:
One that is incredibly consistent:
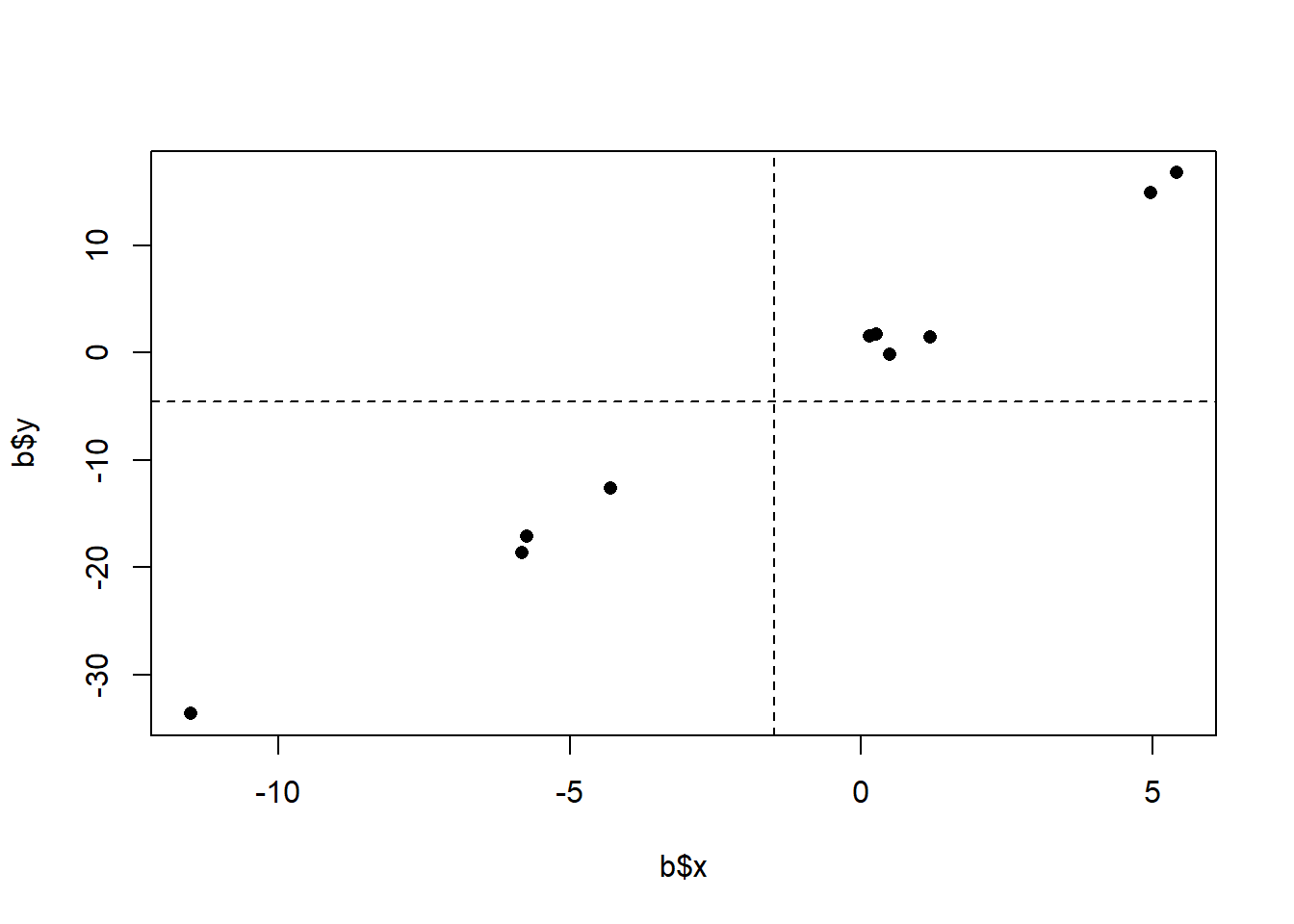
b$x.dev <- b$x - mean(b$x)
b$y.dev <- b$y - mean(b$y)
b$product <- b$x.dev*b$y.dev
b
#> x y x.dev y.dev product
#> 1 -5.7353680 -17.1375687 -4.242922 -12.552367 53.258718
#> 2 -5.8232989 -18.6476386 -4.330853 -14.062437 60.902350
#> 3 -4.2947444 -12.6069980 -2.802299 -8.021796 22.479469
#> 4 0.4840690 -0.2034255 1.976515 4.381776 8.660645
#> 5 0.1415545 1.5042805 1.634000 6.089482 9.950215
#> 6 4.9638353 14.9367649 6.456281 19.521966 126.039302
#> 7 0.2564384 1.7509519 1.748884 6.336154 11.081198
#> 8 1.1786314 1.4359740 2.671077 6.021176 16.083025
#> 9 5.4112385 16.7442084 6.903684 21.329410 147.251513
#> 10 -11.5068133 -33.6285650 -10.014368 -29.043363 290.850916
sum(b$product)/9
#> [1] 82.95082Or where the truth is that there is no relationship between the two variables. Here we see that the positive and negative products cancel each other out, which makes sense!
set.seed(19106)
x <- rnorm(10,mean=0, sd=5)
y <- x*rnorm(10, sd=2)
d <- cbind.data.frame(x,y)
plot(d$x, d$y, pch=16)
abline(v=mean(d$x), lty=2)
abline(h=mean(d$y), lty=2)
d$x.dev <- d$x - mean(d$x)
d$y.dev <- d$y - mean(d$y)
d$product <- d$x.dev*d$y.dev
d
#> x y x.dev y.dev
#> 1 -6.0866587 -0.75613532 -1.0132013 0.3362112
#> 2 -8.7851369 -9.64523909 -3.7116794 -8.5528926
#> 3 -8.7506052 11.66036276 -3.6771477 12.7527093
#> 4 -7.4525445 -9.57732363 -2.3790870 -8.4849771
#> 5 -2.8162482 0.06318308 2.2572093 1.1555296
#> 6 -10.6206995 -7.58143868 -5.5472420 -6.4890922
#> 7 -5.2935076 0.48991352 -0.2200501 1.5822600
#> 8 0.2973094 -0.15902415 5.3707669 0.9333223
#> 9 -3.4008646 5.48742824 1.6725928 6.5797747
#> 10 2.1743811 -0.90519163 7.2478385 0.1871549
#> product
#> 1 -0.3406496
#> 2 31.7455954
#> 3 -46.8935960
#> 4 20.1864988
#> 5 2.6082720
#> 6 35.9965648
#> 7 -0.3481765
#> 8 5.0126568
#> 9 11.0052842
#> 10 1.3564682
sum(d$product)/9
#> [1] 6.70321310.3 Correlation
Covariance is a super helpful tool to have in our pockets, but one of the issues with it is that it doesn’t really tell us anything about the relative strength of the relationship.
For example, let’s take our original dataset where we found a covariance of 60:
cov(a$x, a$y)
#> [1] 60.72786
#The covariance function does the same thing we did above for us...And let’s multiply each of the columns by 100:
cov(a$x*100, a$y*100)
#> [1] 607278.6The covarince is now 607 thousand! Ahhhhhh! But really, this is the same “strength” of relationship, just scaled up by 100
plot(a$x*100, a$y*100, pch=16)
And covariance doesn’t have a really intuitive explanation…. It’s the average product of deviations from the means? Definitely not going to get anyone on-board a policy proposal if you suggest something like that.
We, basically, will make two different modifications/additions to covariance to address these things: correlation and regression. Each of these is helpful, and each has it’s own pitfalls.
We’ll start today with correlation.
The idea behind correlation is simply to standardize a covariance by dividing by the standard deviations of the variables that we are measuring. Specifically, the correlation equals:
\[ \hat{\rho}_{x,y} = \frac{\hat{\sigma}_{x,y}}{\sqrt{var(x)*var(y)}} \]
By dividing away the product of the two variances, we standardize the variables such that all correlations are on the same scale.
Let’s look at how this looks for two variables that are perfectly correlated:
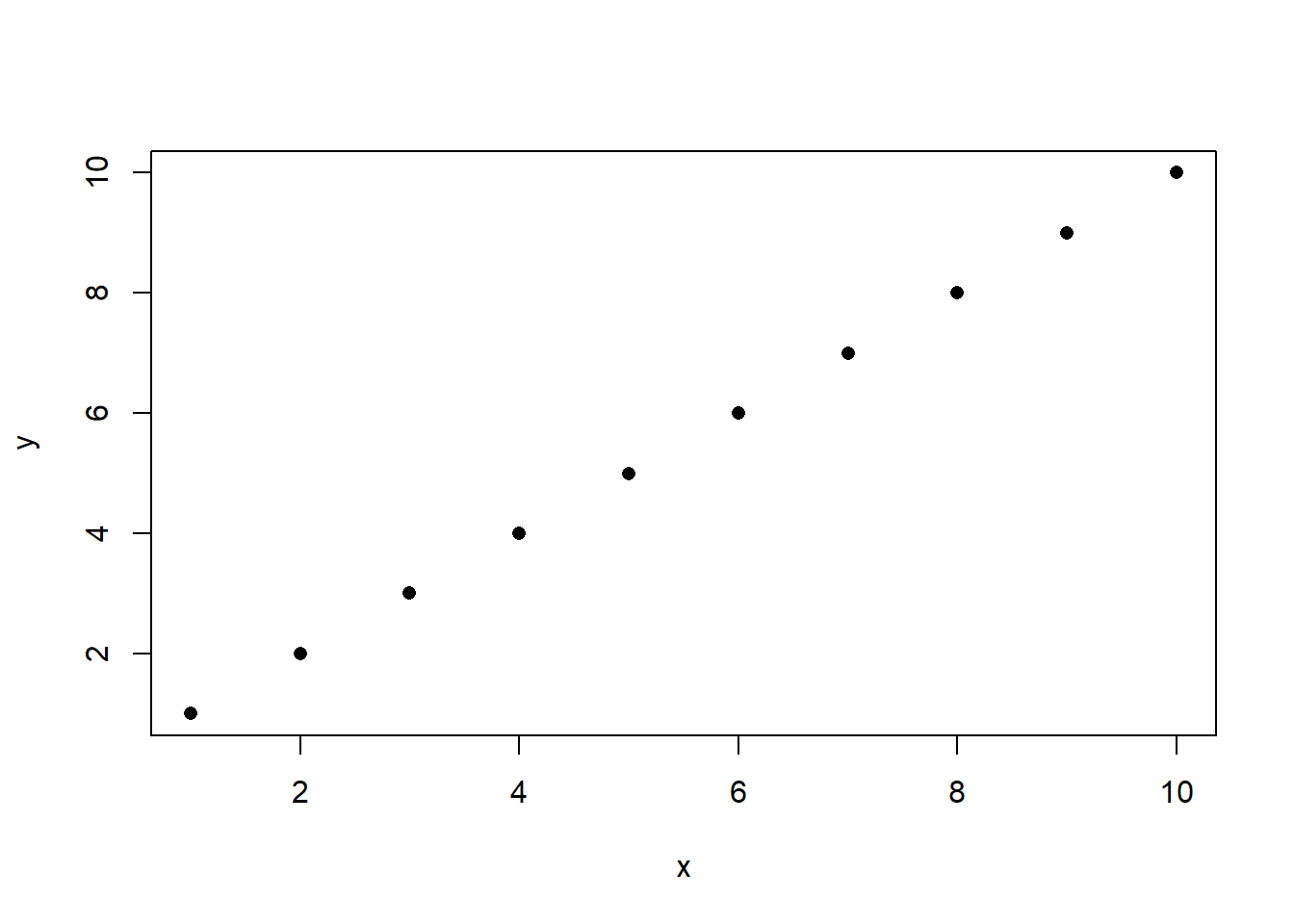
When I say “perfectly correlated”, what I mean here is that every data point has the same value for x any y. If you tell me a data points x coordinate, I can tell you it’s y coordinate because they are the same.
Let’s look at all the components:
cov(x,y)
#> [1] 9.166667
var(x)
#> [1] 9.166667
var(y)
#> [1] 9.166667
var(x)*var(y)
#> [1] 84.02778
sqrt(var(x)*var(y))
#> [1] 9.166667
cov(x,y)/sqrt(var(x)*var(y))
#> [1] 1When two variables are perfectly correlated that equals \(\hat{\rho}_{x,y}=1\). That is the case because when two variables are perfectly correlated their covariance is equal to the variance of each of the variables.
Let’s think about why that’s true. The equation for variance is:
\[ \hat{\sigma_{x,y}} = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2 \]
And equation for covariance is:
\[ \hat{\sigma_{x,y}} = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})(y_i - \bar{y}) \]
But if two variables are perfectly correlated then it is necessarily the case that \((x_i-\bar{x})=(y_i - \bar{y})\). As such the two equations will result in exactly the same thing.
If any of these points is disturbed from this line it means that this perfect balance between x and y will be disturbed, and the correlation will move below 1.
x[3] <- x[3]+.3
plot(x,y)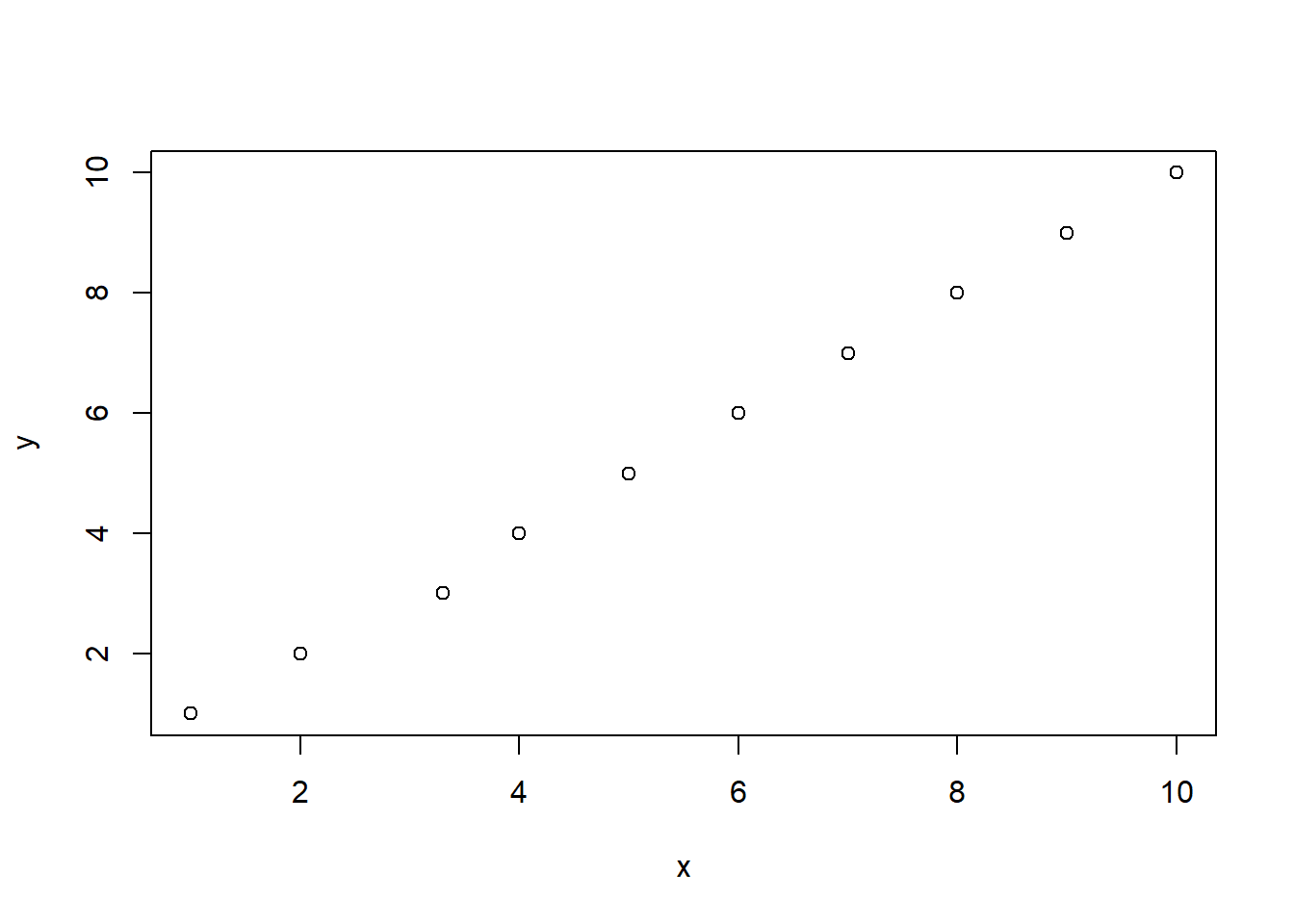
cov(x,y)
#> [1] 9.083333
var(x)
#> [1] 9.009
var(y)
#> [1] 9.166667
var(x)*var(y)
#> [1] 82.5825
sqrt(var(x)*var(y))
#> [1] 9.087491
cov(x,y)/sqrt(var(x)*var(y))
#> [1] 0.9995424What about two variables that are perfectly negatively correlated?

cov(x,y)
#> [1] -9.166667
var(x)
#> [1] 9.166667
var(y)
#> [1] 9.166667
var(x)*var(y)
#> [1] 84.02778
sqrt(var(x)*var(y))
#> [1] 9.166667
cov(x,y)/sqrt(var(x)*var(y))
#> [1] -1Here the covariance is going to be -1 multiplied by the variance of each of the variables (which is the same).
So a correlation coefficient mathematically lies between -1 and 1, and the closer the coefficient is to those two bounds the more “perfectly” correlated the two variables are.
Here are 9 different relationships moving from a very negative to a very positive correlation:
library(MASS)
cors <- seq(-.9,.7,.2)
cors
#> [1] -0.9 -0.7 -0.5 -0.3 -0.1 0.1 0.3 0.5 0.7
#par(mfrow=c(3,3))
for(i in 1:length(cors)){
sigma<-rbind(c(1,cors[i]), c(cors[i],1))
mu <- c(0,0)
d <- mvrnorm(n=100, mu=mu, Sigma=sigma)
plot(d[,1], d[,2], main=paste("Cor =",cors[i] ))
}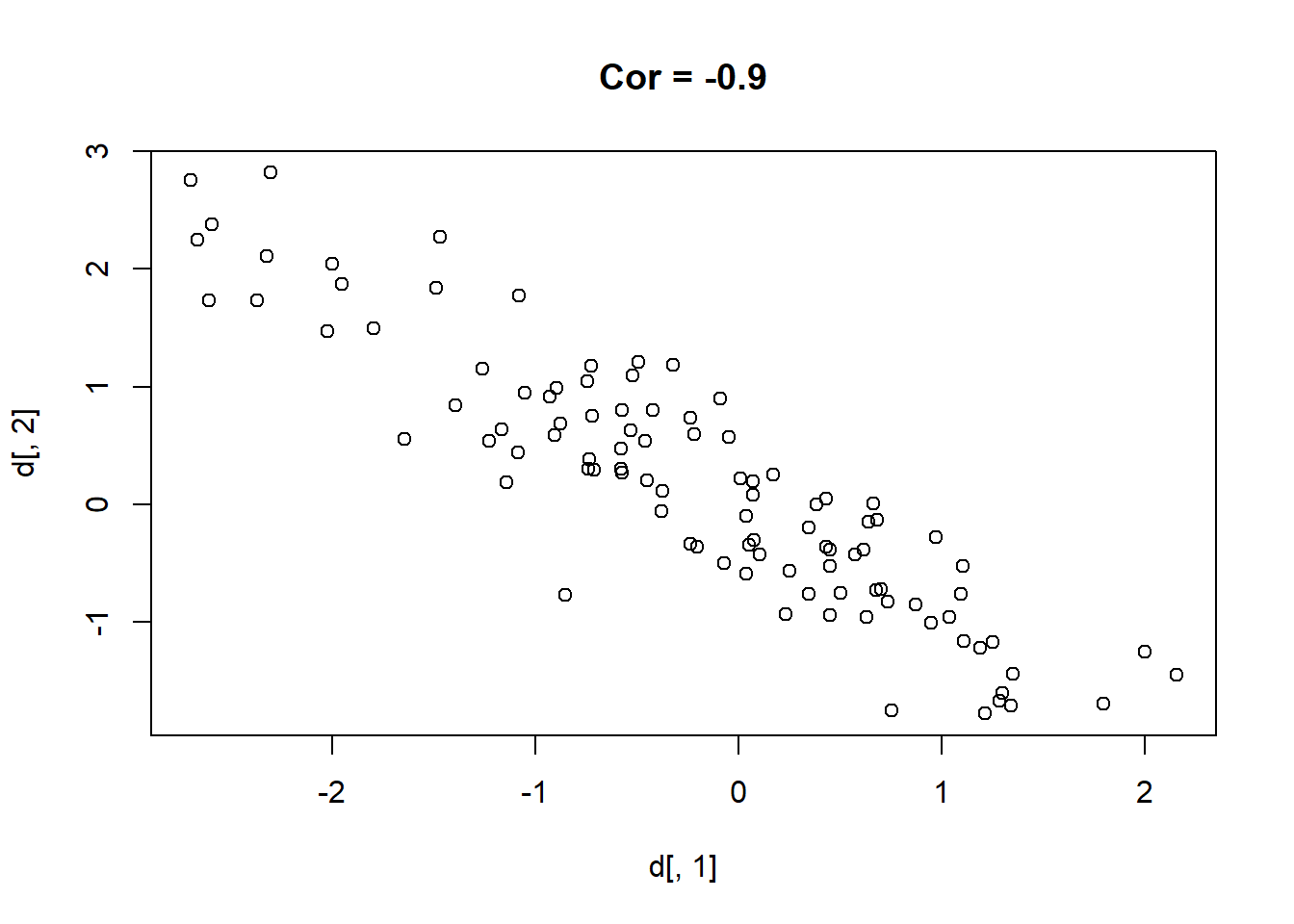
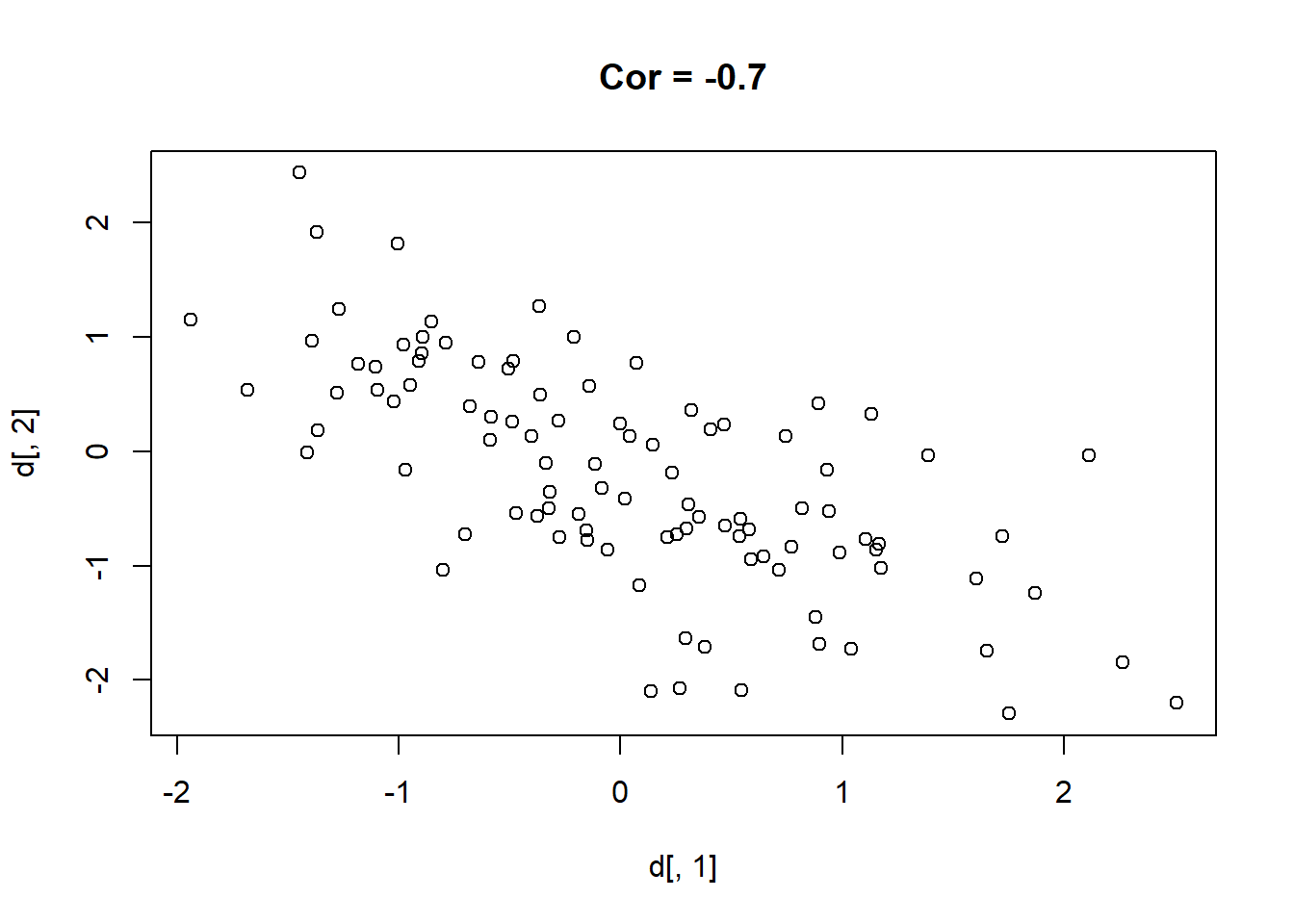
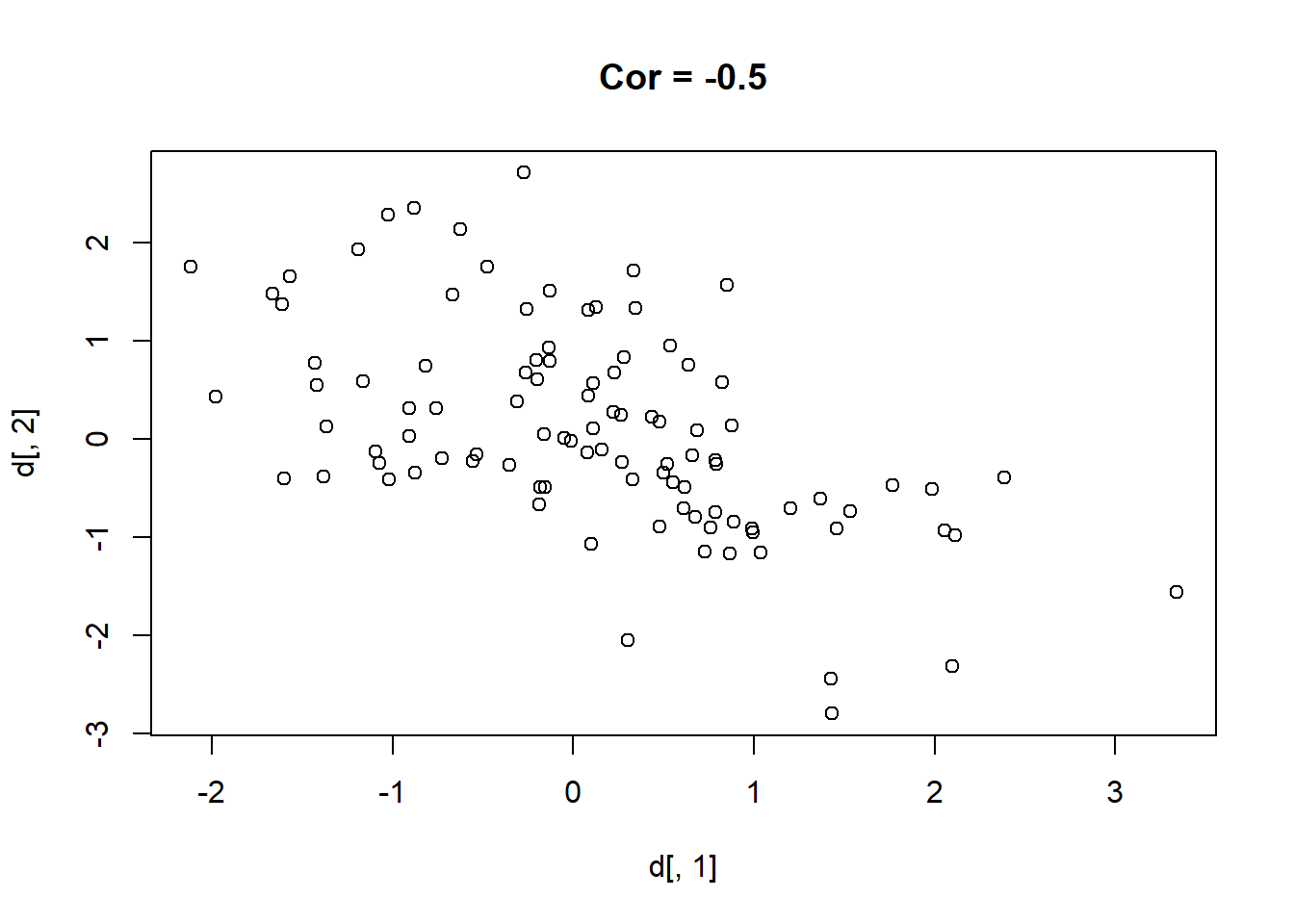


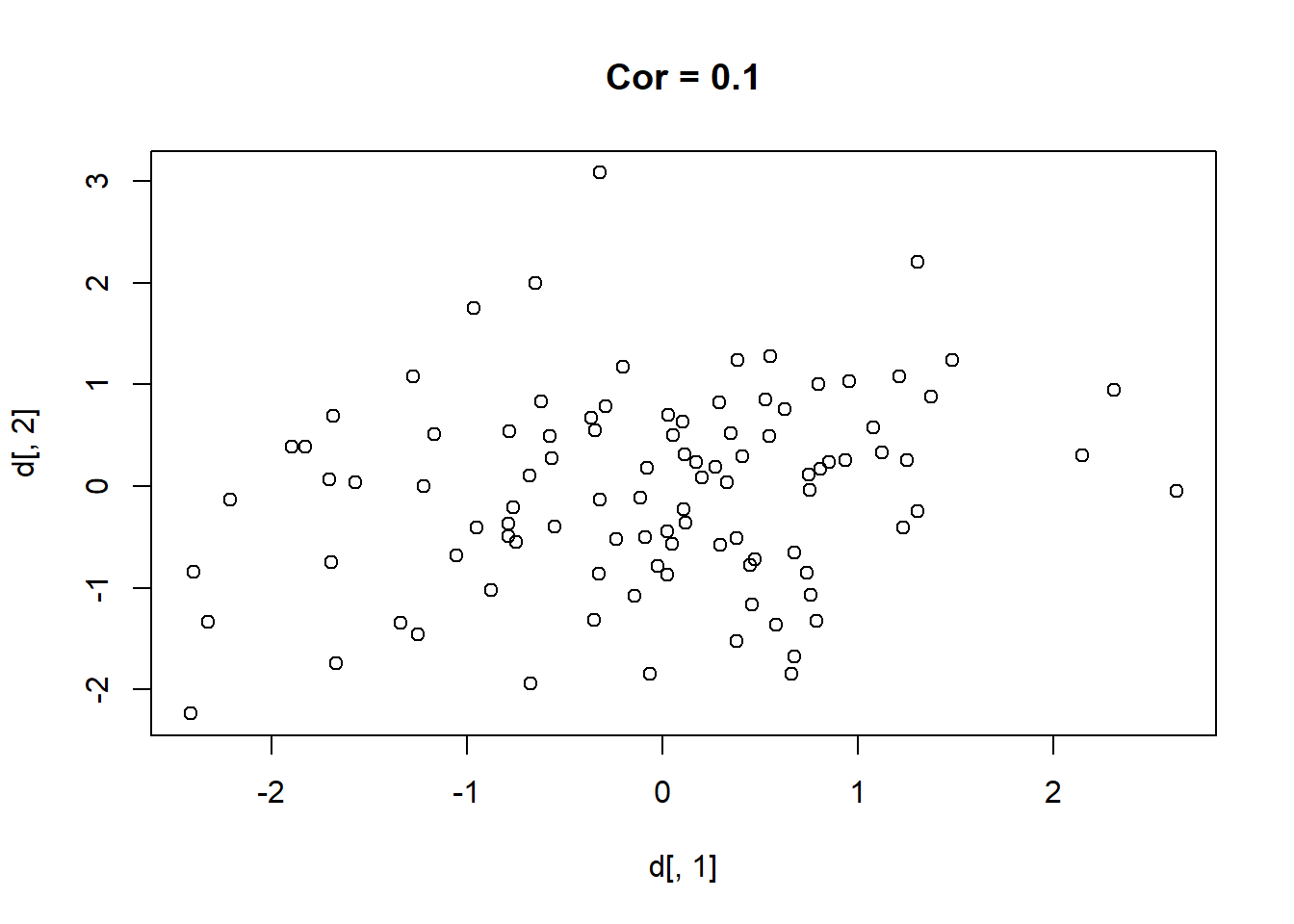
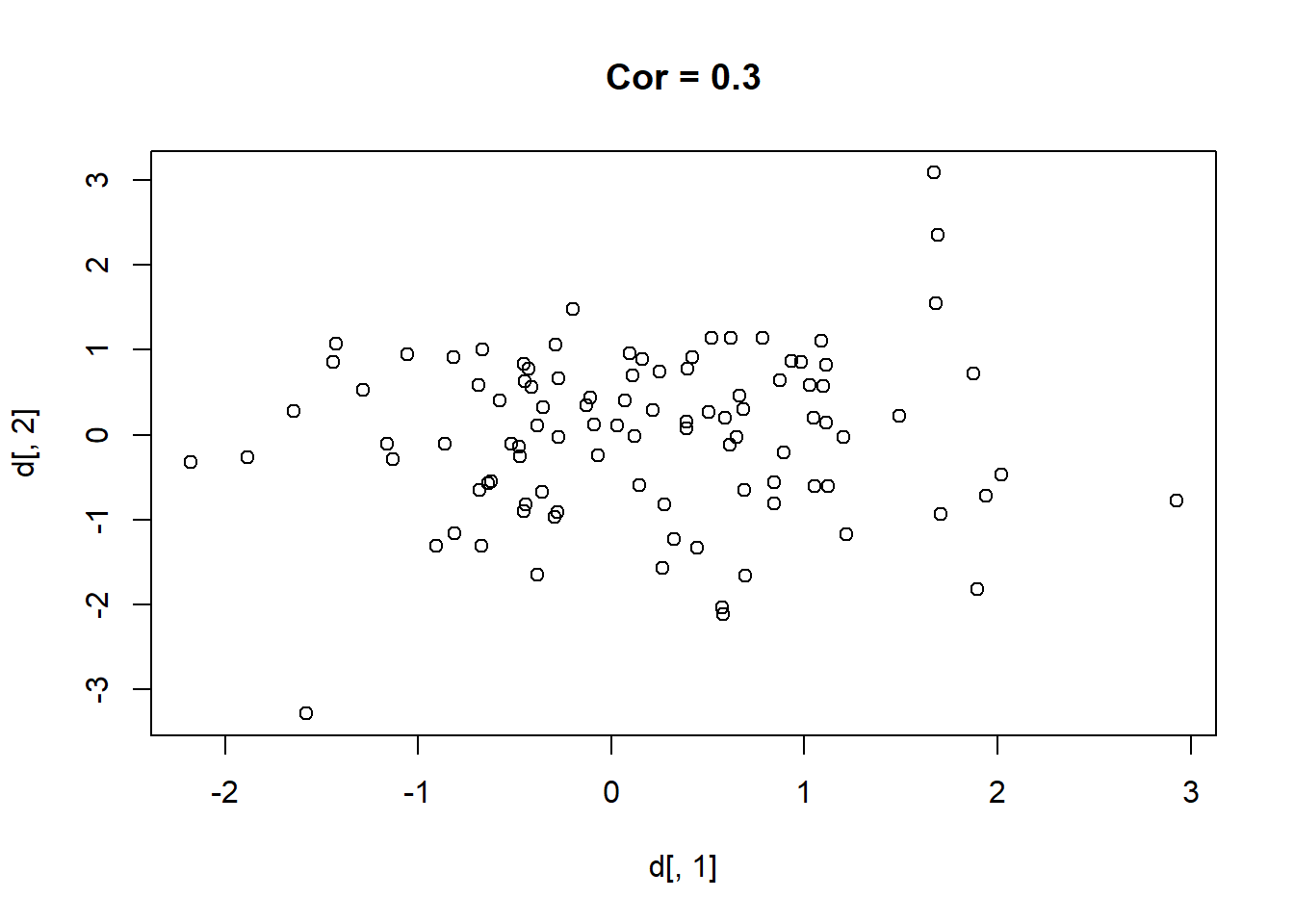
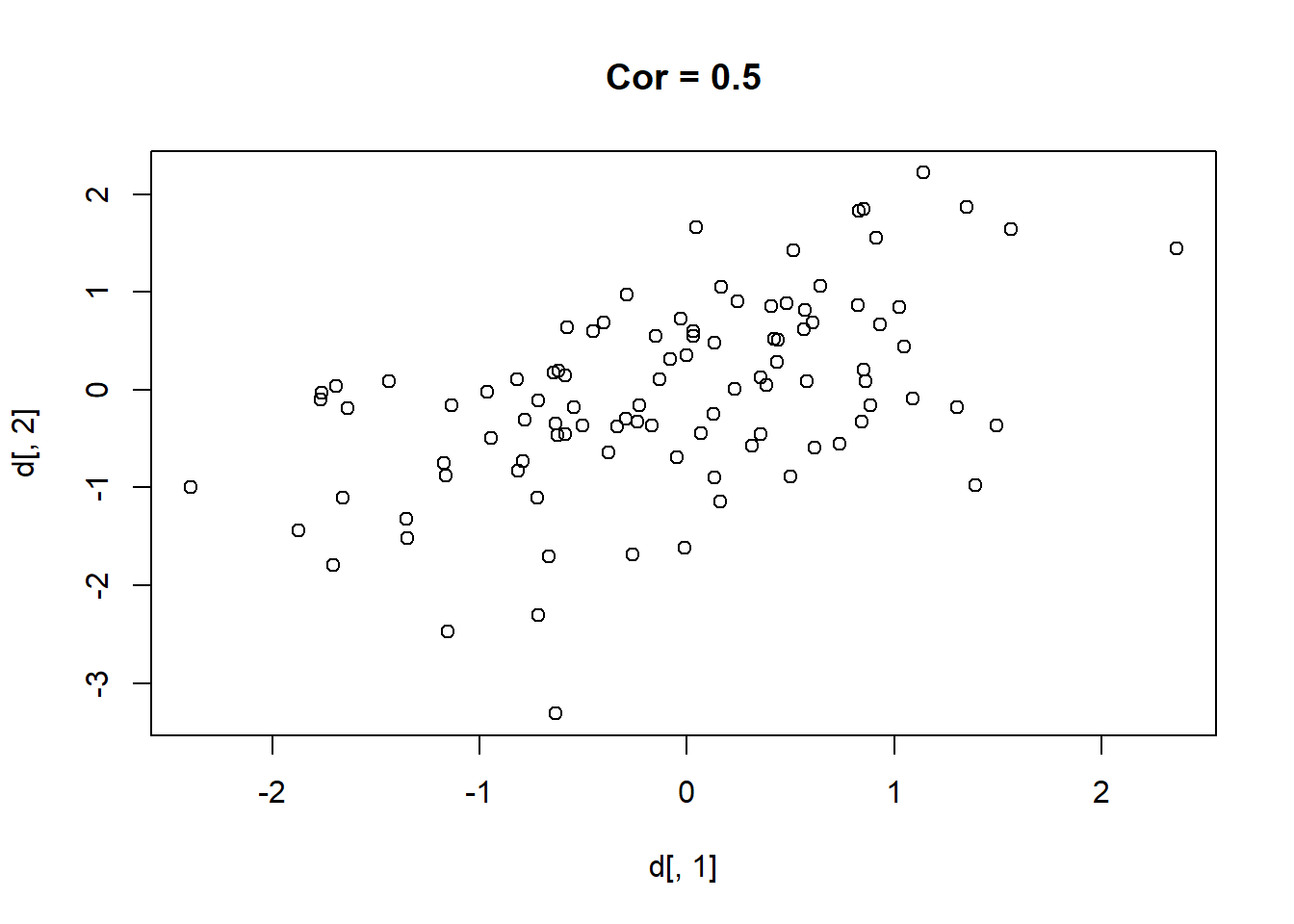
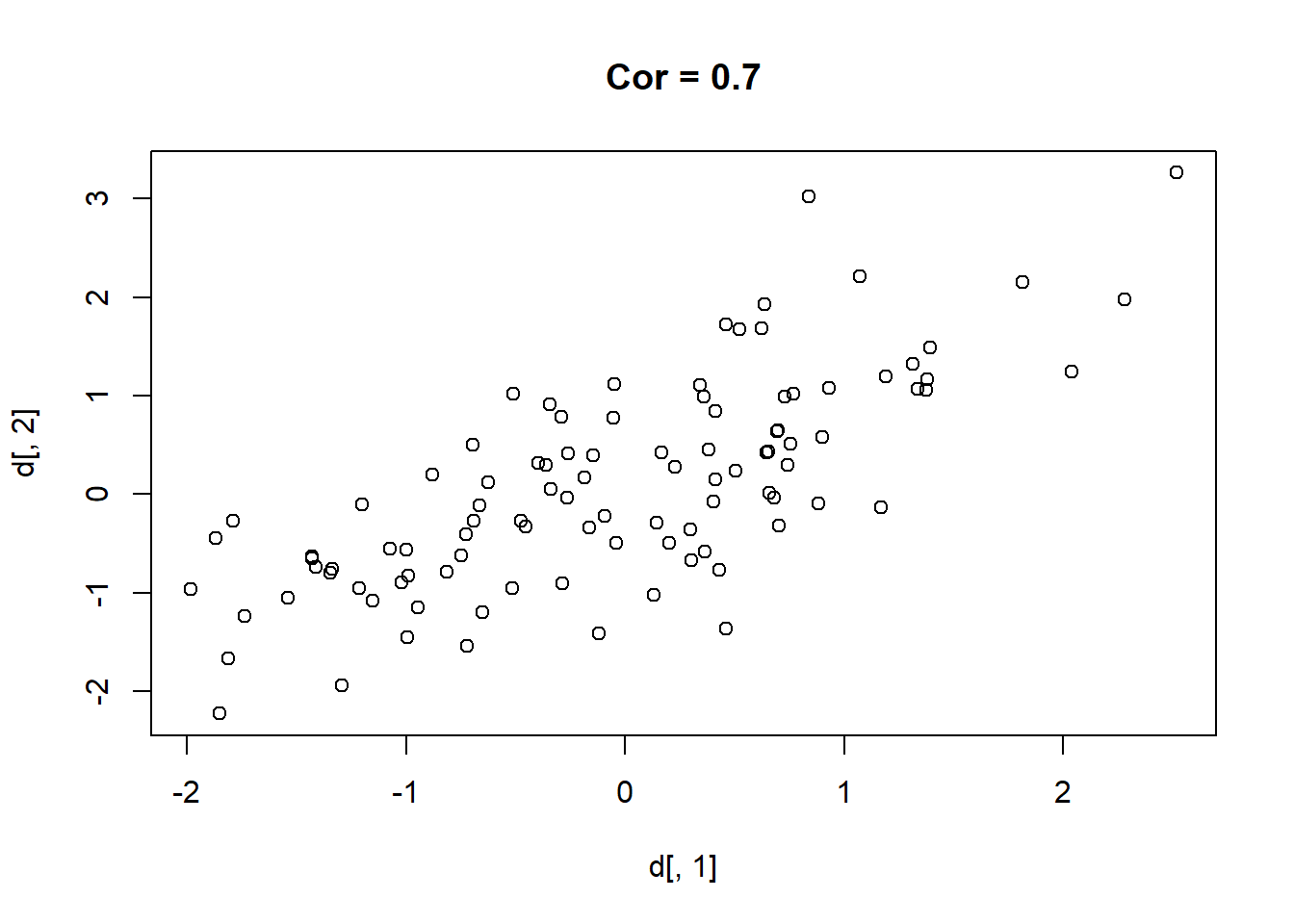
One thing that might be clear from this is that a correlation is hard to “eyeball”.
10.4 The Bootstrap
Of course, like covariance there is a command to do the correlation calculation for us, cor()
set.seed(19103)
sigma<-rbind(c(1,.2), c(.2,1))
d <- as.data.frame(mvrnorm(n=500, mu=c(0,0), Sigma=sigma))
names(d) <- c("x","y")
plot(d$x, d$y )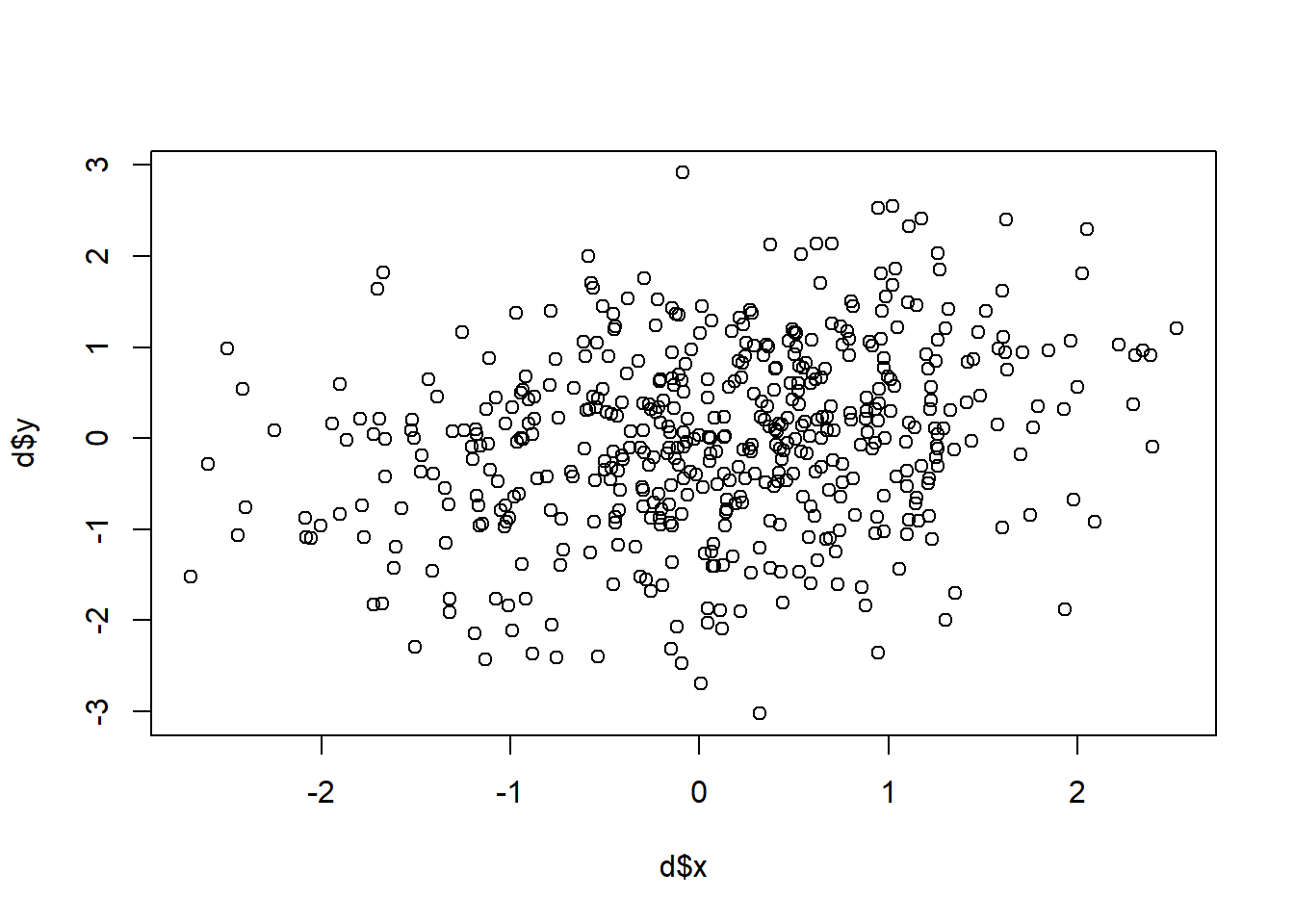
correlation <- cor(d$x, d$y)
correlation
#> [1] 0.2569832One thing to note about the correlation function is that it won’t give you anything back if there missing values in either of the vectors:
z <- d$x
z[5] <- NA
cor(z, d$y)
#> [1] NAOur general answer to how to deal with these things is to use na.rm=T, but that’s not what we do with a correlation. Because there are a few different ways that NA could be dealt with for a correaltion, here we need to specify the method which we want R to deal with NAs. The safe thing to use is:
cor(z, d$y, use="pairwise.complete")
#> [1] 0.2596632That’s really great, but given what we have learned so far in this class about samples and population, what else would we like to know about this correlation coefficient?
Well we know that this sample of data is only one of an infinite number of samples we could get. We know that there is one “true” correlation between these two variables in the world, and we would like to make an inference about what that might be.
As with everything: we want to perform a hypothesis test, so we want a sampling distribution.
So let’s dig in to to the correlation function to find a standard error:
names(correlation)
#> NULLUh-oh! It doesn’t give us one!
And if we go to to the textbook there is no mention of a standard error or sampling distribution for a correlation coefficient!
Well then what are we going to do??
I want to use the rest of class to introduce a method that can give you a sampling distribution for anything you calculate, called the bootstrap.
Why is it called the bootstrap? The phrase “picking yourself up by your bootstraps” specifically refers to doing something impossible. You can’t actually do it. Similarly, the bootstrap statistical method allows you to generate a sampling distribution for anything based off of a single sample, even in cases where there is no known equation for the standard error.
Before we get to the method (which is actually pretty easy), let’s generate the true sampling distribution for this correlation coefficient. In this case we can do so because we generated these data. So let’s repeatedly re-generate these data and calculate the correlation a large number of times so that we can determine the true sampling distribution:
cor.samp.dist <- rep(NA, 10000)
for(i in 1:10000){
sigma<-rbind(c(1,.2), c(.2,1))
samp <- as.data.frame(mvrnorm(n=500, mu=c(0,0), Sigma=sigma))
names(samp) <- c("x","y")
cor.samp.dist[i] <- cor(samp$x, samp$y)
}
plot(density(cor.samp.dist))
abline(v=0, lty=2)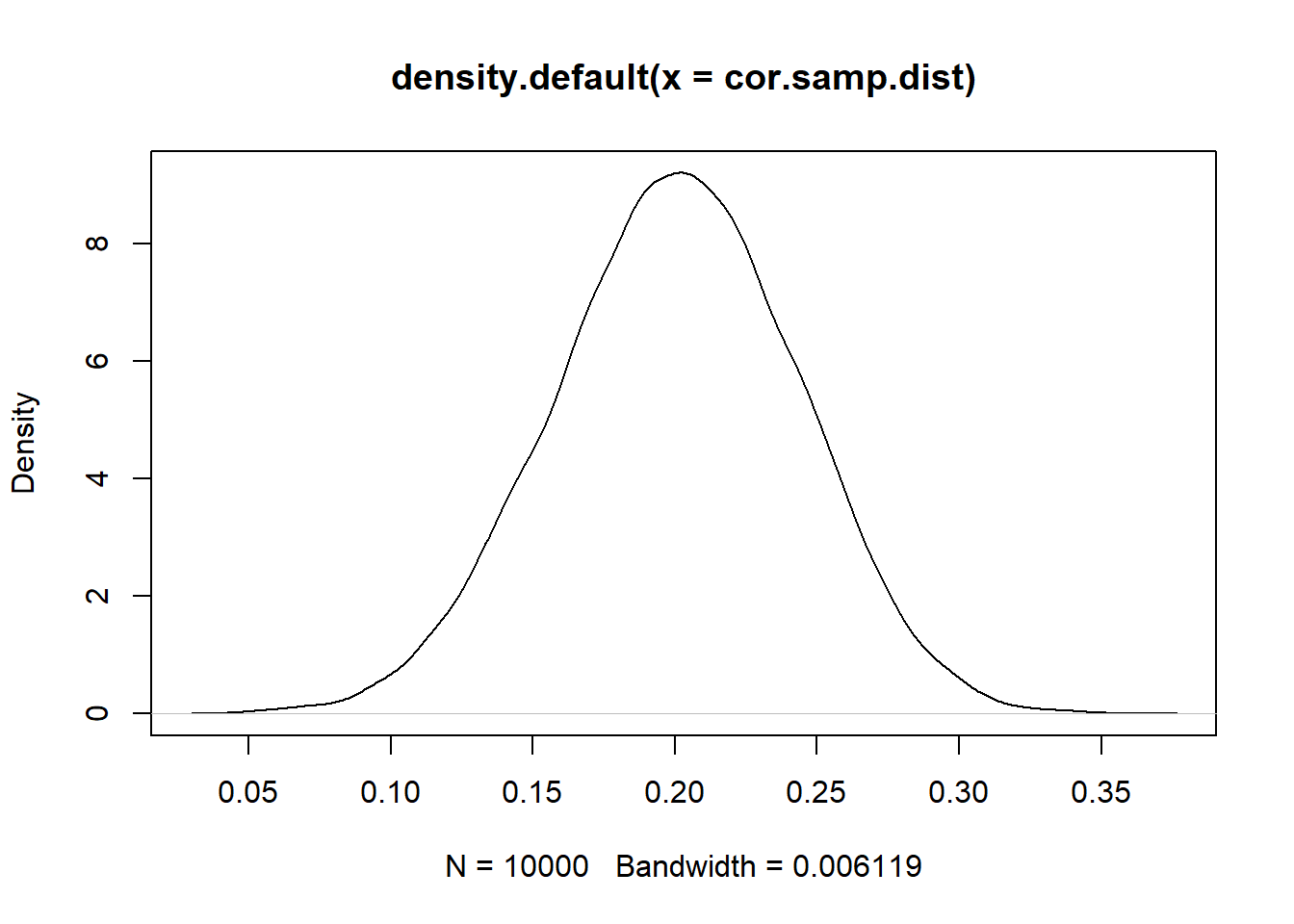
sd(cor.samp.dist)
#> [1] 0.0428987But pretend that all we have is our original dataset, d. Our goal is to recreate the actual sampling distribution using information wholly contained within our one sample.
Here is the key insite to the bootstrap: because our sample of data is assumed to be an iid sample of the population, a random sample of our sample is a new sample.
To put it in more reasonable terms: we have seen already that any given sample is a shadow, or is suggested by, the population. That’s true for the distribution of one variable, but is also true for the relationships between variables (or anything else). What we want to do is to use the fact that our sample is representative of the population to generate new samples to explore the range of possibilities that might occur if we truly re-sampled a large number of times.
The way that we are going to actually do this is to repeatedly generate new datasets of the same length as our original by sampling with replacement from our original dataset. Here is one such new sample:
bs.samp <- d[sample(1:nrow(d), replace=T),]
cor(d$x, d$y)
#> [1] 0.2569832
cor(bs.samp$x, bs.samp$y)
#> [1] 0.2310803
#Not the same!Why is it important that we sample with replacement. Well if we sample without replacement we will just select the rows of the old dataset one at a time until we have selected all of them. In the end we will be left with an exact re-creation of our old dataset in a new order:
bs.samp <- d[sample(1:nrow(d), replace=F),]
cor(d$x, d$y)
#> [1] 0.2569832
cor(bs.samp$x, bs.samp$y)
#> [1] 0.2569832
#The same!Having repeated entries is key into creating variance that generates different samples everytime you generate a new bootstrap sample.
OK, that’s all fine, but does it work? Let’s repeatedly generate new bootstrap samples and calculate the correlation coefficient.
bs.samp.dist <- rep(NA, 10000)
for(i in 1:10000){
bs.samp <- d[sample(1:nrow(d), replace=T),]
bs.samp.dist[i] <- cor(bs.samp$x, bs.samp$y)
}And let’s compare to the true sampling distribution:
plot(density(cor.samp.dist), col="darkblue")
points(density(bs.samp.dist), col="firebrick", type="l")
abline(v=0, lty=2)
Now, these two sampling distributions are not centered in the same place. But does that really matter? The true sampling distribution is centered around the true population correlation, which we are never going to know. The bootstrap sampling distribution is centered around the correlation in the sample.
But think about when we calculate a standard error in a sample using an equation. In that case all we would get is a standard error, we don’t get to recover the true location of a mean, or difference in mean, or correlation.
What we do get is an extremely reasonable approximation of the standard deviation of the sampling distribution. And what is that: the standard error!
What can we do with our bootstrap estimates?
Usually what people do is to use the bootstrap estimates to form a 95% confidence interval. We can determine this empirically by using the quantile function
quantile(bs.samp.dist, .025)
#> 2.5%
#> 0.1764792
quantile(bs.samp.dist, .975)
#> 97.5%
#> 0.3348584If we are willing to assume that the sampling distribution is normally distributed, we can also use the standard error to perform a hypothesis test under a null hypothesis:
More proof that this works on monday!