11 Regression
11.1 A bit more on the bootstrap…
I wanted to talk a bit more about the bootstrap before we move on to regression.
Let’s prove to ourselves that the bootstrap works.
Let’s generate one sample of data from a known normal distribution:
set.seed(19104)
prime.sample <- rnorm(1000, mean=0, sd=5)
mean(prime.sample)
#> [1] 0.1236452
sd(prime.sample)
#> [1] 5.035127From this one sample we can estimate a sampling distribution of this sample mean. To do so we need to calculate a standard error:
Now this sampling distribution is techinically \(t\) distributed, but we have 1000 observations here so the t distribution will have converged on the normal distribution.
So here is this calculated sampling distribution, centered on 0 (though it doesn’t really matter where we center it):
eval <- seq(-1,1, .0001)
plot(eval, dnorm(eval, mean=0, sd=se.calc), col="firebrick", type="l", main="Sampling Distributions")
Now, we know the population in this case, so we can also use that information to calculate the true standard error and sampling distribution:
se.real <- 5/sqrt(1000)
plot(eval, dnorm(eval, mean=0, sd=se.calc), col="firebrick", type="l", main="Sampling Distributions")
points(eval, dnorm(eval, mean=0, sd=se.real), col="darkblue", type="l")
legend("topleft", c("Calculated SampDist", "Real SampDist"), lty=c(1,1), col=c("firebrick","darkblue"))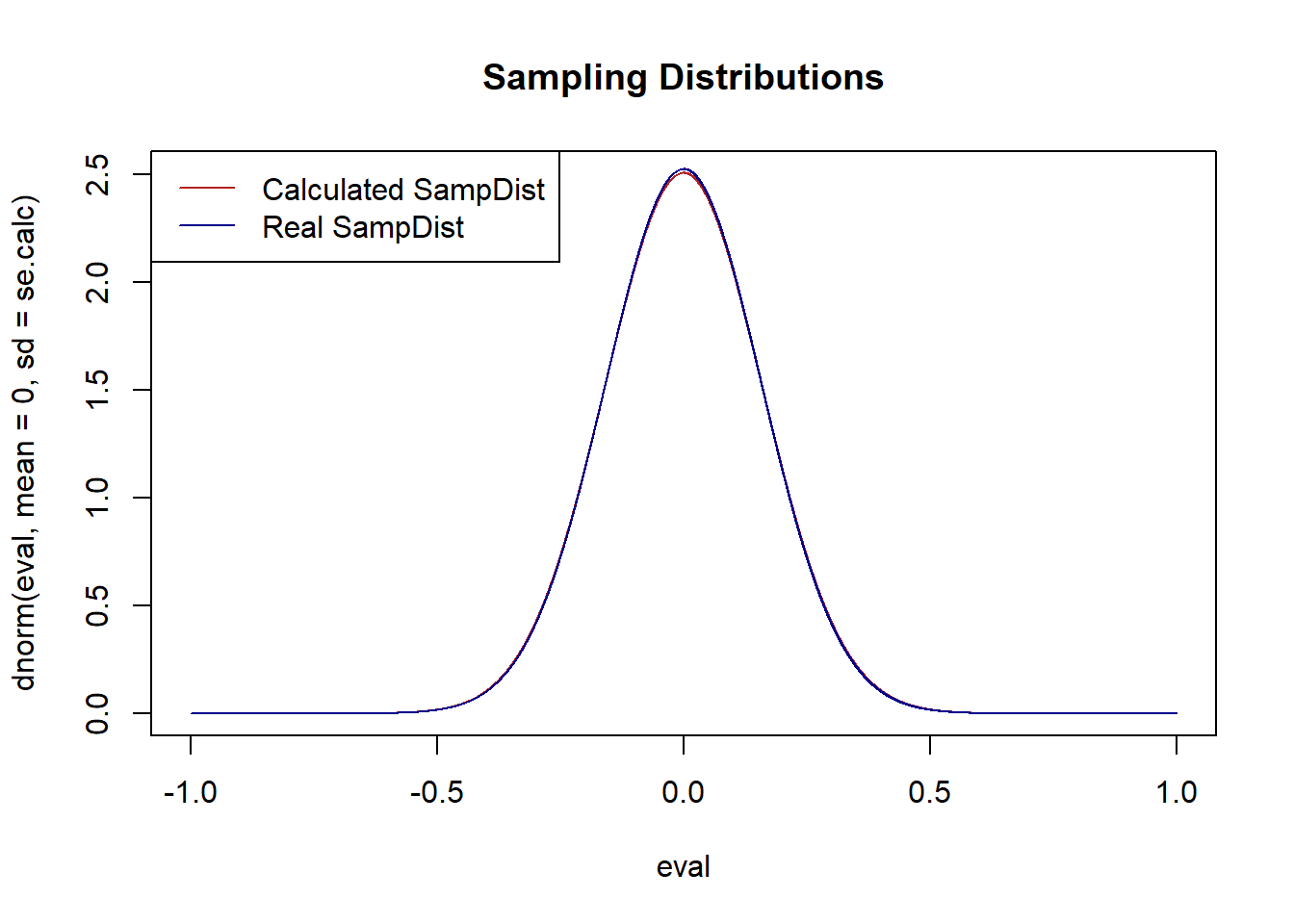
As we have seen they are approximately the exact same shape.
Now, again, because we know the true population we could also repeatedly sample from this population, calculating a mean in each sample, and that should also give us exactly the same sampling distribution.
samp.dist <- rep(NA, 10000)
for(i in 1:10000){
samp.dist[i] <- mean(rnorm(1000, mean=0, sd=5))
}
plot(eval, dnorm(eval, mean=0, sd=se.calc), col="firebrick", type="l", main="Sampling Distributions")
points(eval, dnorm(eval, mean=0, sd=se.real), col="darkblue", type="l")
points(density(samp.dist), col="forestgreen", type="l")
legend("topleft", c("Calculated SampDist", "Real SampDist", "Empirical SampDist"), lty=c(1,1,1), col=c("firebrick","darkblue", "forestgreen"))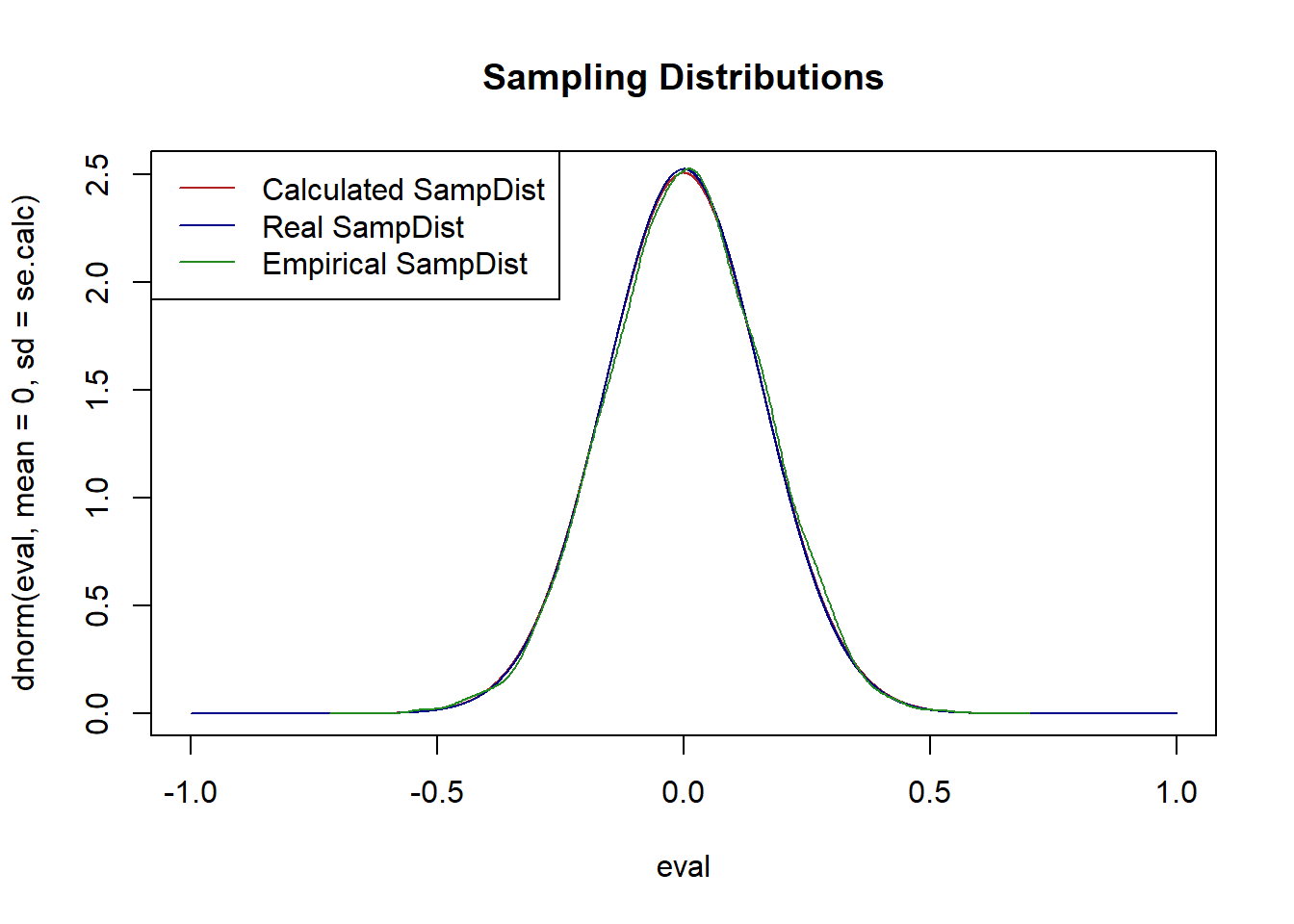
This sampling distribution is also the same.
Finally, what I showed last time is that there is an alternative method to determining the sampling distribution: the bootstrap. To produce the green sampling distribution we repeatedly sampled from our population slightly different sample of 1000, calculating the mean in each, and the resulting distribution is the sampling distribution. What the magic of the bootstrap is that we can get similarly “new samples” by sampling our original data with replacement.
For example here are 9 samples of data compared against the population:
par(mfrow=c(3,3))
eval.pop <- seq(-20,20,.01)
for(i in 1:9){
samp <- rnorm(1000, mean=0, sd=5)
plot(eval.pop, dnorm(eval.pop, mean=0, sd=5), lwd=2, lty=1, type="l",
main=paste("Mean = ", round(mean(samp),2)))
points(density(samp), col="forestgreen", type="l")
}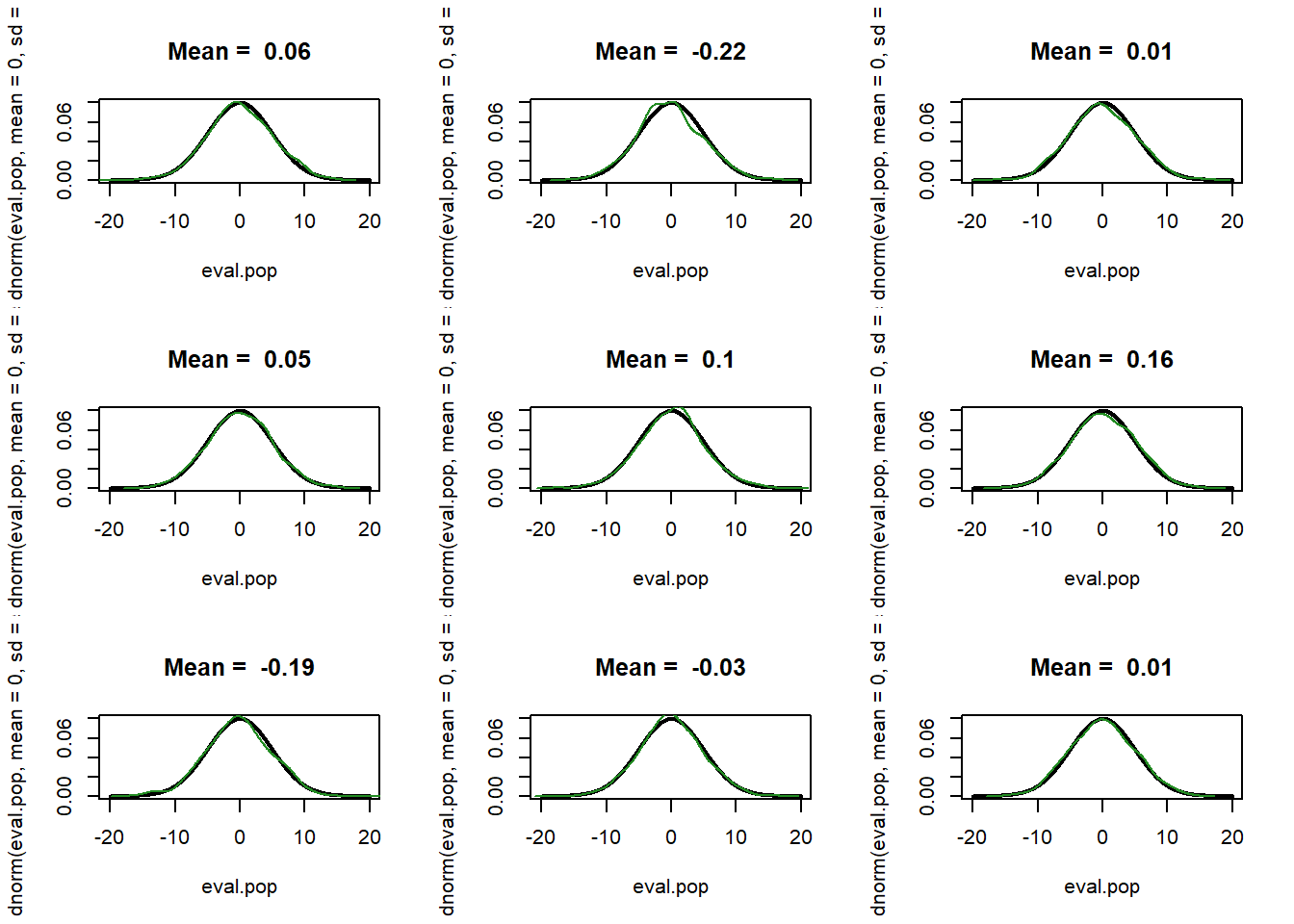
They are all approximately the same, but with a little bit of variation. That “little bit of variation” causes the variation in the mean that generates a sampling distribution.
Again, the claim of the bootstrap is that we can do exactly the same thing by re-sampling from our existing data with replacement:
par(mfrow=c(3,3))
eval.pop <- seq(-20,20,.01)
for(i in 1:9){
samp <- prime.sample[sample(1:length(prime.sample), length(prime.sample), replace=T)]
plot(eval.pop, dnorm(eval.pop, mean=0, sd=5), lwd=2, lty=1, type="l",
main=paste("Mean = ", round(mean(samp),2)))
points(density(samp), col="magenta", type="l")
}
VERY SIMILIARLY, when we re-sample with replacement from our prime sample we get new samples.
If we do this a large number of times (10,000) we will get a new sampling distribution:
bs.samp.dist <- rep(NA,10000)
for(i in 1:10000){
bs.samp.dist[i] <- mean(prime.sample[sample(1:length(prime.sample), length(prime.sample), replace=T)])
}To compare to the other sampling distributions I’m also going to center this distribution on 0, by subtracting the mean from all values (this is only necessary for visualization, this isn’t a usual step in the bootstrap process):
bs.samp.dist <- bs.samp.dist - mean(bs.samp.dist)
plot(eval, dnorm(eval, mean=0, sd=se.calc), col="firebrick", type="l", main="Sampling Distributions")
points(eval, dnorm(eval, mean=0, sd=se.real), col="darkblue", type="l")
points(density(samp.dist), col="forestgreen", type="l")
points(density(bs.samp.dist), col="magenta", type="l")
legend("topleft", c("Calculated SampDist", "Real SampDist", "Empirical SampDist", "BS SampDist"), lty=c(1,1,1,1), col=c("firebrick", "darkblue","forestgreen","magenta"))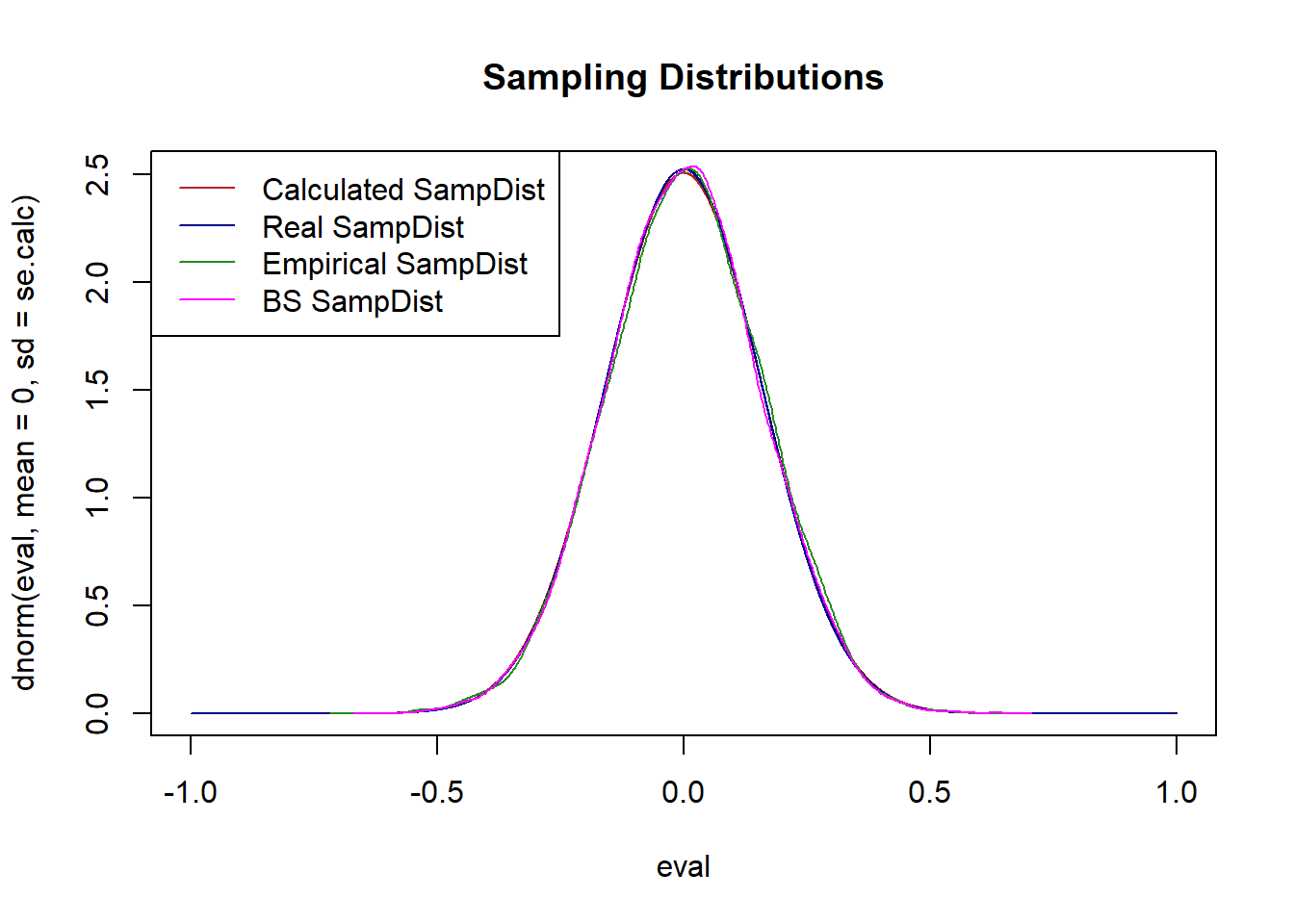
Again, it’s the same!
So 4 ways to calculate a sampling distribution:
- You know the population and you calculate a standard error using the features of the population. (Impossible in real world).
- You know the population and repeatedly sample and calculate the statistic in each. (Impossible in real world).
- You use features of your sample to calculate a standard error using an equation that has been previously worked out by someone. (Requires there to be an equation worked out by someone).
- Generate bootstrap samples and calculate the statistic in each. (Always works.)
So in the real world the options for calculating a standard error/sampling distribution are (3) and (4). If (3) is available to us we always prefer it, but if not, option (4) is available.
Let’s consider a real world example.
Here is some data from the American National Election Study, which is the premier academic study of elections.
library(rio)
anes <- import("https://github.com/marctrussler/IIS-Data/raw/main/ANESFinalProjectData.csv")I’m going to look at how people voted in the democratic primary, classifying candidates into centrist and progressives:
#5 and 6 are Sanders and Warren
anes$vote.centrist.dem[anes$V201021 %in% c(1,2,3,4)] <- 1
anes$vote.centrist.dem[anes$V201021 %in% c(5,6)] <- 0
table(anes$vote.centrist.dem)
#>
#> 0 1
#> 731 1695And I want to know if ideological self placement predicts that:
#1 is very liberal and 7 is very conservative.
anes$ideology <- anes$V201200
anes$ideology[anes$ideology %in% c(-9,-8,99)] <- NA
table(anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 369 1210 918 1818 821 1492 428Here is a cross-table of these two things:
table(anes$vote.centrist.dem, anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 0 165 282 121 89 13 10 4
#> 1 81 492 334 449 74 37 5Even though these are not wide-ranging variables, a correlation can still tell us the degree to which they co-vary:
cor(anes$ideology, anes$vote.centrist.dem, use="pairwise.complete")
#> [1] 0.2734469There is a small correlation between self reported ideology and voting for a centrist candidate in the democratic primary.
Based on recent research by Hakeem Jefferson at Stanford, it might be that the relationship between ideology and vote choice among Black Americans may be different than White Americans. Specifically, Jefferson has found that the cultural context around “liberal” and “conservative” are extraordinarily different for Black Americans such that they are effectively answering a different question, one that (predominantly white) researchers think of completely different.
So let’s look at the correlation among white and among Black Americans sperately.
anes$white.v.black[anes$V201549x==1] <- 1
anes$white.v.black[anes$V201549x==2] <- 0
table(anes$white.v.black)
#>
#> 0 1
#> 726 5963Let’s see if the correlation is different:
#Among White Americans
cor(anes$ideology[anes$white.v.black==1], anes$vote.centrist.dem[anes$white.v.black==1], use="pairwise.complete")
#> [1] 0.2818327
#Among Black Americans
cor(anes$ideology[anes$white.v.black==0], anes$vote.centrist.dem[anes$white.v.black==0], use="pairwise.complete")
#> [1] 0.1446376
#Difference
cor.delta <- cor(anes$ideology[anes$white.v.black==1], anes$vote.centrist.dem[anes$white.v.black==1], use="pairwise.complete") - cor(anes$ideology[anes$white.v.black==0], anes$vote.centrist.dem[anes$white.v.black==0], use="pairwise.complete")
cor.delta
#> [1] 0.1371952Yes! It is substantially lower!
Ok but…. We know that every time we take a new sample we are going to get a slightly different answer. And while the ANES overall is pretty big it only has 700 or so Black Americans, not all of whom voted in the democratic primary. So there theoretically would be a lot of variation in that difference in correlations of .14 if we sampled a large number of times. So we want to perform a hypothesis test of some sort to determine if we can reject the null hypothesis that these two correlations are actually equal to one another in the population.
Looking at our 4 ways of calculating standard errors/sampling distributions above, what can we do to calculate a sampling distribution. Well this is real data so we don’t know the population, which rules out 1 and 2. Do we have a formula to calculate the standard error on the difference between two correlations? No! We don’t even have a formula for one correlation, let alone the difference.
So we have no choice but to use the bootstrap.
What we want to do is to sample rows of our data set with replacement to create “new” datasets. In each we will calculate the difference in the correlations between white and black americans.
To substantially reduce the computing power needed for this, i’m going to reduce the dataset down to just the three variables we need, and only keep observations with non-NA data for all three variables.
boot.data <- anes[c("ideology","vote.centrist.dem","white.v.black")]
boot.data <- boot.data[complete.cases(boot.data),]The bootstrap procedure:
bs.cor.delta <- rep(NA,10000)
for(i in 1:10000){
#Generate the bootstrap dataset
bs.data <- boot.data[sample(1:nrow(boot.data), nrow(boot.data), replace=T),]
#Calculat the same estimate as I calculated in the prime dataset, saving the result each time.
bs.cor.delta[i] <- cor(bs.data$ideology[bs.data$white.v.black==1],bs.data$vote.centrist.dem[bs.data$white.v.black==1],use="pairwise.complete") - cor(bs.data$ideology[bs.data$white.v.black==0],bs.data$vote.centrist.dem[bs.data$white.v.black==0], use="pairwise.complete")
}
Ok! That gave us a sampling distribution for the difference between these two correlations. What can we do with this?
We can use this empirical distribution to generate a confidence interval. We can literally look at the two values which define the range that contains 95% of bootstrap estimates.
#Our original estimate
cor.delta
#> [1] 0.1371952
#CI
quantile(bs.cor.delta, .025)
#> 2.5%
#> 0.01662887
quantile(bs.cor.delta, .975)
#> 97.5%
#> 0.2654626Given that the confidence interval does not overlap 0 we can conclude that there is a lower than 5% probability of seeing a difference in correlation this extreme if the truth was that the two correlations were equal.
We can also use the standard deviation of these bootstrap samples as a standard error:
se <- sd(bs.cor.delta)
#For my own sanity, make sure that the sample distribution is normally distributed:
eval <- seq(-.1, .5, .0001)
plot(density(bs.cor.delta), main="Bootstrap Sampling Distribution")
points(eval, dnorm(eval, mean=cor.delta, sd=se), col="firebrick", type="l")
abline(v=0, lty=2)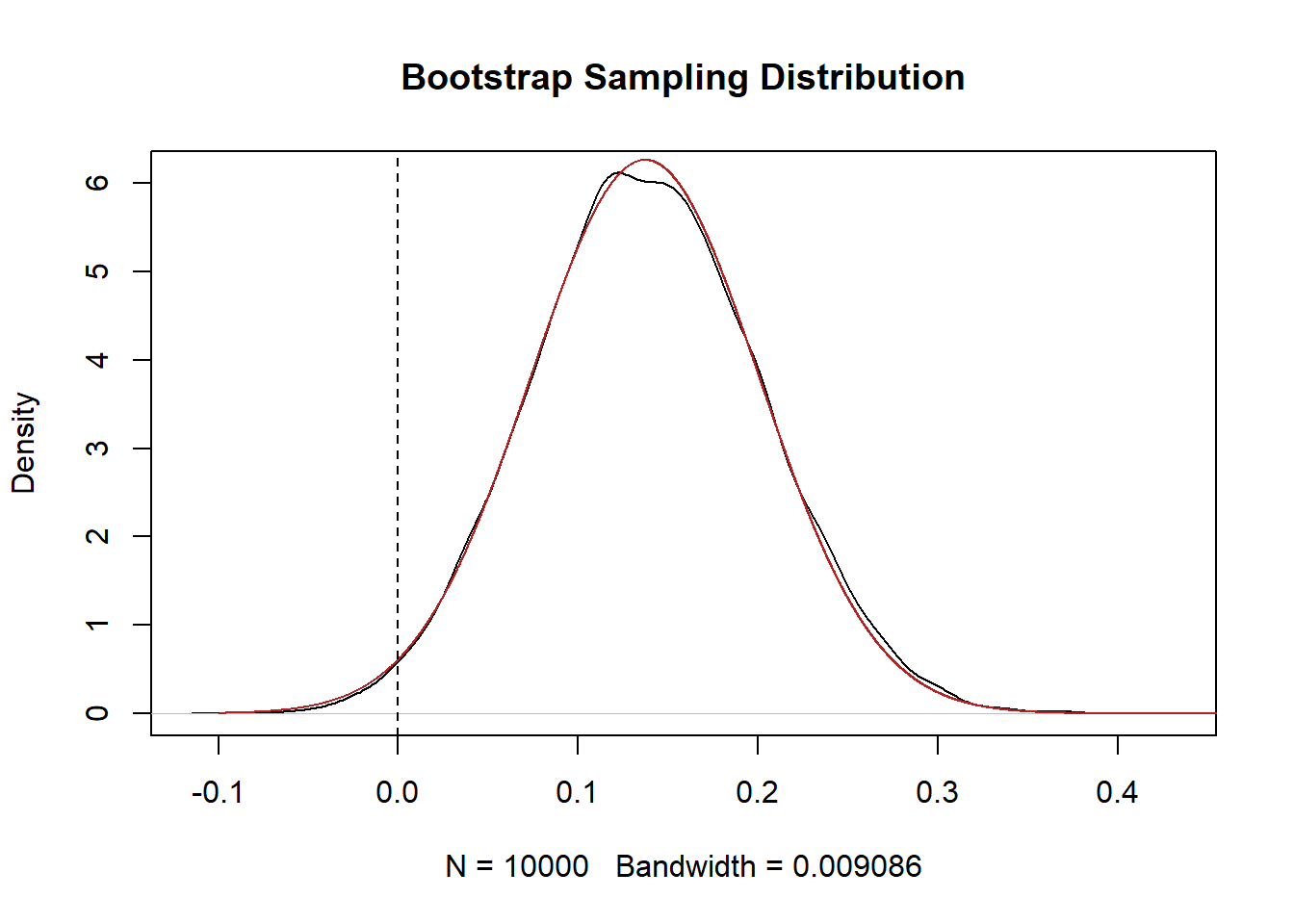
#For null of 0, how many SEs is our test statistic away?
z.score <- (cor.delta-0)/se
#Evalualte under the standard normal
pnorm(z.score, lower.tail=F)*2
#> [1] 0.03125029There is approximately a 3% chance of seeing something as extreme as a difference of .137 if the true difference in correlations was 0.
Cool! That’s genuinely a new thing I didn’t know that we discovered using these data and the bootstrap!
11.2 Regression
So we have correlation, which is fine, but there are two big drawbacks to correlation.
First, the thing that is most helpful about it – that it’s unitless – is also a bit of a drawback. While “correlation” is definitely a word regular people understand, it’s pretty impossible to form a real human sentence about a correlation. Considering what we found above: that the correlation between ideology and voting for a centrist candidate is higher among White then Black Americans. That sentence is fine to say but really lacks nuance. How much does ideology matter? What can I practically say about moving from “very liberal” to “moderate” in terms of the probability of voting for a candidate?
The second thing is that our ability to consider a third variable is very blunt. The only way that we could look at the relationship between ideology and voting for a centrist candidate while taking into account race was very bluntly splitting the sample into two groups. What if our third variable had many levels, or was continuous? Or what if we wanted to also consider the effect of education? Correlation doesn’t really allow us to do any of those things.
What is going to solve both of those problems is regression.
To investigate regression let’s look at the relationship between the age and the feeling thermometer for Black Lives Matter:
summary(anes$V201507x)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -9.00 35.00 51.00 49.04 65.00 80.00
anes$age <- anes$V201507x
anes$age[anes$age<0] <- NA
summary(anes$age)
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 18.00 37.00 52.00 51.59 66.00 80.00 348
summary(anes$V202174)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -9.00 0.00 50.00 47.04 85.00 999.00
anes$blm.therm <- anes$V202174
anes$blm.therm[anes$blm.therm<0 | anes$blm.therm>100] <- NA
summary(anes$blm.therm)
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> 0.0 15.0 60.0 53.3 85.0 100.0 936
#Reduce to only where we have non NAs for those two variables
#this is not strictly necessary but helps with our "by hand" calculations
#down below
anes <- anes[!is.na(anes$age),]
anes <- anes[!is.na(anes$blm.therm),]Before I graph any scatterplot I take a minute to think: what do I expect this graph to look like. What do you expect this graph to look like?
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")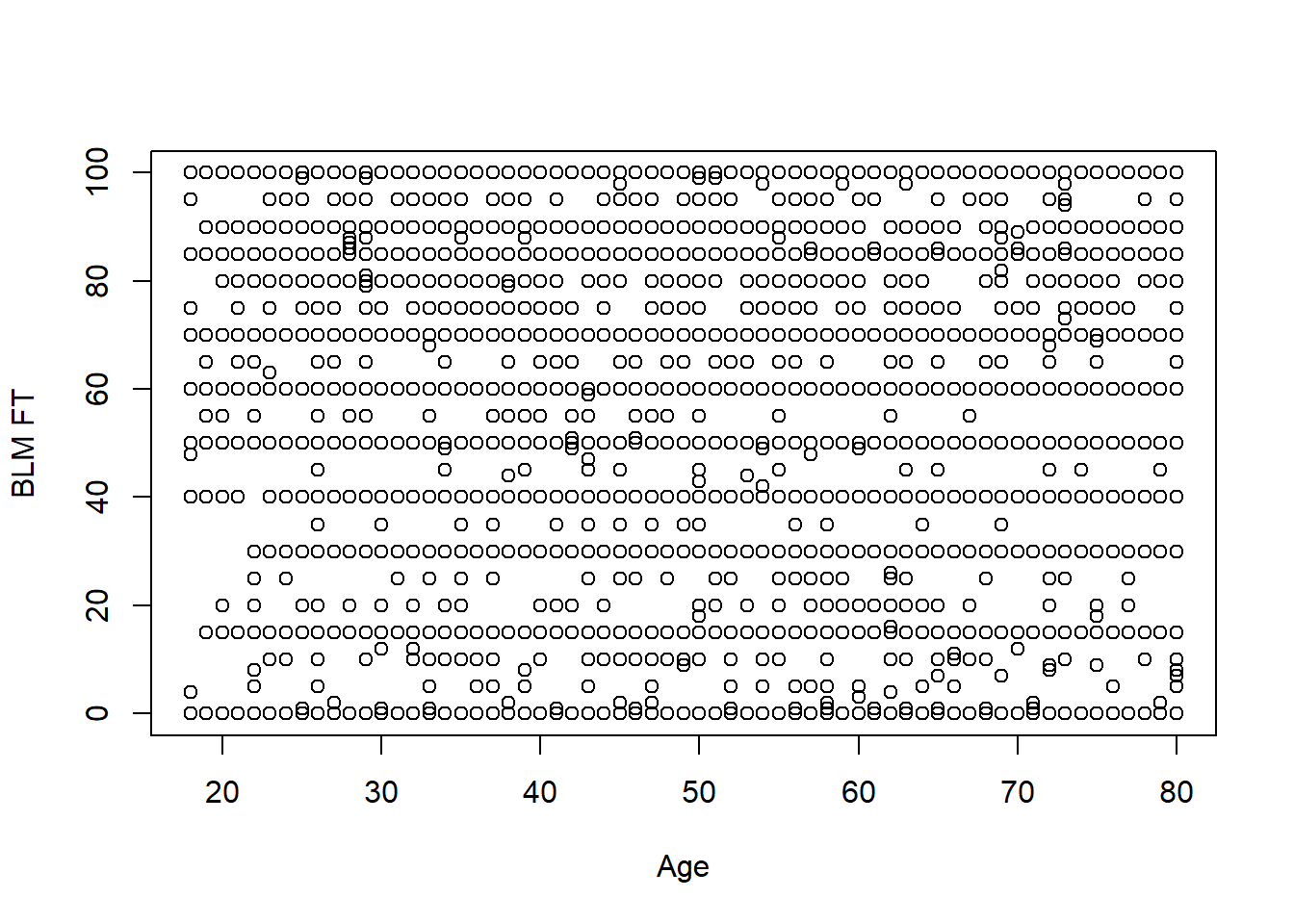
Ah! This looks terrible! It happens, the general problem here is that a lot of people give similar answers on the FT so we have points stacked on top of each other. But still we can also conclude this is not a deterministic relationship: there are lots of 20 year olds that have negative views of BLM and lots of 80 year olds with positive views of BLM.
Now we can use correlation to summarize what’s happening here:
cor(anes$age, anes$blm.therm)
#> [1] -0.1307171There is a very weak negative relationship between these two things.
The goal of regression is to draw a line through these data that summarizes what is going on. How might we do that?
Well one way to do this (this is not the right way) would be to look at each value of age and find the average value of the blm feeling thermometer:
ages <- sort(unique(anes$age))
mean.blm <- rep(NA, length(ages))
for(i in 1:length(ages)){
mean.blm[i] <- mean(anes$blm.therm[anes$age==ages[i]])
}
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
points(ages, mean.blm, type="b", col="firebrick", pch=16, lwd=2)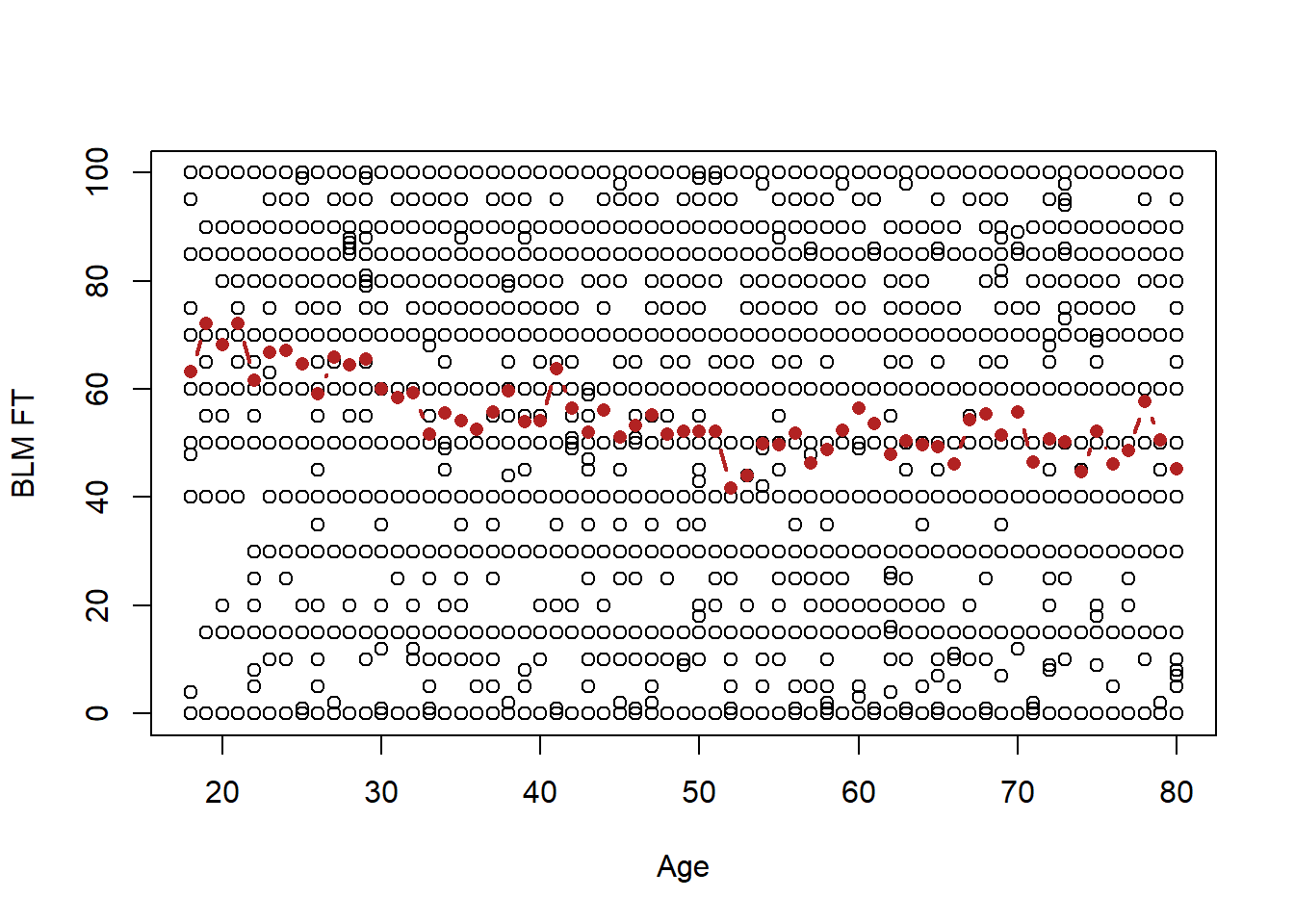
So this progression of averages generally slopes downwards, as we would anticipate given the correlation. But, this doesn’t really allow us to give a answer about the relationship between age and feelings towards BLM.
More problematically, let’s not forget the overall goal of this class, which is to form inferences about the population not just to describe the data that we have. Here we are very religiously following the data from age to age. We would absolutely not claim that each and every up and down of this line is something that is present in the population. For example we are not going to conclude that feelings about BLM generally decline to age 40, but then from age 40 to 41 they go up a bunch, and then they go back down. In other words we are “over-fitting” the data that we have here, taking seriously every quirk in the random sample to be true.
Instead, we want to work to summarize this data in a more averaged way, we want to smooth out the random variations caused by sampling to produce a single line which gives us the overall picture of what is happening between these two variables.
Specifically, we are going to estimate the following equation:
\[ \hat{y} = \hat{\alpha} + \hat{\beta}x_i \]
Where \(\hat{\alpha}\) is the y-intercept, \(\hat{\beta}\) is the slope, and \(x_i\) is each data-points x value.
We are going to get to where these numbers come from shortly, but here are the intercept and slope that the method we are about to cover – Ordinary Least Squares (OLS) regression – will choose:
lm(anes$blm.therm ~ anes$age)
#>
#> Call:
#> lm(formula = anes$blm.therm ~ anes$age)
#>
#> Coefficients:
#> (Intercept) anes$age
#> 67.55 -0.27Here \(\hat{\alpha} = 67.55\) and \(\hat{\beta}=-.27\). What those two pieces of information allow us to do is to draw a line through these data. Specifically, you can evaluate this equation for all values of \(x\), and for each value get a value for \(\hat{y}\), which is the line at that point.
So mechanically
age <- seq(18,80,1)
regression.line <- 67.55 - .27*age
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
points(age, regression.line, type="l", col="firebrick", pch=16, lwd=2)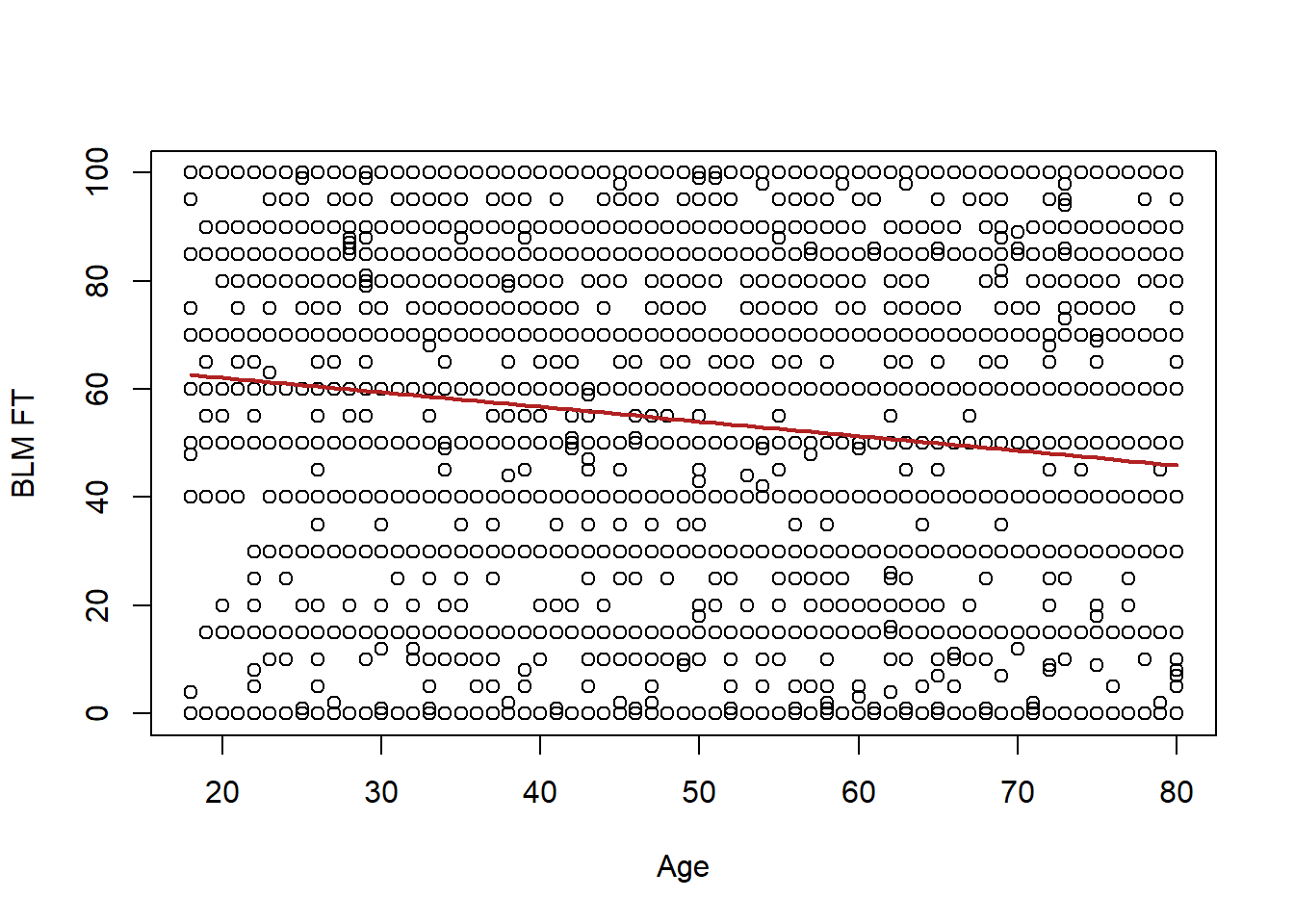
Today we are going to determine (1) how did R choose that line? And on wednesday we will cover (2) How do we interpret that line.
For each data point that we have we can define the residual. The residual is the vertical distance between each data point and the value for the line at that point. Mathematically, the residual is
\[ \hat{u_i} = y_i - \hat{y} \] We would never figure this out one at a time, but for example our first observation is a 46 year old who gave a value of 0 for the blm therm:
anes[1,c("age","blm.therm")]
#> age blm.therm
#> 1 46 0The value of the line at that point would be \(67.55 - .27*46 = 55.13\). As such, the residual for this first individual would be \(0-55.13 = -55.13\).
I mentioned above that the method we use to choose an \(\alpha\) and \(\beta\) is called “Ordinary Least Squares”. It is called this because the method we use to choose these values, is the method which minimizes the sum of the squared residuals.
So specifically, we choose \(\alpha\) and \(\beta\) such that we minimize:
\[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - \hat{y})^2 \]
Subbing in the regression equation above, we get:
\[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - (\hat{\alpha} + \hat{\beta}x_i))^2\\ \hat{u_i}^2 = \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)^2 \]
We want to specifically choose the \(\alpha\) and \(\beta\) values so that this equation generates a small a number of possible.
Now I’ve claimed that the alpha and beta chosen by OLS are the alpha and beta that does that. I will prove that to you in two ways. First through simulation and second through calculus.
Let’s first calculate what the sum of squared residuals is for the chosen alpha and beta
alpha <- 67.55
beta <- -.27
sum.sq <- sum((anes$blm.therm - alpha - beta*anes$age)^2)
sum.sq
#> [1] 8707918Let’s use that sum of the squared residual equation above and first hold constant beta and run through many possibilities for alpha. We should see that the result is the smallest when alpha is equal to 67.55:
alpha <- seq(0,100,1)
beta <- -.27
for(i in 1:length(alpha)){
sum.sq[i] <- sum((anes$blm.therm - alpha[i] - beta*anes$age)^2)
}
plot(alpha, sum.sq, type="l")
abline(v=67.55, lty=2, col="firebrick")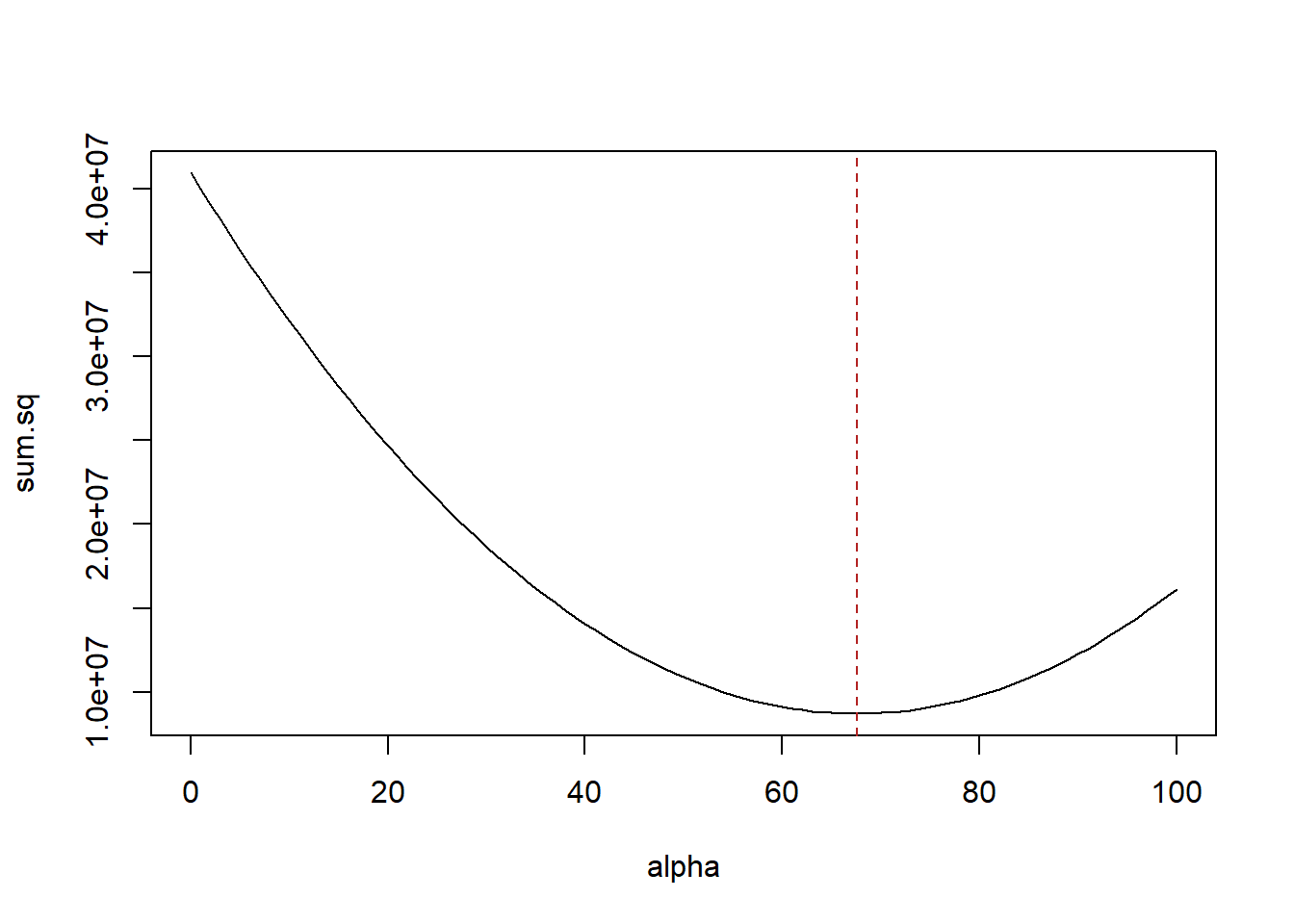
And similarly lets hold constant alpha and cycle through many possibilities for beta:
alpha <- 67.55
beta <- seq(-1,1,.01)
for(i in 1:length(beta)){
sum.sq[i] <- sum((anes$blm.therm - alpha - beta[i]*anes$age)^2)
}
plot(beta, sum.sq, type="l")
abline(v=-.27, lty=2, col="firebrick")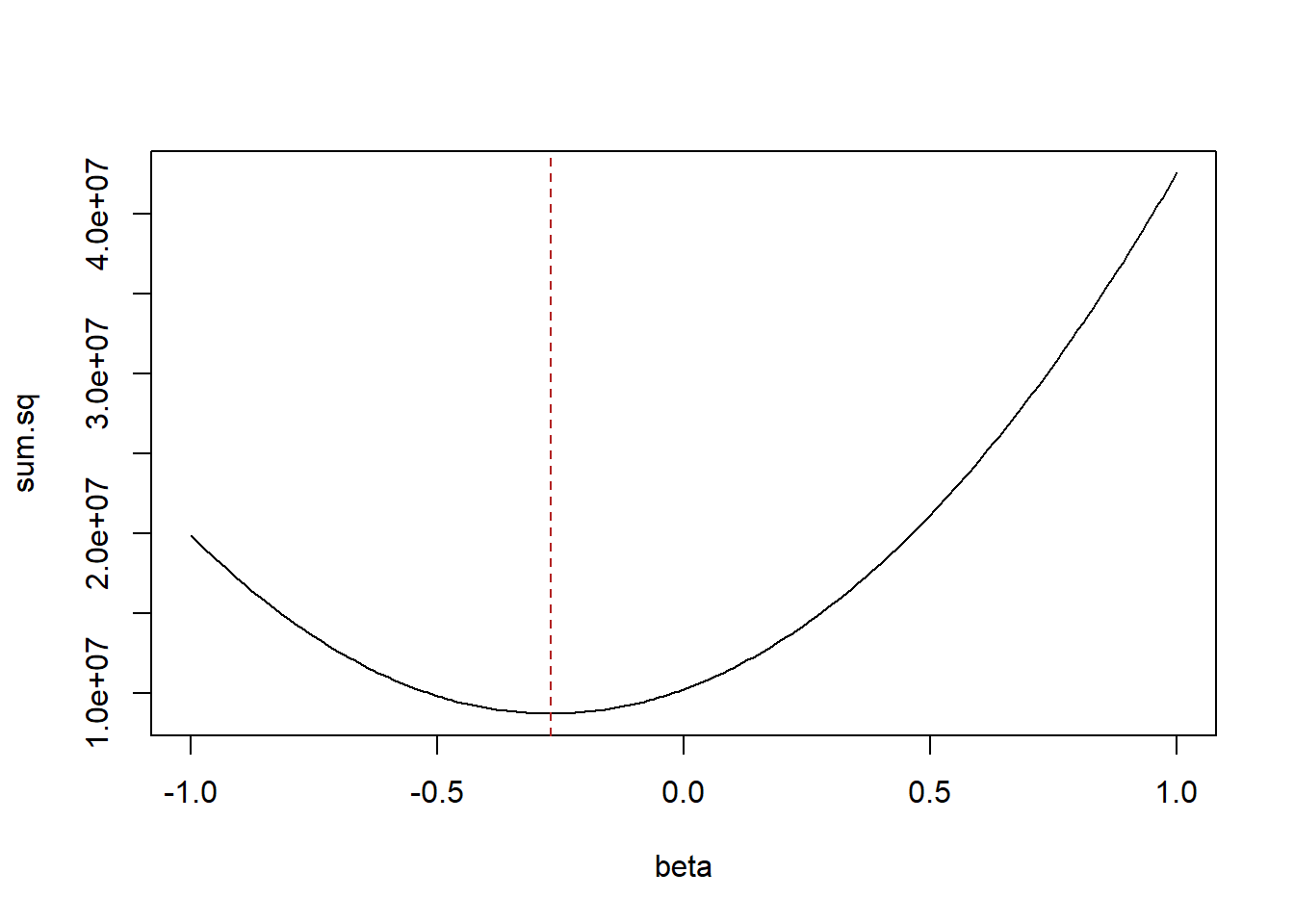
In both cases the sum of the squared residuals is at it’s minimum point at the values for alpha and beta that were chosen by OLS.
We can also show the same thing via calculus. If calculus is not your thing, don’t worry too much about this. But this helps me to mechanically understand what’s happening in OLS regression:
We want to take the partial derivative of the sum of squares equation with respect to both alpha and beta. This will tell us the equations to determine the slope at any point on the above graphs.
For alpha, we can take the first derivative via the power and chain rule:
\[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)^2\\ \frac{\partial \hat{u_i}^2}{\partial \hat{\alpha}} = -2 \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i) \]
If you are rusty on your calculus, the steps we took generate the equation which, for the graphs above, give the slope of the line at any point.
What we are interested partiuclarly interested in is when the slope is equal to zero. Why zero? Because we want the combination of alpha and beta that leads us to the smallest sum of squared residuals, and that happens preceisely when the slope of that curve is zero (a flat line).
So to find this minimum we will set this equation equal to 0 and isolate both \(\hat{\alpha}\) and \(\hat{\beta}\), the two things we need to estimate:
\[ \frac{\partial \hat{u_i}^2}{\partial \hat{\alpha}} = -2 \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)\\ 0 = -2 \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)\\ \]
Divide both sides by \(-2\)
\[ 0 = \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)\\ \]
Distribute the summation operator
\[ 0 = \sum_{i=1}^n y_i - \sum_{i=1}^n\hat{\alpha} - \sum_{i=1}^n\hat{\beta}x_i\\ \]
Because \(\hat{\alpha}\) is a constant, see that is just \(n\) times that constant
\[ 0= \sum_{i=1}^n y_i - n*\hat{\alpha} - \sum_{i=1}^n\hat{\beta}x_i\\ \]
Divide every term by \(n\)
\[ 0= \frac{\sum_{i=1}^n y_i}{n} - \frac{n*\hat{\alpha}}{n} - \hat{\beta}*\frac{\sum_{i=1}^nx_i}{n}\\ \]
Adding up all the values and dividing byt the total \(n\) is just the mean. We can reduce to terms to the mean of y and the mean of x.
\[ 0= \bar{y} - \hat{\alpha}- \hat{\beta}\bar{x}\\ \]
Re-arrange to isolate \(\hat{\alpha}}\)
\[ \hat{\alpha} = \bar{Y} - \hat{\beta}\bar{x} \]
To prove that’s the right equation:
Now we can use that information to isolate beta and minimize.
First do some re-arranging of the sum of squared residuals equation: \[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - \hat{\alpha} - \hat{\beta}x_i)^2\\ \]
Sub in the (now) known definition of \(\hat{\alpha}\)
\[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - (\bar{y} - \hat{\beta}\bar{x}) - \hat{\beta}x_i)^2\\ \]
Distribute the negative 1 and remove the parentheses.
\[ \hat{u_i}^2 = \sum_{i=1}^n (y_i - \bar{y} + \hat{\beta}\bar{x} - \hat{\beta}x_i)^2\\ \] Factor out \(\beta\)
\[ \hat{u_i}^2 = \sum_{i=1}^n [(y_i - \bar{y}) - \hat{\beta}(x_i - \bar{x})]^2\\ \]
Apply the chain and power rule to take the first derivative with respect to \(\beta\)
\[ \frac{\partial \hat{u_i}^2}{\partial \hat{\beta}} = -2 \sum_{i=1}^n (x_i - \bar{x})[(y_i - \bar{y}) -\hat{\beta}(x_i -\bar{x})]\\ \]
Set equal to 0 and divide by -2: \[ 0 = \sum_{i=1}^n (y_i - \bar{y})(x_i - \bar{x}) -\hat{\beta}(x_i -\bar{x})^2\\ \] Move the last term to the other side, and remove the constant \(\beta\) from the summation
\[ \hat{\beta} \sum_{i==1}^n(x_i -\bar{x})^2 = \sum_{i=1}^n (y_i - \bar{y})(x_i - \bar{x}) \\ \] Divid both sides by \(\sum_{i==1}^n(x_i -\bar{x})^2\):
\[ \hat{\beta} = \frac{\sum_{i=1}^n (y_i - \bar{y})(x_i - \bar{x})}{\sum_{i==1}^n(x_i -\bar{x})^2} \\ \]
Again, let’s prove that is the right equation:
sum((anes$blm.therm - mean(anes$blm.therm)) * (anes$age - mean(anes$age)))/
sum((anes$age - mean(anes$age))^2)
#> [1] -0.2699798
#YesSo a little bit of calculus produces the equations for the two paramaters of the line that produce the line which minimizes the sum of the squared residuals.
Looking at the equation for \(\hat{\beta}\) should look familiar.
If we think about the equation for covariance and for variance they are:
\[ \hat{\sigma_{x,y}} = \frac{\sum_{i=1}^n (xi - \bar{x})(y_i - \bar{y})}{n-1}\\ \hat{\sigma_x} = \frac{\sum_{i=1}^n (xi - \bar{x})^2}{n-1}\\ \]
What happens if we divide the covariance by the variance of x?
\[ \hat{\beta} = \frac{\hat{\sigma_{x,y}} = \frac{\sum_{i=1}^n (xi - \bar{x})(y_i - \bar{y})}{n-1} }{\hat{\sigma_x} = \frac{\sum_{i=1}^n (xi - \bar{x})^2}{n-1}}\\ \hat{\beta} = \frac{\sum_{i=1}^n (y_i - \bar{y})(x_i - \bar{x})}{\sum_{i==1}^n(x_i -\bar{x})^2} \\ \hat{\beta} = \frac{\hat{\sigma_{x,y}}}{\hat{\sigma_x}} \\ \]
The regression coefficient is just the covariance of the two variables divided by the variance of one of the variables.
To prove that for the above:
11.3 Interpreting Regression Output
We have uncovered the equations used to generate an alpha and beta to draw the line we see above. Now that we have that line, how do we interpret the main regressionwe have been discussing?
plot(anes$age, anes$blm.therm, xlab="Age", ylab="BLM FT")
abline(lm(anes$blm.therm ~ anes$age), col="firebrick", lwd=2)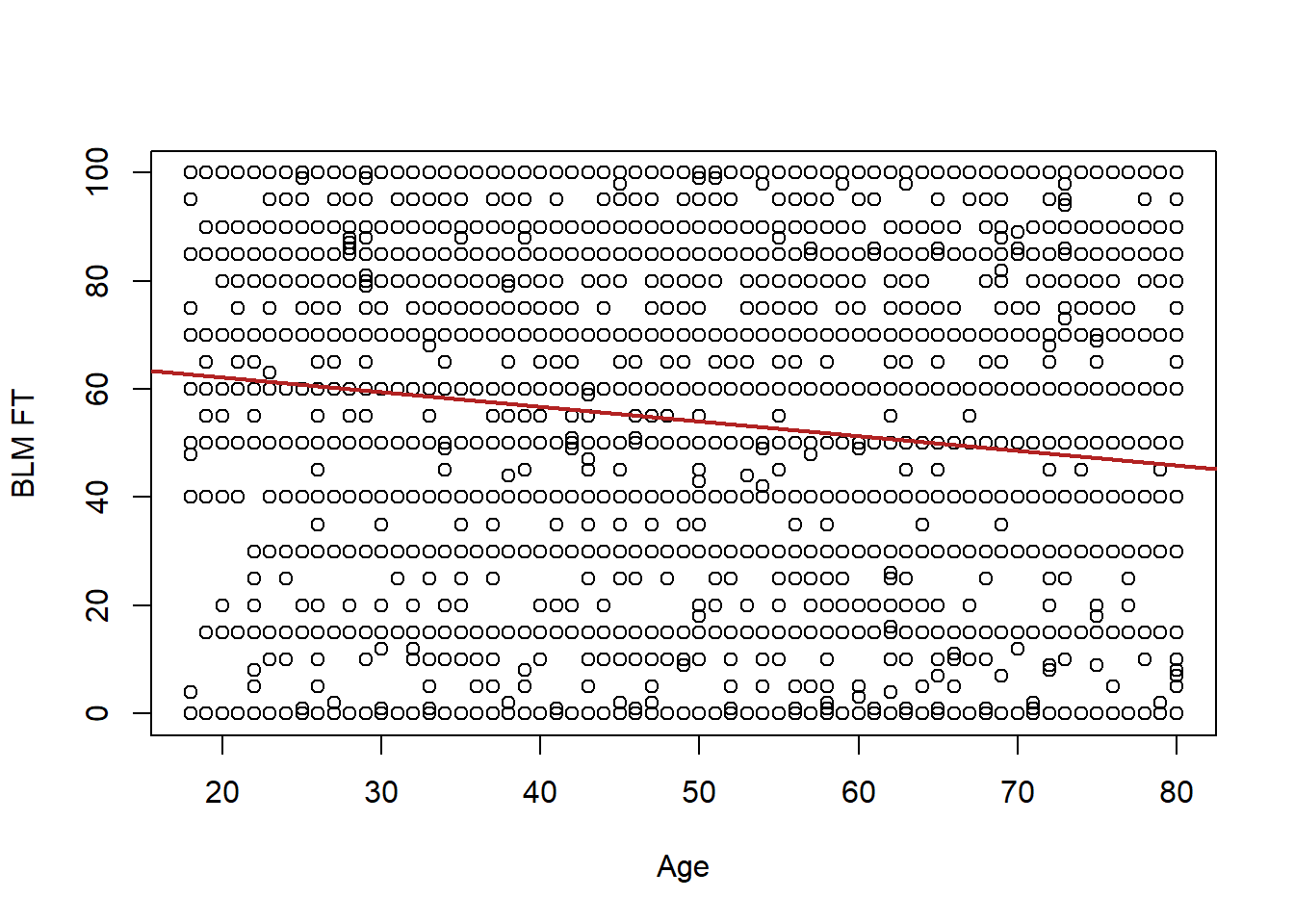
If we save the output of the regression, and use the summary command, we get all sorts of information:
m <- lm(anes$blm.therm ~ anes$age)
#Can also do
m <- lm(blm.therm ~ age, data=anes)
summary(m)
#>
#> Call:
#> lm(formula = blm.therm ~ age, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -62.690 -33.381 4.049 32.202 54.049
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 67.54966 1.32870 50.84 <2e-16 ***
#> age -0.26998 0.02437 -11.08 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.12 on 7062 degrees of freedom
#> Multiple R-squared: 0.01709, Adjusted R-squared: 0.01695
#> F-statistic: 122.8 on 1 and 7062 DF, p-value: < 2.2e-16Let’s use what we know so far to investigate what it is we are seeing here.
At the top we get information on the distribution of the residuals.
To make this explicit, here’s how we could generate that same row:
residuals <- anes$blm.therm - (m$coefficients["(Intercept)"] + m$coefficients["age"]*anes$age)
summary(residuals)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -62.690 -33.381 4.049 0.000 32.202 54.049The two numbers for alpha and beta are present in the “Estimate” column. These are generated using the equations we’ve derived.
The remaining columns give a hypothesis test. How could we determine which hypothesis is being tested? Well a t value is “how many standard errors the estimate is from the null. So:
\[ 50.84 = \frac{67.55 -\beta_{H0}}{1.33}\\ 67.6172 = 67.55 - \beta_{H0}\\ \beta_{H0} \approx 0 \]
So we are getting hypothesis tests that these coefficients are equal to 0, or not.
This makes a lot of sense for the regression coefficient on age. We care a lot about whether a coefficient is 0, or not, because 0 is a flat line! This has a very high t-value and a very low p-score, so we would reject the null hypothesis that the slope in the population is 0. More next week on this hypothesis test!
Do we care if alpha is 0 or not? Well… in real terms what is alpha?
It is the value of \(\hat{y}\) where the line crosses the y axis. We can see that mathematically:
\[ \hat{y} = 65.77 - .27*age_i\\ \hat{y} = 65.77 - .27*0\\ \hat{y} = 65.77 \\ \]
So it is the predicted value of y when x is 0. What does an x of 0 mean here? A newborn? This is how newborns feel about BLM? Do we care about that at all?
No! Of course not. Having an \(\alpha\) is a pre-requisite to drawing a line. Like mechanically, the two ingredients to a line are its intercept and its slope. So we need to define this value, but that does not mean that it is a meaningful number.
What’s more, the hypothesis test is definitely not a meaningful hypothesis test. Do we care if the predicted level of support of BLM of newborns is 0, or not? No! Definitely not. I actually don’t even like that they give you a statistical test for this value.
Let’s move on to beta, which is the estimate for age. We have seen that it is -.27, what does that mean?
You have seen a slope before being defined as rise over run, and this is just what this number is. For every 1 unit increase in X, Y goes down by .27.
When we say 1 unit in a regression, we mean 1 unit in our number system. As in the difference between 1 and 2, and 100 and 101, and 567 and 568. This will be true for absolutely every OLS regression we ever run and you should really internalize it right now. The beta coefficient is how a 1 unit change in x relates to a \(\beta\) change in y.
The best thing about this is how it allows us to form normal human sentences about this relationship. As a person gets 1 year older their feelings about BLM drop .27 points on average.
Note also that we can scale this up or down: If a one unit change in x is -.27, what is a 10 unit change in x? 2.7! So we might also say that as a person gets 10 years older, their feelings about BLM drop 2.7 points on average. Also good!
What this means, however, is that if we re-scale our x variable then \(\beta\) will change, even if the underlying relationship does not.
For example what if we had age in months?
anes$age.months <- anes$age*12
plot(anes$age.months, anes$blm.therm, xlab="Age", ylab="BLM FT")
abline(lm(anes$blm.therm ~ anes$age.months), col="firebrick", lwd=2)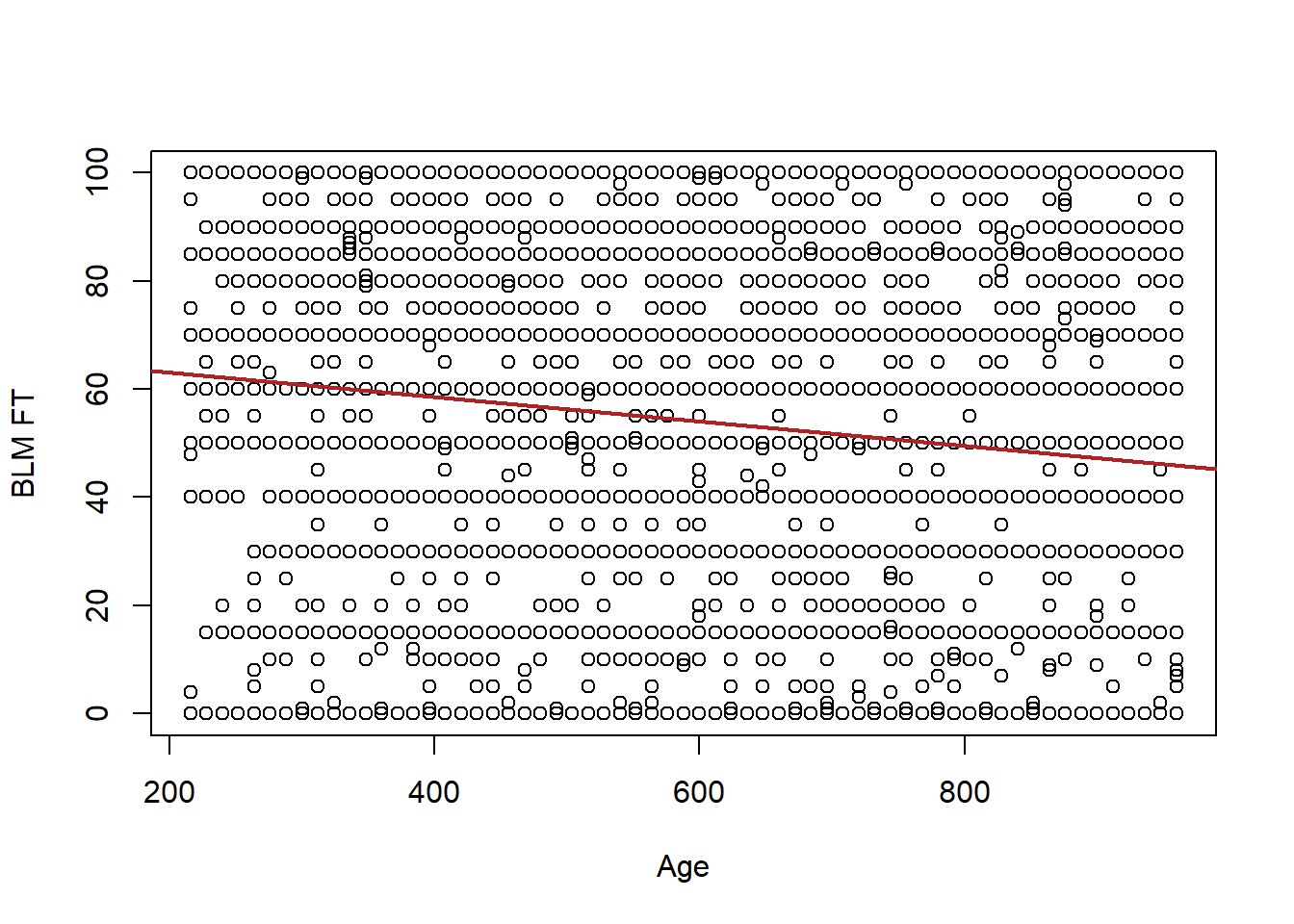
m2 <- lm(blm.therm ~ age.months, data=anes)
summary(m2)
#>
#> Call:
#> lm(formula = blm.therm ~ age.months, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -62.690 -33.381 4.049 32.202 54.049
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 67.549664 1.328699 50.84 <2e-16 ***
#> age.months -0.022498 0.002031 -11.08 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.12 on 7062 degrees of freedom
#> Multiple R-squared: 0.01709, Adjusted R-squared: 0.01695
#> F-statistic: 122.8 on 1 and 7062 DF, p-value: < 2.2e-16Visually we can see that the relationship looks the same, we have just re-scaled the x-axis of the graph. Age explains no more or less than it did when it was measured in years.
Looking at the coefficient on age.months we see that it is smaller than it was before. Because we know that this is how a 1-unit change in x relates to a change in y, we know that this does not mean that age is “less important” in this second regression. Instead, we are now measuring the impact of a change in 1 month on BLM feelings instead of 1 year.
Indeed if we multiply that coefficient by 12:
m2$coefficients["age.months"]*12
#> age.months
#> -0.2699798We return the original coefficient.
Think this through in relation to what we discovered last time that the regression coefficient is simply the covariance of x and y divided by the variance of x. When we were discussing covariance we found that it is completely sensitive to the scale of the variables. Correlation divided by the product of the variance of x and y which standardized the variable to 0,1. Regression, on the other hand, only divides by the variance of the explanatory variable. This means that regression coefficients are standardized based on whatever x is scaled to be at the current moment.
How does this interpretation of the beta coefficient relate to other types of variables?
Let’s look at how being a liberal vs being a conservative or moderate influences your opinions of BLM:
attributes(anes$V201200)
#> NULL
anes$ideology <- anes$V201200
anes$ideology[anes$ideology %in% c(-9,-8,99)] <- NA
table(anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 327 1091 804 1537 696 1267 360
anes$liberal[anes$ideology<4] <- 1
anes$liberal[anes$ideology>=4] <- 0
table(anes$liberal, anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 0 0 0 0 1537 696 1267 360
#> 1 327 1091 804 0 0 0 0Now this scatterplot is not going to look great, because you can only take on two values for the x variable.
plot(anes$liberal, anes$blm.therm)
But all that regression requires is for your two variables to be numeric, and so nothing in the equations for alpha and beta are broken by this.
Let’s see what regression says:
m3 <- lm(blm.therm ~ liberal, data=anes)
summary(m3)
#>
#> Call:
#> lm(formula = blm.therm ~ liberal, data = anes)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -78.439 -23.054 1.946 21.561 61.946
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 38.0544 0.4774 79.71 <2e-16 ***
#> liberal 40.3844 0.7898 51.13 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 29.66 on 6080 degrees of freedom
#> (982 observations deleted due to missingness)
#> Multiple R-squared: 0.3007, Adjusted R-squared: 0.3006
#> F-statistic: 2614 on 1 and 6080 DF, p-value: < 2.2e-16Here we have an intercept of 38.05, and a beta of 40.38.
Let’s start with the intercept, what does this intercept represent? Remember, the intercept is the average value of y when x=0, as shown mechanically by the regression equation.
This is the average value of the BLM thermometer among non-liberals. That is what it means to be 0 on this variable.
What does the slope on liberal mean? This is the effect of a 1 unit change in x on y, so moving one unit on y increases the average person’s blm thermometer by 40.38 points. Ok but what does this mean in real human terms? A one unit change in this variable indicates us moving from one group to another. We have specifically set up this variable in a way that works extremely well with regression, because changing “1-unit” brings us from one group to another. So the difference in blm feelings between liberals and non-liberals is 40.38 points.
What is the average level of feeling towards BLM among liberals?
We can answer this via the regression equation. Our predicted y is equal to
\[ \hat{y} = 38.05 + 40.38*Liberal_i \]
So we can turn liberal on and off to get that answer:
\[ \hat{y} = 38.05 + 40.38*1\\ \hat{y} = 78.43 \]
Let’s compare that to the t.test of the difference in means between these two groups on this variable, which we have already learned about:
t.test(anes$blm.therm ~ anes$liberal)
#>
#> Welch Two Sample t-test
#>
#> data: anes$blm.therm by anes$liberal
#> t = -57.181, df = 6005.6, p-value < 2.2e-16
#> alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
#> 95 percent confidence interval:
#> -41.76891 -38.99987
#> sample estimates:
#> mean in group 0 mean in group 1
#> 38.05440 78.43879The two means are 38.05 and 78.43. So OLS regression with a binary x variable exactly uncovers the means of the two groups, with beta representing the difference between those two means.
This is super helpful, and one of the reasons why I’ve made such a big deal about indicator variables throughout the semester. Indicator variables are great because they work extremely well with the math of OLS. OLS uncovers the effect of 1 unit shifts, and a 1 unit shift in an indicator indicates group membership.
What about if we use the un-altered ideology variable as our dependent variable? Remember that ideology is a 7-point scale where 1 is “very liberal” and 7 is “very conservative”.
table(anes$ideology)
#>
#> 1 2 3 4 5 6 7
#> 327 1091 804 1537 696 1267 360
plot(anes$ideology, anes$blm.therm)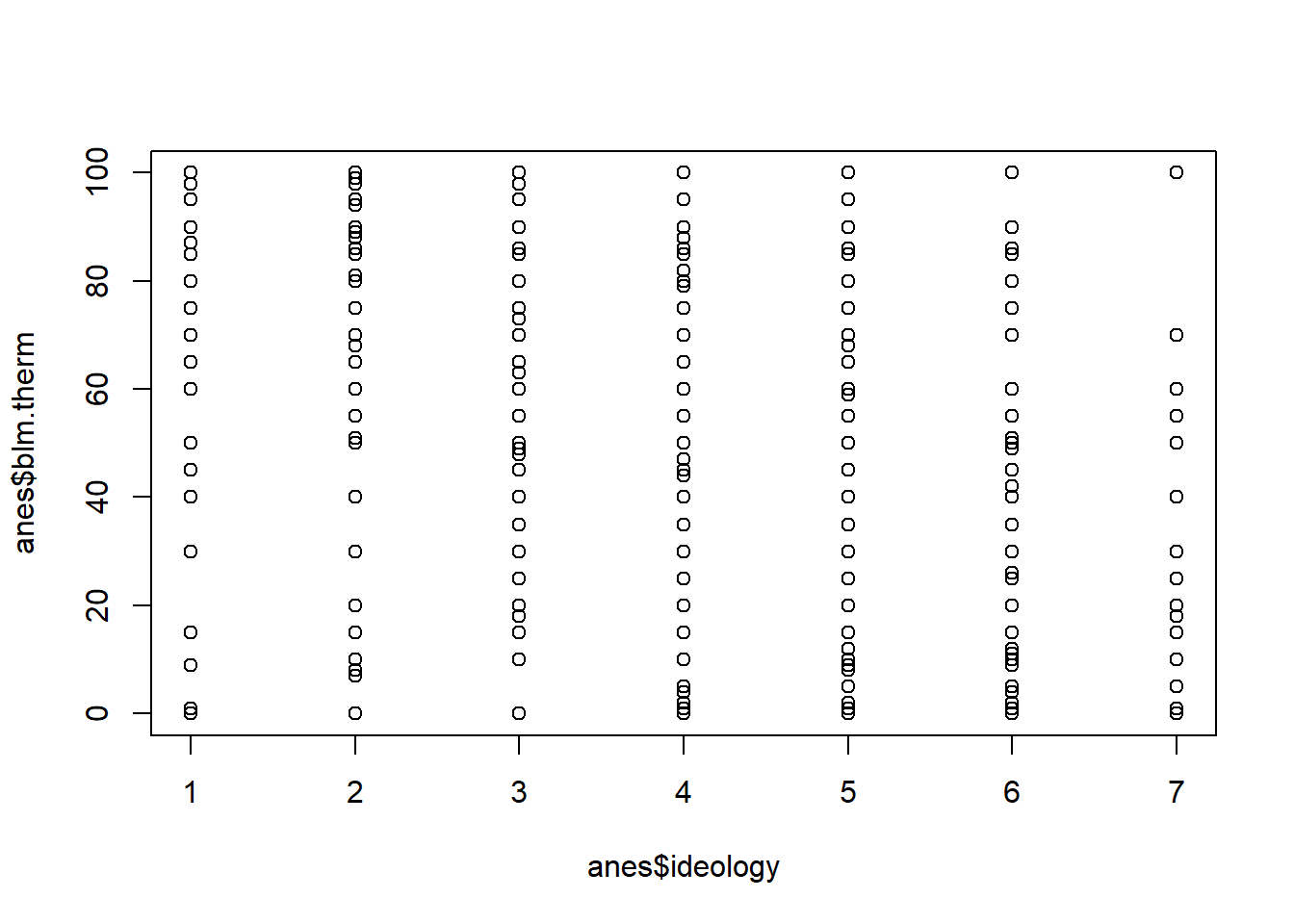
m4 <- lm(blm.therm ~ ideology, data=anes)What does the intercept mean in this case? This is the average value of y when x is 0. Can x be zero? No! Definitely not, so this is a completely meaningless number.
What does beta mean in this case? For every 1 unit change in x your feelings about BLM drop 14.5 points. What does that mean in terms of this variable? Every 1 step more conservative you get you drop 14.5 points in terms of your feelings about BLM.
Now here’s a question, if we use our regression equation to determine the predicted y at 1, 2, 3…7, will that also recover the mean blm thermometer at each of those points?
ideology <- 1:7
yhat <- m4$coefficients["(Intercept)"] + m4$coefficients["ideology"]*ideology
yhat
#> [1] 97.11784 82.62057 68.12331 53.62604 39.12877 24.63150
#> [7] 10.13424
plot(anes$ideology, anes$blm.therm)
points(ideology, yhat, col="firebrick", type="b", pch=16)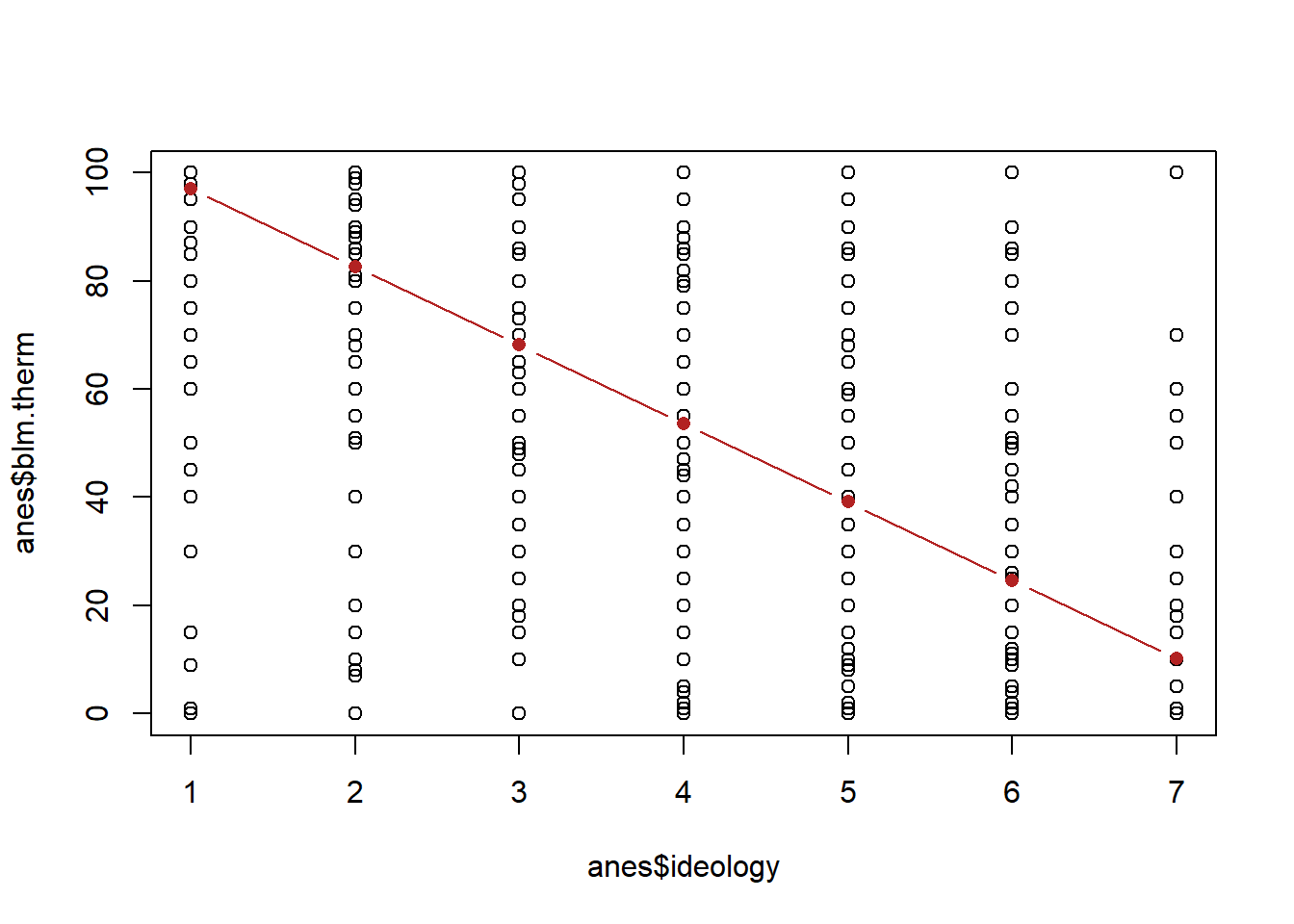
Is that the same as:
ybar <- NA
for(i in 1:7){
ybar[i] <- mean(anes$blm.therm[anes$ideology==i],na.rm=T)
}
plot(anes$ideology, anes$blm.therm)
points(ideology, yhat, col="firebrick", type="b", pch=16)
points(ideology, ybar, col="dodgerblue", type="b", pch=16)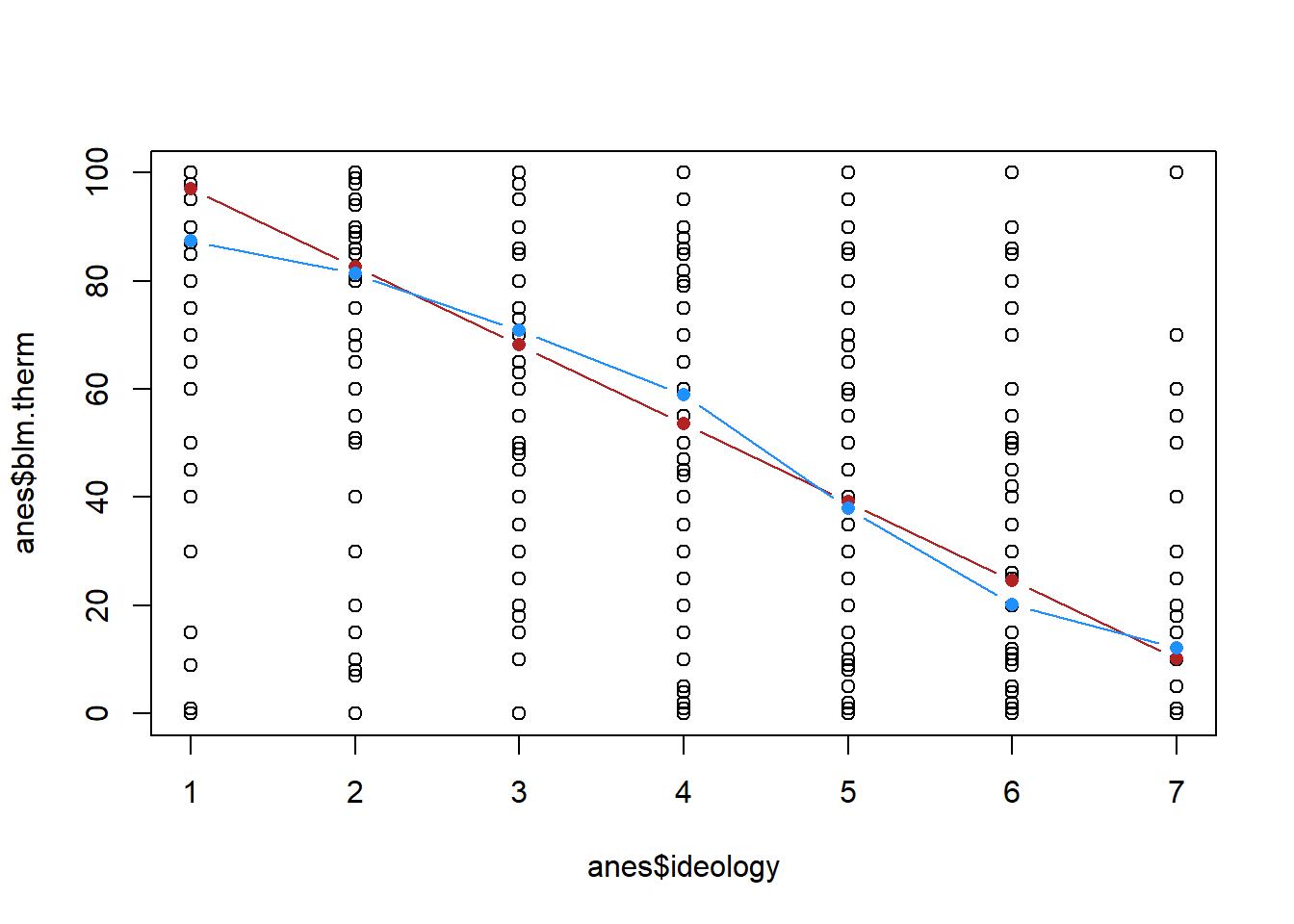
They are definitely not the same! The red line, the regression line, is constrained to being a straight line. the blue line, the connected means, is not. Which of these, in this case, better represents this data?
Regression assumes that everything you put into it is a continuous variable. That means it thinks that the variable ranges from negative to positive infinity, and that each number is evenly spaced. We are necessarily treating, with the red line, the jump from very liberal to liberal the same as the jump from somewhat liberal to moderate. Looking at the blue line, it’s somewhat clear that each of these jumps is not uniformly important. The jump from 1 to 2 and from 6 to 7 is smaller than the jumps in between. Regression returns none of that nuance, it just gives us a straight line that averages across these values.
Neither of these are right or wrong, they just present two different perspectives. But it’s important to know what’s going on under the hood in regression so you understand the assumptions you are making about your variables.
11.4 An example using what we’ve learned so far
Let’s use what we’ve learned so far to investigate the Arizona data from the 2022 election we’ve worked with before:
sm.az <- import("https://github.com/marctrussler/IIS-Data/raw/main/AZFinalWeeks.csv")I want to investigate, relative to the population we are studying (likely Arizona voters) who is in this sample. We are not going to get in to how weighting works in this class, but the basic intuition is that we define groups, and then give individual higher weights if not enough people from their groups are in the sample, relative to the population. So if we run a sample and we don’t have enough women, all women will get a higher weight to make up for it. A weighting algorithm does this simultaneously for many groups (here it is age, gender, education, race, and 2020 presidential vote). But if we see a relationship between a particular variable and the weight variable, it means that we are using weights to make up for the fact that not enough people from that group are in our sample.
Here is the relationship between age and the weight variable
plot(sm.az$age, sm.az$weight, xlab="Age", ylab="Weight")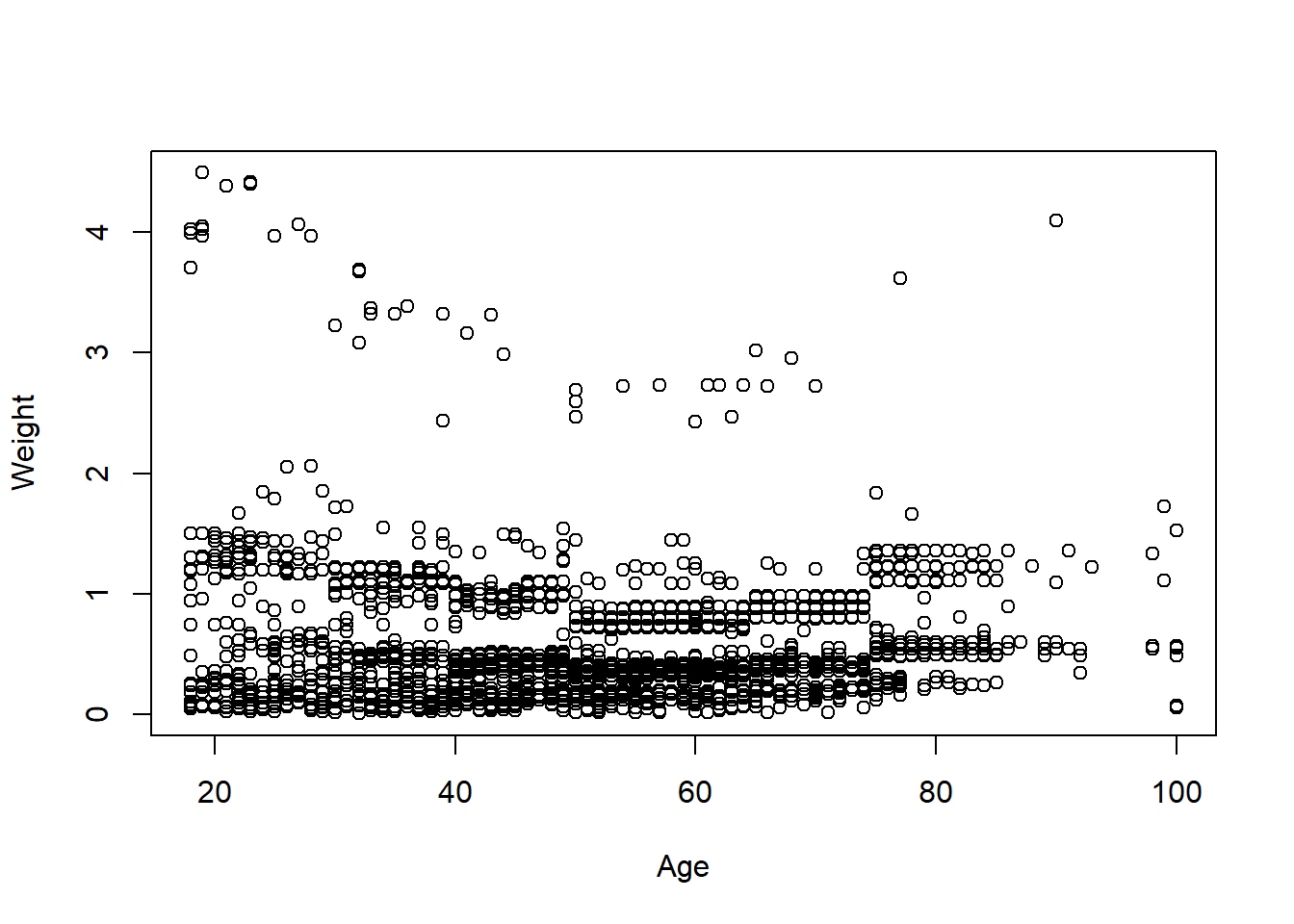
Bit of a messy relationship that is hard to summarize without regression. Here is the regression output for this relationship:
m <- lm(weight ~ age, data=sm.az)
summary(m)
#>
#> Call:
#> lm(formula = weight ~ age, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6194 -0.2602 -0.1573 0.2313 3.8457
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.676267 0.031362 21.563 < 2e-16 ***
#> age -0.001591 0.000545 -2.918 0.00354 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5105 on 3045 degrees of freedom
#> Multiple R-squared: 0.002789, Adjusted R-squared: 0.002462
#> F-statistic: 8.517 on 1 and 3045 DF, p-value: 0.003544What is the interpretation for the coefficient on the Intercept here. The average weight when age is 0 is .67. Again, this is a fairly useless bit of information. We don’t really care what happens when age is 0. This is just a mechanically necessary number to have in order to draw a regression line.
What is the interpretation for the coefficient on age? For every additional year of age, the weight goes down by around .001. If higher weights mean that individuals from that group are less likely to be in our sample, what does this result mean? It means that younger people were harder to get into our sample (despite being online!).
What about the relationship between race and the weight variable?
Here is what race looks like:
head(sm.az$race)
#> [1] "black" "asian" "hispanic" "black" "black"
#> [6] "white"Can we put this variable into the regression as-is? (We actually can, which we will see later on, but for right now….) No. Regression takes numeric variables and this is a bunch of words. We can’t run a regression on this. We have to do some re-coding.
Let’s create a variable that splits the sample into white and non-white:
sm.az$white <- sm.az$race=="white"
table(sm.az$white)
#>
#> FALSE TRUE
#> 875 2172We’ve seen lots of times that R will helpfully treat a binary variable like 0’s and 1’s, which means that we can now put this into a regression:
m2 <- lm(weight ~ white, data=sm.az)
summary(m2)
#>
#> Call:
#> lm(formula = weight ~ white, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6060 -0.2553 -0.1508 0.2304 3.9130
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.61384 0.01727 35.534 <2e-16 ***
#> whiteTRUE -0.03512 0.02046 -1.716 0.0862 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.511 on 3045 degrees of freedom
#> Multiple R-squared: 0.0009664, Adjusted R-squared: 0.0006384
#> F-statistic: 2.946 on 1 and 3045 DF, p-value: 0.08621What’s the interpretation of the intercept? Of the coefficient?
Finally, let’s see if there is a relationship between approval of Biden and the weight. What does the Biden approval variable look like right now?
table(sm.az$biden.approval)
#>
#> Somewhat approve Somewhat disapprove Strongly approve
#> 665 287 623
#> Strongly disapprove
#> 1449Again, these are just words, but in this case the words have an order. Let’s convert this into a numbered ordinal variable and then put that into the regression:
sm.az$biden.approval.num <- NA
sm.az$biden.approval.num[sm.az$biden.approval=="Strongly disapprove"] <- 0
sm.az$biden.approval.num[sm.az$biden.approval=="Somewhat disapprove"] <- 1
sm.az$biden.approval.num[sm.az$biden.approval=="Somewhat approve"] <- 2
sm.az$biden.approval.num[sm.az$biden.approval=="Strongly approve"] <- 3
table(sm.az$biden.approval.num)
#>
#> 0 1 2 3
#> 1449 287 665 623
m3 <- lm(weight~biden.approval.num, data=sm.az)
summary(m3)
#>
#> Call:
#> lm(formula = weight ~ biden.approval.num, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.5869 -0.2573 -0.1651 0.2282 3.9108
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.580937 0.012720 45.671 <2e-16 ***
#> biden.approval.num 0.006676 0.007563 0.883 0.377
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5093 on 3022 degrees of freedom
#> (23 observations deleted due to missingness)
#> Multiple R-squared: 0.0002578, Adjusted R-squared: -7.302e-05
#> F-statistic: 0.7793 on 1 and 3022 DF, p-value: 0.3774What is the interpretation of the Intercept? Is it meaningful? What is the interpretation of the coefficient? Looking ahead, what does it mean that our p-value is .377?
11.5 Regression with a binary dependent variable
So far all of the regressions that we have run have had a continuous dependent variable. Is that our only option? What happens if we want to use regression on a binary dependent variable?
Let’s make a 0,1 variable of whether someone plans to vote for Mark Kelly (the Democrat) or Blake Masters (the Republican).
sm.az$vote.kelly <- NA
sm.az$vote.kelly[sm.az$senate.topline=="Democrat"] <- 1
sm.az$vote.kelly[sm.az$senate.topline=="Republican"] <- 0
table(sm.az$vote.kelly, sm.az$senate.topline)
#>
#> Democrat Other/Would not Vote Republican
#> 0 0 0 1245
#> 1 1368 0 0And use age to predict that variable:
plot(sm.az$age, sm.az$vote.kelly)
Now this is not a very appealing graph. What does the regression line on this look like?
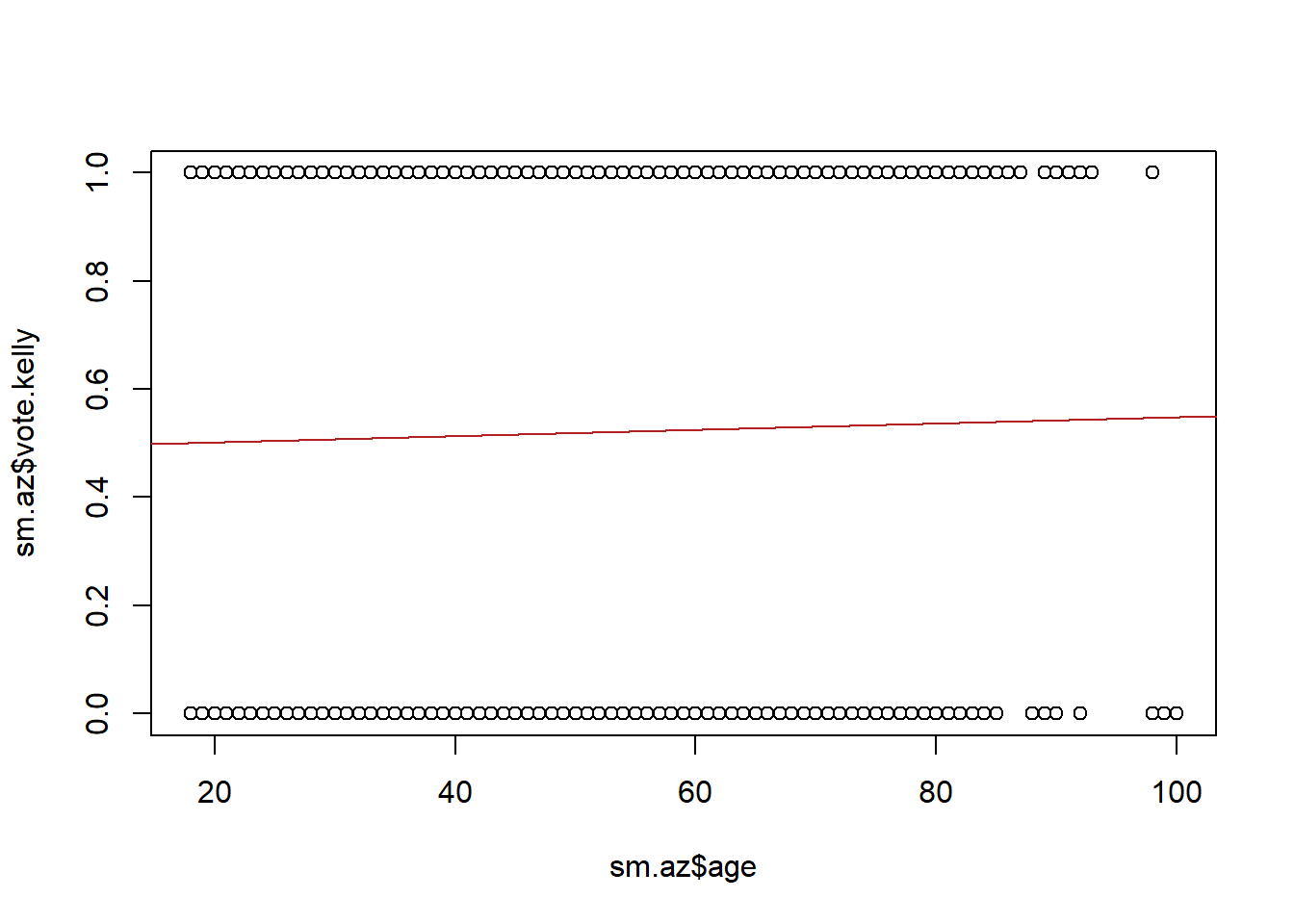
That doesn’t even touch any of the data-points! Is that helpful at all?
Let’s think about what the regression output says:
m4 <- lm(vote.kelly~age, data=sm.az)
summary(m4)
#>
#> Call:
#> lm(formula = vote.kelly ~ age, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.5482 -0.5241 0.4627 0.4753 0.4989
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.4907882 0.0357856 13.715 <2e-16 ***
#> age 0.0005743 0.0006037 0.951 0.342
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4996 on 2611 degrees of freedom
#> (434 observations deleted due to missingness)
#> Multiple R-squared: 0.0003465, Adjusted R-squared: -3.64e-05
#> F-statistic: 0.9049 on 1 and 2611 DF, p-value: 0.3416What is the mathematical interpretation of the intercept?
Remember, that alpha is the average value of y when x is equal to 0. What does it mean when we take the average of a binary/indicator variable? That gives us the probability of that variable being equal to 1. It’s something we have seen repeatedly in this course. So the practical interpretation of this intercept is that the probability of voting for Kelly among a newborn (I know) is approximately 49%.
If that’s what the intercept is giving us, what does the age coefficient mean? For each additional 1 unit change in x, y goes up .0005, on average. This means that every additional year someone ages their probability of voting for Kelly increases by 1 half of a percentage point.
In other words, when we have a binary dependent variable, it converts all of our explanations into probability.
Let’s do another example (with a variable that actually affects Kelly vote prob…)
Let’s look at how the Biden approval variable above relates to voting for Kelly:
m5 <- lm(vote.kelly ~ biden.approval.num, data=sm.az)
summary(m5)
#>
#> Call:
#> lm(formula = vote.kelly ~ biden.approval.num, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.1296 -0.1267 -0.1267 0.2047 0.8733
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.126699 0.007313 17.33 <2e-16 ***
#> biden.approval.num 0.334291 0.004225 79.13 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.2704 on 2595 degrees of freedom
#> (450 observations deleted due to missingness)
#> Multiple R-squared: 0.707, Adjusted R-squared: 0.7069
#> F-statistic: 6261 on 1 and 2595 DF, p-value: < 2.2e-16What is the interpretation of the intercept now? Well we set this variable to be equal to strongly disapprove of Biden at 0, so this is the probability of voting for Kelly when you strongly disapprove of Biden. What is the interpretation of the coefficient on biden.approval.num now? This is now the effect of going from strongly to somewhat disapprove, from somewhat disapprove to somewhat approve, etc. That effect .33. For every step up the approval chain the probability of voting for Kelly increases by 33%. That makes sense!
Now if we try to visualize this it’s going to look terrible:
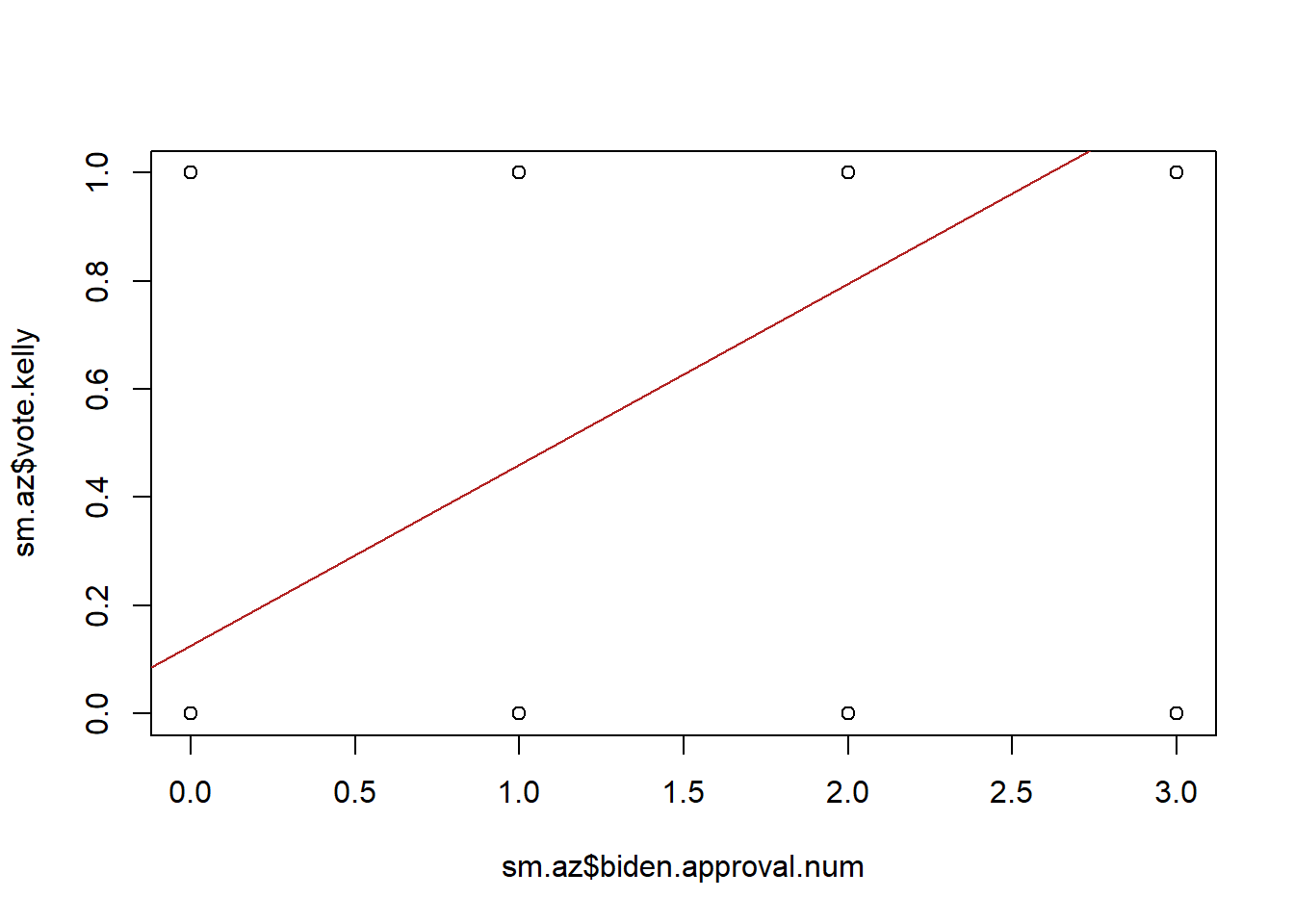
We can somewhat improve this graph by using the jitter feature, which adds a bit of noise to our data so that we can see that each of these dots is actually a fair number of people:
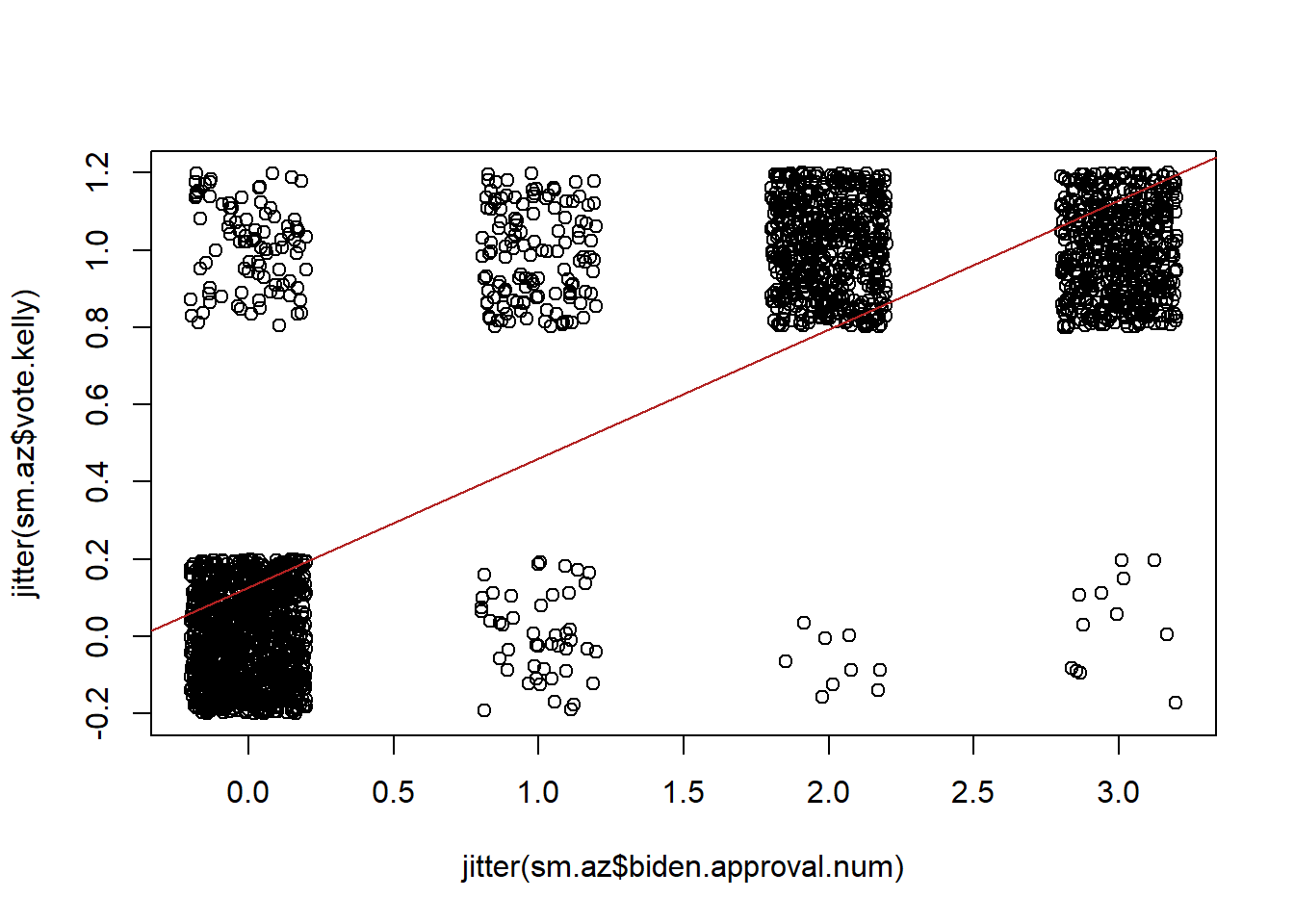
But this graph also reveals another problem here. What is the predicted probability of voting for Kelly at all the levels of Biden approval? How can we mathematically determine that?
m5$coefficients["(Intercept)"] + m5$coefficients["biden.approval.num"]*0:3
#> [1] 0.1266990 0.4609902 0.7952814 1.1295727How would we interpret this last value? If you strongly approve of Biden you have a 112% chance of voting for him! Uh oh! Broken laws of probability!
When we run an OLS regression with a binary dependent variable, it transforms what we are doing into a “Linear Probability Model” or LPM. As we’ve seen, it allows us to interpret our coefficients in terms of the probability of the dependent variable being 1. LPMs are great, and most of the time they work fantastically. I’ve use them throughout my career with no problems.
The major downside to using an LPM is that OLS regression doesn’t know or care what scale your variable are on. It treats every variable like it is a continuous variable that ranges from negative infinity to infinity. There is nothing constraining OLS, in other words, to draw a line that leads to us making a prediction that is outside the interval of \([0,1]\). This is legitimately a big problem if you are specifically using regression to make a prediction, but less of a problem if you are using regression to search for an explanation. Here I’m not super bothered that this prediction falls outside of 0,1 because I am mostly interested in saying that Biden approval has a strong, positive impact on the probability that you are going to vote for Kelly.
If you are interested in using regression for prediction and your outcome variable is binary it is often the case that using an LPM is not appropriate. An example of this would be generating a likely voter model, which definitely needs to range between 0 and 1. In those cases we use a logit or probit model, which are beyond the scope of this course, but are specifically designed to work with binary outcome variables and will not generate predictions outside of the 0,1 interval.
Ultimately any numerical variable can be put into either side of a regression. That being said, you really really have to think about what is happening each and every time. You really have to understand the scale of the variables that you are using in order to correctly interpret what is going on. Every single time.
11.6 Goodness of fit
The final bit of information we get in the regression output is at the bottom, and presents a few different measures of how good your regression fit is, overall.
The value I want to focus on is \(R^2\). Now I may mentioned I have beef with AP stats before. I’ve never actually read an AP stats textbook but for some reason a lot of people come to college with the belief that \(R^2\) is the be all end all of regression. It’s important! But much less so then you might think.
Ok but what is it? \(R^2\) is a measure of how well the \(x\) variable explains the \(y\) variable. It ranges from 0-1 and tells you what percent of the variation in \(y\) is explained by \(x\).
Mathematically:
\[ R^2=\frac{SSR}{SST}\\ SSR=\sum_{i=1}^n (\hat{y_i}-\bar{y})^2\\ SST=\sum_{i=1}^n (y_i - \bar{y_i})^2 \]
So if we visually think about a single point, the SST is how much each point varies from it’s mean. Remember, this is literally the formula for variance, just without the 1/n. So this is giving us the total variation in the y variable.
SSR instead looks at how the predicted variables vary from y. So we are seeing the improvement in fit that is down to having the regression line as opposed to just having the data points.
We can calculate \(R^2\) for the main regression of age on blm.them:
sst <- sum((anes$blm.therm - mean(anes$blm.therm,na.rm=T))^2)
anes$yhat <- coefficients(m)["(Intercept)"] + coefficients(m)["age"]*anes$age
ssr <- sum((anes$yhat - mean(anes$blm.therm,na.rm=T))^2)
r.squared <- ssr/sst
summary(m)
#>
#> Call:
#> lm(formula = weight ~ age, data = sm.az)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6194 -0.2602 -0.1573 0.2313 3.8457
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.676267 0.031362 21.563 < 2e-16 ***
#> age -0.001591 0.000545 -2.918 0.00354 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5105 on 3045 degrees of freedom
#> Multiple R-squared: 0.002789, Adjusted R-squared: 0.002462
#> F-statistic: 8.517 on 1 and 3045 DF, p-value: 0.003544Yes they are the same!
Why is this sometimes helpful to know, but sometimes not?
As above, it really comes down to whether we want to use regression for explanation or prediction.
We will cover prediction in a later week, but right now it should be clear mathematically who we might be able to say: we have a regression for how age predicts BLM thermometer scores. What would our prediction be for how a 120-year-old person would feel about BLM? We can very easily just plug that value in for age and OLS will form a prediction. In these cases, how well your explanatory variable (or variables) is explaining the outcome will be critical in determining whether this is a good or bad prediction.
For explanation we are way less concerned with goodness of fit. Here we might be interested in the question of whether age is an explanation of how people feel about BLM. We find above that it is statistically significant, but the \(R^2\) is very low. Someone might come to me and say: your \(R^2\) is low so your regression is junk! But I don’t really care about that. Of course lots of things influence how someone feels about BLM, so my regression is not going to fully explain each individuals feelings simply based on their age. That’s not what i’m trying to do. I’m simply trying to show that this variable has a non-zero impact.
So \(R^2\) is a helpful number, but a low \(R^2\) does not mean your regression is junk. You have to know what you are using it for.