14 Regression Interaction and Prediction
14.1 Interaction
Let’s continue to work with the California schools data:
library(AER)
#> Loading required package: car
#> Loading required package: carData
#> Loading required package: lmtest
#> Loading required package: zoo
#>
#> Attaching package: 'zoo'
#> The following objects are masked from 'package:base':
#>
#> as.Date, as.Date.numeric
#> Loading required package: sandwich
#> Loading required package: survival
data("CASchools")
#Creating Variables
CASchools$STR <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math)/2
dat <- CASchoolsThe second extension we are interested in are interactions.
Last week we talked about adding polynomial terms. We conceptualized that as a data generating process where the effect of a variable (say, income) changes over its own level. Getting steeper or less steep across its value.
The other thing that we can hypothesize is whether the effect of a variable changes across the levels of a second variable.
Let’s think about this question: Does the effect of income change based on whether the school is a K-6 or K-8? Why might we believe that to be true. It might be that parental income has more effect on learning at lower grade levels, and at higher grade levels teacher quality matters more. So my hypothesis will be that the effect of income will be higher in k-8 schools.
Let’s first look at the base relationship:
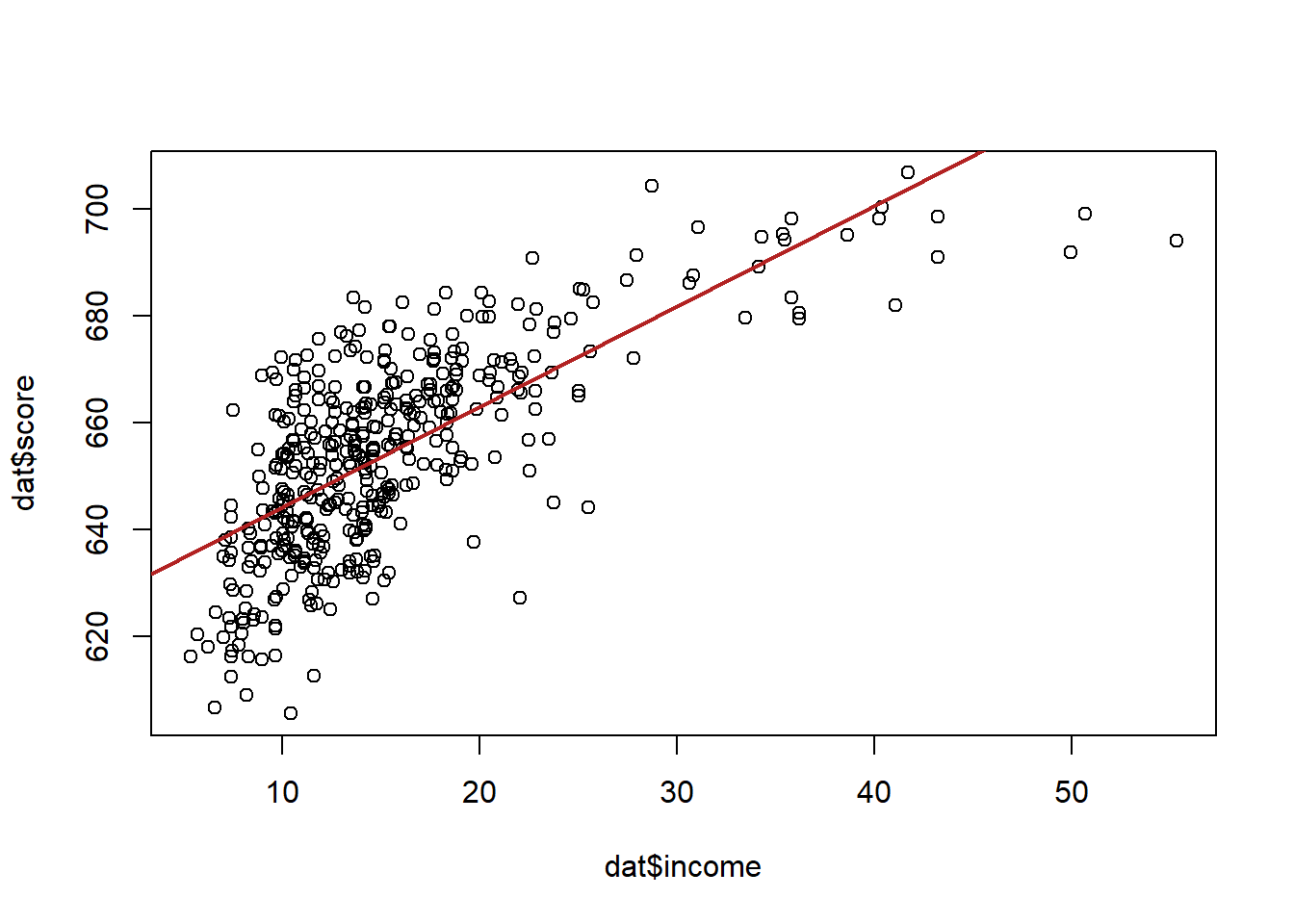
summary(m)
#>
#> Call:
#> lm(formula = score ~ income, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -39.574 -8.803 0.603 9.032 32.530
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 625.3836 1.5324 408.11 <2e-16 ***
#> income 1.8785 0.0905 20.76 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13.39 on 418 degrees of freedom
#> Multiple R-squared: 0.5076, Adjusted R-squared: 0.5064
#> F-statistic: 430.8 on 1 and 418 DF, p-value: < 2.2e-16Similar to when we considered controlling for another variable, we can think about each of these datapoints being of two types, k-6 school or k-8 schools.
Let’s create an indicator variable for k8:
dat$k8 <- NA
dat$k8[dat$grades=="KK-08"] <- 1
dat$k8[dat$grades=="KK-06"] <- 0
table(dat$k8)
#>
#> 0 1
#> 61 359Let’s first determine what the effect of this indicator is on test scores while also taking into account income. Remember that when we do this we are effectively allowing for two intercepts, or having one intercept for the group where k8=0, and then a coefficient to tell us the intercept shift from one type of school to the other.
What does this look like visually:
plot(dat$income[dat$k8==1], dat$score[dat$k8==1], col="forestgreen", pch=16)
points(dat$income[dat$k8==0], dat$score[dat$k8==0], col="goldenrod", pch=16)
abline(m, col="black", lwd=2)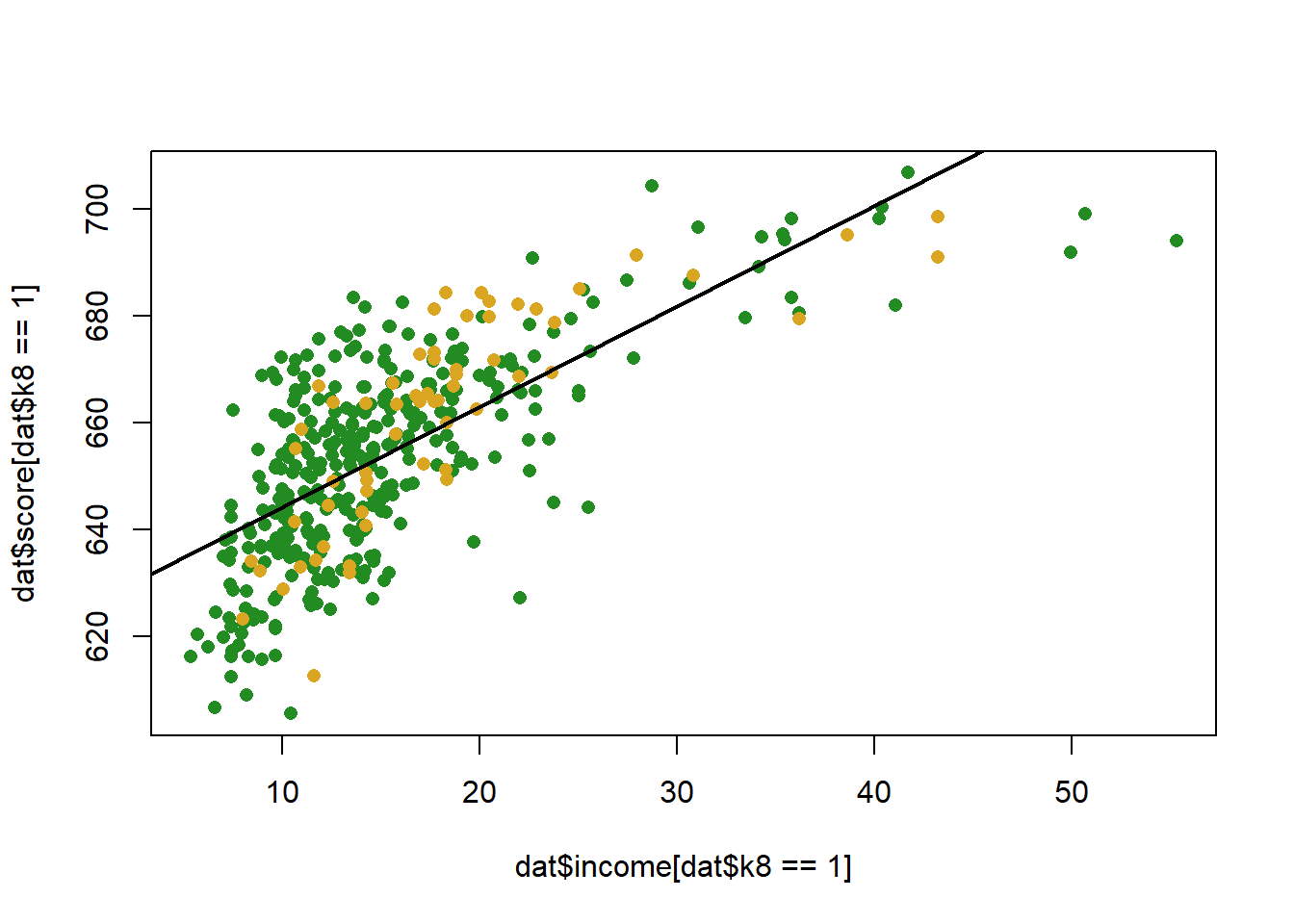
Let’s add in the dummy to our regression equation:
m <- lm(score ~ income + k8, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ income + k8, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -39.126 -9.085 0.649 9.315 32.866
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 627.8774 2.3855 263.209 <2e-16 ***
#> income 1.8585 0.0916 20.288 <2e-16 ***
#> k8 -2.5578 1.8764 -1.363 0.174
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13.37 on 417 degrees of freedom
#> Multiple R-squared: 0.5097, Adjusted R-squared: 0.5074
#> F-statistic: 216.8 on 2 and 417 DF, p-value: < 2.2e-16What does that look like, visually:
income <- seq(0,70, 1)
pred1 <- coef(m)["(Intercept)"] + coef(m)["income"]*income + coef(m)["k8"]
pred0 <- coef(m)["(Intercept)"] + coef(m)["income"]*income
plot(dat$income[dat$k8==1], dat$score[dat$k8==1], col="forestgreen", pch=16)
points(dat$income[dat$k8==0], dat$score[dat$k8==0], col="goldenrod", pch=16)
points(income, pred1, col="forestgreen", lwd=2, type="l")
points(income, pred0, col="goldenrod", lwd=2, type="l")
abline(lm(score ~income, data=dat), lwd=2)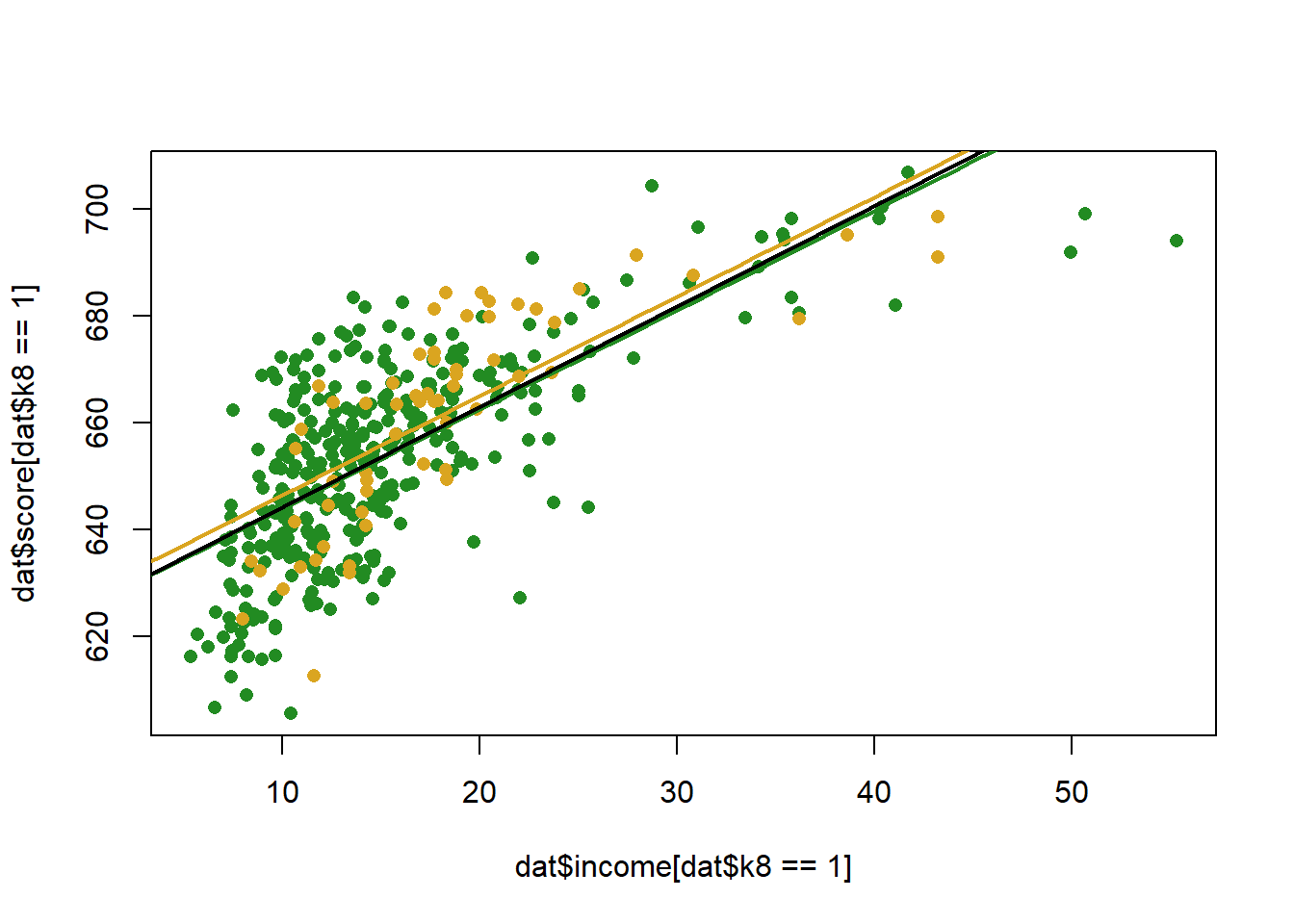
The coefficient indicates that k8 schools have slightly lower test scores than K6, but we fail to reject the null for the hypothesis test….
But we want to answer a separate question, how does the effect of income change in these two different types of schools?
The way that we do this is by interacting, or multiplying, the two variables
m <- lm(score ~ income*k8, data=dat)
summary(m)
#>
#> Call:
#> lm(formula = score ~ income * k8, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -39.257 -8.979 0.734 9.273 32.829
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 625.0716 4.4795 139.541 <2e-16 ***
#> income 2.0132 0.2283 8.820 <2e-16 ***
#> k8 0.6893 4.7717 0.144 0.885
#> income:k8 -0.1845 0.2492 -0.740 0.460
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 13.38 on 416 degrees of freedom
#> Multiple R-squared: 0.5104, Adjusted R-squared: 0.5069
#> F-statistic: 144.6 on 3 and 416 DF, p-value: < 2.2e-16Notice that when we run a regression with an interaction we need three things a term for each constituent part of the interaction, and the two variables interacted together. Helpfully, R does this for you automatically.
How do we interpret a regression with an interaction? We can rely on the power rule and differentiation to do this. Again, taking the first derivative with respect to a variable returns the effect of only that variable. So we can do:
\[ \hat{score} = \alpha + \beta_1Income + \beta_2K8 + \beta_3*Income*K8\\ \frac{\partial Score}{\partial Income} = \beta_1 + \beta_3*K8\\ \frac{\partial Score}{\partial K8} = \beta_2 + \beta_3*Income\\ \]
The key thing here is that now the effect of both of these variables depend on the level of the other. Again, think how this is similar to what we did above with polynomials, where the effect of income depended on itself. Here the effect of one variable depends on the level of the other.(Indeed, polynomial regression is just interaction with itself…)
So for this regression, what is the effect of income?
The effect of income depends on the value of k8, which in this case is just a binary variable:
So the effect of income in k6 schools is
And the effect of income in k8 schools is
We can interpret these two effects in the same way as we have been doing, a 1 unit change in income leads to a blank change in test scores.
So in all actuality the effect of income in k8 schools is lower. How much lower is it? Well, looking at the two equations, it is lower by the size of the interaction coefficient.
To display this visually we can, in this case, just draw two regression lines given the coefficients:
income <- seq(0,70, 1)
pred1 <- coef(m)["(Intercept)"] +coef(m)["income"]*income + coef(m)["k8"] + coef(m)["k8"] + coef(m)["income:k8"]*income
pred0 <- coef(m)["(Intercept)"] + coef(m)["income"]*income
plot(dat$income[dat$k8==1], dat$score[dat$k8==1], col="forestgreen", pch=16)
points(dat$income[dat$k8==0], dat$score[dat$k8==0], col="goldenrod", pch=16)
points(income, pred1, col="forestgreen", lwd=2, type="l")
points(income, pred0, col="goldenrod", lwd=2, type="l")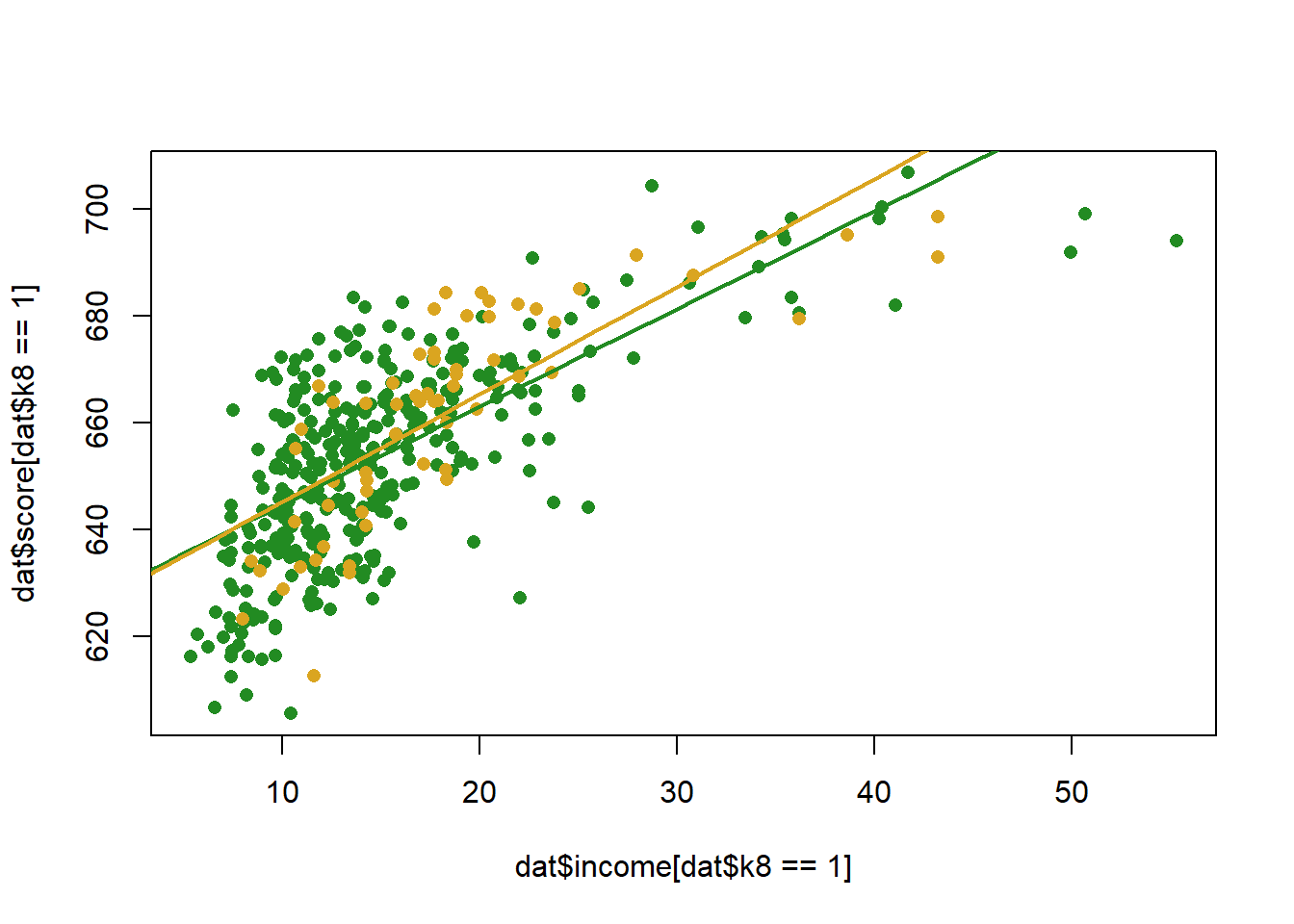
Note a couple of things here
The difference between the two slopes is the coefficient on the interaction term. As such the hypothesis test for the coefficient term tells you if the effect of a variable changes across levels of the interacted variable.
The coefficient on “income” is the effect of income when k8 equals 0. This is ALWAYS the case. This also means that the coefficient on a constituent part of an interaction might be nonsense.
Let’s think about more complex regressions via the ACS data:
What if we want to know the relationship between median income and inequality in counties? To get at that we can use the Gini coefficient, which is a standard measure of income inequality. High numbers are worse.
Let’s re code our variables to aide in interpretability
acs$median.income <- acs$median.income/1000
acs$gini <- acs$gini*100
plot(acs$median.income, acs$gini, xlab="Median Income (thousands)",
ylab="Gini Coefficient")
abline(lm(acs$gini ~ acs$median.income), col="firebrick", lwd=2)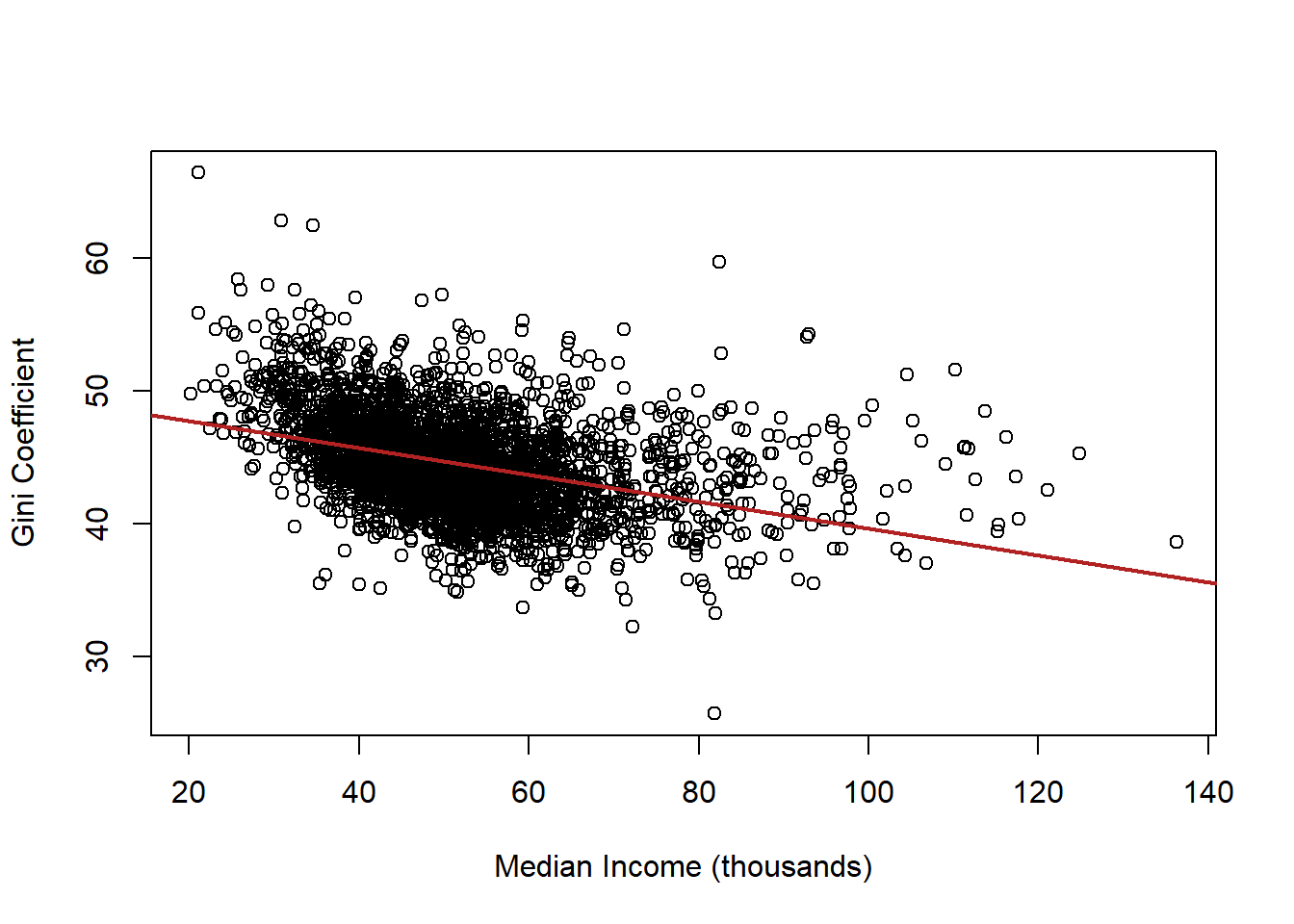
What is the interpretation of this coefficient?
summary(lm(gini ~ median.income, data=acs))
#>
#> Call:
#> lm(formula = gini ~ median.income, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -15.8054 -2.2822 -0.2843 1.9946 18.8559
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 49.7537 0.2348 211.88 <2e-16 ***
#> median.income -0.1011 0.0044 -22.98 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.378 on 3139 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.144, Adjusted R-squared: 0.1437
#> F-statistic: 528.1 on 1 and 3139 DF, p-value: < 2.2e-16Now let’s consider the role of race in this relationship. Let’s use the vairable percent.white to see how taking into account race changes this relationship
Original relationship
m1 <- lm(gini ~ median.income, data=acs)
m2 <- lm(gini ~ median.income + percent.white, data=acs)
#Use stargazer to view two models together
library(stargazer)
#>
#> Please cite as:
#> Hlavac, Marek (2018). stargazer: Well-Formatted Regression and Summary Statistics Tables.
#> R package version 5.2.2. https://CRAN.R-project.org/package=stargazer
stargazer(m1, m2, type="text")
#>
#> =======================================================================
#> Dependent variable:
#> ---------------------------------------------------
#> gini
#> (1) (2)
#> -----------------------------------------------------------------------
#> median.income -0.101*** -0.089***
#> (0.004) (0.004)
#>
#> percent.white -0.070***
#> (0.003)
#>
#> Constant 49.754*** 54.965***
#> (0.235) (0.335)
#>
#> -----------------------------------------------------------------------
#> Observations 3,141 3,141
#> R2 0.144 0.247
#> Adjusted R2 0.144 0.246
#> Residual Std. Error 3.378 (df = 3139) 3.170 (df = 3138)
#> F Statistic 528.123*** (df = 1; 3139) 514.099*** (df = 2; 3138)
#> =======================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01Why does the coefficient on median income get closer to zero? Part of the negative relationship between median income and inequality is caused by race. Being in a county with a high percentage of white people causes both higher income and lower inequality. Put the other way: Being in a county with a low percentage of white people causes both low income and high inequality. Once we take into account the independent relationship of race on inequality, the remaining relationship between income and inequality is smaller.
But this is not quite what we want to do. We want to look at whether the relationship between income and inequality changes based on race.
So far we’ve done this by interacting with a dummy variable like this:
acs$majority.white[acs$percent.white>=50] <- 1
acs$majority.white[acs$percent.white<50] <- 0
m3 <- lm(gini ~ median.income*majority.white, data=acs)
stargazer(m1,m2,m3, type="text")
#>
#> ==========================================================================================================
#> Dependent variable:
#> -----------------------------------------------------------------------------
#> gini
#> (1) (2) (3)
#> ----------------------------------------------------------------------------------------------------------
#> median.income -0.101*** -0.089*** -0.135***
#> (0.004) (0.004) (0.015)
#>
#> percent.white -0.070***
#> (0.003)
#>
#> majority.white -4.492***
#> (0.724)
#>
#> median.income:majority.white 0.046***
#> (0.016)
#>
#> Constant 49.754*** 54.965*** 53.492***
#> (0.235) (0.335) (0.680)
#>
#> ----------------------------------------------------------------------------------------------------------
#> Observations 3,141 3,141 3,141
#> R2 0.144 0.247 0.173
#> Adjusted R2 0.144 0.246 0.172
#> Residual Std. Error 3.378 (df = 3139) 3.170 (df = 3138) 3.322 (df = 3137)
#> F Statistic 528.123*** (df = 1; 3139) 514.099*** (df = 2; 3138) 218.398*** (df = 3; 3137)
#> ==========================================================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01What now is the effect of median income on inequality?
This is fine, but we are throwing out a lot of information by making percent white into an indicator variable.
What does it mean, then, to do this?
m4 <- lm(gini ~ median.income*percent.white, data=acs)
stargazer(m1,m2,m3,m4, type="text")
#>
#> ====================================================================================================================================
#> Dependent variable:
#> -------------------------------------------------------------------------------------------------------
#> gini
#> (1) (2) (3) (4)
#> ------------------------------------------------------------------------------------------------------------------------------------
#> median.income -0.101*** -0.089*** -0.135*** -0.037**
#> (0.004) (0.004) (0.015) (0.018)
#>
#> percent.white -0.070*** -0.039***
#> (0.003) (0.011)
#>
#> majority.white -4.492***
#> (0.724)
#>
#> median.income:majority.white 0.046***
#> (0.016)
#>
#> median.income:percent.white -0.001***
#> (0.0002)
#>
#> Constant 49.754*** 54.965*** 53.492*** 52.576***
#> (0.235) (0.335) (0.680) (0.857)
#>
#> ------------------------------------------------------------------------------------------------------------------------------------
#> Observations 3,141 3,141 3,141 3,141
#> R2 0.144 0.247 0.173 0.249
#> Adjusted R2 0.144 0.246 0.172 0.248
#> Residual Std. Error 3.378 (df = 3139) 3.170 (df = 3138) 3.322 (df = 3137) 3.166 (df = 3137)
#> F Statistic 528.123*** (df = 1; 3139) 514.099*** (df = 2; 3138) 218.398*** (df = 3; 3137) 346.683*** (df = 3; 3137)
#> ====================================================================================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01
summary(m4)
#>
#> Call:
#> lm(formula = gini ~ median.income * percent.white, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -14.7470 -1.9791 -0.2637 1.8651 17.0992
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 52.5755392 0.8567078 61.369
#> median.income -0.0365980 0.0178957 -2.045
#> percent.white -0.0386569 0.0109061 -3.545
#> median.income:percent.white -0.0006808 0.0002248 -3.029
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> median.income 0.040932 *
#> percent.white 0.000399 ***
#> median.income:percent.white 0.002476 **
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.166 on 3137 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.249, Adjusted R-squared: 0.2483
#> F-statistic: 346.7 on 3 and 3137 DF, p-value: < 2.2e-16What is now the marginal impact of median income?
\[ \hat{gini} = \alpha + \beta_1M.Income + \beta_2Perc.White + \beta_3 M.Income*Perc.White\\ \frac{\partial Gini}{\partial M.Income} = \beta_1 + \beta_3*Perc.White \]
So again, a “one unit change in income” is different based off of what value of percent white we have. But now percent white isn’t just a binary variable but a continuous one. So now every one unit change in percent white changes the effect of income by \(\beta_3\)
Indeed, looking at the coefficient on the interaction term, for every one unit change in percent white the effect of income declines by .001. This change is statistically significant.
How might we visualize this?
One way might be to pick some meaningful values of percent white, and plot the predicted effects for each
median.income <- seq(0,150,.01)
pred0 <- coef(m4)["(Intercept)"] +
coef(m4)["median.income"]*median.income +
coef(m4)["percent.white"]*0 +
coef(m4)["median.income:percent.white"]*0*median.income
pred25 <- coef(m4)["(Intercept)"] +
coef(m4)["median.income"]*median.income +
coef(m4)["percent.white"]*25 +
coef(m4)["median.income:percent.white"]*25*median.income
pred50 <- coef(m4)["(Intercept)"] +
coef(m4)["median.income"]*median.income +
coef(m4)["percent.white"]*50 +
coef(m4)["median.income:percent.white"]*50*median.income
pred75 <- coef(m4)["(Intercept)"] +
coef(m4)["median.income"]*median.income +
coef(m4)["percent.white"]*75 +
coef(m4)["median.income:percent.white"]*75*median.income
pred100 <- coef(m4)["(Intercept)"] +
coef(m4)["median.income"]*median.income +
coef(m4)["percent.white"]*100 +
coef(m4)["median.income:percent.white"]*100*median.income
library(RColorBrewer)
#> Warning: package 'RColorBrewer' was built under R version
#> 4.1.3
cols <- brewer.pal(7, "Set2")
plot(acs$median.income, acs$gini, col="gray80")
points(median.income, pred0,lwd=2, type="l", col=cols[1])
points(median.income, pred25,lwd=2, type="l", col=cols[2])
points(median.income, pred50,lwd=2, type="l", col=cols[3])
points(median.income, pred75,lwd=2, type="l", col=cols[4])
points(median.income, pred100,lwd=2, type="l", col=cols[5])
legend("topleft", c("0% White",
"25% White",
"50% White",
"75% White",
"100% White"),
lty=rep(1,6), col=cols)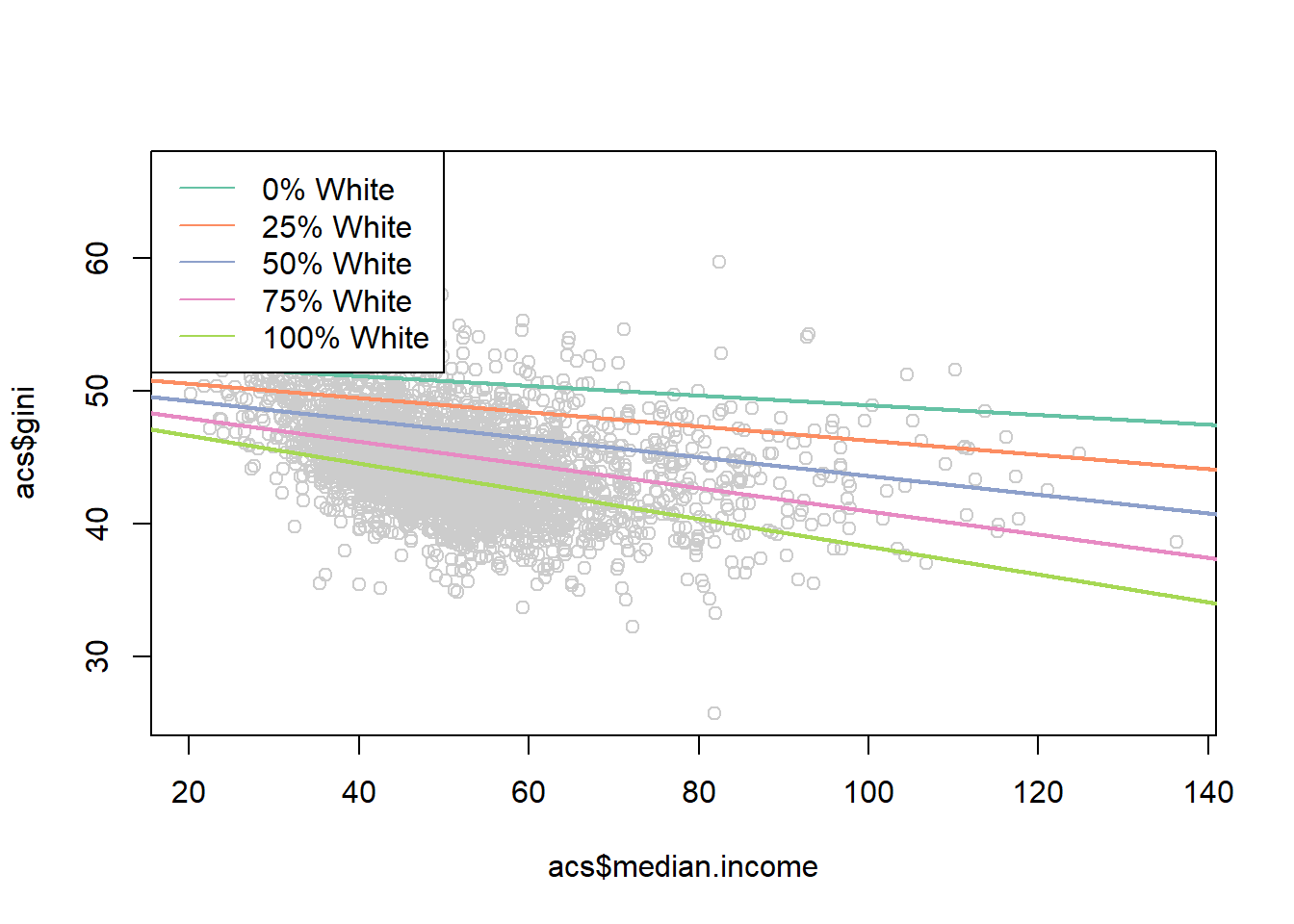
Not bad!
But for interaction with continuous variables often what is more helpful to plot is the marginal effect of the variable that we care about across levels of the other variable.
Here the effect of median income is given by the equation
\[ \frac{\partial Gini}{\partial M.Income} = \beta_1 + \beta_3*Perc.White \]
So the marginal effect of median income is
percent.white <- seq(0,100,.01)
margin <- coef(m4)["median.income"] + coef(m4)["median.income:percent.white"]*percent.white
plot(percent.white, margin, type="l", ylim=c(-0.15,0))
abline(h=0, lty=2)
rug(acs$percent.white)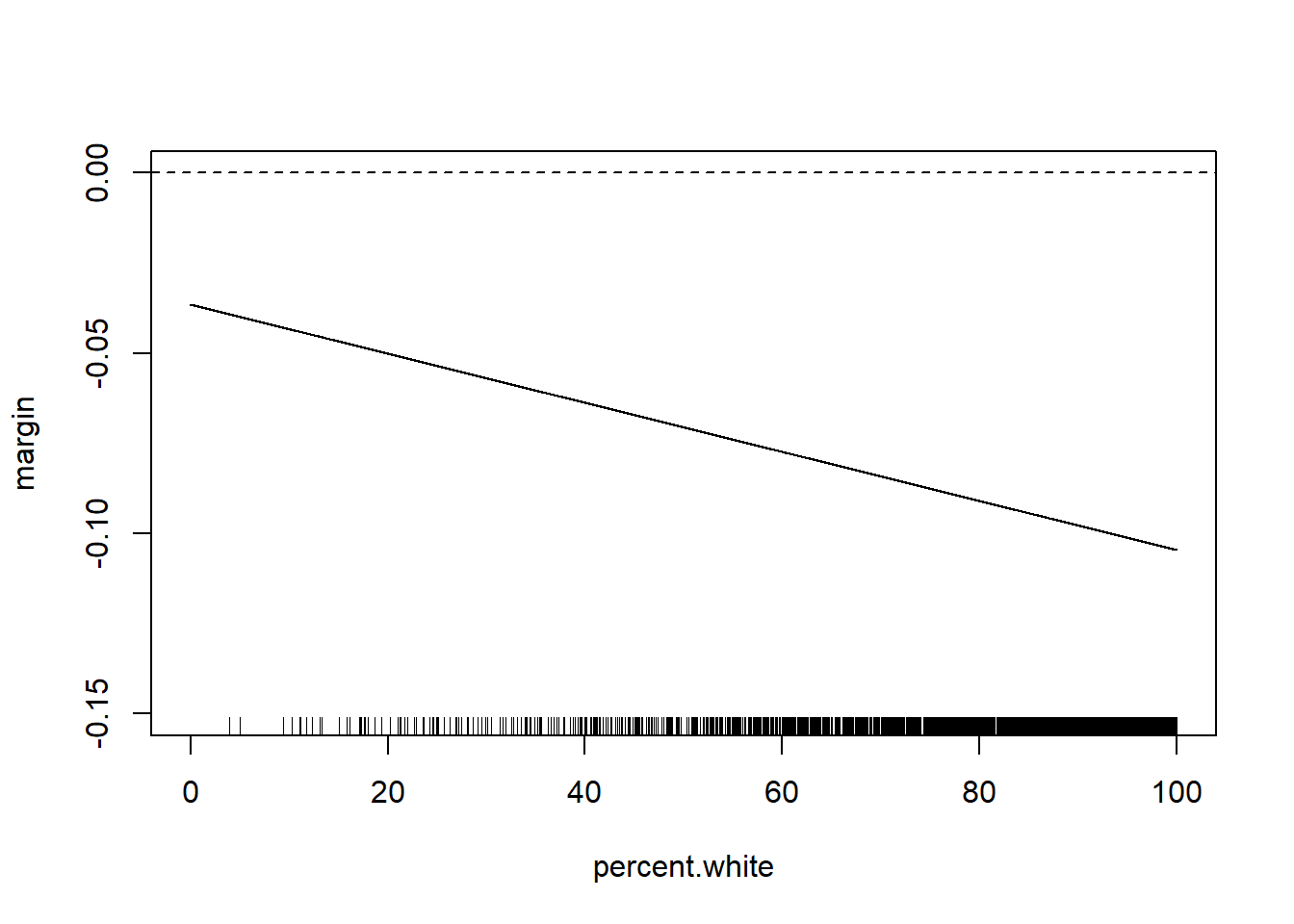
Note that we can easily think about the inverse of this
median.income <- seq(0,140,1)
margin <- coef(m4)["percent.white"] + coef(m4)["median.income:percent.white"]*median.income
plot(median.income, margin, type="l", ylim=c(-0.15,0))
abline(h=0, lty=2)
rug(acs$median.income)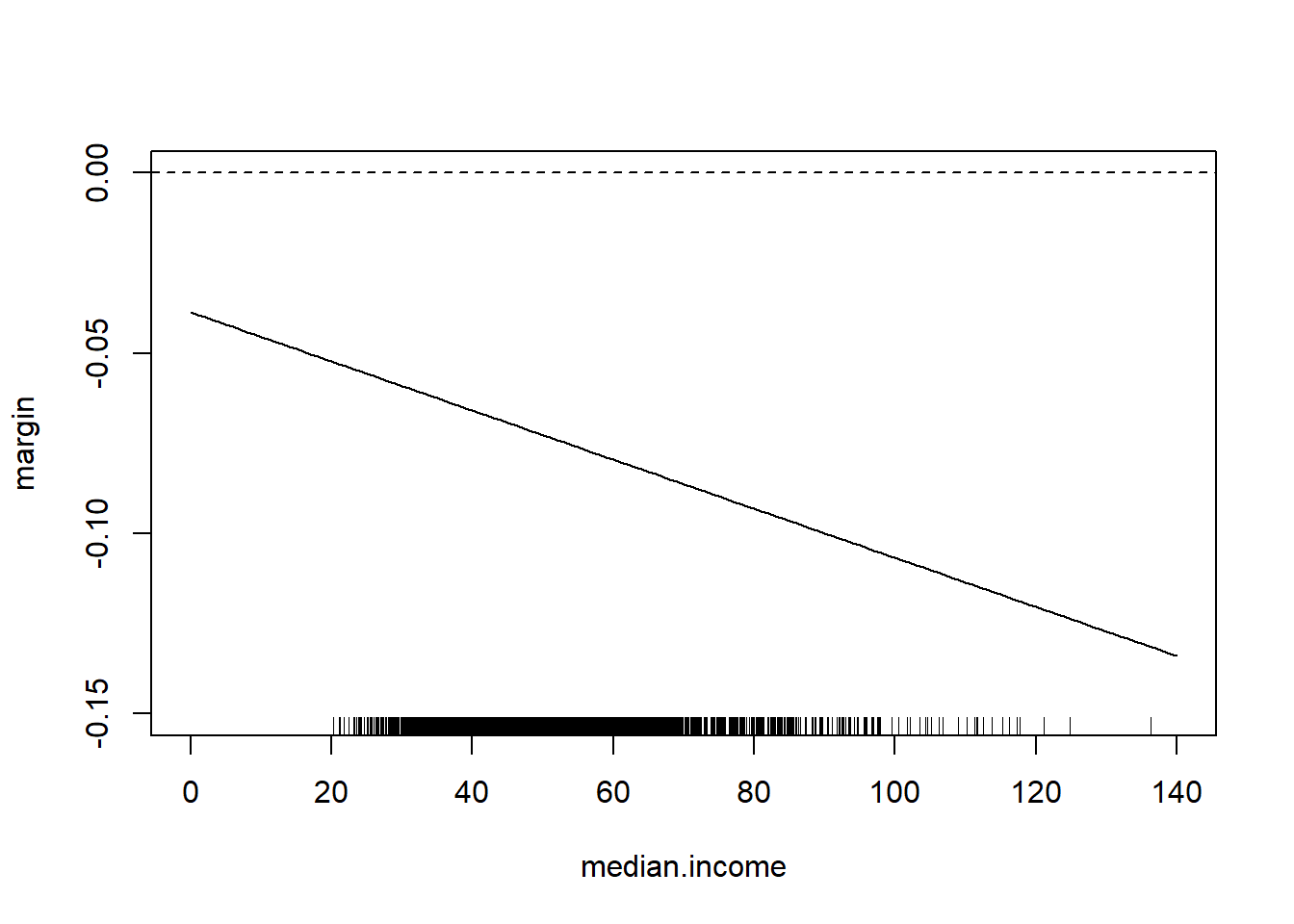
Would you like this to be a bit easier?
From the maker of the rio package: margins!
library(margins)
#> Warning: package 'margins' was built under R version 4.1.3
cplot(m4, x="median.income",dx="percent.white", what="effect")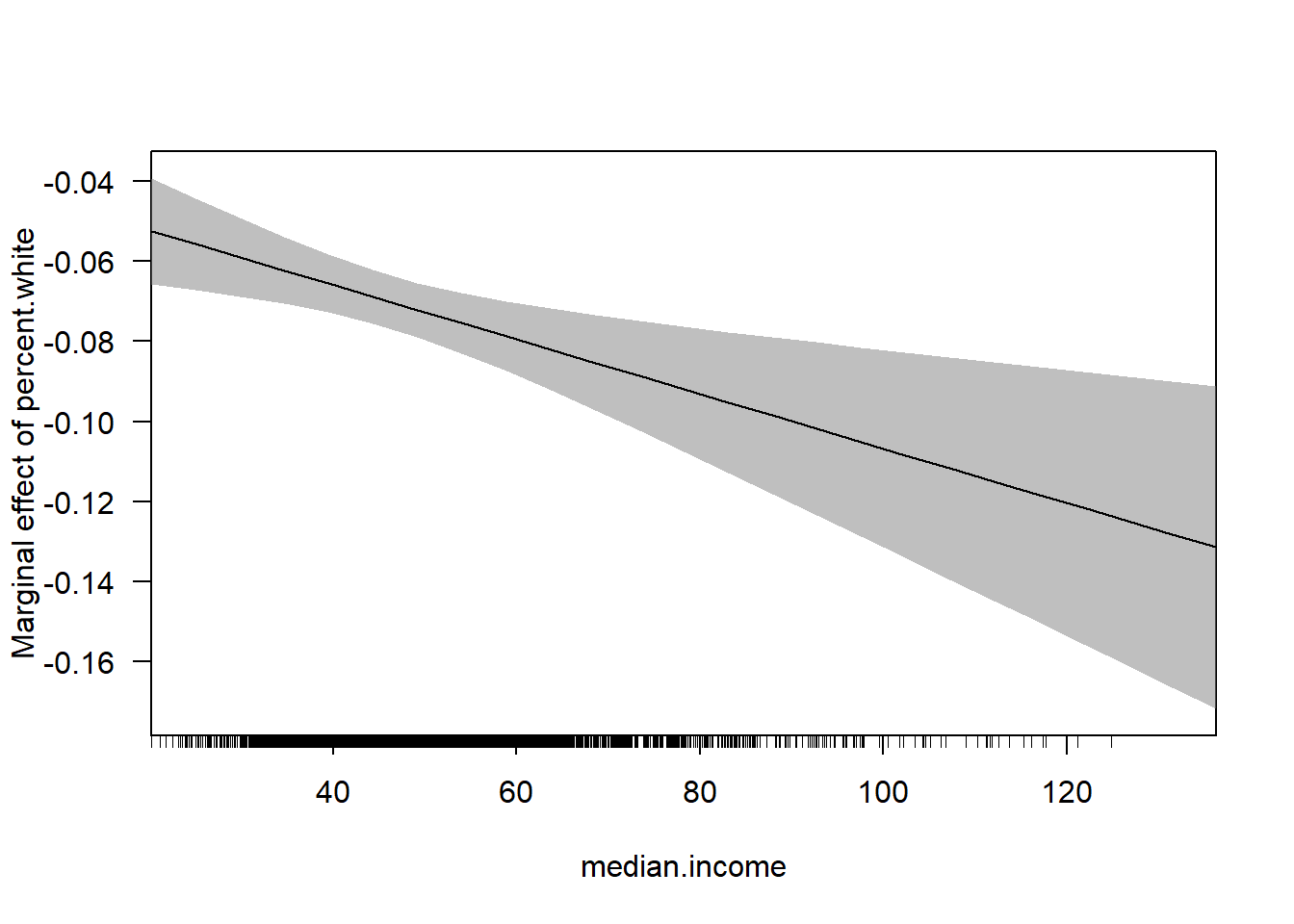
cplot(m4, dx="median.income",x="percent.white", what="effect")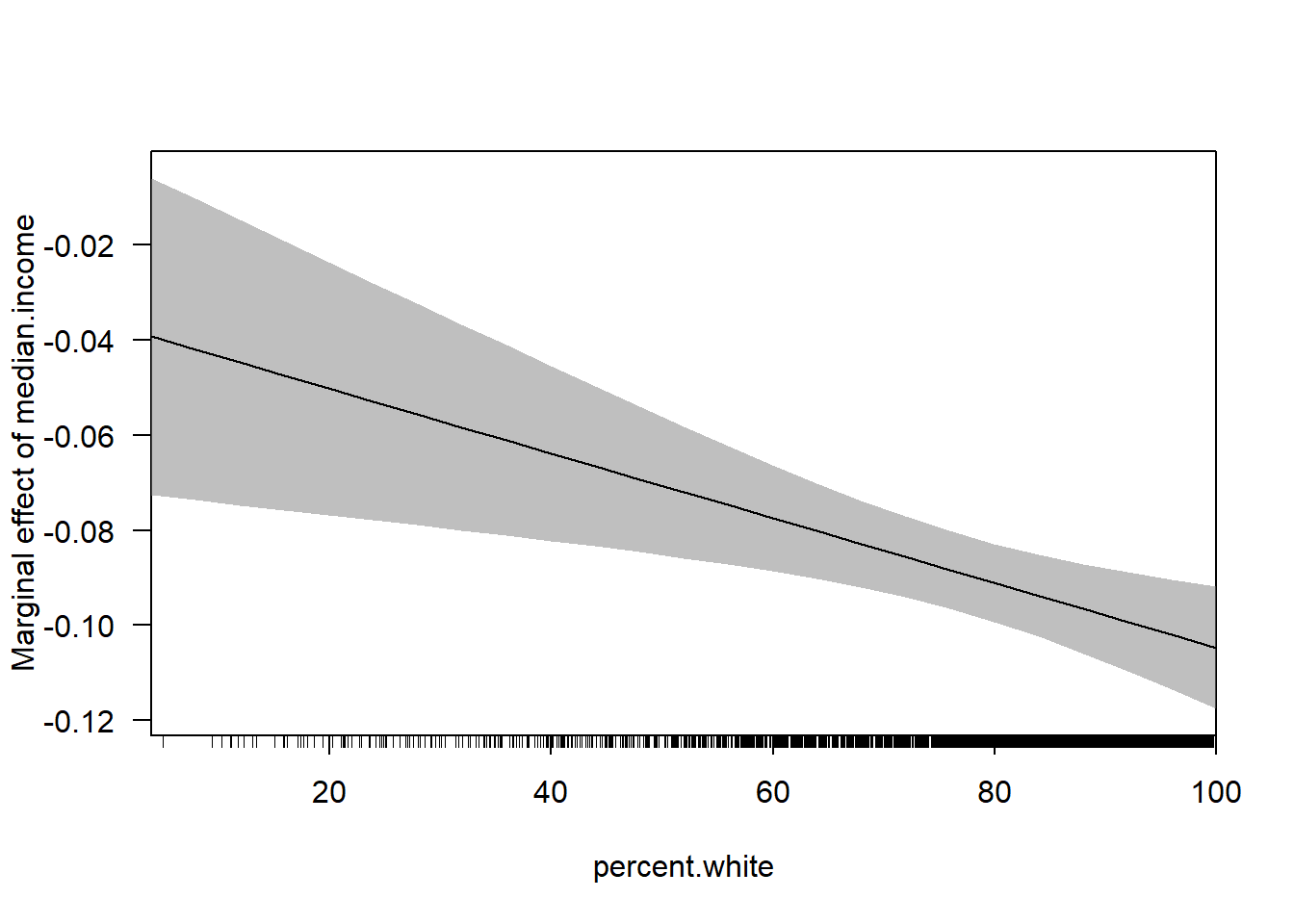
With the huge benefit of there being confidence intervals included!
We can also use the margins package to get marginal effects across levels:
margins(m4, at=list(percent.white=c(0,25,50,75,100)))
#> Warning in check_values(data, at): A 'at' value for
#> 'percent.white' is outside observed data range
#> (3.89119297389607,100)!
#> Average marginal effects at specified values
#> lm(formula = gini ~ median.income * percent.white, data = acs)
#> at(percent.white) median.income percent.white
#> 0 -0.03660 -0.07377
#> 25 -0.05362 -0.07377
#> 50 -0.07064 -0.07377
#> 75 -0.08766 -0.07377
#> 100 -0.10468 -0.07377
margins(m4, at=list(median.income=c(0,50,150)))
#> Warning in check_values(data, at): Some 'at' values for
#> 'median.income' are outside observed data range
#> (20.188,136.268)!
#> Average marginal effects at specified values
#> lm(formula = gini ~ median.income * percent.white, data = acs)
#> at(median.income) median.income percent.white
#> 0 -0.09315 -0.03866
#> 50 -0.09315 -0.07270
#> 150 -0.09315 -0.14078How does this change when we add additional control variables?
m5 <- lm(gini ~ median.income*percent.white + population.density +
percent.adult.poverty + percent.car.commute, data=acs)
summary(m5)
#>
#> Call:
#> lm(formula = gini ~ median.income * percent.white + population.density +
#> percent.adult.poverty + percent.car.commute, data = acs)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -13.8154 -1.7762 -0.2256 1.6935 18.6010
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 4.137e+01 1.279e+00 32.348
#> median.income 1.377e-02 1.759e-02 0.783
#> percent.white -2.108e-02 1.026e-02 -2.053
#> population.density 2.727e-04 3.226e-05 8.455
#> percent.adult.poverty 2.893e-01 1.365e-02 21.202
#> percent.car.commute 7.685e-03 7.824e-03 0.982
#> median.income:percent.white -2.105e-04 2.124e-04 -0.991
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> median.income 0.4340
#> percent.white 0.0401 *
#> population.density <2e-16 ***
#> percent.adult.poverty <2e-16 ***
#> percent.car.commute 0.3261
#> median.income:percent.white 0.3217
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.923 on 3134 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.3604, Adjusted R-squared: 0.3591
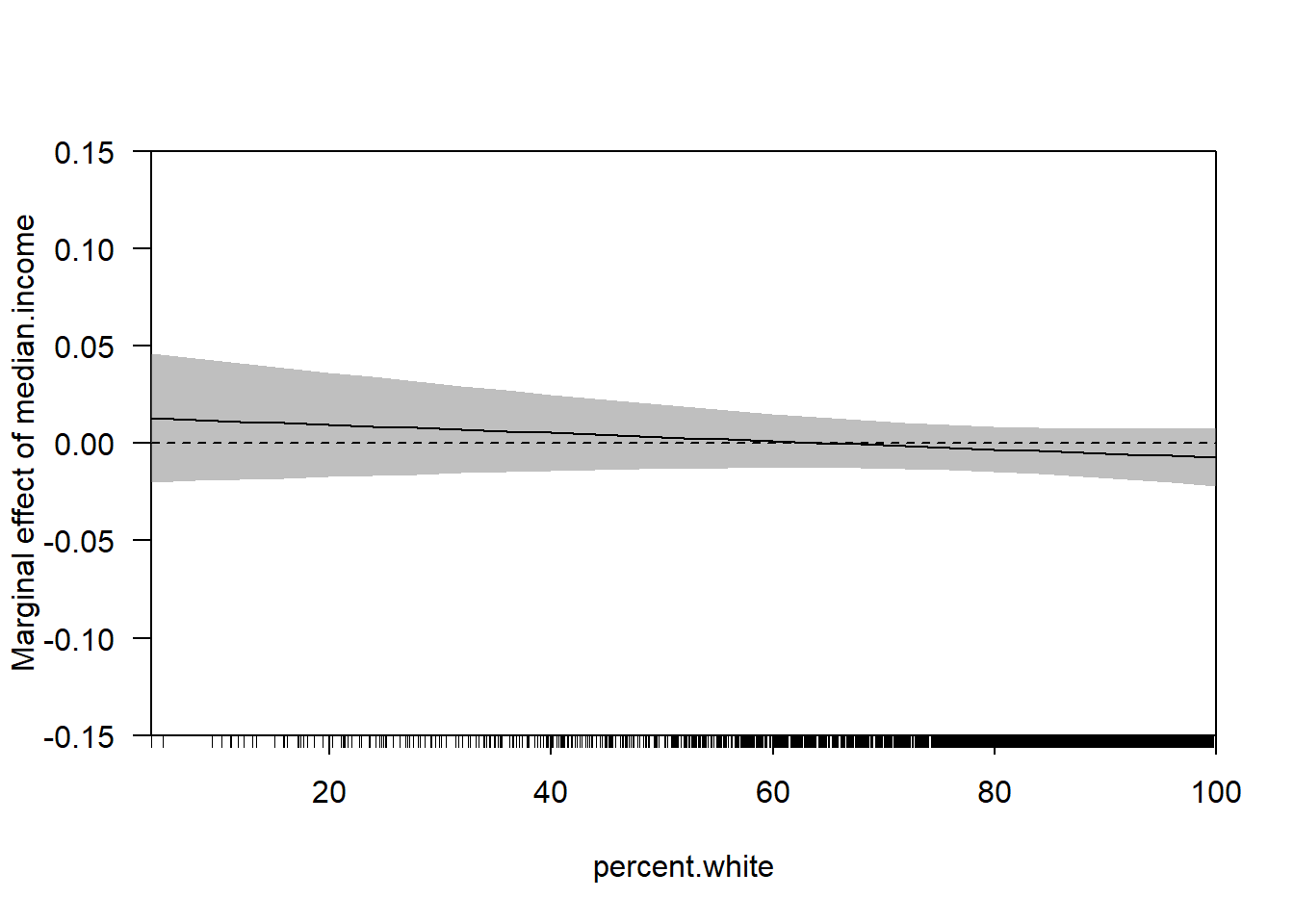
#> F-statistic: 294.3 on 6 and 3134 DF, p-value: < 2.2e-16This is a more complicated regression… but the way we approach the margina effect is identical, because of the calculus. If we apply the power rule we get the exact same outcome:
\[ \hat{gini} = \alpha + \beta_1M.Income + \beta_2Perc.White + \beta_3 M.Income*Perc.White\\ + \beta_4* population.density + \beta_5* adult.poverty + \beta_6 * percent.car.commute \\ \frac{\partial Gini}{\partial M.Income} = \beta_1 + \beta_3*Perc.White \]
So we can still do:
percent.white <- seq(0,100,.01)
margin <- coef(m5)["median.income"] + coef(m5)["median.income:percent.white"]*percent.white
plot(percent.white, margin, type="l", ylim=c(-0.15,0.15))
abline(h=0, lty=2)
rug(acs$percent.white)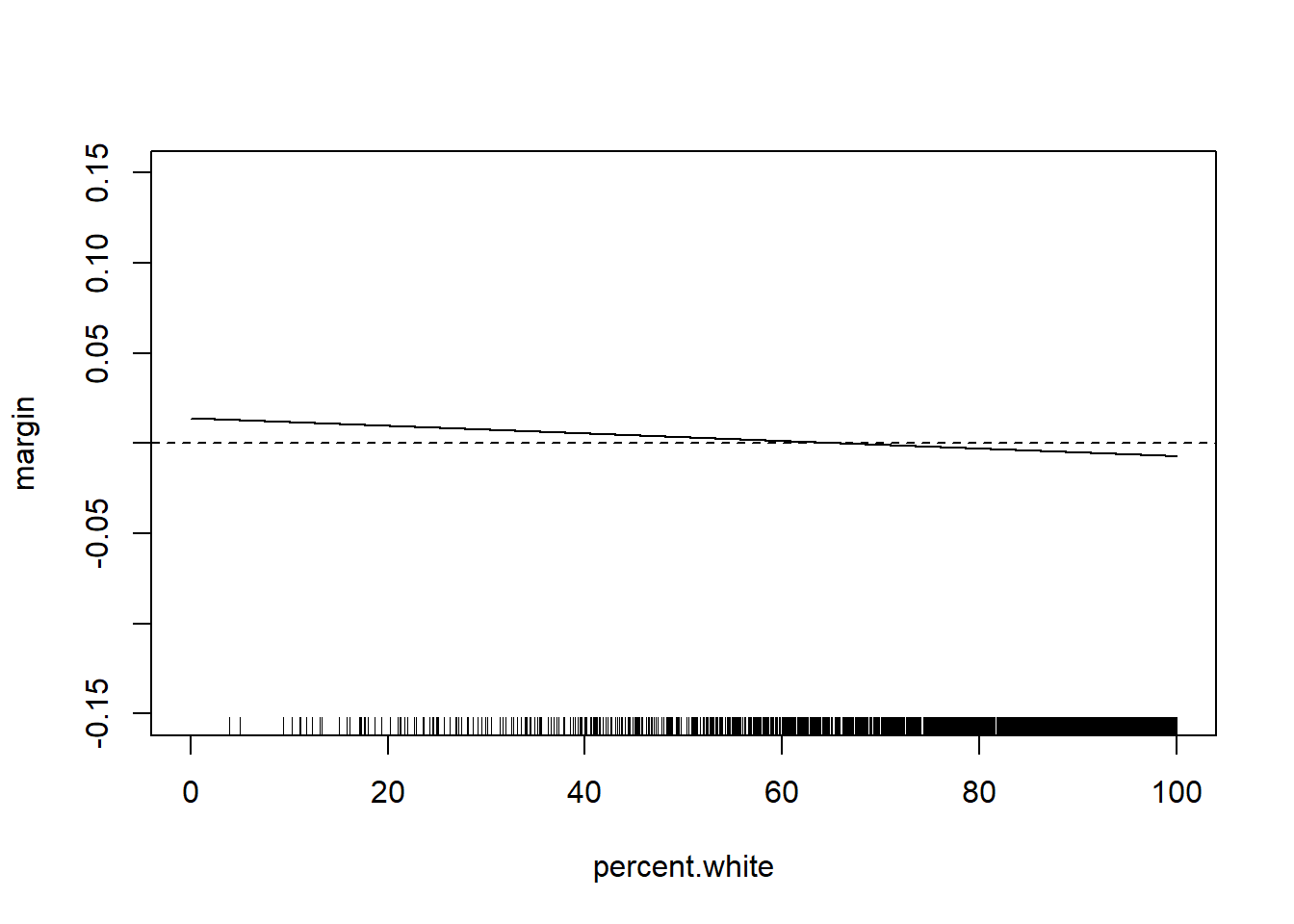
The relationship has changed substantially with these additional control variables. But the way we examine the marginal effect does not. Can get the same thing with:
Let’s do one more example of an interaction using the ACS data:
How does the effect of the percent who commute by car on commute time change as population density increases?
What do we mean by this question? First, we think there is some sort of unconditional relationship between the percent of people who commute by transit and commuting time. Given that, in the US at least, transit commuting is a real second-class option, my expectation is that the more people who commute by transit in a location the longer average commute times will be.
We can confirm that using a bivariate regression:
library(stargazer)
m <- lm(average.commute.time ~ percent.transit.commute, data=acs)
stargazer(m, type="text")
#>
#> ===================================================
#> Dependent variable:
#> ---------------------------
#> average.commute.time
#> ---------------------------------------------------
#> percent.transit.commute 0.353***
#> (0.032)
#>
#> Constant 23.225***
#> (0.105)
#>
#> ---------------------------------------------------
#> Observations 3,140
#> R2 0.037
#> Adjusted R2 0.037
#> Residual Std. Error 5.630 (df = 3138)
#> F Statistic 121.671*** (df = 1; 3138)
#> ===================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01Indeed, for every additional percent of people commuting by transit average commute times increase by .353.
An objection to that regression might be that rural places have both low transit commuting and low commute times (if people work on their farms, for example). So we may want to take into account the independent effect of population density on both the percent who commute by transit and average commute times:
m2 <- lm(average.commute.time ~ percent.transit.commute + population.density, data=acs)
stargazer(m,m2, type="text")
#>
#> ==========================================================================
#> Dependent variable:
#> --------------------------------------------------
#> average.commute.time
#> (1) (2)
#> --------------------------------------------------------------------------
#> percent.transit.commute 0.353*** 0.391***
#> (0.032) (0.056)
#>
#> population.density -0.0001
#> (0.0001)
#>
#> Constant 23.225*** 23.209***
#> (0.105) (0.107)
#>
#> --------------------------------------------------------------------------
#> Observations 3,140 3,140
#> R2 0.037 0.038
#> Adjusted R2 0.037 0.037
#> Residual Std. Error 5.630 (df = 3138) 5.631 (df = 3137)
#> F Statistic 121.671*** (df = 1; 3138) 61.166*** (df = 2; 3137)
#> ==========================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01Actually this relationship gets stronger once we take into account the independent effect of population density.
But that’s not the question we asked, we want to know if the effect of the percent transit commuters changes as population density increases. To do that we have to multiply the two variables:
m3 <- lm(average.commute.time ~ percent.transit.commute*population.density, data=acs)
stargazer(m,m2,m3, type="text")
#>
#> ======================================================================================================================
#> Dependent variable:
#> ---------------------------------------------------------------------------
#> average.commute.time
#> (1) (2) (3)
#> ----------------------------------------------------------------------------------------------------------------------
#> percent.transit.commute 0.353*** 0.391*** 0.272***
#> (0.032) (0.056) (0.061)
#>
#> population.density -0.0001 0.001***
#> (0.0001) (0.0002)
#>
#> percent.transit.commute:population.density -0.00002***
#> (0.00000)
#>
#> Constant 23.225*** 23.209*** 23.110***
#> (0.105) (0.107) (0.109)
#>
#> ----------------------------------------------------------------------------------------------------------------------
#> Observations 3,140 3,140 3,140
#> R2 0.037 0.038 0.045
#> Adjusted R2 0.037 0.037 0.044
#> Residual Std. Error 5.630 (df = 3138) 5.631 (df = 3137) 5.610 (df = 3136)
#> F Statistic 121.671*** (df = 1; 3138) 61.166*** (df = 2; 3137) 49.045*** (df = 3; 3136)
#> ======================================================================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01Let’s break down what it is that we are seeing here.
The intercept here is 23.110. I have said many times that the intercept is the average value of the outcome when all variables in the regression are equal to 0, so this is the average commute time in a place with 0 transit commuters and 0 population density. So, as often is this case, this is a nonsense number.
To get the effect of the percent commuting by transit we can deploy a derivative:
\[ \hat{commute} = \alpha + \beta_1 Transit + \beta_@ Dens + \beta_3 Transity*Dens\\ \frac{\partial\hat{commute} }{\partial Transit} = \beta_1 + \beta_3*Dens\\ \]
As we wanted, the effect of the percent who commute by transit changes across levels of population density. If this equation describes the effect of % transit, under what conditions is the effect \(\beta_1\)? This is only the case when population density is equal to 0. So in a county with zero people the effect of an additional transit commuter is to increase average commute times by .272. Is this an important number? No! You have to know to ignore this number.
To determine what the effect of percent transit commute is, we have to evaluate at many values of of population density. Again, we have to be smart here. Try to think: what values does density take on?
summary(acs$population.density)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.04 16.69 44.72 270.68 116.71 72052.96OK! Let’s just do the math:
population.density <- seq(0,73000,1)
marginal.effect <- coef(m3)["percent.transit.commute"] + population.density*coef(m3)["percent.transit.commute:population.density"]
plot(population.density, marginal.effect, type="l", xlab="Population Density", ylab="Effect of % Transit Commute on Commute Time")
abline(h=0, lty=2)
rug(acs$population.density)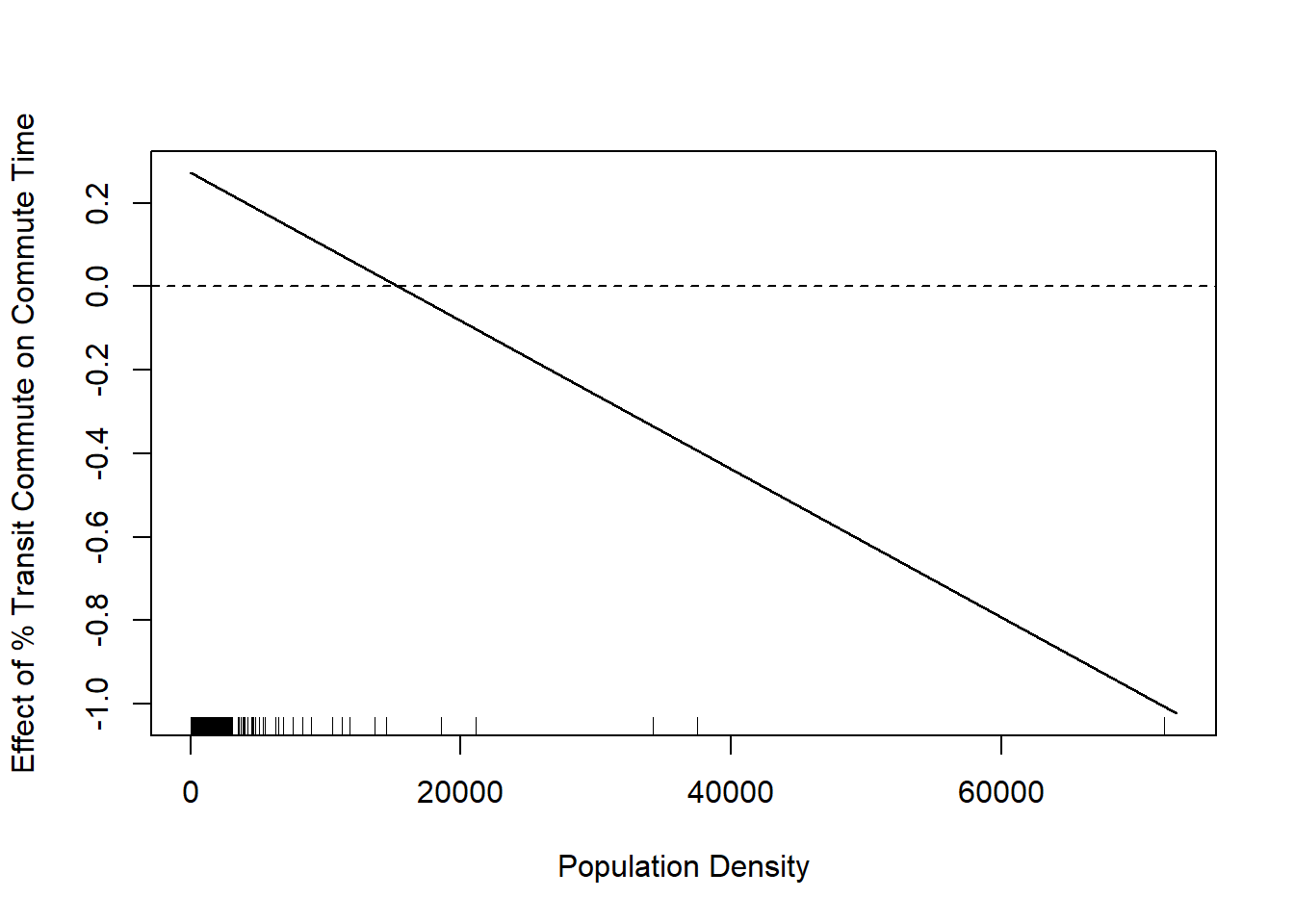
We see that this line is negative. This is saying that the effect of percent commuting by transit decreases as population density increases. In other words, when a place gets more dense having more people commute by transit moves from a net time suck on commute times to a net positive.
I have added the rug plot here to show where counties population densities actually are, and that rug plot somewhat tempers this finding. The truth is that the majority of counties have very small population densities and so this negative relationship is not true for many places.
This graph is not particularly helpful without some sense of the error. Can we conclude with any certainty that the effect of the percent commuting by transit on commute times is truly negative at any point?
What is the variance of this marginal effect? In other words what is:
\[ V(\beta_1 + \beta_3*Dens)=? \]
Is it just:
\[ V(\beta_1 + \beta_3*Dens) \neq V(\beta_1) + V(\beta_3*Dens) \]
No! When we are adding variance we critically need to know if there is any covariance between the two things. That is because:
\[ V(X+Y) = V(X) + V(Y) + 2*COV(X,Y) \]
So we could ignore the covariance if there was 0 covariance between these two features. Do the coefficients co-vary? Let’s simulate via bootstrap to see if beta 1 and beta 3 covary:
small <- acs[c("percent.transit.commute","population.density","average.commute.time")]
b1 <- rep(NA, 1000)
b3 <- rep(NA, 1000)
for(i in 1:1000){
bs.data <- small[sample(1:nrow(small), nrow(small),replace=T),]
m.bs <- lm(average.commute.time ~ percent.transit.commute*population.density, data=bs.data)
b1[i] <- coef(m.bs)["percent.transit.commute"]
b3[i] <- coef(m.bs)["percent.transit.commute:population.density"]
}
cor(b1,b3)
#> [1] 0.2401167Yes! There is a non-zero correlation between these two things.
As such the variance of the marginal effect is:
\[ V(\beta_1 + \beta_3*Dens) = V(\beta_1) + V(\beta_3*Dens) + 2*Cov(\beta_1, \beta_3*Dens)\\ = V(\beta_1) + Dens^2*V(\beta_3) + 2*Dens*Cov(\beta_1, \beta_3)\\ \] Sidebar for that final term:
Notice how population density is a variable in this equation. The standard error of the marginal effect changes across levels of density. We will see this visually in a second.
How can we get these variances and co-variances?
vcov(m3)
#> (Intercept)
#> (Intercept) 1.177826e-02
#> percent.transit.commute -1.378290e-03
#> population.density -2.825708e-06
#> percent.transit.commute:population.density 7.390022e-08
#> percent.transit.commute
#> (Intercept) -1.378290e-03
#> percent.transit.commute 3.752489e-03
#> population.density -1.011826e-05
#> percent.transit.commute:population.density 8.850673e-08
#> population.density
#> (Intercept) -2.825708e-06
#> percent.transit.commute -1.011826e-05
#> population.density 6.223717e-08
#> percent.transit.commute:population.density -8.328641e-10
#> percent.transit.commute:population.density
#> (Intercept) 7.390022e-08
#> percent.transit.commute 8.850673e-08
#> population.density -8.328641e-10
#> percent.transit.commute:population.density 1.316543e-11The “variance-covariance” matrix is generated by the regression and tells us the variances (the diagonals) and the covariances (the off diaganoals) of all of the coefficients including the intercept.
So to get the standard error of the marginal effect at all the levels we calculated above:
var.margin <- vcov(m3)["percent.transit.commute","percent.transit.commute"] +
population.density^2*vcov(m3)["percent.transit.commute:population.density","percent.transit.commute:population.density"] +
population.density*2*vcov(m3)["percent.transit.commute:population.density","percent.transit.commute"]
This is variance, so to get the standard errors we take the square root:
se.margin <- sqrt(var.margin)Each entry here is the standard deviation of the sampling distribution at that point. If each of those sampling distributions is normally distributed, then the 95% confidence interval will run 1.96 standard errors above and below our estimate:
upper.bounds <- marginal.effect +se.margin*1.96
lower.bounds <- marginal.effect - se.margin*1.96Now for this graph we can add in that confidence interval:
population.density <- seq(0,73000,1)
marginal.effect <- coef(m3)["percent.transit.commute"] + population.density*coef(m3)["percent.transit.commute:population.density"]
plot(population.density, marginal.effect, type="l", xlab="Population Density", ylab="Effect of % Transit Commute on Commute Time")
abline(h=0, lty=2)
points(population.density, upper.bounds, type="l", lty=2)
points(population.density, lower.bounds, type="l", lty=2)
rug(acs$population.density)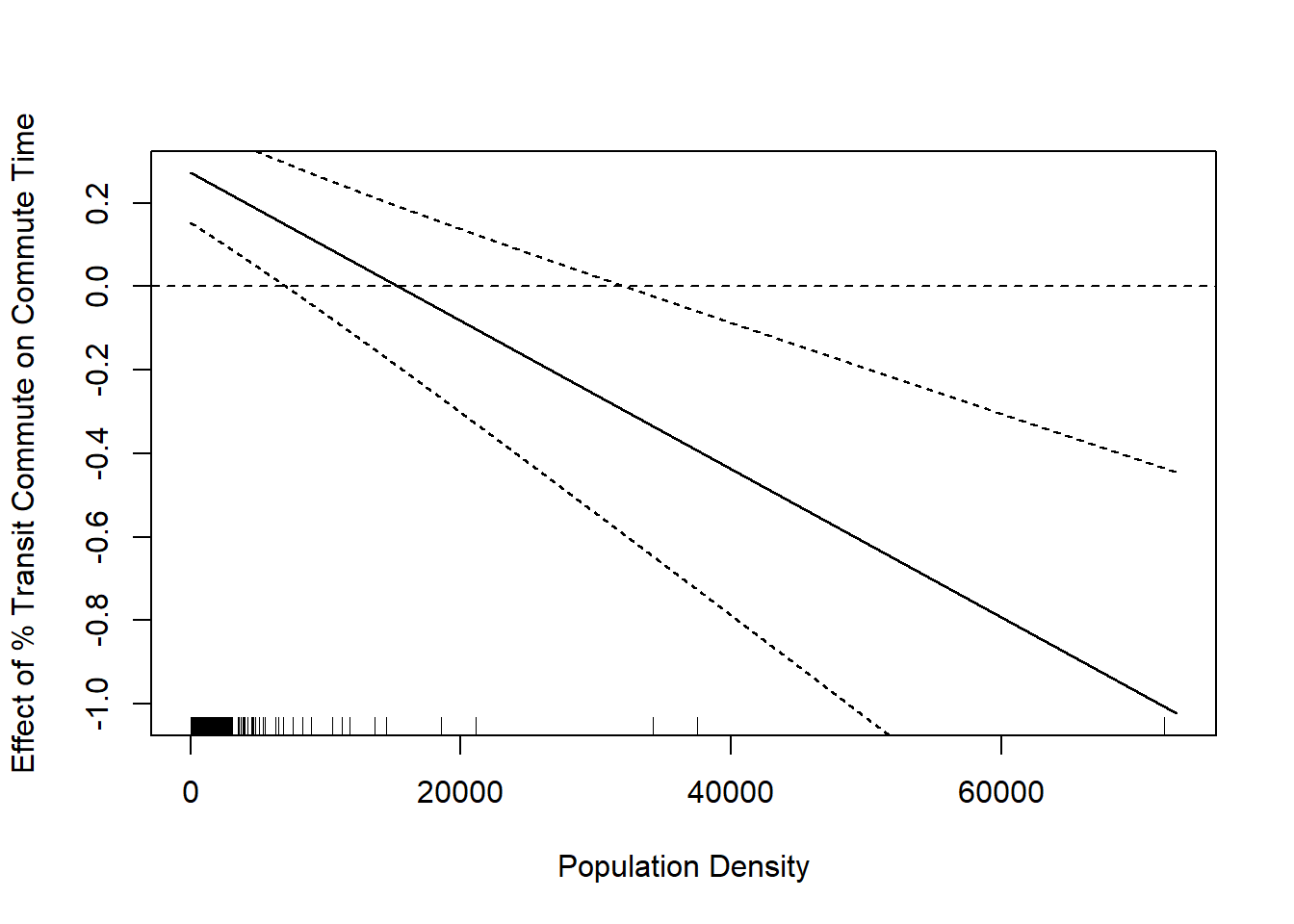
This should be the same as what we get in the margins package:
library(margins)
cplot(m3, x="population.density",dx="percent.transit.commute", what="effect")
abline(h=0)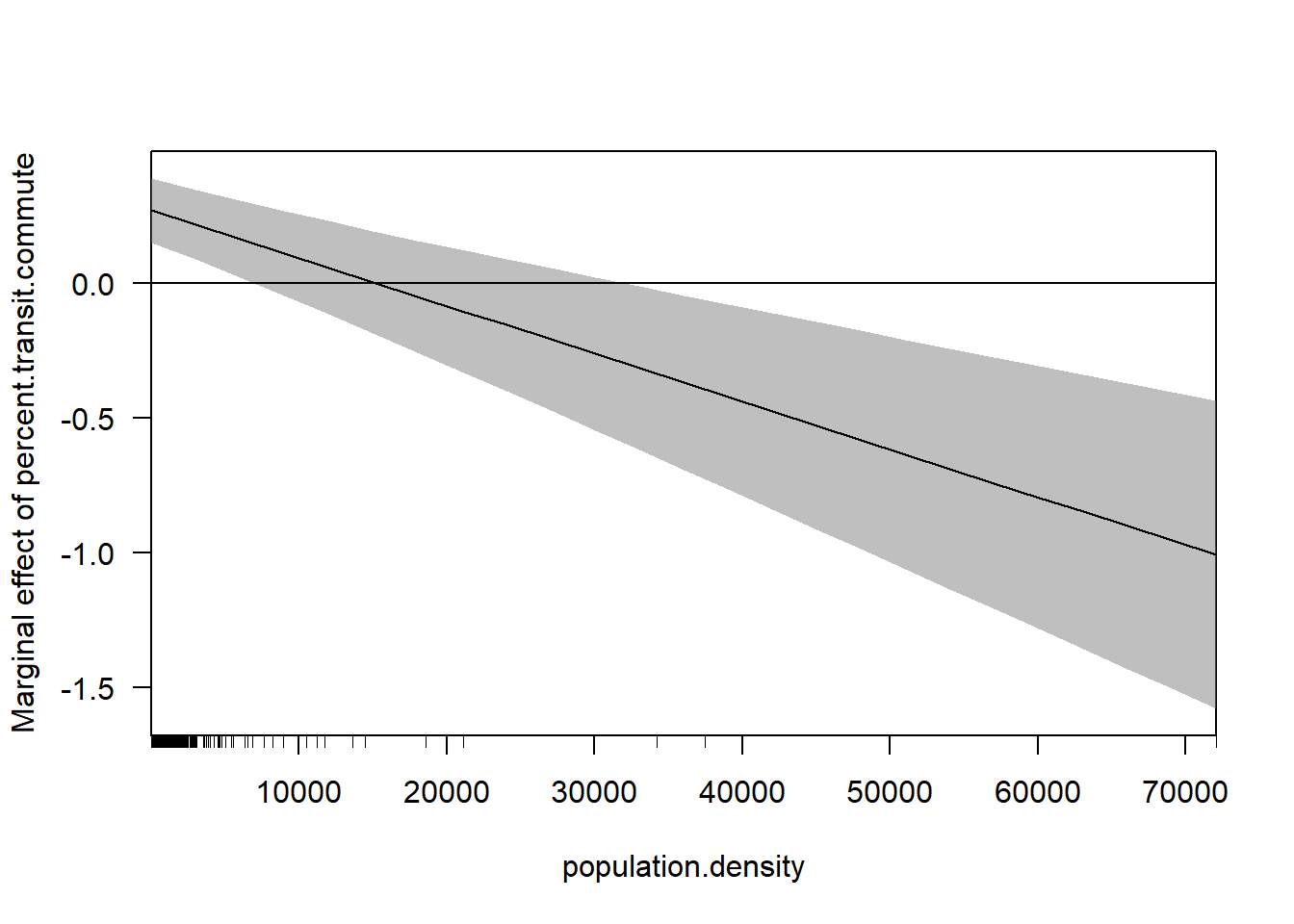
Additional Example:
m1 <- lm(gini ~ median.rent, data=acs)
m2 <- lm(gini ~ median.rent + factor(census.region), data=acs)
stargazer(m1, m2, type="text")
#>
#> =================================================================================
#> Dependent variable:
#> --------------------------------------------------
#> gini
#> (1) (2)
#> ---------------------------------------------------------------------------------
#> median.rent -0.001*** -0.002***
#> (0.0003) (0.0003)
#>
#> factor(census.region)northeast 1.834***
#> (0.263)
#>
#> factor(census.region)south 2.910***
#> (0.139)
#>
#> factor(census.region)west 1.032***
#> (0.200)
#>
#> Constant 45.346*** 44.193***
#> (0.236) (0.230)
#>
#> ---------------------------------------------------------------------------------
#> Observations 3,138 3,138
#> R2 0.004 0.131
#> Adjusted R2 0.004 0.130
#> Residual Std. Error 3.624 (df = 3136) 3.387 (df = 3133)
#> F Statistic 12.375*** (df = 1; 3136) 117.841*** (df = 4; 3133)
#> =================================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01
#Let the relationship change in each region
m3 <- lm(gini ~ median.rent*factor(census.region), data=acs)
stargazer(m1, m2,m3, type="text")
#>
#> ======================================================================================================================
#> Dependent variable:
#> ---------------------------------------------------------------------------
#> gini
#> (1) (2) (3)
#> ----------------------------------------------------------------------------------------------------------------------
#> median.rent -0.001*** -0.002*** -0.002***
#> (0.0003) (0.0003) (0.001)
#>
#> factor(census.region)northeast 1.834*** -5.365***
#> (0.263) (0.993)
#>
#> factor(census.region)south 2.910*** 4.867***
#> (0.139) (0.652)
#>
#> factor(census.region)west 1.032*** -1.515**
#> (0.200) (0.766)
#>
#> median.rent:factor(census.region)northeast 0.008***
#> (0.001)
#>
#> median.rent:factor(census.region)south -0.003***
#> (0.001)
#>
#> median.rent:factor(census.region)west 0.003***
#> (0.001)
#>
#> Constant 45.346*** 44.193*** 44.557***
#> (0.236) (0.230) (0.563)
#>
#> ----------------------------------------------------------------------------------------------------------------------
#> Observations 3,138 3,138 3,138
#> R2 0.004 0.131 0.170
#> Adjusted R2 0.004 0.130 0.168
#> Residual Std. Error 3.624 (df = 3136) 3.387 (df = 3133) 3.311 (df = 3130)
#> F Statistic 12.375*** (df = 1; 3136) 117.841*** (df = 4; 3133) 91.768*** (df = 7; 3130)
#> ======================================================================================================================
#> Note: *p<0.1; **p<0.05; ***p<0.01
median.rent <- seq(200,2500,1)
pred.midwest <- coef(m3)["(Intercept)"] +
coef(m3)["median.rent"]*median.rent
pred.northeast <- coef(m3)["(Intercept)"] +
coef(m3)["factor(census.region)northeast"] +
coef(m3)["median.rent"]*median.rent +
coef(m3)["median.rent:factor(census.region)northeast"]*median.rent
pred.south <- coef(m3)["(Intercept)"] +
coef(m3)["factor(census.region)south"] +
coef(m3)["median.rent"]*median.rent +
coef(m3)["median.rent:factor(census.region)south"]*median.rent
pred.west <- coef(m3)["(Intercept)"] +
coef(m3)["factor(census.region)west"] +
coef(m3)["median.rent"]*median.rent +
coef(m3)["median.rent:factor(census.region)west"]*median.rent
cols <- brewer.pal(4, "Set2")
plot(acs$median.rent, acs$gini, col="gray80")
points(median.rent, pred.midwest, lwd=2, col=cols[1], type="l")
points(median.rent, pred.northeast, lwd=2, col=cols[2], type="l")
points(median.rent, pred.south, lwd=2, col=cols[3], type="l")
points(median.rent, pred.west, lwd=2, col=cols[4], type="l")
legend("topright", c("Midwest","Northeast","South","West"), lty=1, col=cols)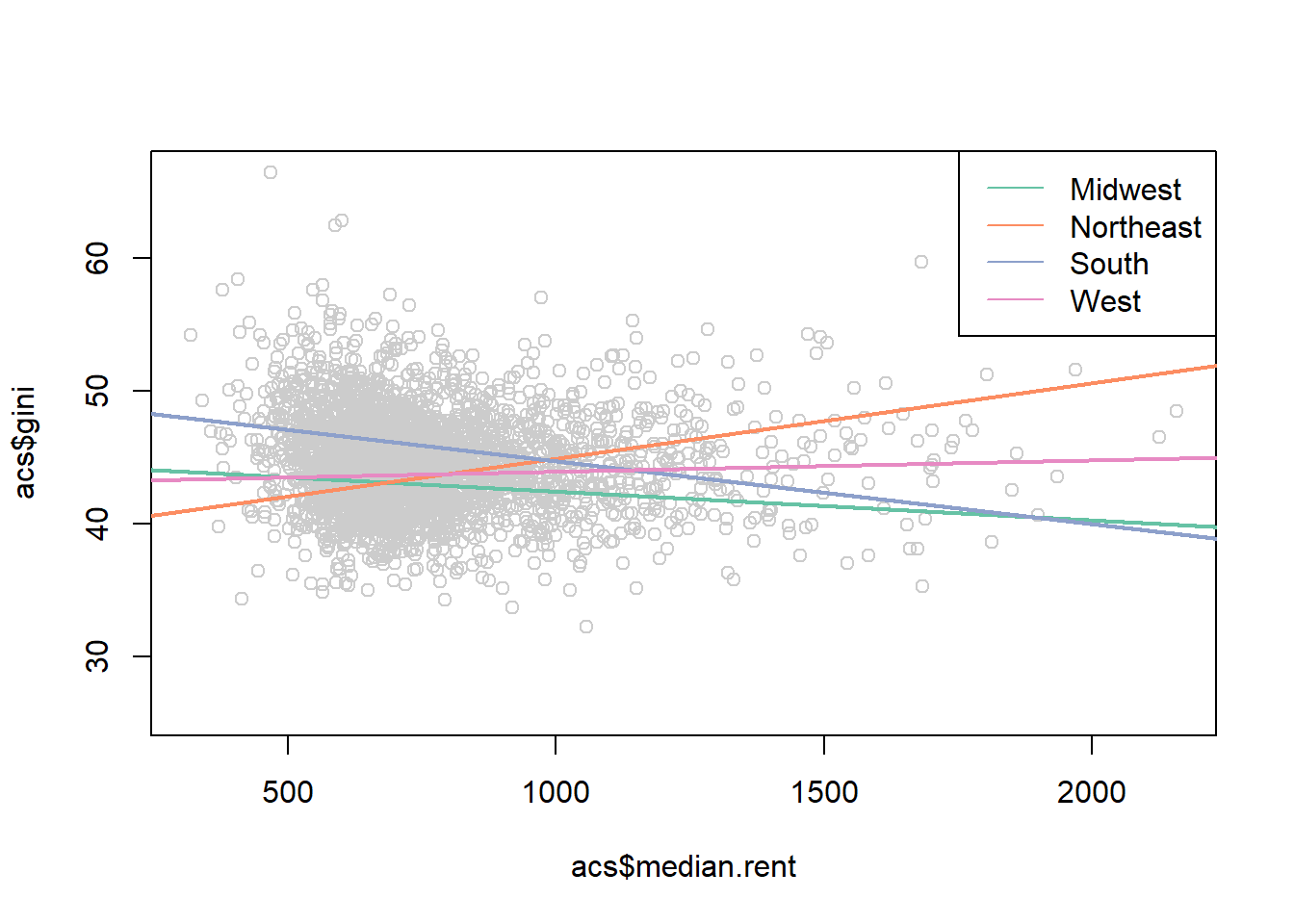
14.2 Predicting with regression
We have defined regression with this equation:
\[ \hat{y} = \hat{\alpha} + \hat{\beta}x \]
The regression line \(\hat{y}\) is determined by an intercept, slope coefficient, and x values.
For the most part we have used this information to literally draw a regression line:
x <- runif(100,0,100)
y <- 3 + 5*x + rnorm(100,0,40)
#Scatterplot
plot(x,y)
#Regression
m <- lm(y~x)
#Predicted values
pred <- coef(m)["(Intercept)"] + coef(m)["x"]*x
#Draw lines
plot(x,y)
points(x, pred, type="l", col="firebrick")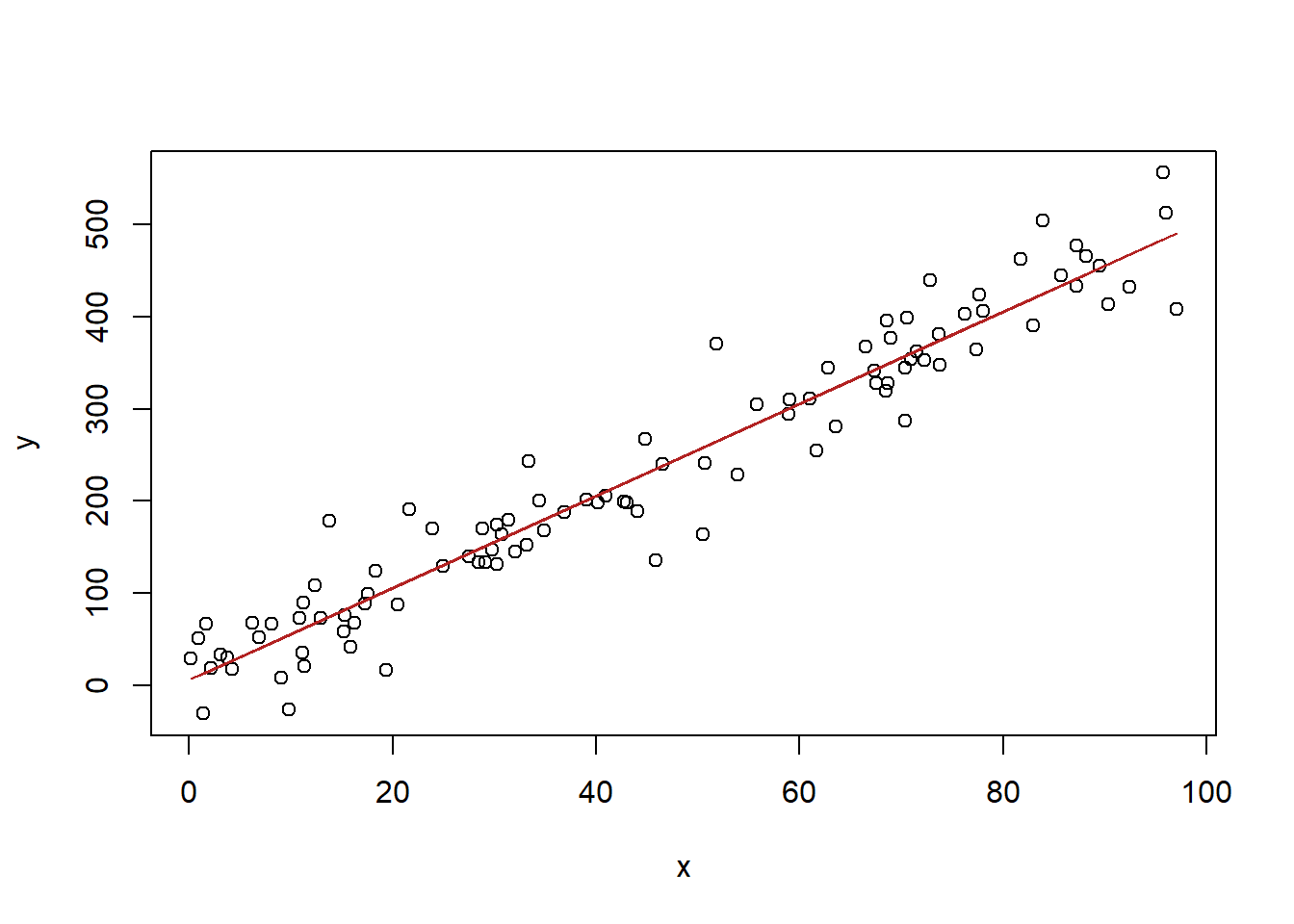
In this case our x runs from 0-100. What if we wanted to predict what y would be when x equaled 200? There is nothing stopping us from doing the math for this:
In other words, we can use the output of the regression to generate new predictions based on new values for \(x\).
We have primarily been using and conceptualizing regression as a tool of explanation thus far. Questions of the order: how does \(x\) effect \(y\)? The other tool we use regression for is prediction. Given the existing relationship, what do we expect to happen if we were to receive new data? How sure or unsure would we be of those predictions?
To be honest, most of my experience with regression is in explnation, though I increasingly do work with prediction in my election work. The good thing is: nothing changes about the math of regression when we are using it for this other purpose. There are some additional considerations to make, but those just build on the tools that we already have.
We are going to do a couple of examples here. The first (unsurprising for me) is to look at data on marathon running.
We are going to load in data on all of the marathon world records over time.
(Note that I downloaded this data in 2022, before Kevin Kiptums insanse 2:00:35 in Chicago).
library(lubridate)
#> Warning: package 'lubridate' was built under R version
#> 4.1.3
#>
#> Attaching package: 'lubridate'
#> The following objects are masked from 'package:base':
#>
#> date, intersect, setdiff, union
library(rio)
mwr <- import("https://github.com/marctrussler/IIS-Data/raw/main/MarathonWR.csv")
#Some cleaning because I copied data from wikipedia
names(mwr) <- c("time","date")
mwr <- mwr[-5,]
mwr$seconds <- seconds(hms(mwr$time))
mwr$date <- dmy(mwr$date)
mwr$date[1:30] <- mwr$date[1:30]-years(100)
mwr$year <- year(mwr$date)
mwr$seconds <- as.numeric(mwr$seconds)
mwr$year <- as.numeric(mwr$year)
#How many seconds is 2 hours?
2*3600
#> [1] 7200
#What does data look like?
head(mwr)
#> time date seconds year
#> 1 2:55:18 1908-07-24 10518 1908
#> 2 2:52:45 1909-01-01 10365 1909
#> 3 2:46:53 1909-02-12 10013 1909
#> 4 2:46:05 1909-05-08 9965 1909
#> 6 2:40:34 1909-08-31 9634 1909
#> 7 2:38:16 1913-05-12 9496 1913We are going to look at year as our main explanatory variable, and as our outcome variable we will look at marathon time in seconds.
A critical question is: when do we expect a male runner to run a 2:00 marathon that qualifies for a world record*.
*(Kipchoge’s 2 hour marathon time in Austria does not count for a world record for several reasons, the largest being that he had pacers who rotated in and out of running so he had a draft effect for the full 26.2 miles.)
Let’s visualize this relationship using bivariate regression:
#Plotting this relationship:
library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.1.3
p <- ggplot(mwr, aes(x=year, y=seconds)) + geom_point() +
labs(x="Date", y = "Time") +
geom_smooth(method = lm, formula = y ~ poly(x, 1), se = FALSE)
p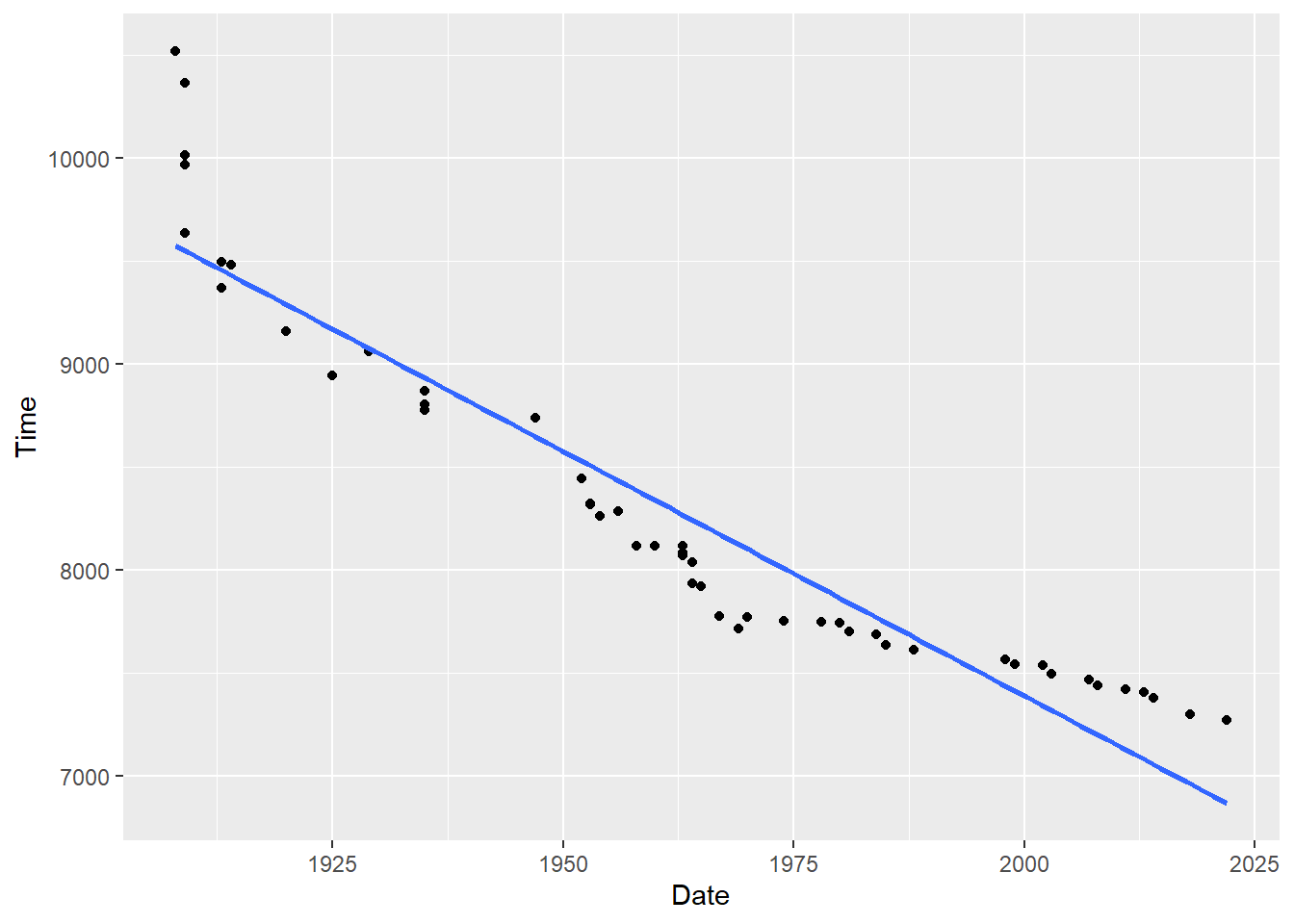
m <- lm(seconds ~ year, data=mwr)
summary(m)
#>
#> Call:
#> lm(formula = seconds ~ year, data = mwr)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -410.6 -188.4 -100.2 166.1 944.4
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 54898.384 2406.743 22.81 <2e-16 ***
#> year -23.755 1.227 -19.36 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 291.5 on 48 degrees of freedom
#> Multiple R-squared: 0.8865, Adjusted R-squared: 0.8842
#> F-statistic: 375 on 1 and 48 DF, p-value: < 2.2e-16In the output we see that the coefficient on year is -23.755. This is telling us that each additional year the marathon world record is expected to drop by around 24 seconds.
Now we can see that a linear relationship is not a particularly good fit for this data. We will address that shortly. But first, we can use the output of this regression to predict future year’s marathon times.
As above, all we need to do is to simply input future years (2023-2050) into the regression equation and it will spit out what the value of the line will be at those points. I will divide by 3600 to get the answer in hours:
future.years <- seq(2023,2050,1)
prediction <- coef(m)["(Intercept)"] + coef(m)["year"]*future.years
cbind(future.years, prediction/3600)
#> future.years
#> [1,] 2023 1.900505
#> [2,] 2024 1.893906
#> [3,] 2025 1.887308
#> [4,] 2026 1.880709
#> [5,] 2027 1.874110
#> [6,] 2028 1.867512
#> [7,] 2029 1.860913
#> [8,] 2030 1.854314
#> [9,] 2031 1.847716
#> [10,] 2032 1.841117
#> [11,] 2033 1.834518
#> [12,] 2034 1.827920
#> [13,] 2035 1.821321
#> [14,] 2036 1.814722
#> [15,] 2037 1.808124
#> [16,] 2038 1.801525
#> [17,] 2039 1.794927
#> [18,] 2040 1.788328
#> [19,] 2041 1.781729
#> [20,] 2042 1.775131
#> [21,] 2043 1.768532
#> [22,] 2044 1.761933
#> [23,] 2045 1.755335
#> [24,] 2046 1.748736
#> [25,] 2047 1.742137
#> [26,] 2048 1.735539
#> [27,] 2049 1.728940
#> [28,] 2050 1.722342Like everything in this class: we know that this data is just a sample and that if we sampled many times we would get slightly different answers and slightly different predictions for all of these years.
One method to get a sense of how variable these predictions are would be the bootstrap, but we don’t actually have to do that here.
For interaction we determined how to work out the variance of the sum of two regression coefficients, and that’s really all we are doing here:
\[ V(\alpha + \beta*years)=V(\alpha) + years^2 *V(\beta) + 2*years*Cov(\alpha,\beta) \]
Let’s input that information:
var <- vcov(m)["(Intercept)","(Intercept)"] + future.years^2 * vcov(m)["year","year"] + 2*future.years * vcov(m)["year","(Intercept)"]
se.pred <- sqrt(var)
upper <- (prediction + se.pred*1.96)/3600
lower <- (prediction - se.pred*1.96)/3600And graph that information:
plot(future.years, prediction/3600, type="l", ylim=c())
points(future.years, lower, type="l", lty=2)
points(future.years, upper, type="l", lty=2)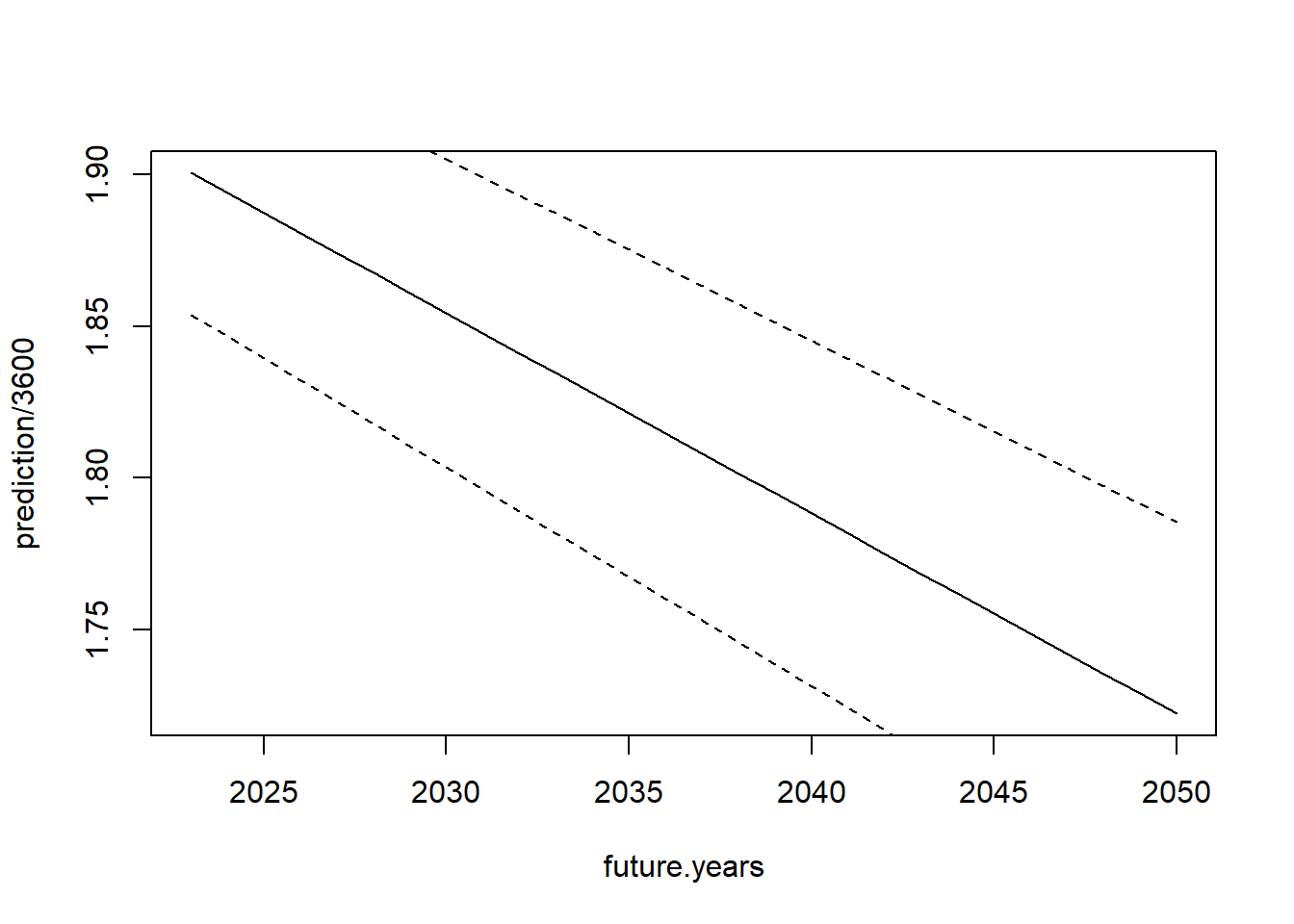
Thankfully, we don’t have to manually work out the math. R has a built in function predict() which can simplify this procedure for us.
In it’s basic form predict will spit out the value of the line for all the actual data points in our dataset.
mwr$prediction <- predict(m)
head(mwr)
#> time date seconds year prediction
#> 1 2:55:18 1908-07-24 10518 1908 9573.654
#> 2 2:52:45 1909-01-01 10365 1909 9549.899
#> 3 2:46:53 1909-02-12 10013 1909 9549.899
#> 4 2:46:05 1909-05-08 9965 1909 9549.899
#> 6 2:40:34 1909-08-31 9634 1909 9549.899
#> 7 2:38:16 1913-05-12 9496 1913 9454.878But helpfully we can also feed new data into the predict function with new values for the x variable
prediction2 <- predict(m, newdata=data.frame(year=future.years))
cbind(prediction, prediction2)
#> prediction prediction2
#> 1 6841.817 6841.817
#> 2 6818.062 6818.062
#> 3 6794.307 6794.307
#> 4 6770.552 6770.552
#> 5 6746.797 6746.797
#> 6 6723.042 6723.042
#> 7 6699.287 6699.287
#> 8 6675.532 6675.532
#> 9 6651.776 6651.776
#> 10 6628.021 6628.021
#> 11 6604.266 6604.266
#> 12 6580.511 6580.511
#> 13 6556.756 6556.756
#> 14 6533.001 6533.001
#> 15 6509.246 6509.246
#> 16 6485.491 6485.491
#> 17 6461.736 6461.736
#> 18 6437.981 6437.981
#> 19 6414.225 6414.225
#> 20 6390.470 6390.470
#> 21 6366.715 6366.715
#> 22 6342.960 6342.960
#> 23 6319.205 6319.205
#> 24 6295.450 6295.450
#> 25 6271.695 6271.695
#> 26 6247.940 6247.940
#> 27 6224.185 6224.185
#> 28 6200.430 6200.430(this produces identical predictions as doing the math by “hand”).
What’s more, the predict function will also determine the confidence interval for you:
prediction2 <- predict(m, newdata=data.frame(year=future.years), interval="confidence")
prediction2
#> fit lwr upr
#> 1 6841.817 6669.355 7014.280
#> 2 6818.062 6643.432 6992.692
#> 3 6794.307 6617.503 6971.112
#> 4 6770.552 6591.565 6949.539
#> 5 6746.797 6565.620 6927.974
#> 6 6723.042 6539.668 6906.415
#> 7 6699.287 6513.710 6884.864
#> 8 6675.532 6487.745 6863.318
#> 9 6651.776 6461.773 6841.780
#> 10 6628.021 6435.796 6820.247
#> 11 6604.266 6409.812 6798.720
#> 12 6580.511 6383.823 6777.199
#> 13 6556.756 6357.829 6755.684
#> 14 6533.001 6331.829 6734.173
#> 15 6509.246 6305.824 6712.668
#> 16 6485.491 6279.814 6691.168
#> 17 6461.736 6253.799 6669.672
#> 18 6437.981 6227.779 6648.182
#> 19 6414.225 6201.756 6626.695
#> 20 6390.470 6175.727 6605.214
#> 21 6366.715 6149.695 6583.736
#> 22 6342.960 6123.658 6562.262
#> 23 6319.205 6097.618 6540.793
#> 24 6295.450 6071.573 6519.327
#> 25 6271.695 6045.525 6497.865
#> 26 6247.940 6019.473 6476.406
#> 27 6224.185 5993.418 6454.951
#> 28 6200.430 5967.359 6433.500This seems minimally helpful here where the math is so easy. The real value of the predict function comes when we have much more complicated regressions.
Above we can see that the linear regression is not a very good fit for these marathon data. Instead, I’m going to propose that a 3rd order polynomial fit is what is best to fit to these data. That would look like this:
#Plotting this relationship:
library(ggplot2)
p <- ggplot(mwr, aes(x=year, y=seconds)) + geom_point() +
labs(x="Date", y = "Time") +
geom_smooth(method = lm, formula = y ~ poly(x, 3), se = FALSE)
p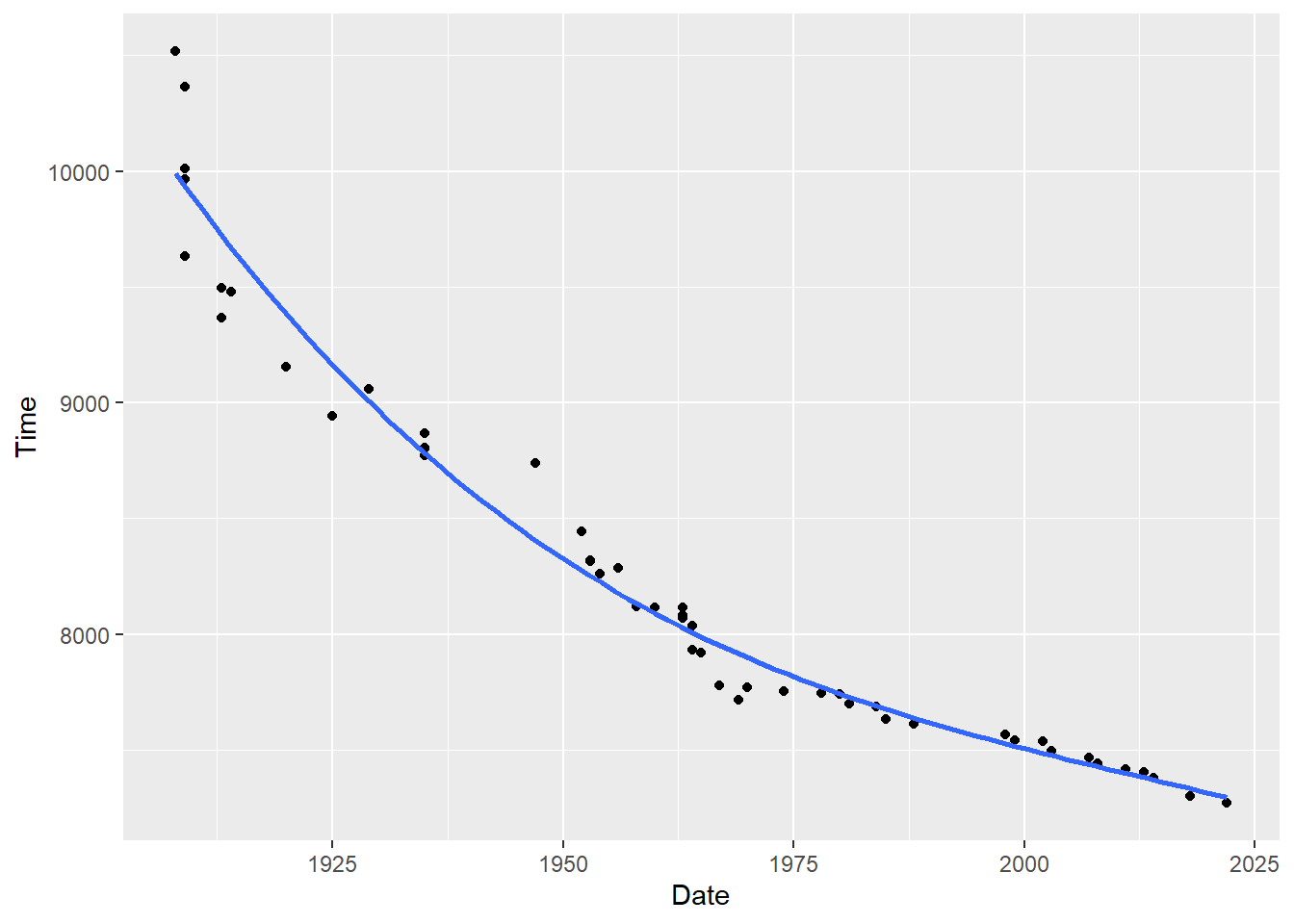
m2 <- lm(seconds ~ poly(year, 3), data=mwr)
summary(m2)
#>
#> Call:
#> lm(formula = seconds ~ poly(year, 3), data = mwr)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -357.07 -41.24 18.96 48.94 526.26
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8298.48 22.67 366.133 < 2e-16 ***
#> poly(year, 3)1 -5644.47 160.27 -35.219 < 2e-16 ***
#> poly(year, 3)2 1678.50 160.27 10.473 9.16e-14 ***
#> poly(year, 3)3 -281.26 160.27 -1.755 0.0859 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 160.3 on 46 degrees of freedom
#> Multiple R-squared: 0.9671, Adjusted R-squared: 0.965
#> F-statistic: 451.1 on 3 and 46 DF, p-value: < 2.2e-16It’s not too bad to use the math to predict the fitted values for all of the future years, but calculating the standard error for the confidence band at each of those fitted values would be extremely difficult.
Thankfully, we can just pipe in the model to the predict function and generate predictions and a confidence interval around those predictions:
prediction.poly <- predict(m2, newdata=data.frame(year=future.years), interval="confidence")
plot(future.years, prediction.poly[,1], type="l", ylim=c(6000,8000))
points(future.years, prediction.poly[,2], type="l")
points(future.years, prediction.poly[,3], type="l")
abline(h=7200, lty=3)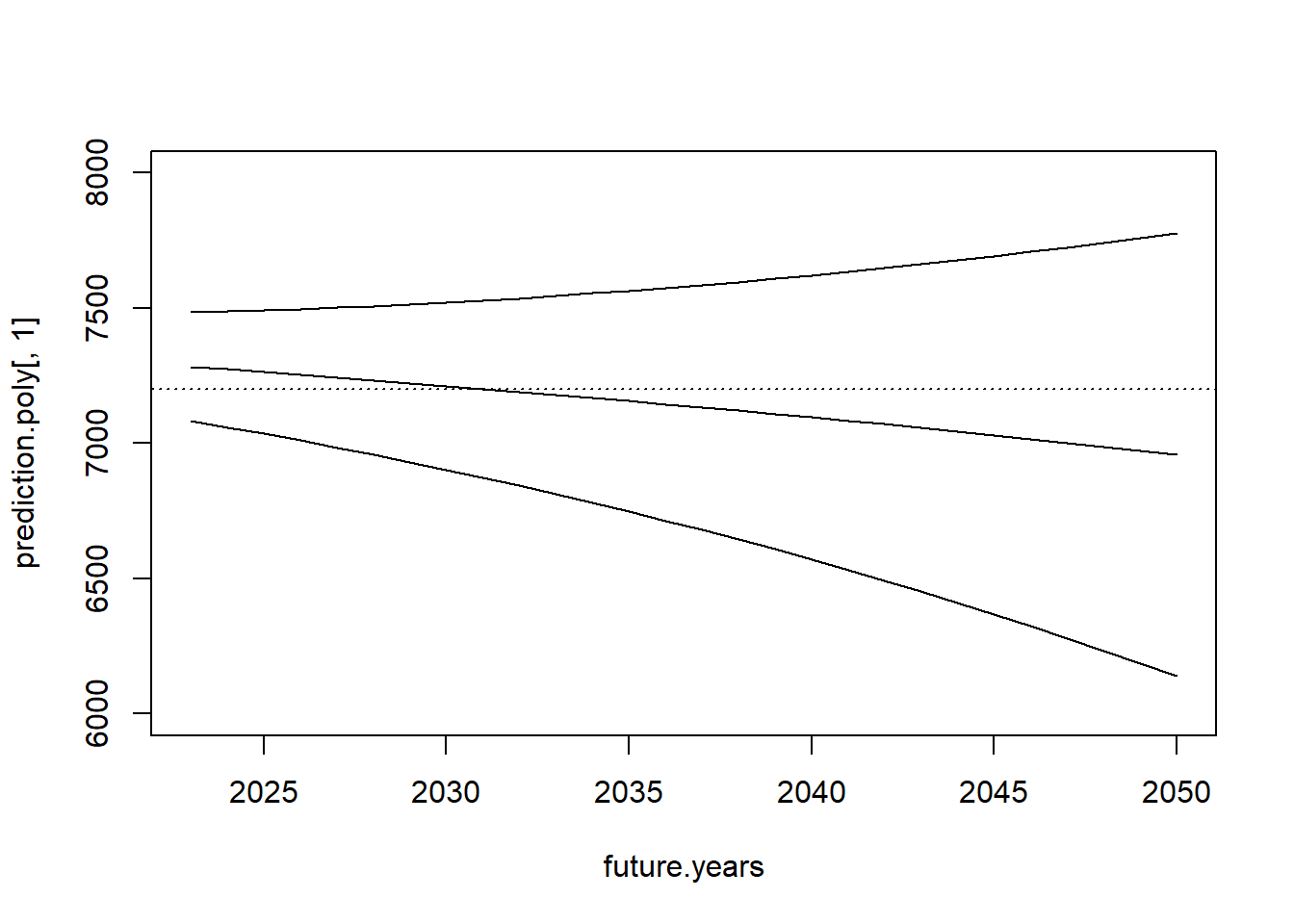
Let’s examine what that looks like in the context of the full dataset:
prediction.poly <- predict(m2, newdata=data.frame(year=future.years), interval="confidence")
plot(future.years, prediction.poly[,1], type="l", ylim=c(6000,11000), xlim=c(1900,2050))
points(future.years, prediction.poly[,2], type="l")
points(future.years, prediction.poly[,3], type="l")
points(mwr$year, mwr$seconds, pch=16)
abline(h=7200, lty=3)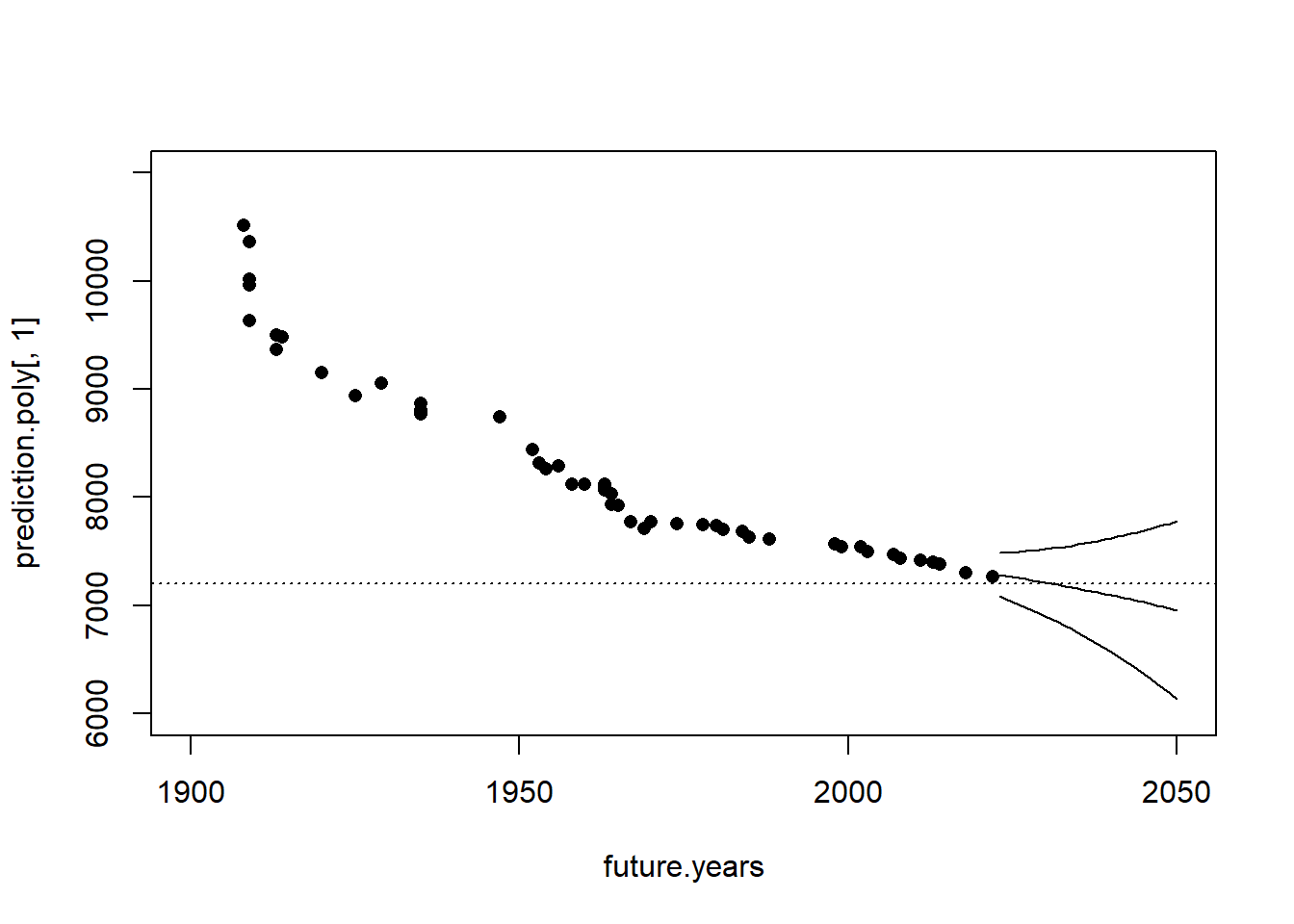
That’s pretty reasonable! Our prediction is that the 2 hour marathon barrier will be broken in around 2030 given current trends, though our confidence in that prediction is pretty wide.
That being said, since I first wrote this lecture the world record was dropped to 2:00:35 on October 8th 2023 by Kevin Kiptum. Let’s look at what that looks like in the context of our regression and prediction:
head(mwr)
#> time date seconds year prediction
#> 1 2:55:18 1908-07-24 10518 1908 9573.654
#> 2 2:52:45 1909-01-01 10365 1909 9549.899
#> 3 2:46:53 1909-02-12 10013 1909 9549.899
#> 4 2:46:05 1909-05-08 9965 1909 9549.899
#> 6 2:40:34 1909-08-31 9634 1909 9549.899
#> 7 2:38:16 1913-05-12 9496 1913 9454.878
prediction.poly <- predict(m2, newdata=data.frame(year=future.years), interval="confidence")
plot(future.years, prediction.poly[,1], type="l", ylim=c(6000,11000), xlim=c(2000,2050))
points(future.years, prediction.poly[,2], type="l")
points(future.years, prediction.poly[,3], type="l")
points(mwr$year, mwr$seconds, pch=16)
points(2023,7235, pch=16, col="firebrick" )
abline(h=7200, lty=3)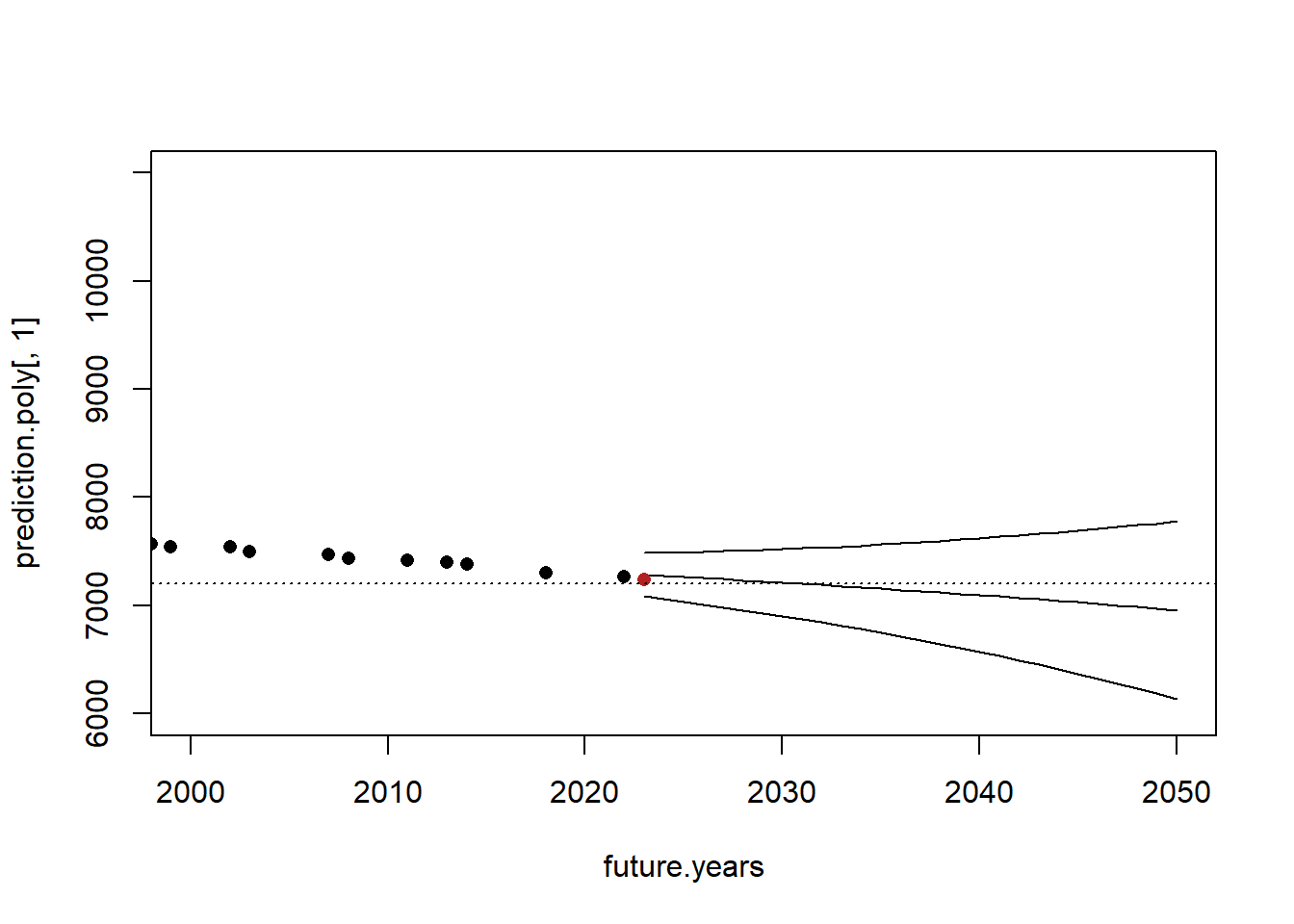
This isn’t a particularly shocking data point, but it is a good amount off the line and might make us reconsider when 2 hour barrier will be broken. One of the downsides to prediction is that we can only use what we have, and have to make the assumption that current trends will continue. We can’t “model in” the possibilities of future intercept shifts due to new advancements.
In this case all of endurance sport saw an intercept shift before and after the pandemic. The possibilities for this ocurring are potentially nefarious – i.e. doping, particularly during lock downs when there was no at-home testing – but also might be due to advances in technology (super shoes, better understanding of aerodynamics), training (the use of lactate monitoring and a better understanding of recovery), and nutrition (a huge increase in the amount of fueling happening in long activities). None of this is important to this class I just enjoy this stuff!
14.3 Out of Sample Prediction
Let’s go through another example of making out of sample predictions.
In order to conduct a pre-election survey a necessary step is to predict who is likely to vote and who is not. This is critical because a pre-election poll is not meant to predict the opinions of all Americans, but rather the opinions of voters specifically. Making a judgement on who that is a critical step.
We are going to look at building a likely voter model using CCES data. One of the nice things about the CCES is that, post election, they use the voter file to determine who actually voted out of the people that they surveyed. This is great information because people lie like crazy when we ask them if they voted or not.
library(rio)
cces <- import("https://github.com/marctrussler/IIS-Data/raw/main/CCES.csv")
head(cces)
#> V1 year vv.turnout educ white female agegrp
#> 1 1 2016 1 HS or less white 1 40-49
#> 2 2 2016 1 HS or less white 1 18-29
#> 3 3 2016 0 HS or less nonwhite 1 50-64
#> 4 4 2016 1 HS or less nonwhite 1 18-29
#> 5 5 2016 1 college white 1 30-39
#> 6 6 2016 0 HS or less nonwhite 1 50-64
#> vote.intent pid3 prim.turnout
#> 1 Maybe 3 0
#> 2 Yes 3 0
#> 3 Yes 1 0
#> 4 Yes 3 0
#> 5 Yes 1 0
#> 6 Maybe 1 0
table(cces$year)
#>
#> 2016 2018 2020
#> 64600 60000 61000The models we want to build here are to predict vv.turnout, whether someone voted (1) or not (0). So for example, taking the 2016 voters, we can determine how an individual’s vote intention predicts whether they will vote, or not.
table(cces$vote.intent)
#>
#> Already voted Maybe No Yes
#> 16563 23491 15139 130199
cces$vote.intent <- factor(cces$vote.intent)
cces$vote.intent <- relevel(cces$vote.intent, ref="No")
cces.16 <- cces[cces$year==2016,]
m <- lm(vv.turnout ~ vote.intent, data=cces.16)
summary(m)
#>
#> Call:
#> lm(formula = vv.turnout ~ vote.intent, data = cces.16)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.6969 -0.6499 0.3502 0.3502 0.9261
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 0.073882 0.006337 11.66
#> vote.intentAlready voted 0.623028 0.013332 46.73
#> vote.intentMaybe 0.174263 0.008153 21.37
#> vote.intentYes 0.575972 0.006660 86.48
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> vote.intentAlready voted <2e-16 ***
#> vote.intentMaybe <2e-16 ***
#> vote.intentYes <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4575 on 64484 degrees of freedom
#> (112 observations deleted due to missingness)
#> Multiple R-squared: 0.1528, Adjusted R-squared: 0.1528
#> F-statistic: 3877 on 3 and 64484 DF, p-value: < 2.2e-16Because the intercept is the probability of voting when all other variables are 0, this is the probability of voting for someone who said they would not vote in the upcoming election (about 7.3%). Each of these coefficients indicates the change of probability of moving from being an expressed non-voter to each of those categories. We can do the math ourselves or use predict:
predict(m, newdata= data.frame(vote.intent=c("No", "Maybe", "Yes", "Already voted")))
#> 1 2 3 4
#> 0.07388217 0.24814489 0.64985443 0.69690993So for the 2016 data only 70% of those who said they already voted actually voted. The lies!
Now pretend that it’s fall of 2020 and we have collected the data but the election hasn’t happened yet. How can we use the other data to predict, for the 2020 respondents, whether they are going to vote or not. Now we actually have this information and can verify how we do with our predictions, but that’s not something that would actually be available to us at the time.
Let’s use the 2016 and 2018 data to build a couple of models that predict whether someone voted or not. I’m going to use 4 models from simple to complex:
cces.training <- cces[cces$year %in% c(2016,2018),]
cces.test <- cces[cces$year==2020,]
m1 <- lm(vv.turnout ~ vote.intent, data=cces.training)
m2 <- lm(vv.turnout ~ vote.intent +prim.turnout + educ:white, data=cces.training)
m3 <- lm(vv.turnout ~ female + vote.intent +prim.turnout + educ:white:agegrp + pid3, data=cces.training)These are 3 models with increasingly complicated equations. We haven’t seen regressions with this many variables but, rest assured, everything we’ve talked about so far applies. These are (mostly) just a series of indicator variables and interactions.
The important thing here is that because the 2020 data has the exact same variables in it, we can use the coefficients in these models to form predictions in the 2020 data.
Consider the first model:
summary(m1)
#>
#> Call:
#> lm(formula = vv.turnout ~ vote.intent, data = cces.training)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.7710 -0.6675 0.3325 0.3325 0.9336
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 0.066432 0.004318 15.39
#> vote.intentAlready voted 0.704534 0.007914 89.02
#> vote.intentMaybe 0.175119 0.005477 31.97
#> vote.intentYes 0.601085 0.004565 131.67
#> Pr(>|t|)
#> (Intercept) <2e-16 ***
#> vote.intentAlready voted <2e-16 ***
#> vote.intentMaybe <2e-16 ***
#> vote.intentYes <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4482 on 124444 degrees of freedom
#> (152 observations deleted due to missingness)
#> Multiple R-squared: 0.1851, Adjusted R-squared: 0.1851
#> F-statistic: 9423 on 3 and 124444 DF, p-value: < 2.2e-16
predict(m1, newdata= data.frame(vote.intent=c("No", "Maybe", "Yes", "Already voted")))
#> 1 2 3 4
#> 0.06643162 0.24155081 0.66751633 0.77096562The people in 2020 also have a variable named vote.intent with the same response labels. As such we can do:
cces.test$predict1 <- predict(m1, newdata=cces.test)
head(cces.test)
#> V1 year vv.turnout educ white female
#> 124601 124601 2020 1 some college white 0
#> 124602 124602 2020 0 postgrad white 1
#> 124603 124603 2020 0 college white 1
#> 124604 124604 2020 1 college white 1
#> 124605 124605 2020 0 college white 0
#> 124606 124606 2020 1 some college white 0
#> agegrp vote.intent pid3 prim.turnout predict1
#> 124601 50-64 Already voted 2 1 0.77096562
#> 124602 65-74 No 1 0 0.06643162
#> 124603 65-74 Yes 3 0 0.66751633
#> 124604 50-64 Yes 1 1 0.66751633
#> 124605 50-64 Yes 3 0 0.66751633
#> 124606 50-64 Yes 2 0 0.66751633
table(cces.test$predict1)
#>
#> 0.066431619966184 0.241550808184305 0.667516327713994
#> 4361 5797 38790
#> 0.770965622946551
#> 11996The predict1 column takes on 4 possible values based on the individuals vote intention.
We can classify each person as a likely voter or not if there probability of voting is above or below 50%. From that we can determine how good of a job this model does in predicting 2020 voters. We can look to see the proportion of voters who are incorrectly classified. IE, how many are predicted to vote but don’t, and how many are predicted not to vote but do?
#Classification Error
mean((cces.test$predict1>.5 & cces.test$vv.turnout==0) | (cces.test$predict1<.5 & cces.test$vv.turnout==1),na.rm=T)
#> [1] 0.2363153The two other models both have a substantially higher \(R^2\), meaning that the models fit the 2016/2018 data much better. The question is whether this better fitting data also reduces the classification error. Notice that even though these models have lots of complicated interactions and many variables the code to actually form predictions is really easy! Wee! Regression is fun!
cces.test$predict2 <- predict(m2, newdata=cces.test)
#> Warning in predict.lm(m2, newdata = cces.test): prediction
#> from a rank-deficient fit may be misleading
cces.test$predict3 <- predict(m3, newdata=cces.test)
#> Warning in predict.lm(m3, newdata = cces.test): prediction
#> from a rank-deficient fit may be misleading
#Classification Error Model 2
mean((cces.test$predict2>.5 & cces.test$vv.turnout==0) | (cces.test$predict2<.5 & cces.test$vv.turnout==1),na.rm=T)
#> [1] 0.2115221
#Classification Error Model 3
mean((cces.test$predict3>.5 & cces.test$vv.turnout==0) | (cces.test$predict3<.5 & cces.test$vv.turnout==1),na.rm=T)
#> [1] 0.1948018Yes, in this case we do make a few fewer classification errors when we better fit the data. Taking into account more features gives us a fuller picture of why some people vote and why some do not, and ultimately that allows us to make a better prediction.
But is that always true?
Let’s go crazy with this interacting everything we everything:
#Stupid model
m4 <- lm(vv.turnout ~ pid3:vote.intent:prim.turnout + female:educ:white:agegrp, data=cces.training)
cces.test$predict4<- predict(m4, newdata=cces.test)
#Classification Error Model 4
mean((cces.test$predict4>.5 & cces.test$vv.turnout==0) | (cces.test$predict4<.5 & cces.test$vv.turnout==1),na.rm=T)
#> [1] 0.2268804What happened!? The classification error went up.
Here is where things get tricky with prediction, and links directly to the through-line of this course about trying to uncover what is true in the population. Remember that our 2016 and 2018 data are samples from a broader population, and due to that there are small random bits of noise present. If we go crazy with our regression, estimating interactions for every possible sub-category, we are over-fitting our model to the specifics of the 2016 and 2018 cases. At some point, a better fit on these data mean a worse fit on out-of-sample data.
This problem: optimizing the fit of a model to maximize out of sample predictiveness is….. machine learning! That’s all that is. There are some more complicated models and some other details, but it’s not that far of a stretch from this lesson to what happens with machine learning.