3 Probability
Pretty much all classes and textbooks that teach statistics start with some introductory material on probability theory. They get in the weeds of dice, card games, lotteries, colored balls in hats in a way that thoroughly confuses the students. There is then some hand-waving over the course of a week and then… ta-dah! P-values! If I’m to be honest, it was years before I was able to properly articulate the connection between probability theory and day-to-day statistics. It is indeed helpful to learn a bit of probability theory in order to understand the foundation of inferential statistics, but I promise here not to get too bogged down in weird probability exercises.
One resource that helped me enormously in seeing the connection between probability and statistics was the book “The Drunkard’s Walk” by Leonard Mlodinow. It’s a very entertaining read in the style of Malcolm Gladwell or Michael Lewis that tells the story of how statistics was founded. Here is an excerpt that is a good starting point:
Bill Miller was the sole portfolio manager of Legg Mason Value Trust Fund, who in each year of his fifteen-year streak beat the portfolio of equity securities that constitute Standard & Poor’s 500. For his accomplishments, Miller was heralded “the Greatest Money Manager of the 1990s” by Money magazine. In the fourteenth year of Miller’s streak, one analyst put the odds of a fourteen-year streak by chance alone at 372,529:1. Those who quoted the low odds were right in one sense: if you had singled out Bill Miller in particular at the start of 1991 in particular and calculated the odds that by pure chance the specific person you selected would beat the market for precisely the next fifteen years then those odds would indeed have been astronimcally low. But those are not the relevant odds because there are thousands of mutual fund managers (over 6000 currently) and there are many fifteen year periods in which the feat could have been accomplished. So the relevant question is, if thousands of people are tossing coins once a year and have been doing so for decades, what are the chances that one of them, for some peiod of fifteen years or longer, will toss all heads?
Mlodinow is providing an example of the “Hot Hand Fallacy”, which is the mistaken belief that streaks are less likely than they really are. This fallacy is very common in sports, for example, where coaches, analysts, and fans all assume a run of success (or failure!) for a player is meaningful, when in reality such streaks are quite common.
The question at hand here is whether what this particular investor has done is special, or not. We understand that there is a lot of randomness in the stock market, yet it is tempting to believe that there are individuals who can out-smart it and continuously win. The existence of a streak of winning this long must be nearly impossible to achieve only due to chance, right?
This question, which we’ll answer together via simulation below, helps clarify why probability is an important component of statistical inference. When trying to decide whether to be impressed by not by Bill Miller, our baseline is the question: if success and failure on the stock market was just random chance, how likely would it be that we see someone have 15 years of success? In order for us to calculate this, we first need a way to calculate what is likely to happen due to chance variation alone. In other words, we need to be able to calculate the probability of random events.
This will tie in directly with our ability to make inferences about populations from samples in future parts of this course. When we calculate regression coefficients and find, for example, that there is a positive relationship between age and feelings towards Trump in our sample the question we will ask is: if there is no relationship between age and feelings towards Trump in the population, what is the probability of seeing a relationship this extreme in our sample?
3.1 The Basics of Probability
It is odd to define something that we use all the time in everyday language, but it’s helpful to lay out some clear definitions of what we mean by probability.
What do we mean, for example, when we say that a coin comes up heads 50% of the time? Or that a dice4 comes up as 4 \(\frac{1}{6}\) of the time?
We clearly do not mean that, for example, a coin must come up tails after coming up heads. Barring magic, each flip of the coin is independent of from the last. Probability has nothing to say about what must happen on any particular coin flip.
Instead, what probability denotes is the expected long-term frequency of events. A definition that I find helpful:
The chance of something gives the percentage of time it is expected to happen, when the basic process is done over and over again, independently and under the same conditions.
This is a particularly helpful frame because, as we’ll see below, a good way for us to estimate probability is to simply to get R to repeat a process a whole bunch of times to determine the percentage of time an event is likely to happen.
To formalize our look into probability, two key terms are events and a sample space. Events are simply outcomes of a particular thing: the outcome of the roll of a dice or a flip of a coin; or the outcome of a presidential election; or whether a randomly sampled individual is favorable towards the President or not. A sample space is set of all possible outcomes of the thing we are considering. So for the roll of a dice the sample space is all of the numbers \(\lbrace 1,2,3,4,5,6 \rbrace\). For a flip of a coin \(\lbrace H,T \rbrace\). For the outcome of a presidential election $Dem, Rep, Third$. For whether an individual is favorable towards the President \(\lbrace Fav, Unfav, NoOpinion \rbrace\).
When the probability of all events are equal (which of the above are equal?) we can then define the probability of an event occuring by dividing the number of elements in the event by the total number of events in the sample space.
So the probability of getting a heads on a coin flip is \(P(H) = \frac{1}{2}\). The probability of rolling a 2 is \(P(2) = \frac{1}{6}\).
This helpfully scales up when we are interested in multiple events ocurring. For example what is the probability of rolling an even number? \(P(even) = \frac{3}{6} = \frac{1}{2}\)
This method does not apply to when the probability of events ocurring is not equal. For example we cannot calculate the probability of a third party candidate winning an election by \(P(third) \neq \frac{1}{3}\).
There are a couple of “rules” (axioms) about probability that are helpful to keep in mind.
- The probability of any event A is non-negative: \(P(A)\geq 0\).
An event can’t have a 0 or negative probability of occurring.
- The probability that one of the outcomes in the sample space occurs is 1. \(P(\Omega)==1\)
The probability that something happens is a certainty, or 1.
Together these two axioms also tell us that probability ranges between 0 and 1 (or 0% and 100%, if we want to express it like that).
- If events A and B are mutually exclusive: \(P(AorB) = P(A) + P(B)\).
What do we mean by mutually exclusive? Simply that A ocurring precludes B from ocurring, and vice versa. We can ask, for example, what is the probability of rolling a 2 or a 3? If you roll a 2 you can’t roll a 3, and vice versa.
So here: \(P(2or3) = P(2) + P(3) = \frac{1}{6} + \frac{1}{6} = \frac{1}{3}\). We could confirm this visually by looking at the sample space \(\lbrace 1,\mathbf{2},\mathbf{3},4,5,6\rbrace\).
But what if we ask a different question: what is the probability of rolling a 4 or an even number? Are these events mutually exclusive? No! If you roll an even number it doesn’t preclude rolling a 4.
Just looking visually if we think about the events in the sample space that satisfy this statement we see that the probability of this combined event is \(\frac{1}{2}\): \(\lbrace 1,\mathbf{2},3,\mathbf{4},5,\mathbf{6}\rbrace\).
But if we (incorrectly) apply Axiom 3 we get: \(P(4orEven) \neq P(4) + P(Even) = \frac{1}{6} + \frac{1}{2} = \frac{4}{6}\).
Because of this we use a more general formula for Axiom 3: \(P(AorB) = P(A) + P(B) - P(A\&B)\). Notice what the last part of this equation is doing. We need to subtract off the probability of then events that are contained in both A & B so we don’t double count. In the example above the probability of rolling a 4 and rolling an even number is \(\frac{1}{6}\). So using this formula we get: \(P(4orEven) = P(4) + P(Even) - P(4\&Even) = \frac{1}{6} + \frac{1}{2} - \frac{1}{6}= \frac{1}{2}\).
Helpfully, this more general formula also applies to events that are mutually exclusive, because the probability of both of them occurring is 0!
The other helpful bit of notation is to think about the complement of an event, which is simply everything in the sample space that is not that event.
For example what is the complement of rolling a 2(\(2^c\))? \(\lbrace 1,3,4,5,6 \rbrace\).
What is the complement of rolling an odd number (\(odd^c\))? \(\lbrace 2,4,6 \rbrace\).
This is helpful for the following reason: What is \(P(2 or 2^c)\)? Using the formula from above: \(P(2) + P(2^c) + P(2\&2^c) = \frac{1}{6} + \frac{5}{6} + 0 = 1\). An event either happens or doesn’t happen, so any event plus it’s complement by definition equals 1.
So if we generalize that \(P(A) + P(A^c)=1\), then re-arranging we get: \(P(A) = 1- P(A^c)\) and \(P(A^c) = 1- P(A)\). The probability of an event occuring is 1 minus the probability of that event not ocurring. This ends up being very helpful!
3.2 Simulating Probability in R
There are ways of calculating probability mathematically that we will get to, but one of the most beautiful things about learning statistics in the computer age is the ability to obtain estimates of probability via simulation. Instead of calculating what happens when you throw a dice an infinite number of times, we can just simulate the throwing of a dice a large number of times to get a proximate answer.
The way that we do that using R is a for() loop. The basic logic of a for() loop is that it lets you repeat the same code many, many times. Because, as defined above, all probability represents is the long term frequency of events, we can simulate something approaching “long term” by simulating the outcome of a process many times.
Here is the basic setup for a for() loop:
for(i in 1:3){
#CODE HERE
}We can look at the for loop as having two parts. Everything from the start to the opening squiggly bracket are the instructions for the loop. It basically tells the loop how many times to repeat the same thing. “i” in this case is the variable that is going to change its value each time through the loop. Having this variable is what allows the loop to do something slightly different each time through the loop. The second part is whatever you put in between the squiggly brackets. This is the code that will be repeated again, and again the specified number of times.
Let’s put a simple bit of code in the loop to see how these work. I’m just going to put the command print(i) in the loop so that all the loop does is print the current value of i.
for(i in 1:3){
print(i)
}
#> [1] 1
#> [1] 2
#> [1] 3What a loop does is the following: on the first time through the loop it sets our variable (i) to the number 1. Literally. Anywhere we have the variable i, R will replace it with the integer 1. Once all the code has been executed and R reaches the closing squiggly bracket it goes back up the start. Now it will set i equal to 2. Anywhere in our code where there is currently the variable “i”, R will literally treat this as the integer 2. After it reaches the end of the code again, it will go back to the beginning and run the code again, this time making “i” equal to 3.
So the result of running this code is to simply print out the numbers 1, then 2, then 3.
To make this crystal clear, here is what code is literally being executed by R here. It is just the print command 3 times, the first time changing the variable i to the integer 1, the second time changing it to 2, and the third time changing it to 3.
Let’s take a second to think through the options at the start of this loop; everything that is contained in the opening parentheses.
Right now it says for(i in 1:3). This is saying: the variable that’s going to change everytime through the loop is called “i”, and the things we want to change it to is the sequence of numbers 1, 2, and then 3. Each of these things is customizable.
First, there is nothing special about “i”. We can name the variable that changes everytime through the script to anything we want.
So, for example, we can edit this same code to be for(batman in 1:3), and have the variable be called batman. And if we run this we get the exact same result.
for(batman in 1:3){
print(batman)
}
#> [1] 1
#> [1] 2
#> [1] 3This being said, it is convention to use the letter “i” as the indexing variable in a for loop. This is true across coding platforms so it’s a good idea to just use that.
Second, we can put any sort of vector into the second part. We can make it longer, for example, by running from 1 to 50.
for(i in 1:50){
print(i)
}
#> [1] 1
#> [1] 2
#> [1] 3
#> [1] 4
#> [1] 5
#> [1] 6
#> [1] 7
#> [1] 8
#> [1] 9
#> [1] 10
#> [1] 11
#> [1] 12
#> [1] 13
#> [1] 14
#> [1] 15
#> [1] 16
#> [1] 17
#> [1] 18
#> [1] 19
#> [1] 20
#> [1] 21
#> [1] 22
#> [1] 23
#> [1] 24
#> [1] 25
#> [1] 26
#> [1] 27
#> [1] 28
#> [1] 29
#> [1] 30
#> [1] 31
#> [1] 32
#> [1] 33
#> [1] 34
#> [1] 35
#> [1] 36
#> [1] 37
#> [1] 38
#> [1] 39
#> [1] 40
#> [1] 41
#> [1] 42
#> [1] 43
#> [1] 44
#> [1] 45
#> [1] 46
#> [1] 47
#> [1] 48
#> [1] 49
#> [1] 50We could also use the concatenate (or c() function) to give it a sequence of numbers to loop through. So here the first time through the loop i will be set equal to 2, the second time through it will be set equal to 15, and the third time through it will be set equal to 45.
Before you run this code, think: what code would the following produce?
How can we use this functionality to simulate probability?
Let’s say we want to know the odds of getting 0 heads when we flip a coin 7 times. There is a way to calculate this mathematically, but remember the probability of an event can be defined as the frequency that event occurs over the long run. We can get at this in R by literally flipping 7 coins a large number of times and seeing how often we get 0 heads.
Before we do this a large number of times, let’s create the code to do it once.
First, let’s create an object called coin that is just a vector with 0 and 1 in it. We’ll define 0 as tails, and 1 as heads.
coin <- c(0,1)The sample() command take a random sample from an object a specific number of times. Here we are going to sample from our object “coin” 7 times with replacement. The 7 times represents 7 flips of the coin. We are sampling with replacement here because each time you flip a coin you can get either heads or tails. It’s not the case that once you get a heads you can only get a tails.
Running this once we get the following output. As we’ve defined tails as 0 and heads as 1,
sample(coin,7,replace=T)
#> [1] 1 0 0 1 1 1 0Sample() is a random command, however, so each time we run it we’ll get something different.
sample(coin,7,replace=T)
#> [1] 1 0 1 0 1 1 0
sample(coin,7,replace=T)
#> [1] 1 1 1 0 1 1 1
sample(coin,7,replace=T)
#> [1] 1 1 1 1 0 0 1Finally, we aren’t interested in the specific sequence of heads and tails but just the number of heads each time we flip a coin 7 times. Because we’ve defined heads as the number 1 and tails as 0, taking the sum of the sample will give us the number of heads.
Now we need to repeat this a large number of times. Let’s do 100000! A loop lets us repeat this same code as many times as we want. We’ll set up our loop just as we did above, going from 1 to 100,000. We can put our coin flipping code in the loop and see what happens.
One nuance of running loops in R is that by default R will run the code in the background and not display anything. So in this case R did sample 7 coins 100,000 times, but because we didn’t save it anywhere there is no record of this. We need to explicitly save what is happening. We’ll create an empty vector “num.heads” to save these, and then each time through the loop save the outcome in each successive position in num.heads.
num.heads <- NA
for(i in 1:100000){
num.heads[i] <- sum(sample(coin,7,replace=T))
}
head(num.heads)
#> [1] 3 4 3 3 4 4Finally, using the table command we can see exactly how often each of these outcomes happened. Only 780 out of the 100,000 times did none of the coins come up heads. Less than 1% of the time.
table(num.heads)
#> num.heads
#> 0 1 2 3 4 5 6 7
#> 811 5515 16382 27419 27325 16340 5437 771
prop.table(table(num.heads))
#> num.heads
#> 0 1 2 3 4 5 6
#> 0.00811 0.05515 0.16382 0.27419 0.27325 0.16340 0.05437
#> 7
#> 0.00771Now let’s simulate the throwing of a dice in R. First, how might we set it up so we throw a dice once? I am going to create an object called “dice” that is a vector containing the possible outcomes of a dice throw. I’m then going to use the sample() function to randomly sample 1 number from this vector. The beginning of the code uses set.seed see the footnote for what this is.5
Here the random sampling produced a dice roll of 4.
Let’s go further to roll this dice a large number of times in a way that approximates the probability of getting each number, 1 through 6. To do so I will use a loop, which is how we will simulate things a large number of times. I create a loop that is 10,000 iterations. In each iteration I sample from our object dice and save the output in the empty vector result. At the end of the loop the vector result will be 10,000 items long, with each being the result of a single dice throw.
set.seed(19104)
dice <- c(1,2,3,4,5,6)
result <- rep(NA,10000)
for(i in 1:10000){
result[i] <- sample(dice,1,replace=T)
}
table(result)
#> result
#> 1 2 3 4 5 6
#> 1684 1653 1710 1682 1676 1595We know that each number of a fair dice will come up 1/6 of the time, so our expectation would be that each of these numbers would be drawn \(10000/6=1666\) times. Obviously with random chance we don’t get that number exactly, but each is quite close.
3.3 Permutations & Combinations
It’s pretty easy to talk about the probability with one coin or easy things like that, which might have you thinking we are over-complicating something that is very straightforward. Where probability is more helpful is sharpening our thinking for more complex events.
Consider the following problem. I have a locker in Pottruck and I’m worried about someone trying to guess the code to my locker. The lock on my locker has 50 numbers and my code (and any code) has three unique numbers that need to be put in the right order. What is the probability that someone guesses my combination?
Using the probability we have learned so far, we can break this problem down in the following way. Each event is a possible combination. There is only 1 correct event, so we need to know the probability of selecting the 1 right answer out of all the possible answers. In other words: \(P(GuessRight) = \frac{1}{AllPermutations}\).
Now I’ve used “Permutation” instead “Combination” here on purpose. In probability theory a permutation is a sequence where the order matters (as it does when putting in a locker code), where “combination” is a sequence that doesn’t matter (like a lottery drawing).
So how many different 3-digit permutations are there to a lock with 50 numbers? We can break it down like this: There are 50 possibilities for the first number in the code. Because the numbers have to be unique, there are 49 digits for the second number. Finally, because the first two numbers can’t be repeated, there are 48 possibilities for the last number. In total the number of permutations is: \(50*49*48=117600\).
Therefore the probability of guessing my code is \(\frac{1}{117600}\).
As above, we can similarly use R to get an answer to this question:
#Estimating the probability of guessing a locker combination
#Set Seed
set.seed(19104)
#Draw prime combination
prime <- sample(seq(1,50),3, replace=F)
#How do we determine if two vectors are exactly equal?
c(2,34,29)==prime
#> [1] FALSE FALSE FALSE
#Use the all command to determine if all numbers match
all(c(28,21,37)==prime)
#> [1] TRUE
#Use a loop to repeatedly sample and check
results <- rep(NA, 1E6)
for(i in 1:length(results)){
results[i] <- all(sample(seq(1,50),3, replace=F)==prime)
}
prop.table(table(results))
#> results
#> FALSE TRUE
#> 0.99999 0.00001
#Approximately equivalent to what we calculated via math. There is a more generalized formula to determine the number of permutations which is \(_nP_k = \frac{n!}{(n-k)!}\), which gives the number of permutatations where \(n\) is the number of options and \(k\) is the number of selections. Plugging the numbers from above into this: \(_{50}P_3 = \frac{50!}{(50-47)!} = \frac{50*49*48*47*46 \dots *2*1}{47*46 \dots *2*1} = 50*49*48=1176000\).
A combination differs from a permutation because with a combination the order does not matter. A lottery is a great example of this. You win the lottery if the numbers you selected come out of the bin, regardless of the order of the balls.
Let’s try to calculate the probability of winning the Mega Millions lottery. For this lottery you have to match 5 white balls that are drawn from a pool of 70, as well as one gold “MegaBall” drawn from a pool of 25. To win the jackpot you need the exact winning combination so the probability of winning is: \(\frac{1}{\#Of Possiblg Combos}\).
Let’s deal first with the white balls. Using the permutations formula (which is wrong) we would get: \(_nP_k = \frac{70!}{(70-5)!} \approx 1.5bil\). But that’s the number of permutations such that two sequences with the same numbers in a different order would be treated as different lottery drawings. So to get the number of combinations do we have to increase or decrease this number?
Decrease! If any sequence of the same numbers is treated as equal, we collapse all of those into 1. So to get the number of combinations we have to divide by the number of ways to sequence a series of 5 numbers. The ways to sequnece 5 numbers is \(5!\). So to generalize, the formula for combinations just modifies the permutations formula to be \(_nC_k = \frac{n!}{k!(n-k)!}\). Therefore the number of combinations for the 5 white balls is: \(_{70}C_5 =\frac{70!}{5!(70-5)!} = 12103014\). A lot less!
To get this number I used R. There is a very helpful function for combinations:
choose(70,5)
#> [1] 12103014To get the total odds of winning the lottery we also have to deal with the gold ball. The way to think about that is that for every possible sequence of white numbers there are 25 possibilities for the gold ball. So the total number of possible lottery numbers are: \(12103014*25 = 302575350\).
Let’s stop here for a second and have you do some of the work: can you write a simulation of the probability of winning the lottery in R? Remember: first write it to simulate the lottery once, and then place that code in a loop to simulate the lottery a large number of times. Don’t forget the Gold ball!
Here’s a problem for us to solve: To get the expected value of winning the lottery we can compare the cost ($2) to the “Expected Value” of winning. The expected value is the odds of winning (which we calculated above), multiplied by the jackpot. At what point is playing the lottery a good idea?
We can solve this via algebra, solving for \(P\), the prize: \[ \begin{aligned} \frac{1}{302575350}*P &=&2\\ P&=&2*302575350 \\ P &=& 605150700 \end{aligned} \]
The expected value of playing Mega Millions becomes positive when the jackpot is just over 600 million. Which it is frequently! Should you therefore play the lottery everytime the value gets over this number? No. You shouldn’t, because we are ignoring a critical and unknown component to the lottery. Can you guess what it is? 6
Another common probability problem we can solve with permutations is the “Birthday problem”. What is the probability in a classroom of 20 people that two people will have the same birthday? To solve this it is helpful to use what we learned above about compliments. It turns out re-framing this question makes things a bit easier: what is the probability that nobody shares a birthday in a class?
The sample space we are interested in here is all possible permutations of 20 birthdays. Each “event” is a sequence of 20 birthdays. The probability we want to calculate is \(P(No Shared Birthdays) = \frac{\text{Number of sequences with no shared birthdays}}{\text{All possible sequences of birthdays}}\).
Let’s start with the denominator what is the size of the entire sample space? Here we are interested in every possible set of 20 birthdays, including the ones with repeats. So if we take the first person in a class of 20 there are 365 possible birthdays for them to have. Because we are not interested in unique birthdays for the denominator, the second person also has 365 options for a birthday. And so on. So to get the total number of sequences 20 people can have birthdays on we get \(365*365*365*365 \dots\), or \(365^{20}\). Note that this calculation gives the total number of sequences where order matters.
For the numerator, we need to find the number of sequences where there is no repeating birthdays. In other words, how many ways are there to uniquely order 20 birthdays when there are 365 possible birthdays. This is just like the locker permutation but scaled up. We get: \(_{365}P_{20} = \frac{365!}{(365-20)!}\).
So to calculate the probability of no-two people sharing a birthday in a class of 20 we will calculate: \(\frac{\frac{365!}{(365-20)!}}{365^{20}}\).
OK, let’s try to do that:
We get nothing! What! Why?? Because \(365!\) is an absolutely gigantic number that R literally cannot calculate.
In order to calculate this we can make use of the choose() function in R which we used above. Because this calculates a combination, however, it is calculating: \(\frac{365!}{20!(365-20)!}\). To get the permutations we multiply the whole thing by \(20!\).
So the probability of nobody in a class of 20 people sharing a birthday is only 58.9 percent. Using our knowledge of complements, this means the probability that two people (or more) share a birthday in a class of 20 people is 41%! That’s very high.
Again, we can make our lives less mathy by simulating the birthday problem in R:
First, how can we randomly assign birthdays to 20 people using R? We can think of this in the same way as above. We can create a vector birthdays that is numbered 1 to 365 to represent all the possible days of the year (sorry, leap day babies). We can then sample from that vector 20 possibilities, with replacement. anyDuplicated() returns a 0 if there are no duplicates in a vector, and returns the index position of the first duplicate if there is one. So, if this returns a number greater than 0, there is a duplicate in the sampled vector.
set.seed(19104)
birthdays <- seq(1,365,1)
s <- sample(birthdays, 20, replace=T)
s
#> [1] 156 277 119 101 334 276 86 279 178 225 305 329 212 195
#> [15] 5 261 365 335 192 24
anyDuplicated(s)>0
#> [1] FALSEIn this first run of the simulation, all 20 students have a unique birthday.
Now, again, let’s run this a large number of times to estimate the probability of people sharing a birthday:
set.seed(19104)
birthdays <- seq(1,365,1)
result <- rep(NA, 10000)
for(i in 1:10000){
s <- sample(birthdays, 20, replace=T)
result[i] <- anyDuplicated(s)>0
}
table(result)
#> result
#> FALSE TRUE
#> 5891 4109In these 10,000 runs, over 41% of them had duplicated birthdays – The exact same as we calculated with math!
Can we make a graph that is the probability of at least two people sharing a birthday for every class size from 5 to 100? Can we make it both using math and simulation?
set.seed(19104)
birthdays <- seq(1,365,1)
class.size <- seq(5,100,1)
prob.sim <- rep(NA, length(class.size))
prob.math <- rep(NA, length(class.size))
for(j in 1:length(class.size)){
result <- rep(NA, 10000)
for(i in 1:10000){
s <- sample(birthdays, class.size[j], replace=T)
result[i] <- anyDuplicated(s)>0
}
prob.sim[j] <- mean(result)
prob.math[j] <- 1-(choose(365,class.size[j])*factorial(class.size[j]))/365^class.size[j]
}
plot(class.size, prob.math, col="dodgerblue", type="b", xlab="Class Size",
ylab="Probability of Shared Birthday", pch=16)
points(class.size, prob.sim, col="firebrick", type="b", pch=16)
legend("topleft", c("Math","Simulation"), pch=c(1,1), col=c("dodgerblue", "firebrick"))
Some more practice writing loops to simulate probability (see end of chapter for answers).
Rolling 4 dice, and we want to know the odds of the dice all coming up as the same number.
Rolling two dice, what are the odds of the sum of the two dice equaling 10?
Rolling two dice, what are the odds of each sum, 2 to 12? Plot the result.
Bag 1 containes 3 red and 5 black balls. Bag 2 contains 4 red and 4 black balls. A bag is chosen at random, and then a ball is chosen at random from that bag. What’s the probability a red ball is drawn?
The Philadelphia Phillies are expected to beat the Washington Nationals 60% of the time. In a stretch of 7 games, what are the odds that the Phillies win a majority (4 games)?
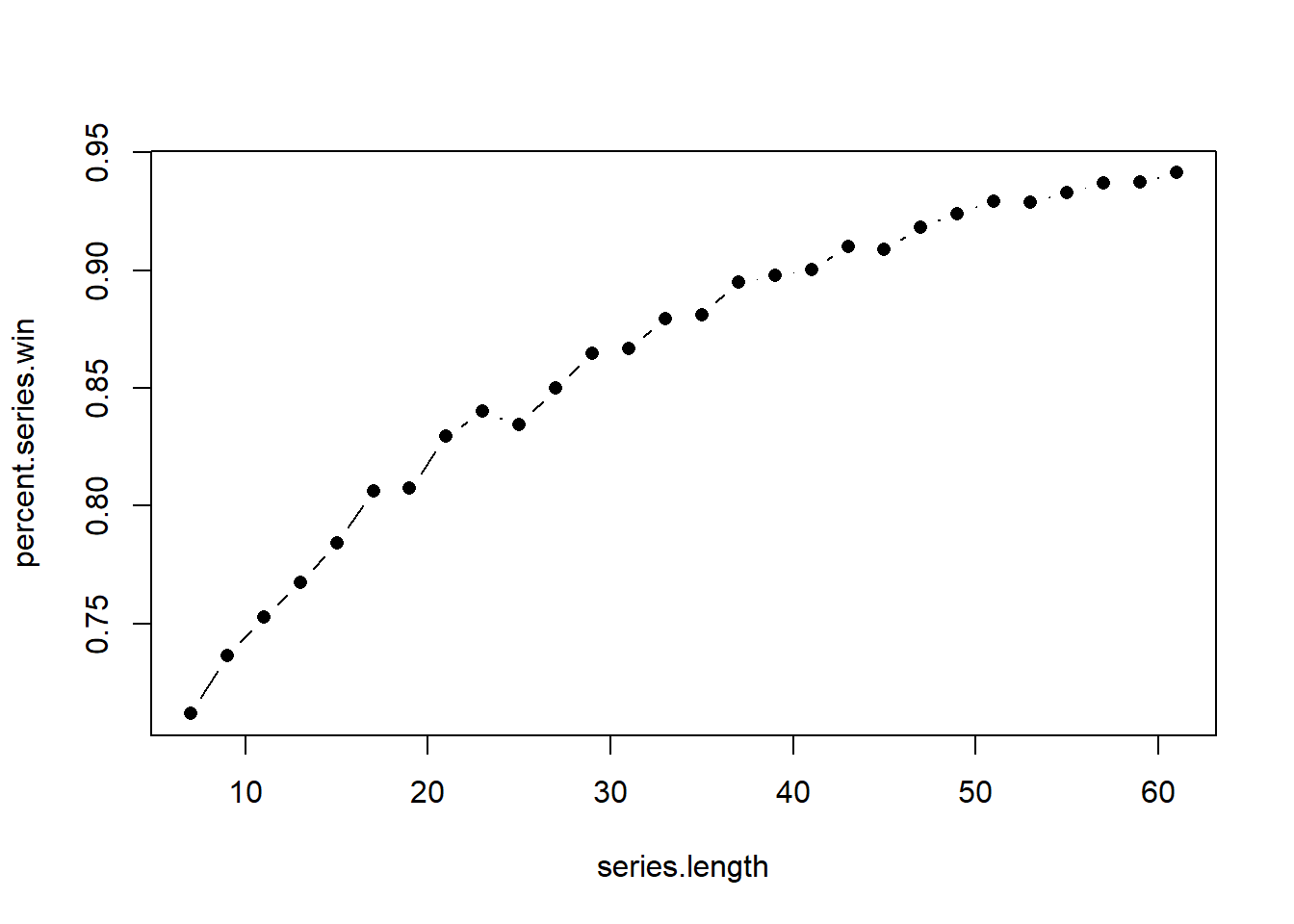
Estimate the probability the Phillies win the majority of 9,11,13,15…61 games, and plot the result.
3.4 Conditional probability
An additional complication with probability is to think about conditional probability: or how the probability of some event changes based on the outcome of a seperate event.
Consider the following: You first flip a coin. If the coin comes up tails you have to roll one dice. If the coin comes up heads you have to roll two dice. What is the probability the sum of the two dice rolls is greater than, or equal to, 4? Clearly, the likelihood is contingent on the coin flip. It’s way more likely when you get a heads and roll two dice. But how much more likely?
In this case we can write out the full sample space.
| T1 | H11 | H22 | H33 | H44 | H55 | H66 |
| T2 | H12 | H23 | H34 | H45 | H56 | |
| T3 | H13 | H24 | H35 | H46 | ||
| T4 | H14 | H25 | H36 | |||
| T5 | H15 | H26 | ||||
| T6 | H16 |
Looking through this sample space there are 27 possible outcomes: 6 for when you flip a tails and 21 for when you flip a head. We also see that all but 5 of these events results in a dice or a pair of dice summing to a number greater than, or equal to, 4.
Regardless of the possibility of changes based on conditions, our estimate for the probability of a sum greater than or equal to 4 remains the same: count up the number of events where it happens and divide by the total number of events in the sample space: \(P(sum\geq 4)=\frac{22}{27}\).
But does the probability of a 4 change if you toss a tails?
The key insight to conditional probability is that it is about subsetting. To visually answer this question, think about subsetting down to the “condition” we have set and to use that as out denominator.
So using just the “Tails” events as our whole sample space we get: \(P(sum\geq 4| T) = \frac{3}{6} = \frac{1}{2}\).
And for the other condition: \(P(sum\geq 4| H) = \frac{19}{21}\).
As a gut check: Does \(P(sum \geq 4 | T) = P(T | sum \geq 4)\)? No! It’s a completely different, almost unrelated, question. The answer there is \(P(T | sum \geq 4) = \frac{3}{21} = \frac{1}{7}\)
The more general formula for conditional probability is given by : \(P(A|B) = \frac{P(A\&B)}{P(B)}\).
So for the above example we can use this equation to give us \(P(sum \geq 4 | T) = \frac{\frac{3}{27}}{\frac{6}{27}} = \frac{3}{27}*\frac{27}{6} = \frac{1}{2}\)
We can consider conditional probability in a more practical way using some data.
Consider race in the American National Election Study. Now remember: this is just a sample of data and the percentages we calculate are not necessarily true in the population. But regardless: using real data can help us to focus on what we mean when we are talking about conditional probability.
anes <- read.csv("https://raw.githubusercontent.com/marctrussler/IIS-Data/main/ANES2020Clean.csv")We can first determine what we will call the marginal probability of each race. This is simply the probability that someone identifies as each option:
table(anes$race)
#>
#> Asian/Hawaiian/Pacific-Islander
#> 284
#> Black, non-Hispanic
#> 726
#> Hispanic
#> 762
#> Multiple races, non-Hispanic
#> 271
#> Native American
#> 172
#> White, non-Hispanic
#> 5963
prop.table(table(anes$race))
#>
#> Asian/Hawaiian/Pacific-Islander
#> 0.03472732
#> Black, non-Hispanic
#> 0.08877476
#> Hispanic
#> 0.09317682
#> Multiple races, non-Hispanic
#> 0.03313769
#> Native American
#> 0.02103204
#> White, non-Hispanic
#> 0.72915138And similarly we can compute the marginal probability of being female:
table(anes$gender)
#>
#> Female Male
#> 4450 3763But let’s say that we are interested in the conditional probability of being a certain race based on if someone is a woman.
Given that we have learned that conditional probability is just subsetting it should be very clear how we would calculate this in R:
table(anes$race[anes$gender=="Female"])
#>
#> Asian/Hawaiian/Pacific-Islander
#> 133
#> Black, non-Hispanic
#> 466
#> Hispanic
#> 404
#> Multiple races, non-Hispanic
#> 156
#> Native American
#> 78
#> White, non-Hispanic
#> 3177
prop.table(table(anes$race[anes$gender=="Female"]))
#>
#> Asian/Hawaiian/Pacific-Islander
#> 0.03013140
#> Black, non-Hispanic
#> 0.10557318
#> Hispanic
#> 0.09152696
#> Multiple races, non-Hispanic
#> 0.03534209
#> Native American
#> 0.01767105
#> White, non-Hispanic
#> 0.71975532That answers the probability that an individual in this data set is a certain race given that they are a women, but is that the same as the probability that somebody is both of these things? For example is the probability you are black and a women, 10.5%?
No. That’s two separate questions.
To get these probability we have to consider the joint probability of gender and race, wihch again we can uncover in R using:
joint.prob <- prop.table(table(race=anes$race, gender=anes$gender))
joint.prob
#> gender
#> race Female Male
#> Asian/Hawaiian/Pacific-Islander 0.016331041 0.018541257
#> Black, non-Hispanic 0.057220039 0.031311395
#> Hispanic 0.049607073 0.043835953
#> Multiple races, non-Hispanic 0.019155206 0.013998035
#> Native American 0.009577603 0.011051081
#> White, non-Hispanic 0.390103143 0.339268173These are the individual probabilities of being each of these things. Note that the sum of all of these probabilities equal 1, because you have to be in exactly one of the cells.
sum(joint.prob)
#> [1] 1From a table of joint probabilities we can actually calculate any marginal probability or any conditional probability, which is helpful in us understanding the relationship between the three.
For example, the probability that someone is Female can be recovered by summing across all of the individual probabilities of being Female AND each race:
sum(joint.prob[,1])
#> [1] 0.5419941
mean(anes$gender=="Female",na.rm=T)
#> [1] 0.5418239
#(There is some rounding error...)Or the probability that someone is White can be given by summing across that row:
sum(joint.prob[6,])
#> [1] 0.7293713
mean(anes$race=="White, non-Hispanic", na.rm=T)
#> [1] 0.7291514And remember that the formula for a conditional probability is \(P(A|B) = \frac{P(A\&B)}{P(B)}\).
So we have all of the information to calculate: \(P(White|Female) = \frac{P(White\&Female)}{P(Female)}\)
3.5 Independence
Now that we have the concept of conditional probability in our pockets it allows us to formally define the concept of “independent” events.
Simply: two events A&B are independent when the probability of A does not change when B takes on different values.
Formally: \(P(A|B)=P(A) \& P(B|A)=P(B)\).
To give a (purposely) absurd example, consider rolling a dice and flipping a coin. What is the probability of rolling a 2 conditional on flipping a head?
The sample space is:
T2 | H2
T3 | H3
T4 | H4
T5 | H5
T6 | H6
So to test for independence we can determine if \(P(2|H)=P(2)\).
\[ \begin{aligned} P(2|H)&=&P(2)\\ \frac{P(H\&2)}{P(2)} &=& \frac{2}{12}\\ \frac{\frac{1}{12}}{\frac{2}{12}} &=& \frac{1}{6}\\ \frac{1}{6} &=& \frac{1}{6} \end{aligned} \]
We can also consider an example with data:
It should be (maybe?!) that gender should be independent from race. Gender is evenly distributed in all races so knowing someone’s gender shouldn’t tell us anything about their race and vice versa.
We can test this pretty easily by comparing the probability of being female conditional on being each race to the probability of being female:
joint.prob
#> gender
#> race Female Male
#> Asian/Hawaiian/Pacific-Islander 0.016331041 0.018541257
#> Black, non-Hispanic 0.057220039 0.031311395
#> Hispanic 0.049607073 0.043835953
#> Multiple races, non-Hispanic 0.019155206 0.013998035
#> Native American 0.009577603 0.011051081
#> White, non-Hispanic 0.390103143 0.339268173
conditional.prob <- rep(NA, nrow(joint.prob))
for(i in 1:nrow(joint.prob)){
conditional.prob[i] <- joint.prob[i,1]/sum(joint.prob[i,])
}
conditional.prob
#> [1] 0.4683099 0.6463245 0.5308804 0.5777778 0.4642857
#> [6] 0.5348485
sum(joint.prob[,1])
#> [1] 0.5419941In this case these two things do not seem to be wholly independent. But that makes sense here. This is not a perfectly representative sample of the population!
Perhaps the most famous of all conditional probability problems is the “Monty Hall” problem. This was a real TV show that even I’m not old enough to have actually seen. Here’s the setup to the problem:
You are on a game show and must choose one of three doors, where one conceals a new car and two conceal goats. After you randomly choose one door, the host of the game show, Monty, opens a different door, which does not conceal a car. Then, Monty asks you if you would liek to switch to the unopened third door. You will win the new car if it is behind the door of your final choice. Should you switch, or stay with your original choice?
Clearly, at the start of the game you have an obvious \(\frac{1}{3}\) probability of winning the car. There are three possibilities and one contains the car.
It is very tempting to think that your odds won’t change if you switch once a goat is revealed. The doors all have a \(\frac{1}{3}\) chance, so why does revealing additional information change that?
There is a mathematical solution to this problem which you can go through in the textbook. But here let’s use R to simulate this situation to see what happens.
The most critical thing to realize about the Monty Hall problem is this: Monty know where they car is and will never reveal it in the second stage of the game. Put another way: he is not revealing a random door. Because of this the odds shift dramatically towards the door you didn’t open.
I’m going to set this up in R where we will play the monty hall game 10,000 times. Each of the 10,000 times we will (1) randomly assign the car to a door, (2) have the player randomly choose a door, (3) Have Monty semi-randomly open a door, (4) record whether the car is won if the player stays, and if the car is won if they player switches.
#One Monty Hall game
set.seed(19104)
#Randomply place the Cars and goats
placement <- sample(c("Goat", "Goat","Car"),3, replace=F)
#In this case the placement is Goat, Goat, Car
#Person randomly selects a door:
door.selection <- sample(seq(1,3),1)
#In this case the person has selected door 1, that has a goat
#Now Monty must open a door
#He can't open the door we have opened, and can't open the door with the car
#Record which doors have goats:
goats <- which(placement=="Goat")
#Can't open the door you've selected
goats <- goats[goats!=door.selection]
#We are going to use an if statement here to represent the two situations
#In this situation there is only one door Monty can open, but if we had chosen the car first
#there would be two doors that monty can open and he has to choose one
if(length(goats)==1){
open <- goats
} else {
open <- sample(goats,size=1)
}
#
#The door that is switched to is the remaining door
switch.selection <- c(1,2,3)[c(-door.selection,-open)]
#Finally we see if the car is won either in the stay or switch condition
#Stay
placement[door.selection]=="Car"
#> [1] FALSE
#Switch
placement[switch.selection]=="Car"
#> [1] TRUE
#In this case the car is won when switching.
#It should be clear from this that if you pick a goat initially and switch you *necessarily* win
#the car. Because you have a 2/3 probability of picking a goat, you win the car 2/3 of the time if you
#switch. Is that what R says?
win.stay <- rep(NA, 1000)
win.switch <- rep(NA, 1000)
for(i in 1:1000){
#Placement
placement <- sample(c("Goat", "Goat","Car"),3, replace=F)
#Person randomly selects a door:
door.selection <- sample(seq(1,3),1)
#Now Monty must open a door
goats <- which(placement=="Goat")
goats <- goats[goats!=door.selection]
if(length(goats)==1){
open <- goats
} else {
open <- sample(goats,size=1)
}
switch.selection <- c(1,2,3)[c(-door.selection,-open)]
win.stay[i] <- placement[door.selection]=="Car"
win.switch[i] <- placement[switch.selection]=="Car"
}
table(win.stay)
#> win.stay
#> FALSE TRUE
#> 670 330
table(win.switch)
#> win.switch
#> FALSE TRUE
#> 330 6703.6 Calculating the odds of Stock Market Predictions
Let’s return to the motivating example of this chapter: financial adviser Bill Miller. Remember that Miller had an “unprecedented” streak of 15 straight years of success in beating the S&P 500. Is this an interesting or impressive thing to happen?
How can we go about examining this? The way probability (and eventually, statistics) focuses our minds is to have us answer the following question: If an investor’s ability to beat the S&P 500 is truly random (50% Success, 50% failure), how likely is it that an investor will have a streak of 15 consecutive years of success?
There are ways to calculate this mathematically, but R allows us to get at these answers in a different way: through simulation. If our baseline model is that success and failure is 50/50, then we can think about it as flipping a coin. As we saw above, with R we don’t have to calculate what happens when we flip a coin a bunch of times, we can just flip a coin a bunch of times.
Above, Mlodinow pointed out that some pundits calculated the odds of this happening as being extremely low, but this calculation was wrong.
Let’s first calculate this the wrong way. Here’s what we want to simulate for this wrong way: if we flip a coin 15 times, how often do we get all heads? This represents the situation where a particular investor, over a particular period of time, has all successes.
Here is the code that simulates this in R:
set.seed(19104)
coin <- c(0,1)
all.heads <- rep(NA, 1000000)
for(i in 1:length(all.heads)){
s <- sample(coin, 15, replace=T)
all.heads[i] <- sum(s)==15
}
sum(all.heads)
#> [1] 33Here is a breakdown of what is happening in this code:
The first command is
set.seed(19104): this command makes it so R’s random number generator will start in the same place each time we run this code. The following is still a “random” process, this command just makes it so we have the same “random” process each time this code is run. Otherwise we’d get a slightly different answer each time.I then create an object that will function as a coin, which is just a vector of 0 (tails) and 1 (heads).
This code flips a coin 15 times, one million times. That is, imagine a flipping a coin 15 times: this is doing this process once. We then flip that coin 15 times, 999,999 more times.
all.heads <- rep(NA,1000000)creates an empty vector 1 million spaces long to store the results of the simulation.We then begin a loop that runs one million times.
s <- sample(coin, 15, replace=T)takes a sample of the coin object that is 15 units long, and saves it to an objects.Finally,
all.heads[i] <- sum(s)==15evaluates whether in this sample all the flips are heads (True) or not (False).
We see that the output of this simulation above is that in 33/1000000 simulations does the coin come up all heads. So if this is the question we are asking, it is indeed very special for that to happen.
What Mlodinow is pointing out, however, is that this is the wrong question to be asking. Miller was not the only financial adviser working during this period (there are thousands), and a streak doesn’t have to happen in the exact 15 year period for which it happened to Miller.
So we need to re-frame the question. If 6000 financial advisers are picking stocks for 40 years, what are the odds that any of them have a 15 year run of success? Put into the terms of a coin: if 6000 people are all flipping a coin once a year for 40 years, what are the odds that any of them get a streak of 15 heads in a row during that time period?
Here is a simulation of this situation happening once in R. That is, 6000 advisers flipping a coin once a year for 40 years. It’s a bit more complicated! Don’t worry right now if you don’t understand this whole thing. Each time through the loop represents each of our 6000 financial advisers. They flip the coin 40 times, and then a separate loop looks to see if in anywhere in those 40 flips is a run of 15 heads. We then record for that adviser whether they had a run of 15 years of success or not.
set.seed(19104)
coin <- c(0,1)
success <- rep(NA, length(6000))
for(advisers in 1:6000){
s <- sample(coin, 40, replace=T)
#Find streaks of 15#
streak <- rep(NA, 26)
for(k in 1:26){
streak[k] <- sum(s[k:(k+14)])==15
}
success[advisers] <- any(streak==T)
}
sum(success)
#> [1] 4In this simulation, 4 of the advisers had a run of 15 heads. So already, having just looked at one randomly chosen simulation, Bill Miller’s success is looking a lot less special.
We can now simulate this situation happening a bunch of times (let’s do 10,000) to determine what the long run probability of this situation is. All I am doing here is adding an outer loop to the code above that records the number of successful financial advisers in each simulation
set.seed(19104)
coin <- c(0,1)
number.successes <- rep(NA, 1000)
for(i in 1:1000){
success <- rep(NA, length(6000))
for(advisers in 1:6000){
s <- sample(coin, 40, replace=T)
#Find streaks of 15#
streak <- rep(NA, 26)
for(k in 1:26){
streak[k] <- sum(s[k:(k+14)])==15
}
success[advisers] <- any(streak==T)
}
number.successes[i]<-sum(success)
}
hist(number.successes)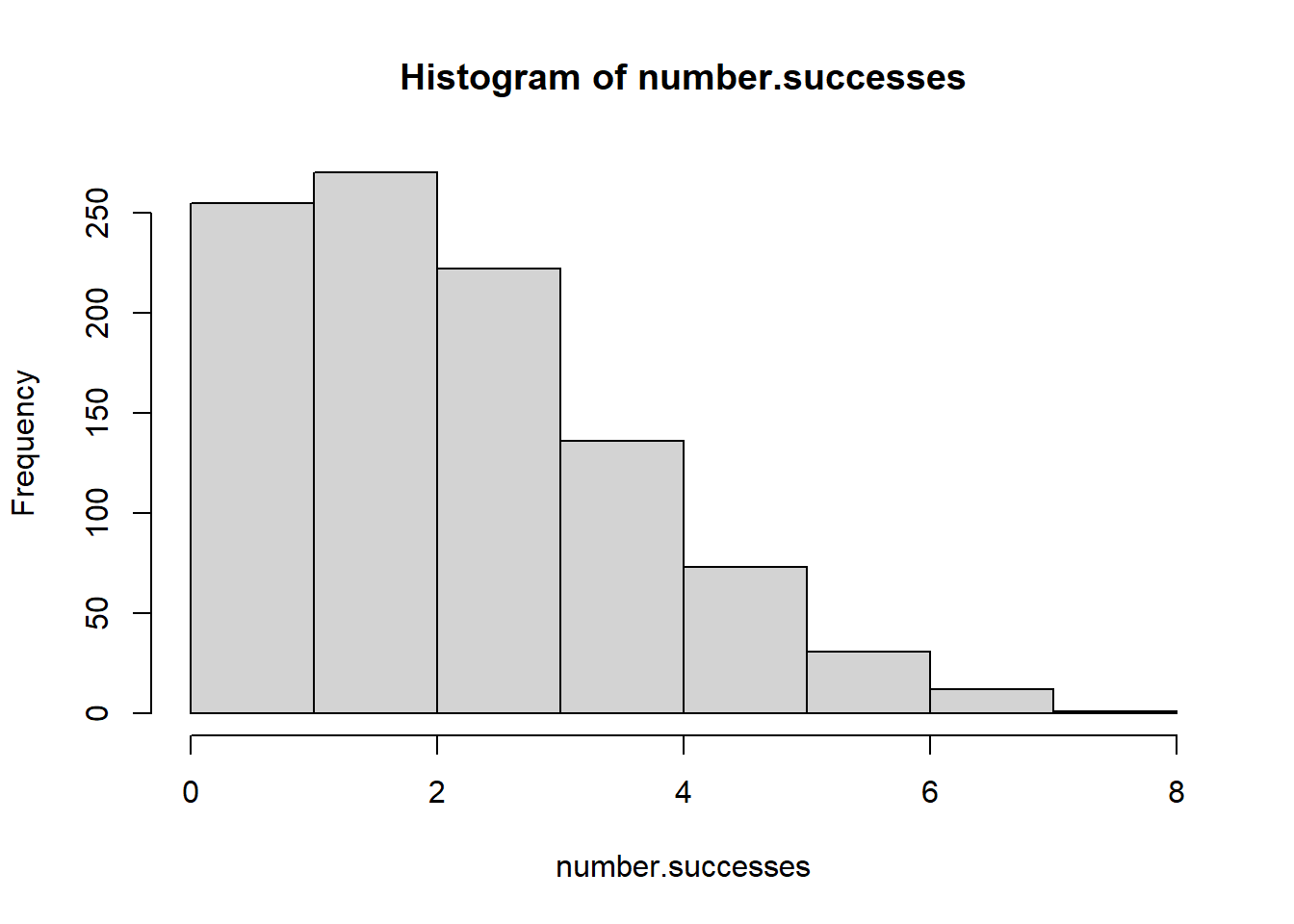
prop.table(table(number.successes>0))
#>
#> FALSE TRUE
#> 0.078 0.922In a full 92% of the 1000 simulations did at least one financial adviser have a run of 15 successful years in a row. Indeed, looking at the histogram lots of times 2, 3, or 4 advisers would have such a run. Indeed, it would be incredibly weird if someone didn’t have a run of 15 successes in a row!
We can conclude from this, more generally, to be wary of when people claim that a run of success (or a run of failure) is meaningful. Sometimes it is, surely. There exist runs of success and failure that are far beyond what would be expected by chance alone. But chance alone predicts far more frequent, and far longer, runs of success and failure than what seems logical.
3.7 Problem Answers
- Rolling 4 dice, and we want to know the odds of the dice all coming up as the same number.
#> [1] 0.0051- Rolling two dice, what are the odds of the sum of the two dice equaling 10?
set.seed(19104)
dice <- c(1,2,3,4,5,6)
result <- rep(NA, 10000)
for(i in 1:10000){
roll <- sample(dice,2, replace=T)
result[i] <- sum(roll)==10
}
mean(result)
#> [1] 0.0835- Rolling two dice, what are the odds of each sum, 2 to 12? Plot the result.
set.seed(19104)
dice <- c(1,2,3,4,5,6)
result <- rep(NA, 10000)
for(i in 1:10000){
roll <- sample(dice,2, replace=T)
result[i] <- sum(roll)
}
table(result)
#> result
#> 2 3 4 5 6 7 8 9 10 11 12
#> 290 549 837 1122 1419 1648 1377 1122 835 531 270
barplot(prop.table(table(result)),
xlab="Sum of Two Dice",
ylab="P(Sum)")
- Bag 1 containes 3 red and 5 black balls. Bag 2 contains 4 red and 4 black balls. A bag is chosen at random, and then a ball is chosen at random from that bag. What’s the probability a red ball is drawn?
set.seed(19104)
bag1 <- c(rep("R",3), rep("B",5))
bag2 <- c(rep("R",4), rep("B",4))
bags <- cbind(bag1,bag2)
result <- rep(NA,10000)
for(i in 1:length(result)){
bag <- sample(1:2,1)
ball <- sample(bags[,bag], 1)
result[i] <- ball=="R"
}
mean(result)
#> [1] 0.4343- The Philadelphia Phillies are expected to beat the Washington Nationals 60% of the time. In a stretch of 7 games, what are the odds that the Phillies win a majority (4 games)?
philly.truth <- c(rep(1,6), rep(0,4))
result <- rep(NA,10000)
for(i in 1:length(result)){
result[i] <- mean(sample(philly.truth, 7, replace=T))>.5
}
mean(result)
#> [1] 0.7103- Estimate the probability the Phillies win the majority of 9,11,13,15…61 games, and plot the result.
philly.truth <- c(rep(1,6), rep(0,4))
series.length <- seq(7,61,2)
percent.series.win <- rep(NA, length(series.length))
for(j in 1:length(percent.series.win)){
result <- rep(NA,10000)
for(i in 1:length(result)){
result[i] <- mean(sample(philly.truth, series.length[j], replace=T))>.5
}
percent.series.win[j] <- mean(result)
}
plot(series.length, percent.series.win, type="b", pch=16)