3.7 Normal distributions and standard deviation: SAT scores
In the previous section we assumed a Uniform(200, 800) distribution for \(X\), the SAT Math score of a single randomly selected student. The corresponding spinner would be like the one in Figure 2.2 but now labeled with equally spaced values from 200 to 800 (instead of 0 to 1). However, this would not lead to very realistic SAT scores. The average SAT Math score is around 500, and a much higher percentage of students score closer to average than to the extreme scores of 200 or 800.
To simulate SAT Math scores, we might use a spinner like the following. Notice that the values on the spinner axis are not equally spaced. Even though only some values are displayed on the spinner axis, imagine this spinner represents an infinitely fine model where any value between 200 and 800 is possible56.
Figure 3.9: A spinner representing the “Normal(500, 100)” distribution. The spinner is duplicated on the right; the highlighted sectors illustrate the non-linearity of axis values and how this translates to non-uniform probabilities.
Since the axis values are not evenly spaced, different intervals of the same length will have different probabilities. For example, the probability that this spinner lands on a value in the interval [400, 500] is about 0.341, but it is about 0.136 for the interval [300, 400].
Consider what the distribution of values simulated using this spinner would look like.
- About half of values would be below 500 and half above
- Because axis values near 500 are stretched out, values near 500 would occur with higher frequency than those near 200 or 800.
- The shape would be symmetric since the spacing below 500 mirrors that above. For example, about 34% of values would be between 400 and 500, and also 34% between 500 and 600.
- About 68% of values would be between 400 and 600.
- About 95% of values would be between 300 and 700.
And so on. We could compute percentages for other intervals by measuring the areas of corresponding sectors on the circle to complete the pattern of variability that values resulting from this spinner would follow. This particular pattern is called a “Normal(500, 100)” distribution. Note that the arguments for a Normal distribution play a different role than those for a Uniform distribution. In a Uniform(\(a, b\)) distribution, \(a\) represents the minimum possible value and \(b\) the maximum. In a Normal(\(\mu\), \(\sigma\)) distribution, \(\mu\) represents the long run mean (a.k.a. long run average) and \(\sigma\) the standard deviation. We will discuss standard deviation in more detail soon.
As in the previous section we can define a random variable by specifying its distribution.
We can then simulate values. Remember that the Normal distribution is only a model for the distribution of SAT Math scores. In particular, a Normal distribution assumes values on a continuous scale. Also, it is possible to see values outside of the range \([200, 800]\), though such values do not occur often.
## Index Result
## 0 437.26703701078793
## 1 386.2335035826363
## 2 491.06530479918763
## 3 483.97673072965017
## 4 273.28662563112033
## 5 450.2164105825055
## 6 488.60746385091267
## 7 751.4431281976571
## 8 514.0313078454432
## .. .................
## 99 509.7550993808241Plotting the values, we see that values near 500 occur more frequently than those near 200 or 800.
We now simulate many values.
## Index Result
## 0 624.1755617862292
## 1 558.4217482637338
## 2 439.7257087343732
## 3 567.5269124321483
## 4 582.5381306763719
## 5 649.6529489466335
## 6 517.0128928607962
## 7 533.0515231654022
## 8 507.54887494013224
## .... .................
## 9999 509.1912570431512We see that the histogram appears like it can be approximated by a smooth, “bell-shaped” curve, called a Normal density.
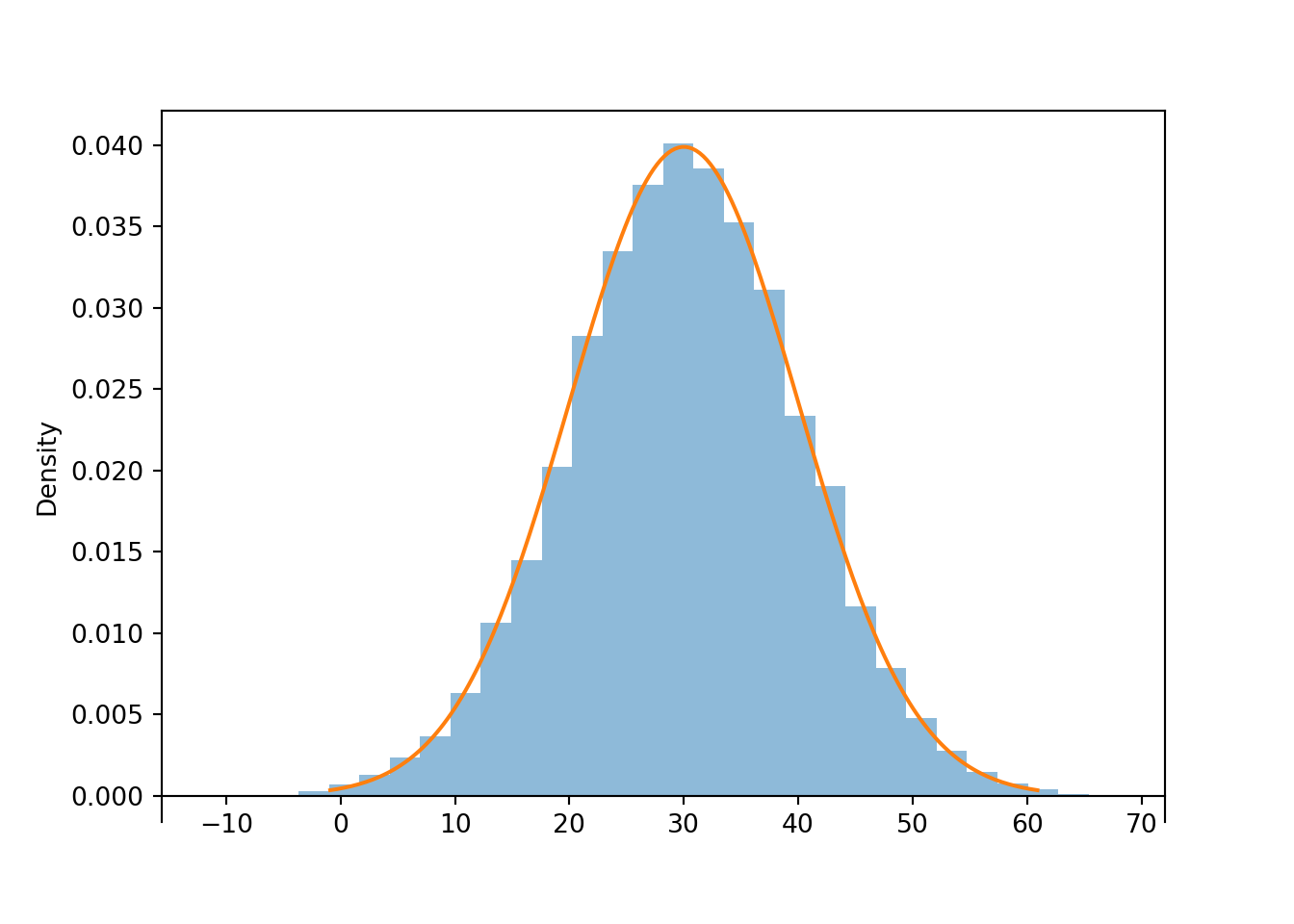
Figure 3.10: Histogram representing the approximate distribution of values simulated using the spinner in Figure 3.9. The smooth solid curve models the theoretical shape of the distribution of \(X\), called the “Normal(500, 100)” distribution).
The parameter 500 represents the long run average (a.k.a. mean) value. Calling x.mean() will compute an average as usual: sum the 10000 simulated values in x and divide by 10000. This average should be close to 500. The more simulated values included in the average, the closer we would expect the simulated average value to be to 500.
## 500.59439081818783.7.1 Standard deviation
The parameter 100 represents the standard deviation, which is a measure of degree of variability. While the average is 500, the values vary about that average. Many values are close to the average, but some are farther away. The standard deviation measures, roughly, the average distance of the values from their mean. Calling x.sd() will compute the standard deviation of the simulated values in x.
## 100.44448576668793Roughly, standard deviation measures the average distance from the mean: For each simulated value compute its absolute distance from the mean, and then average these distances.
## Index Result
## 0 123.58117096804142
## 1 57.827357445546
## 2 60.868682083814576
## 3 66.93252161396049
## 4 81.94373985818413
## 5 149.05855812844572
## 6 16.418502042608452
## 7 32.45713234721438
## 8 6.954484121944461
## .... .................
## 9999 8.596866224963435## 80.37159562780154Unfortunately, the above calculation yields roughly 80 rather than the value of roughly 100 that x.sd() returns. The above calculation illustrates the concept of standard deviation as average distance from the mean, but the actual calculation of standard deviation is a little more complicated. Technically, you must first square all the distances and then average; the result is the variance. The standard deviation is then the square root of the variance. The standard deviation is measured in the measurement units of the random variable. For example, if the random variable is measured in inches, then standard deviation is also measured in inches, while variance is measured in square-inches. We will see the theory of variance and standard deviation LATER.
## Index Result
## 0 15272.305817832283
## 1 3344.0032691349443
## 2 3704.9964586204896
## 3 4479.962449603288
## 4 6714.776501945755
## 5 22218.45375133123
## 6 269.5672093231379
## 7 1053.4654402045903
## 8 48.364849402377615
## .... .................
## 9999 73.90610888991706## 10089.094720934376## 100.44448576668793For comparison, consider values from the Uniform(200, 800) distribution. While the Uniform(200, 800) and Normal(500, 100) distributions have the same mean, the Uniform(200, 800) has a larger standard deviation than the Normal(500, 100) distribution. In comparison to a Normal(500, 100) distribution, a Uniform(200, 800) distribution will give higher probability to ranges of values near the extremes of 200 and 800, as well as lower probability to ranges of values near 500. Thus, there will be more values far from the mean of 500 and fewer values close, and so the average distance from the mean and hence standard deviation will be larger for the Uniform(200, 800) distribution than for the Normal(500, 100) distribution.
In a Uniform(200, 800) distribution, values are “evenly spread” from 200 to 800, so distances from the mean are “evenly spread” from 0 (for 500) to 300 (for 200 and 800). We might expect the standard deviation to be about 150; it turns out to be about 173. While the “average distance” interpretation helps our conceptual understanding of standard deviation, the process of squaring the distances, then averaging, and then taking the square root makes guessing the actual value of standard deviation difficult.
## 175.2208680511372Some lessons from this example.
- Spinners with non-evenly spaced values can be used to generate values from non-Uniform distributions
- Normal distributions are common models of situations where the pattern of variability follows a bell-shaped curve centered at the average value.
- Variability is an essential feature of a distribution. Standard deviation measures degree of variability in terms of, roughly, the average distance from the mean.
Technically, for a Normal distribution, any real value is possible. But values that are more than 3 or 4 standard deviations occur with small probability.↩︎