5 Day 5 (June 7)

5.1 Announcements

  • Tutoring for program R
    • Dickens Hall room 108
    • 12:30 - 1:30 Monday - Friday

5.2 Estimation

  • Three options to estimate \(\boldsymbol{\beta}\)
    • Minimize a loss function
    • Maximize a likelihood function
    • Find the posterior distribution
    • Each option requires different assumptions

5.3 Loss function approach

  • Define a measure of discrepancy between the data and the mathematical model
    • Find the values of \(\boldsymbol{\beta}\) that make \(\mathbf{X}\boldsymbol{\beta}\) “closest” to \(\mathbf{y}\)
    • Visual
  • Classic example \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}}\sum_{i=1}^{n}(y_i-\mathbf{x}_{i}^{\prime}\boldsymbol{\beta})^2\] or in matrix form \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^{\prime}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})\] which results in \[\hat{\boldsymbol{\beta}}=(\mathbf{X}^{\prime}\mathbf{X})^{-1}\mathbf{X}^{\prime}\mathbf{y}\]
  • Three ways to do it in program R
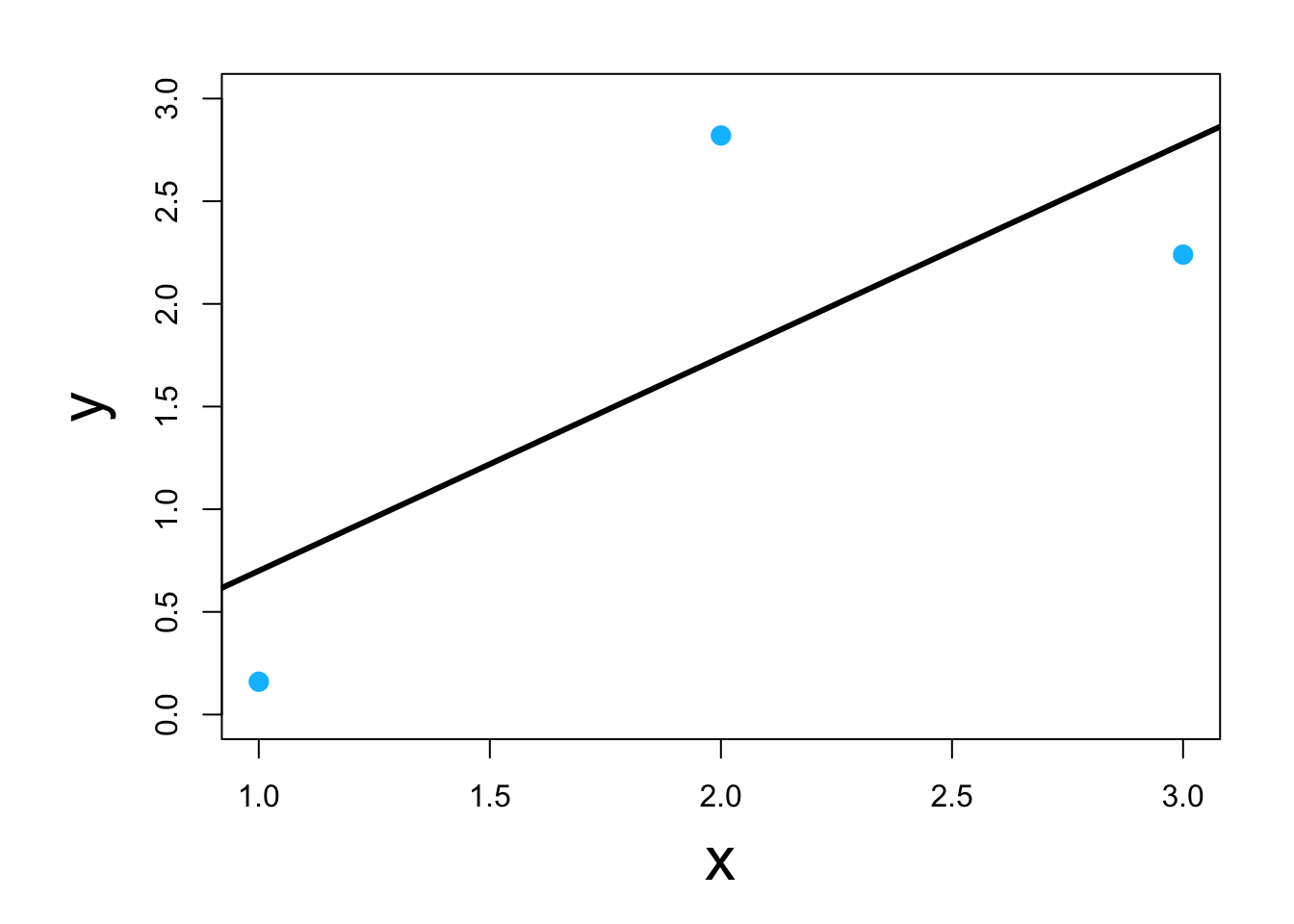
    • Using scalar calculus and algebra (kind of)
    y <- c(0.16,2.82,2.24)
x <- c(1,2,3)

y.bar <- mean(y)
x.bar <- mean(x)

# Estimate the slope parameter
beta1.hat <- sum((x-x.bar)*(y-y.bar))/sum((x-x.bar)^2)
beta1.hat
    ## [1] 1.04
    # Estimate the intercept parameter
beta0.hat <- y.bar - sum((x-x.bar)*(y-y.bar))/sum((x-x.bar)^2)*x.bar
beta0.hat
    ## [1] -0.34
    • Using matrix calculus and algebra
    y <- c(0.16,2.82,2.24)
X <- matrix(c(1,1,1,1,2,3),nrow=3,ncol=2,byrow=FALSE)
solve(t(X)%*%X)%*%t(X)%*%y
    ##       [,1]
## [1,] -0.34
## [2,]  1.04
    • Using modern (circa 1970’s) optimization techniques
    y <- c(0.16,2.82,2.24)
x <- c(1,2,3)

optim(par=c(0,0),method = c("Nelder-Mead"),fn=function(beta){sum((y-(beta[1]+beta[2]*x))^2)})
    ## $par
## [1] -0.3399977  1.0399687
## 
## $value
## [1] 1.7496
## 
## $counts
## function gradient 
##       61       NA 
## 
## $convergence
## [1] 0
## 
## $message
## NULL
    • Using modern and user friendly statistical computing software
    df <- data.frame(y = c(0.16,2.82,2.24),x = c(1,2,3))
lm(y~x,data=df)
    ## 
## Call:
## lm(formula = y ~ x, data = df)
## 
## Coefficients:
## (Intercept)            x  
##       -0.34         1.04
  • Live example