37 Day 36 (July 26)

37.1 Announcements

  • Today is our last day :(

37.2 Regression trees

  • Example: Change point analysis
    • Motivation: Annual mean temperature in Ann Arbor Michigan
    library(faraway)
plot(aatemp$year,aatemp$temp,xlab="Year",ylab="Annual mean temperature",pch=20,col=rgb(0.5,0.5,0.5,0.7))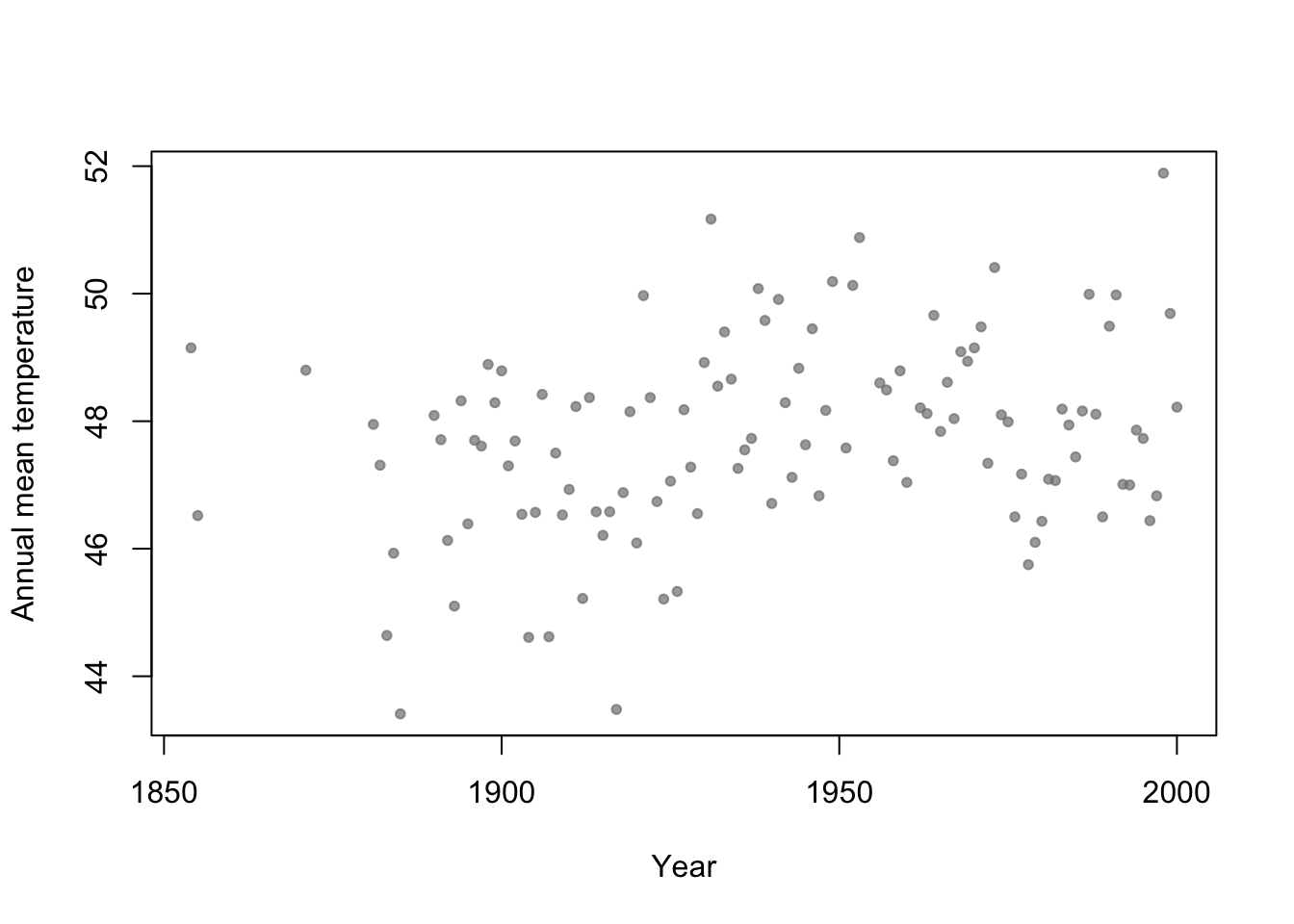
    • Basis function \[f_1(x)=\begin{cases} 1 & \text{if}\;x<c\\ 0 & \text{otherwise} \end{cases}\] and \[f_2(x)=\begin{cases} 1 & \text{if}\;x\geq c\\ 0 & \text{otherwise} \end{cases}\]
    • In R
    # Change point basis function
f1 <- function(x,c){ifelse(x<c,1,0)}
f2 <- function(x,c){ifelse(x>=c,1,0)}

# Fit linear model
m1 <- lm(temp ~ -1 + f1(year,1930) + f2(year,1930),data=aatemp)
summary(m1)
    ## 
## Call:
## lm(formula = temp ~ -1 + f1(year, 1930) + f2(year, 1930), data = aatemp)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5467 -0.8962 -0.1157  1.1388  3.5843 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## f1(year, 1930)  46.9567     0.1990   236.0   <2e-16 ***
## f2(year, 1930)  48.3057     0.1684   286.8   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.378 on 113 degrees of freedom
## Multiple R-squared:  0.9992, Adjusted R-squared:  0.9992 
## F-statistic: 6.899e+04 on 2 and 113 DF,  p-value: < 2.2e-16
    # Plot predictions
plot(aatemp$year,aatemp$temp,xlab="Year",ylab="Annual mean temperature",pch=20,col=rgb(0.5,0.5,0.5,0.7))
points(aatemp$year,predict(m1),type="l")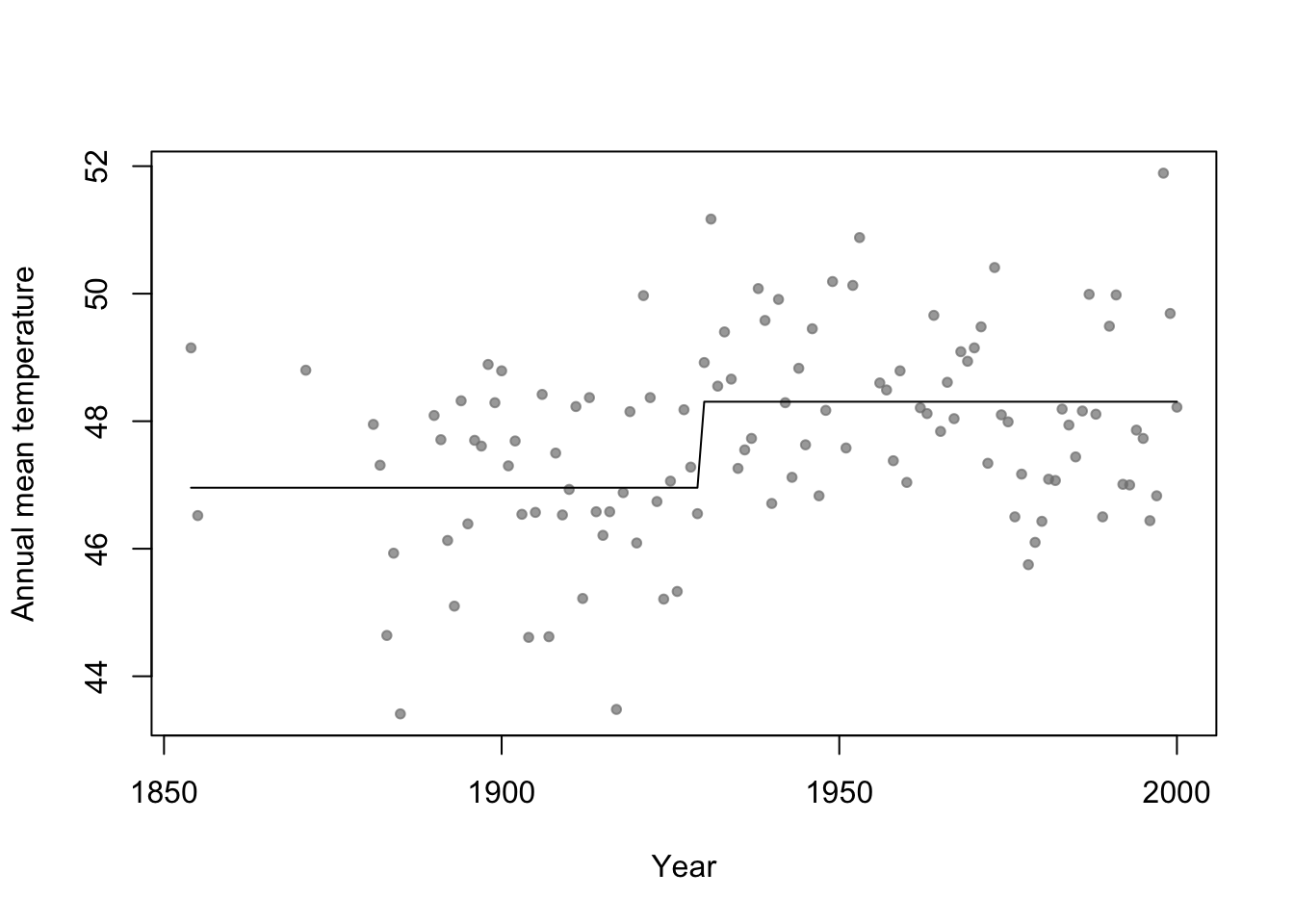
    • Connection to regression trees
      • For a single predictor, a regression tree can be though of as a linear model that uses the “change point” basis function, but tries to estimate the location (or time) and number of change points.
      • Example in R
    library(rpart)

# Fit regression tree model
m2 <- rpart(temp ~ year,data=aatemp)

# Plot predictions
E.y <- predict(m2,data.frame(year=seq(1850,2023,by=1)))
plot(aatemp$year,aatemp$temp,xlab="Year",ylab="Annual mean temperature",pch=20,col=rgb(0.5,0.5,0.5,0.7),xlim=c(1850,2023))
points(1850:2023,E.y,type="l")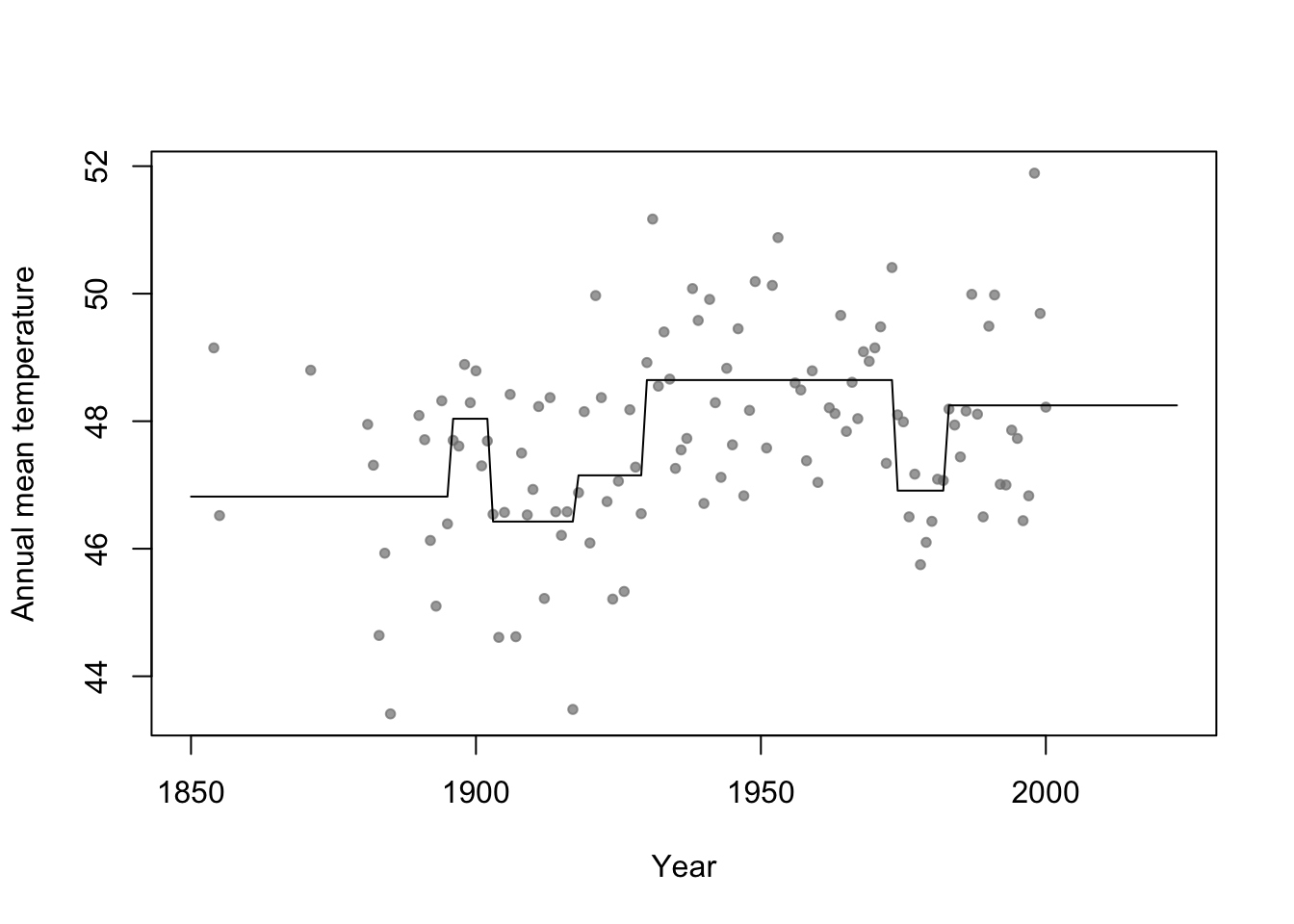

37.3 Random forest

  • Breiman 2001 link

  • Example

    n.boot <- 1000 # Number of bootstrap samples
x.new=seq(1850,2023,by=1) # New values of x that I want predicitons at
E.y <- matrix(,length(x.new),n.boot) # Matrix to save predictions
x <- aatemp$year
y <- aatemp$temp

for(i in 1:n.boot){

  # Resample data
  df.temp <- data.frame(y=y,x=x)[sample(1:length(y),replace=TRUE,size=51),]

  # Fit tree
  m1 <- rpart(y~x,data=df.temp)

  # Get and save predictions
  E.y[,i] <- predict(m1,data.frame(x=x.new))
}

plot(aatemp$year,aatemp$temp,xlab="Year",ylab="Annual mean temperature",pch=20,col=rgb(0.5,0.5,0.5,0.7),xlim=c(1850,2023))



# Aggregate predictions
E.E.y <- rowMeans(E.y)
points(1850:2023,E.E.y,type="l")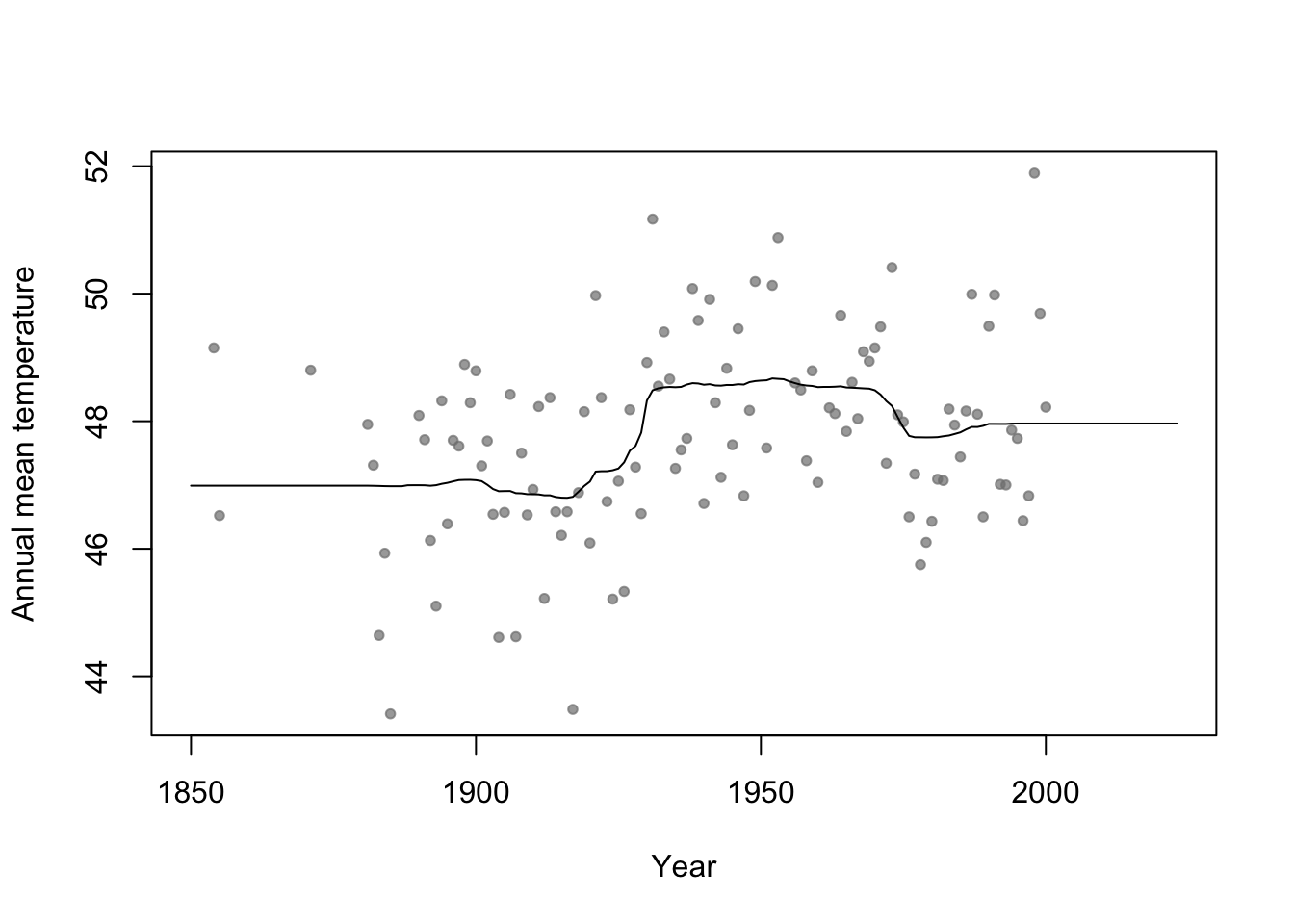

  • Summary

    • Bootstrap aggregating (or bagging) can be used with any statistical model
    • Usually increases predictive accuracy but reduces ability to understand (and write-out) the model(s) and make inference

37.4 Generalized additive model

  • Write out on white board

  • Difference between interpretable vs. non-interpretable model/machine learning approaches

  • My personal use of gams

    • The functions lm() and glm() and packages lme4, nlme, etc
    • Why I use the mgcv package
    • Wood (2017)

  • Example

    library(faraway)
library(mgcv)

m1 <- gam(temp ~ s(year,bs="tp"),family=Gamma(link="log"),data=aatemp)

# Plot predictions
E.y <- predict(m1,data.frame(year=seq(1850,2023,by=1)),type="response")
ui <- E.y + 1.96*predict(m1,data.frame(year=seq(1850,2023,by=1)),type="response",se=TRUE)$se.fit
li <- E.y - 1.96*predict(m1,data.frame(year=seq(1850,2023,by=1)),type="response",se=TRUE)$se.fit
plot(aatemp$year,aatemp$temp,xlab="Year",ylab="Annual mean temperature",pch=20,col=rgb(0.5,0.5,0.5,0.7),xlim=c(1850,2023))
points(1850:2023,E.y,type="l",lwd=3)
points(1850:2023,ui,type="l",lwd=2,lty=2)
points(1850:2023,li,type="l",lwd=2,lty=2)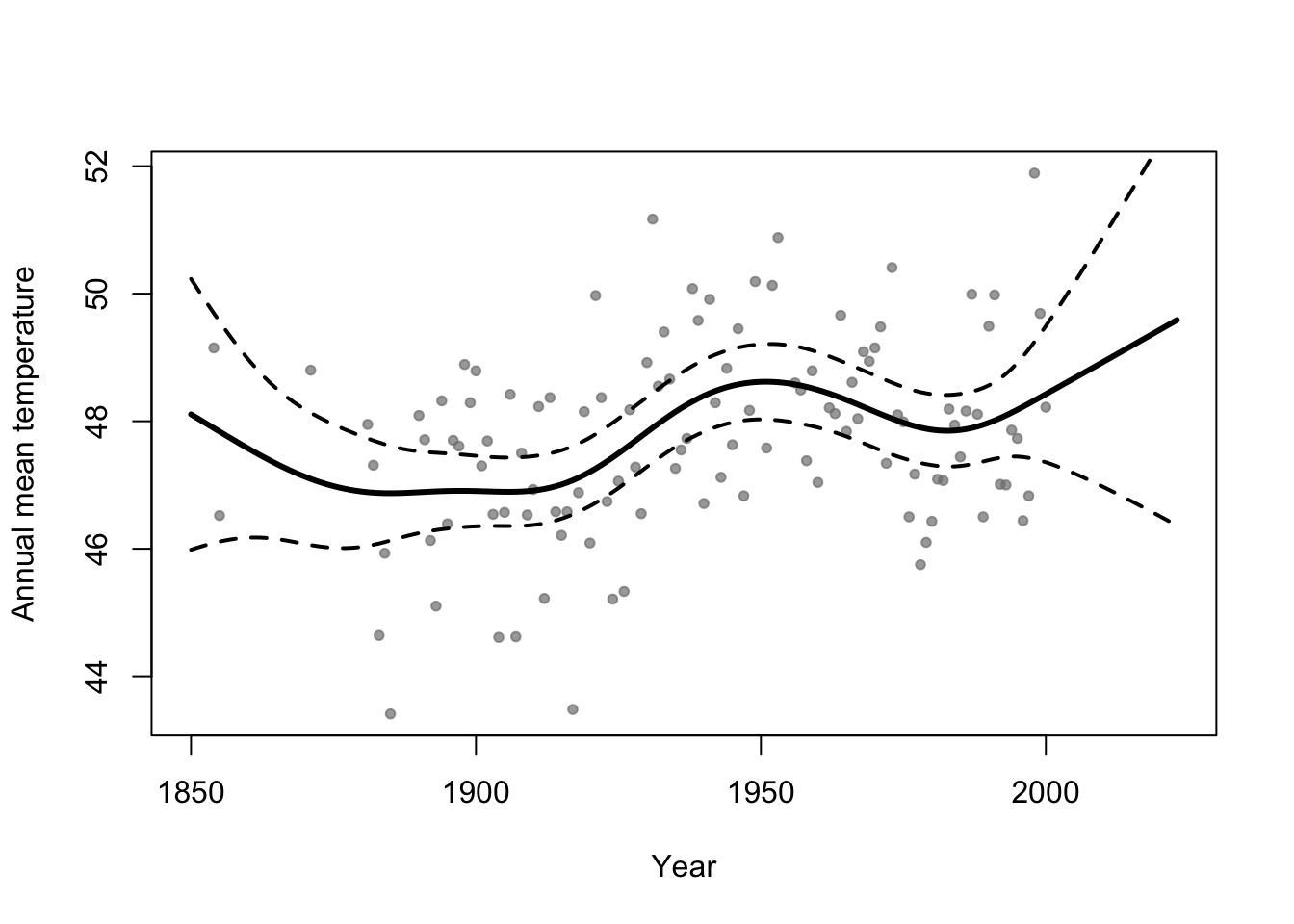

37.5 Shrinkage methods

  • Ridge regression (Hoerl and Kennard 1970)

    • See pgs. 174-177 of Chapter 11 in (Faraway 2014)
    • Minimize the loss function \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}} (\mathbf{y}-\mathbf{X}\boldsymbol{\beta})^{'}(\mathbf{y}-\mathbf{X}\boldsymbol{\beta})+\lambda\sum_{j=1}^{p}\beta_{j}^{2}\]
    • Properties of ridge regression
      • Connection to the linear model with random effects
      • \(\hat{\boldsymbol{\beta}}=\left(\mathbf{X}^{'}\mathbf{X}+\lambda\mathbf{I}\right)^{-1}\mathbf{X}^{'}\mathbf{y}\)
      • \(\text{rank}(\mathbf{X}^{'}\mathbf{X}+\lambda\mathbf{I})\)
      • \(\hat{\boldsymbol{\beta}}\) when \(\lambda=0\)
      • \(\hat{\boldsymbol{\beta}}\) when \(\lambda=\infty\)
      • Recall \[\begin{equation} \begin{split} \hat{\text{E}(\mathbf{y})} & = \mathbf{X}\hat{\boldsymbol{\beta}} \\ & = \mathbf{X}\left(\mathbf{X}^{\prime}\mathbf{X}+\lambda\mathbf{I}\right)^{-1}\mathbf{X}^{\prime}\mathbf{y}\\ & = \mathbf{H}\mathbf{y}\\ \end{split} \end{equation}\]
      • Effective number of coefficients \(=\text{trace}(\mathbf{H})\)
      • If \(\lambda=0\), then \(\text{trace}(\mathbf{H}) = \text{?}\)
      • If \(\lambda=\infty\), then \(\text{trace}(\mathbf{H}) = \text{?}\)
    • Estimation requires selecting a value for \(\lambda\)
    • Example: Variable selection and dealing with collinearity
      • Linear model with \(\lambda=0\)
    library(httr)
library(readxl)

url <- "https://doi.org/10.1371/journal.pone.0148743.s005"
GET(url, write_disk(path <- tempfile(fileext = ".xls")))
    df1 <- read_excel(path = path, sheet = "Data", col_names = TRUE, col_types = "numeric")
df1 <- df1[complete.cases(df1),]
    m1 <- lm(CDEP ~ NCAT + WPOP + WKIL, data = df1)
summary(m1)
    ## 
## Call:
## lm(formula = CDEP ~ NCAT + WPOP + WKIL, data = df1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -18.483  -9.151  -1.477   3.985  78.775 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 14.5176798  6.6712280   2.176   0.0339 *  
## NCAT        -0.0014333  0.0008412  -1.704   0.0941 .  
## WPOP         0.0108041  0.0159751   0.676   0.5017    
## WKIL         0.6864227  0.0985674   6.964 4.71e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.95 on 54 degrees of freedom
## Multiple R-squared:  0.7784, Adjusted R-squared:  0.7661 
## F-statistic: 63.23 on 3 and 54 DF,  p-value: < 2.2e-16
    cor(df1[,c(7,5,4)])
    ##             NCAT       WPOP        WKIL
## NCAT  1.00000000 -0.3547717 -0.05005347
## WPOP -0.35477170  1.0000000  0.79070496
## WKIL -0.05005347  0.7907050  1.00000000
    • Linear model with \(\lambda=10\)
    X <- scale(df1[,c(7,5,4)])
y <- df1$CDEP

m2 <- lm(y ~ X)
summary(m2)
    ## 
## Call:
## lm(formula = y ~ X)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -18.483  -9.151  -1.477   3.985  78.775 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   28.776      1.964  14.655  < 2e-16 ***
## XNCAT         -3.944      2.314  -1.704   0.0941 .  
## XWPOP          2.554      3.776   0.676   0.5017    
## XWKIL         24.615      3.535   6.964 4.71e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.95 on 54 degrees of freedom
## Multiple R-squared:  0.7784, Adjusted R-squared:  0.7661 
## F-statistic: 63.23 on 3 and 54 DF,  p-value: < 2.2e-16
    library(MASS)
m3 <- lm.ridge(y ~ X,lambda = 10)
coef(m3)
    ##               XNCAT     XWPOP     XWKIL 
## 28.775862 -2.243853  7.196794 17.936405
    • Ridge regression using glmnet() and multiple values of \(\lambda\)
    library(glmnet)
lambda <- seq(0,400,by=0.1)
m4 <- glmnet(X,y,family=c("gaussian"),alpha=0,standardize=FALSE,lambda=lambda)
plot(m4, xvar = "lambda", label = TRUE)

    plot(m4, xvar = "dev", label = TRUE)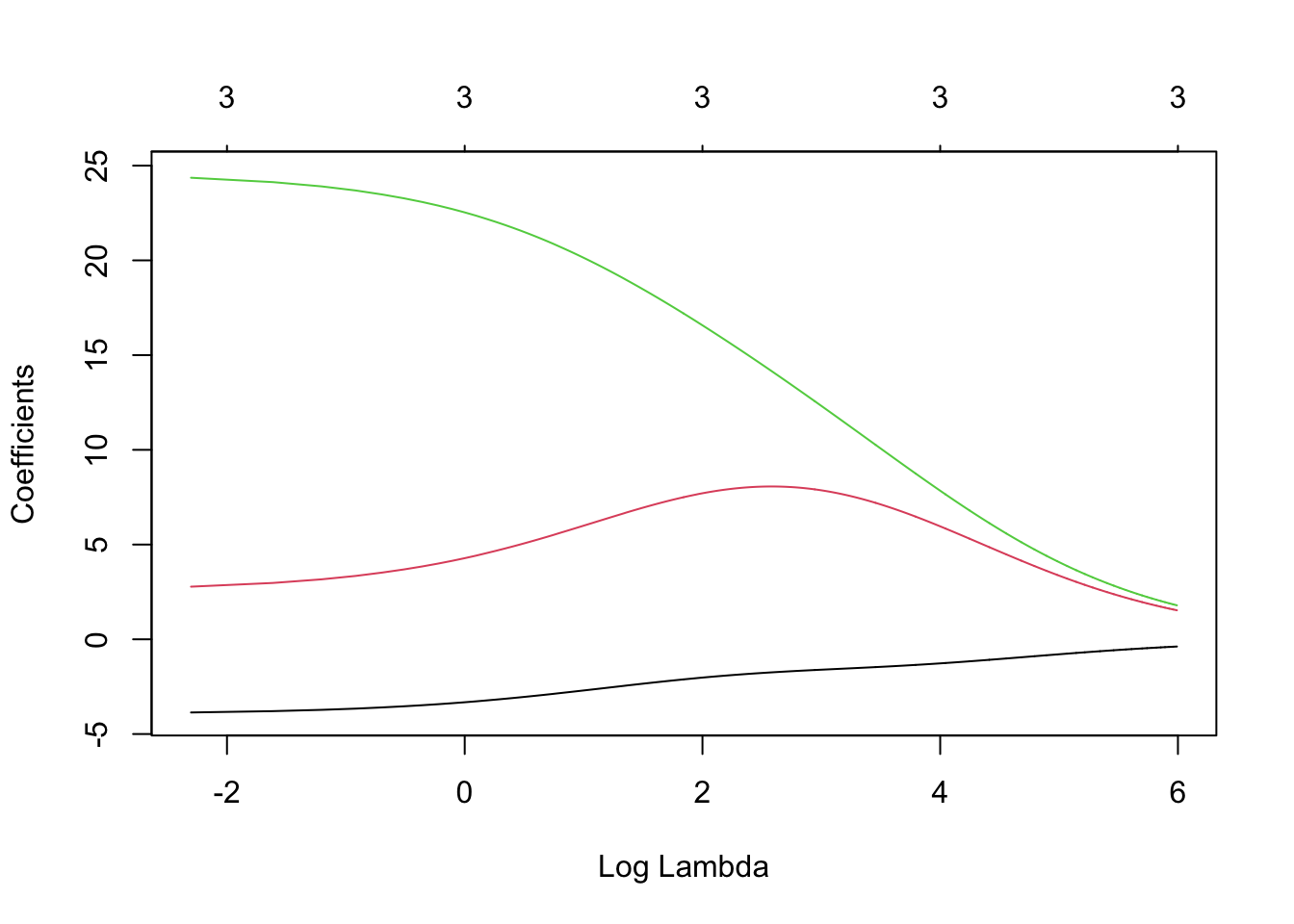

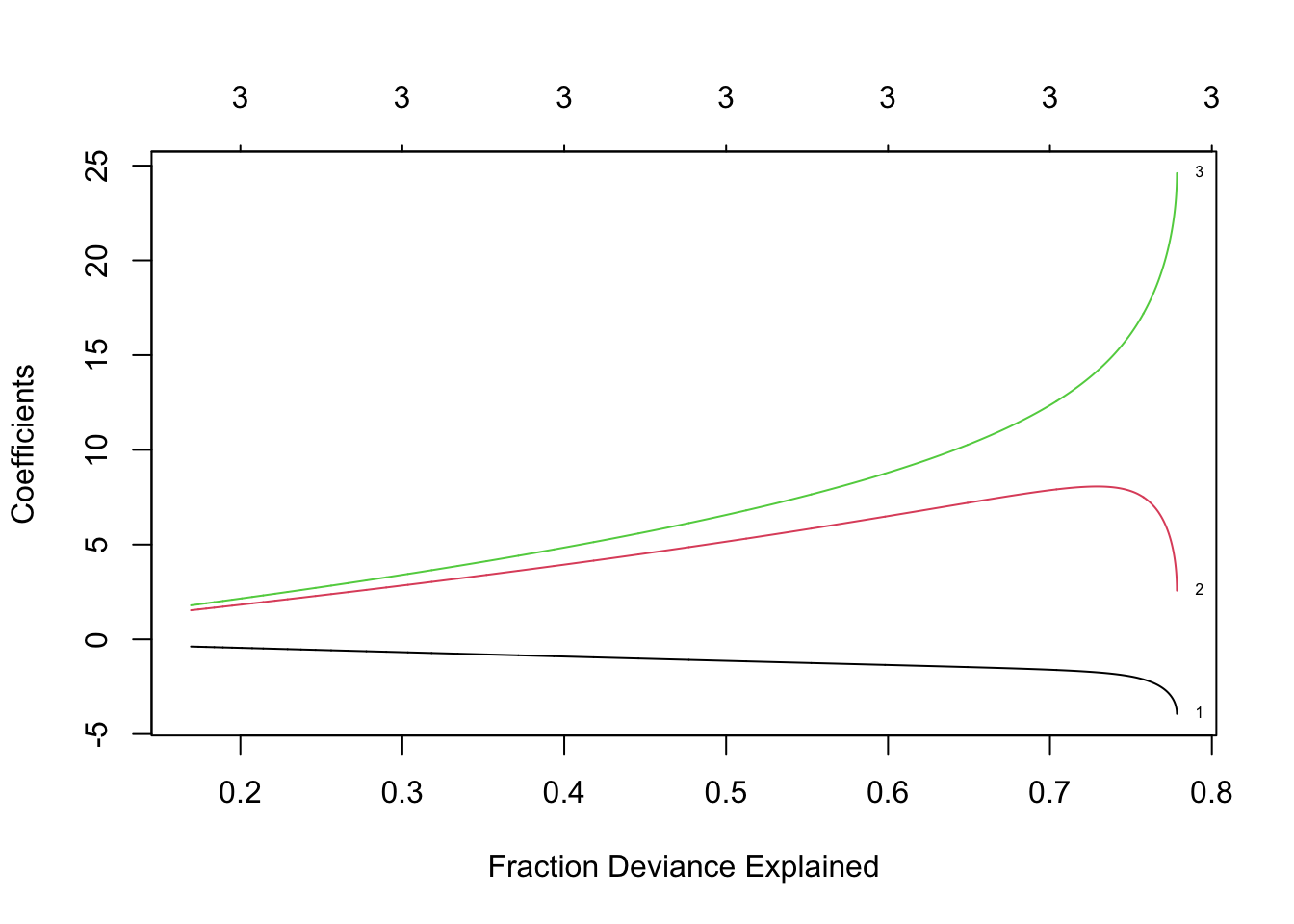
    • Ridge regression using 10 fold cross-validation
    m5 <- cv.glmnet(X,y,family=c("gaussian"),alpha=0,standardize=FALSE,lambda=lambda,nfolds = 10)
plot(m5)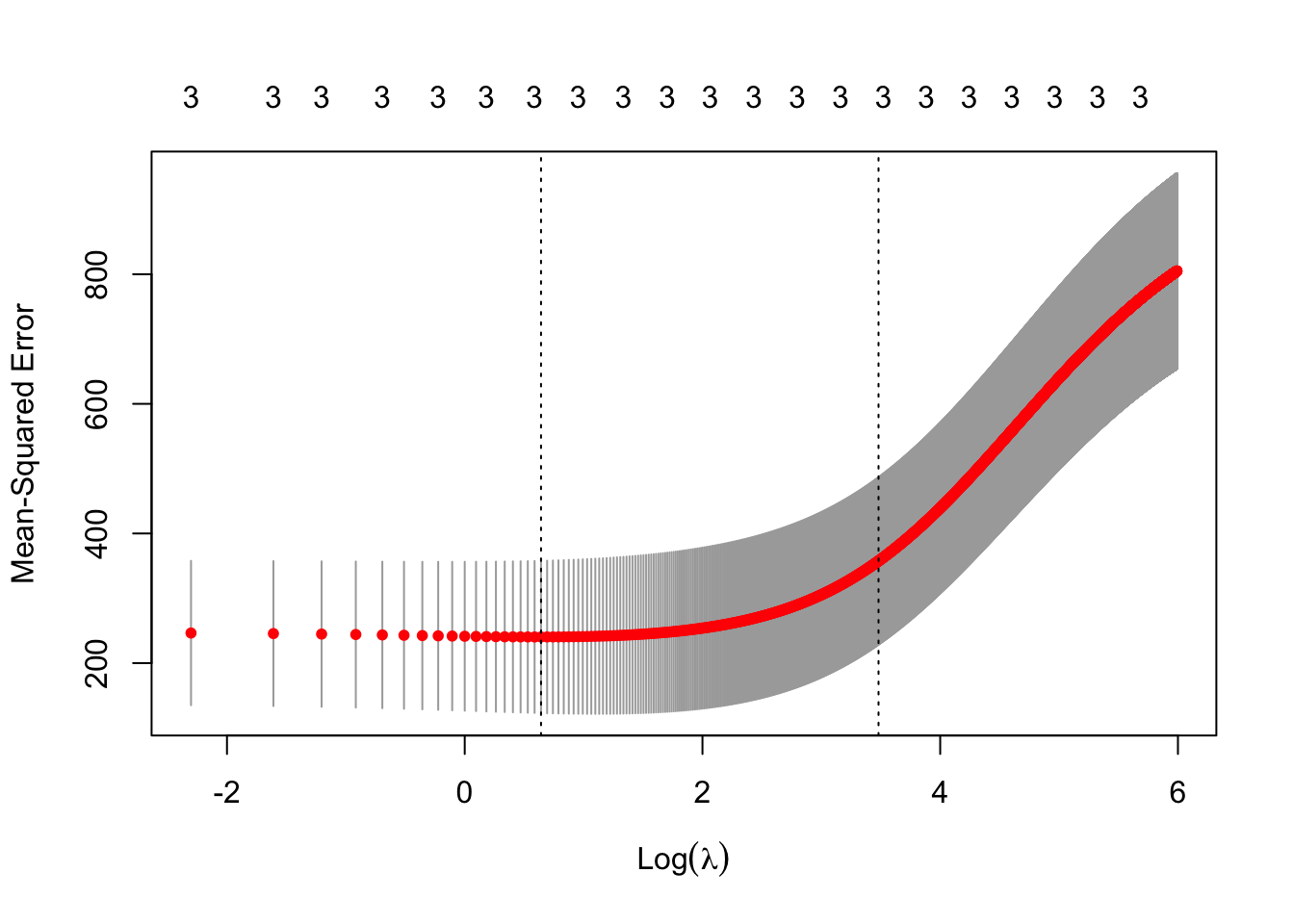

    m5$lambda.min
    ## [1] 1.9
    m6 <- glmnet(X,y,family=c("gaussian"),alpha=0,standardize=FALSE,lambda=m5$lambda.min)
coef(m6)
    ## 4 x 1 sparse Matrix of class "dgCMatrix"
##                    s0
## (Intercept) 28.775862
## NCAT        -2.950257
## WPOP         5.314891
## WKIL        21.147750

  • LASSO (Tibshirani 1996)

    • Minimize the loss function \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}} (\mathbf{y}-\mathbf{X}\boldsymbol{\beta})^{'}(\mathbf{y}-\mathbf{X}\boldsymbol{\beta})+\lambda\sum_{j=1}^{p}|\beta_{j}|\]
    • Properties of LASSO
      • Connection to the linear model with random effects
      • No closed-form solution for \(\hat{\boldsymbol{\beta}}\)
      • Shrinks and selects (Least Absolute Shrinkage and Selection Operator)
      • Good to use when collinearity is not a huge problem and when some of the \(\boldsymbol{\beta}\) are thought to be zero.
    • Example: LASSO using glmnet() and multiple values of \(\lambda\)
    X <- scale(df1[,c(7,5,4)])
y <- df1$CDEP

library(glmnet)
lambda <- seq(0,400,by=0.1)
m7 <- glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=lambda)
plot(m7, xvar = "lambda", label = TRUE)

    plot(m7, xvar = "dev", label = TRUE)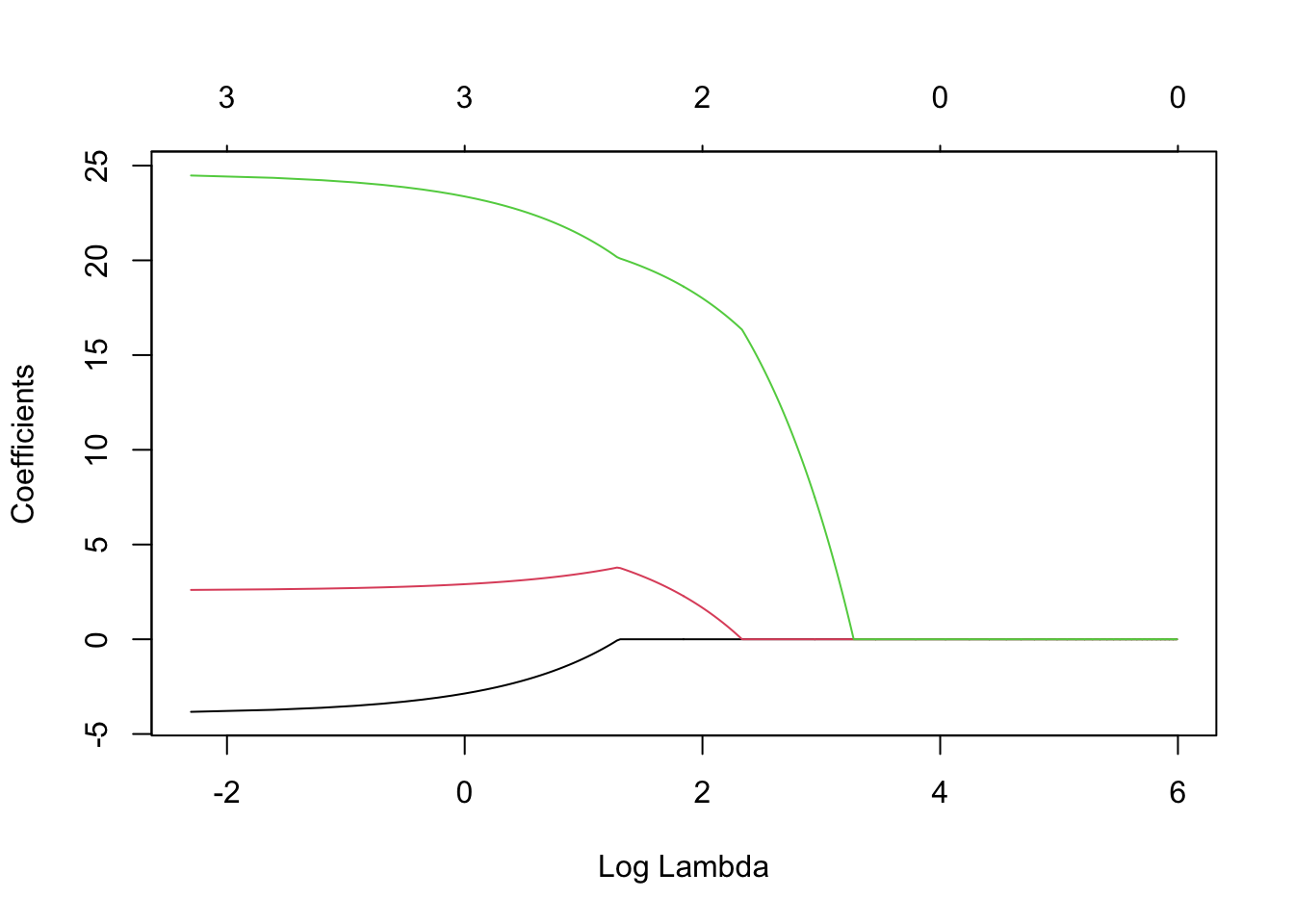

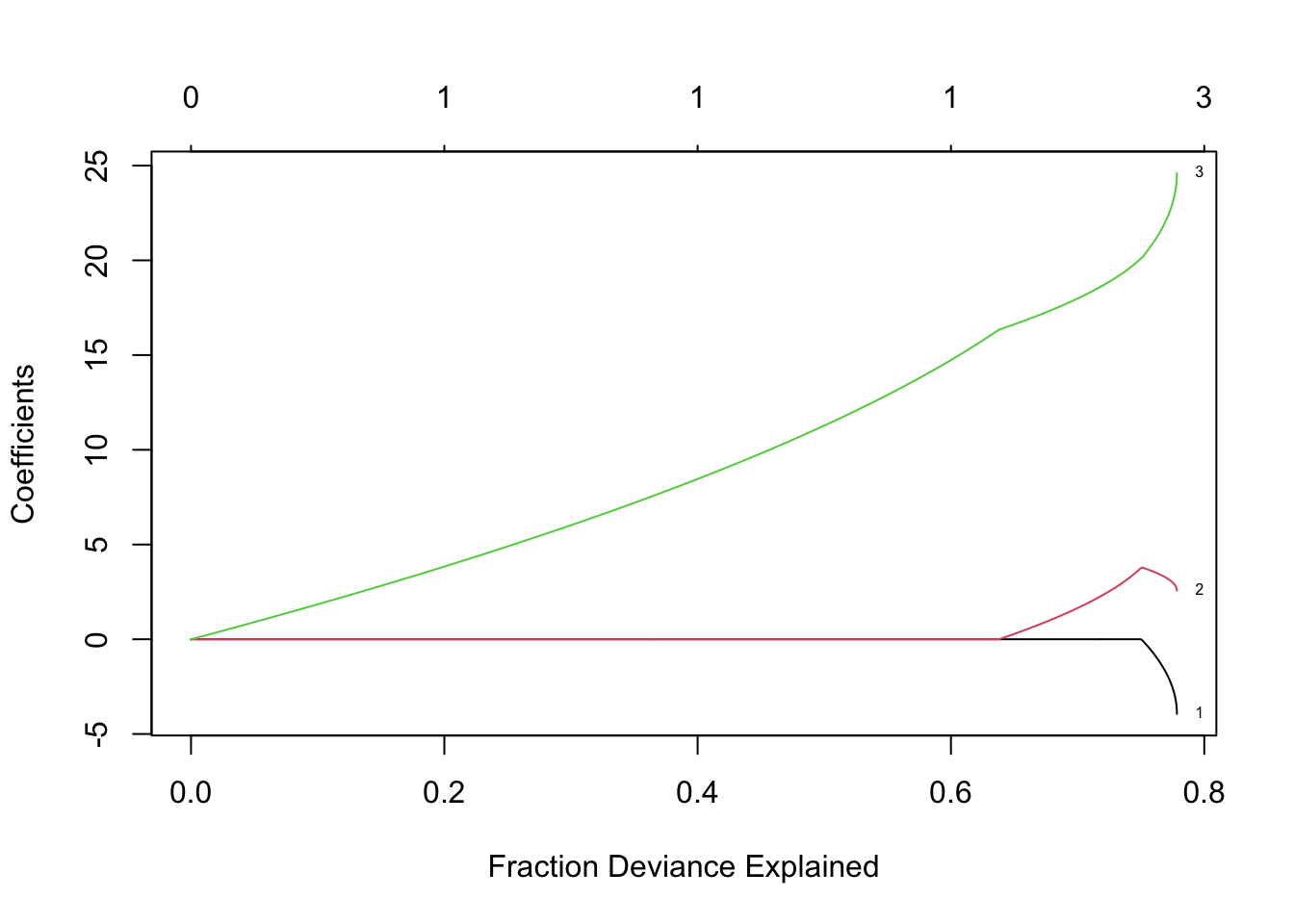    - LASSO using 10 fold cross-validation

    m8 <- cv.glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=lambda,nfolds = 10)
plot(m8)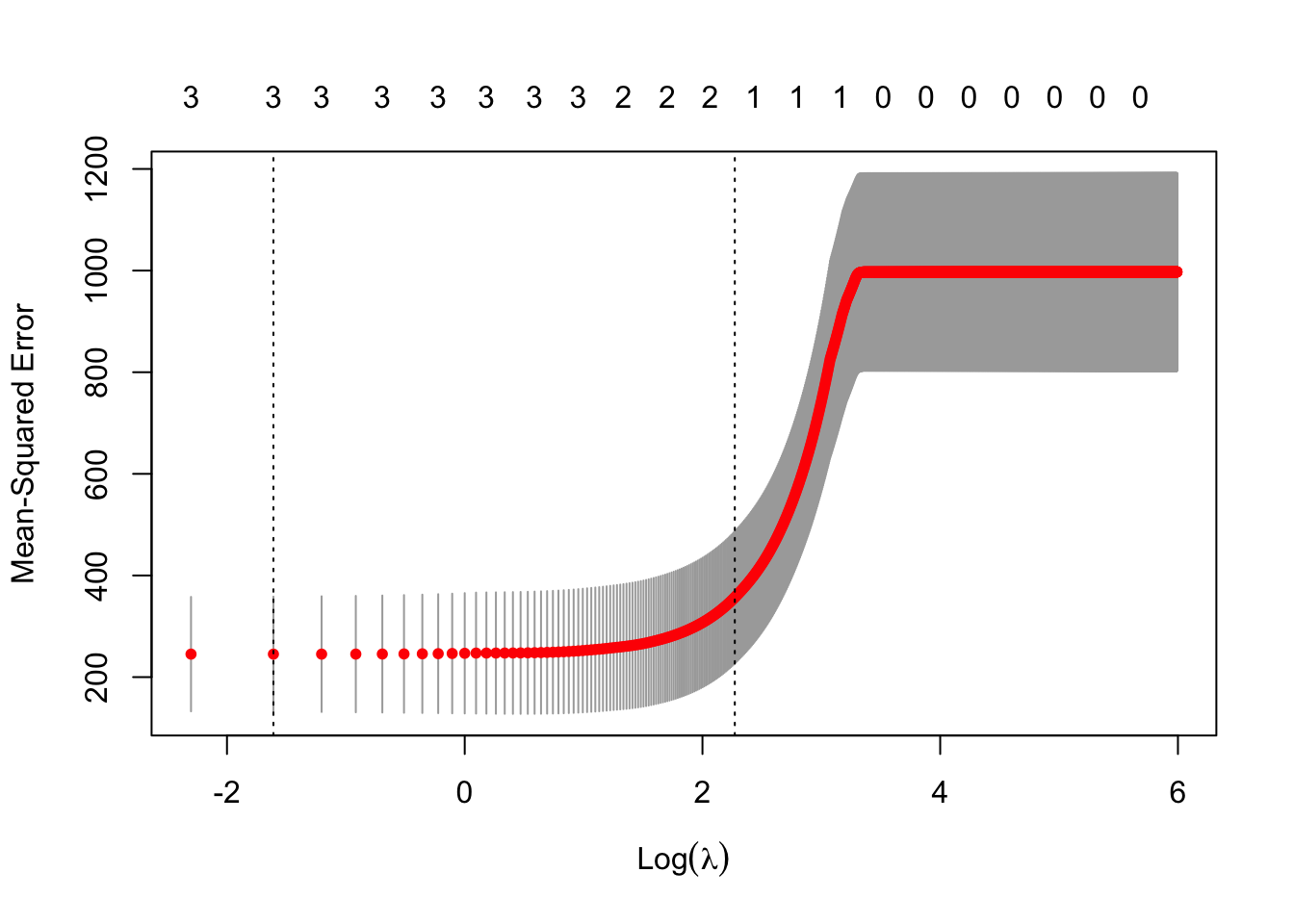

    m8$lambda.min
    ## [1] 0.2
    m9 <- glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=m8$lambda.min)
coef(m9)
    ## 4 x 1 sparse Matrix of class "dgCMatrix"
##                    s0
## (Intercept) 28.775862
## NCAT        -3.722689
## WPOP         2.634395
## WKIL        24.358870
    m10 <- glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=m8$lambda.1se)
coef(m10)
    ## 4 x 1 sparse Matrix of class "dgCMatrix"
##                     s0
## (Intercept) 28.7758621
## NCAT         .        
## WPOP         0.3655531
## WKIL        16.6725216

  • Elastic net (Zou and Hastie 2005)

    • Mix of ridge and lasso penalty
    • Example: Elastic net using glmnet() and multiple values of \(\lambda\)
    lambda <- seq(0,400,by=0.1)
m11 <- glmnet(X,y,family=c("gaussian"),alpha=0.5,standardize=FALSE,lambda=lambda)
plot(m11, xvar = "lambda", label = TRUE)

    plot(m11, xvar = "dev", label = TRUE)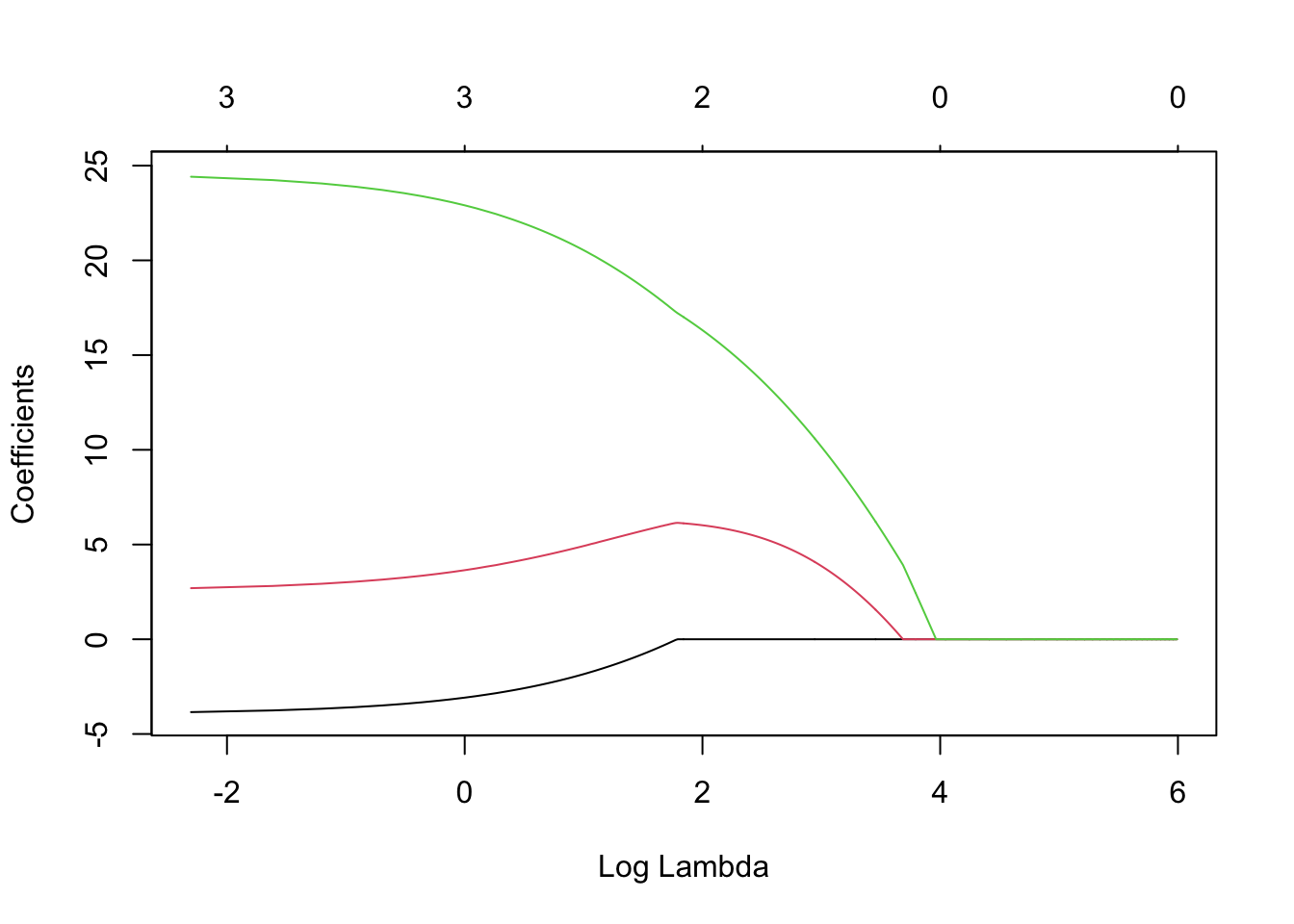

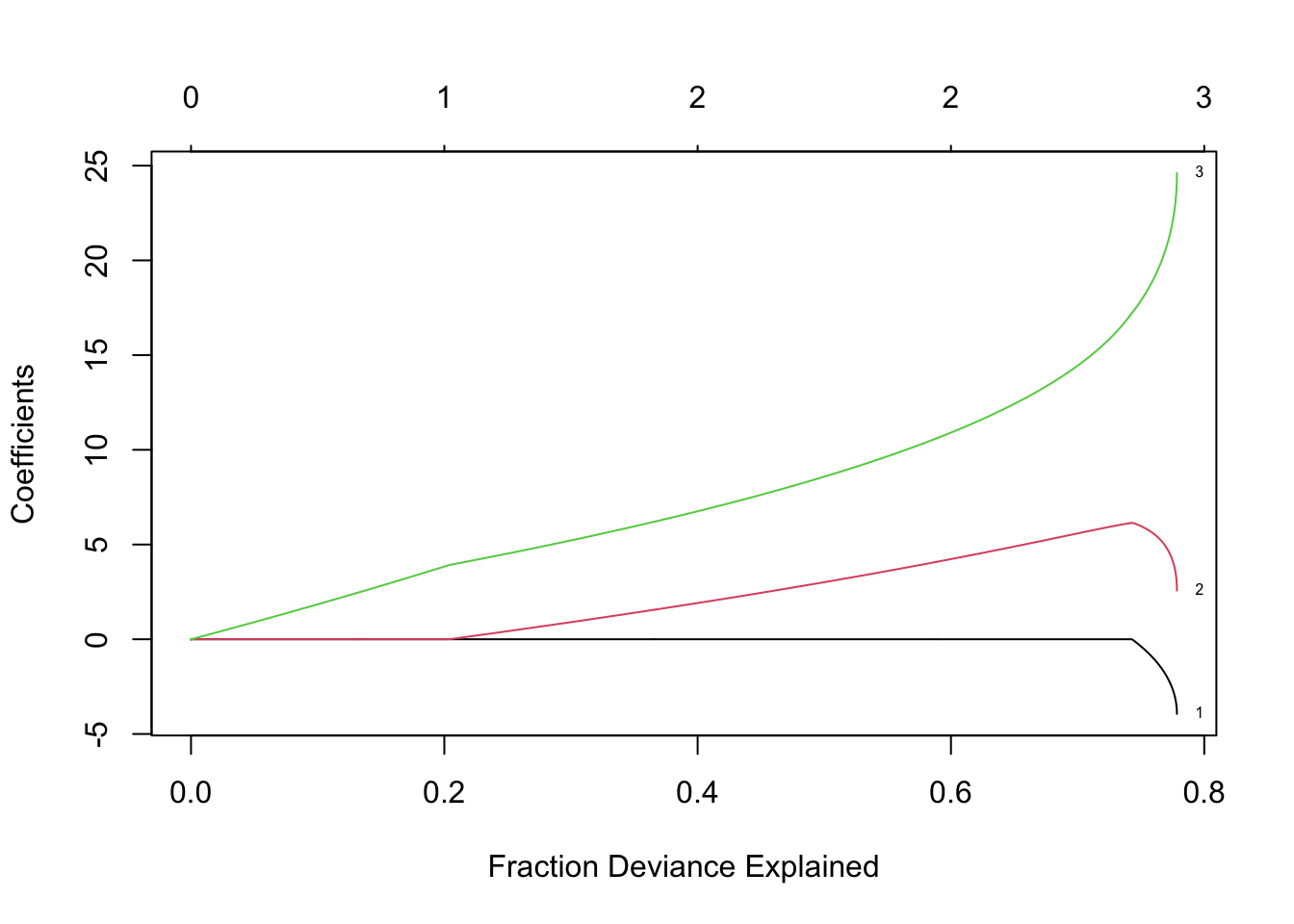    - Elastic net using 10 fold cross-validation

    m12 <- cv.glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=lambda,nfolds = 10)
plot(m11)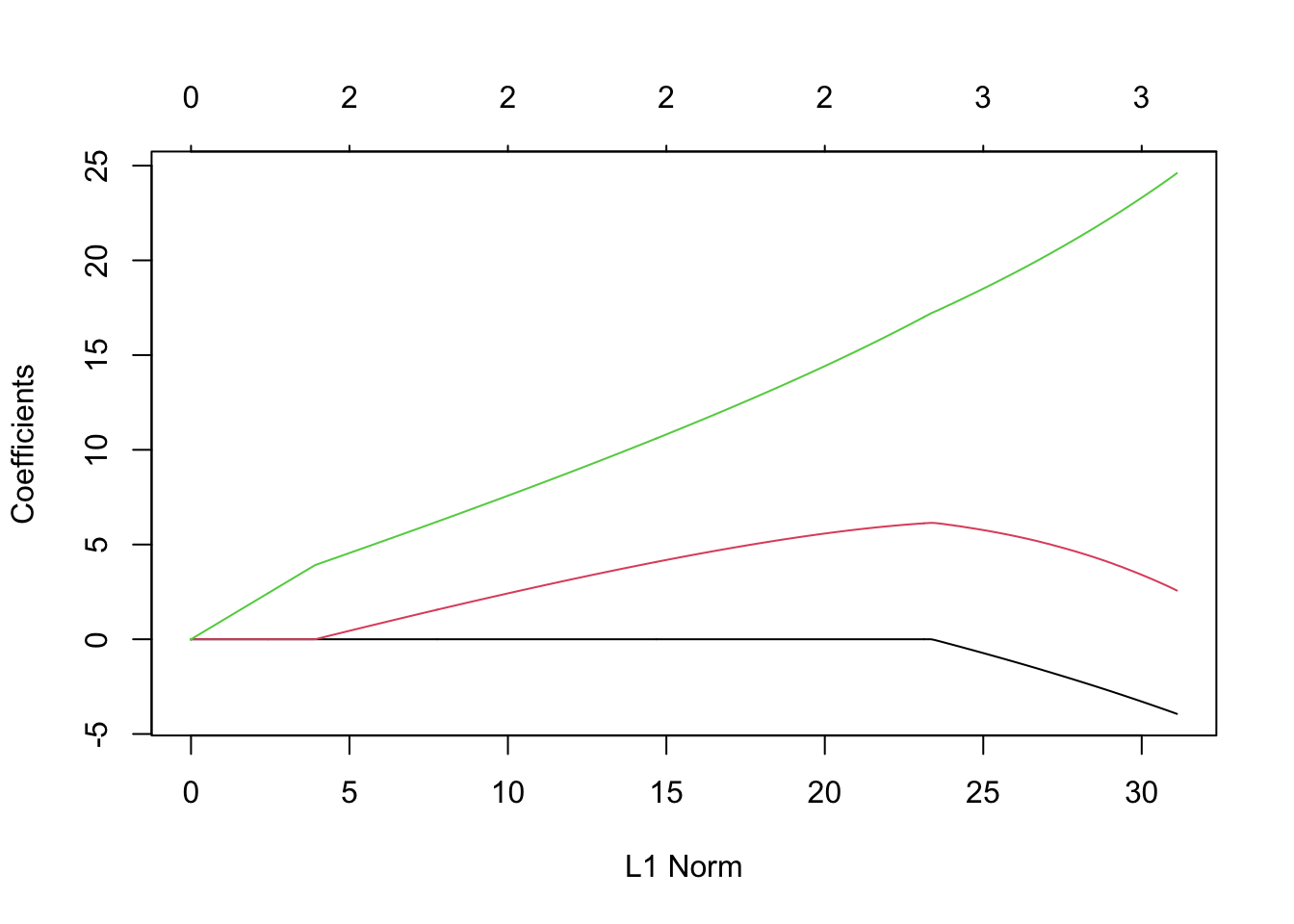

    m12$lambda.min
    ## [1] 1.4
    m13 <- glmnet(X,y,family=c("gaussian"),alpha=1,standardize=FALSE,lambda=m12$lambda.min)
coef(m13)
    ## 4 x 1 sparse Matrix of class "dgCMatrix"
##                    s0
## (Intercept) 28.775862
## NCAT        -2.431400
## WPOP         3.039959
## WKIL        22.881770

  • Summary

    • Non-Bayesian inference (e.g., confidence intervals) is an open question
    • Methods that shrink coefficients can be used to introduce bias which reduces variance
      • Methods that do continuous shrinkage are preferend to binary shrinkage (e.g., variable selection with AIC).
      • Shrinking coefficients is one way to deal with collinearity.
    • Most continuous shrinkage methods are some gernalization of ridge or LASSO penalty.
    • Good references
      • Statistical Learning with Sparsity: the Lasso and Generalizations (link)
      • An Introduction to Statistical Learning: with Applications in R (link)
        • Ch. 6 (Linear Model Selection and Regularization)

Literature cited

Faraway, J. J. 2014. Linear Models with r. CRC Press.
Hoerl, Arthur E, and Robert W Kennard. 1970. “Ridge Regression: Biased Estimation for Nonorthogonal Problems.” Technometrics 12 (1): 55–67.
Tibshirani, Robert. 1996. “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society. Series B (Methodological), 267–88.
Zou, Hui, and Trevor Hastie. 2005. “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67 (2): 301–20.