14 Day 14 (June 21)

14.1 Announcements

  • Read Ch. 3 in linear models with R (inference)

14.2 Confidence intervals for derived quantities

14.3 Bootstrap confidence intervals

  • Google scholar demonstration

  • Motivation (see section 3.6 in Faraway (2014))

    • Functions of parameters (i.e., “derived” quantities)
    • Difficult to obtain the sampling distribution for non-linear functions of estimated parameters
    • Further reading (Hesterberg 2015)
    • Example: When do we expect the population to go extinct?
    y <- c(63, 68, 61, 44, 103, 90, 107, 105, 76, 46, 60, 66, 58, 39, 64, 29, 37,
27, 38, 14, 38, 52, 84, 112, 112, 97, 131, 168, 70, 91, 52, 33, 33, 27,
18, 14, 5, 22, 31, 23, 14, 18, 23, 27, 44, 18, 19)
year <- 1965:2011
df <- data.frame(y = y, year = year)
plot(x = df$year, y = df$y, xlab = "Year", ylab = "Annual count", main = "",
col = "brown", pch = 20, xlim = c(1965, 2040))
m1 <- lm(y~year)
abline(m1)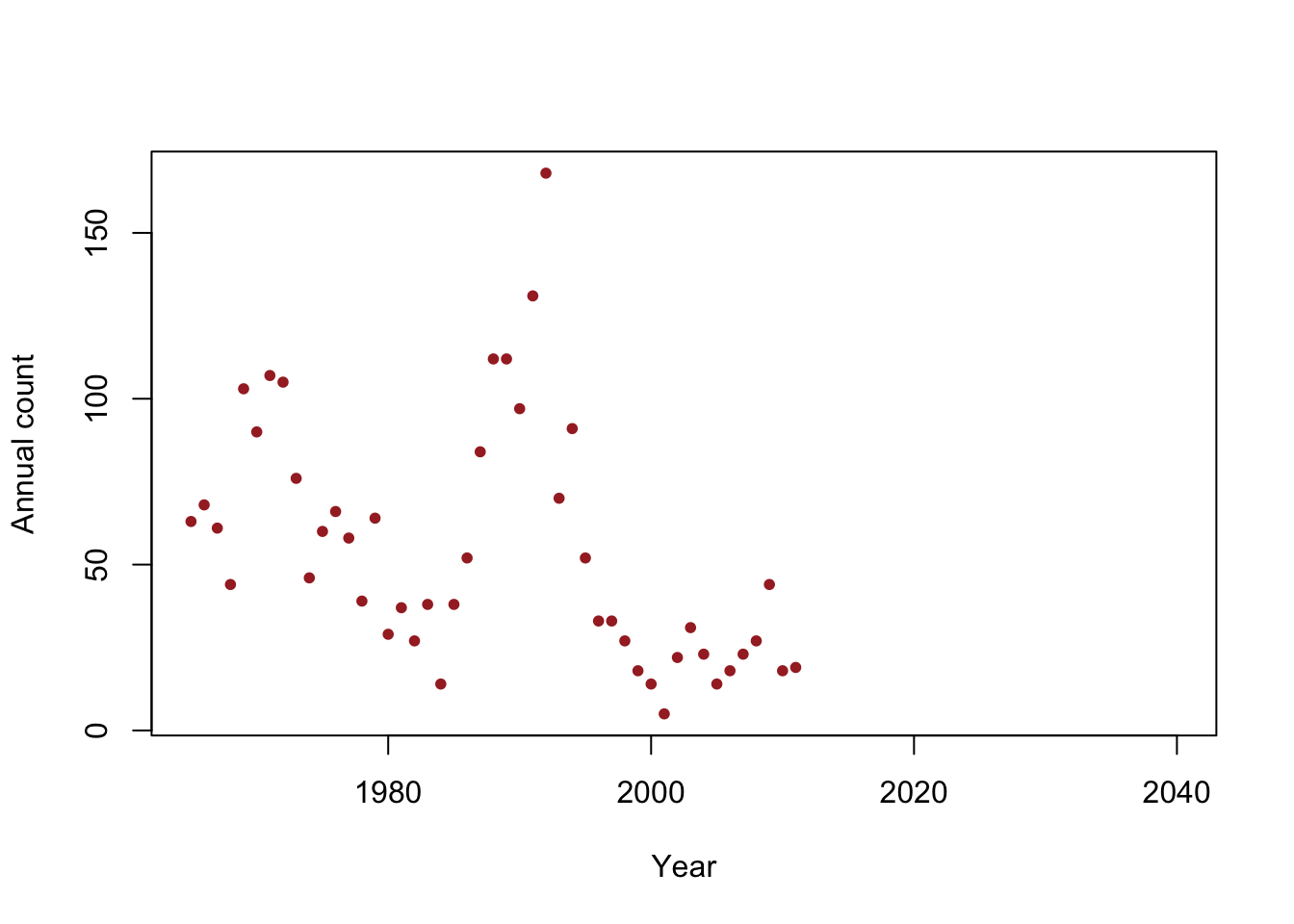

  • Non-parametric bootstrap (see Efron and Tibshirani (1994)).

    1. From a data set with n observations, take a sample of size n with replacement. For a linear model, the sample should include both the observed response (\(y_{i}\)) and covariates (\(x_{1}\),\(x_{2}\),…,\(x_{p}\)).
    2. Estimate the parameters for a statistical model using the sampled data from step 1.
    3. Save the estimates of interest. This could be parameters of interest (e.g., \(\boldsymbol{\beta}\)) or a a derived quantity (e.g., \(R^{2}\), \(\frac{1}{\boldsymbol{\beta}}\)).
    4. Repeats steps (1)-(3) \(m\) times.

  • Inference

    • The \(m\) samples of the quantities of interest are samples from the empirical distribution.
    • The empirical distribution can summarized using sample statistics (e.g., quantiles, mean, variance, etc). Conceptually, this is similar to Monte Carlo integration.

  • Example in R

    library(latex2exp)
# Number of bootstrap samples (m)
m.boot <- 1000   

# Create matrix to save empirical distribution of -beta2.hat/beta1.hat (expected time of extinction)
ed.extinct.hat <- matrix(,m.boot,1)

# Set random seed so results are the same if we run it again
# Results would be different due to random resampling of data
set.seed(1940)   

# Start for loop for non-parametric boostrap
for(m in 1:m.boot){

  # Sample data with replacement
  # boot.sample gives the rows of df that we use for estimation
  boot.sample <- sample(1:nrow(df),replace=TRUE) 

  # Make temporary data frame that contains the resamples
  df.temp <- df[boot.sample,]

  # Estimate parameters for df.temp
  m1 <- lm(y~year,data=df.temp)

  # Save estimate of -beta0.hat/beta1.hat (expected time of extinction)
  ed.extinct.hat[m,] <- -coef(m1)[1]/coef(m1)[2]
}
par(mar=c(5,4,7,2))
hist(ed.extinct.hat,col="grey",xlab="Year",main=TeX('Empirical distribuiton of $$-$$\\hat{\\frac{$\\beta_0}{$\\beta_1}}'),freq=FALSE,breaks=20)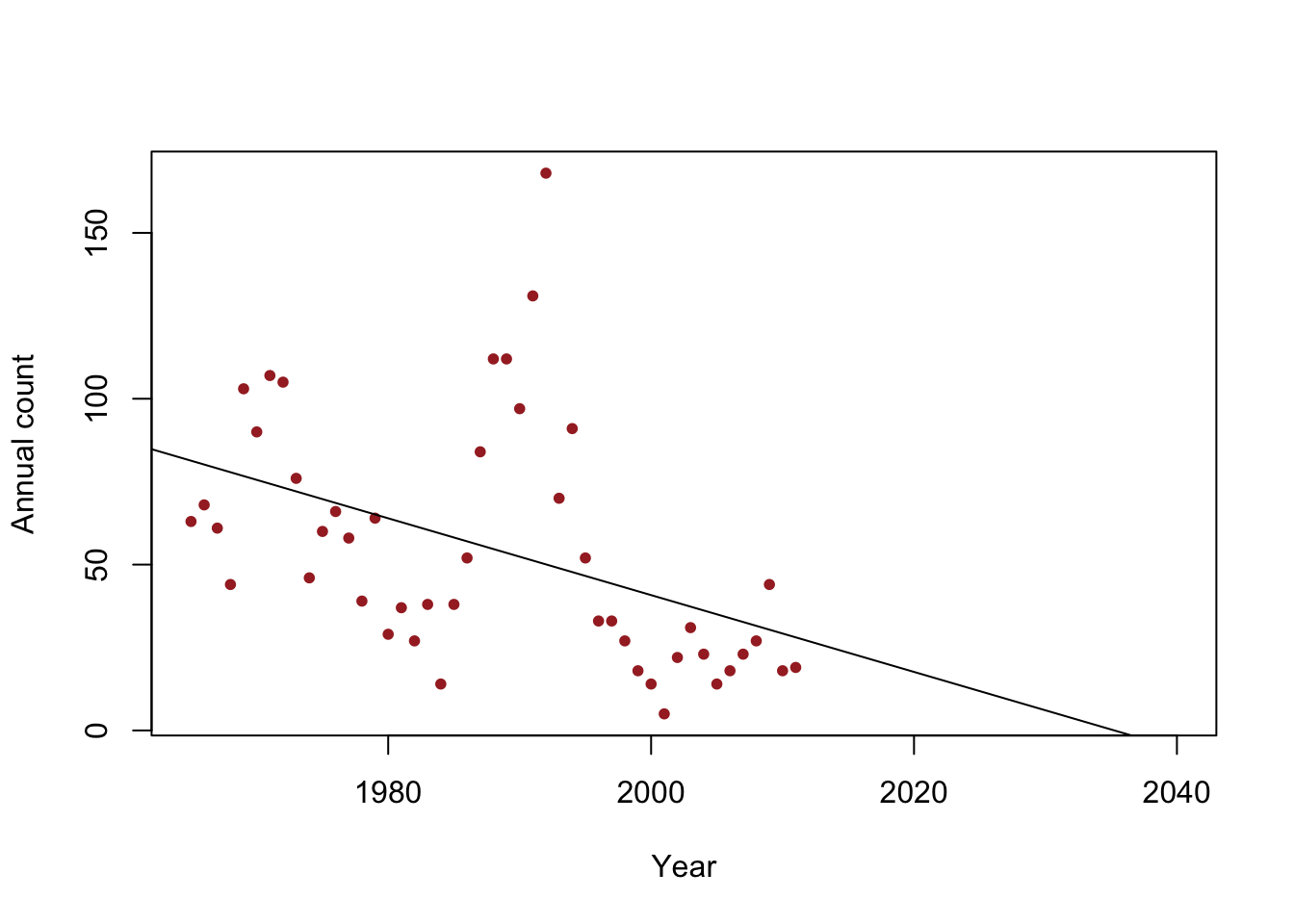

    # 95% equal-tailed CI based on percentiles of the empirical distribution
quantile(ed.extinct.hat,prob=c(0.025,0.975))
    ##     2.5%    97.5% 
## 2021.203 2077.168

Literature cited

Efron, Bradley, and Robert J Tibshirani. 1994. An Introduction to the Bootstrap. CRC press.
Faraway, J. J. 2014. Linear Models with r. CRC Press.
Hesterberg, Tim C. 2015. “What Teachers Should Know about the Bootstrap: Resampling in the Undergraduate Statistics Curriculum.” The American Statistician 69 (4): 371–86.