40 Assignment 2 (Guide)

  1. A mathematical model is a simplification and description of some real-world phenomenon. The model is usually expressed and communicated using a mathematical equation. The equation is deterministic and does not allow for the real-world phenomenon to have any randomness in it.

  2. A statistical model is a simplification and description of some real-world phenomenon. The model is usually expressed and communicated using a mathematical equation and a probability density/mass function (e.g., the normal distribution). The combination of the mathematical equation and probability density/mass function enables to model to be stochastic and account for randomness in a real-world phenomenon that the model describes.

  3. Everyone did great answering this question!!!

  4. A <- matrix(c(1,2,3,2,5,6,3,6,9),3,3,byrow=TRUE)
B <- diag(1,3)
C <- t(A)
    A+C
    ##      [,1] [,2] [,3]
## [1,]    2    4    6
## [2,]    4   10   12
## [3,]    6   12   18
    A-C
    ##      [,1] [,2] [,3]
## [1,]    0    0    0
## [2,]    0    0    0
## [3,]    0    0    0
    A%*%B
    ##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    2    5    6
## [3,]    3    6    9
    solve(A+B)%*%(C+B)
    ##               [,1]          [,2]          [,3]
## [1,]  1.000000e+00 -8.881784e-16 -1.554312e-15
## [2,]  1.665335e-16  1.000000e+00  1.110223e-16
## [3,] -5.551115e-17  1.110223e-16  1.000000e+00

  5. Which of the models below are a linear statistical model? Please justify your answer using words.

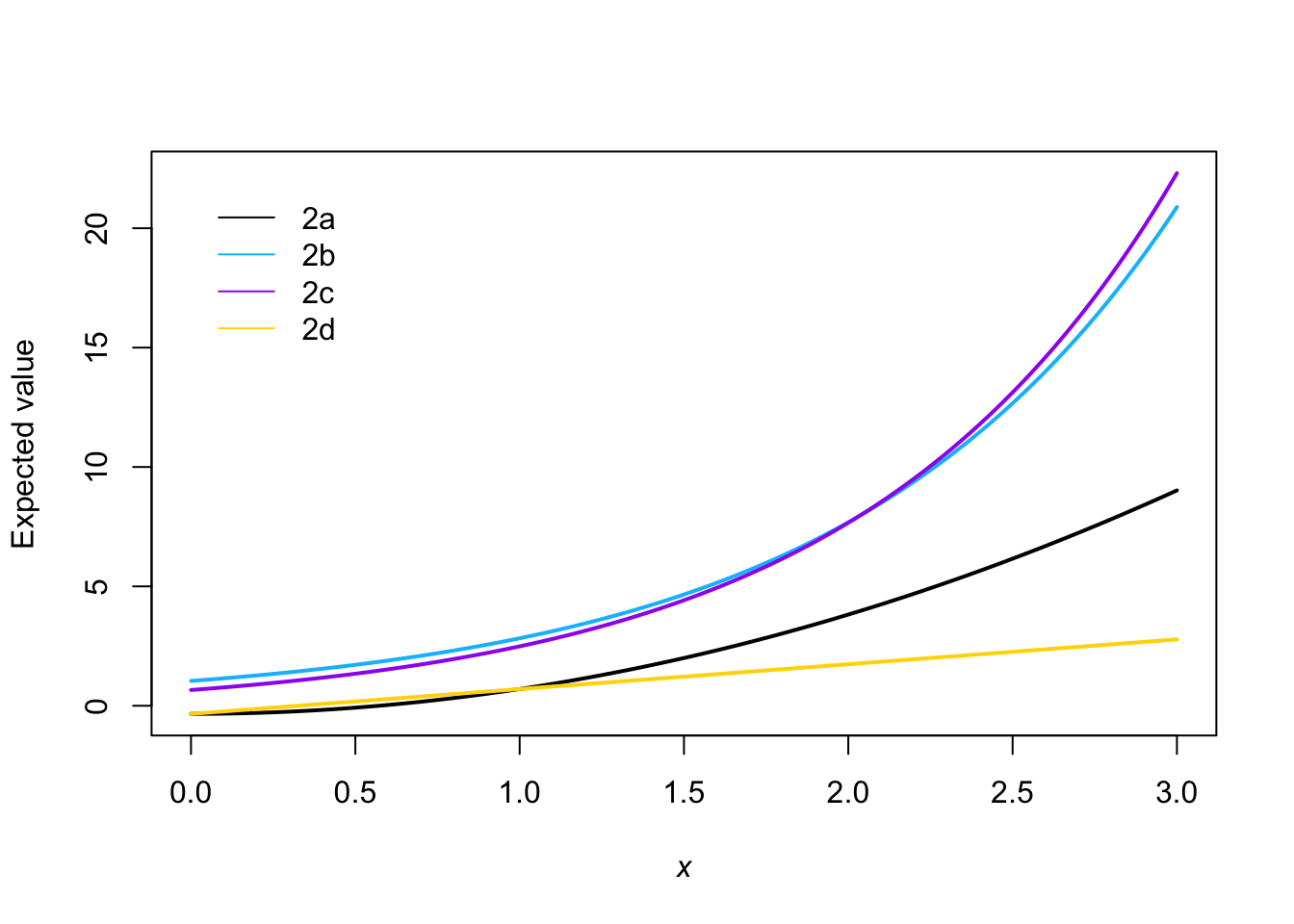
    1. Multiple answers are correct here. This is a linear model because the only non-linear part is where the predictor variable (i.e., \(\mathbf{x}\)) is squared. Any linear or non-linear transformation of the predictor variable does not change if a model is linear or non-linear. Another correct answer is that this is not a linear model because the error term (i.e., \(\boldsymbol{\varepsilon}\)) is missing. If the error term was not missing, then it would be a linear model.
    2. This is a linear model because the only non-linear part is where Euler’s number (i.e., \(e\)) is raised to the \(\mathbf{x}\) power. Any linear or non-linear transformation of the predictor variable does not change if a model is linear or non-linear.
    3. This is not a linear model because Euler’s number is raised to the parameter \(\beta_{1}\) power (i.e., the parameter shows up in the model inside of a non-linear function).
    4. See comment about my typo in original question. Multiple answers are correct here. This is not a linear model because the parameter shows up in the model inside of a non-linear function. Another correct answer is that you can easily simplify the model and show that it is the same as \(\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}+\boldsymbol{\varepsilon}.\)
  6. x <- seq(0,3,by=0.01)
beta <- c(-0.34,1.04)
E.y_a <- beta[1]+beta[2]*x^2
E.y_b <- beta[2]*exp(x)
E.y_c <- beta[1]+exp(beta[2]*x)
E.y_d <- beta[1]+beta[2]*x
col <- c("black","deepskyblue","purple","gold")

plot(x,E.y_a,ylim=c(range(E.y_a,E.y_b,E.y_c,E.y_d)),
 typ="l",col=col[1],
 xlab=expression(italic(x)),
 ylab="Expected value",lwd=2)
points(x,E.y_b,typ="l",col=col[2],lwd=2)
points(x,E.y_c,typ="l",col=col[3],lwd=2)
points(x,E.y_d,typ="l",col=col[4],lwd=2)
legend(x=0,y=22,legend=c("2a","2b","2c","2d"),bty="n",lty=1,
   col=col)