35 Day 34 (July 24)

35.1 Announcements

  • Teval
  • Final grades
  • More about challenger example here

35.2 Transformations of the response

  • Big picture idea

    • Select a function that transforms \(\mathbf{y}\) such that the assumptions of normality are approximately correct.

  • Two cultures

    • This is with respect to \(\mathbf{y}\) and not the predictors. Transforming the predictors is not at all controversial.
    • Trade offs
    • Difficult to apply sometimes (e.g., \(\text{log(}\mathbf{y}+c)\) for count data)
    • Difficult to interpret on the transformed scale
    • If normality is an appropriate assumption, we can use the general linear model \(\textbf{y}\sim\text{N}(\mathbf{X}\boldsymbol{\beta},\mathbf{V})\)

  • Example

    • Number of whooping cranes each year
    url <- "https://www.dropbox.com/s/ihs3as87oaxvmhq/Butler%20et%20al.%20Table%201.csv?dl=1"
df1 <- read.csv(url)
plot(df1$Winter,df1$N,typ="b",xlab="Year",ylab="Population Size",ylim=c(0,300),lwd=1.5,pch="*")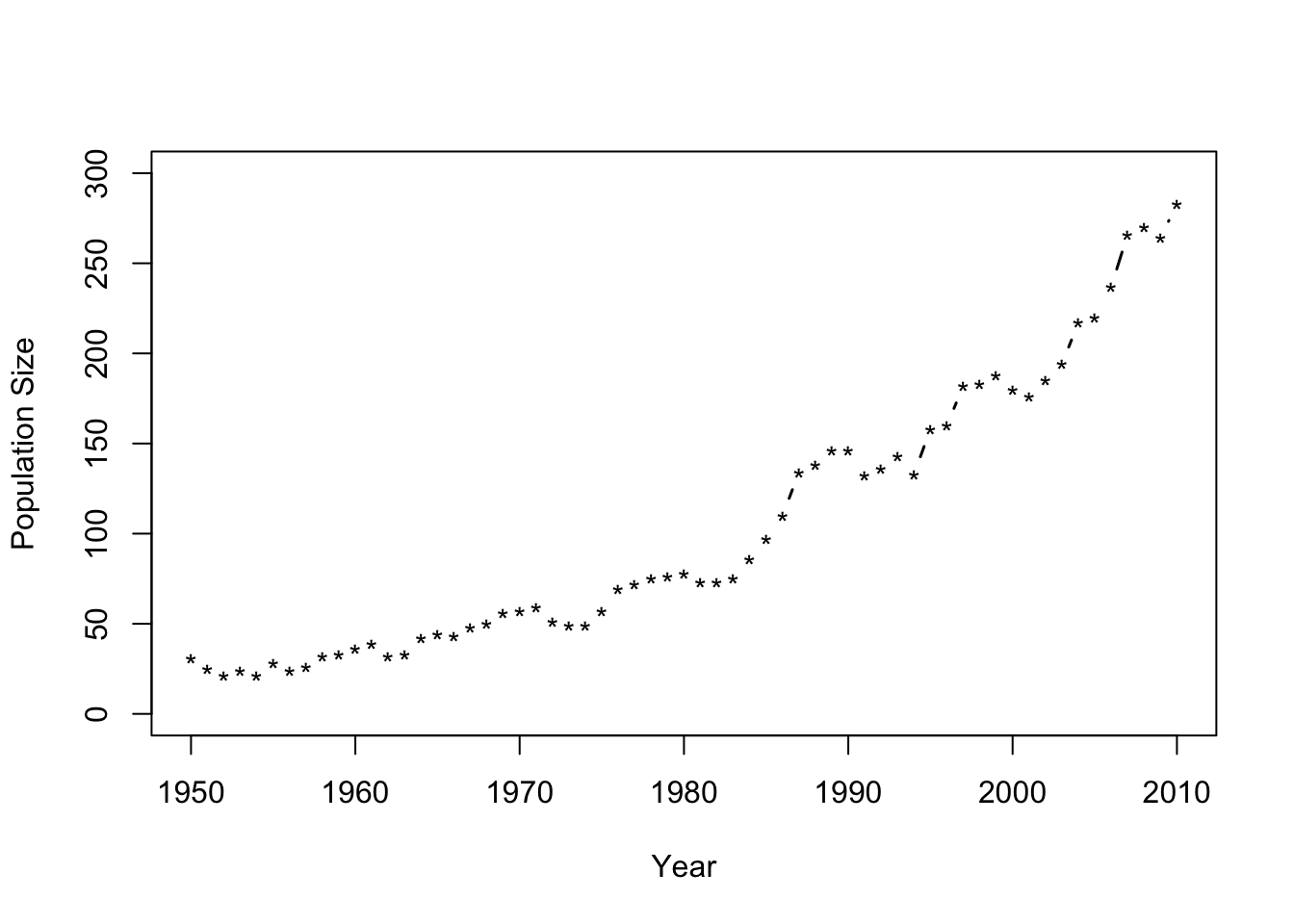

    • Fit the model \(\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}+\boldsymbol{\varepsilon}\) where \(\boldsymbol{\varepsilon}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{I})\) and \(\mathbf{x}\) is the year.
    m1 <- lm(N~Winter,data=df1)
plot(df1$Winter,df1$N,typ="b",xlab="Year",ylab="Population Size",ylim=c(0,300),lwd=1.5,pch="*")
abline(m1,col="gold")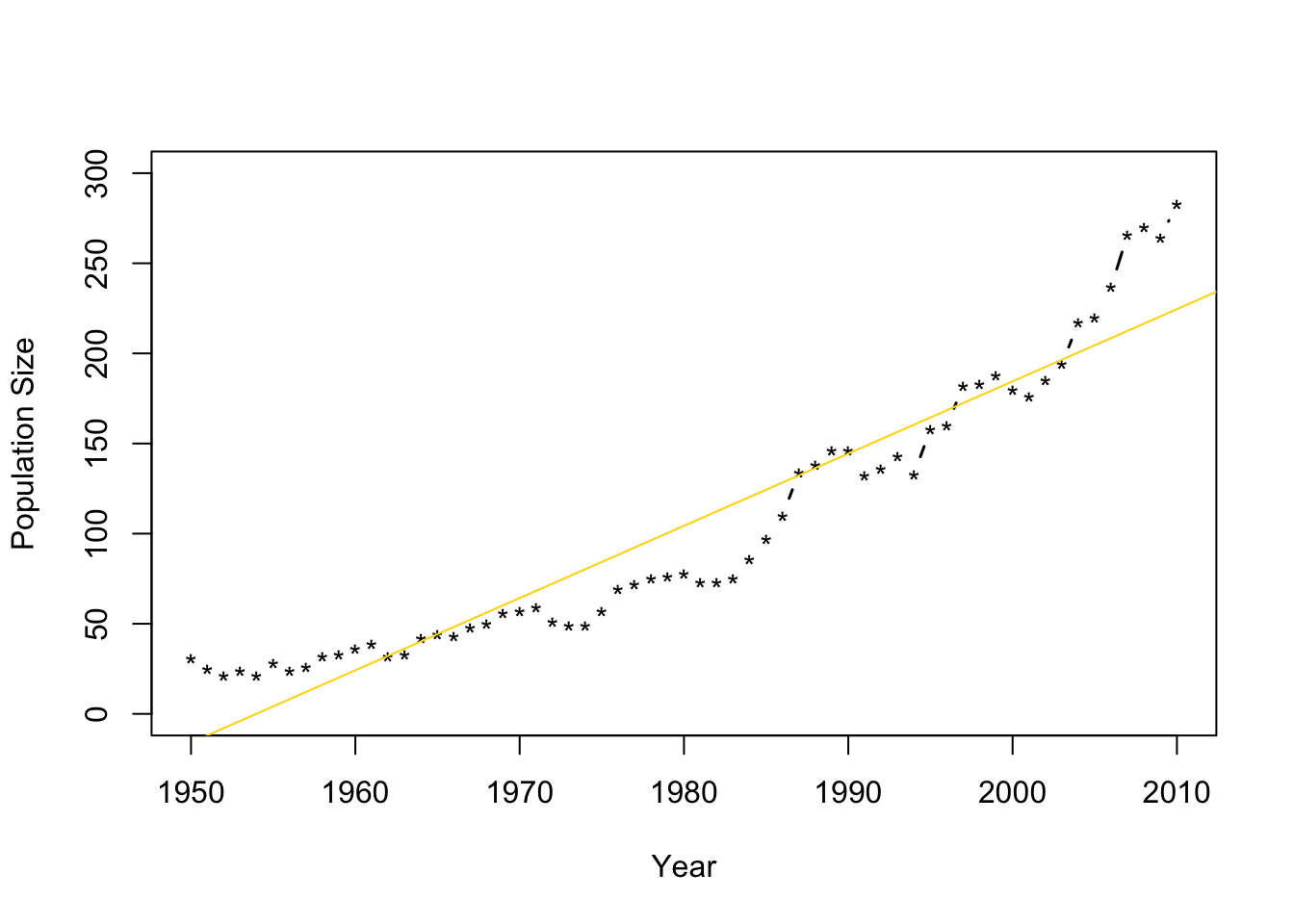

    • Check model assumptions
    e.hat <- residuals(m1)

#Check normality
hist(e.hat,col="grey",breaks=10,main="",xlab=expression(hat(epsilon)))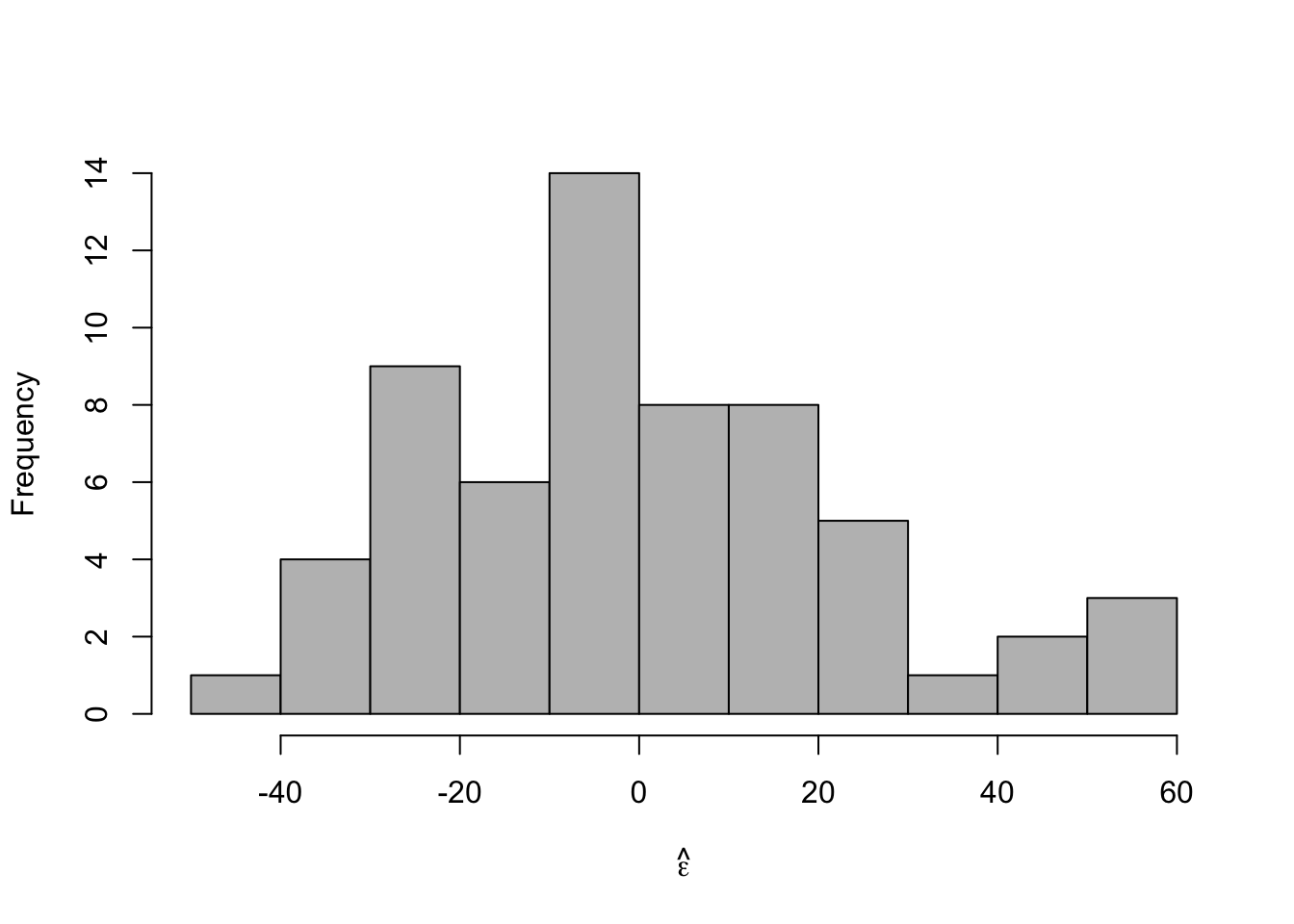

    shapiro.test(e.hat)
    ## 
##  Shapiro-Wilk normality test
## 
## data:  e.hat
## W = 0.96653, p-value = 0.09347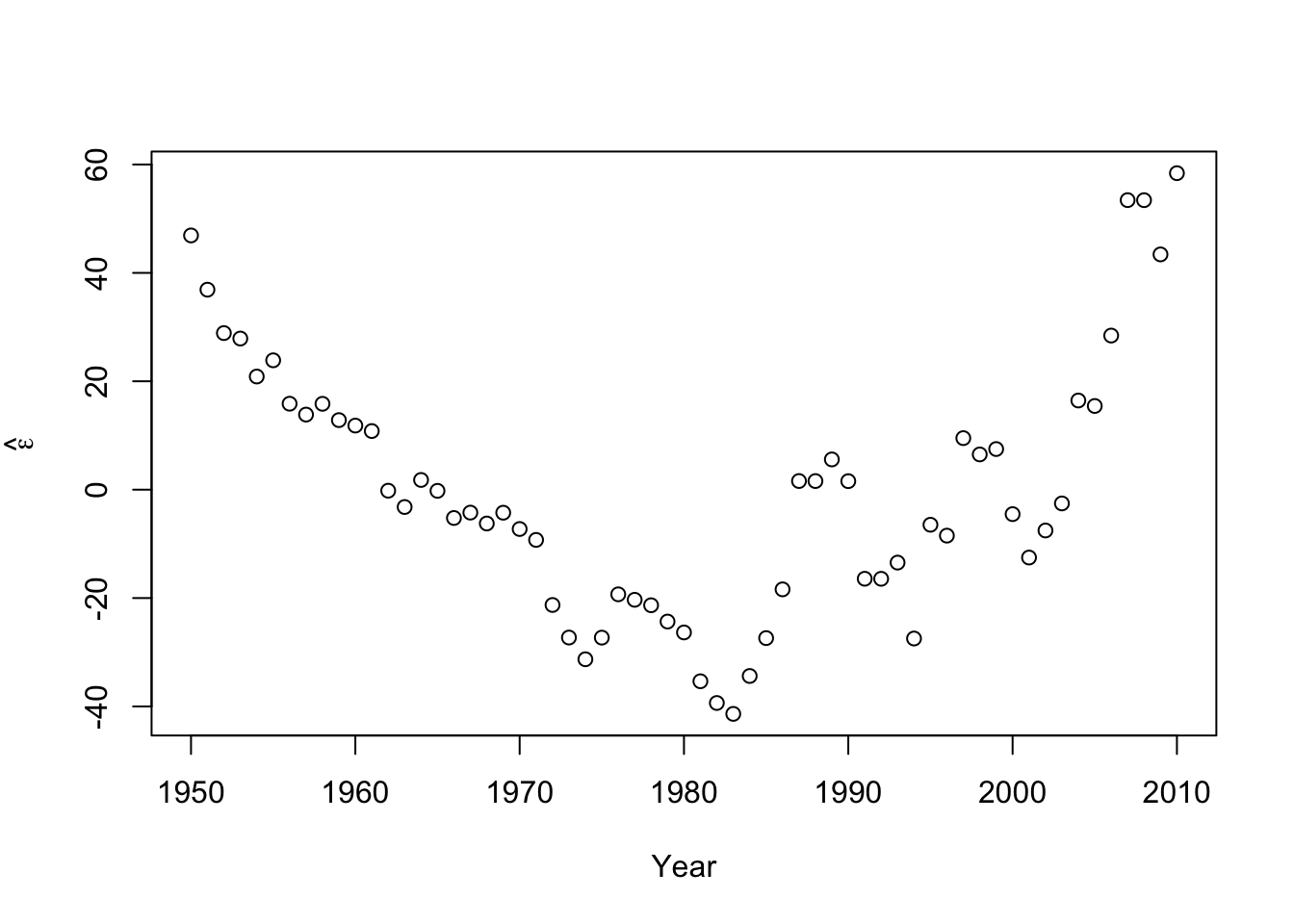
    #Check constant variance
plot(df1$Winter,e.hat,xlab="Year",ylab=expression(hat(epsilon)))

    #Check for autocorrelation among residuals
plot(e.hat[1:60],e.hat[2:61],xlab=expression(hat(epsilon)[t]),ylab=expression(hat(epsilon)[t+1]))

    cor(e.hat[1:60],e.hat[2:61])
    ## [1] 0.9273559
    library(lmtest)
dwtest(m1)
    ## 
##  Durbin-Watson test
## 
## data:  m1
## DW = 0.13355, p-value < 2.2e-16
## alternative hypothesis: true autocorrelation is greater than 0
    • Log transformation (i.e., \(\text{log}(\mathbf{y})\)).
      • \(\text{log}(\mathbf{y})=\beta_{0}+\beta_{1}\mathbf{x}+\boldsymbol{\varepsilon}\) where \(\boldsymbol{\varepsilon}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{I})\) and \(\mathbf{x}\) is the year.
      • What model is implied by this transformation?
        • If \(z\sim\text{N}(\mu,\sigma^{2})\), then \(\text{E}(e^{z})=e^{\mu+\frac{\sigma^{2}}{2}}\) and \(\text{Var}(e^{z})=(e^{\sigma^{2}}-1)e^{2\mu+\sigma^{2}}\)
      • Fit the model
    m2 <- lm(log(N)~Winter,data=df1)
plot(df1$Winter,df1$N,typ="b",xlab="Year",ylab="Population Size",ylim=c(0,300),lwd=1.5,pch="*")
abline(m1,col="gold")

ev.y.hat <- exp(predict(m2)) # Possible because of invariance property of MLEs
points(df1$Winter,ev.y.hat,typ="l",col="deepskyblue")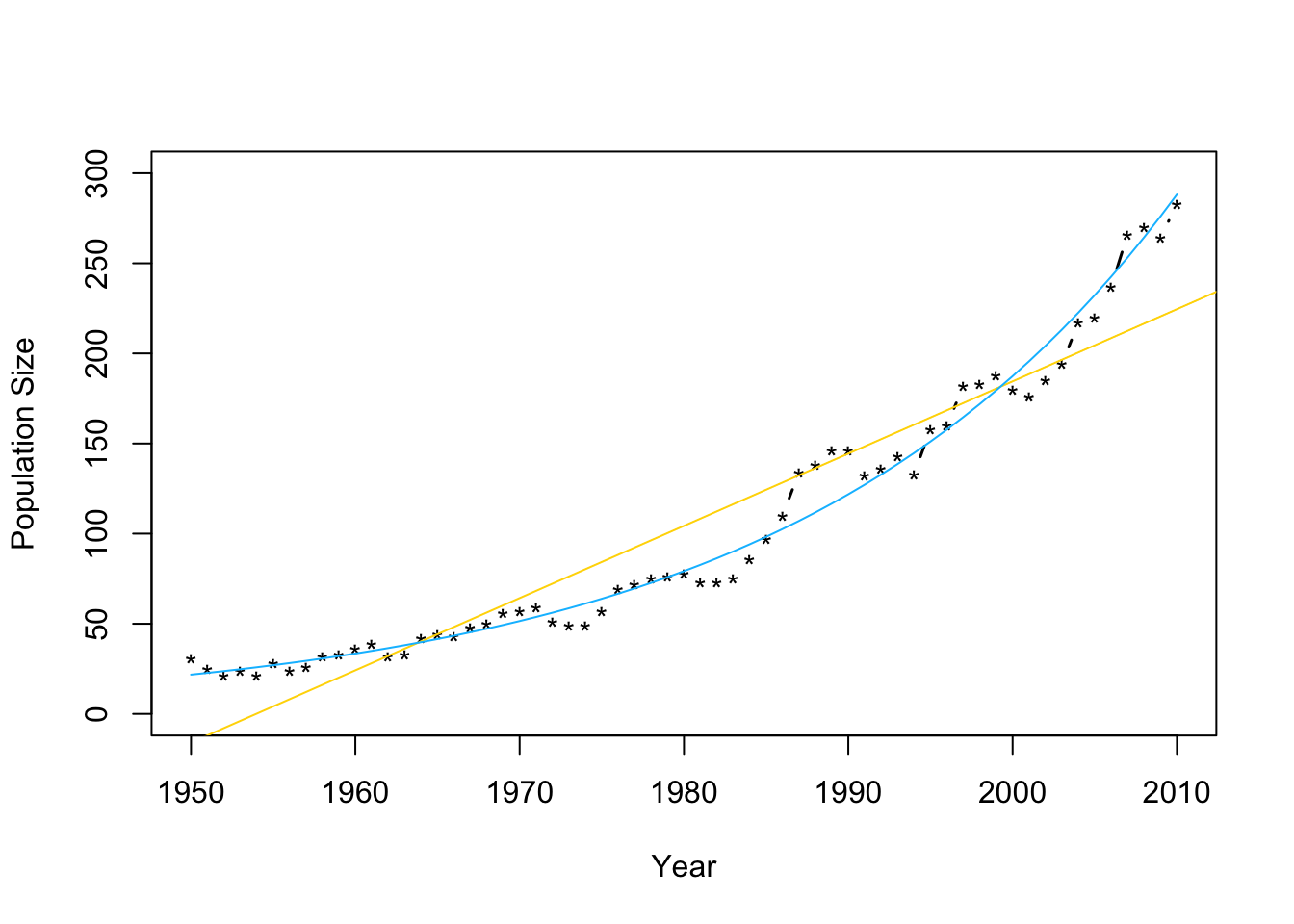

    - Check model assumptions

    e.hat <- residuals(m2)

#Check normality
hist(e.hat,col="grey",breaks=10,main="",xlab=expression(hat(epsilon)))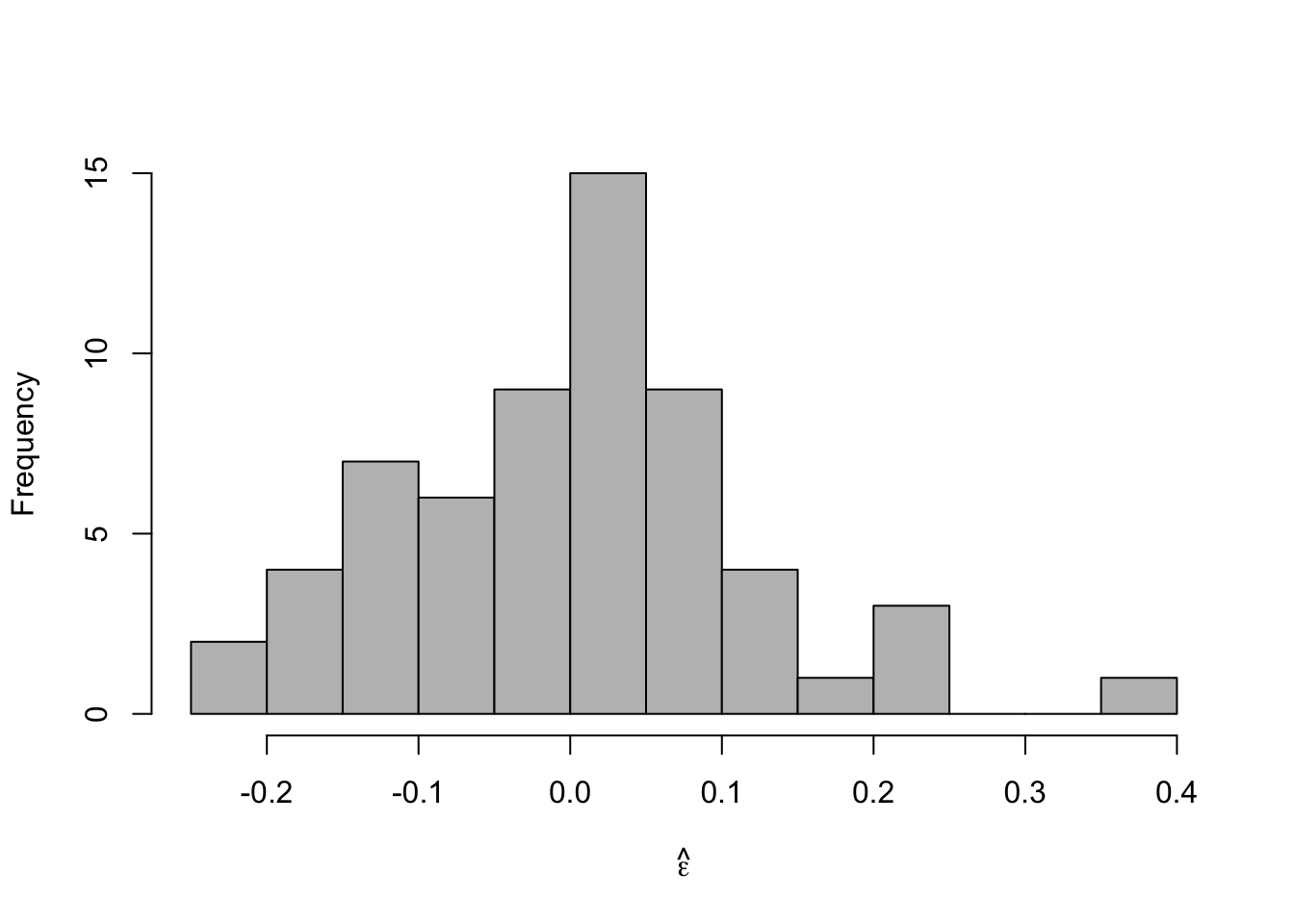

    shapiro.test(e.hat)
    ## 
##  Shapiro-Wilk normality test
## 
## data:  e.hat
## W = 0.97059, p-value = 0.1489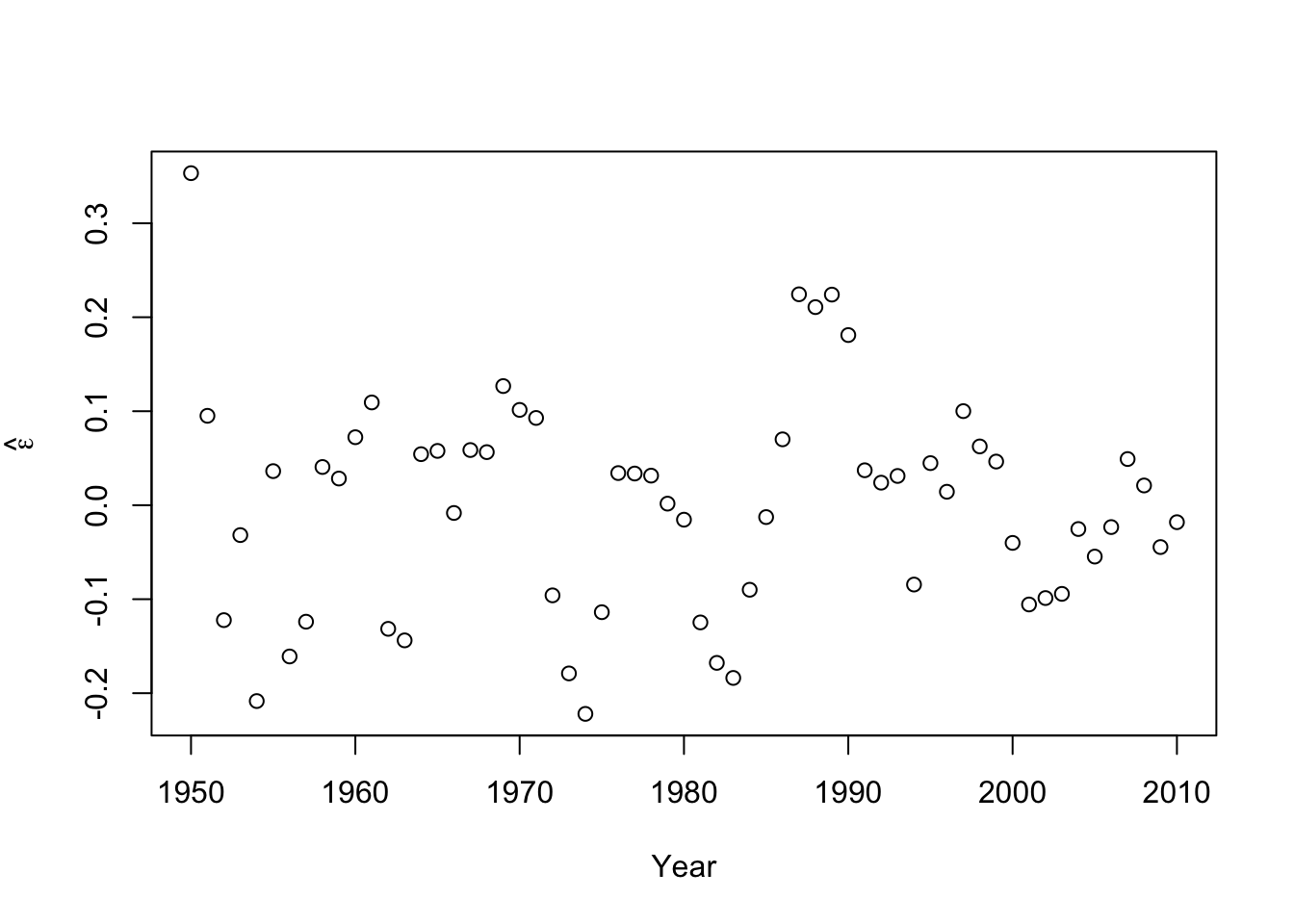
    #Check constant variance
plot(df1$Winter,e.hat,xlab="Year",ylab=expression(hat(epsilon)))

    - Confidence intervals and prediction intervals

    plot(df1$Winter,df1$N,typ="b",xlab="Year",ylab="Population Size",ylim=c(0,300),lwd=1.5,pch="*")
ev.y.hat <- exp(predict(m2)) # Possible because of invariance property of MLEs
points(df1$Winter,ev.y.hat,typ="l",col="deepskyblue")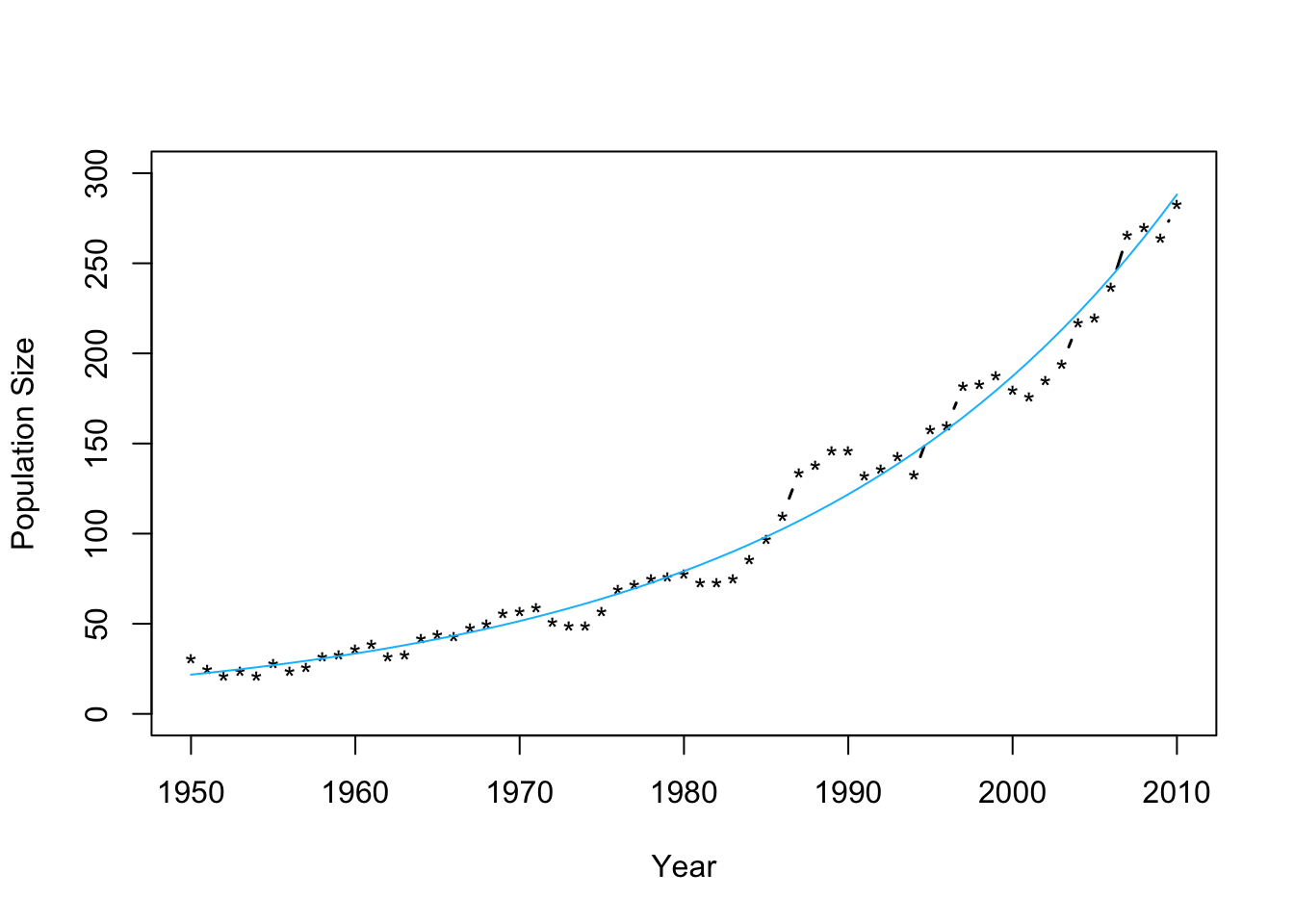

    # CI and PI for log(y)
predict(m2,newdata=df1[1,],interval="confidence")
    ##        fit    lwr      upr
## 1 3.080718 3.0223 3.139136
    predict(m2,newdata=df1[1,],interval="prediction")
    ##        fit      lwr      upr
## 1 3.080718 2.842504 3.318933