4 Day 4 (June 6)
4.1 Announcements
Tutoring for program R
- Dickens Hall room 108
- 12:30 - 1:30 Monday - Friday
Recommended reading
- Chapters 1 and 2 (pgs 1 - 28) in Linear Models with R
- Chapter 2 in Applied Regression and ANOVA Using SAS
Final project is posted
Assignment 2 is posted a due Wednesday June 12
Special in-class event on Friday!
4.2 Introduction to linear models
What is a model?
What is a linear model?
Most widely used model in science, engineering, and statistics
Vector form: \(\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\mathbf{x}_{2}+\ldots+\beta_{p}\mathbf{x}_{p}+\boldsymbol{\varepsilon}\)
Matrix form: \(\mathbf{y}=\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon}\)
Which part of the model is the mathematical model
Which part of the model makes the linear model a “statistical” model
Visual
Which of the four below are a linear model \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\mathbf{x}^{2}_{1}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\beta_{2}\text{log(}\mathbf{x}_{1}\text{)}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}e^{\beta_{2}\mathbf{x}_{1}}+\boldsymbol{\varepsilon}\] \[\mathbf{y}=\beta_{0}+\beta_{1}\mathbf{x}_{1}+\text{log(}\beta_{2}\text{)}\mathbf{x}_{1}+\boldsymbol{\varepsilon}\]
Why study the linear model?
- Building block for more complex models (e.g., GLMs, mixed models, machine learning, etc)
- We know the most about it
4.3 Estimation
- Three options to estimate \(\boldsymbol{\beta}\)
- Minimize a loss function
- Maximize a likelihood function
- Find the posterior distribution
- Each option requires different assumptions
4.4 Loss function approach
- Define a measure of discrepancy between the data and the mathematical model
- Find the values of \(\boldsymbol{\beta}\) that make \(\mathbf{X}\boldsymbol{\beta}\) “closest” to \(\mathbf{y}\)
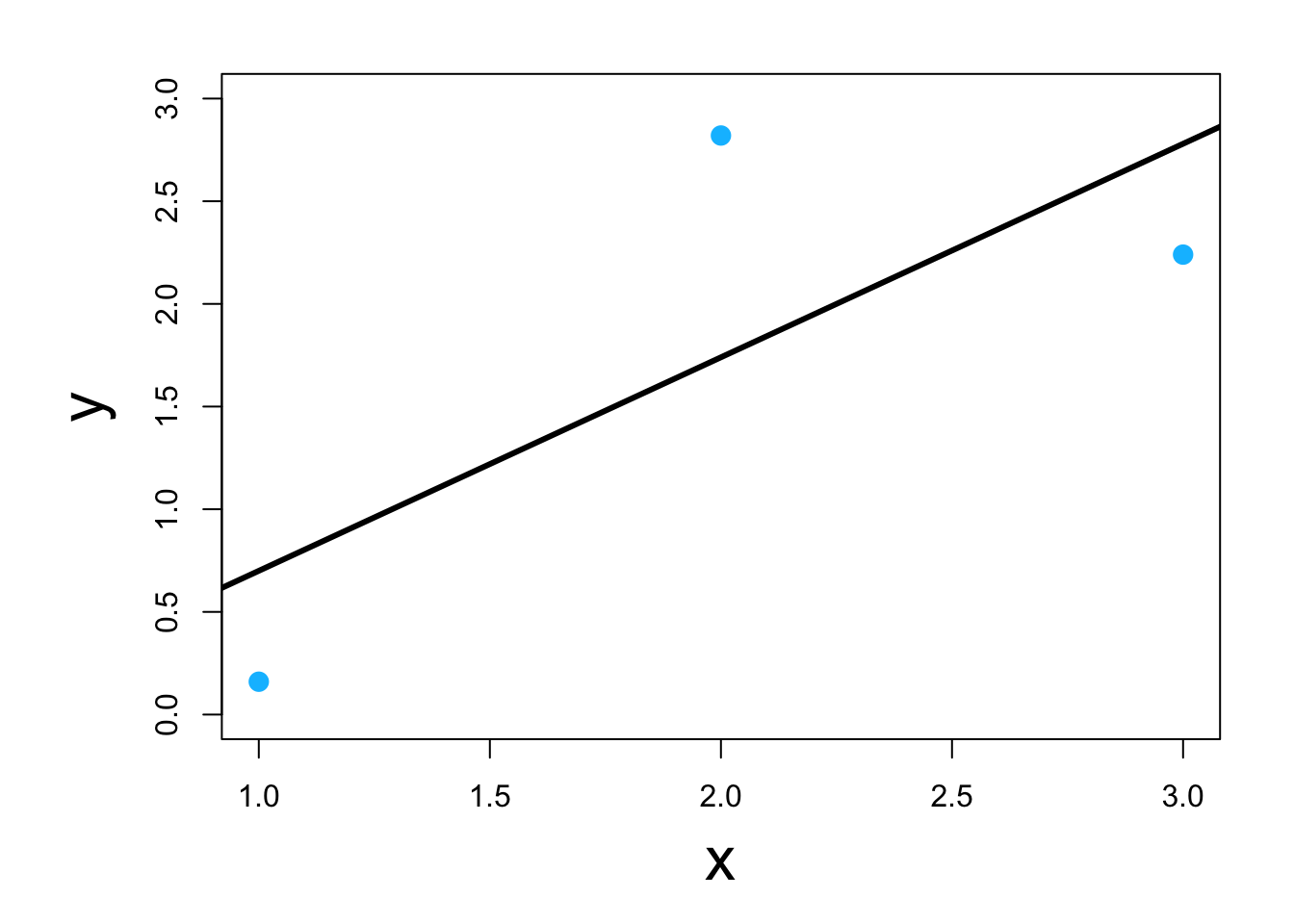
- Visual
- Classic example \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}}\sum_{i=1}^{n}(y_i-\mathbf{x}_{i}^{\prime}\boldsymbol{\beta})^2\] or in matrix form \[\underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^{\prime}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})\] which results in \[\hat{\boldsymbol{\beta}}=(\mathbf{X}^{\prime}\mathbf{X})^{-1}\mathbf{X}^{\prime}\mathbf{y}\]
- Three ways to do it in program R
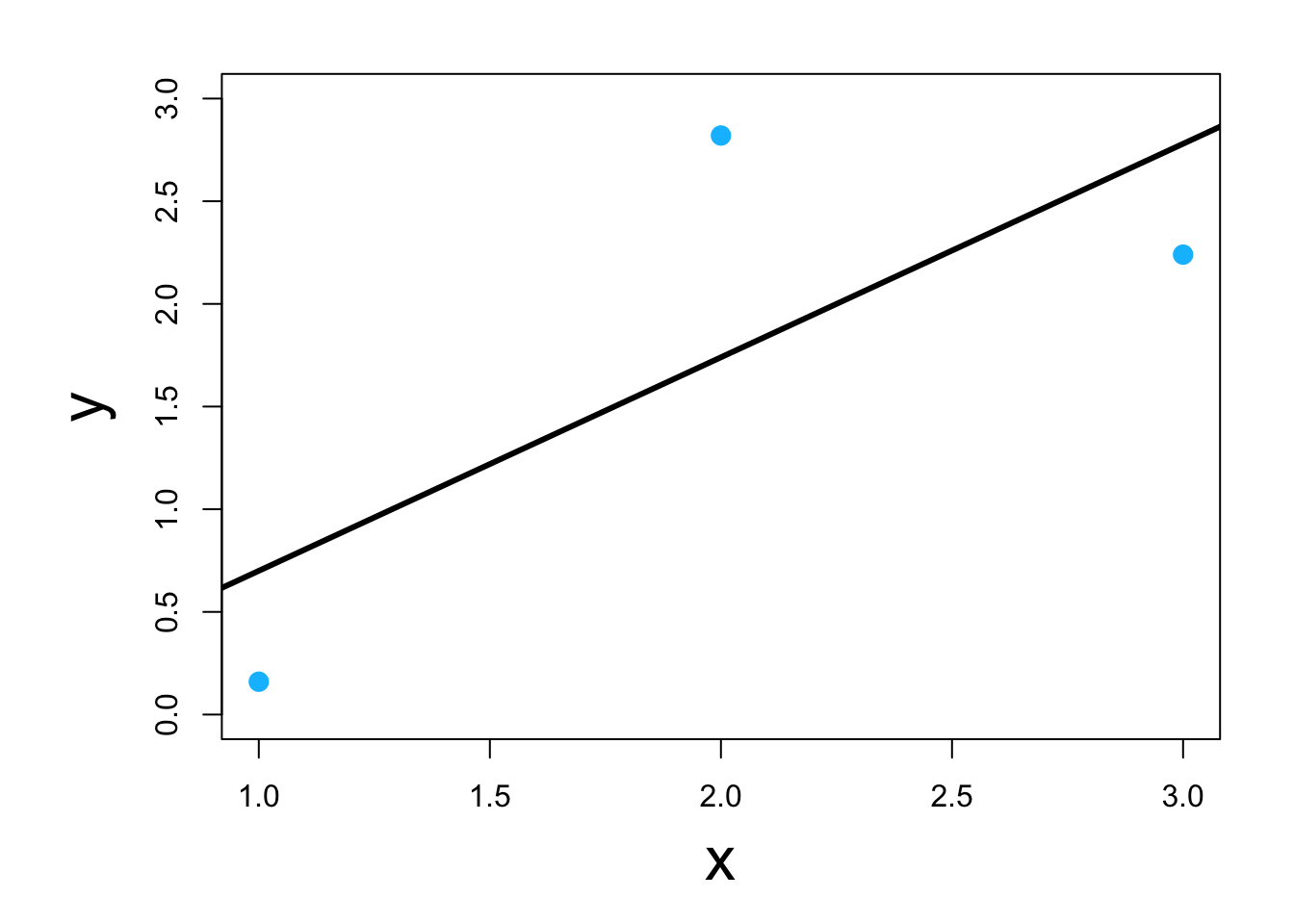
- Using scalar calculus and algebra (kind of)
y <- c(0.16,2.82,2.24) x <- c(1,2,3) y.bar <- mean(y) x.bar <- mean(x) # Estimate the slope parameter beta1.hat <- sum((x-x.bar)*(y-y.bar))/sum((x-x.bar)^2) beta1.hat## [1] 1.04# Estimate the intercept parameter beta0.hat <- y.bar - sum((x-x.bar)*(y-y.bar))/sum((x-x.bar)^2)*x.bar beta0.hat## [1] -0.34