Chapter 7 Principal Component Analysis
7.1 Reminder
So far, we have focused on linear models of the form \[ y= \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_p x_p +\epsilon \] and argued in favour of selecting sparser models which are simpler to interpret and also have better predictive performance in comparison to the model that includes all \(p\) predictors.
Specifically, we saw
- Model-search methods: discrete procedures which require full or partial enumeration of all possible models and select one best model.
- Coefficient shrinkage methods: continuous procedures which shrink the coefficients of the full model to zero (penalised regression).
Note that both are supervised learning approaches and effectively reduce the dimensionality of the problem.
There is another alternative unsupervised learning approach for dimension reduction, where only the predictors are of the interest. Here comes the principal component analysis.
7.2 Linear approximation
Consider that there is a \(q\)-dimensional random vector \[ \boldsymbol{X} \sim (\boldsymbol{m} , \boldsymbol{\Sigma}), \] where
\[\boldsymbol{m}=E(\boldsymbol{X})=\begin{bmatrix} m_1 \\ \vdots \\ m_q \end{bmatrix} \] and
\[\boldsymbol{\Sigma}=Var(\boldsymbol{X})=\begin{bmatrix} \Sigma_{11} & \dots & \Sigma_{1q} \\ \vdots & \ddots & \vdots\\ \Sigma_{q1} & \dots & \Sigma_{qq} \end{bmatrix} \] If we were to approximate \(\boldsymbol{X}\) through a single straight line, what is the ``best’’ line?
One approach to solve this problem dates back to Pearson (1901): Minimize the expected squared distances between \(\boldsymbol{X}\) and their projections \(\boldsymbol{X}^{\prime}\) onto the line. We make in the following use of geometrical considerations which are provided in Figure 7.1.
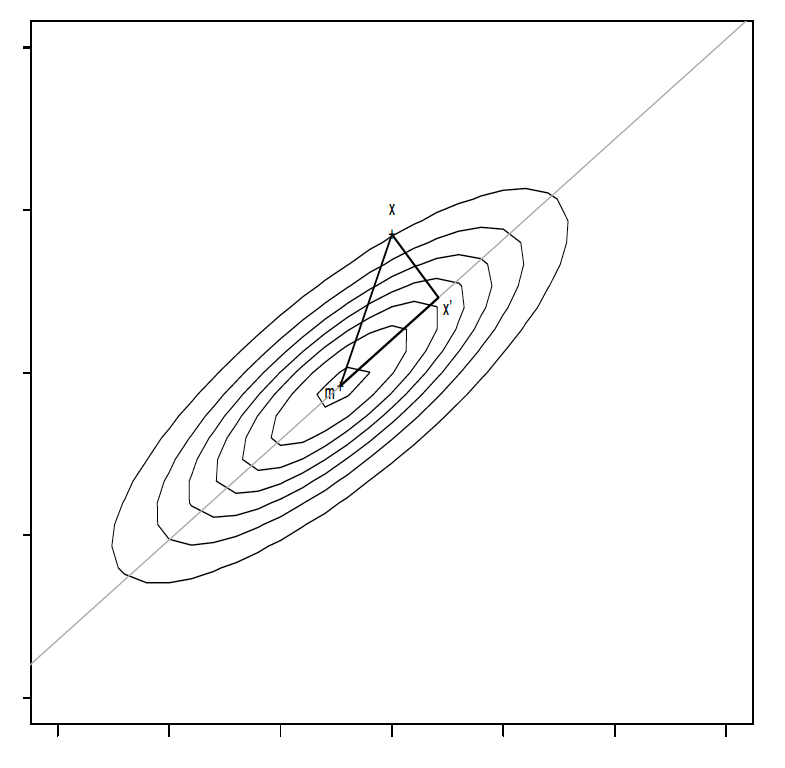
Figure 7.1: Geometrical considerations for PCA
By Pythagoras, \[ E(\overline{\boldsymbol{X}\boldsymbol{X}^{\prime}}^2)= E(\overline{\boldsymbol{m} \boldsymbol{X}}^2)-E(\overline{\boldsymbol{m}\boldsymbol{X}^{\prime}}^2) \]
where \(\overline{\boldsymbol{X}\boldsymbol{X}^{\prime}}\) denotes the length of the line segment connecting \(X\) and \(\boldsymbol{X}^{\prime}\), i.e. \(\overline{\boldsymbol{X}\boldsymbol{X}^{\prime}}= ||\boldsymbol{X}-\boldsymbol{X}^{\prime}||\). As \(E(\overline{\boldsymbol{m} \boldsymbol{X}}^2)\) does not depend on the fitted line, minimizing \(E(\overline{\boldsymbol{X}\boldsymbol{X}^{\prime}}^2)\) is the same as maximizing \(E(\overline{\boldsymbol{m}\boldsymbol{X}^{\prime}}^2)\). Investigating this quantity further, let \(\boldsymbol{\gamma}\) be a unit vector pointing in the direction of the vector \(\boldsymbol{X}^{\prime}-\boldsymbol{m}\) and let \(t\in \mathbb{R}\) be a scalar such that the projected point is given by \[\boldsymbol{X}^{\prime}= \boldsymbol{m}+t \boldsymbol{\gamma}\in\mathbb{R}^q.\] The Euclidean distance between \(\boldsymbol{m}\) and \(\boldsymbol{X}^{\prime}\), \(\overline{\boldsymbol{m}\boldsymbol{X}^{\prime}}\), equals \(|t|\). We have by definition \[ cos(\boldsymbol{\gamma}, \boldsymbol{X}-\boldsymbol{m})=\frac{t}{||\boldsymbol{X}-\boldsymbol{m}||}\] and, using the properties of the dot product gives \[\boldsymbol{\gamma}^T(\boldsymbol{X}-\boldsymbol{m})=||\boldsymbol{\gamma}||||\boldsymbol{X}-\boldsymbol{m}||cos(\boldsymbol{\gamma}, \boldsymbol{X}-\boldsymbol{m})=t.\] To maximizing \(E(\overline{\boldsymbol{m}\boldsymbol{X}^{\prime}}^2)\), we have \[\begin{eqnarray*} E(\overline{\boldsymbol{m} \boldsymbol{X}^{\prime}}^2) &=& E(\overline{\boldsymbol{m} \boldsymbol{X}^{\prime}}\, \overline{\boldsymbol{m} \boldsymbol{X}^{\prime}} )= E(\boldsymbol{\gamma}^T(\boldsymbol{X}-\boldsymbol{m}) (\boldsymbol{X}-\boldsymbol{m})^T\boldsymbol{\gamma})=\\ &=& \mbox{Var}(\boldsymbol{\gamma}^T(\boldsymbol{X}-\boldsymbol{m}))= \mbox{Var}(\boldsymbol{\gamma}^T\boldsymbol{X})= \boldsymbol{\gamma}^T\mbox{Var}(\boldsymbol{X})\boldsymbol{\gamma}= \boldsymbol{\gamma}^T\boldsymbol {\Sigma} \boldsymbol{\gamma}. \end{eqnarray*}\]
Hence, we need to maximize \(\boldsymbol{\gamma}^T\boldsymbol{\Sigma} \boldsymbol{\gamma}\) under the constraint \(||\boldsymbol{\gamma}||^2=\boldsymbol{\gamma}^T\boldsymbol{\gamma}=1\). This is a constrained maximization problem which can be addressed through the use of a Lagrange multiplier. Define \[ P(\boldsymbol{\gamma})= \boldsymbol{\gamma}^T \boldsymbol{\Sigma} \boldsymbol{\gamma}-\lambda(\boldsymbol{\gamma}^T\boldsymbol{\gamma}-1). \]
Then from Chapter 12 Mardia, Kent, and Bibby (1979) \[ \frac{\partial P}{\partial\boldsymbol{\gamma}}= 2 \boldsymbol{\Sigma} \boldsymbol{\gamma} - 2 \lambda \boldsymbol{\gamma}, \] and setting this equal to zero yields \[\begin{equation} \boldsymbol{\Sigma}\boldsymbol{\gamma} = \lambda \boldsymbol{\gamma} \tag{7.1} \end{equation}\] So, \(\boldsymbol{\gamma}\) must be an eigenvector of \(\boldsymbol{\Sigma}\). But which one? (To fix terms, order the \(q\) eigenvalues of \(\boldsymbol{\Sigma} \in \mathbb{R}^{q\times q}\) such that \(\lambda_1 \ge \ldots \ge \lambda_q\), and let the orthogonal vectors \(\boldsymbol{\gamma}_1, \ldots, \boldsymbol{\gamma}_q\) denote the corresponding eigenvectors.) Multiplying ((7.1)) with \(\boldsymbol{\gamma}^T\), one has
\[\begin{eqnarray*} \boldsymbol{\gamma}^T\boldsymbol{\Sigma} \boldsymbol{\gamma}&=& \lambda \boldsymbol{\gamma}^T \boldsymbol{\gamma}\\ \mbox{Var}(\boldsymbol{\gamma}^T\boldsymbol{X})&=& \lambda \end{eqnarray*}\] The left hand side is now exactly what we want to maximize. Maximizing \(\mbox{Var}(\boldsymbol{\gamma}^T\boldsymbol{X})\) means then that we need to choose the eigenvector \(\boldsymbol{\gamma}_1\) corresponding to the largest eigenvalue \(\lambda_1\).
Some notes:
The new random variable \(\boldsymbol{\gamma}_1^T \boldsymbol{X}\) is that linear combination of \(\boldsymbol{X}=(X_1, \ldots,X_q)^T\) with maximal variance, and is called the first principal component (PC) of \(\boldsymbol{X}\). The line \[ g_1(t)= \boldsymbol{m}+ t\boldsymbol{\gamma}_1, \qquad (t \in \mathbb{R}) \] is the corresponding first principal component line.
Similarly, we define higher-order PC’s: The \(j-\)th eigenvector \(\boldsymbol{\gamma}_j\) maximizes \(\mbox{Var}(\boldsymbol{\gamma}^T\boldsymbol{X})\) over all \(\boldsymbol{\gamma}\) which are orthogonal to \(\boldsymbol{\gamma}_1, \ldots, \boldsymbol{\gamma}_{j-1}\). The \(j-\)th PC is given by \(\boldsymbol{\gamma}_j^T\boldsymbol{X}\), and \(g_j(t)=\boldsymbol{m}+t\boldsymbol{\gamma}_j\) is the corresponding \(j-\)th PC line (See Krzanowski (2000)).
For data \(\boldsymbol{Z}\), we need to replace \(\boldsymbol{m}\) by \(\hat{\boldsymbol{m}}\), and \(\boldsymbol{\Sigma}\) by some estimate \(\hat{\boldsymbol{\Sigma}}\) (ML or sample), yielding \(\hat{\lambda}_1, \ldots, \hat{\lambda}_q\), \(\hat{\boldsymbol{\gamma}}_1, \ldots, \hat{\boldsymbol{\gamma}}_q\).
From now on for the rest of this section, we will omit all “hats” on \(\boldsymbol{\Sigma}\), \(\boldsymbol{m}\), \(\lambda\), etc, meaning that the formulas hold for either the random vector or the corresponding estimate, depending on context.
Note that principal components minimize the (sum of squared) orthogonal distances between data \(\boldsymbol{X}_1, \ldots, \boldsymbol{X}_n\) and the line, unlike vertical distances as in the regression context. For example:
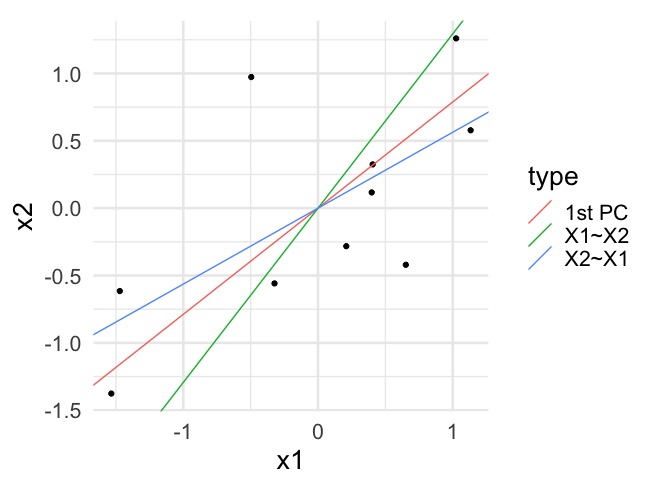
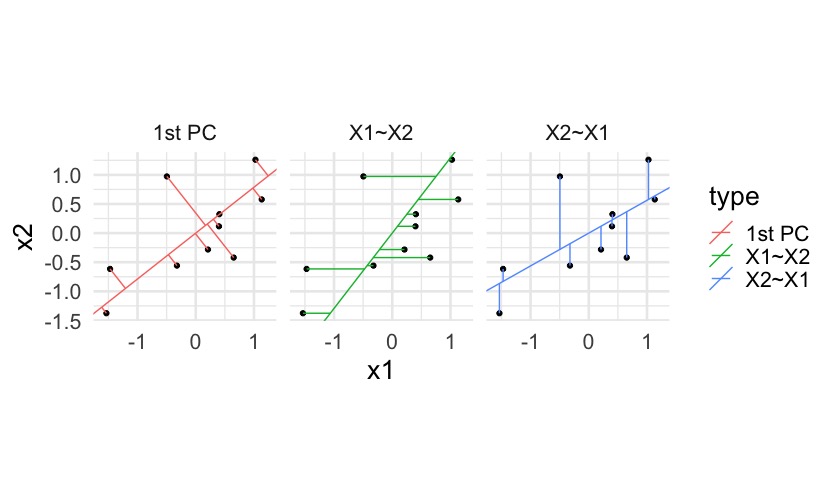
7.3 Decomposing variance
Recall that, for the \(j-\)th eigenvector \(\boldsymbol{\gamma}_j\) of \(\boldsymbol{\Sigma}\), one has \[ \boldsymbol{\Sigma}\boldsymbol{\gamma}_j= \lambda_j\boldsymbol{\gamma}_j \,\qquad j=1, \ldots,q \]
For each \(j\), either side of this equation is a \(q \times 1\) vector. We can bind these \(q\) vectors together to form \(q \times q\) matrices:
\[\begin{eqnarray} \nonumber \left(\boldsymbol{\Sigma}\boldsymbol{\gamma}_1, \ldots, \boldsymbol{\Sigma}\boldsymbol{\gamma}_q\right) &=& \left(\lambda_1 \boldsymbol{\gamma}_1, \ldots, \lambda_1\boldsymbol{\gamma}_q\right)\\ \nonumber \boldsymbol{\Sigma}\left(\boldsymbol{\gamma}_1, \ldots, \boldsymbol{\gamma}_q\right) &=& \left(\boldsymbol{\gamma}_1, \ldots, \boldsymbol{\gamma}_q\right) \left(\begin{array}{ccc} \lambda_1& & \\ & \ddots& \\ & & \lambda_q \\ \end{array}\right)\\ \nonumber \boldsymbol{\Sigma} \boldsymbol{\Gamma} &=& \boldsymbol{\Gamma} \boldsymbol{\Lambda} \\ \label{eigdec}\boldsymbol{\Sigma}&=& \boldsymbol{\Gamma} \boldsymbol{\Lambda} \boldsymbol{\Gamma}^{-1} = \boldsymbol{\Gamma} \boldsymbol{\Lambda} \boldsymbol{\Gamma}^T \end{eqnarray}\]
This decomposition is called the eigen decomposition of \(\boldsymbol{\Sigma}\). Some software packages use this in order to find the \(\lambda_j's\) and \(\boldsymbol{\gamma}_j's\).
Now, we have \[ \lambda_j=\mbox{Var}(\boldsymbol{\gamma}_j^T\boldsymbol{X}) \] so the \(\lambda_j\) provide some decomposition of variance. So, each \(\lambda_j\) takes the share of something - but the share of what? Let’s therefore compute their sum: \[ \lambda_1+\ldots +\lambda_q=\mbox{Tr}(\boldsymbol{\Lambda}) {=} \mbox{Tr}(\boldsymbol{\Gamma}^T\boldsymbol{\Sigma} \boldsymbol{\Gamma}) {=} \mbox{Tr} (\boldsymbol{\Gamma}\boldsymbol{\Gamma}^T \boldsymbol{\Sigma})= \mbox{Tr}(\boldsymbol{\Sigma}) \equiv \mbox{TV}(\boldsymbol{X}) \]
The trace of the variance matrix is called the total variance. Therefore \[ \frac{\lambda_j}{\lambda_1+\ldots + \lambda_q}= \frac{\mbox{Var}(\boldsymbol{\gamma}_j^T\boldsymbol{X})}{\mbox{TV}(\boldsymbol{X})} \] is the proportion of total variance explained by the \(j-\)th principal component. A simple graphical tool illustrating this decomposition is the scree plot, which plots \(\lambda_j\) vs. \(j\).
Practical Example
For the 4-dimensional space spanned by the four variables “TAX”, “DLIC”, “INC”, “ROAD” of the fuel consumption data set, we obtain a scree plot in R as follows:
fuelcons <- read.table("https://www.maths.dur.ac.uk/users/hailiang.du/data/FUEL.dat", header=TRUE)
fuel <- fuelcons[,c("TAX", "DLIC", "INC", "ROAD")]
fuel.pr <- prcomp(fuel)
plot(fuel.pr)
Can we create it by hand? Let’s look at the output of the prcomp function:
fuel.pr## Standard deviations (1, .., p=4):
## [1] 5.5610991 3.5210898 0.7482262 0.5562322
##
## Rotation (n x k) = (4 x 4):
## PC1 PC2 PC3 PC4
## TAX -0.04687723 0.15579496 -0.96634218 0.19928183
## DLIC 0.99686606 -0.05351563 -0.05128624 0.02763787
## INC 0.01607022 -0.01033709 -0.20428171 -0.97872564
## ROAD -0.06166301 -0.98628452 -0.14772101 0.04023709Here, the item Standard deviations contains the (ordered) values
\[
SD[\boldsymbol{\gamma}_j^T\boldsymbol{X}] = \sqrt{Var[\boldsymbol{\gamma}_j^T\boldsymbol{X}]} = \sqrt{\lambda_j},
\]
and the item Rotation is the same as \(\boldsymbol{\Gamma}\). Both items can be extracted directly from the prcomp object (here: fuel.pr) through the components \$sdev and \$rot, respectively. Hence, we get the \(\lambda_j\) via
fuel.pr$sdev^2## [1] 30.9258227 12.3980734 0.5598424 0.3093942which is immediately confirmed to be the same as
eigen(var(fuel))$values## [1] 30.9258227 12.3980734 0.5598424 0.3093942and the proportions of variance explained are given by
fuel.pr$sdev^2/ sum(fuel.pr$sdev^2)## [1] 0.699787972 0.280542985 0.012668086 0.007000957One may also want to look at the built-in R summary output.
summary(fuel.pr)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 5.5611 3.5211 0.74823 0.5562
## Proportion of Variance 0.6998 0.2805 0.01267 0.0070
## Cumulative Proportion 0.6998 0.9803 0.99300 1.0000We would conclude from the scree plot and the summary output that \(d=2\) principal components capture the essential information provided by the data cloud.
7.4 Scaling
If the variables operate on different scales/units, the decomposition of variance may not be meaningful as it depends on the units chosen. It is a problem for the fuel data as all units are different, and our decomposition of variance may just reflect which variables are recorded on smaller or larger units! Assume, for instance, that INC had been measured in \(\$\) (instead of \(1000\$\)), or the proportions DLIC had been measured on the interval [0,1] (rather than in percent). This would have had a massive impact on \(\boldsymbol{\Sigma}\) in the corresponding directions, and, hence, on the principal components found for this data set (Try this!).
To avoid problems of this type, standardize all variables by dividing through their standard deviation, i.e. set \(\tilde{X}_j= X_j/SD(X_j)\), and then apply PCA to \(\tilde{\boldsymbol{X}}= (\tilde{X}_1, \ldots, \tilde{X}_q)^T\). Also, observe that for eigenvalues \(\lambda_1, \ldots, \lambda_q\) of the variance matrix of \(\tilde{\boldsymbol{X}}\), \[ \lambda_1+\ldots +\lambda_q= \ldots = \mbox{Tr}(Var[\tilde{\boldsymbol{X}}])= 1+ \ldots+ 1= q \] i.e. the eigenvalues of the correlation matrix always add up to the dimension of the random vector.
Practical Example - Scaling for fuel data
fuel.pr1 <- prcomp(fuel, scale=TRUE)
fuel.pr1## Standard deviations (1, .., p=4):
## [1] 1.2567608 1.0695586 0.9578833 0.5992131
##
## Rotation (n x k) = (4 x 4):
## PC1 PC2 PC3 PC4
## TAX 0.7101892 -0.08133737 0.1902941 0.6729069
## DLIC -0.3185570 -0.68187354 -0.5219691 0.4013952
## INC -0.1241055 -0.61747664 0.7603559 -0.1586799
## ROAD -0.6154271 0.38360828 0.3364450 0.6007486plot(fuel.pr1)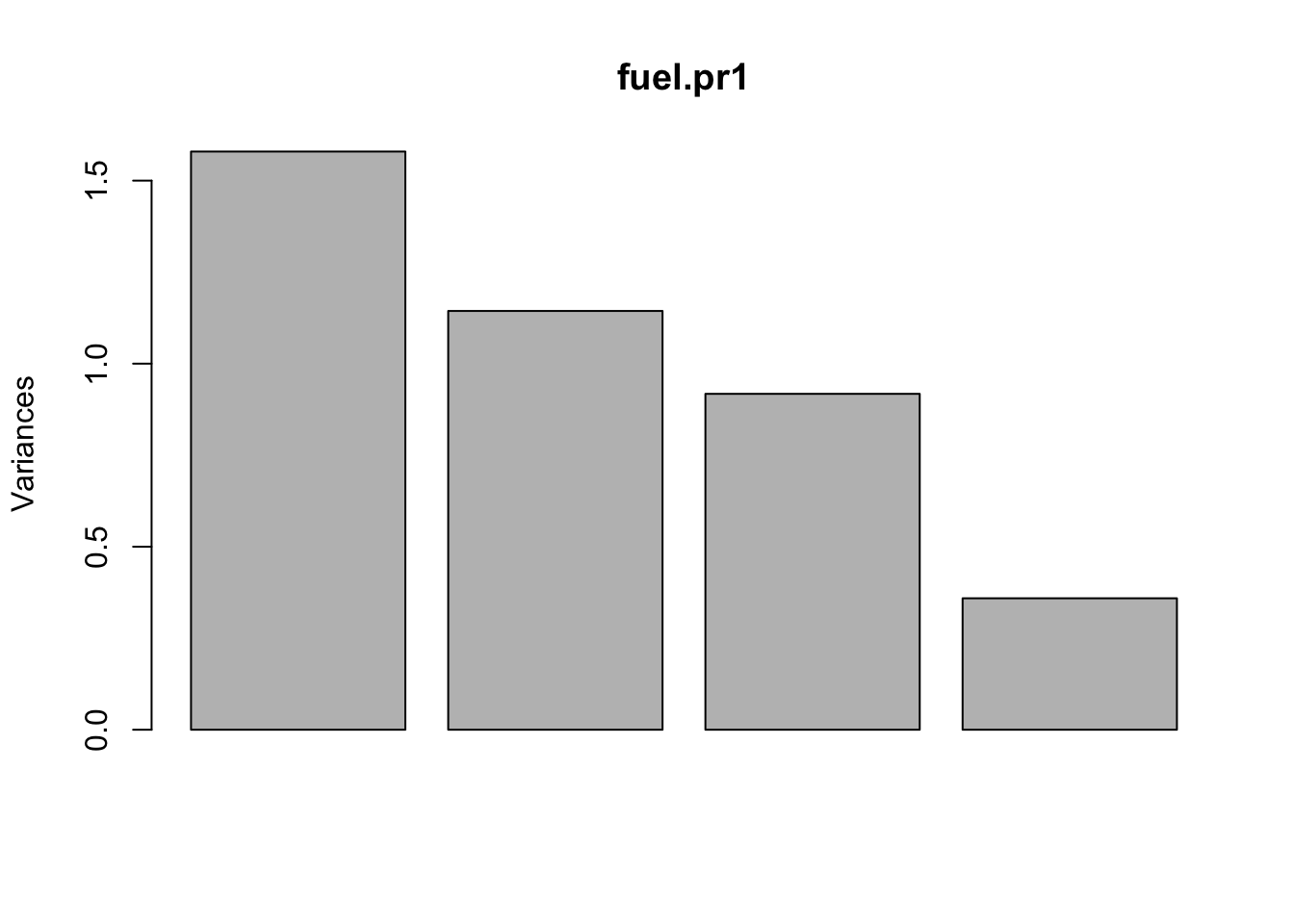
sum(fuel.pr1$sdev^2)## [1] 4Note carefully that the values given at Standard deviations: are \(SD(\boldsymbol{\gamma}_j^T\tilde{\boldsymbol{X}})\); NOT \(SD(\tilde{X}_j)\). We also verify that \(\sum \lambda_j = 4\).
7.5 Data compression (Dimension reduction)
Let \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_n\) be sampled from the \(q-\) dim. r.v. \(X \sim (\boldsymbol{m}, \boldsymbol{\Sigma})\), yielding a data matrix (or ‘data frame’) \[ \left(\begin{array}{c} \boldsymbol{x}_{1}^T \\ \vdots \\ \boldsymbol{x}_{n}^T \end{array}\right) = \left(\begin{array}{ccc} x_{11} &\cdots & x_{1q}\\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{nq} \end{array}\right) \in \mathbb{R}^{n \times q}. \]
Assume a PCA has been carried out as usual, yielding \(\boldsymbol{m}\), \(\boldsymbol{\Sigma}\), \(\boldsymbol{\gamma}_1, \ldots \boldsymbol{\gamma}_q\), \(\lambda_1, \ldots \lambda_q\). Suppose we wish to compress the data towards a smaller dimension \(d \le q\) (for instance, in order to have fewer predictors or save storage space and computing time, etc.). How to choose \(d\)? There are different conventions (all more or less heuristic) on how to extract such information from a scree plot (of \(\lambda_j\) versus \(j\)), but the general idea is the following: The scree plot usually can be split into a left–hand part (which contains the components which capture significant variation in the data) and a right–hand part (which just contains noise or “scree”). So, one cuts off where this breakpoint, also called “knee”, is deemed to be situated.
How does the actual compression step work? Data compression means projection. We project all data points \(\boldsymbol{x}_i\), \(i=1, \ldots, n\) onto the \(d-\)dim subspace spanned by the \(d\) largest principal components: \[ f:\mathbb{R}^q\longrightarrow \mathbb{R}^d, \, \boldsymbol{x}_i \mapsto (\boldsymbol{\gamma}_1, \cdots, \boldsymbol{\gamma}_d)^T(\boldsymbol{x}_i - \boldsymbol{m}), \quad i=1, \ldots, n \] (the \(f(\boldsymbol{x}_i)\equiv \boldsymbol{t}_i\) are called principal component scores).
If desired, scores can be mapped back to the data space: \[ g:\mathbb{R}^d \longrightarrow \mathbb{R}^q, \, \boldsymbol{t}_i \mapsto \boldsymbol{m} +(\boldsymbol{\gamma}_1, \cdots, \boldsymbol{\gamma}_d)\boldsymbol{t}_i, \quad i=1, \ldots, n \] which leads to ‘reconstructed’ values \(\boldsymbol{r}_i\equiv (g \circ f)(\boldsymbol{x}_i)\). Obviously, the original data will not be exactly reconstructed (as we have dismissed some information), unless \(d=q\). In the latter case, using the orthogonality of \(\boldsymbol{\Gamma}\),
\[\begin{eqnarray*} (g \circ f)(\boldsymbol{x}_i) &=& g(f(\boldsymbol{x}_i)) = \boldsymbol{m}+ (\boldsymbol{\gamma}_1, \cdots, \boldsymbol{\gamma}_d)(\boldsymbol{\gamma}_1, \cdots, \boldsymbol{\gamma}_d)^T (\boldsymbol{x}_i- \boldsymbol{m}) \\ &=& \boldsymbol{m} + \boldsymbol{\Gamma}\boldsymbol{\Gamma}^T(\boldsymbol{x}_i - \boldsymbol{m})= \boldsymbol{m} + \boldsymbol{x}_i - \boldsymbol{m} = \boldsymbol{x}_i \end{eqnarray*}\]
The following R code implements the above procedure. We consider firstly just a single data point, and proceed with compression/reconstruction of the full fuel data set, each using \(d=2\), without scaling.
# Work firstly with a single observation. Say, case 1:
x1 <- fuel[1,]
mode(x1) # wrong data type: lists can't be used for computation ## [1] "list"x1<- as.numeric(x1)
mode(x1) # that does it.## [1] "numeric"m <- colMeans(fuel)
t1 <- t(fuel.pr$rot[,c(1,2)]) %*% (x1-m) # Score for case 1
r1 <- m+ fuel.pr$rot[,c(1,2)]%*% t1 # Reconstruction for case 1
x1## [1] 9.000 52.500 3.571 1.976t1## [,1]
## PC1 -4.370997
## PC2 3.997192r1## [,1]
## TAX 8.495976
## DLIC 52.462122
## INC 4.130271
## ROAD 1.892577plot(rbind(fuel,t(r1)), col=c(2, rep(1,47),3))# red=original, green=approx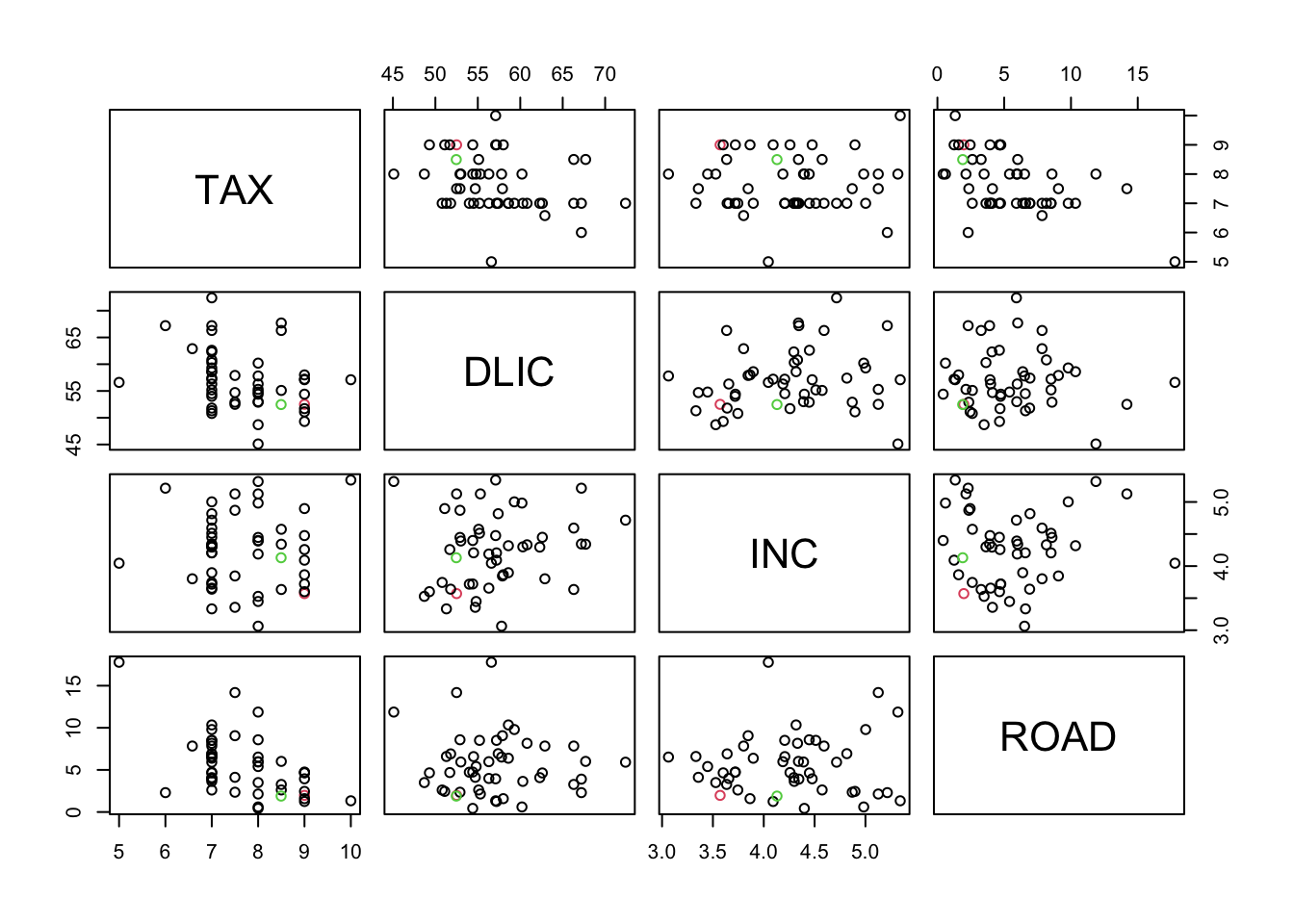
# For the full data matrix, we make use of the scores delivered by prcomp:
# fuel.pr$x # is the same as:
# t(fuel.pr$rot[,]) %*% (t(fuel)-m)
T <- t(fuel.pr$x[,c(1,2)]) # All scores
R <- t(m + fuel.pr$rot[,c(1,2)]%*% T) # All reconstructed values
plot(rbind(fuel, R), col=c(rep(1,48),rep(3,48)))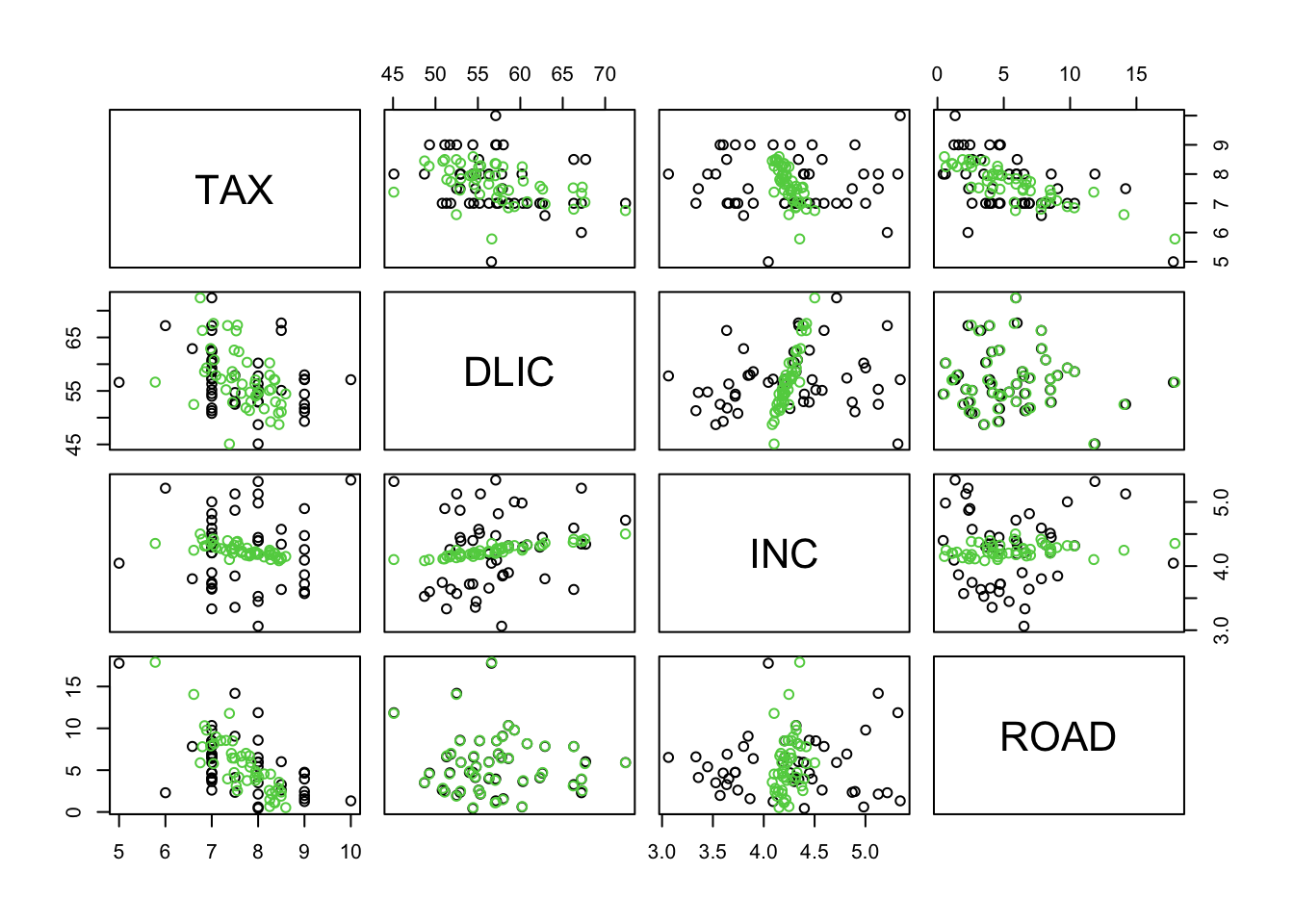
# black=original, green=approx
boxplot(fuel)
Obviously, PCA favors ROAD and DLIC which have the largest variance. Hence, when “compressing” the data we have essentially eliminated the “less variable” variables, TAX and INC. Note that the results would have changed dramatically if, for instance, INC would have been measured in \(\$\) (instead of \(1000\$\)).
To eliminate the effect of the units, we repeat the same analysis using scaled data.
s <- apply(fuel, 2, sd) # calculates the column standard deviations
fuel.s <- sweep(fuel, 2, s, "/") # divides all columns by their standard deviations
boxplot(fuel.s) 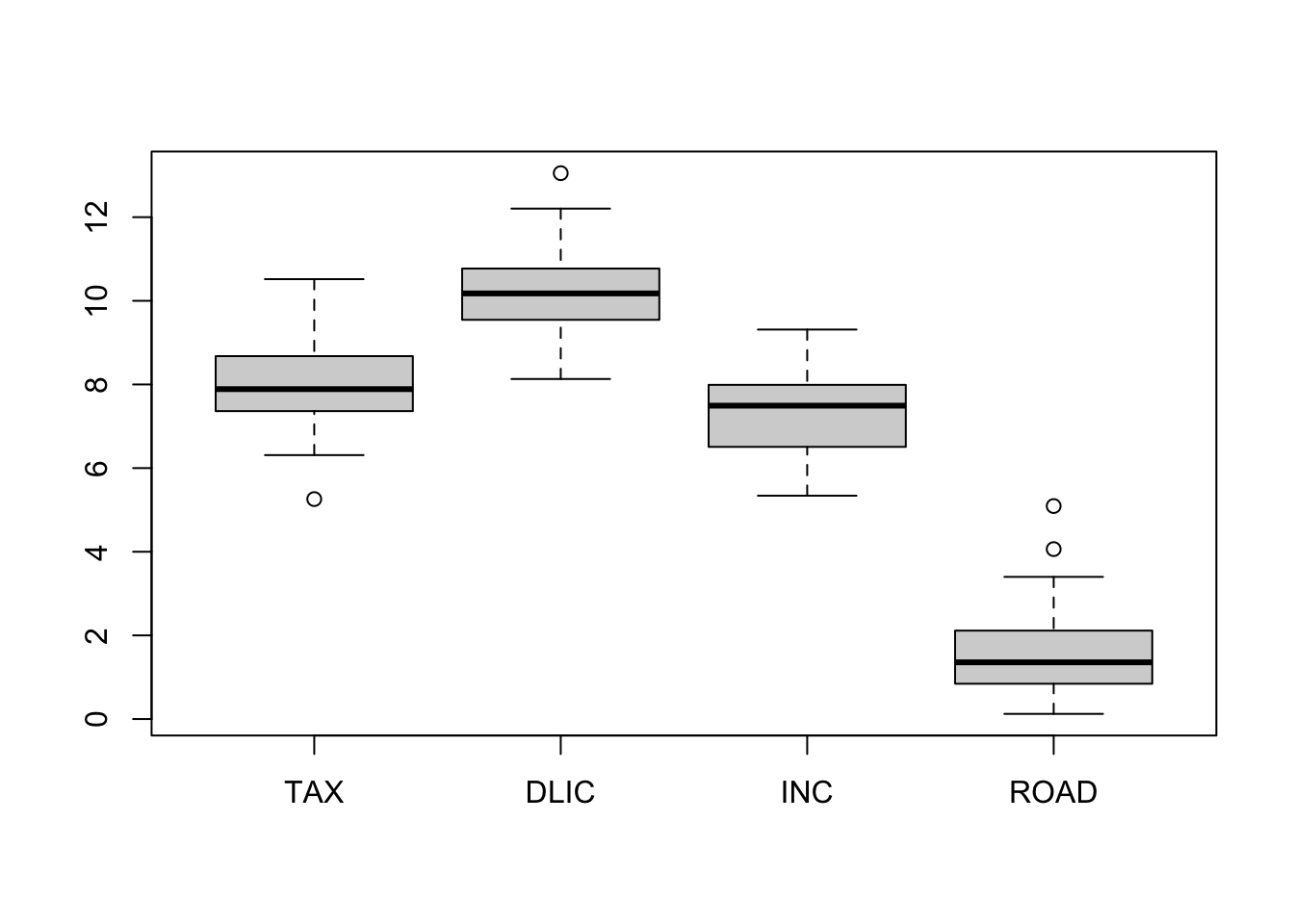
fuel.pr1 <- prcomp(fuel.s)
# (equivalent to fuel.pr1 in the example in previous section).
plot(fuel.pr1) # suggests d=3 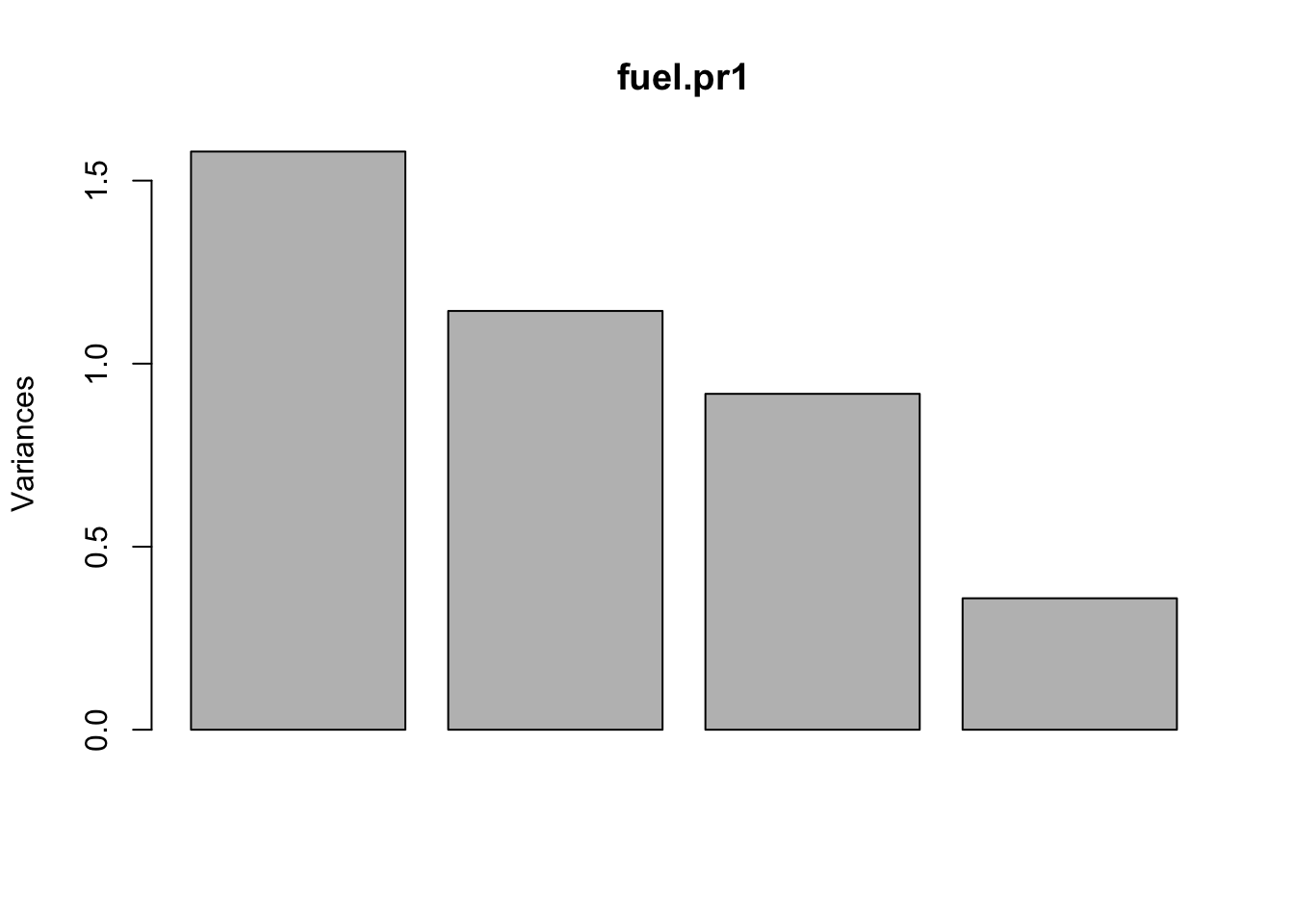
ms <- colMeans(fuel.s) # calculates means of scaled data set
Ts <- t(fuel.pr1$x[,c(1,2,3)]) # 3d-scores for scaled data
Rs <- t(ms + fuel.pr1$rot[,c(1,2,3)]%*% Ts) # Reconstructed scaled data
plot(rbind(fuel.s, Rs), col=c(rep(1,48),rep(3,48)))# black=original, green=approx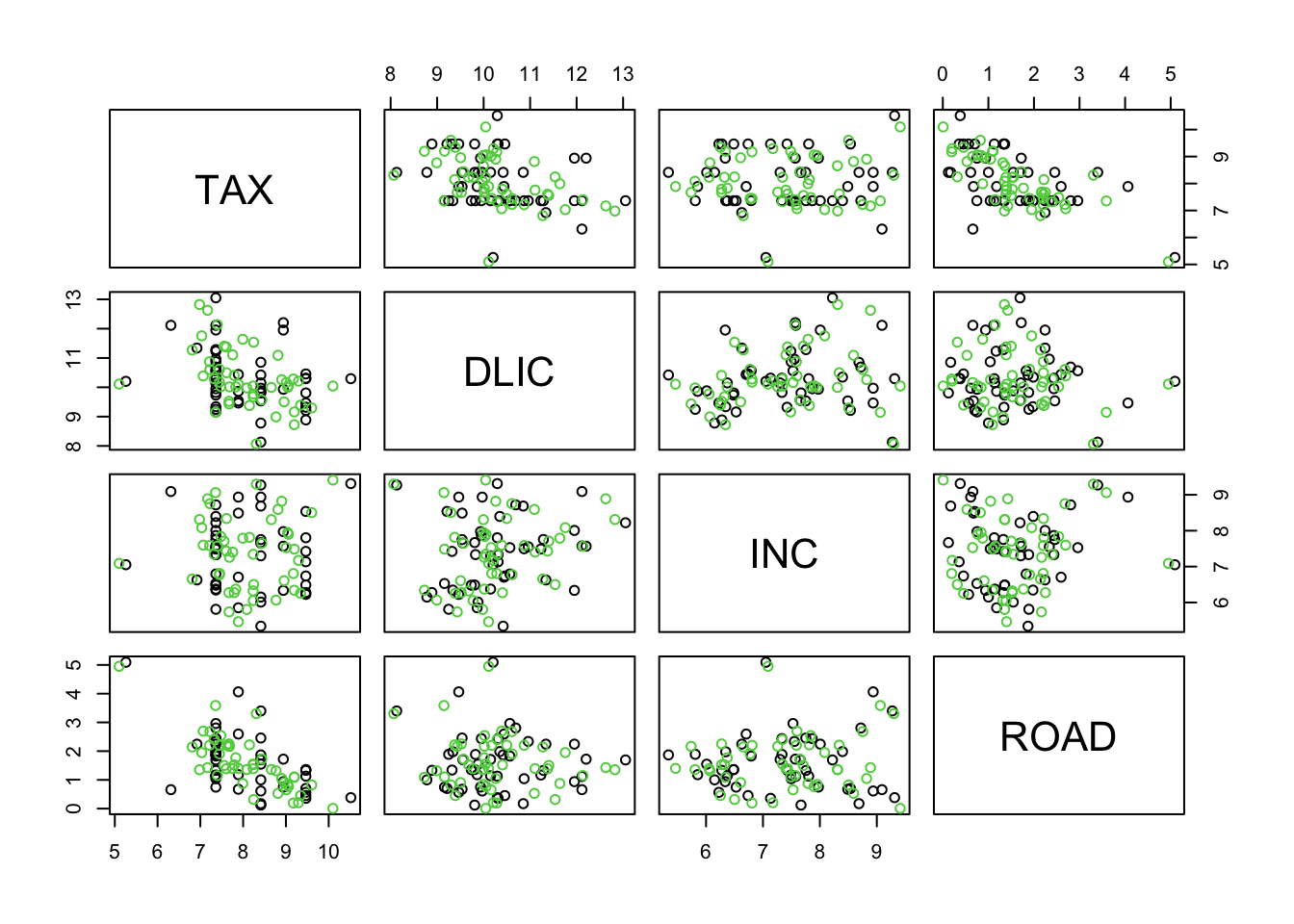
7.6 Principal Component Regression
Principal Component Regression
Consider a linear regression problem with the model form \[ y= \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_p x_p +\epsilon \] Assume that \(p\) is quite large, which may be impractical in practice. In such a case, may consider reducing the number of “predictors”, prior to regression, via PCA. That is instead of utilizing the \(p\) original predictors, this approach utilises \(d\) transformed variables (principal components) which are linear combinations of the original predictors, where \(d<p\), then fit a regression model using the principal components. This technique, which combines the worlds of unsupervised and supervised learning, is known as principal component regression (PCR).
Mathematically:
- Define \(d < p\) linear transformations \(Z_k, k = 1,...,d\) of \(X_1,X_2,\ldots,X_p\) as
\[Z_k= \sum_{j =1}^{p}\phi_{jk}X_j,
\]
when applying PCA, \(\phi_{1k},...,\phi_{pk}\) is simply the \(\boldsymbol{\gamma}_k\) obtained from eigen decomposition of the sample variance of data \(\boldsymbol{X}\). - Fit a linear regression model of the form \[y_i = \theta_0 + \sum_{k =1}^d \theta_k z_{ik}, \, i = 1,\ldots, n. \]
We have dimension reduction: Instead of estimating \(p+1\) coefficients we estimate \(d+1\)!
Interestingly, with some re-ordering we get: \[ \sum_{k =1}^d \theta_k z_{ik} = \sum_{k =1}^d \theta_k \left( \sum_{j =1}^{p}\phi_{jk}x_{ij}\right) = \sum_{j =1}^{p} \left(\sum_{k =1}^d \theta_k \phi_{jk}\right)x_{ij} = \sum_{j =1}^p \beta_j x_{ij} \]
The key idea is that often a small number of principal components suffice to explain most of the variability of the data, as well as the relationship with the response. In other words, we assume that the directions in which \(X_1,...,X_p\) show the most variation are the directions that are associated with Y. This assumption is not guaranteed, but it is often reasonable enough to give good results.
Another nice property of the new transformed variables (principal components) is that they are uncorrelated this would give a solution to the problem of multicollinearity.
How Many Components?
- Once again we have a tuning problem.
- In ridge and lasso the tuning parameter (\(\lambda\)) was continuous - in PCR the tuning parameter is the number of components (\(d\)), which is discrete.
- Some methods calculate the total variance of X explained as we add further components. When the incremental increase is negligible, we stop. One such popular method is the scree plot (we have seen it in the previous session.
- Alternatively, we can use (yes, you guessed it…) cross-validation!
What about Interpretability?
- One drawback of PCR is that it lacks interpretability, because the estimates \(\hat{\theta}_k\) for \(k = 1,\ldots, d\) are the coefficients of the principal components, which have no meaningful interpretation.
- Well, that is partially true, but there is one thing we can do: once we fit LS on the transformed variables we can use the transformation to obtain the corresponding estimates of the original predictors \[ \hat{\beta}_j = \sum_{k =1}^d \hat{\theta}_k \phi_{jk}, \] for \(j = 1,\ldots, p\)
- However, for \(d < p\) these will not correspond to the LS estimates of the full model. In fact, the PCR estimates get shrunk in a discrete step-wise fashion as \(d\) decreases (this is why PCR is still a shrinkage method).
PCR - a Summary
Advantages:
- Similar to ridge and lasso, it can result in improved predictive performance in comparison to Least Squares by resolving problems caused by multicollinearity and/or large \(p\).
- It is a simple two-step procedure which first reduces dimensionality from \(p+1\) to \(d+1\) and then utilizes LS.
Disadvantages:
- It does not perform feature selection.
- The issue of interpretability.
- It relies on the assumption that the directions in which the predictors show the most variation are the directions which are predictive of the response. This is not always the case. Sometimes, it is the last principal components which are associated with the response! Another dimension reduction method, Partial Least Squares, is more effective in such settings, but we do not have time in this course to cover this approach.
Final Comments:
- In general, PCR will tend to do well in cases when the first few principal components are sufficient to capture most of the variation in the predictors as well as the relationship with the response.
- We note that even though PCR provides a simple way to perform regression using \(d<p\) predictors, it is not a feature selection method. This is because each of the \(d\) principal components used in the regression is a linear combination of all \(p\) of the original features.
- In general, dimension-reduction based regression methods are not very popular nowadays, mainly due to the fact that they do not offer any significant advantage over penalised regression methods.
- However, PCA is a very important tool in unsupervised learning where it is used extensively in a variety of applications!
Practical Demonstration
For PCR, we will make use of the package pls, so we have to install this before first use by executing install.packages('pls'). The main command is called pcr(). The argument scale=TRUE standardises the columns of the predictor matrix, while argument validation = 'CV' picks the optimal number of principal components via cross-validation. The command summary() provides information on CV error and variance explained (RMSEP - Root Mean Squared Error (of Prediction)). Note that adjCV is an adjusted estimate of CV error accounting for bias. Under TRAINING, we can see the proportion of the variance of training data explained by the \(q\) largest PCs, \(q=1,...,p\).
library(pls) # for performing PCR##
## Attaching package: 'pls'## The following object is masked from 'package:stats':
##
## loadingslibrary(ISLR) # for Hitters dataset
set.seed(1)
pcr.fit = pcr( Salary ~ ., data = Hitters, scale = TRUE, validation = "CV" )
summary(pcr.fit)## Data: X dimension: 263 19
## Y dimension: 263 1
## Fit method: svdpc
## Number of components considered: 19
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 452 352.5 351.6 352.3 350.7 346.1 345.5
## adjCV 452 352.1 351.2 351.8 350.1 345.5 344.6
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 345.4 348.5 350.4 353.2 354.5 357.5 360.3
## adjCV 344.5 347.5 349.3 351.8 353.0 355.8 358.5
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 352.4 354.3 345.6 346.7 346.6 349.4
## adjCV 350.2 352.3 343.6 344.5 344.3 346.9
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps 8 comps
## X 38.31 60.16 70.84 79.03 84.29 88.63 92.26 94.96
## Salary 40.63 41.58 42.17 43.22 44.90 46.48 46.69 46.75
## 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps 15 comps
## X 96.28 97.26 97.98 98.65 99.15 99.47 99.75
## Salary 46.86 47.76 47.82 47.85 48.10 50.40 50.55
## 16 comps 17 comps 18 comps 19 comps
## X 99.89 99.97 99.99 100.00
## Salary 53.01 53.85 54.61 54.61We can use the command validationplot() to plot the validation error. The argument val.type = 'MSEP' specifies to select Mean Squared Error (of Prediction), other options are Root Mean Squared Error (of Prediction), RMSEP and \(R^2\); type ?validationplot for help.
validationplot( pcr.fit, val.type = 'MSEP' )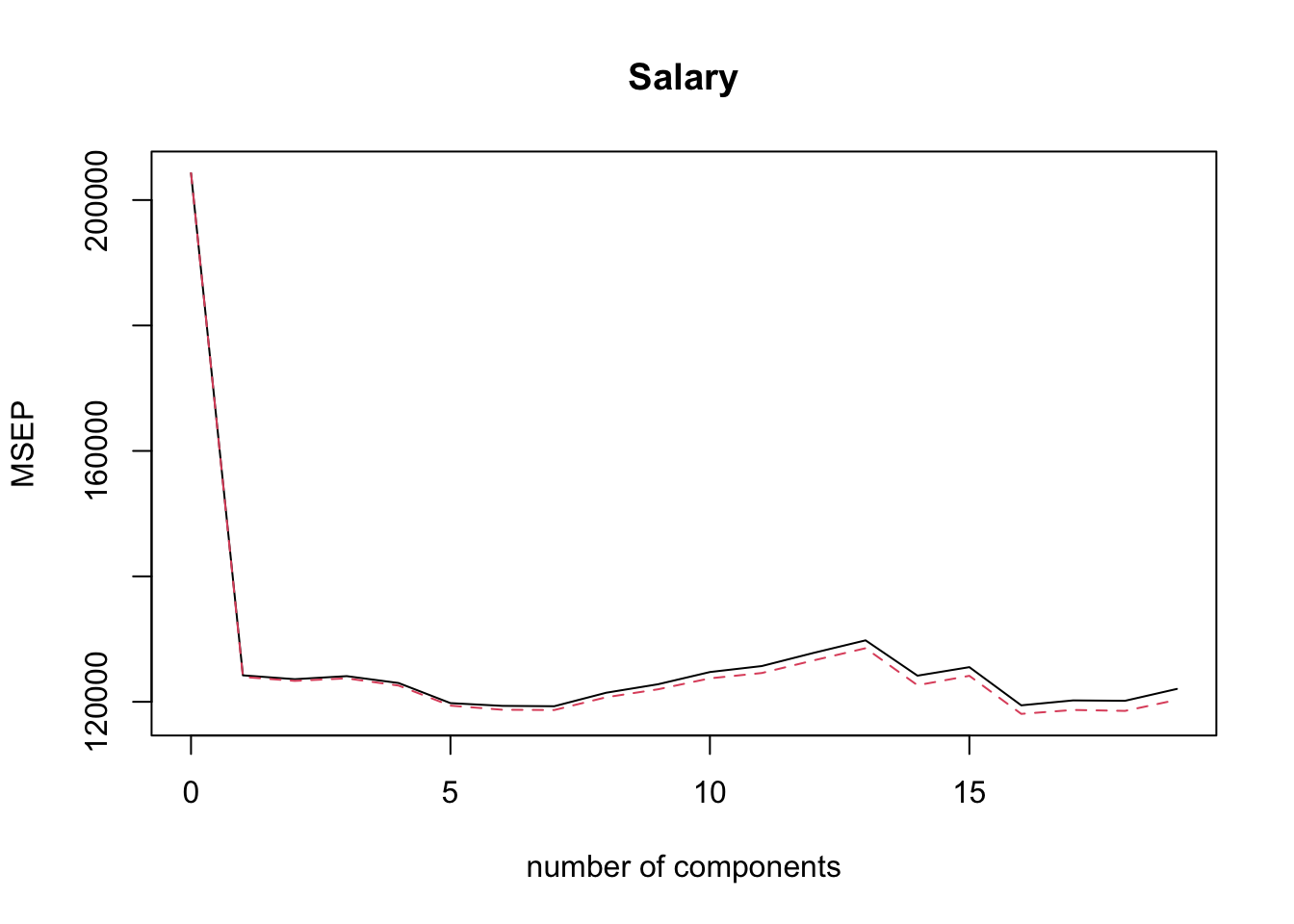
From the plot above it is not obvious which PCR model minimises the CV error. We would like to extract this information automatically, but it turns out that is not so easy with pcr()! One way to do this is via the code below (try to understand what it does!).
min.pcr = which.min( MSEP( pcr.fit )$val[1,1, ] ) - 1
min.pcr## 7 comps
## 7So, it is the model with 7 principal components that minimises CV. Now that we know which model it is we can find the corresponding estimates in terms of the original \(\hat{\beta}\)’s using the command coef() we have used before. Also we can generate predictions via predict() (below the first 6 predictions are displayed).
coef(pcr.fit, ncomp = min.pcr)## , , 7 comps
##
## Salary
## AtBat 27.005477
## Hits 28.531195
## HmRun 4.031036
## Runs 29.464202
## RBI 18.974255
## Walks 47.658639
## Years 24.125975
## CAtBat 30.831690
## CHits 32.111585
## CHmRun 21.811584
## CRuns 34.054133
## CRBI 28.901388
## CWalks 37.990794
## LeagueN 9.021954
## DivisionW -66.069150
## PutOuts 74.483241
## Assists -3.654576
## Errors -6.004836
## NewLeagueN 11.401041head( predict( pcr.fit, ncomp = min.pcr ) )## , , 7 comps
##
## Salary
## -Alan Ashby 568.7940
## -Alvin Davis 670.3840
## -Andre Dawson 921.6077
## -Andres Galarraga 495.8124
## -Alfredo Griffin 560.3198
## -Al Newman 135.5378Extension: Regularisation Paths for PCR
What about regularisation paths with pcr()? This is again tricky because there is no built-in command. The below piece of code can be used to produce regularisation paths. The regression coefficients from all models using 1 up to 19 principal components are stored in pcr.fit$coefficients, but this is an object of class list which is not very convenient to work with. Therefore, we create a matrix called coef.mat which has 19 rows and 19 columns. We then store the coefficients in pcr.fit$coefficients to the columns of coef.mat, starting from the model that has 1 principal component, using a for loop. We then use plot() to plot the path of the first row of coef.mat, followed by a for a for loop calling the command lines() to superimpose the paths of the rest of the rows of coef.mat.
coef.mat = matrix(NA, 19, 19)
for(i in 1:19){
coef.mat[,i] = pcr.fit$coefficients[,,i]
}
plot(coef.mat[1,], type = 'l', ylab = 'Coefficients',
xlab = 'Number of components', ylim = c(min(coef.mat), max(coef.mat)))
for(i in 2:19){
lines(coef.mat[i,], col = i)
}
abline(v = min.pcr, lty = 3)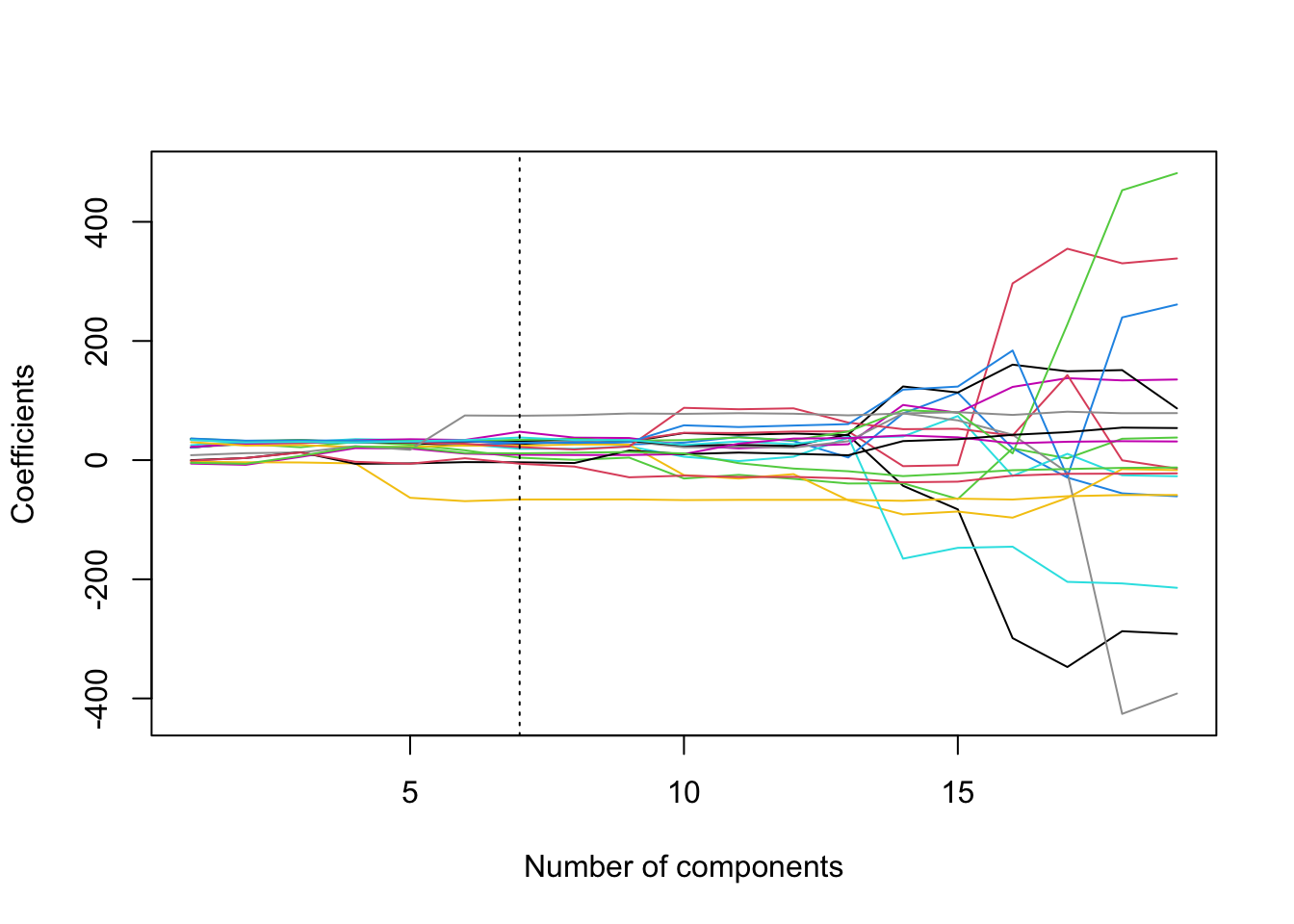
We can see from the plot the somewhat strange way in which PCR regularises the coefficients.
Scree plots
Finally, consider here that we used the in-built CV within the function pcr to select the number of coefficients. We can, however, use the visual aid of a scree plot to help us decide on the appropriate number of principal components. This amounts to plotting as a bar chart the cumulative proportion of variance attributed to the first \(q\) principal components, such as was shown in the X row of the % variance explained matrix when we called summary(pcr.fit). This information is a little difficult to extract from the summary object, however, so we construct the scree plot manually as shown below (try to understand what is happening):
PVE <- rep(NA,19)
for(i in 1:19){ PVE[i]<- sum(pcr.fit$Xvar[1:i])/pcr.fit$Xtotvar }
barplot( PVE, names.arg = 1:19, main = "scree plot",
xlab = "number of PCs",
ylab = "proportion of variance explained" )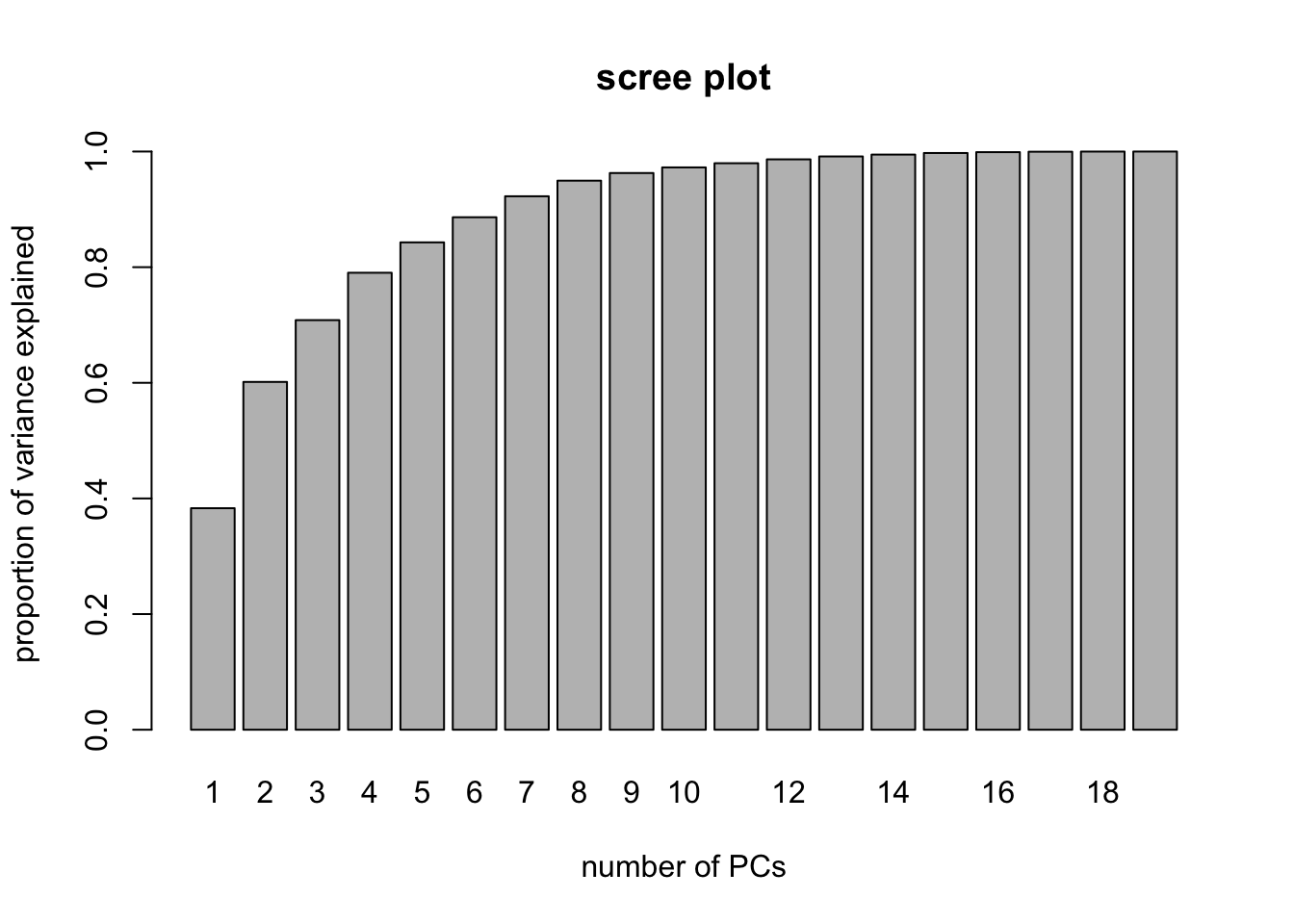
We may, for example, decide that we need the number of principal components required to explain 95% of the variance in the predictors. In this case, we could look at the scree plot and the output from summary(pcr.fit) to elicit that we need to select the first 9 principal components in order to explain 95% of the variance in X.