| ID | Musician |
|---|---|
| 1 | Taylor Swift |
| 2 | Drake |
| 3 | Taylor Swift |
| 4 | Drake |
| 5 | Drake |
| 6 | Drake |
18 Chi-square
18.1 Background
Until now, we have largely dealt with continuous variables or some combination of continuous and categorical variables at the same time. We haven’t ran into solely categorical (i.e., nominal) variables only. Fortunately, the Chi-square (pronounced “kai”) is a statistic we can use to help us. Under the Chi-square, we can test for independence in categorical variables.
The Chi-square is a ubiquitous statistic that we have used previously; you just didn’t know it. Please see the section on the F-distribution or here for more details. We will first explore the Chi-square Goodness of Fit and then the Chi-square Test of Independnece.
18.2 Chi-Square Goodness of Fit
18.2.1 Our Research
Let’s explore who is Grenfell students’ favourite musician. I think it is Taylor Swift (\(H_A\)). The null hypothesis is that Grenfell students like all artists equally (\(H_0\)).
18.2.2 Our Data
To test this, I wait outside the library one day and ask students to write down their favorite music artist. I recruit 70 individuals. These are the results; note: each person represents one row. They have an ID and their listed artist:
To easily summarize the results, let’s create a contingency table:
| Artist | Frequency |
|---|---|
| Drake | 18 |
| Harry Style | 4 |
| Taylor Swift | 53 |
These table are sometimes called cross tabulations or crosstabs (e.g., SPSS). The table displays the frequency of each level of the variable. Out of the 70 people we recruited, 18 said Drake was their favorite, 4 said Harry Styles, and 53 said Taylor Swift.
We can test our research question and hypothesis (\(H_0=\) all artists liked equally) using a ‘goodness-of-fit’ test. The null hypothesis for this test assumes that an equal frequency for each level of the variable.
18.2.3 Our Analysis
For one categorical variable, chi-square is defines as:
\(\chi^2=\sum^n_{i=1}\frac{(O_i-E_i)^2}{E_i}\)
where:
- \(O_i\) is the observed frequency for cell \(i\)
- \(E_i\) is the expected frequency for cell \(i\)
We observed the following:
Drake Harry Style Taylor Swift
18 4 53 However, under the null hypothesis, we expected an equal distribution across levels. Thus, we would expect under \(H_0\) that each group would have \(\frac{n=75}{3 groups}=25\).
Now we can calculate the Chi-square statistic. We subsract the observed from the expected, square the result, and divide one more for teh expected. We then sum each:
\(\chi^2=\frac{(18-25)^2}{25}+\frac{(4-25)^2}{25}+\frac{(53-25)^2}{25}\)
\(=1.96+17.64+31.36=50.96\)
The resulting \(\chi^2\) has groups - 1 degrees of freedom:
\(df=k-1=3-1=2\)
We can then compare our observed Chi-square statistic to the chi-square distribution to make a conclusion about the results. Note, this is simply getting a p-value.
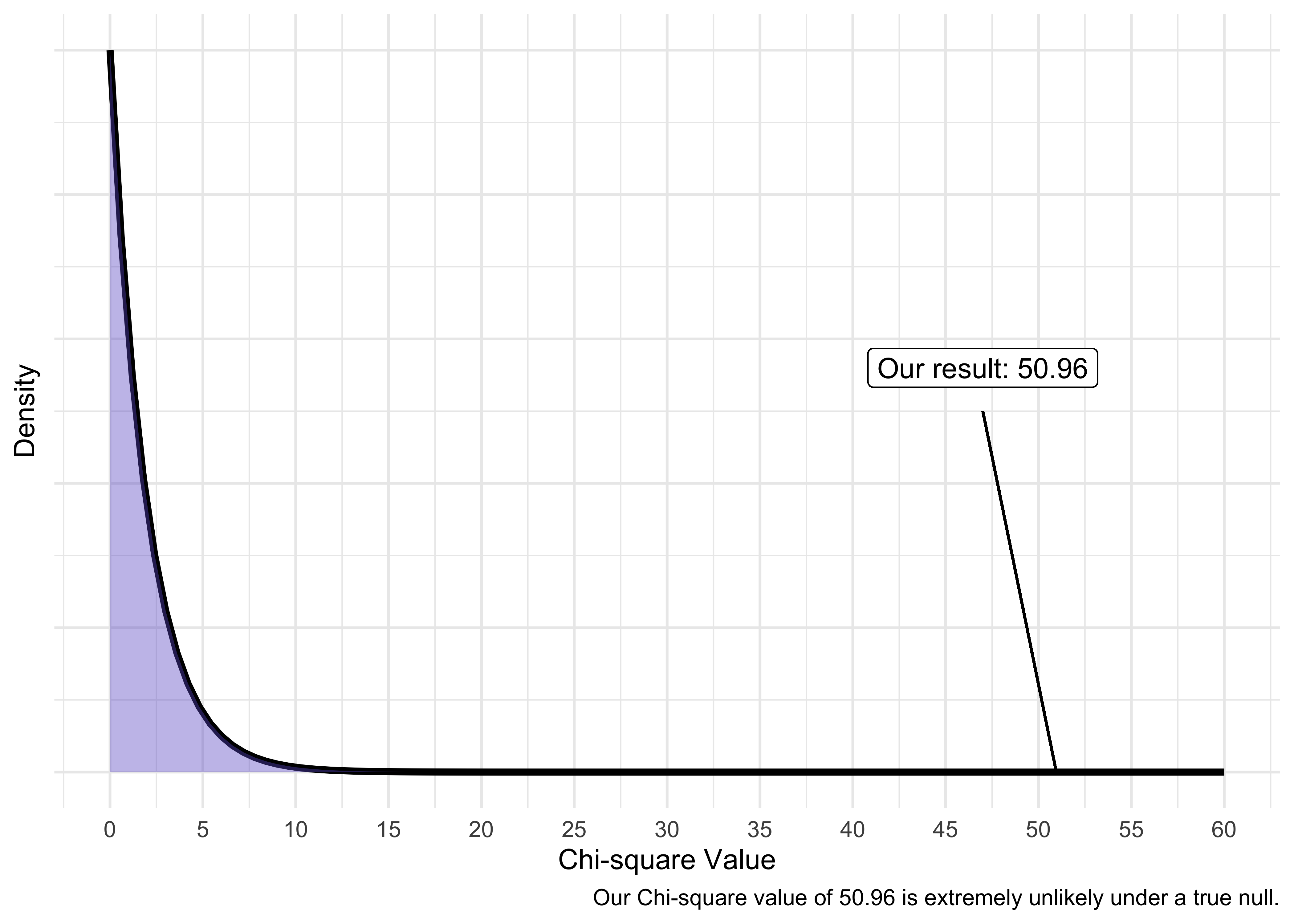
18.2.4 Our Results
Our formal analysis would yield the following results in R.
Chi-squared test for given probabilities
data: c(18, 4, 53)
X-squared = 50.96, df = 2, p-value = 8.594e-12Thus, we would reject the null hypothesis. We could write it up as the following:
A chi-square goodness-of-fit test was conducted to determine which musicians are preferred at Grenfell. The results suggest that our sample is unlikely given a true null hypothesis that musicians are equally preferred, \(\chi^2(2)=50.96, p<.001.\)
In previous analyses, we used post-hoc to determine where the differences lie (e.g., Tukey’s test for ANOVA). We can do a similar analysis for chi-square to determine if a certain musician is exspecially preferred or disliked.
18.3 Residuals and Post-Hoc Analysis
We will calculate residuals to help us with our post-hoc analyses.
18.3.0.1 Raw Residuals
First, raw residuals are simply \(O_i-E_i\). These may provide a quick number to assess residuals, but do not adjust based on relative magnitude of differences. For us, the unstandardized residuals are:
| Musician | Unstandardized Residual |
|---|---|
| Drake | -7 |
| Harry Style | -21 |
| Taylor Swift | 28 |
Interpreting these is more difficult than the following types of residuals because these residuals must be interpreted in the context of the sample size. If we sample 10,000 people, these residuals may be considered small. If we sampled 50 people, they may be considered large.
18.3.0.2 Pearson’s Residual
Second, Pearson’s residuals allow us to determine which cells are most unlikely while considered the relative differences in observed and expected. Typically, residuals bigger than \(|2|\) (i.e., the absolute value of 2) are considered to deviate substantially from the expected counts. Pearson residuals are calculated using:
- \(res=\frac{O_i-E_i}{\sqrt{E_i}}\)
For our data, the residuals are:
- Drake: \(res_{D}=\frac{(18-25)}{\sqrt25} = -1.40\)
- Harry Styles: \(res_{HS}=\frac{(4-25)}{\sqrt25} = -4.20\)
- Taylor Swift: \(res_{TS}=\frac{(53-25)}{\sqrt25} = 5.60\)
We can interpret these as Drake and Harry Styles were favored less than expected, while Taylor Swift was more than expected. However, looking at the magnitudes, it would seem that only Harry and Taylor occurred differently than expected. Specifically, Harry seemed to be favoured less likely than expected and Taylor seemed to be favoured more likely than expected under a true null hypothesis.
18.3.0.3 Standardized Residuals
Standardized residuals (or sometimes referred to as adjusted standardized residuals) take into account the row and column totals. I’m not concerned whether you know the formula. R can calculate these for us using the chi.residuals() function from the questionr package. Here is the results from R for the standardized residuals:
| Musician | Adjusted Residual |
|---|---|
| Drake | -1.71 |
| Harry Style | -5.14 |
| Taylor Swift | 6.86 |
We can interpret these using the same \(|2|\) threshold as above. As such, we could add to our results:
A chi-square goodness-of-fit test was conducted to determine which musicians are preferred at Grenfell. The results suggest that our sample is unlikely given a true null hypothesis that musicians are equally preferred, \(\chi^2(2)=50.96, p<.001\).
Specifically, people seemed to favour Taylor Swift more than expected (Pearson’s residual = 5.60) and prefer Harry Style less than expected (Pearson’s residual = -4.20).
18.3.1 Multiple comparisons and residuals
Why do we use a 2 for a residual threshold? The chi-square residuals represent z-scores from a normal distribution. Using a z-score of 1.96 or greater (one both tails) represents the extreme 5% of the distribution. We rounded to 2 for convenience. Thus, we are looking for the extreme 5% of values from a normal distribution. This is visualized as:

However, given you knowledge about multiple comparisons, assessing the size of multiple residuals may induce a type 1 error. As such, some people suggest dividing your \(\alpha\) by the number of cells for which you are calculating the residuals – or, at least, the ones you will be interpreting. You can then use this new \(alpha\) to get an associated z-score and cut-off. For us:
- \(\alpha=\frac{.05}{3}=.0167\)
This new \(\alpha\) aligns with with a z-score of 2.39 and, thus, represents the extreme 16.7% of values. This is what we could compare our residuals with. We can, again, visualize this:

[Here is a useful reference about residuals.](https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1269&context=pare](https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1269&context=pare).
Here is a website that will convert alpha to an associated z-score.
18.4 Chi-square Test of Independence (TOI)
In the above examples, we had one variable. Often in research we are dealing with more than one variable. We are in luck. The Chi-square Test of Independence (TOI) test is a logical extension to what we have already done and used in many research contexts. Luckily, the calculations are similar. The TOI will compare the association between two or more categorical/nominal variables.
18.4.1 Our Data
You run a randomized trial and randomly assign participants to the placebo or treatment group. You can test if men and women were randomly assigned to each experimental condition. Your data is:
| ID | Sex | Group |
|---|---|---|
| 1 | Male | Treatment |
| 2 | Female | Treatment |
| 3 | Male | Treatment |
| 4 | Female | Placebo |
| 5 | Male | Placebo |
| 6 | Female | Placebo |
It’s useful to put this data into a continency table:
Placebo Treatment
Female 7 13
Male 6 14And what might be more helpful is to also put row, columns and total counts, which we will use in our analyses:
| Placebo (j=1) | Treatment (j=2) | ||
|---|---|---|---|
| Female (i=1) | 7 | 13 | Row total: 20 |
| Male (i=2) | 6 | 14 | Row total: 20 |
| Column total: 13 | Column total: 27 | Total sample size: 40 |
18.4.2 Our Analyses
For 2+ variables, Chi-square is defined as:
\(\chi^2=\sum^n_{i=1, j=1}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\)
where:
- i is the row number
- j is the column number
- \(O_{ij}\) is the observed frequency
- \(E_{ij}\) is the expected frequency and
- \(E_{ij}=\frac{n_{row}\times n_{col}}{N}\)
Note that for the expected value we need the row, column, and table frequencies. Let’s calculate the expected value for the cell in row 1 (\(i=1\)), column 1 (\(j=1\)).
\(E_{11}=\frac{13 \times 20}{40}=6.5\)
Try to calculate the expected value for cell \(i=2\), \(j=2\) before proceeding.
The expected value of \(2,2\) is: \(E_{2,2}=\frac{27\times20}{40}=13.5\)
Here are the observed and expected (in brackets) values for the complete table:
| Placebo (j=1) | Treatment (j=2) | ||
|---|---|---|---|
| Female (i=1) | 7 (6.5) | 13 (13.5) | Row total: 20 |
| Male (i=2) | 6 (6.5) | 14 (13.5) | Row total: 20 |
| Column total: 13 | Column total: 27 | Total sample size: 40 |
We can now compute a Chi-square the same way using \(df=(n_{row}-1) \times (n_{col}-1)\) degrees of freedom!
\(\chi^2=\frac{(7-6.5)^2}{6.5}+\frac{(6-6.5)^2}{6.5}+\frac{(13-13.5)^2}{13.5}+\frac{(14-13.5)^2}{13.5}=0.114\)
\(df=(n_{row}-1) \times (n_{col}-1)=(2-1)\times(2-1)=1\times1=1\)
We are more likely to use statistical software, such as R, for these analyses:
Cell Contents
|-------------------------|
| Count |
| Expected Values |
| Chi-square contribution |
| Std Residual |
|-------------------------|
Total Observations in Table: 40
|
| Placebo | Treatment | Row Total |
-------------|-----------|-----------|-----------|
Female | 7 | 13 | 20 |
| 6.500 | 13.500 | |
| 0.038 | 0.019 | |
| 0.196 | -0.136 | |
-------------|-----------|-----------|-----------|
Male | 6 | 14 | 20 |
| 6.500 | 13.500 | |
| 0.038 | 0.019 | |
| -0.196 | 0.136 | |
-------------|-----------|-----------|-----------|
Column Total | 13 | 27 | 40 |
-------------|-----------|-----------|-----------|
Statistics for All Table Factors
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 0.1139601 d.f. = 1 p = 0.7356799
Pearson's Chi-squared test with Yates' continuity correction
------------------------------------------------------------
Chi^2 = 0 d.f. = 1 p = 1
Minimum expected frequency: 6.5 18.4.3 Our Effect Size - Cramer’s V
Cramer’s V is the typical effect size used for a Chi-square. It can be calculated as:
\(V=\sqrt{\frac{\chi^2/n}{min(r-1, c-1)}}\)
So, in our above example, \(V=\sqrt{\frac{0.114/40}{1}}=\sqrt{0.0029}=.05\)
Although I am not a fan of pre-determined cut-offs for effect sizes, the standard cut-offs used in the literature are:
- .1 - Small
- .3 - Med
- .5 - Large
18.4.4 Our Results
There was not a statistically significant association between the sex and randomization into the placebo versus treatment group, \(\chi^2=0.114, p=.736, V=.05\).
18.4.5 Our Assumptions
There are two major assumptions we will consider relevant to the Chi-square test.
- Independence of observations
Each observation in a Chi-square test must be independent of all others. For example, in our first example using favourite musicians, we could not two of each individuals favourite musician, because these two observations would be correlated. Someone who like Taylor Swift is probably going to prefer similar pop artist, whereas someone who likes ACDC is more probably going to prefer similar rock artists.
There are options when dealing with correlated observations or repeated measures data. It is beyond the scope of this course, but additional details can be found here (McNemar’s test).
- Expected frequencies greater than 5
The results are unreliable when some cells have expected frequency counts less than 5. You can likely understand how this is linked to sample size. Some say that for larger tables no more than 20% of cells having lower than 5 for their expected frequencies.
18.5 Practice
You are researching whether certain diagnoses are more prevalent in certain health authorities in NL. You are interested in the potential diagnoses for children in Western and Eastern Health. You review the 1,000 health records from 2022 (250 from Western and 750) and gather the following data:
| Anxiety | Depression | None | |
|---|---|---|---|
| Eastern | 52 | 71 | 127 |
| Western | 290 | 73 | 387 |
By hand or statistical software, calculate the expected frequencies, Chi-square, df, and Cramer’s V. Use this website to get the exact p-value.
Cell Contents
|-------------------------|
| Count |
| Expected Values |
| Chi-square contribution |
|-------------------------|
Total Observations in Table: 1000
|
| Anxiety | Depression | None | Row Total |
-------------|------------|------------|------------|------------|
Eastern | 52 | 71 | 127 | 250 |
| 85.500 | 36.000 | 128.500 | |
| 13.126 | 34.028 | 0.018 | |
-------------|------------|------------|------------|------------|
Western | 290 | 73 | 387 | 750 |
| 256.500 | 108.000 | 385.500 | |
| 4.375 | 11.343 | 0.006 | |
-------------|------------|------------|------------|------------|
Column Total | 342 | 144 | 514 | 1000 |
-------------|------------|------------|------------|------------|
Statistics for All Table Factors
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 62.89469 d.f. = 2 p = 2.200854e-14
Minimum expected frequency: 36 Cramer’s V
\(V=\sqrt{\frac{\chi^2/n}{min(r-1, c-1)}}\)
Therefore:
\(V=\sqrt{\frac{62.89469/1000}{1}}=\sqrt{0.063}=0.251\)