11.14 Lab1

We start with a simple dataset in Table 11.4 that involves 3 variables (Y = trust, D = threat, X = education) measured for three individuals (units) at three time points (resulting in 3 observations per unit and 15 observations in total).

data <- structure(list(
name = c("Brittany", "Ethan", "Kyle", "Jacob", "Jessica"), 
trust.2006 = c(4, 5, 0, 5, 7), 
trust.2007 = c(4, 6, 7, 3, 9), 
trust.2008 = c(2, 4, 5, 6, 4), 
threat.2006 = c(0,1, 0, 0, 1), 
threat.2007 = c(0, 0, 1, 1, 0), 
threat.2008 = c(1, 0, 0, 1, 0), 
education.2006 = c(0, 3, 1, 2, 0), 
education.2007 = c(0, 3, 1, 2, 0), 
education.2008 = c(0, 3, 1, 2, 0)), 
row.names = c(NA, 
-5L), class = c("tbl_df", "tbl", "data.frame"))

Table 11.4: Data for 3 variables across time points (cut off)
name	trust.2006	trust.2007	trust.2008	threat.2006	threat.2007	threat.2008	education.2006	education.2007	education.2008
Brittany	4	4	2	0	0	1	0	0	0
Ethan	5	6	4	1	0	0	3	3	3
Kyle	0	7	5	0	1	0	1	1	1
Jacob	5	3	6	0	1	1	2	2	2
Jessica	7	9	4	1	0	0	0	0	0

We convert this dataset to long format in Table 11.5. That’s what we generally do for FD or FE models. In Table 11.5 treated observations are coloured red, control observations are coloured blue.

data <- data %>% pivot_longer(-name, names_to = "variable", values_to = "value") %>%
      separate(col = "variable", into = c("variable", "time"), sep = "\\.") %>% 
      pivot_wider(names_from = variable, values_from = value) 
data <- data %>% mutate(time = as.numeric(time), # Converting time variable
                        unit = as.numeric(factor(name))) %>% # Add unit index
                        dplyr::select(name, unit, time, everything()) # Reorder variables

Table 11.5: Toy data in long format
name	unit	time	trust	threat	education
Brittany	1	2006	4	0	0
Brittany	1	2007	4	0	0
Brittany	1	2008	2	1	0
Ethan	2	2006	5	1	3
Ethan	2	2007	6	0	3
Ethan	2	2008	4	0	3
Kyle	5	2006	0	0	1
Kyle	5	2007	7	1	1
Kyle	5	2008	5	0	1
Jacob	3	2006	5	0	2
Jacob	3	2007	3	1	2
Jacob	3	2008	6	1	2
Jessica	4	2006	7	1	0
Jessica	4	2007	9	0	0
Jessica	4	2008	4	0	0

The recently published PanelMatch package includes very useful graphing functions (we’ll see how they work later on). Figure 11.2 displays the treatment status across time (naturally the question occurs how we would choose treatment and control units):

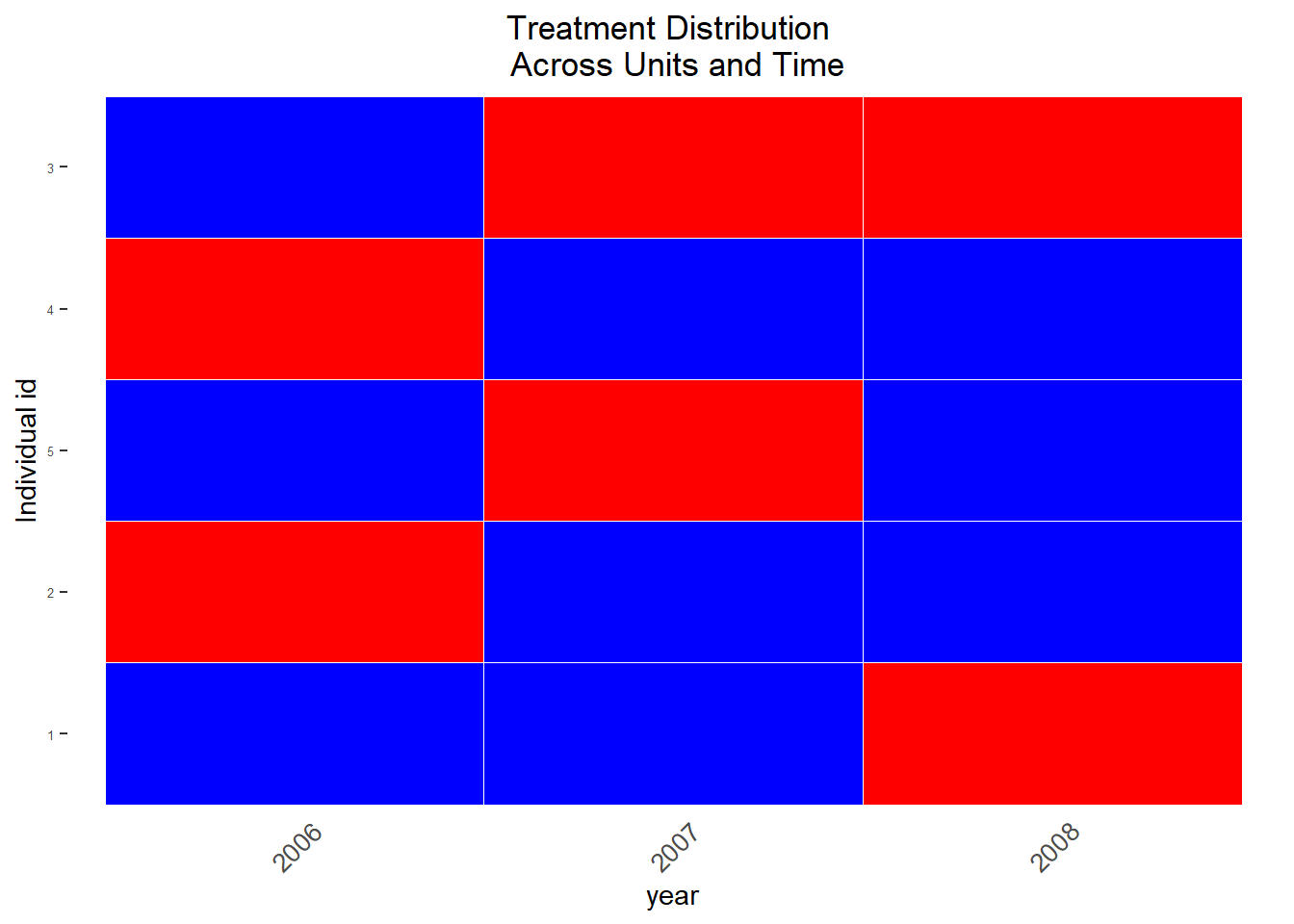
Figure 11.2: Visualization of treated observations across time, across units

11.14.1 Pooled model

The rows in the long format are unit(=individual) \(\times\) time(=year). In other words, across years units may have been never, sometimes or always treated. If we simply pool the data, i.e. lump them together ignoring the time dimension/variable, we can calculate the difference between the average trust among treated observations (red in Table 11.5) and among non-treated observations (blue in Table 11.5). Again, if we do that we ignore the fact that the same units are observed several times. And as you can see in Table 11.5) the same units may appear several times in either/or treatment and control group because they were observed several times. We calculate this pooled estimate in Table 11.6 below.

fit.pooled <- plm(trust ~ threat, 
                  data = data,
                  index = c("name", "time"),
                  model = "pooling") # pooled model
# Alternatively
fit <- lm(trust ~ threat, data = data)

stargazer(fit.pooled, fit, 
          type = "html", no.space = TRUE, single.row = TRUE, header = FALSE,
                    title = "(#tab:tab-pooled-estimate)Model based on pooled data (ignoring time)")

**Table 11.6: Model based on pooled data (ignoring time)**

	Dependent variable:

	trust
	panel	OLS
	linear
	(1)	(2)

threat	0.444 (1.190)	0.444 (1.190)
Constant	4.556^*** (0.752)	4.556^*** (0.752)

Observations	15	15
R²	0.011	0.011
Adjusted R²	-0.065	-0.065
Residual Std. Error		2.257 (df = 13)
F Statistic (df = 1; 13)	0.140	0.140

Note:	p<0.1; p<0.05; p<0.01

The regression estimate in the pooled model (without controls such as education) is simply the difference between the outcome means that is trust means comparing treatment and control observations. To illustrate that we simply aggregate the data as in Table 11.7 to get the group means of treatment and control group. Compare the trust difference in Table 11.7 to the coefficients we estimated in Table 11.6.

Table 11.7: Aggregated data (Pooled data)
threat	trust	n
0	4.555556	9
1	5.000000	6

We could also control for time, i.e. estimate the effects within the years 2006, 2007, 2008 and the corresponding rows in Table 11.5. Conceptually, this would makes sense. At the moment the same units may appear several times in the treatment and control group. If we control for time we are dividing the dataset into three subsets for each year. In these subsets units only appear once. The effect is then estimated in these subsets and the final estmiate is a combination of the effects in these subsets. You try to estimate the results by using summary(lm(trust ~ threat + time, data = data)).

11.14.2 First-differences (FD) Model

For the FD model we need the first differences, i.e. the difference between t₁ and t₀ for each variable. We can manually calculate the first differences. Below we do so and create another dataset called data_fd which is depicted in Table 11.8. The NAs will drop out once we estimate a model based on trust_fd and threat_fd.

data_fd <- data %>% dplyr::select(-education) %>%
  group_by(name) %>% 
  mutate(trust_fd = trust - dplyr::lag(trust)) %>% # Why do we need to specify the dplyr package here?
  mutate(threat_fd = threat - dplyr::lag(threat))
# filter(!is.na(trust_fd)) # we could filter out NAs but leave them in the data

Table 11.8: First differences of data (data_fd from above)
name	unit	time	trust	threat	trust_fd	threat_fd
Brittany	1	2006	4	0	NA	NA
Brittany	1	2007	4	0	0	0
Brittany	1	2008	2	1	-2	1
Ethan	2	2006	5	1	NA	NA
Ethan	2	2007	6	0	1	-1
Ethan	2	2008	4	0	-2	0
Kyle	5	2006	0	0	NA	NA
Kyle	5	2007	7	1	7	1
Kyle	5	2008	5	0	-2	-1
Jacob	3	2006	5	0	NA	NA
Jacob	3	2007	3	1	-2	1
Jacob	3	2008	6	1	3	0
Jessica	4	2006	7	1	NA	NA
Jessica	4	2007	9	0	2	-1
Jessica	4	2008	4	0	-5	0

Then we run a normal regression in Table 11.9. The outcome is now change in trust from t₀ to t₁. The estimate of threat_fd is the increase of the trust average when threat_fd increase by one unit. This is the ‘manual’ way, i.e., we don’t use the plm or the wfe package.

fit <- lm(trust_fd ~ threat_fd, data = data_fd)
stargazer(fit, type = "html", no.space = TRUE, single.row = TRUE,
                    title = "(#tab:model-lm-fd)Linear model based on first-differenced data")

**Table 11.9: Linear model based on first-differenced data**

	Dependent variable:

	trust_fd

threat_fd	0.333 (1.467)
Constant	-0.000 (1.137)

Observations	10
R²	0.006
Adjusted R²	-0.118
Residual Std. Error	3.594 (df = 8)
F Statistic	0.052 (df = 1; 8)

Note:	p<0.1; p<0.05; p<0.01

Fortunately, the plm function will do the first differencing in the background so we can provide it with our simple long-format data (also plm will estimate proper SEs). The results are shown in Table 11.10.

  fit_fd <- plm(trust ~ threat, data = data,
                    index = c("name", "time"),
                    model = "fd", # first differences
                    effect = "individual") # Check ? plm for specification
#  the kind of effects to include in the model, i.e. individual effects, time effects or both
  stargazer(fit_fd, type = "html", no.space = TRUE, single.row = TRUE,
                    title = "(#tab:model-plm-fd)First-differences: plm function")

**Table 11.10: First-differences: plm function**

	Dependent variable:

	trust

threat	0.333 (1.467)
Constant	0.000 (1.137)

Observations	10
R²	0.006
Adjusted R²	-0.118
F Statistic	0.052 (df = 1; 8)

Note:	p<0.1; p<0.05; p<0.01

Analogue K. Imai and Kim (2019 b) provide functions to estimate a first difference model in their package as well (the estimate is the same, albeit the se differs; See ?wfe and hetero.se and auto.se).

  library(wfe)
  mod.fd <- wfe(trust ~ threat, data = data, 
                treat = "threat",
               unit.index = "unit", 
               time.index = "time", 
               method = "unit",
               qoi = "ate", 
               estimator ="fd",
               verbose = FALSE)
  summary(mod.fd)

## 
## Method: unit Fixed Effects
## 
## Quantity of Interest: ATE (Average Treatment Effect)
## Estimator: FD (First-Difference)
## Standard Error: Heteroscedastic / Autocorrelation Robust Standard Error
## 
## Call:
## wfe(formula = trust ~ threat, data = data, treat = "threat", 
##     unit.index = "unit", time.index = "time", method = "unit", 
##     qoi = "ate", estimator = "fd", verbose = FALSE)
## 
## Coefficients:
##        Estimate Std.Error t.value p.value
## threat  0.33333   1.82870  0.1823  0.8594
## 
## Residual standard error: 2.079 on 9 degrees of freedom
## White statistics for functional misspecification: -0.5493388 with Pvalue= 1
## Reject the null of NO misspecification: FALSE

Table 11.11: Aggregating the differenced data (means)
threat_fd	trust_fd	n
-1	0.3333333	3
0	-1.0000000	4
1	1.0000000	3
NA	NaN	5

Again we can also aggregate the first-differenced data in Table 11.8 to get a better grasp in terms of averages as depicted in Table 11.11. Table 11.11 we see that averages that underly model above. The transformed treatment variable has three values: -1, 0, 1, NA (the NA values stem from the first time point for which we can not calculate a difference). In Figure 11.3 depicts a scatterplot with those values on the x-axis and the trust values (averages on the y axis).

Q: Conceptually does it make sense to include observations with first-differenced treatment values of -1?

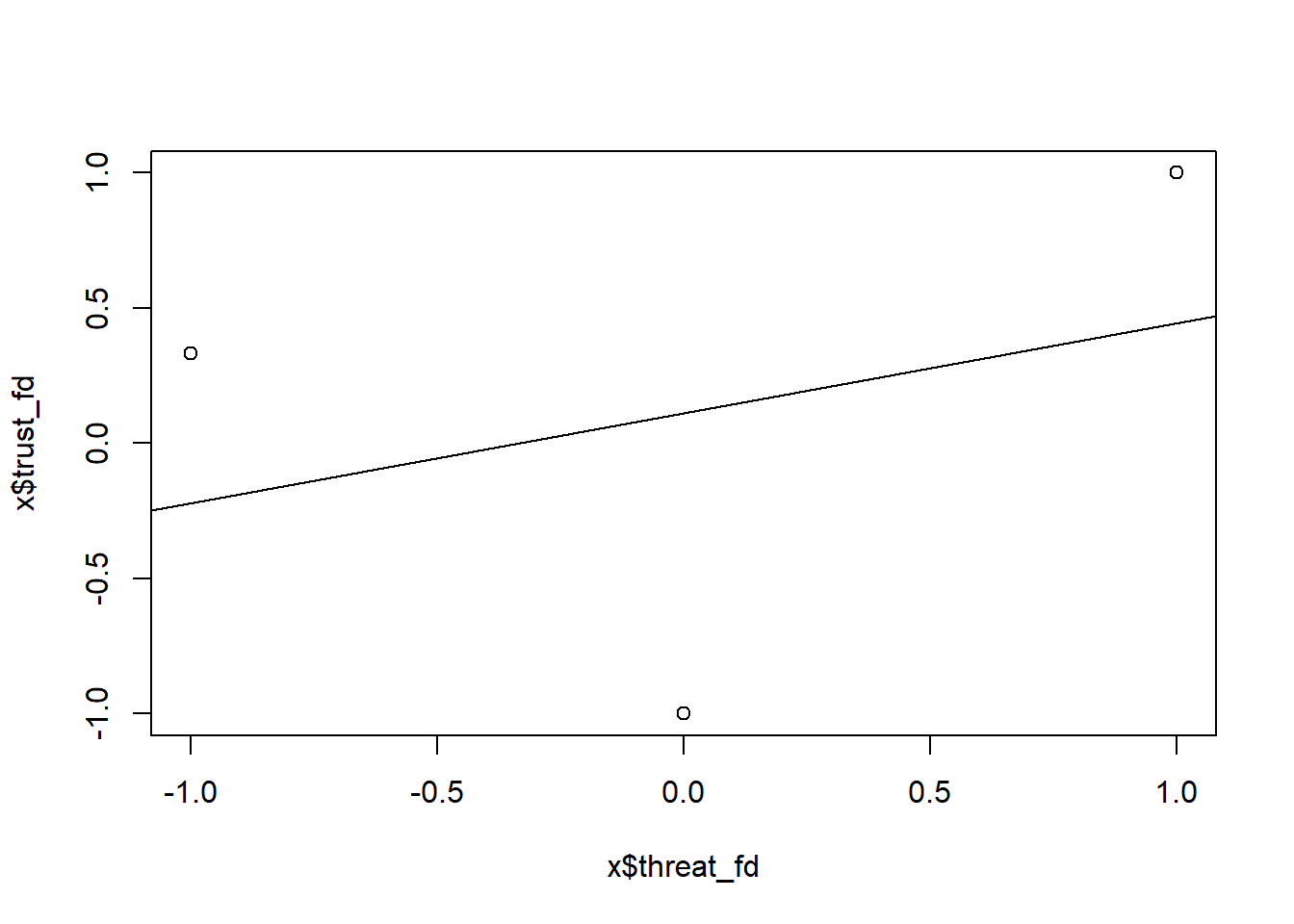
Figure 11.3: Scatterplot of first-differences treatment variable and outcome

11.14.3 Fixed effect (FE) Model (This is outdated since provision of PanelMatch package)

We can do the same for the FE model. To estimate the FE model we need to de-mean the data instead of taking first differences. Below we do so ‘manually’ and generate the dataset data_fe that is depicted in Table 11.12. Then we run a normal regression in Table 11.13. It’s immediatly visible that we end up with more observations as compared to first-differencing the data.

data_fe <- data %>% dplyr::select(-education) %>% 
        group_by(name) %>% 
        mutate(trust.mean = mean(trust)) %>% # calculate trust individual mean
        mutate(threat.mean = mean(threat)) %>% # calculate threat individual mean
        mutate(trust.dmean = trust - trust.mean) %>% # calculate diff to ind. mean
        mutate(threat.dmean = threat - threat.mean) %>% # calculate diff to ind. mean
        ungroup()

Table 11.12: De-meaned data (data_fe)
name	unit	time	trust	threat	trust.mean	threat.mean	trust.dmean	threat.dmean
Brittany	1	2006	4	0	3.333333	0.3333333	0.6666667	-0.3333333
Brittany	1	2007	4	0	3.333333	0.3333333	0.6666667	-0.3333333
Brittany	1	2008	2	1	3.333333	0.3333333	-1.3333333	0.6666667
Ethan	2	2006	5	1	5.000000	0.3333333	0.0000000	0.6666667
Ethan	2	2007	6	0	5.000000	0.3333333	1.0000000	-0.3333333
Ethan	2	2008	4	0	5.000000	0.3333333	-1.0000000	-0.3333333
Kyle	5	2006	0	0	4.000000	0.3333333	-4.0000000	-0.3333333
Kyle	5	2007	7	1	4.000000	0.3333333	3.0000000	0.6666667
Kyle	5	2008	5	0	4.000000	0.3333333	1.0000000	-0.3333333
Jacob	3	2006	5	0	4.666667	0.6666667	0.3333333	-0.6666667
Jacob	3	2007	3	1	4.666667	0.6666667	-1.6666667	0.3333333
Jacob	3	2008	6	1	4.666667	0.6666667	1.3333333	0.3333333
Jessica	4	2006	7	1	6.666667	0.3333333	0.3333333	0.6666667
Jessica	4	2007	9	0	6.666667	0.3333333	2.3333333	-0.3333333
Jessica	4	2008	4	0	6.666667	0.3333333	-2.6666667	-0.3333333

fit <- lm(trust.dmean ~ threat.dmean, data = data_fe)
stargazer(fit, type = "html", no.space = TRUE, single.row = TRUE,
                    title = "(#tab:model-lm-fe)FE model: Linear model based on de-meaned data")

**Table 11.13: FE model: Linear model based on de-meaned data**

	Dependent variable:

	trust.dmean

threat.dmean	0.500 (1.043)
Constant	-0.000 (0.492)

Observations	15
R²	0.017
Adjusted R²	-0.058
Residual Std. Error	1.905 (df = 13)
F Statistic	0.230 (df = 1; 13)

Note:	p<0.1; p<0.05; p<0.01

Fortunately, the plm function will do the de-meaning in the background (also plm will estimate proper SEs) and the results are shown in Table 11.14.

  fit_fe <- plm(trust ~ threat, data = data,
                    index = c("name", "time"),
                    model = "within",
                    effect = "individual")
  stargazer(fit_fe, type = "html", no.space = TRUE, single.row = TRUE,
                    title = "(#tab:model-plm-fe)FE model: plm function")

**Table 11.14: FE model: plm function**

	Dependent variable:

	trust

threat	0.500 (1.254)

Observations	15
R²	0.017
Adjusted R²	-0.529
F Statistic	0.159 (df = 1; 9)

Note:	p<0.1; p<0.05; p<0.01

Analogue K. Imai and Kim (2019 b) provide functions to estimate a fe model in their package as well.

  library(wfe)
  mod.fe <- wfe(trust ~ threat, data = data, 
                treat = "threat",
               unit.index = "unit", 
               time.index = "time", 
               method = "unit",
               qoi = "ate",
               verbose = FALSE)
  summary(mod.fe)

## 
## Method: unit Fixed Effects
## 
## Quantity of Interest: ATE (Average Treatment Effect)
## Estimator: NULL
## Standard Error: Heteroscedastic / Autocorrelation Robust Standard Error
## 
## Call:
## wfe(formula = trust ~ threat, data = data, treat = "threat", 
##     unit.index = "unit", time.index = "time", method = "unit", 
##     qoi = "ate", verbose = FALSE)
## 
## Coefficients:
##        Estimate Std.Error t.value p.value
## threat    0.500     1.122  0.4456  0.6664
## 
## Residual standard error: 3.028 on 9 degrees of freedom
## White statistics for functional misspecification: 0 with Pvalue= 1
## Reject the null of NO misspecification: FALSE

Table 11.15: Aggregating the de-meaned data (means)
threat.dmean	trust.dmean	n
-0.6666667	0.3333333	1
-0.3333333	-0.2500000	8
0.3333333	-0.1666667	2
0.6666667	0.5000000	4

Again we can also aggregate the de-meaned data in Table 11.12 to get a better grasp in terms of averages as depicted in Table 11.15. In Table 11.15 we can see that our the transformed treatment variable takes on different values: -0.6666667, -0.3333333, 0.3333333, 0.6666667. Again imagine a scatterplot with those values on the x-axis and the trust values (averages on the y axis).

11.14.4 Digging into control and treatment group specification

NOTE: Sound causal analysis requires a deeper consideration of time from a causal perspective. For instance, we might contemplate how long it takes for a treatment (e.g. university education) to lead to identifiable changes in an outcome variable. When we rely on such a perspective we may want to construct our comparison groups (treatment and control) manually (or in a different way) as to adapt them to our research question. For instance, we might decide to focus on outcome changes that span longer periods than the usual yearly panel periods.

Q: Please draw a picture how the treatment variable may change between two time points t₀ and t₁?⁴⁶
Q: Why does the number of observations differ between FD (Table 11.10) and the FE model (Table 11.14)?⁴⁷ You might find a hint when you compare Table 11.8 to Table 11.12.

Now conceptually, if you look at Table 11.8 and Table 11.12 you can see that units may turn up several times. And the transformed differenced/de-meaned treatment variables threat_fd and threat.demean can take on different values (-1, 0, 1 in the case of the first-difference model, see Table 11.11 and 11.15).

From a causal perspective we need to consider what these three values of the transformed treatment variable stand for in terms of our original 0/1 treatment variable (victimization). More generally, we need to clarify how the comparison groups treatment/control are constructed here.

We’ll focus on first-differences here:

Q: What values in the original treatment variable did individual i have when the transformed value is a -1, 1 or 0?

For first differences a (transformed) individual gets…

…-1 if he/she had D = 1 at t₀ and D = 0 at t₁ (from treated to control/untreated)
…0 if he/she had D = 1/0 at t₀ and D = 0/0 at t₁ (no change in treatment status = control to control = treatment to treatment)
…1 if he/she had D = 0 at t₀ and D = 1 at t₁ (from control/untreated to treated)

In the case of fixed effects it’s a bit more complicated because the de-meaned value depends on the mean across all of an individuals’ values (so we’ll skip that here)…

Then, the question is what contrast interests us.

Q: Which units would you use to built your treatment and control group?

…yes, we would normally say that observations (time points \(\times\) unit) where units move from control to control (0), i.e., stay in control, are the control observations while observations where units move from control to treated (1) are the treatment observations.

Hence, a potential solution would be to filter out observation periods of individual units where the development in the treatment status from t₀ (the time point before) to t₁ (the actual time point) was either treated → treated or treated → control.

The problem is that the 0s in the original dataset (no change in treatment status, see threat_fd below) may contain both observations where units move from treated t₀ to treated t₁ and observations where units move from control t₀ to control t₁.

Q: Which are those observations below in Table 11.16?

Table 11.16: First differences of data (data_fd from above)
name	unit	time	trust	threat	trust_fd	threat_fd	treatment_status
Brittany	1	2006	4	0	NA	NA	NA-0
Brittany	1	2007	4	0	0	0	0-0
Brittany	1	2008	2	1	-2	1	0-1
Ethan	2	2006	5	1	NA	NA	NA-1
Ethan	2	2007	6	0	1	-1	1-0
Ethan	2	2008	4	0	-2	0	0-0
Kyle	5	2006	0	0	NA	NA	NA-0
Kyle	5	2007	7	1	7	1	0-1
Kyle	5	2008	5	0	-2	-1	1-0
Jacob	3	2006	5	0	NA	NA	NA-0
Jacob	3	2007	3	1	-2	1	0-1
Jacob	3	2008	6	1	3	0	1-1
Jessica	4	2006	7	1	NA	NA	NA-1
Jessica	4	2007	9	0	2	-1	1-0
Jessica	4	2008	4	0	-5	0	0-0

Q: Which observations would we throw out in Table 11.16? How would we go about observations where we don’t have information on the previous wave?

Using the data above we could exclude them as follows (Q: What does the code actually do?):

# Importantly, the data does not contain units that hat status treated -> treated
data_fd <- data_fd %>% mutate(treatment_status = paste(dplyr::lag(threat), "-", threat, sep=""))
d_fd_filtered <- data_fd %>% 
         filter(!treatment_status == "1-0") %>% 
         filter(!treatment_status == "1-1")

Let’s have a look at the filtered data in Table 11.17:

Q: What does treatment status NA-1 mean in Table 11.17? Would you exclude them as well?⁴⁸

Table 11.17: Filtered data
name	unit	time	trust	threat	trust_fd	threat_fd	treatment_status
Brittany	1	2006	4	0	NA	NA	NA-0
Brittany	1	2007	4	0	0	0	0-0
Brittany	1	2008	2	1	-2	1	0-1
Ethan	2	2006	5	1	NA	NA	NA-1
Ethan	2	2008	4	0	-2	0	0-0
Kyle	5	2006	0	0	NA	NA	NA-0
Kyle	5	2007	7	1	7	1	0-1
Jacob	3	2006	5	0	NA	NA	NA-0
Jacob	3	2007	3	1	-2	1	0-1
Jessica	4	2006	7	1	NA	NA	NA-1
Jessica	4	2008	4	0	-5	0	0-0

Subsequently, we can reestimate the FD model in Table 11.18 using the first-difference treatment variable threat_fd and outcome variable trust_fd to see whether we get another point estimate for the effect as compared to Table 11.9 and Table 11.10. Note also that 3 observations were deleted through the filtering.

fit <- lm(trust_fd ~ threat_fd, data = d_fd_filtered)
stargazer(fit, type = "html", no.space = TRUE, single.row = TRUE,
                    title = "(#tab:model-fd-filtered-data)FD model: Re-estimated")

**Table 11.18: FD model: Re-estimated**

	Dependent variable:

	trust_fd

threat_fd	3.333 (3.333)
Constant	-2.333 (2.357)

Observations	6
R²	0.200
Adjusted R²	0.000
Residual Std. Error	4.082 (df = 4)
F Statistic	1.000 (df = 1; 4)

Note:	p<0.1; p<0.05; p<0.01

Table 11.18 illustrates that the estimate changes quite drastically as a function of our changing composition of treated and control groups. In other words, treatment and control group construction is central to estimating causal effects based on panel data.

The problem is that in classic applications of these models it’s not entirely clear how how these models use observed data to estimate relevant counterfactual quantities (@ K. Imai and Kim 2019 b) (in addition the linearity assumption may be too stringent). In other words, it’s not really clear which observations actually make up the treatment and control group in those models. And as discussed earlier departing from a counterfactual perspective for each treated unit we would normally seek a control unit that had exactly the same pre-treatment trajectories (in terms of covariates, treatment and outcome) and only differs in the treatment status. A new package (2020) that automizes this process and provides transparency in terms of how treatment and control group are constructed is PanelMatch

11.14.5 Quick overview of PanelMatch

Summary: “This R package provides a set of methodological tools that enable researchers to apply matching methods to time-series cross-sectional data. Imai, Kim, and Wang (2018) proposes a nonparametric generalization of difference-in-differences estimator, which does not rely on the linearity assumption as often done in practice. Researchers first select a method of matching each treated observation from a given unit in a particular time period with control observations from other units in the same time period that have a similar treatment and covariate history. These methods include standard matching and weighting methods based on propensity score and Mahalanobis distance. Once matching is done, both short-term and long-term average treatment effects for the treated can be estimated with standard errors. The package also offers a visualization technique that allows researchers to assess the quality of matches by examining the resulting covariate balance” (Source) (see also Imai, Kim, and Wang 2018).

In my view PanelMatch seems the most promising candidate when it comes to estimating causal effects based on panel data (I only learned about it in May 2020). It is one of the first packages that takes treatment/control group construction with panel data seriously (see also the wfe package) and it provides more transparency. Here we will just provide a very short example that is closely based on the official vignette (the latter is longer and uses different data). For more extensive explanations I refer the reader to this vignette.

We’ll start by visualizing treatment status across units, across time of our toy dataset (see Imai, Kim, and Wang 2018 Figure 1 for more examples). The graph allows for a discussion of which units & time periods are usable to construct our treatment and control group. For that some modification of the data are necessary (converting unit and time to integers). For illustration purposes we work we very few units here (see the vignette for an example with more observations). Figure 11.4 displays the treatment status across time (see also Figure 11.2 above):

library(PanelMatch)
# Necessary modifications
data <- data.frame(data) %>% mutate(time = as.integer(time), # required transformations for PanelMatch
                                        unit = as.integer(unit))
DisplayTreatment(unit.id = "unit",
                 time.id = "time", 
                 legend.position = "none",
                 xlab = "year", 
                 ylab = "Individual id",
                 treatment = "threat", data = data)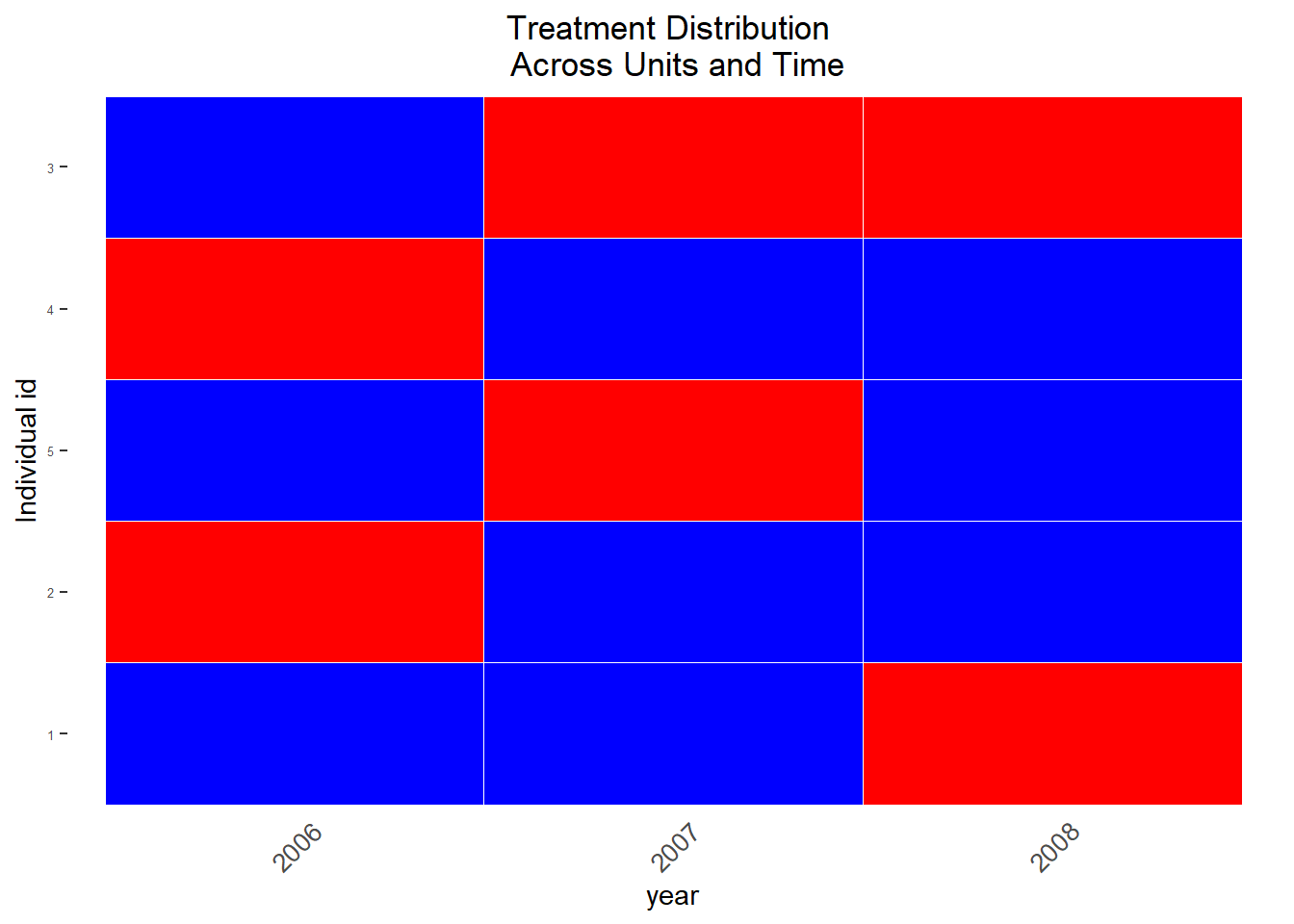

Figure 11.4: Visualization of treated observations across time, across units

The PanelMatch function has the aim of…

1. creating matched sets that contain control units that have been matched to treatment units
- here units that receive treatment after previously being untreated (that move from 0 to 1 in the example above) are matched with units that have matching treatment histories in a specified lag window, but are untreated in the specific time window (move from 0 to 0)
1. determining weights for each control unit in a given matched set (units with higher weights factor more heavily into the estimations).
- here we choose variables for measuring similarity/distance between units, determining the most comparable control units to be included in the matched set, and assigning weights to control units as (argument refinement.method) There are different weighting methods. The “weighting” methods will generate weights in such a way that control units that are more similar to treated units will be assigned higher weights.

We start with an example that sets refinement.method to none meaning that all control units receive equal weights (we don’t refine the control units to which we compare):

PM_results_none <- PanelMatch(lag = 1, time.id = "time", unit.id = "unit", 
                         treatment = "threat", refinement.method = "none", 
                         data = data, match.missing = TRUE, 
                         size.match = 1, qoi = "att", outcome.var = "trust",
                         lead = 0, forbid.treatment.reversal = FALSE, 
                         use.diagonal.variance.matrix = TRUE)

The PanelMatch function returns a PanelMatch object, which contains a matched.set object (here we call it msets_none) which informs us about the matches we get (see here for further explanations):

msets_none <- PM_results_none$att

##   unit time matched.set.size
## 1    1 2008                2
## 2    3 2007                1
## 3    5 2007                1

Table 11.19: Matched sets
unit	time	matched.set.size
1	2008	2
3	2007	1
5	2007	1

The matched.set object object msets_none informs us about the matched sets and is shown in Table 11.19. For treated observation unit1/2008 we found two control observations. For treated observations unit3/2007 and unit5/2007 we found one control observation for each.

We can also display the matches with code below (refers to the first unit) as illutrated in Figure 11.5, 11.6 and 11.7:

# Display matched sets for unit one
DisplayTreatment(time.id = "time", unit.id = "unit", 
                 treatment = 'threat', data = data, matched.set = msets_none[1])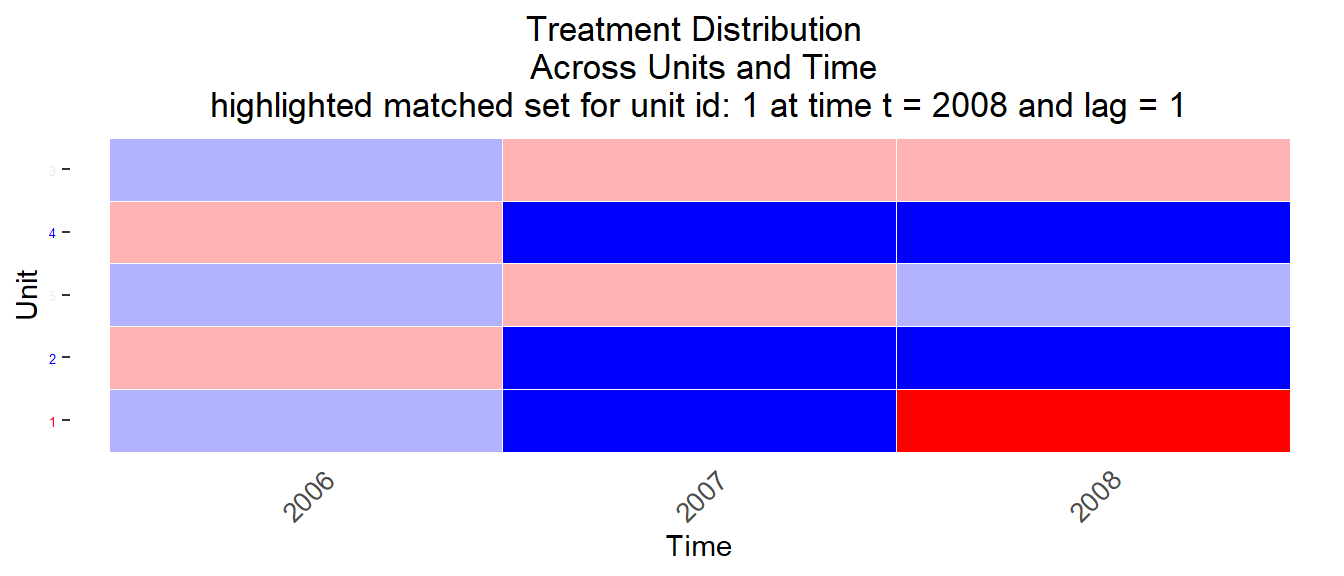

Figure 11.5: Matched sets 1

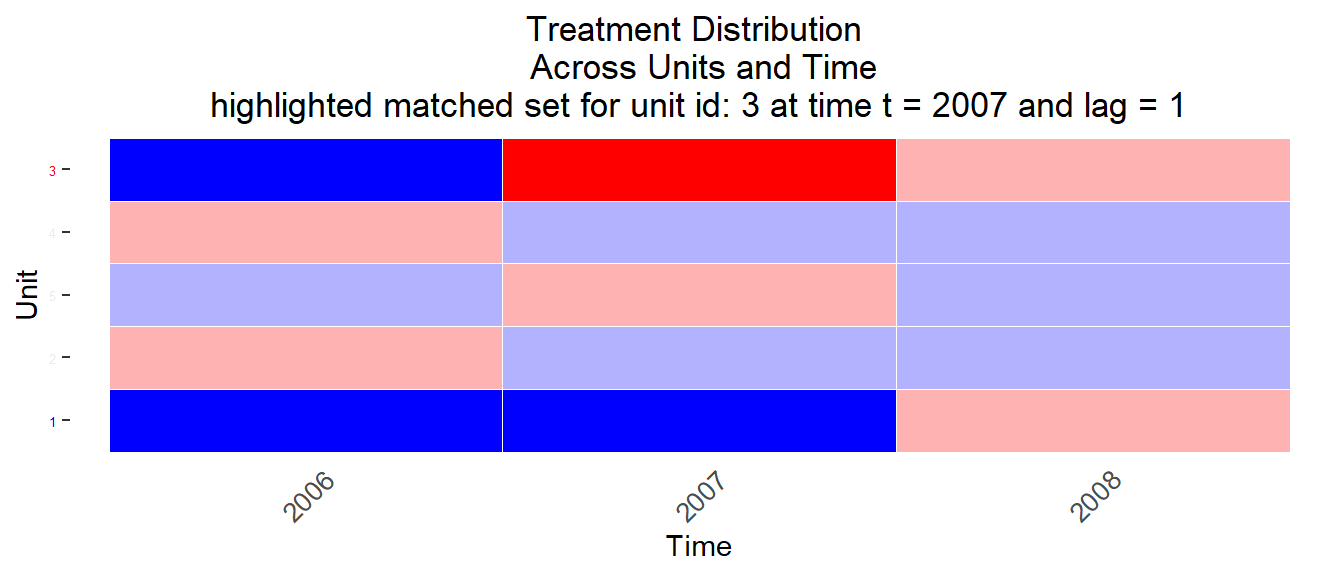
Figure 11.6: Matched sets 2

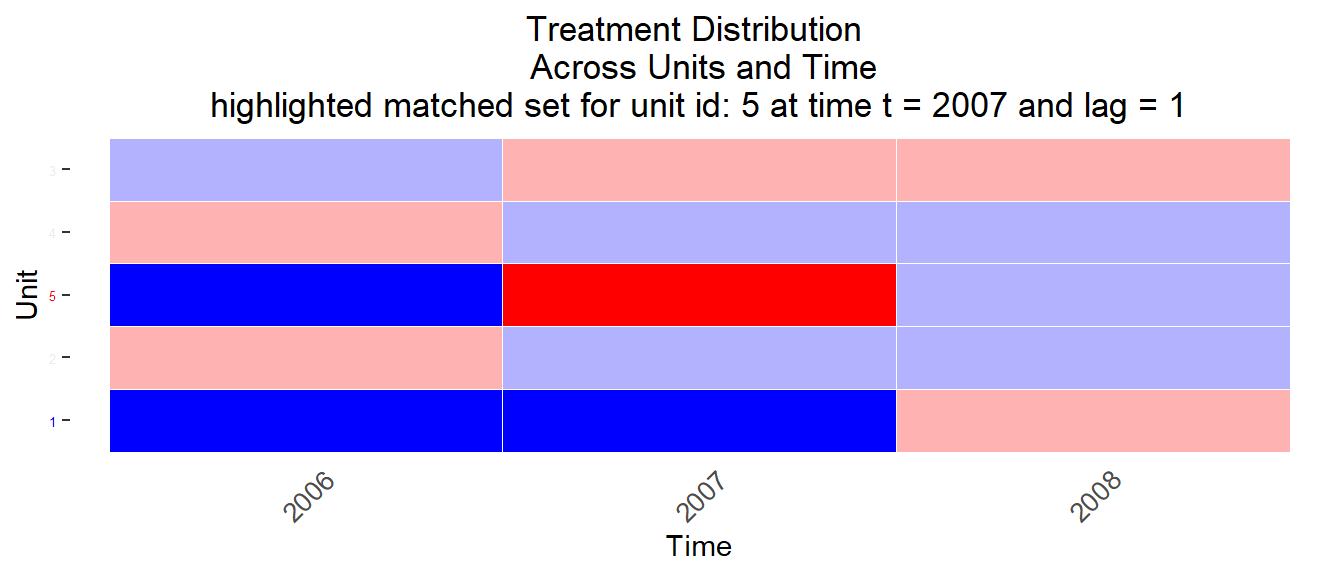
Figure 11.7: Matched sets 3

In searching for those matches we took into account the treatment history but just for one lagged time period (we can use more by specifying the lag argument).

Q: Can you identify one matched control unit/observation in Figure 11.5 that differs in terms of treatment history from the treated unit? What would you recommend?

Moreover, we ignored other covariates. For instance, we might want to find control units that are similar in terms of education, the only coviariate we have in the dataset (or even the outcome trajectory).

Below we’ll start with exact matching (the approach we mostly focused on in our session on Matching). Exact matching is restricted to variables that are stable over time (which is the case for the variable education).

PM_results_exact <- PanelMatch(lag = 1, time.id = "time", unit.id = "unit", 
                         treatment = "threat",
                         refinement.method = "none", # no refinement method 
                         exact.match.variables = "education",
                         data = data, match.missing = TRUE, 
                         covs.formula = ~ education, 
                         size.match = 1, qoi = "att" , outcome.var = "trust",
                         lead = 0, forbid.treatment.reversal = FALSE, 
                         use.diagonal.variance.matrix = TRUE)

msets_exact <- PM_results_exact$att

##   unit time matched.set.size
## 1    1 2008                1
## 2    3 2007                0
## 3    5 2007                0

Table 11.20: Matched sets
unit	time	matched.set.size
1	2008	1
3	2007	0
5	2007	0

Table 11.20 depicts msets_exact and informs us about the matched sets. In contrast to before (see Table 11.19) we only find one match because we now search for control units that additionally have exactly the same values on the education variable. Similarly, if we visualize the matched sets we’ll see that no control units/observations were found for two units (try out the code below).

DisplayTreatment(time.id = "time", unit.id = "unit", 
                 treatment = 'threat', data = data, matched.set = msets_exact[1])
DisplayTreatment(time.id = "time", unit.id = "unit", 
                 treatment = 'threat', data = data, matched.set = msets_exact[2])
DisplayTreatment(time.id = "time", unit.id = "unit", 
                 treatment = 'threat', data = data, matched.set = msets_exact[3])

With exact matching there is normally no need for balance tests (maybe if we want to check whether there were any problems; get_covariate_balance does not work here because we have a single treated/control observation after matching).

Importantly, in real applications we will probably rely on other distance measures (not exact matching), especially if we match on many covariates as well as non-categorical ones. For instance, we can use use the mahalanobis option for refinement.method and will use only contemporaneous values of the education to define similarity.

PM_results_mahalanobi <- PanelMatch(lag = 1, time.id = "time", unit.id = "unit", 
                         treatment = "threat", refinement.method = "mahalanobis", # use Mahalanobis distance 
                         data = data, match.missing = TRUE, 
                         covs.formula = ~ education, 
                         size.match = 1, qoi = "att" , outcome.var = "trust",
                         lead = 0, forbid.treatment.reversal = FALSE, 
                         use.diagonal.variance.matrix = TRUE)

msets_mahalanobi <- PM_results_mahalanobi$att

##   unit time matched.set.size
## 1    1 2008                2
## 2    3 2007                1
## 3    5 2007                1

Table 11.21: Matched sets
unit	time	matched.set.size
1	2008	2
3	2007	1
5	2007	1

Table 11.21 informs us about the matched sets. In contrast to before (see Table 11.20) more observations are acceptable as controls now. Again we could visualize those matched sets.

For now we only check the balance betweet treatment and control group using the get_covariate_balance() function which provides the means in treatment and control (see ?get_covariate_balance for details on calculation). (see also the balance_scatter() function).

get_covariate_balance(PM_results_mahalanobi$att,
                      data = data,
                      covariates = c("education", "trust"),
                      plot = FALSE)

	education	trust
t_1	0	-0.6299408
t_0	0	0.0000000

“While there are no hard rules for how to set the many different PanelMatch parameters, in general, you want to find a balance between having a good number of matched sets and having matched sets that are large enough in size. Having many small matched sets will lead to larger standard errors. You also want to create sets with good covariate balance, which will be discussed later.” (Source)

The PanelMatch vignette provides further examples of visualizing the distribution of matched set sizes.

Finally, we can obtain point estimates (of our causal effect) and standard errors relying on bootstrapping to obtain standard errors (see ?PanelMatch for default values).

# Store the results
PE_results <- PanelEstimate(sets = PM_results_mahalanobi, data = data)

# Display names of results
names(PE_results)

##  [1] "estimates"              "bootstrapped.estimates" "bootstrap.iterations"  
##  [4] "standard.error"         "method"                 "lag"                   
##  [7] "lead"                   "confidence.level"       "qoi"                   
## [10] "matched.sets"

# Display summary of results
summary(PE_results)

## Weighted Difference-in-Differences with Mahalanobis Distance
## Matches created with 1 lags
## 
## Standard errors computed with 1000 Weighted bootstrap samples
## 
## Estimate of Average Treatment Effect on the Treated (ATT) by Period:

## $summary
##     estimate std.error 2.5% 97.5%
## t+0 1.666667  2.622277   -2     9
## 
## $lag
## [1] 1
## 
## $iterations
## [1] 1000
## 
## $qoi
## [1] "att"

# See also 
  # PE_results[["estimates"]] # View the point estimates
  # plot(PE_results) # plot results

References

Imai, Kosuke, and In Song Kim. 2019b. “When Should We Use Unit Fixed Effects Regression Models for Causal Inference with Longitudinal Data?” Am. J. Pol. Sci. 63 (2): 467–90.

Imai, Kosuke, In Song Kim, and Erik Wang. 2018. “Matching Methods for Causal Inference with Time-Series Cross-Section Data.” Princeton University 1.

Lesson: Just a reminder that the observations at t₀ and t₁ do not actually tell us something about the trajectory of the treatment variable, i.e., when the change occurs.↩
Lesson: We loose observations (rows in the data) through first-differencing.. not when we demean the data.↩
They stem from the first time point (which can not be differenced). We don’t need to exclude them as they will drop out anyways when we estimate the model (since the get an NA when first-differenced) but we could check how many drop out etc. if we want.↩