Chapter 3 Odd lattice simulations

Here we are going to describe the technique we use to simulate lattices with odd number of points. Since the interaction are first neighbor we need to divide the lattice sectors that can be updated simultaneously.

In general three sectors need to be considered. For each direction $\mu$ we define $c_\mu= 2$ if the number of points in that directions $L_\mu$ are even or $c_\mu=3$ if the number of point are odd.

We assign each point to a different sector according to the value of $s$ defined as $$s=\left[\sum_\mu (x_\mu \,\%\, c_\mu+ I_{\mu}^6) \right] \,\%\, c_{tot}$$

with $c_{tot}=3$ if there is at least one dimension odd, otherwise $c_{tot}=2$. $I_{\mu}^6(x_\mu)$ is a special unit addition in the case of $L_\mu=7, 13, 25, ...$ i.e.: $$I_{\mu}^6(x_\mu) = \begin{cases} 1 \quad\mbox{if}\quad (L_\mu-1)\%6=0 \quad\mbox{and}\quad x_\mu= L_\mu-1\\ 0 \quad\mbox{elsewhere} \end{cases}$$ We test the correctness of this partitioning for the lattices of the form $T\times L^3$ for all combination $T=[4,24]$ and $L=[4,24]$

library(ggplot2)
colorise_lattice<- function(nx,ny){
  latt<- data.frame("x"=c(1:ny*ny),"y"=c(1:ny*ny), "color"=c(1:ny*ny) )
  
  cx<- if (nx %% 2==0) 2 else 3
  cy<- if (ny %% 2==0) 2 else 3
  ctot<- if(nx%%2==1 || ny%%2==1) 3 else 2
  for(x in c(0:(nx-1))){
    for(y in c(0:(ny-1))){
      i<- x+ y*(nx)
      latt[i+1,1]<- x
      latt[i+1,2]<- y
      color <- ((x %% cx)+ (y %% cy)) %% ctot
      if ( (nx-1)%% 6==0 && x==nx-1) color <- (color + 1) %% ctot 
      if ( (ny-1)%% 6==0 && y==ny-1) color <- (color + 1) %% ctot  
      latt[i+1, 3] <- color
    }
  }
  gg<- ggplot(latt)+theme_bw()
  gg<- gg+geom_point(aes(x=x, y=y, color=as.factor(color), shape=as.factor(color) ), size=5)
  return(gg)
}

gg<- colorise_lattice(4,4)
gg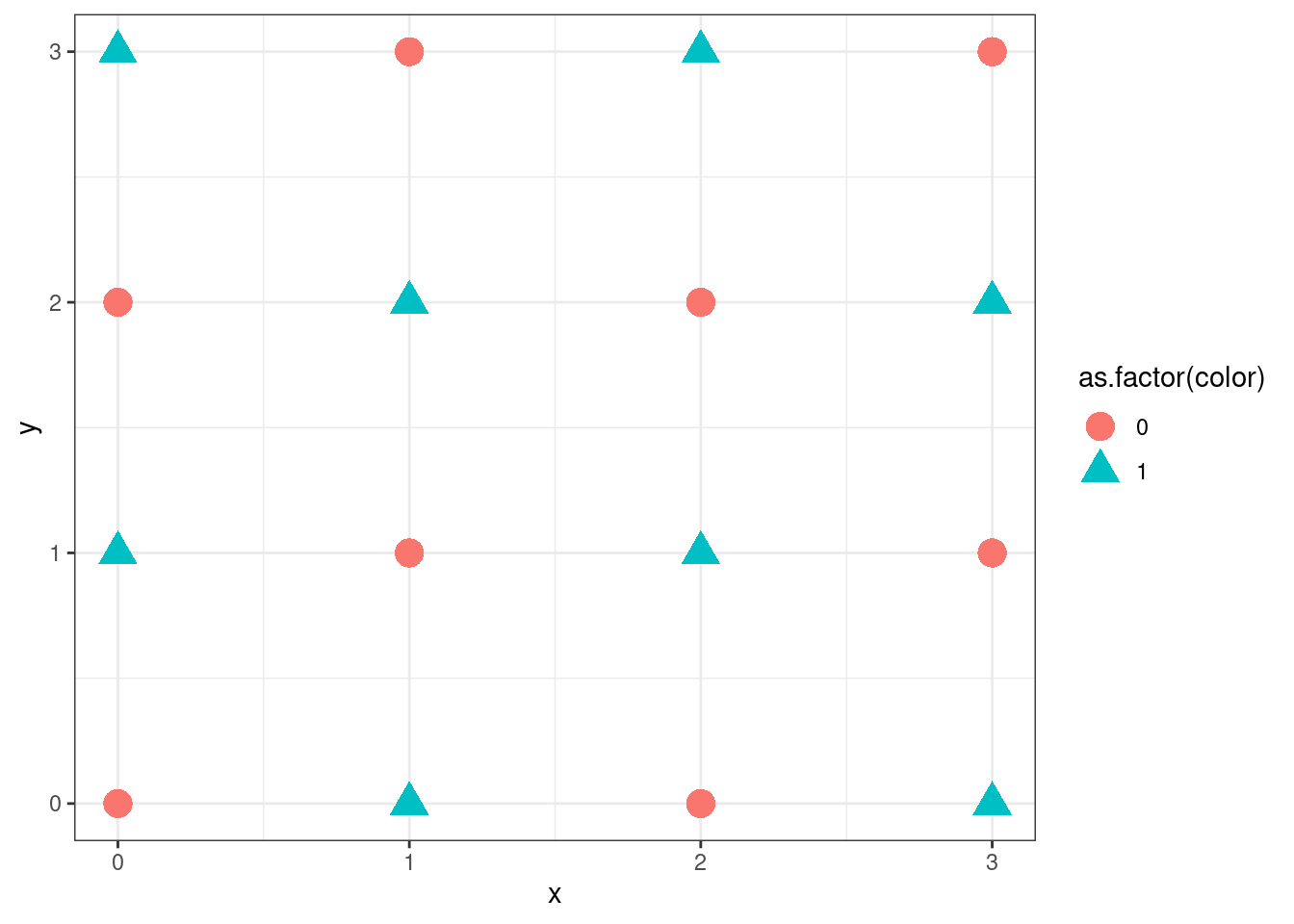

gg<- colorise_lattice(4,5)
gg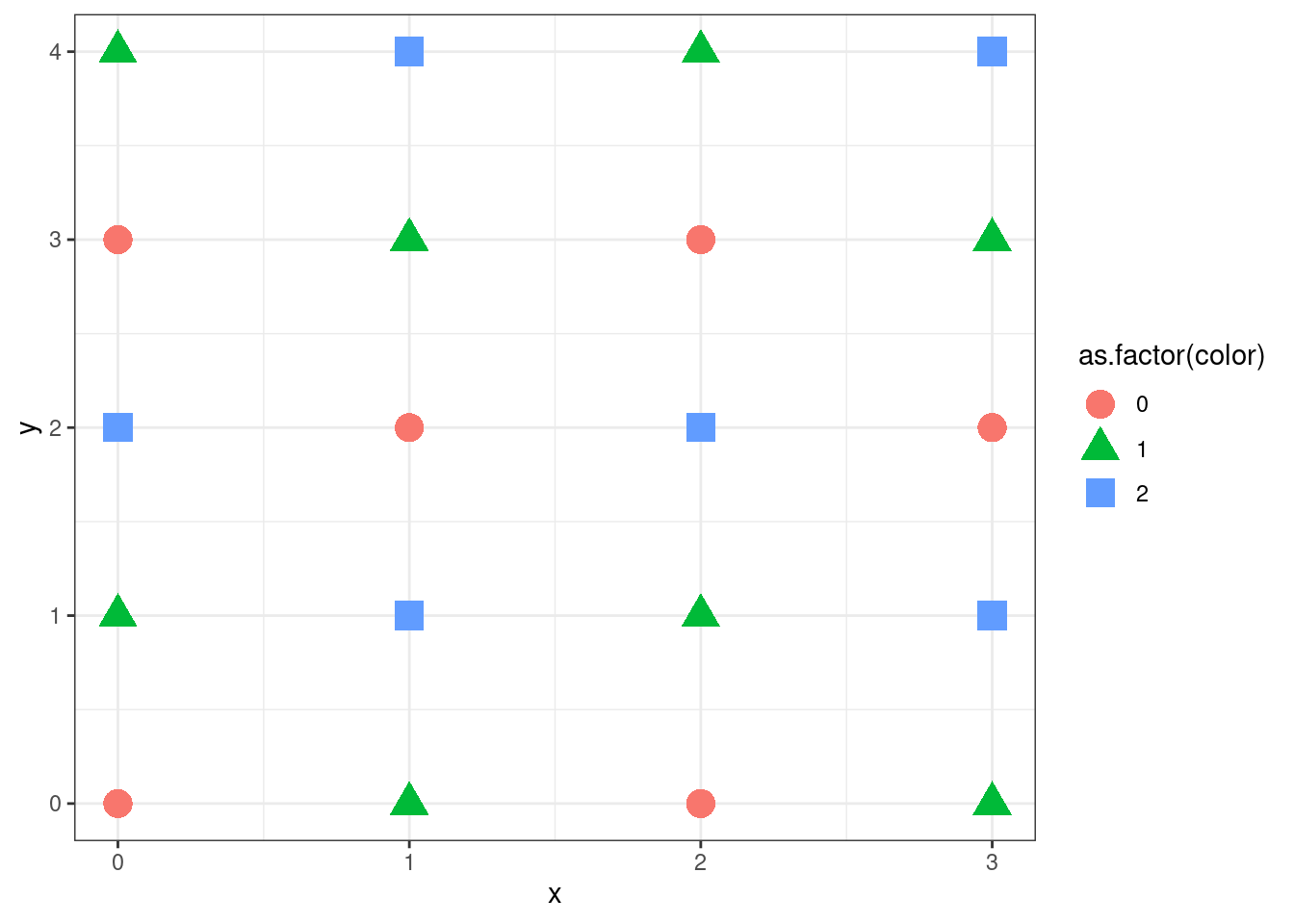

gg<- colorise_lattice(5,5)
gg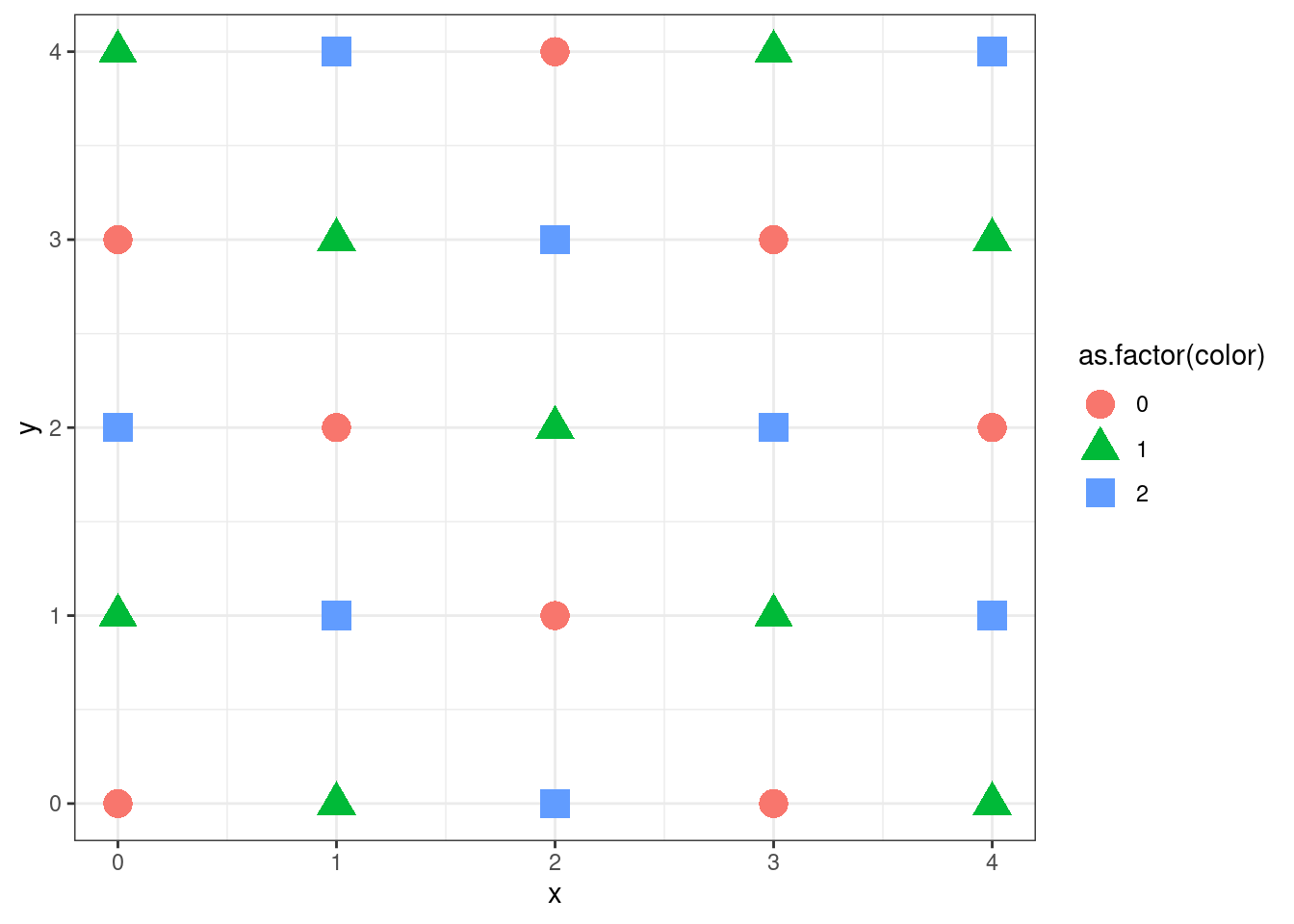

3.0.1 problem with L-1 multiple of 6

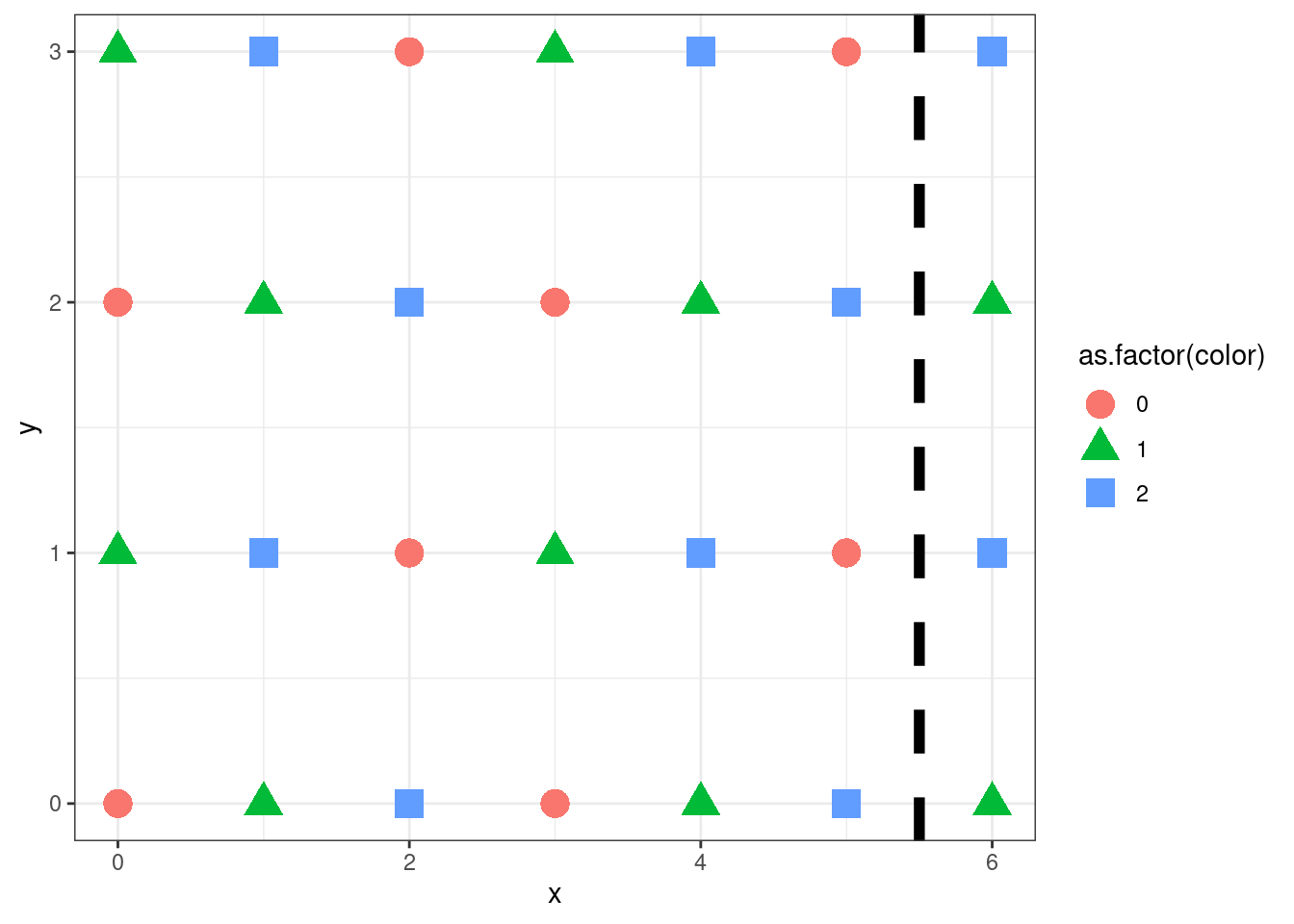
gg<- colorise_lattice(7,7)
gg<- gg + geom_vline(xintercept=5.5, size=2 , linetype = "dashed" )
gg<- gg + geom_hline(yintercept=5.5, size=2 , linetype = "dashed" )
gg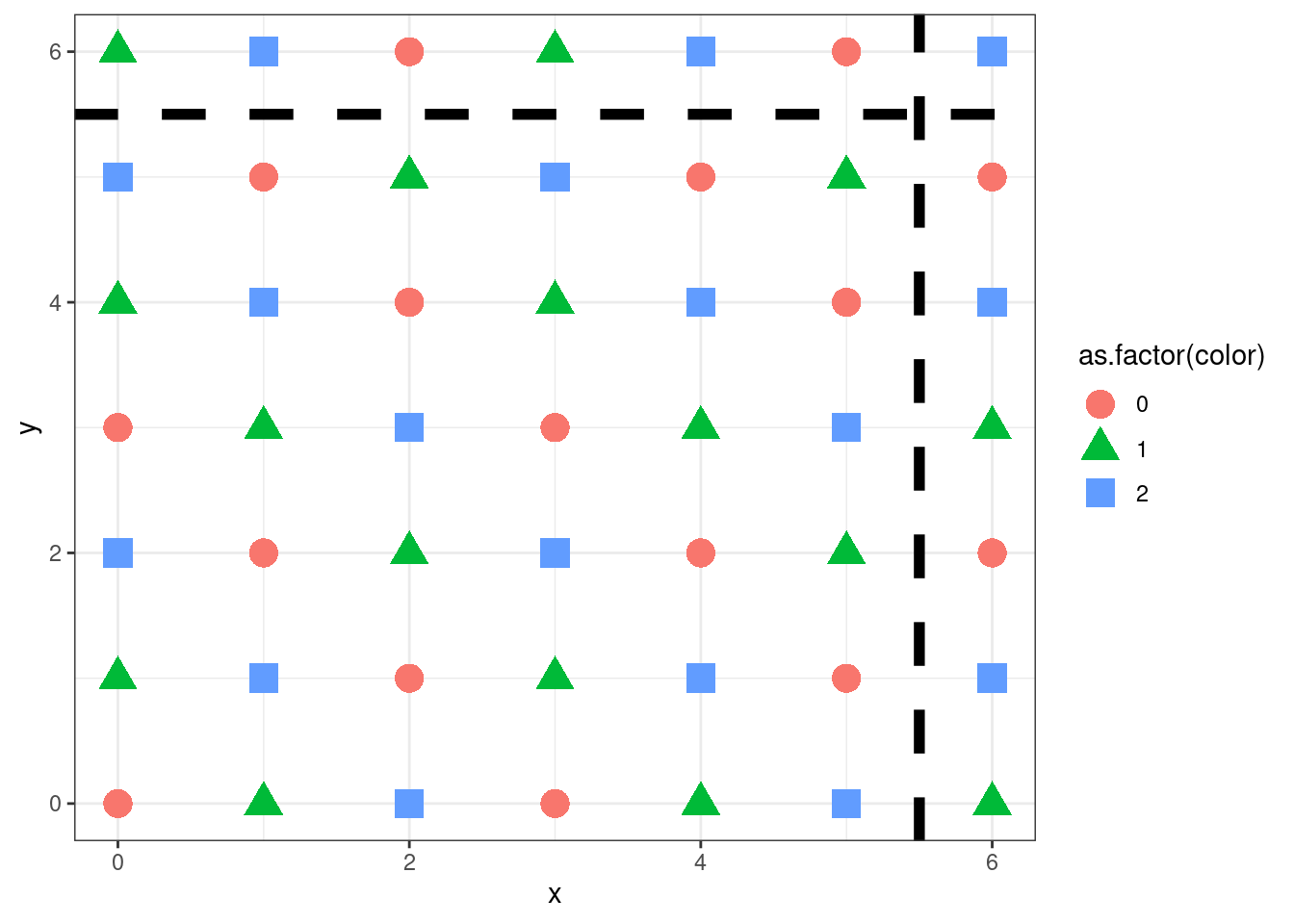

gg<- colorise_lattice(7,5)
gg<- gg + geom_vline(xintercept=5.5, size=2 , linetype = "dashed" )
gg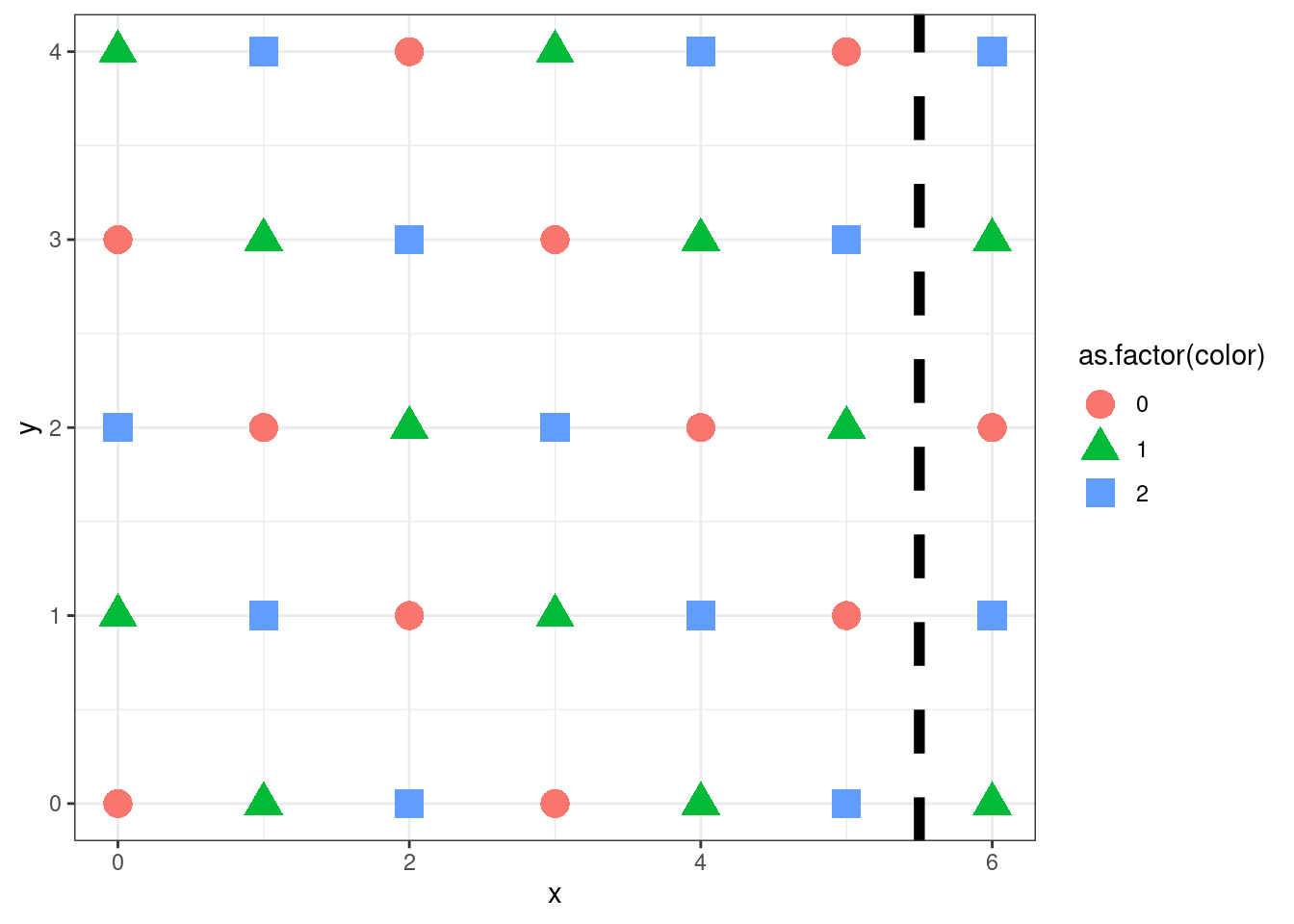

gg<- colorise_lattice(7,4)
gg<- gg + geom_vline(xintercept=5.5, size=2 , linetype = "dashed" )
gg