7.2 Das Beispiel Technikbereitschaft
Am Beispiel der Technikbereitschaft wird nachfolgend einmal beispielhaft das Vorgehen bei der Modell(re)spezifikation verdeutlicht.
Gemessen wurden die vier Indikatorvariablen auf einer fünfstufigen Skala mit den Antwortoptionen „stimmt gar nicht“ (1), „stimmt wenig“ (2), „stimmt teilweise“ (3), „stimmt ziemlich“ und „stimmt völlig“ (5).
Dabei sollten die Befragten anhand dieser Skalierung ihre persönliche Einschätzung zu den folgenden vier Aussagen abgeben:
- “Hinsichtlich technischer Neuentwicklungen bin ich sehr neugierig.” (ta1)
- “Ich finde schnell Gefallen an technischen Neuentwicklungen.” (ta2)
- “Ich bin stets daran interessiert, die neuesten technischen Geräte zu verwenden.” (ta3)
- “Wenn ich Gelegenheit dazu hätte, würde ich noch viel häufiger technische Produkte nutzen, als ich das gegenwärtig tue.” (ta4)
Verschaffen wir uns zunächst einen Überblick über die Zusammenhänge der Variablen der Technikbereitschaft
#Übersicht über die Ausprägung der Variablen
#Hierzu muss zunächst das für die Funktion "describe" notwendige r-package psych geladen werden
library(psych)
describe(daten_latente_konstrukte[, c("ta1","ta2","ta3","ta4")])## vars n mean sd median trimmed mad min max range skew kurtosis se
## ta1 1 455 3.6 1.1 4 3.7 1.5 1 5 4 -0.53 -0.55 0.05
## ta2 2 455 3.1 1.1 3 3.1 1.5 1 5 4 -0.08 -0.68 0.05
## ta3 3 455 2.5 1.2 2 2.4 1.5 1 5 4 0.43 -0.69 0.05
## ta4 4 455 2.5 1.2 2 2.4 1.5 1 5 4 0.47 -0.71 0.05Mit dem Paket PerformanceAnalytics und der Funktion chart.Correlation kann man sich einen guten Überblick über die Zusammenhänge und Verteilungen der einzelnen Variablen verschaffen.9
#Übersicht über die Zusammenhänge der Variablen untereinander
library("PerformanceAnalytics")
data_corr <- daten_latente_konstrukte[, c("ta1","ta2","ta3","ta4")]
chart.Correlation(data_corr, histogram=TRUE, pch=3)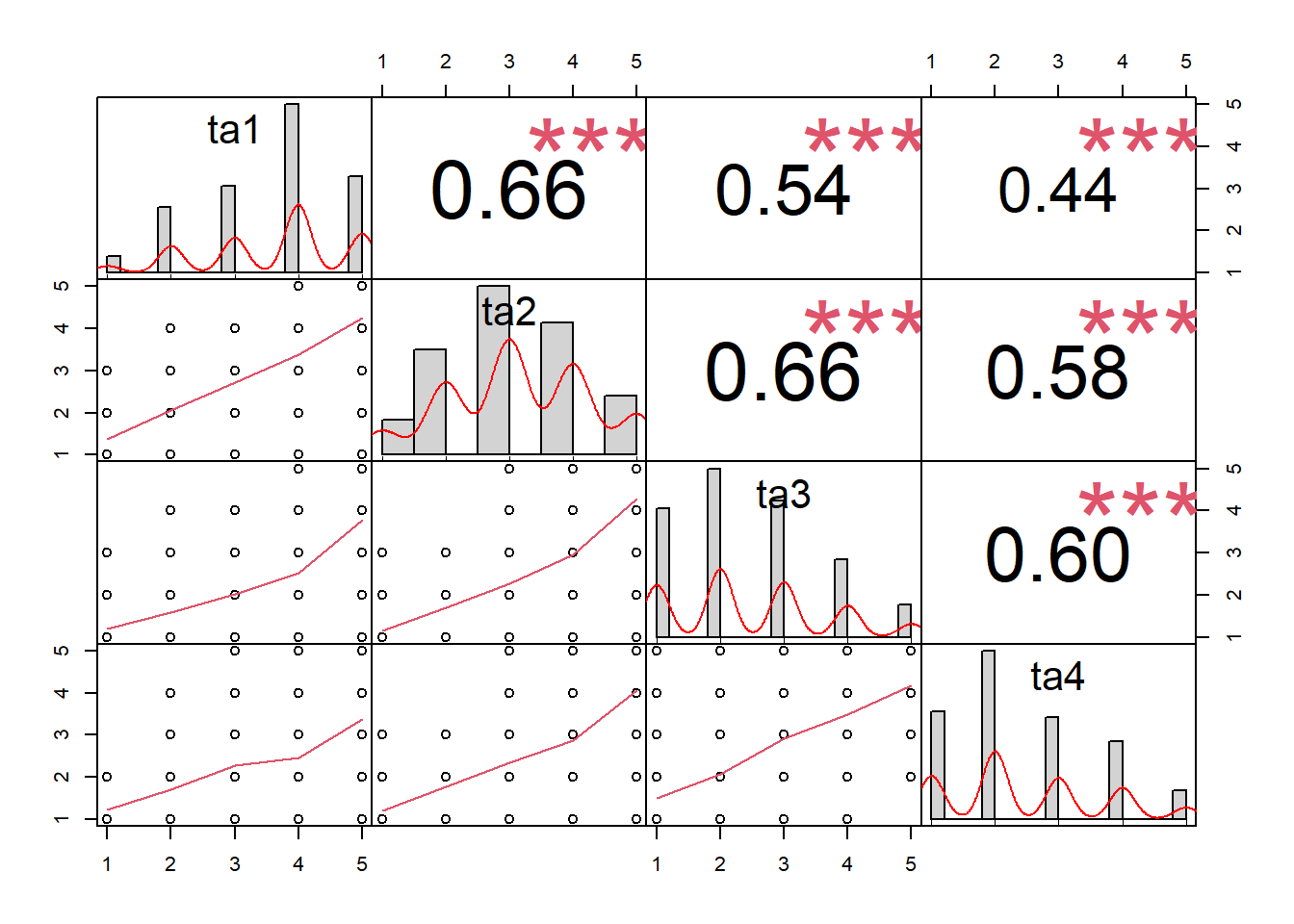
Zusätzlich lassen wir uns noch die altbekannten Reliabilitätswerte ausgeben (hier Cronbachs Alpha sowie Omega).
#Reliabilitätswere der Variablen: Cronbachs Alpha und Omega
library(psych)
omega(data_corr)## Omega
## Call: omegah(m = m, nfactors = nfactors, fm = fm, key = key, flip = flip,
## digits = digits, title = title, sl = sl, labels = labels,
## plot = plot, n.obs = n.obs, rotate = rotate, Phi = Phi, option = option,
## covar = covar)
## Alpha: 0.85
## G.6: 0.82
## Omega Hierarchical: 0.79
## Omega H asymptotic: 0.91
## Omega Total 0.87
##
## Schmid Leiman Factor loadings greater than 0.2
## g F1* F2* F3* h2 u2 p2
## ta1 0.61 0.44 0.60 0.40 0.63
## ta2 0.76 0.46 0.77 0.23 0.74
## ta3 0.84 0.66 0.34 1.05
## ta4 0.74 0.56 0.44 0.98
##
## With eigenvalues of:
## g F1* F2* F3*
## 2.20 0.00 0.41 0.03
##
## general/max 5.4 max/min = Inf
## mean percent general = 0.85 with sd = 0.2 and cv of 0.23
## Explained Common Variance of the general factor = 0.84
##
## The degrees of freedom are -3 and the fit is 0
## The number of observations was 455 with Chi Square = 0 with prob < NA
## The root mean square of the residuals is 0
## The df corrected root mean square of the residuals is NA
##
## Compare this with the adequacy of just a general factor and no group factors
## The degrees of freedom for just the general factor are 2 and the fit is 0.12
## The number of observations was 455 with Chi Square = 56 with prob < 6.1e-13
## The root mean square of the residuals is 0.08
## The df corrected root mean square of the residuals is 0.14
##
## RMSEA index = 0.24 and the 10 % confidence intervals are 0.19 0.3
## BIC = 44
##
## Measures of factor score adequacy
## g F1* F2* F3*
## Correlation of scores with factors 0.91 0 0.69 0.27
## Multiple R square of scores with factors 0.83 0 0.48 0.07
## Minimum correlation of factor score estimates 0.66 -1 -0.04 -0.85
##
## Total, General and Subset omega for each subset
## g F1* F2* F3*
## Omega total for total scores and subscales 0.87 NA 0.81 0.78
## Omega general for total scores and subscales 0.79 NA 0.57 0.78
## Omega group for total scores and subscales 0.07 NA 0.24 0.00Auf den ersten Blick scheint es hier keine großen Überraschungen zu geben. Die visuelle Inspektion der Verteilung sieht in Ordnung aus, auch wenn man strikterweise die Annahme der Normalverteilung, wie bei sozialwissenschaftlichen Daten leider üblich, sicherlich ablehnen müsste.
Für diese vier Indikatoren spezifizieren wir nun ein Modell bei dem alle vier Indikatoren durch einen gemeinsamen zugrundeliegenden latenten Faktor erklärt werden. Im nachfolgenden Abschnitt finden Sie die den kommentierten Code für R.