Chapter 21 PCA
Hello! In this tutorial, we will be learning about principal component analysis (PCA). PCA is considered a “data reduction” variable: it is used when researchers have a large number of variables that they want to represent with a smaller number of variables (called “[principal] components”). The idea behind this strategy is that researchers can represent their data using a linear combination of variables (i.e., a weighted average). The goal of the PCA algorithm is to identify those optimal weights.
To learn more about PCA, let’s use our survey data. PCA is often used in survey data to test whether indicies are meaningful together or to try and group multiple questions. This helps to reduce dimensionality (and, by extension, multicollinearity issues).
21.1 Set Up
Let’s set our data up by bringing in tidyverse. Because of the popularity of PCA, base R contains substantial support for conducting a PCA.
library(tidyverse)
survey_data <- read_csv("data/pew_AmTrendsPanel_110_2022_revised.csv")
colnames(survey_data)## [1] "...1" "perceived_party_difference" "gun_bill_approval" "personal_fin" "party"
## [6] "abortion_opinion" "age" "education" "income" "voter"To use this data, we need to select the variables we want to focus on and clean them. While saving the variables as characters or factors is useful for human interpretation, PCA takes numeric variables specifically, so likert scales and other variables must be converted.
survey_data_trim <- survey_data %>% select(perceived_party_difference, gun_bill_approval, personal_fin, abortion_opinion, age)Importantly, we will remove data rows with missing observations. Traditional PCA does not support missing data, but there are PCA variants (like bpca, or Bayesian Principal Component Analysis) that can handle missing data (for bpca, I recommend using the pcaMethods package, which you can learn about here). We can subset our data to focus on the rows with all their responses using complete.cases().
survey_data_trim[survey_data_trim == "NaN"] <- NA
survey_complete <- survey_data_trim[complete.cases(survey_data_trim),]21.1.1 Centering
In some instances (i.e., when you are using variables with different levels of analysis), it is often helpful to center the variables.
#apply(survey_complete, 2, var) #use this line to calculate the variance of each variable
#?scale #use scale() center columns of a numeric matrix
scaled_df <- apply(survey_complete, 2, scale)
head(scaled_df)## perceived_party_difference gun_bill_approval personal_fin abortion_opinion age
## [1,] -0.1395452393 0.5558159 -0.16356318 -0.34543710 0.184887641
## [2,] -0.1395452393 -0.1149440 -0.16356318 -0.34543710 0.184887641
## [3,] -0.1395452393 -0.1149440 -0.01039481 -0.34543710 0.005124445
## [4,] 0.1405432872 0.3322293 0.14277356 -0.34543710 0.005124445
## [5,] 0.0004990239 0.1086427 -0.16356318 -0.34543710 -0.354401947
## [6,] 0.0004990239 -0.3385306 0.14277356 -0.01592245 -0.174638751Now that our data are prepared, let’s look at this data further.
21.2 Descriptive Analysis
PCA is especially effective when the variables are highly correlated (0.3 or higher). If the variables are not strongly correlated, they will be difficult to combine into an index (“component”).
To identify how strongly correlated these variables are, we will use cor():
## perceived_party_difference gun_bill_approval personal_fin abortion_opinion age
## perceived_party_difference 1.00000000 0.01542172 0.032231101 0.211518972 0.029760235
## gun_bill_approval 0.01542172 1.00000000 0.163473970 0.141640764 -0.010785667
## personal_fin 0.03223110 0.16347397 1.000000000 0.048013644 -0.008167237
## abortion_opinion 0.21151897 0.14164076 0.048013644 1.000000000 -0.008922412
## age 0.02976024 -0.01078567 -0.008167237 -0.008922412 1.000000000It looks like quite a few of our variables are strongly correlated, so let us proceed with our analysis!
21.3 PCA Basics
In this tutorial, I will walk through two processes for conducting a PCA. The first approach is the “older” coding approach: we will calculate eigenvalues/eigenvectors from a covariance matrix and use this to identify the optimal number of components as well as to construct our components. In the newer coding approach, we use prcomp, which is great for PCA analysis and is especially useful for the interpretation of data. At this point, prcomp is the more popular approach, but the emphasis on data visualizations can obfuscate the back-end math, which is why I also discuss the older method.
PCA takes the following steps: (1) Calculate eigenvalues from covariance matrix, (2) determine the optimal number of components, and then (3) plot the data based on these components.
21.3.1 (1) Eigenvalues/vectors
This process of identifying our data’s eigenvalues and eigenvectors is fairly straightforward: we use cov() to calculate the covariate matrix and then eigen() to calculate eigenvectors/eigenvalues. Recall from our class that eigenvectors are used to represent (matrix) data because some vectors contains special properties that, in the case of PCA, are useful for aggregating multiple variables. Learn more about eigenvectors and eigenvalues here.
## List of 2
## $ values : num [1:5] 1.315 1.085 0.996 0.865 0.739
## $ vectors: num [1:5, 1:5] -0.471049 -0.502777 -0.401197 -0.60363 0.000212 ...
## - attr(*, "class")= chr "eigen"## eigen() decomposition
## $values
## [1] 1.3149517 1.0845356 0.9960530 0.8651995 0.7392602
##
## $vectors
## [,1] [,2] [,3] [,4] [,5]
## [1,] -0.471048758 0.5675086 -0.07892895 -0.4004943 0.53797915
## [2,] -0.502777186 -0.4659175 0.10875962 0.5436650 0.47194884
## [3,] -0.401196809 -0.5391333 0.21785455 -0.6640245 -0.24492299
## [4,] -0.603630056 0.3036400 -0.17345626 0.3010754 -0.65015388
## [5,] 0.000212002 0.2792721 0.95099626 0.1116143 -0.0718010421.3.2 (2) Component selection
Next, we will need to determine the number of components we want in our analysis. To figure this out, it is helpful to calculate the proportion of variance explained (PVE). The goal of PVE is to have as much of the variance explained by as few components as possible (because what’s the point of reducing a 28-variable dataset to 28 components? hint: there isn’t one). One straightforward way to calculate the PVE of each component is to simply divide the eigenvalue by the sum of all the eigenvalues.
## [1] 0.26 0.22 0.20 0.17 0.15Note that, in our data, the first 3 variables explain 66%+ of the data, so let’s focus on these (the percent explained drops a little after this). We’ll talk about whether this is really the right approach at the end.
To visualize how meaningful this PCA is, it is often helpful to include a visual about how the data are reduced. To do this, we’ll
Notably, R reverses the numbers (https://uc-r.github.io/pca), so you need to flip it back, which we do in the first line of this chunk. Each statistical software varies in whether they reverse the numbers or not, so it may be helpful to look into what other softwares use. For interpretability, we will also add variable names to our matrix to make this easier to interpret.
components <- -(eigen_survey$vectors[,1:3]) #negate
row.names(components) <- colnames(survey_complete) #save the variable names
colnames(components) <- c("PC1", "PC2", "PC3")
components## PC1 PC2 PC3
## perceived_party_difference 0.471048758 -0.5675086 0.07892895
## gun_bill_approval 0.502777186 0.4659175 -0.10875962
## personal_fin 0.401196809 0.5391333 -0.21785455
## abortion_opinion 0.603630056 -0.3036400 0.17345626
## age -0.000212002 -0.2792721 -0.95099626Based on this data we can tell that PC1 seems to distinguish strongly between variables like covid, aca opinion, medicare4ll opinion, and opinions about a public option for healthcare and variables such as approval of Trump, party affiliation and swing vote. PC2 distinguishes between the healthcare variable and the covid variable and opinions about a public option for healthcare. We’ll explore this distinction further.
21.3.3 (3) Plotting
To plot the results of our PCA, let’s calculate the principal component score for each observation (in this case, for each participant).
PC1 <- as.matrix(scaled_df) %*% components[,1]
PC2 <- as.matrix(scaled_df) %*% components[,2]
PC3 <- as.matrix(scaled_df) %*% components[,3]
PC <- data.frame(Participant = row.names(survey_complete), PC1, PC2, PC3)
head(PC)## Participant PC1 PC2 PC3
## 1 1 -0.06045748 0.303229695 -0.2715772
## 2 2 -0.39770025 -0.009289081 -0.1986256
## 3 3 -0.33621148 0.123491933 -0.0610399
## 4 4 0.08200305 0.255463288 -0.1209356
## 5 5 -0.21920398 0.166016071 0.3009731
## 6 6 -0.12226434 -0.027430121 0.1690729We can then use this data to plot the poll data on a two-dimensional scale using the principal components as axes (i.e., using the eigenvectors as directions in a feature space):
ggplot(PC, aes(PC1, PC2, PC3)) +
modelr::geom_ref_line(h = 0) +
modelr::geom_ref_line(v = 0) +
geom_text(aes(label = Participant), size = 3) +
xlab("First Principal Component") +
ylab("Second Principal Component") +
ggtitle("First Two Principal Components of Poll Data")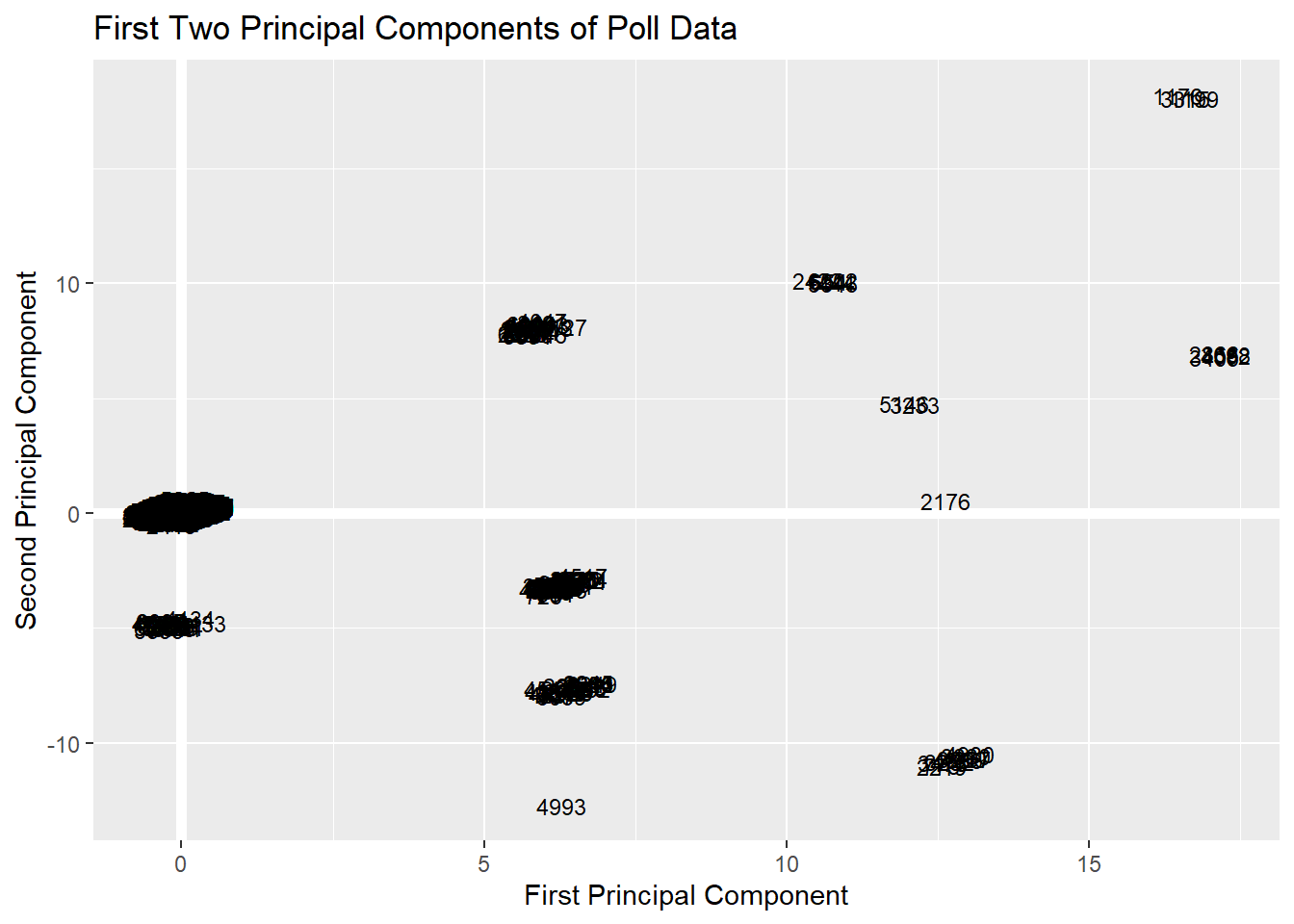
While possibly interpretable, this figure is somewhat difficult to interpret. This is a big reason why folks have move onto more advanced and interpretable visualizations for showing their principal component analysis.
21.4 PCA, Intermediate
21.4.1 (1) Eigenvectors/values
Using the function prcomp(), we can also calculate the eigenvectors/eigenvalues. We will set scale == TRUE to scale the data as well.
## Standard deviations (1, .., p=5):
## [1] 1.1467134 1.0414104 0.9980245 0.9301610 0.8598024
##
## Rotation (n x k) = (5 x 5):
## PC1 PC2 PC3 PC4 PC5
## perceived_party_difference 0.471048758 -0.5675086 0.07892895 0.4004943 -0.53797915
## gun_bill_approval 0.502777186 0.4659175 -0.10875962 -0.5436650 -0.47194884
## personal_fin 0.401196809 0.5391333 -0.21785455 0.6640245 0.24492299
## abortion_opinion 0.603630056 -0.3036400 0.17345626 -0.3010754 0.65015388
## age -0.000212002 -0.2792721 -0.95099626 -0.1116143 0.0718010421.4.2 (2) scree plots
While PCE is great for some straightforward numbers, it sometimes also helps to visualize the PVE to show how meaningful each component is. We can use factoextra (which is a separate library) to plot such a visualization (this is called a scree plot).
As we saw in the first analysis, the first component. explains a majority of the variance, and the second component explains a little more.
factoextra also has a useful function, get_eigenvalue(), for creating a dataframe of eigenvalue information.
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 1.3149517 26.29903 26.29903
## Dim.2 1.0845356 21.69071 47.98975
## Dim.3 0.9960530 19.92106 67.91081
## Dim.4 0.8651995 17.30399 85.21480
## Dim.5 0.7392602 14.78520 100.0000021.4.3 (3) factoextra visualizations
We can also use factoextra to visualize the meaningfulness of our components “more elegantly.” In factoextra, there is a great visualization called fviz_pca that can help you plot the participants (similar to what we did above), the variables, or both. Since you already know how to visualize the participants, let’s focus on the variables.
fviz_pca_var(df_pca,
col.var = "contrib", # Color by contributions to the component
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE)
We can also visualize this using ggfortify, which adds additional support to ggplot2 for visualizing PCA results. One advantage of this method is that you have much more control of your visualization.
## Warning: package 'ggfortify' was built under R version 4.2.2ggplot2::autoplot(df_pca, data = survey_complete,
shape = TRUE, #if you set this to false, it will show you the participant id's
loadings.colour = 'blue', loadings = TRUE, #style of variable arrows
loadings.label.colour = 'red', loadings.label = TRUE, loadings.label.size = 3, #style of variable names
loadings.label.repel=T) + #this is the eqivalent of repel in fviz_pca_var
theme_minimal()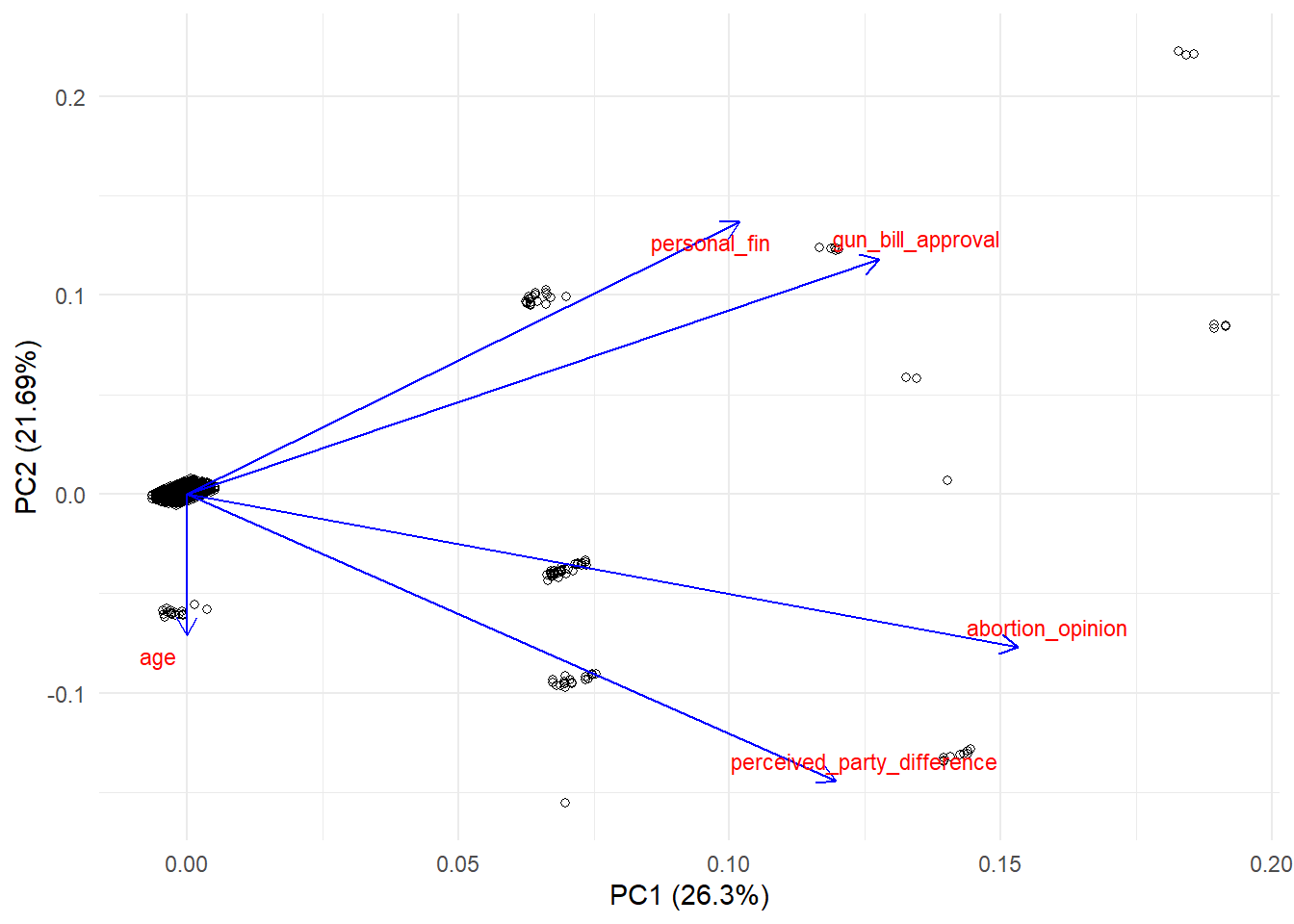
More Resources:
1. PCA tutorial which has great information about how to report on a PCA.
2. PCA tutorial using state data (this helps with the interpretation of individual data points since you’d be using state names rather than participant numbers, as we had).
3. PCA tutorial; I like the way this one is written.
4. More on prcomp()
5. If you want to use this sort of approach on categorical variable, I encourage you to look into factor analysis.
6. If you want to use this approach on mixed data (categorical or numeric), look into factor analyses of mixed data.
+ Note: sometimes, you’ll see categorical variables be called “qualitative” and numeric variables called “quantitative” in this literature.