15 Model selection and model averaging
15.1 Introduction
So far we have used statistical models, such as general and generalized linear (mixed) models, and accompanied these with statistical tests to adjudicate on hypotheses. These statistical testings have all taken the form of null hypothesis significance testing (NHST). The software calculated a probability that a parameter estimate as extreme as the one we got from the data would arise under the null hypothesis, that is the hypothesis that the parameter in question is in fact zero. If this probability, the p-value, was significantly small, we felt some justification in concluding that the parameter in the world probably was not zero; and therefore that the null hypothesis could be rejected; and therefore that we should embrace the alternative hypothesis, that the variable in question does have some non-zero effect.
NHST is a very standard approach in many areas of science, but it is not the only and not always the best approach one can take to choosing what, given the data, one should believe to be true about the world. I believe that, despite the caveats about p-values discussed in an earlier unit, NHST has useful applications. But, it does not make sense for everything. In particular, there are two kinds of cases where its utility is quite low. People often use it in these cases, but there are better alternatives.
The first kind of case is where the researcher is entertaining multiple hypotheses, none of which is null, and wishes to say something about which hypothesis is best supported by the data. For example, consider how the diameters of the trunks of trees relate to their height. Obviously, taller trees tend to have thicker trunks. Thus, testing (and rejecting) the hypothesis that there is no relationship between trunk diameter is not very interesting. However, there are multiple possible hypotheses about how trunk diameter might relate to height. For example: is there a linear relationship; does height increase with the square root of diameter; is height related to diameter to the power of 2/3, and so on. You could turn each of these possible ideas into a hypothesis; and then you would want to evaluate each of these hypotheses against one another given the data, not evaluate each of them against the null hypothesis that there is no relationship.
The second kind of case where NHST might not be useful is where you have observational data, quite a few potential predictor variables, and your objectives are exploratory rather than confirmatory. As soon as this is the case, there are many models you could test. Because you have so many combinations of predictors, you are very likely to find several that do better than the null hypothesis (that all parameters are zero). Finding some models where some parameters have small p-values is to be expected. But how do you know which of these models to prefer to the others?
The question in these cases is: of all the various combinations of predictors that do a better job than the null hypothesis at predicting the outcome, which one should I think of as the best? Which one should I take to represent the causal forces that really generated this data; and, hence, which one is likely to predict the outcome in novel samples?
We have to be careful here. One traditional approach was to find the combination of predictors that minimizes the variance of the residuals. That is, the more closely your combination of predictors predicts the actual data points, the better your model is. The problem with this is that it always leads you to include more predictors in the model. This is because adding further predictors can only ever increase the amount of variance explained by your model. (If you think about it, adding an extra predictor could never reduce the amount of variance explained, only leave it the same or increase it to some degree). In the limit, where you had 100 data points and 100 predictors, you could predict every value of the outcome variable exactly, because you would have a unique combination of predictor values for each point in the data.
However, though such a complex model would minimize the variance of the residuals in the current dataset, it would be very unlikely to be the best model at out-of-sample generalization, that is, predicting the values in a novel dataset. This is because you would have overfitted your model, bending its predictions to every random wrinkle and bump that happens to be in the current dataset, instead of capturing the probably simpler set of influences that generated the repeatable patterns that are going to be seen in other datasets as well. What you want is a model that captures the major systematic forces shaping the outcome, without overfitting.
In this session, I will introduce an alternative approach to inference, model selection or information theoretic model selection. Model selection allows you to test between multiple non-null hypotheses; and to find the best model in exploratory analysis of datasets with many predictor variables. Model selection does not involve p-values or significance tests in the way you are used to, so we will have to learn some new terminology.
15.2 The Akaike Information Criterion and the basics of model selection
The Akaike Information Criterion (AIC) is a quantity that can be calculated for any statistical model, whether a linear mixed model, general linear model, or generalized linear model. It is named after the Japanese mathematician Hirotugu Akaike and it forms the basis of model selection. You can get the AIC for any R model using the function AIC(). The lower the AIC, the ‘better’ the model is, in the sense of capturing the data generating forces well and hence being likely to predict patterns in a new sample well. Of two competing models, the one with the lower AIC is to be preferred.
The AIC is the sum of two terms. One term is a measure of goodness of fit: basically, how well the right-hand side of the model predicts the outcome variable on the left-hand side. The better the model fits the data, the smaller this term gets, and hence the lower the AIC becomes.
The other term reflects the number of parameters in the model. As the model gets more complex, this term gets bigger and hence makes the AIC worse. Of two models where the right-hand side predicts the variation in the outcome equally well, the one with more predictors in it will have a worse AIC due to the increase in this term.
Of a set of models, the one with the lowest AIC is therefore going to be the one that does the best at predicting variation in the outcome, given its complexity. It turns out, mathematically, that selecting the one with the lowest AIC should reliably find the one that is going to be best at out-of-sample prediction. The one with the lowest AIC represents the optimal trade-off between including enough predictors to capture the important systematic forces, and the risk of overfitting and excessive model complexity.
Model selection therefore proceeds by defining a set of models of interest. Obviously, all the models must have the same outcome variable, and all must be fitted on exactly the same dataset. This has implications for datasets in which some values are missing for some variables; you need to fit all the models to the subset of cases where all variables are non-missing. Having defined your set, you calculate AICs for all the models, and the smallest wins.
It is not quite this simple. Often, several models have AICs that are very similar. In this case, the software gives you an AIC weight for each of the nearly-equal models. You can interpret this as the probability that that particular model is the best one. You might for example have a situation where model m1 has an AIC weight of 0.72 and model m2 has an AIC weight of 0.28. In such a case, the data suggest a 72% probability of m1 being the best model, and a 28% probability that it is m2.
All of this will seem less abstract when we work through examples. We will have two: first, an example where we use model selection to adjudicate between multiple non-null hypotheses; then second, a case of using AIC in an exploratory manner.
15.3 Using model selection to test between multiple non-null hypotheses
15.3.1 The Changing Cost of Living Study
For our examples, we will use the data from a study called The Changing Cost of Living Study (Nettle et al. 2024). This longitudinal study aimed to investigate the impact of financial circumstances on people’s psychological well-being over the course of a year. Every month, the participants (232 adults in France and 240 in the UK) filled in a financial report including how much income they had earned that month as well as their expenditures of various kinds. They also completed a number of psychological measures, notably measures of depression and anxiety symptoms.
In this first example, we are going to examine the relationship between income earned, and depressive symptoms. It will be no surprise that when people’s earnings are smaller, their depressive symptoms are higher. This is one of the best known patterns in all of psychiatric epidemiology. The null hypothesis (no relationship) is therefore not plausible and rejecting it would not be interesting.
Instead, we can entertain the following set of hypotheses about the association:
Linear negative association. Depressive symptoms reduce by a constant amount for each euro increase in income.
Logarithmic negative association. Depressive symptoms reduce by a constant amount for each unit increase in the logarithm of income. This would imply a benefit of earning more that flattens off, so the first 500 euros you earn would reduce your symptoms a lot, the second 500 a bit less, the next 500 less still, and so on.
Quadratric association. Depressive symptoms are related to income via a quadratic function. This is a function that has the potential to be U-shaped or inverted U-shaped. That is, depressive symptoms might go down with increasing income up to a certain point, and then start to increase again as income goes up still further.
Quadrative logarithmic association. This possibility, included for completeness, is that depressive symptoms are related to the logarithm of income, via a quadratic function. This would accommodate both the fact that the first 500 euros had a greater impact than the next 500 euros, and the possibility of a U-shaped situation where depressive symptoms first go down and then start to go up again as income increases.
We will define a model corresponding to each of these hypotheses and select between them.
15.3.2 Getting the data and the MuMIn package
The data for the study are at: https://osf.io/d9qb6/. Under ‘Data’, you will see that there are two versions available, .csv and .Rdata. .Rdata is an R-specific format that keeps things like the classes of variables and the levels of factors from the preparation of the data, so download this one and put it in your working directory. Then we need:
You should see dataframe d appear in your environment. The codebook of what all the variables represent is available in the OSF repository with the data, under ‘Documents’.
Now, let’s install the contributed package MuMIn (which stands for Multi_Model Inference) and attach it. We are also going to need tidyverse and lmerTest, packages you have met before.
## Error in install.packages : Updating loaded packagesNow, we need to do two things before we can work with MuMIn. As mentioned, model selection only works if all the models are fitted to exactly the same dataset; otherwise the measures of how well the models fit the data are not comparable. MuMIn therefore requires us to set the options such that models will not get fitted if there are any missing values in any variable. We do this as follows:
Now, we have to make sure that we only have the set of cases where none of the variables of interest has a missing value. The variables of interest are: depressive symptoms (variable PHQ); income (variable incomec); and gender (mgender), which needs to be in all the models as a covariate, since women have higher depressive symptoms than men on average, and may have different salaries too. We will also need the variable pid (participant ID), but this never has missing values.
We need therefore to select the set of cases from d that are not missing values for PHQ, incomec or mgender. In R, != is the equivalent of ==, but means ‘is not the case’. So, we select our non-missing cases as follows:
We lost 39 cases due to a missing value; your observations in c in your environment window should be 4843 rather than 4882.
15.3.3 Setting up your models and doing the selection
Now we come to setting up the four models corresponding to the four hypotheses (linear, logarithmic, quadratic, quadratic-logarithmic). These are going to include some transformed versions of income (logged and squared). To make things as smooth as possible, let’s define these as separate variables first. We are also going to scale them at the same time, to make the coefficients in the models more comparable. A few people received incomes of zero in the month in question, and the logarithm of zero does not exist, so we have to add 1 to all the income values for the logged variables.
c <- c %>% mutate(income.scaled = scale(incomec),
log.incomec = scale(log(incomec + 1)),
sq.incomec = scale(incomec^2),
sq.log.incomec = scale(log(incomec+1)^2))Now let’s set up the models. These are linear mixed models with a random intercept for participant, to account for the repeated measurements from the same people. The lmer function has two options for fitting the model, reduced maximum likelihood (REML=TRUE), and maximum likelihood (REML=FALSE). When comparing models by AIC we want them to all be fitted by maximum likelihood, hence the REML=FALSE in the calls below.
m1 <- lmer(PHQ ~ income.scaled + mgender + (1|pid), data=c, REML=FALSE)
m2 <- lmer(PHQ ~ log.incomec + mgender + (1|pid), data=c, REML=FALSE)
m3 <- lmer(PHQ ~ income.scaled + sq.incomec + mgender + (1|pid), data=c, REML=FALSE)
m4 <- lmer(PHQ ~ log.incomec + sq.log.incomec + mgender + (1|pid), data=c, REML=FALSE)If you run the summary() on these models, you will see that all other than m1 contain at least one income-related parameter estimate that is significantly different from zero. Thus, the models seem to be telling us that income is related to depressive symptoms in some way, but NHST does not much help us adjudicate what kind of association it is.
To do the model selection, we need to assign the set of models to a class of object called a list and then call model.sel from the MuMIn package.
## Model selection table
## (Int) incom.scl mgn log.incmc sq.incmc sq.log.incmc df
## 2 5.643 + -0.3063 6
## 4 5.640 + -0.5707 0.3026 7
## 3 5.646 -0.69280 + 0.4878 7
## 1 5.642 -0.09599 + 6
## logLik AICc delta weight
## 2 -12050.73 24113.5 0.00 0.547
## 4 -12049.92 24113.9 0.40 0.448
## 3 -12054.53 24123.1 9.61 0.004
## 1 -12061.00 24134.0 20.54 0.000
## Models ranked by AICc(x)
## Random terms (all models):
## 1 | pidHave a good look at this output (you might need to resize your console window to see it all at one glance). For each model, you can see which variables are included (gender is in all of them). For the various income variables, you can see their parameter estimates where they are included. And, you can see the AIC (column AICc) for each model, and then the AIC weight.
In this case, the AICs for models 2 and 4 are pretty similar, whilst models 3 and 1 lag further behind. In terms of the AIC weights, m2 gets 0.547 of the weight (i.e. 55%), with a substantial minority report of 0.448 (45%) for m4. Support for the other two models is negligible.
Both m2 and m4 share the same feature: depressive symptoms decrease with the log of income. The additional twist of model m4 is that it also has a squared term, allowing for a possible increase again as income becomes very high. But the simple possibility, symptoms just going down and down as the log of income increases, is more strongly supported.
Thus, if I were writing this analysis up, I would say that the all the models that received any support featured a decrease in depressive symptoms as the log of income increases. The strongest support (55%) is for a model with no deviation from this relationship, with some support (45%) for a quadratic model allowing for an additional re-increase as the log of income becomes very large. Then I would report the parameter estimates and their 95% confidence intervals from the two models that received support. In the section on model averaging I will return to the question of which parameter estimates to report when you do model selection, but here I would fully report the estimates and their confidence intervals from both m2 and m4.
Note that AIC weights are defined relative to this particular set of models (m1, m2, m3 and m4), not any other set. If we include some other model in the set, the AIC weights can change, and the new model can even be better than any of the currently included ones.
We can try to understand why we got the results we got by plotting depressive symptoms against the log of income, and displaying with a locally-estimated smooth fit (this is a line that tracks the local average of y variable across the range of x). We do this as follows:
## `geom_smooth()` using method = 'gam' and formula = 'y ~
## s(x, bs = "cs")'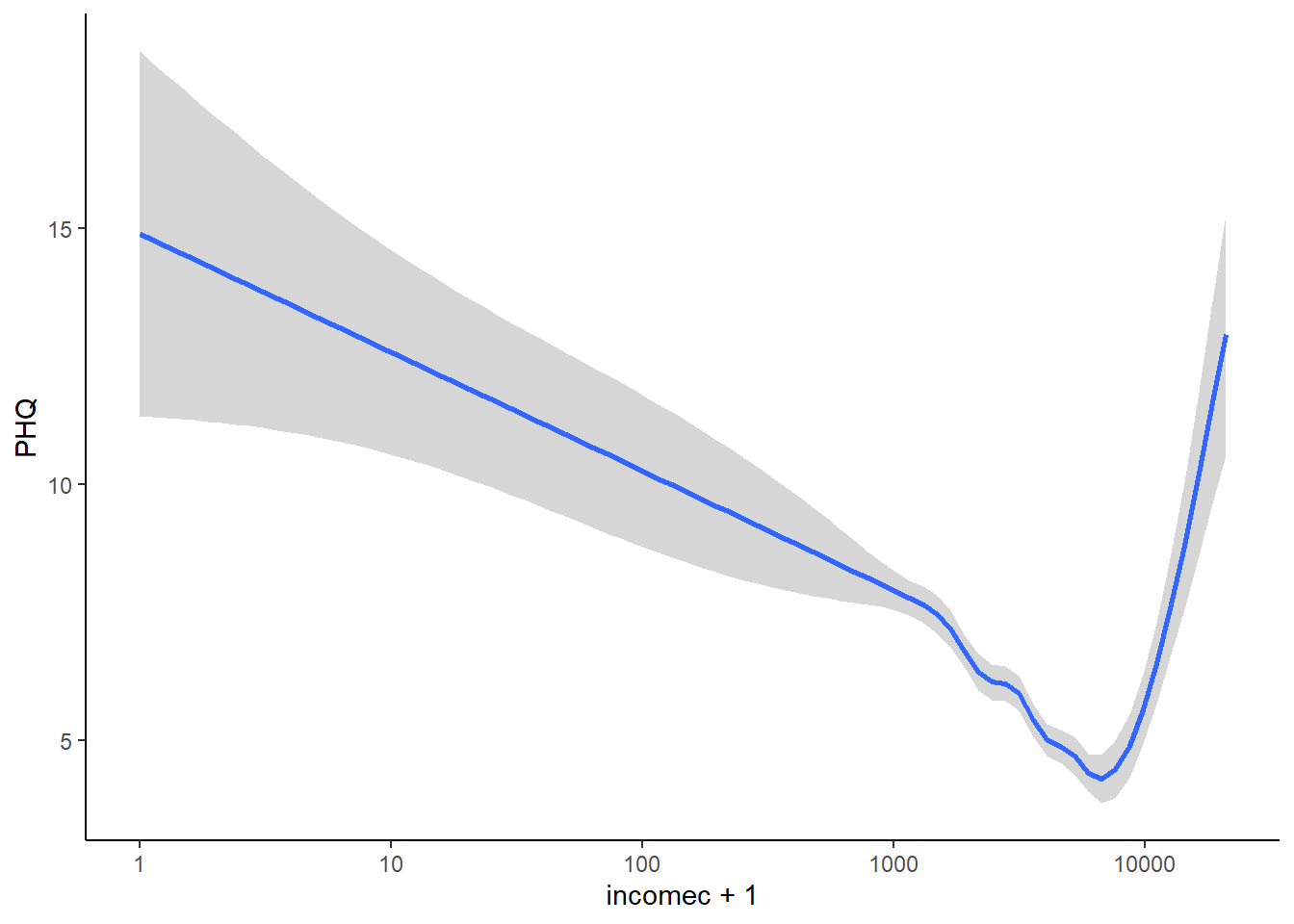
By eye, you can see very clearly how depressive symptoms go down and down as the log of income goes up. You can also see the apparent uptick especially from incomes of 10,000 euros upwards. This must be what is causing the quadratic-logarithmic model m4 to get some support.
The uptick looks so clear on the graph that you must be wondering why the support for m4 is not stronger. It must be because there are very few cases in this range of the data. Let’s check that:
## c$incomec > 10000
## FALSE TRUE
## 4777 66This means: give me a cross-tabulation of how many cases do and do not meet the condition incomec > 10000. And the answer is that only 66 cases do (about 1% of cases). And these cases belong to even fewer individuals (remember, each individual filled in their income up to 12 times).
Given the small number of cases, the evidence for any change in relationship after 10,000 euros is fairly weak, whereas the evidence for the negative relationship before 10,000 euros is very clear and based on many more cases. This is why m2 wins out.
Although I have stressed that model selection is different from NHST, you can include a null model in your set, so that this is one of the hypotheses that gets compared. The difference from more usual NHST is that all the non-null models are compared to one another, as well as the null model, during selection. Here, we would do this by making a model m5 that does not include incomec at all:
Now let us rerun the model selection including m5 in the set:
## Model selection table
## (Int) incom.scl mgn log.incmc sq.incmc sq.log.incmc df
## 2 5.643 + -0.3063 6
## 4 5.640 + -0.5707 0.3026 7
## 3 5.646 -0.69280 + 0.4878 7
## 1 5.642 -0.09599 + 6
## 5 5.639 + 5
## logLik AICc delta weight
## 2 -12050.73 24113.5 0.00 0.547
## 4 -12049.92 24113.9 0.40 0.448
## 3 -12054.53 24123.1 9.61 0.004
## 1 -12061.00 24134.0 20.54 0.000
## 5 -12062.35 24134.7 21.23 0.000
## Models ranked by AICc(x)
## Random terms (all models):
## 1 | pidThere is no support at all for model m5. Whatever we believe, we should not believe that there is no relationship between income and depressive symptoms. On the other hand, m5 is barely worse than m1. We should not believe that there is a linear relationship between income and depressive symptoms either. This makes sense. A linear relationship would imply that an extra 100 euros of income has an equal impact on the mental health of someone who already has an income 5000 a month as on the mental health of someone who currently has an income of 500 a month. We can see that this will not be so. Indeed, the fact that a given increment of income has a bigger effect when you don’t have much - the so-called diminishing marginal returns of income - is one of the best established findings in all of social science. Thus, the failure of m1 is expected, and reassuring.
15.4 Model selection for exploratory analysis: What drives temporal discounting?
We are now going to work through another example of using model selection, from the same dataset. This is a case where our objectives are exploratory.
The dataset contains a measure of temporal discounting. Temporal discounting is the extent to which you value an outcome realised sooner in time more highly than the same outcome realised further into the future. So, the higher your temporal discounting, the more you value the present over the future. Temporal discounting was measured in The Changing Cost of Living Study in a variable called timediscounting. The participants were offered seven hypothetical choices between smaller-sooner and larger-later amounts of money, and the variable is the number of smaller-sooner choices they made (so, the higher the score from 0-7, the more they discount the future).
Let’s say we don’t know what predicts temporal discounting and we want to explore. Here are some candidates:
Age. Perhaps you get more patient as you get older; or alternatively, you have not got so long left so you become more impatient! We will include both age and age squared, to allow of the possibility of some U-shaped or inverted U-shaped relationship.
Gender. Perhaps there are gender differences.
Income. If you are financially pressed because your income is low, you might well value some immediate financial input and hence have a higher rate of income. We will use logged income, which is almost always the right decision, as the last example showed.
Ill health. If your health is poor, you might be more focused on the here and now. The study has a self-rated general health variable (scale of 1-10) called
health. In fact, higher on this scale represents a worse health rating, so this is really a measure of ill health. (The codebook is misleading on this, I now notice).
There are other predictors we could imagine including, but for the sake of the excercise, we will limit consideration to these ones. We will also consider only the additive models (i.e. we are not going to consider the possibility that income and age interact, or age and gender interact, etc.). Again, you could explore these - in fact I encourage you to do so - but the number of possible models explodes exponentially and so for the current example we will limit ourselves to the additive models.
15.4.1 Preparing the data frame
You should still have data frame d in your environment from the previous section. If not, reload The Changing Cost of Living data as outlined earlier in the chapter.
Now, we need to select the cases that are complete for all of the variables we are going to need in the present analysis. We will do this by making a new data frame c2.
c2 <- d %>% subset(!is.na(timediscounting) &
!is.na(incomec) &
!is.na(mgender) &
!is.na(health) &
!is.na(age))Now, we want a logged income variable and an age squared variable. We also want our continuous predictors to be scaled. Let’s do all this ahead of time.
15.4.2 Running the model selection
There are quite a lot of possible models to consider this time. We could set them up manually and make a list, as in the previous example. However, we can also cheat this, where our objectives are exploratory and hence our a priori set of models is open, using a function called dredge(). To use dredge(), you define a maximal model, that is, the biggest set of predictors you are prepared to consider. dredge() then generates all possible simpler sub-models of the maximal model.
Let’s try this. Here is our maximal model:
max.model <- lmer(timediscounting ~
age.scaled +
age.squared +
gender +
log.income +
health.scaled + (1|pid), data=c2, REML=FALSE)Now we do the model selection on the set of models made by applying dredge() to max.model.
## Fixed term is "(Intercept)"## Global model call: lmer(formula = timediscounting ~ age.scaled + age.squared + gender +
## log.income + health.scaled + (1 | pid), data = c2, REML = FALSE)
## ---
## Model selection table
## (Int) age.scl age.sqr gnd hlt.scl log.inc df
## 29 2.947 + 0.1598 -0.05331 8
## 31 2.948 -0.10050 + 0.1603 -0.05399 9
## 30 2.947 -0.08921 + 0.1603 -0.05383 9
## 13 2.947 + 0.1636 7
## 15 2.948 -0.09781 + 0.1640 8
## 14 2.947 -0.08704 + 0.1641 8
## 32 2.949 0.27920 -0.38260 + 0.1599 -0.05426 10
## 16 2.949 0.26500 -0.36560 + 0.1637 9
## 25 3.195 0.1602 -0.05353 5
## 27 3.189 -0.11710 0.1607 -0.05432 6
## 26 3.190 -0.10420 0.1608 -0.05414 6
## 9 3.195 0.1640 4
## 11 3.189 -0.11440 0.1645 5
## 28 3.190 0.31880 -0.43930 0.1603 -0.05463 7
## 10 3.190 -0.10200 0.1646 5
## 12 3.190 0.30470 -0.42230 0.1641 6
## 21 2.945 + -0.06366 7
## 23 2.946 -0.09686 + -0.06433 8
## 22 2.945 -0.08408 + -0.06418 8
## 24 2.947 0.33750 -0.43810 + -0.06463 9
## 5 2.945 + 6
## 7 2.945 -0.09355 + 7
## 6 2.945 -0.08129 + 7
## 8 2.947 0.32240 -0.41950 + 8
## 17 3.195 -0.06387 4
## 19 3.190 -0.11370 -0.06466 5
## 18 3.190 -0.09930 -0.06448 5
## 20 3.190 0.37680 -0.49460 -0.06499 6
## 1 3.196 3
## 3 3.190 -0.11040 4
## 2 3.191 -0.09652 4
## 4 3.191 0.36160 -0.47610 5
## logLik AICc delta weight
## 29 -8226.448 16468.9 0.00 0.226
## 31 -8225.719 16469.5 0.55 0.172
## 30 -8225.845 16469.7 0.80 0.152
## 13 -8228.039 16470.1 1.17 0.126
## 15 -8227.350 16470.7 1.80 0.092
## 14 -8227.466 16471.0 2.04 0.082
## 32 -8225.559 16471.2 2.24 0.074
## 16 -8227.206 16472.5 3.52 0.039
## 25 -8232.841 16475.7 6.77 0.008
## 27 -8231.858 16475.7 6.81 0.008
## 26 -8232.024 16476.1 7.14 0.006
## 9 -8234.441 16476.9 7.96 0.004
## 11 -8233.505 16477.0 8.10 0.004
## 28 -8231.651 16477.3 8.40 0.003
## 10 -8233.661 16477.3 8.41 0.003
## 12 -8233.317 16478.7 9.72 0.002
## 21 -8239.627 16493.3 24.35 0.000
## 23 -8238.967 16494.0 25.04 0.000
## 22 -8239.105 16494.2 25.31 0.000
## 24 -8238.739 16495.5 26.59 0.000
## 5 -8241.893 16495.8 26.88 0.000
## 7 -8241.281 16496.6 27.66 0.000
## 6 -8241.408 16496.8 27.91 0.000
## 8 -8241.073 16498.2 29.25 0.000
## 17 -8246.041 16500.1 31.16 0.000
## 19 -8245.139 16500.3 31.36 0.000
## 18 -8245.319 16500.7 31.72 0.000
## 20 -8244.857 16501.7 32.80 0.000
## 1 -8248.317 16502.6 33.71 0.000
## 3 -8247.471 16503.0 34.02 0.000
## 2 -8247.639 16503.3 34.36 0.000
## 4 -8247.212 16504.4 35.51 0.000
## Models ranked by AICc(x)
## Random terms (all models):
## 1 | pidThere are a lot of models! To reduce the busyness of the display, you can just ask for the software to display those within a few of AIC units of the best model (the variable delta in the output is the difference in AIC between a model and the best model of the set). Restricting the display to models to, say, delta < 4 is going to show you just those models that get at least some AIC weight.
## Fixed term is "(Intercept)"## Global model call: lmer(formula = timediscounting ~ age.scaled + age.squared + gender +
## log.income + health.scaled + (1 | pid), data = c2, REML = FALSE)
## ---
## Model selection table
## (Int) age.scl age.sqr gnd hlt.scl log.inc df
## 29 2.947 + 0.1598 -0.05331 8
## 31 2.948 -0.10050 + 0.1603 -0.05399 9
## 30 2.947 -0.08921 + 0.1603 -0.05383 9
## 13 2.947 + 0.1636 7
## 15 2.948 -0.09781 + 0.1640 8
## 14 2.947 -0.08704 + 0.1641 8
## 32 2.949 0.27920 -0.38260 + 0.1599 -0.05426 10
## 16 2.949 0.26500 -0.36560 + 0.1637 9
## logLik AICc delta weight
## 29 -8226.448 16468.9 0.00 0.235
## 31 -8225.719 16469.5 0.55 0.179
## 30 -8225.845 16469.7 0.80 0.158
## 13 -8228.039 16470.1 1.17 0.131
## 15 -8227.350 16470.7 1.80 0.095
## 14 -8227.466 16471.0 2.04 0.085
## 32 -8225.559 16471.2 2.24 0.077
## 16 -8227.206 16472.5 3.52 0.040
## Models ranked by AICc(x)
## Random terms (all models):
## 1 | pidNow, there are quite a few models that get at least some support. At this point, you would want to ask what the supported models have in common. One thing is that they all include gender. There is no support at all for any model omitting gender. The second thing to note is that all the models with any weight include health, with a positive coefficient. Thus, people in worse health are more present-oriented. And quite a few of the models getting some weight include logged income.
A way of expressing the degree of support for logged income (or any other variable) being important is to sum up the total AIC weight received by models including that term. For example, for logged income, this would be `0.235 + 0.179 + 0.158 + 0.077 = 0.649’. So about 65% of the AIC weight goes to models including logged income. For gender and self-rated health, it is 100%: the model selection is unequivocal that these variables are important.
To report this analysis, I would explain that eight models received at least some support, and then provide the total AIC weight received by the different variables that are included in at least some of those eight. If you look at the model selection table above, the parameter estimate for health.scaled varies a bit across those eight. Should you just report the one from the first model in the table, or all eight?
15.5 Model averaging
The model selection table allows us to say how much support there is for the inclusion of a particular variable in the best model. But we don’t just want to know that, say, health is included. We want to know what the strength and direction of the association between health and time discounting is. That is, we want to provide a parameter estimate.
The problem is: which parameter estimate do we choose? There are eight different models receiving at least some support.
The solution to this dilemma is to report the average of the parameter estimates for health.scaled across the eight models, specifically the average weighted according to the degree of support that model received. We get this information using the function model.avg(), which we apply to the model selection table we have already generated.
##
## Call:
## model.avg(object = results, subset = delta < 4)
##
## Component models:
## '345' '2345' '1345' '34' '234' '134' '12345'
## '1234'
##
## Coefficients:
## (Intercept) genderPNTS genderSelf-describe
## full 2.94752 0.07023177 -0.1054886
## subset 2.94752 0.07023177 -0.1054886
## genderWoman health.scaled log.income age.squared
## full 0.4826788 0.1614065 -0.03484015 -0.07146609
## subset 0.4826788 0.1614065 -0.05373503 -0.18254723
## age.scaled
## full 0.01070094
## subset 0.02973999What we see is that the average parameter estimate for health.scaled is 0.1614065; the average parameter estimate for being a woman as opposed to a man is 0.4826788 (women are, it seems, more present oriented than men).
For some variables, there is a difference between the full and the subset parameter estimate. The full parameter estimate averages across all models in the set, taking the parameter estimate to be 0 in models where that variable is absent. The subset one averages only across the models in which that variable is included. (Hence, for variables that appear in all eight models, there is no difference between the two.) The one you should report is usually the full. When there is a support for some models omitting a particular variable, that is in effect support for the proposition that the parameter is zero for that variable, and this should be incorporated in your estimation.
Having given the total AIC weight going to the inclusion of particular variables, I would go on to give the model-averaged parameter estimates for the potentially important variables, either in a table or in the text.
In sum, our model selection and model averaging provides very strong support for gender and health status being associated with temporal discounting; weaker but still substantial support for (logged) income; and some support for age differences.
15.6 Summary
Model selection and model averaging are very powerful and flexible tools for certain kinds of data analysis. This session has given some examples of how to use them. Compared to NHST, model selection produces less of a bright line between ‘significant’ and ‘not significant’. It can produce degrees of support for the importance of a predictor on a more continuous scale. It also captures the uncertainty of inferential quite well, often finding some degree of support in the same dataset for several different models.
In the next session, we will consider the question of when you would choose model selection and when you would choose NHST as your analysis strategy.