7 Going a bit further with the General Linear Model
This session will go a little bit further than we did in the last session with the analysis of the behavioural inhibition data (Paál, Carpenter, and Nettle 2015). The aim is to get you to the point where you are able to do as much as the researchers did in the paper.
Start by reloading in the data as you did last time. You should have a script file somewhere with your work from last week, and it should contain the lines you need to load in the data.
7.1 Multiple predictors and partial coefficients
Last week, we considered a case of a General Linear Model with a binary predictor (experimental condition), and also the case of a General Linear Model with a continuous predictor (Age). But what about when you have several predictors at the same time? In the paper, the researchers had such a situation, because they wanted to consider the impact on SSRT of their experimental manipulation, Condition, and childhood socioeconomic deprivation, Deprivation Score, whilst controlling for Age and GRT (overall reaction time), which are covariates likely to explain some of the variation.
We fit this model exactly as in our existing cases, but now there are multiple variables on the right-hand side:
m3 <- lm(SSRT ~ Condition + scale(Deprivation_Score) + scale(Age) + scale(GRT), data = d)
summary(m3)##
## Call:
## lm(formula = SSRT ~ Condition + scale(Deprivation_Score) + scale(Age) +
## scale(GRT), data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -89.698 -23.490 -1.642 22.456 119.963
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 234.749 7.725 30.388
## ConditionNegative 7.638 10.789 0.708
## scale(Deprivation_Score) 14.210 5.354 2.654
## scale(Age) 17.004 6.164 2.759
## scale(GRT) -12.787 6.163 -2.075
## Pr(>|t|)
## (Intercept) < 2e-16 ***
## ConditionNegative 0.48212
## scale(Deprivation_Score) 0.01052 *
## scale(Age) 0.00799 **
## scale(GRT) 0.04297 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 39.64 on 52 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.2553, Adjusted R-squared: 0.198
## F-statistic: 4.457 on 4 and 52 DF, p-value: 0.003585Notice that I standardize all the continuous predictors. Now we have a parameter estimate (and standard error, and p-value) for each of the various things we thought might affect or be associated with SSRT. We have estimated them all simultaneously.
The intercept is again equal to the mean SSRT in the neutral condition. The parameter estimates are interpreted nearly as before: for Condition, the effect of moving from Neutral to Negative; and for the others, the impact on SSRT of a one standard deviation increase in the variable. However, the interpretation of these coefficients is not completely straightforward. Observe for example that the coefficient for Age is about 17 here. If you look back to the model that only had age as a predictor, it was less than 14. So, does SSRT increase by 17 msec per standard deviation of age, or 14 msec?
In a model with multiple predictors, the parameter estimates are called partial coefficients. They model the effect of a one-unit change in that variable on the outcome on the assumption that all other variables in the model are unchanged (they all stay at zero, if you like). In the model where age was the only predictor, the coefficient for age represented the change in SSRT that would be expected if age increased by a standard deviation. In the model m3, the coefficient for age represents the change in SSRT that would be expected if age increase by a standard deviation, and Condition, Deprivation_Score, and GRT stayed the same. Why are the two numbers different from one another (14 and 17).
It turns out that as you get older, your total reaction time, GRT, goes up. And a higher GRT means a lower SSRT. So as you age, two things happen that affect SSRT:
the direct effect: SSRT goes up;
the indirect effect: GRT goes up, and a higher GRT means a lower SSRT.
These two things partially offset one another: the direct effect causes SSRT to increase with age, and the indirect one causes it to decrease a bit with age. In model m2, we were estimating the sum of the direct and indirect associations; the total impact of age on SSRT which comes from both processes. In model m3, we are estimating only the direct effect; the model estimates the impact of an increase in age on SSRT in the case where GRT does not change at all, thus eliminating the indirect effect from consideration.
It is really important to understand that, comparing the parameter estimate for Age in m2 and in m3, one is not ‘better’ or ‘more accurate’ than the other. They are estimating two different quantities. In one case, the total effect on SSRT of age increasing by a standard deviation; and in the other, the effect on SSRT of age increasing by a standard deviation in a hypothetical case where GRT stays exactly the same.
In other words, the intepretation of a coefficient a General Linear Model depends what other variables are included in the model as predictors. As a corollorary, you have to think really hard about which variables to include, and which to not include, in your models. The right model for answering your question depends exactly what quantity you want to estimate, and that depends what your hypotheses and predictions are. In the present case, including GRT makes only a modest difference to what we conclude about age and SSRT (the parameter estimate is still in the same direction, and not much different in magnitude), but this is not always the case.
7.2 A more formal presentation of the General Linear Model
I have introduced the General Linear Model, using the R function lm() as a practical tool for you to estimate parameters that you care about using your data. It’s time to discuss a little more detail of what the model assumes and what is going on under the hood. Let’s consider the case of the model m2 that predicts SSRT from age. Everything we are going to say applies to more complex models like m3 as well, but it is easier to explain it for the simple case where there is only one predictor.
Formally, the model assumes that any value of SSRT, say the value of participant i, is going to be equal to \(\beta_0\), the intercept, plus \(\beta_1\) times the participant’s age.
\[ SSRT_i = \beta_0 + \beta_1 * Age_i \]
This cannot be all, however. If we plot the straight line of SSRT against Age, we do see a relationship, but the points do not line up neatly along the line. Look:
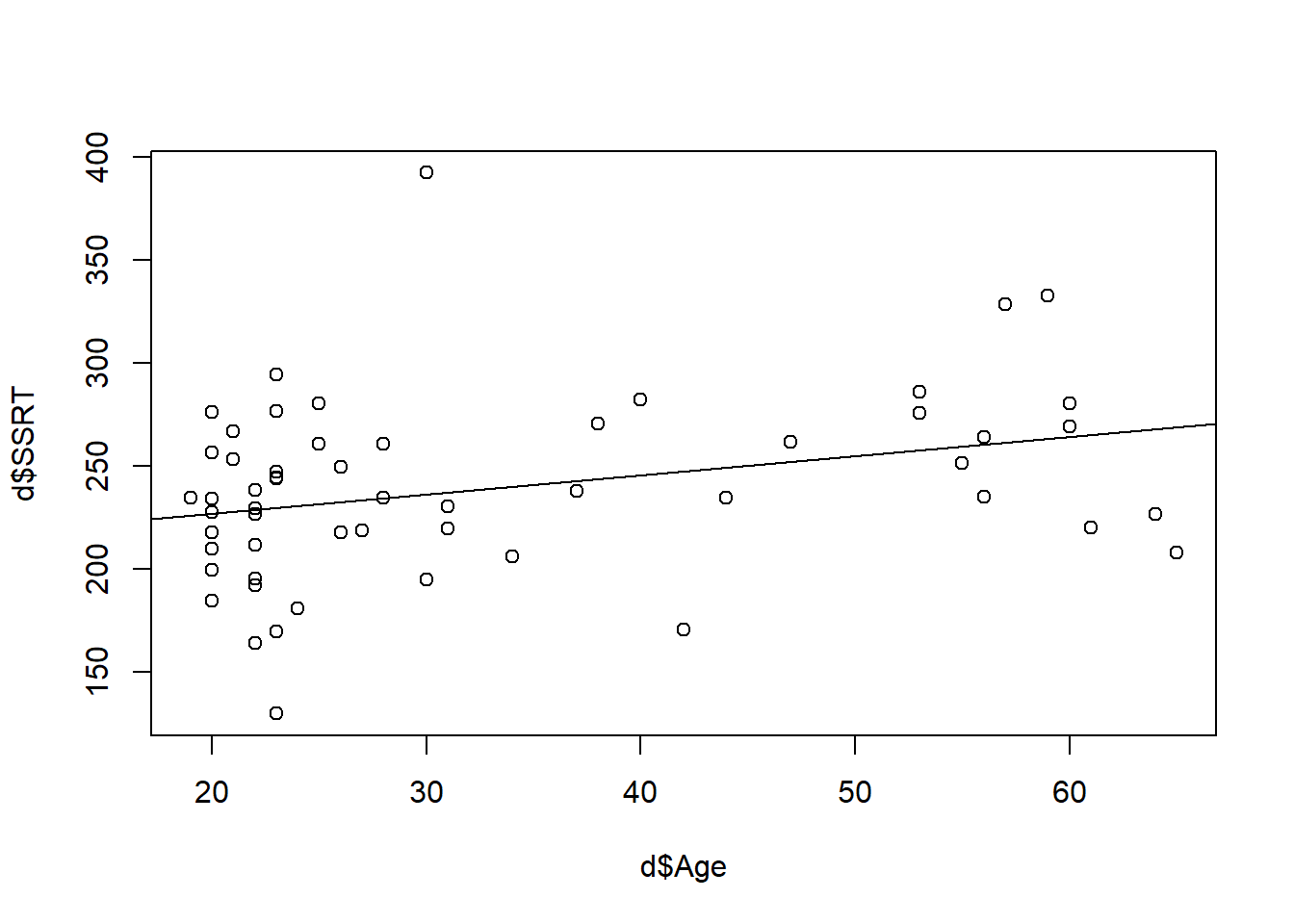As you can see, each point is either above or below the line predicted by just \(\beta_0 + \beta_1 * Age\), by varying distances. The model handles this by including an error term for each case, which means the actual values are a bit higher or lower than \(\beta_0 + \beta_1 * Age\). This could be to do with measurement error, or the fact that in the real world there are many other influences on SSRT other than just the variable include in our model. We don’t know what the value of the error term is going to be for any particular case of course; that is assumed to be beyond the scope of our knowledge. But the model makes two assumptions: one, that the average error is 0 (that is, some points are above and some below the line but there is no systematic direction); and that the errors are generated by something like a Normal distribution, which means a bell shaped distribution where most of the errors are small and larger errors are rarer.
So the full model is actually: \[ SSRT_i = \beta_0 + \beta_1 * Age_i + \epsilon_i \\ \epsilon \sim N(0, \sigma^2) \]
What does this mean?
The first line says: the SSRT of participant i will be \(\beta_0\), plus \(\beta_1\) times their age, plus some error term \(\epsilon\) whose value is unpredictable from any information included in the model.
The second line says: although we don’t know the values of the individual error terms for specific participants, we can assume that they are generated from a Normal distribution with a mean value of 0, and a variance \(\sigma^2\). We don’t know the value of \(\sigma^2\), but just like \(\beta_0\) and \(\beta_1\), we can estimate it using the data. This is what the model fitting does.
7.3 Checking assumptions: Distributions of residuals
The difference between the predicted value for each case (the point on the straight line shown on the scatter plot above which is at the appropriate place on the horizontal axis), and the actual value, is known as the residual. The residuals are the empirical manifestation of the errors \(\epsilon\). Because the model assumes that errors are generated from a Normal distribution, the residuals should have a symmetrical, roughly bell-shaped distribution. If this assumption is badly violated, our parameter estimates may be misleading. It is therefore worth checking what the distribution of the residuals looks like for any given model.
The residuals are stored in a variable that is part of the model object. Let’s look at them:
## 1 3 4 5
## -60.7790629 39.2654062 4.8850813 -76.9239995
## 6 7 8 9
## 0.6982350 -41.0462340 -6.8628822 7.3982350
## 10 11 12 13
## -27.2017650 -16.9017650 16.2850813 -41.1300534
## 14 15 16 17
## -14.6896572 27.2073159 9.8118563 -25.4836033
## 18 19 20 21
## 18.0148832 3.7163967 49.1340908 67.1835679
## 22 23 24 25
## 28.6148832 -14.7315669 36.8416582 69.6179102
## 26 27 28 29
## -14.7987380 -33.4674226 -27.0017650 29.9982350
## 30 31 32 33
## -49.6330803 -8.0507745 -42.2017650 -9.2017650
## 34 35 36 37
## 14.9997485 -17.1674226 25.3654062 -33.9613688
## 38 39 40 41
## 9.5325774 64.7997485 156.1699466 -17.3628822
## 42 43 44 45
## 14.1997485 29.2340908 -59.7002515 26.7356043
## 46 47 48 49
## 17.1012620 17.7997485 -36.6674226 -44.9477475
## 50 51 52 53
## 49.5982350 46.8997485 0.9325774 -64.7674226
## 54 55 56 57
## -99.7002515 0.3356043 8.7310639 -4.6598553
## 58
## -2.0674226Some SSRTs are close to the predicted line, so the residual is close to zero; others are 40, 50 or even 60 msec off, in either the positive or negative direction. The critical thing is the shape of the distribution of the residuals, so let’s use hist() to look at that:
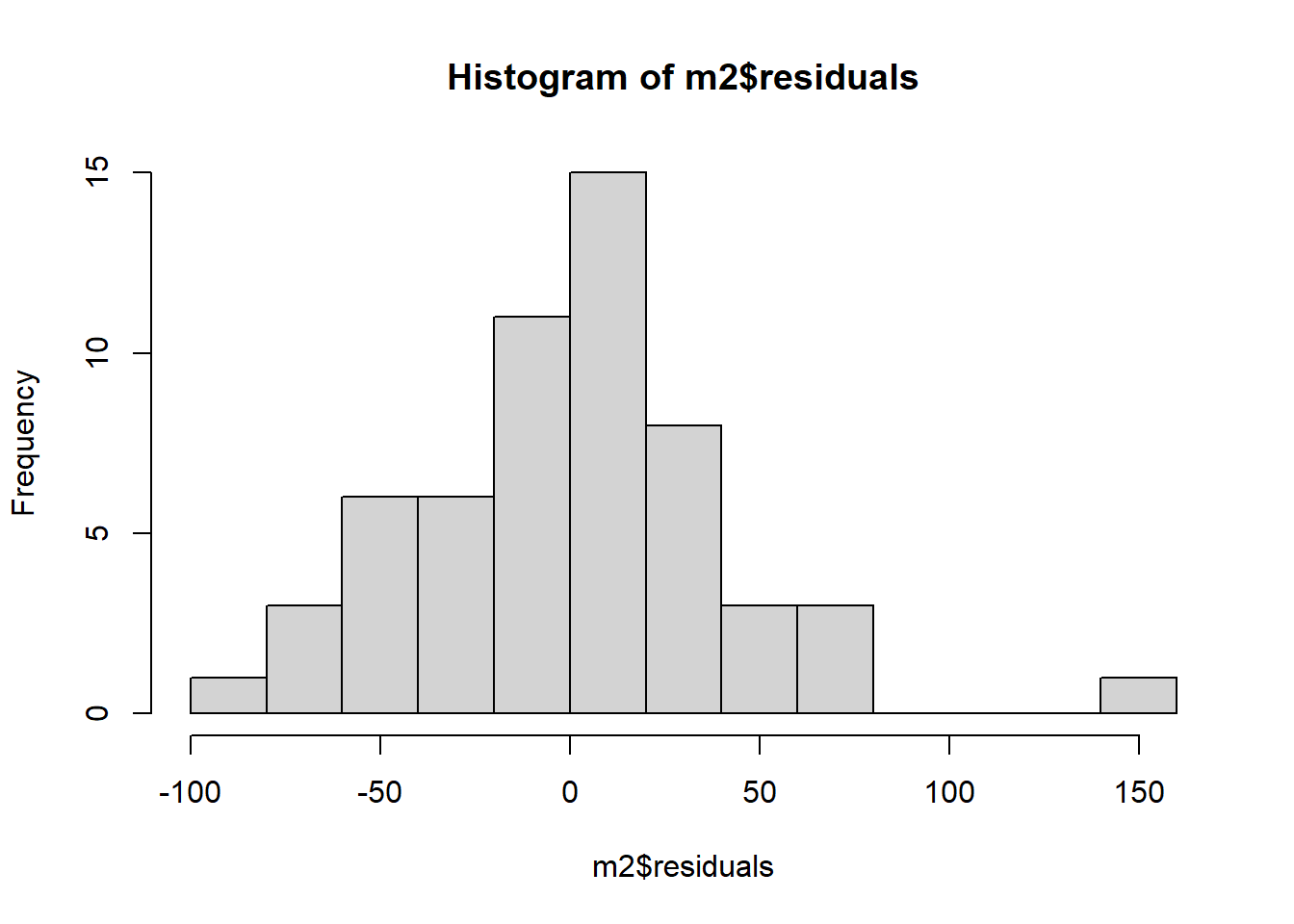It’s not a disaster, but the distribution is not quite symmetric. The positive residuals are made up of many very small values and one really big one (about 150 msec) that has no correspondingly large counterpart on the negative side.
The question arises: how asymmetric does the distribution of residuals have to be for us to worry about the intepretability of our parameter estimates? It’s a reasonable question but there is not a simple answer.
Some people are keen on doing ‘Normality tests’, statistical tests that are supposed to tell you if your residuals are ‘significantly’ different from those generated by a Normal distribution function. These should be avoided. Why? Because, as we said last week, whether a statistical test is significant depends to a great extent on the sample size. If the sample size is small, these tests won’t give you a significant p-value even if the departures from Normality of the residuals are really quite consequential. If the sample size is large, the tests will almost always be significant. The Normal distribution is a theoretical distribution after all, and no actual dataset corresponds exactly to its distribution function. Even human heights, the classic example of a Normally distributed variable, depart subtly from the theoretical distribution. So in a large sample, your Normality test would be significant even if the departures from Normality were inconsequential.
Some statistics courses even tell you to do Normality tests on the outcome variable itself, rather than the residuals! I can only think that origin of this nonsense is that, if all the parameters are exactly zero, the distribution of the outcome variable is the same as the distribution of the residuals. Thus, in a world where all associations and effects are very weak, the distribution of the outcome variable approximates the distribution of the residuals. It is still nonsense, though.
We will return below to the issue of what to do if your residual distribution is asymmetric, but only after looking at another important assumption.
7.4 Checking assumptions: Heteroscedasticity
If you look back to our equation for our General Linear Model, the variance of the residuals is a constant, \(\sigma^2\). This means that the dispersion of the residuals should be the same from the whole dataset. It should not change across the range of our predictor variables. It should not, for example look like this (which is based on some made up data):
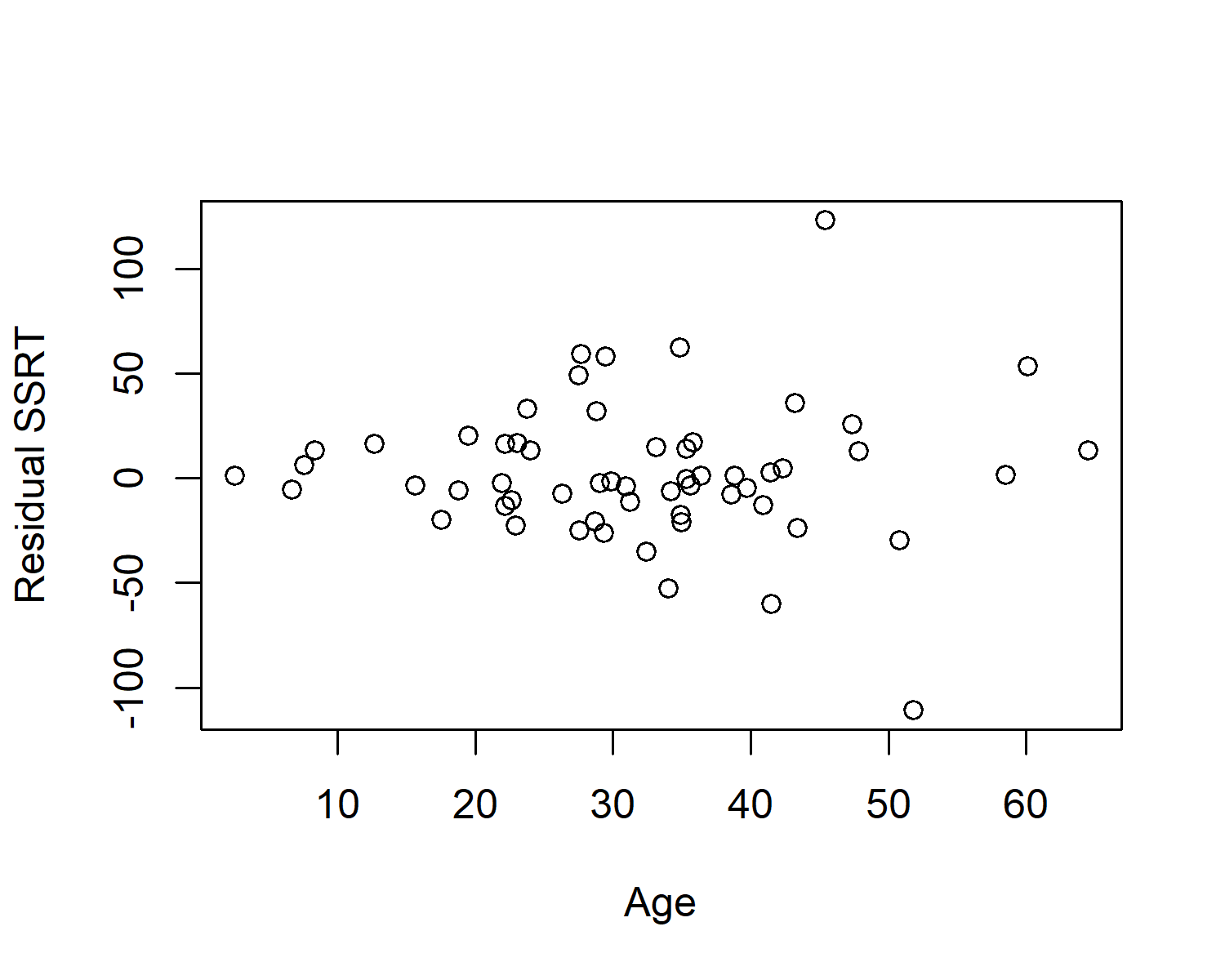
In this case, the residuals are tightly clustered around zero in the young people in the sample, but much more variable for the older people in the sample.
The assumption that the variance of the residuals is constant across the range of the predictor variables is known as heteroscedasticity.
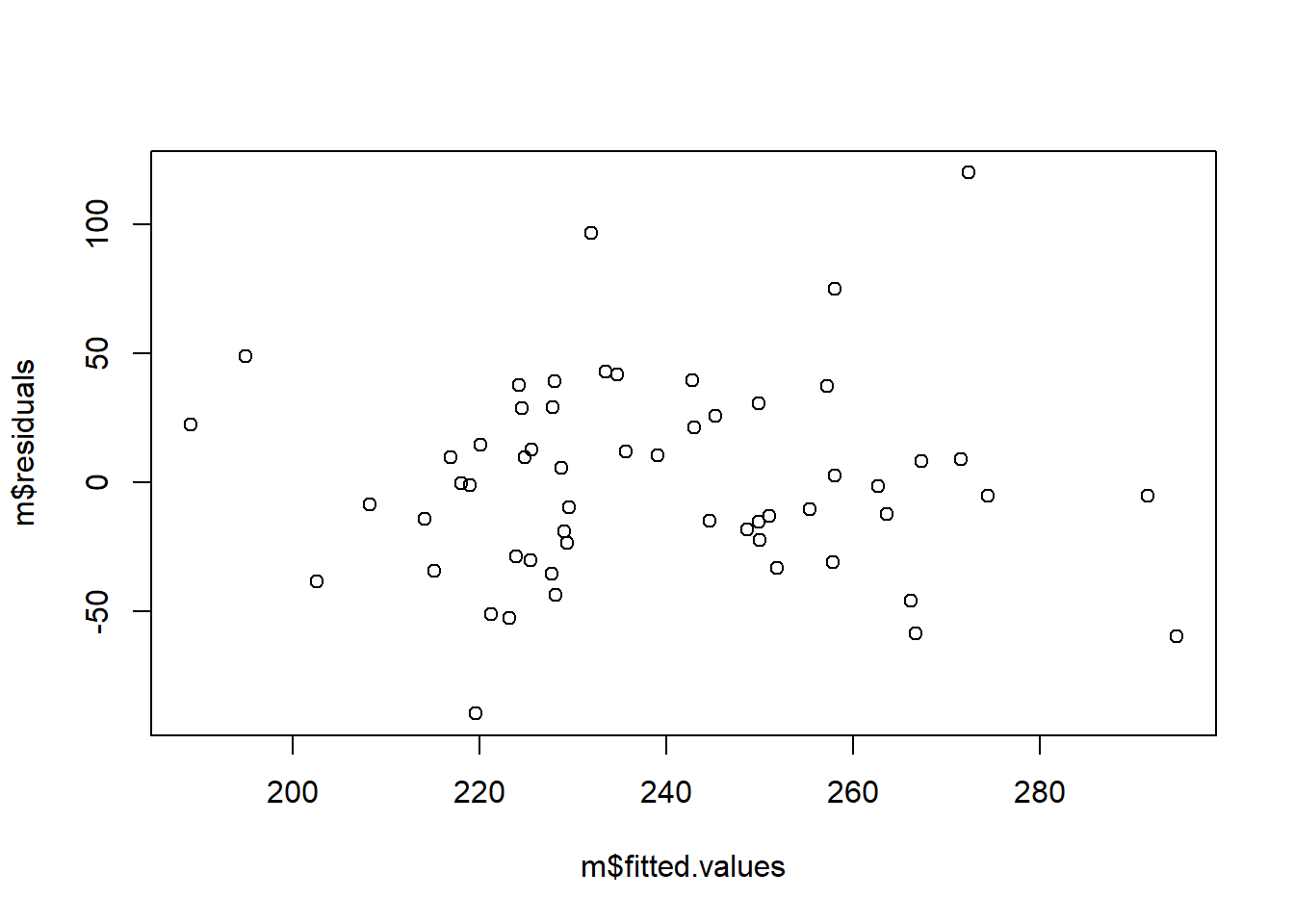
You can assess to what extent your data are compatible with the assumption of heteroscedasticity by making a plot of the residuals against the fitted values of the model:
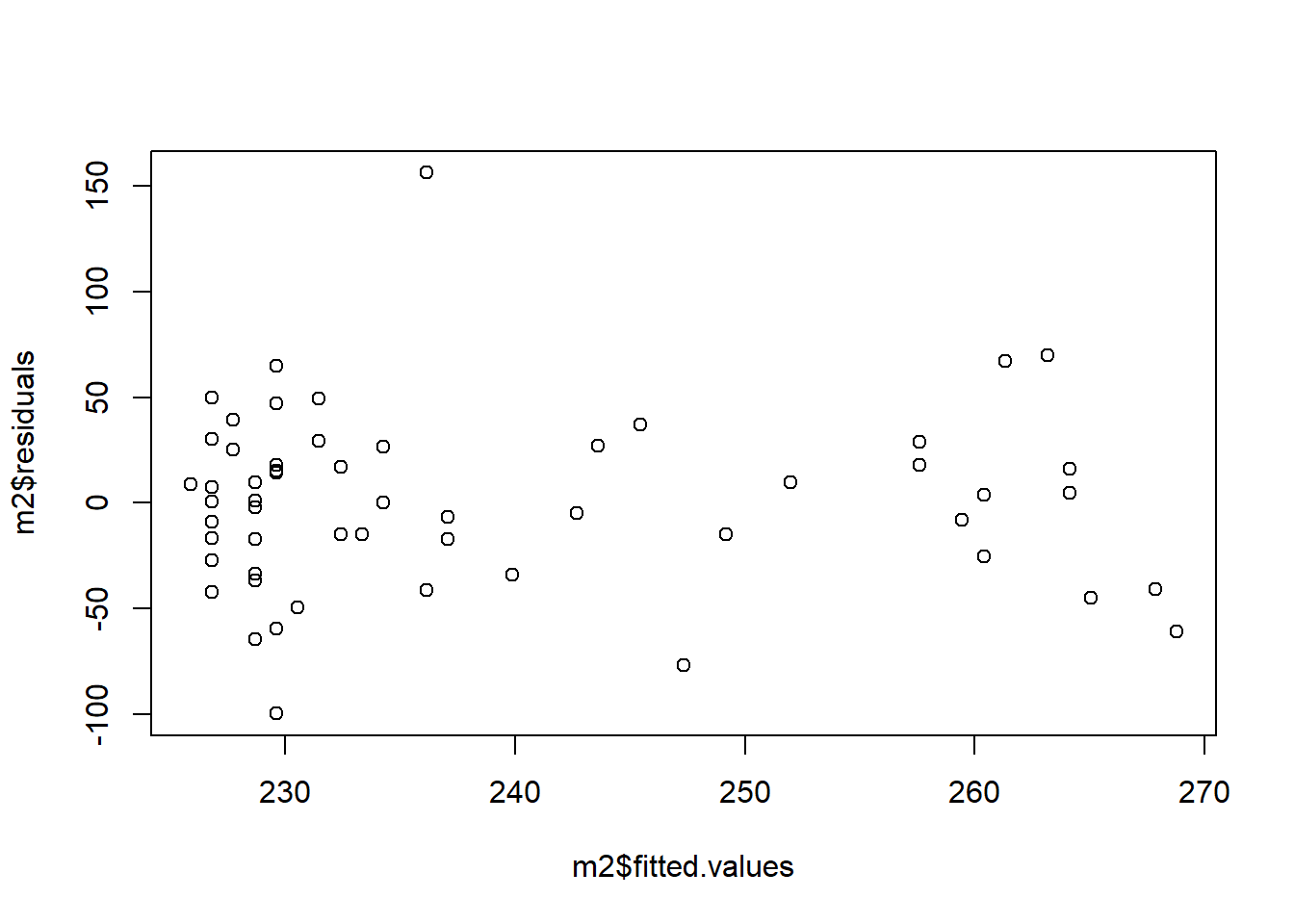
What you are looking for is not to see any obvious pattern like the expanding funnel in my made up example, or a contracting funnel either. If there is no obvious pattern, the assumption is not too badly violated.
7.5 Transformations
Something I have not addressed thus far is what you do if the distribution of your residuals is asymmetric or there is an obvious violation of heteroscedasticity. The solution ‘lite’ is to transform your outcome variable. The solution ‘dramatic’ is to use a different kind of model than a General Linear Model (a Generalized Linear Model of a different class). I won’t say much about the solution ‘dramatic’ today, as we will cover Generalized Linear Models in a future week.
The rest of the section will treat how you transform your data for the solution ‘lite’.
If your problem is that the residuals are right-skewed and/or there is more variation in the residuals at large values of the predictors, then you should consider logarithmic transformation of your data. A right-skewed distribution is one that looks something like this:
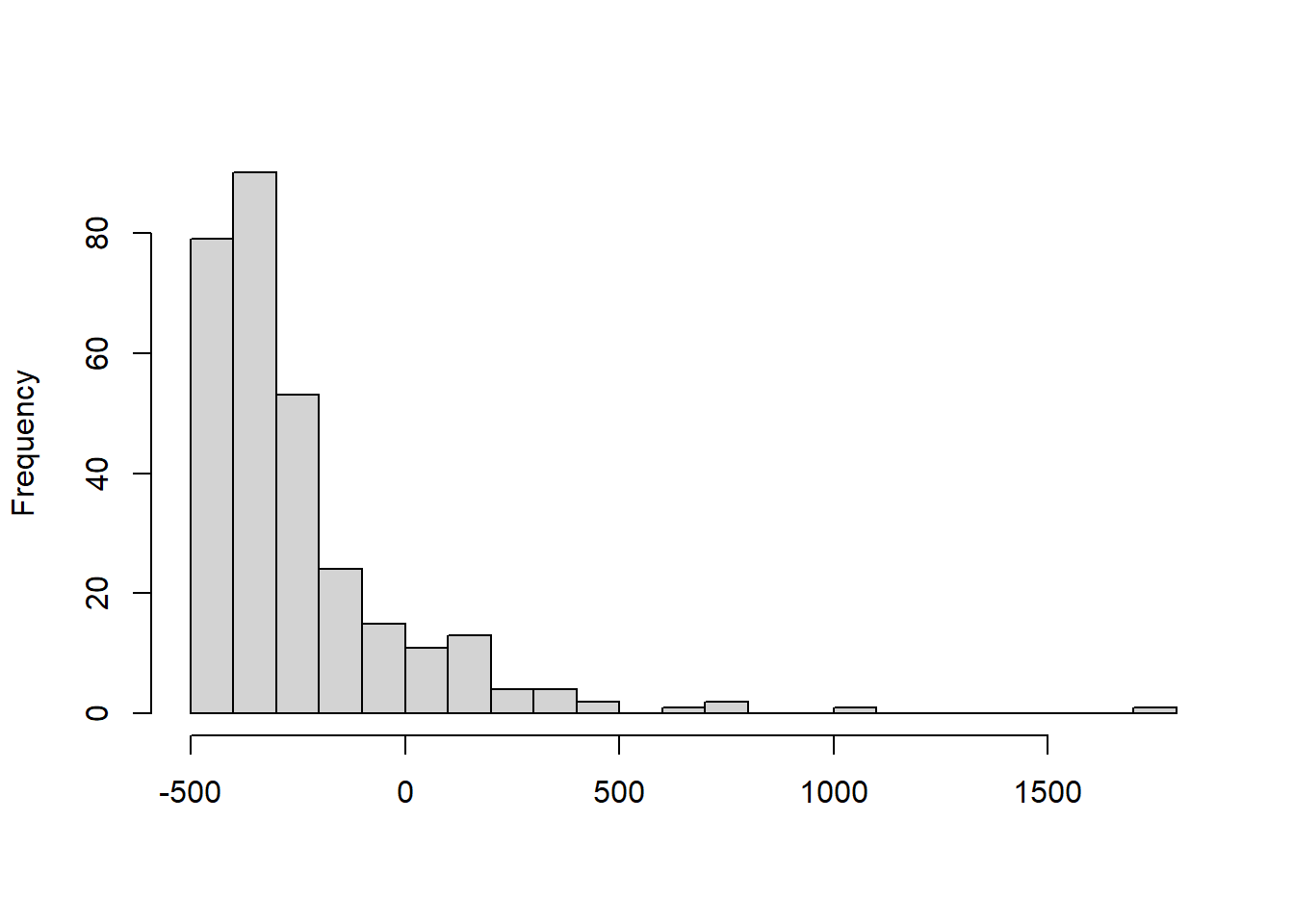
In this case, if you take the logarithm of your outcome variable, the extreme high cases will be ‘pulled in’ towards the centre of the data (because taking the logarithm has a proportionally larger impact the larger the value). Your residual distribution will be compressed to the left to look more like this:
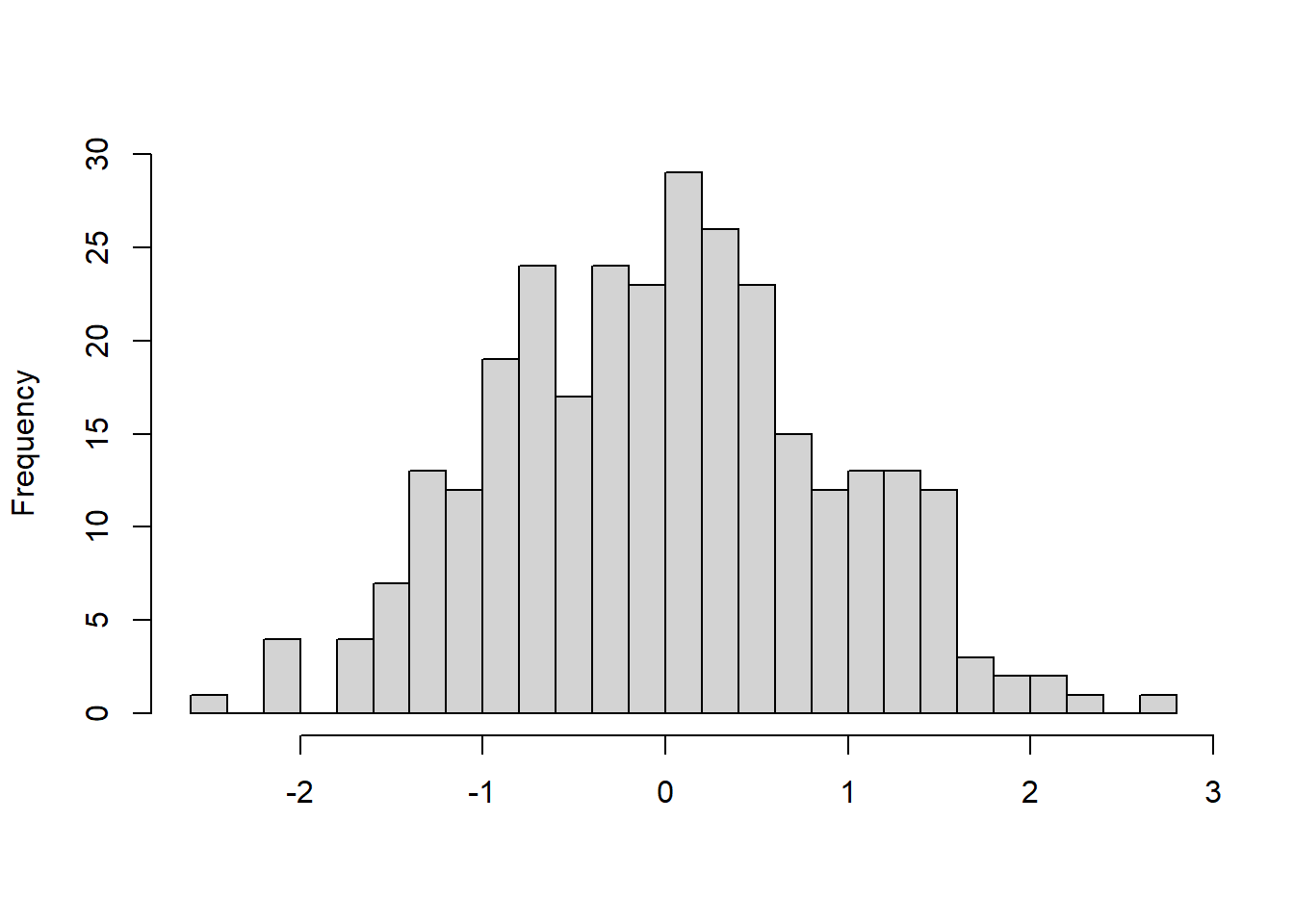
Lovely! You take the (natural) logarithm in R using the function log().
Note that you can only take logarithms of positive numbers, so if your variable contains zeros, you will have to add 1 to every value before logging. If your variable contains negative values, you will need to add the minimum value plus 1 to make everything positive prior to logging.
What if your dataset shows the opposite pattern, left-skewness (long tail to the left) or greater residual variation at low values? You might want to try subtracting the variable values from their maximum value plus 1, to turn the low numbers into high ones and the left-skew into a right-skew, and then logging. Remember though that when you interpret your parameter estimates, high values are now low and vice versa.
There are also other transformations (square root, inverse, arcsin) that can be helpful, but we don’t say anything more about them here.
Going back to the behavioural inhibition data and model m2, we thought that the heteroscedasticity looked ok, but maybe the residuals were a bit right-skewed. So there would be some justification for running the model using a logarithmic transformation of SSRT instead of the raw values. There are no negative or zero values and so logging will not be a problem. Here is how we do it:
##
## Call:
## lm(formula = log(SSRT) ~ scale(Age), data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.55315 -0.11079 0.01905 0.11869 0.52456
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.45838 0.02373 230.032 <2e-16 ***
## scale(Age) 0.05829 0.02394 2.435 0.0182 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1791 on 55 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.09729, Adjusted R-squared: 0.08088
## F-statistic: 5.928 on 1 and 55 DF, p-value: 0.01818This model produces the same conclusion as the untransformed variable: SSRT increases significantly with age. The parameter estimate for Age has a different value, of course, because in m2.logged it represents the change in the logarithm of SSRT with every increase of one standard deviation in age, rather than the chance in SSRT itself.
If you read the paper carefully, you will see that the researchers considered whether a logarithmic transformation of SSRT might be better, and fitted models this way too. In the end they report the non-logged ones in the paper since, as they say, it leads to identical conclusions in this case. This is not necessarily always the case though: it can make a dramatic difference to what you conclude, especially if the violations are marked. You should therefore always check carefully for residual normality and violations of heteroscedasticity when you use a General Linear Model.
7.6 Reporting your analysis
Having run a data analysis as we have done here, you need to do two things. The first is to make the definitive analysis script, to show to your collaborators and publish in the repository; and the second is to write up the analysis in the relevant section of your paper or thesis.
Here is the script I would file for the data analysis that we have produced so far (I would probably want to do some other things, like make some nice figures). Note how I use comments to make it comprehensible for readers and for myself if I come back to it in the future. Make sure you understand what all of this code is doing. (I assume in the following that we have settled on the model with all the predictors, m3 in the naming we used so far, as the definitive model.)
# Script to analyse the Paal et al. data
### Preliminaries #####
# Load up required packages
library(tidyverse)
library(table1)
# Read in the data
d <- read_csv("https://dfzljdn9uc3pi.cloudfront.net/2015/964/1/data_supplement.csv")## New names:
## Rows: 58 Columns: 13
## ── Column specification
## ─────────────────────────────────── Delimiter: "," chr
## (1): Experimenter dbl (12): ...1, Sex, Age,
## Deprivation_Rank, Deprivation...
## ℹ Use `spec()` to retrieve the full column specification
## for this data. ℹ Specify the column types or set
## `show_col_types = FALSE` to quiet this message.
## • `` -> `...1`# Rename the first column
colnames(d)[1] = "Participant_Number"
# Calculate a change in mood variable
d <- d %>% mutate(Difference_Mood = Final_Mood - Initial_Mood)
# Recode the Condition variable nicer and make Neutral the reference category
d <- d %>% mutate(Condition = case_when(Mood_induction_condition == 1 ~ "Negative", Mood_induction_condition == 2 ~ "Neutral"))
d$Condition = factor(d$Condition, levels=c("Neutral", "Negative"))
### Descriptive statistics #####
table1(~ SSRT + Deprivation_Score + Age + Difference_Mood|Condition, data=d,
overall=c(left="Total"))
### Fit the statistical model ####
m <- lm(SSRT ~ Condition + scale(Deprivation_Score) + scale(Age) + scale(GRT), data = d)
summary(m)
### Check model assumptions ####
# Plot a histogram the residuals for model m
hist(m$residuals, breaks=10)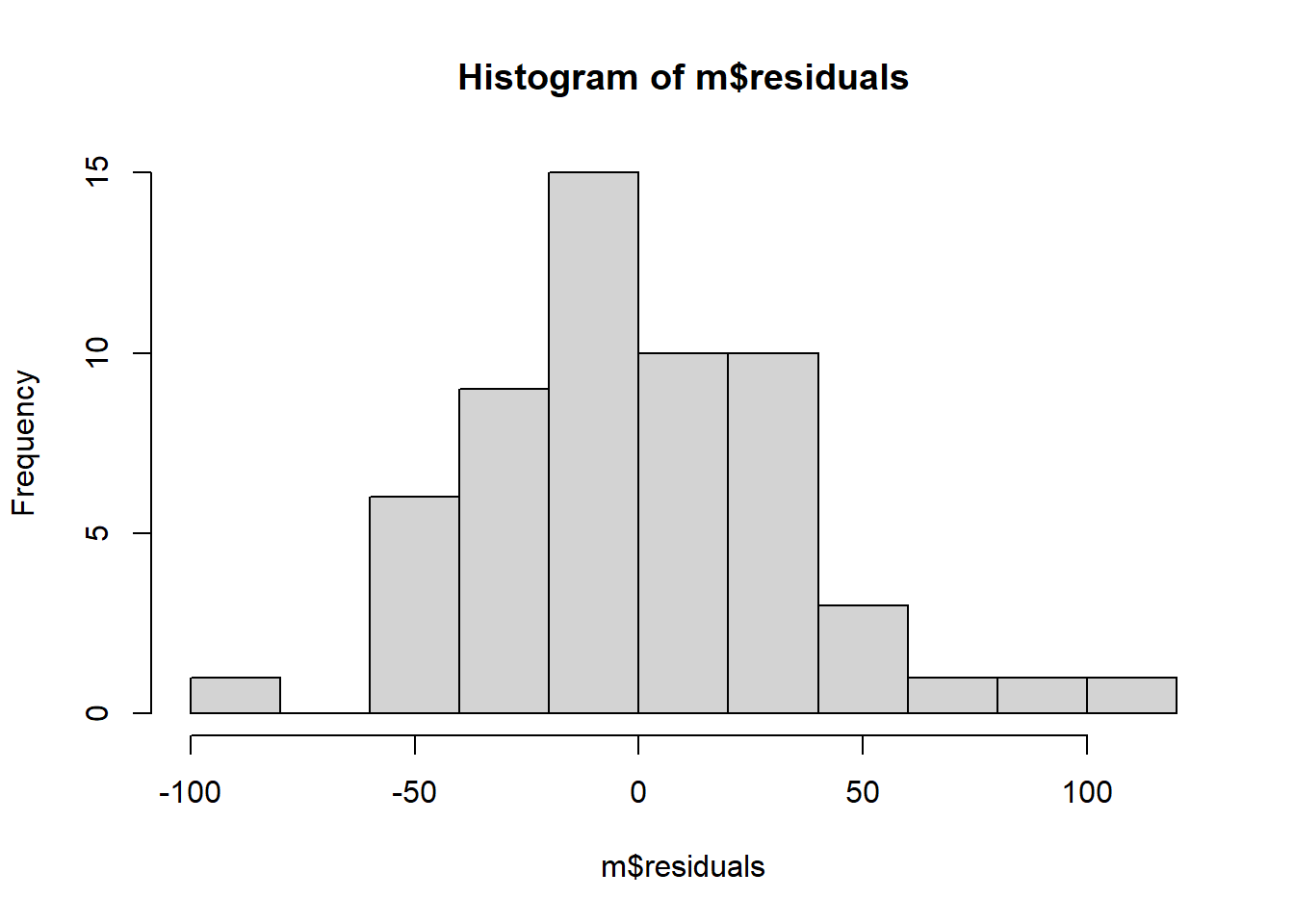
Now, the write up. With a General Linear Model, you have the choice between describing the results within the continuous prose, or putting some of the statistical values into a table that you refer to in the continuous prose. I will show you both versions here.
Continuous prose version, roughly:
We fitted a general linear model with SSRT as the outcome variable and condition, deprivation score, age and GRT as predictors. The residuals were checked for asymmetry and heteroscedasticity revealing no concerns. The effect of condition was not significantly different from zero (\(B_{negative}\) = 7.64, se = 10.79, t = 0.71, p =0.482). However, there was a significant positive association between SSRT and deprivation score, with individuals with higher deprivation scores having higher SSRTs (\(B\) = 14.21, se = 5.35, t = 2.65, p = 0.011). SSRT was also significantly positive associated with age (\(B\) = 17, se = 6.16, t = 2.76, p = 0.008), and inversely associated with GRT (\(B\) = -12.79, se = 6.16, t = -2.07, p = 0.043).
Note that we tend to refer to the parameter estimates as \(B\). Where it is a binary variable, as for condition, we indicate with a subscript which category the parameter estimate reflects the effect of. No such subscript is required for a continuous variable.
Now for the table version:
We fitted a general linear model with SSRT as the outcome variable and condition, deprivation score, age and GRT as predictors. The residuals were checked for asymmetry and heteroscedasticity revealing no concerns. Table 2 summarises the results. As the table shows, the difference in SSRTs between the neutral and negative conditions was small and not significantly different from zero. However, SSRT was significantly positively associated with deprivation score (increasing by 14 msec per standard deviation of deprivation score), and with age (increasing by 17 msec per standard deviation of age). It was also negatively associated with GRT (decreasing by 13 msec per standard deviation of GRT).
| Variable | B | se | t | p |
|---|---|---|---|---|
| Intercept | 234.75 | 7.73 | 30.39 | 0.000 |
| Condition (negative) | 7.64 | 10.79 | 0.71 | 0.482 |
| Deprivation score | 14.21 | 5.35 | 2.65 | 0.011 |
| Age | 17.00 | 6.16 | 2.76 | 0.008 |
| GRT | -12.79 | 6.16 | -2.07 | 0.043 |
This table was (like this whole course document) was actually made directly from R without any need for any manual typing of numbers. We will learn how to do this in a later week.
7.7 Summary
Today’s practical has continued our use of the General Linear Model to analyse the behavioural inhibition data. We have:
fitted a model with multiple predictors and learned how to interpret the coefficients;
examined the underpinning assumptions of the General Linear Model;
learned how to inspect residuals for evidence of violation of assumptions;
discussed logarithmic transformation of variables;
looked at how to report General Linear Model output.