16 Developing your analysis strategy
16.1 Introduction
In the course so far, we have met a number of statistical tools, and a number of ways of testing hypothesis using them. On the tools side, we have the General Linear Model (continuous outcomes); Generalised Linear Model (outcomes that are binary or counts); Linear Mixed Model (when there is clustering in your data, e.g. by participant); and Generalised Linear Mixed Model (when the outcome is binary or count and there is clustering). On the hypothesis testing side, we have comparing parameter estimates to zero; ANOVA tables; or model selection using AIC. (These are, by the way, not the only hypothesis testing tools that exist, just those we have covered in this course).
This session brings all the work so far together, to answer the following question: which strategy is most suited to which kind of situation? How do I plan how to go about my data analysis?
This question arises most obviously in the case of writing a preregistration. This must contain a section called ‘Analysis strategy’ or ‘Analysis plan’. In this, you will say how you propose to pursue your research questions or test your predictions once you start on the data analysis. Getting your analysis strategy right before you start will save you a lot of mess and difficulty later. Specifying the analysis plan ahead of time is not just good from an epistemic point of view, since it reduces researcher degrees of freedom. It is also tremendously helpful for you as a researcher. It means you have to think hard about what you are trying to do; it saves time later; it helps you remember what your goals were; and above all it reduces the probability that you will design your study wrong, and then end up having to do it all over again.
In this session, we will talk about the principles that might guide your choice of analysis strategy. There are no very hard and fast rules, and people’s preferences vary. The rules of thumb I will set out are the ones that seem most often appropriate in my own experience.
At a very minimum, you should plan your analysis strategy ahead of time (even if the data have already been collected). An even more thorough option is to simulate a dataset. You then write the code to analyse the simulated data and draw the figures. That way when the actual data come, you can plug them more or less straight in to the code that you developed on the simulated data. You can vary the parameters of the simulation code so you get a sense of what it will look like if your predictions are met, and if they are not. It is very easy to write R code to simulate data; we will briefly encounter this in a later session.
16.2 My rules of thumb
Now we come to my analysis strategy rules of thumb. I summarise them in the table below, before discussing each row in more detail in the text that follows.
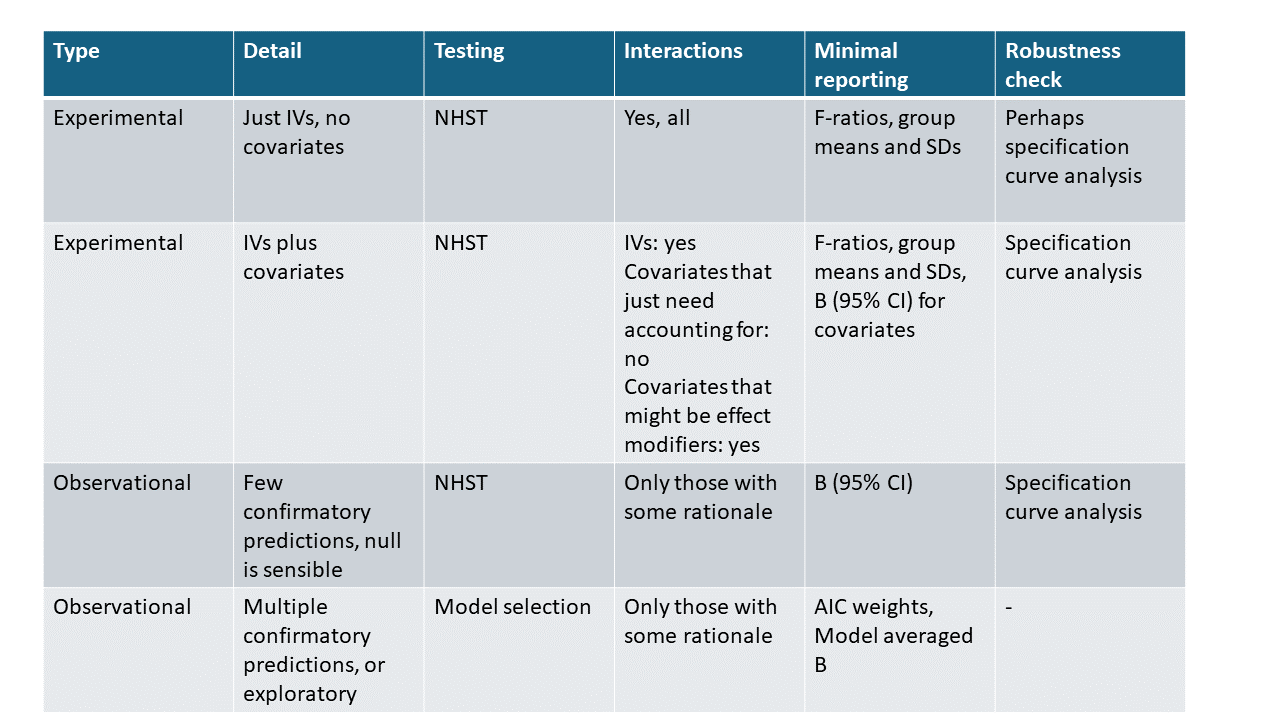
I see four common situations you might face. Sometimes your study falls a bit in the grey zone, or does not correspond to any of these. This can make it hard, and you will have to use judgement. Even then, it is useful to have these four prototypical cases in your mind when deciding on intermediate ones.
The situation you face is determined by the type of study (experimental or observational); the variables you need to account for; the confirmatory or exploratory nature of the goal; and the kinds of predictions you want to test. We will now go through the four situations one after the other.
16.2.1 Case one: Experiments with no covariates
This is the classic situation where you want to predict a DV from some set of IVs, which are usually cross-balanced, so that every level of the first IV is equally likely to appear with every level of the other IVs. Moreover, there are no covariates: you randomly assigned individuals to treatments (or to an order of treatments in cases of within-subjects manipulation), and you simply want to know whether each treatment has an effect.
Here, I would fit the model with the IVs on the right-hand side and the DV on the left-hand side. I would include all possible interactions between IVs. Even if you have no strong reason to expect interactions, it is important to know whether one of your treatments modifies the effect of the other(s).
In terms of statistical tests, I would usually present F-ratios from the ANOVA table. As we saw in the session on ANOVA, this is a form of NHST; it tests the null hypothesis that all the group scores are generated from a distribution with the same mean. It is a simple approach to hypothesis testing that is unaffected by how many levels each IV has. However, as well as knowing whether any group differs from any other, you want to know which ones differ, and in what direction. I would therefore include the means and standard errors from each experimental group, on a graph or in a table, plus an effect size measure like Cohen’s d in the case of comparison of two means (Cohen’s d is the difference between the two means expressed in units of their pooled standard deviation; there are R packages that will calculate it for you). Alternatively, you might want to present some or all individual parameter estimates and their 95% confidence intervals.
At this point, you might be wondering, in an experimental study, when should I include covariates, and when should I not do so? After all, there is almost always something that you have recorded that you could conceivably include.
This can be a tricky question, but there are a couple of things to bear in mind. First, you rarely want to include a covariate that could be influenced by your IV. For example, if you are showing people scary films, don’t include negative emotion as a covariate. Watching a scary film could induce negative emotion, which could in turn influence your DV. The moment that you include a covariate that can be influenced by your IV, you are no longer estimating the simple, total, causal effect of your intervention on the DV. You are estimating something more complex (the part of the total causal effect that is not brought about by changes in the covariate), and that is a whole different question, probably not the one you are trying to address.
What about covariates that cannot be influenced by your IV? Sometimes you need to include these because you know that they drive quite a lot of the variation in your DV that is not to do with your IV. In the name of simplicity us much as anything else, it is usually a good principle to balance these variables. This may obviate the need to include them as covariates. For example, design your experimental groups so that the gender ratio, mean age, or whatever, are equal.
Sometimes your possible covariate is something generated by your method, such as experimental session, experimenter, or which specific stimulus was used. In this case, if the variable has more than four or so levels, consider treating it as a random effect in a Linear Mixed Model, rather than an additional predictor in a General Linear Model.
Even so, sometimes you do need to include covariates as additional predictors in the analysis of experimental data. We will come to these situations in case two.
For case one, there is often no need for much in the way of robustness analysis. The exception would be if there are multiple ways of specifying your DV (for example, log transformed or not), or multiple subsets of observations you might run the analysis on (all participants, only those participants who successfully completed an attention check, etc.). To explore robustness to these variations, use specification curve analysis on the different possibilities. However, don’t consider models that omit any of your IVs. These are part of your design. No reasonable analysis would not have included them, and it makes no real sense to consider models that omit them.
16.2.2 Case two: Experiments with covariates
Case two is when you have an experiment, and you feel you really need to include one or more covariates. There are two possible reasons for this. The first is that the covariate is something you could not entirely balance for, is not affected by your IV, and drives variation in the DV to a considerable extent. An example might be body size in a study of energy expenditure. You know that, whatever your IV did, there will be a basic scaling relationship where larger people expend more energy, and you want to correct for this.
In such a sitation, do exactly the analysis described in case one (report ANOVAs, etc.), but additionally include your covariate(s) on the right-hand side of the model. Typically, you don’t want to include interactions between the covariate(s) and your IVs, or of covariates with one another. You still want to include all the interactions of your IVs with one another though. This is the approach to modelling and reporting that was traditionally called ANCOVA (analysis of covariance). If you are in this situation, you should check robustness using specification curve analysis that considers all the possible combinations of covariates, or their absence.
The other situation is where there is a covariate that you think could be an effect modifier. A classic example would be gender: you can’t randomly assign it, but you do think it could modify the effect of your IV(s) on your DV. In such a case, you want to include both gender and its interactions with all the IVs in the model. Effect modification would show up in a significant interaction term. If you think there is a possibility of effect modification like this, still try to balance your experimental groups for numbers of men and women. Relying on random assignment alone can leave you with very small numbers of one gender in some groups, unless your overall sample size is very large.
As for robustness checking, your specification curve analysis should probably not consider models that omit your potential effect modifier and its interactions with the IVs. The possibility of effect modification was presumably part of your design and intentions, and the set of specifications you consider should be limited to which nuisance covariates are included, which subsets of cases you use, and which transformations of the DV you use.
16.2.3 Case three: Observational study with a small number of confirmatory predictions
Case three is observational studies where you have a small number of confirmatory predictions, and where a null association is a serious and sensible possibility. In such a case, it can be ok to use NHST; though, the more numerous your predictions, and the greater the number of variables involved, the more I tend to prefer model selection and model averaging.
For case three, use a General Linear Model and include your putative predictor on the right-hand side, and your outcome variable on the left-hand side. The tricky decisions are about which other variables to include. Here, it is important to be very clear about what your claim is going to be. If you are looking for a negative association between age and depressive symptoms, is your question: (1) “Are older people less depressed?”; or (2) “Are older people less depressed for reasons above and beyond the fact that they tend to have higher incomes and be more likely to be married?”. In case (1), the simple association with no other predictors might make sense. In case (2), the parameter you want to estimate is the association between age and depressive symptoms after controlling for income and marital status. The parameter estimate in case (2) is not a more precise estimate of the same quantity as estimated in case (1). It is an estimate of a wholly different quantity, that could be different in magnitude and even direction. For this reason, it is important to think hard about what predictors other than the ones that are the subject of your hypothesis you include. These should be causally justified in ways that relate to your questions and claims.
Be careful also that if you include on the right-hand side of your model an additional variable that is causally influenced by both your predictor and the outcome variable, you can bias your estimate of the association between predictor and outcome (the association you actually want to know about). This is known as collider bias. It is hard to know a priori what the direction or magnitude of collider bias will be. The possibility of collider bias argues for the importance of considering models that are as simple as possible; and of doing plenty of robustness analysis.
As a default, I would not include all possible interactions in models of observational data, as these rapidly proliferate exponentially. Include interactions where your hypothesis or question relates to them.
If you are using NHST on observational data, specification curve analysis becomes particularly important. You want to consider which variables are absolutely integral. That is, what are the variables it would make no sense not to include. Above and beyond this, examine how the parameter estimates change with the addition of further predictors, and with changes in which cases are included or how variables are statistically transformed. This will help you and your readers understand what might be going on causally as well as evaluate the importance of any ‘significant’ association you might be reporting.
16.2.4 Case four: Observational study with multiple predictions or exploratory goals
Case four is when you have observational data and multiple different predictions to test. It also applies where the goals are more exploratory than confirmatory, or where a null hypothesis makes no real sense. Here, I would strongly recommend using model selection and model averaging, in the way we worked on in the earlier session. Model selection is the best way of addressing the question: “what factors predict such-an-such an outcome?” in observational data. You don’t need to do specification curve analysis in conjunction with model selection. The model selection by AIC uses the data to tell you which models are worthy of consideration.
One issue that can arise a lot in observational data is that there may be important non-linear associations. We have already seen examples of this with age and income. You can sometimes allow for this by taking the logarithm of the predictor, or including a quadratic term to allow for U-shaped relationships. But this is not a panacea: what if the relationship has an even more complex shape, with two or even three inflection points?
There are classes of models, notably General Additive Models, that allow you to deal with non-linear relationship shapes of indefinite complexity. We will not deal with these models in this course. Their strength is their lack of strong assumptions about the form relationships must take. Their difficulty is that they can be difficult to interpret and compare, as well as the risk of overfitting.
16.3 The relationship of your analysis strategy to your preregistration
16.3.1 Departures from the preregistration
You should preregister your analysis strategy, even for data that already exist. This helps everyone be clearer about what your ideas were beforehand, and what the evidential status is of any results that you present. Try to be as detailed as possible in your analysis plan: go into detail about what each model will be, which variables you anticipate including and excluding, and what kinds of statistical tests you will report.
Personally speaking, I like to preregister exploratory analyses as well as confirmatory ones. I identify them as exploratory in the preregistration, to make clear that I did not have well-developed predictions, but it is worth signalling the intention to do them nonetheless.
However, even with the best intentions, you are likely to need to depart from your preregistered analysis plan. A variable turns out not to have the kind of distribution you anticipated, or has many missing values, or an incidental variable has an unexpectedly strong relationship with the outcome. Or, you simply made a mistake in specifying your plan.
In these cases, it is fine to depart from the preregistered plan. You must however indicate in your reporting where you have done so; and give some justification of why you did. Where you can, present the results of your pre-registered analysis alongside the analysis that you eventually came to favour, so that everything is transparent.
You may also add additional analyses at a later stage that you simply had not thought of at the planning stage. Sometimes the results or the suggestions of reviewers lead you to do this, or you just realise you can ask an extra question. This is fine too. Just make sure that these analyses are explicitly identified in your write-up not just as exploratory but also as non-preregistered.
16.3.2 Studies that are not preregistered
You cannot report as confirmatory any analyses or studies where you did not verifiably preregister a prediction in a location such as OSF. This is tough love but you need to bind yourself to this mast to avoid the temptation or the perception of hypothesizing after the results are known. So, there are only three types of results: confirmatory and preregistered; exploratory and preregistered; and exploratory and not preregistered. Non-preregistered studies should be clearly and explicitly identified as exploratory in prominent places such as the title and abstract.
Perhaps you feel aggrieved by this. You have a result for something you did not preregister and it clearly supports some hypothesis you can specify. In this case, preregister the prediction and do the (relevant part of) the study again. In the paper, the current result can be the exploratory study 1, and the preregistered follow-up can be the confirmatory study 2. It’s good practice to include replication within your workflow anyway.
Maybe you do the kind of research where you cannot easily repeat the study. You rely on unpredictable observations of a rare wild animal, for example. Fine, but if you cannot pre-register predictions and plans, your research is exploratory and must be described as such. This does not mean it is any less valuable. It is just about being clear.
16.4 Trimming your analysis strategy
Once you have decided on the broad outlines of your analysis strategy, it is time to get into the details of which models you are going to run. Often, first drafts of analysis strategies are too messy and too big. What you need to do is trim them down at this point to make them clearer, leaner and more convincing.
Trimming the analysis strategy can involve pruning the number of models you fit. In my experience though it more often involves going back to the measures you intend to collect and removing some. Sometimes it even involves deleting some of your research questions better to focus on the main ones. This is why it is so crucial to think in detail about data analysis before the design is finalized and the data collected.
16.4.1 Too many variables !
My observation is that most people, including myself, have tendencies to collect too many variables and to make their designs too complex. This can stem from various anxieties: uncertainty about the best measure of the outcome; uncertainty about which manipulations work; the desire to make sure you ‘find something’; that you ‘might not have enough’ for publication in a good journal; or the fact that you have lots of follow-up questions about your effect or association.
Try to resist these temptations. The very great experiments in the history of science have been very simple. That is the key to their enduring influence. The studies that were premature or too complex are mostly on the scrap heap of science. A study with more going on is usually worse.
Try to proceed one question at a time. For example, why think about effect modifiers or mediating variables for your effect before you have really shown that your effect reliably exists? Modern papers in the cognitive and behavioural sciences almost always include multiple studies in series. Save those follow up questions for studies 2, 3 and 4. Including them prematurely will just lead to a mass of confusing analyses in which it is hard to see the forest for the trees. The whole will be rhetorically and epistemically unconvincing.
Your temptation to stuff the study with more variables might come from the existence of multiple possible ways of measuring the outcome, such as different self-report scales, or explicit and implicit measures. There are better ways of addressing this temptation than just gathering all the measures. Review the literature on the properties of the different measures, or perform a validation study. In a validation study, you assess the measurement properties of all the candidate measures. This can involve investigating how they relate to one another - maybe they are so highly correlated that in the main study it does not matter which one you choose. More often, validation involves relating the measures to some unambiguous ‘gold standard’ criterion. For example, putative measures of physical activity ought to distinguish professional endurance athletes from the general population. Those that don’t are not very good measures.
Sometimes in an experimental study, you are not sure what the best way of manipulating your IV is. Here, again, proceed by preliminary investigation and validation, rather than just throwing a lot of different manipulations directly at your DV. You can start by doing a preparatory study where you measure an outcome that should umambiguously be changed by any decent manipulation of the construct you want to manipulate. In biomedical science, this is often called a positive control.
Say that you are interested in whether using more elaborate and effortful cognitive processing affects moral decisions. Think of all the ways you might induce more elaborate and effortful cognitive processing. Do an initial study where you do not measure your eventual DV, but you do measure decision latency and measures of effort. The manipulation that has the biggest effects on decision latency and measures of effort is probably to be preferred. In this piloting stage, you can also include negative controls, things that you ideally do not want your manipulation to affect. For example you don’t want your manipulation of elaborate and effortful cognitive processing to make people bored or angry. You might want to measure boredom and anger in the pilot studies to select a manipulation that does not unduly increase these quantities.
Only once you have done this kind of preparatory work should you think of unleashing your IVs on your actual DVs. It saves a lot of tears and waste later on.
16.4.2 Keeping to ‘one question, one model’
A principle that you should try to follow is: one question, one model. That is, each prediction or research question should be tested using a single main statistical model, not more than one. You can then use specification curve analysis where appropriate to understand how robust the inference from this model is to variations in its specification.
Even if you have tried to reduce your number of measures, you can still end up with multiple variables that are at least kind-of measuring the same thing. This is not ideal - you should probably have gone further in reducing your measures at the piloting stage. Still, it does happen. You have an implicit and an explicit measure of hostility; or you have several related behavioural measures, such as proportion of time spend looking at the stimulus, duration of first look, and number of returns of the gaze to the stimulus.
The temptation then becomes to fit a separate model using each one of these versions of the outcome variable. This is bad because it violates the principle of one question, one model. What if you get significant results for some of your measures, but not others? Is the prediction then supported, not supported, or what? The more measures there are, the greater the chance that one of them shows some significant difference or association even if the null hypothesis is actually true. It is also true that the more measures you have, the greater the chance that (in a modest sample) one of them fails to show a significant difference or association even if the null hypothesis is false. So if you consider all the possible versions of the outcome measure, the results will likely be a confusing mixture. On the other hand, if you just select one of the measures, you are throwing away the information potentially contained in all the others.
There are various strategies available to you if you have ended up with several possible measures and yet you want to respect the principle of one question, one model. If your different outcome variables are highly correlated, you might be able to reduce them to a single dimension using Principal Components Analysis. If they are not highly correlated, then you can consider making your main model a multivariable model.
16.4.2.1 Principal Components Analysis
Let’s imagine you have four possible measures of your outcome, and they are all correlated with one another to varying but substantial degrees. This means that they all capture the same underlying variation (with each measure additionally capturing some additional specificity or noise, which is why the correlations are not perfect).
A simple solution is take to their mean. Since they are all correlated, then they are all getting at the same thing to some degree. Their mean is going to be a more accurate reflection of this underlying thing, you would think, than the four individual scores. An the mean is just one number, so the principle of one question, one model can be reflected in your analysis.
However, simply taking their mean is not smart. One of the measures might be more correlated with the others, another one less. This would be true, for example, if one measure was more directly related than the others to the underlying quantity that all your measures are reflecting to different degrees. A smarter approach would be to take a kind of mean where the different contributing variables were weighted according to how well they each predicted all the others.
This is what you do in Principal Components Analysis (PCA). PCA uses the correlation matrix between your variables. It then computes a PC score, which is a composite of the scores on the individual variables, in which those variables that better predict the others are given more weight. You can only do PCA legitimately if the degree of correlation between your variables is sufficient. You test this with the Kaiser–Meyer–Olkin (KMO) test prior to running the PCA. You can perform PCA and the KMO test with many contributed R packages, including psych.
By the way, in more complex PCA analyses, you may extract more than one PC score. Your set of variables may fall into two subsets, each correlated with the others in its own subset, but not those in the other set. This would be because you had variables capturing two different quantities in the set. In this case, we would extract two PC scores. The topics of PCA - and factor analysis, which is also about extracting underlying redundancy in a set of variables - is complex and I will not say more about it here.
16.4.2.2 Multivariable models
Let’s imagine the case where you have two possible outcome measures for the same question, and they are not that highly correlated. You cannot just take their mean. But what you could do is consider, for each participants, both data points to be instances of a single underlying variable, say score. You could then fit a Linear Mixed Model with score as the outcome, your IVs plus which measure it was as the predictors, and a random intercept for participant.
Let me explain with a more concrete example. You have an IV which is experimental condition (Condition). You want to know whether your intervention has an effect on bias, and you have two measures of bias, Implicit.bias and Explicit.bias. The beginning of your data frame looks like this:
## Participant Condition Implicit.bias Explicit.bias
## 1 1 Control 2.3 4
## 2 2 Experimental 3.4 6
## 3 3 Control 3.1 2
## 4 4 Experimental 2.9 4
## 5 5 Control 3.7 7
## 6 6 Experimental 1.9 3You find yourself tempted to run two models with these specifications:
m1 <- lm(Condition ~ Implicit.bias, data=d)
and:
m2 <- lm(Condition ~ Explicit.bias, data=d)
This would violate the principle of one question, one model.
Instead, I would first scale both outcome measures so the data frame looks like this:
## Participant Condition Implicit.bias Explicit.bias
## 1 1 Control -0.86226777 -0.1790287
## 2 2 Experimental 0.76372288 0.8951436
## 3 3 Control 0.32027089 -1.2532010
## 4 4 Experimental 0.02463622 -0.1790287
## 5 5 Control 1.20717488 1.4322297
## 6 6 Experimental -1.45353710 -0.7161149Then, reorganise your data frame to look like this one:
## # A tibble: 12 × 4
## Participant Condition Measure Score[,1]
## <dbl> <chr> <chr> <dbl>
## 1 1 Control Implicit.bias -0.862
## 2 1 Control Explicit.bias -0.179
## 3 2 Experimental Implicit.bias 0.764
## 4 2 Experimental Explicit.bias 0.895
## 5 3 Control Implicit.bias 0.320
## 6 3 Control Explicit.bias -1.25
## 7 4 Experimental Implicit.bias 0.0246
## 8 4 Experimental Explicit.bias -0.179
## 9 5 Control Implicit.bias 1.21
## 10 5 Control Explicit.bias 1.43
## 11 6 Experimental Implicit.bias -1.45
## 12 6 Experimental Explicit.bias -0.716Your model specification would then look something like this:
l1 <- lmer(Score ~ Condition + Measure + Condition:Measure + (1|Participant), data=l)
In this analysis, a significant main effect of condition would mean that Condition had affected the total set of the two measures. A significant interaction between Condition and Measure would mean that Condition had affected one of the measures differently from the other. You could find both a main effect and an interaction, or just a main effect of condition, or just the interaction, or neither. Each of these results would be richly informative about your question. In the case of significant interaction, and perhaps in any case, you could then do models m1 and m2 as follow ups. But, for the main analysis, the principle of one question, one model would have been respected, and you would nonetheless have used the information in both of your two measures.
In the above model l1, it is important that I scaled the two measures first, so that they have the same mean and standard deviation. Also, it is important that they both have the same direction (that it is a higher score is higher bias for both measures, or a higher score is lower bias for both measures, not any incongruent combination).
By the way, you may be wondering how I got the second form of the data frame from the first. I used the pivot_longer() function from tidyverse as follows.
16.5 Keeping it small and simple
It’s worth reiterating, in closing this unit, how valuable it is to follow the principle ‘Keep It Small and Simple’ (KISS) in designing your studies and analysis strategies. Your overall research programme may be grand, ambitious, and incorporate many eventual subquestions and nuances. But each individual empirical study does not have to. The bricks can be simple so that the building can be solid and durable. Try to establish one thing clearly with each study; try to measure the right number of things; try to prune premature extensions, equivocations and side hustles. You can take these on in later studies.
Of course, your study needs to be complex enough. You have to incorporate all the crucial variables, not leave one out. You may need to measure several things. But don’t make it any more complex than it has to be. And, however complex it is, write a set of predictions and then an analysis strategy that really boils down the sparest form of what it is you are trying to find out.
Albert Einstein is often credited as saying ‘everything should be made as simple as possible, but not simpler’. As often is the case with quotations, their history turns out to be more complex than it appears, and the attribution may be apocryphal. Still, it remains good advice.
16.6 Summary
In this unit, we have discussed principles for developing your analysis strategy. Notably, we discussed different typical analysis strategies for:
- Experimental studies with no covariates;
- Experimental studies with covariates;
- Observational studies with a few simple predictions to be compared against the null;
- Observational studies with many possible predictions, no sensible null, or that are exploratory.
We discussed how to handle analytical departures from your preregistration, and ways of making your analysis strategy as trim as possible.