Chapter 10 Correlation
Our book uses “measurement variables” for quantitative variables at the ordinal, interval, or ratio level of measurement. The majority of our examples will be from the strongest level (ratio).
I’m choosing to include material on correlation as chapter 10 and linear regression as chapter 11 of my notes, although your textbook scatters this material throughout these two chapters.
10.1 Univariate Statistics vs Bivariate Statistics
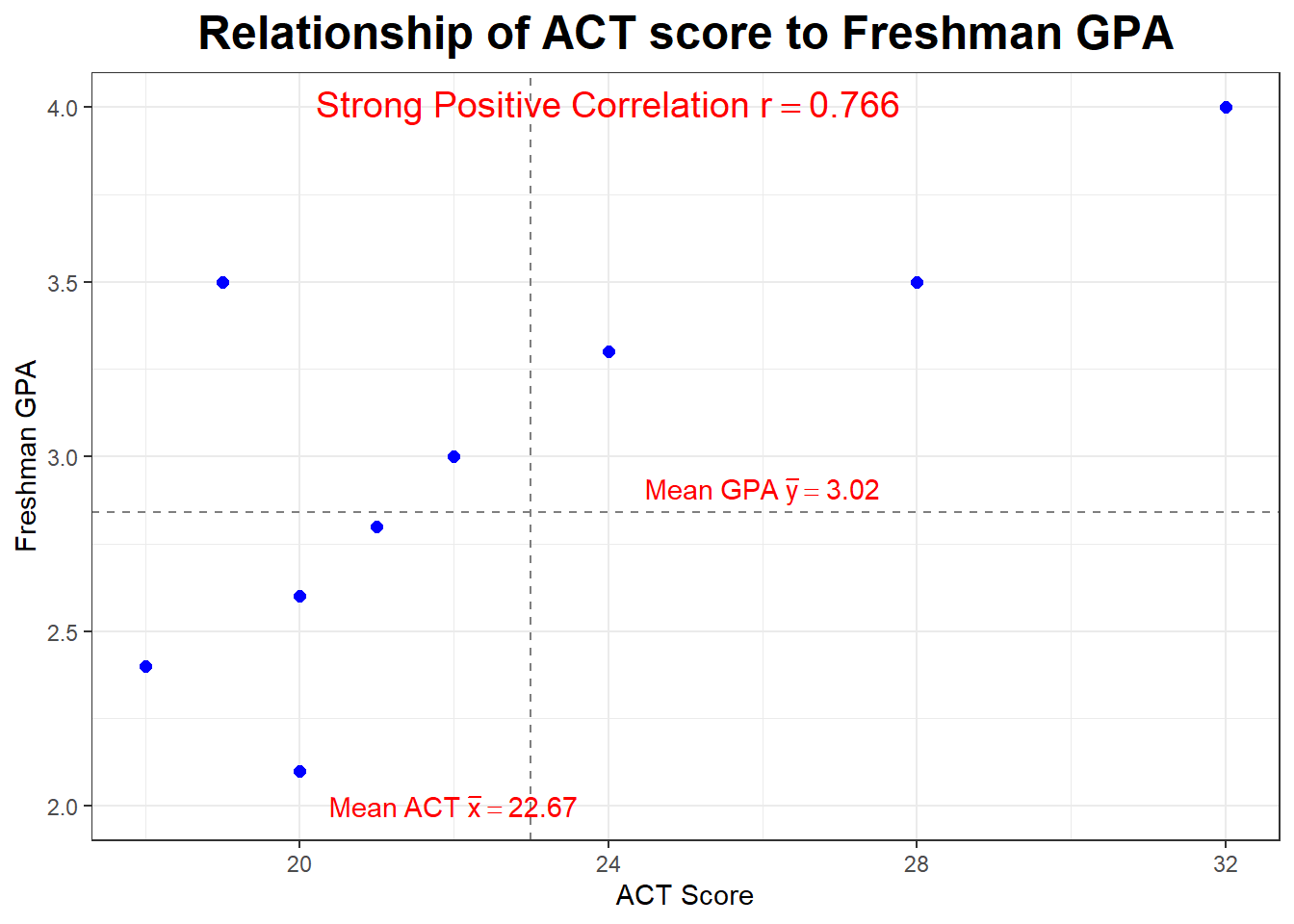
Data Set: Variable \(X\) is ACT composite score; the \(X\) variable will be referred to as the explanatory variable, predictor variable, or independent variable
Variable \(Y\) is the freshman college GPA; the \(Y\) variable will be referred to as the response variable or dependent variable
In statistic, we often want to know if two variables \(X\) and \(Y\) are mathematically related to each other, and eventually if we can form a mathematical model to explain or predict variable \(Y\) based on variable \(X\)
This is a sample of \(n=10\) college students. I have computed the means and standard deviations of both variables.
| \(X\) | \(Y\) |
|---|---|
| 32 | 4.0 |
| 28 | 3.5 |
| 26 | 1.2 |
| 24 | 3.3 |
| 22 | 3.0 |
| 21 | 2.8 |
| 20 | 2.6 |
| 20 | 2.1 |
| 19 | 3.5 |
| 18 | 2.4 |
## [1] "Variable X (ACT Score)"## mean sd
## 23 4.472136## [1] "Variable Y (GPA)"## mean sd
## 2.84 0.812677310.2 Scatterplot
We will construct a scatterplot with the explanatory variable on the horizontal \(x\)-axis and the response variable on the vertical \(y\)-axis. I will draw by hand on the board and below with my software
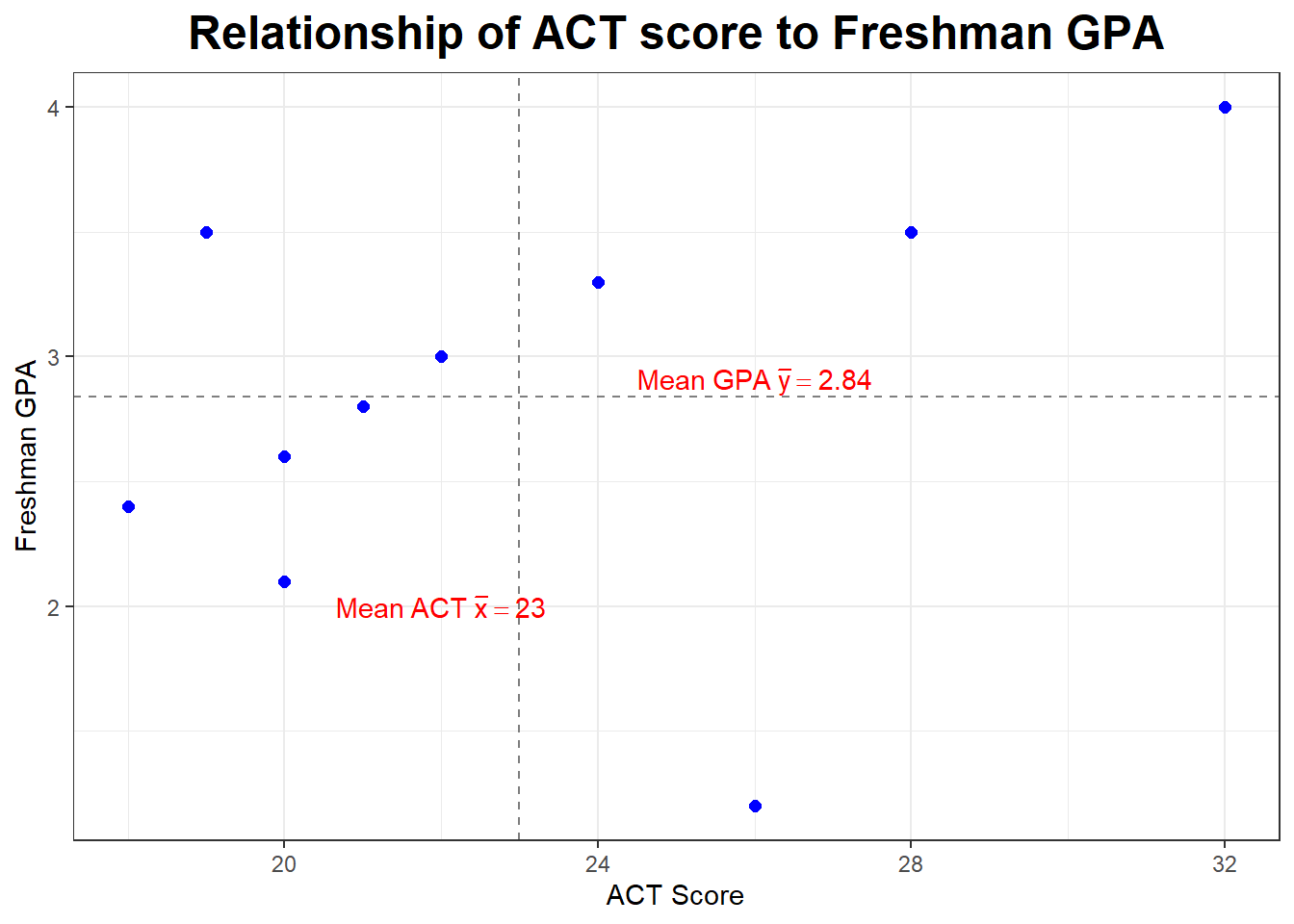
What sort of mathematical model could we use to try to explain the student’s freshman GPA, using their ACT score?
Are there any points that seem to be “outliers”?
10.3 The Correlation Coefficient
A statistic that is commonly used to quantify the strength of a linear relationship between two variables is the correlation coefficient. There are many such coefficients; the most common one, which we will use in this course, is sometimes called Pearson’s correlation coefficient.
If our bivariate data represent an entire population, we use the Greek letter “rho”, \(\rho\), to represent the population correlation as a parameter.
More commonly, our data is a sample and we compute the sample statistic \(r\) as our estimate of the population correlation \(\rho\), similarly to using \(\bar{x}\) to estimate \(\mu\) or \(s^2\) to estimate \(\sigma^2\).
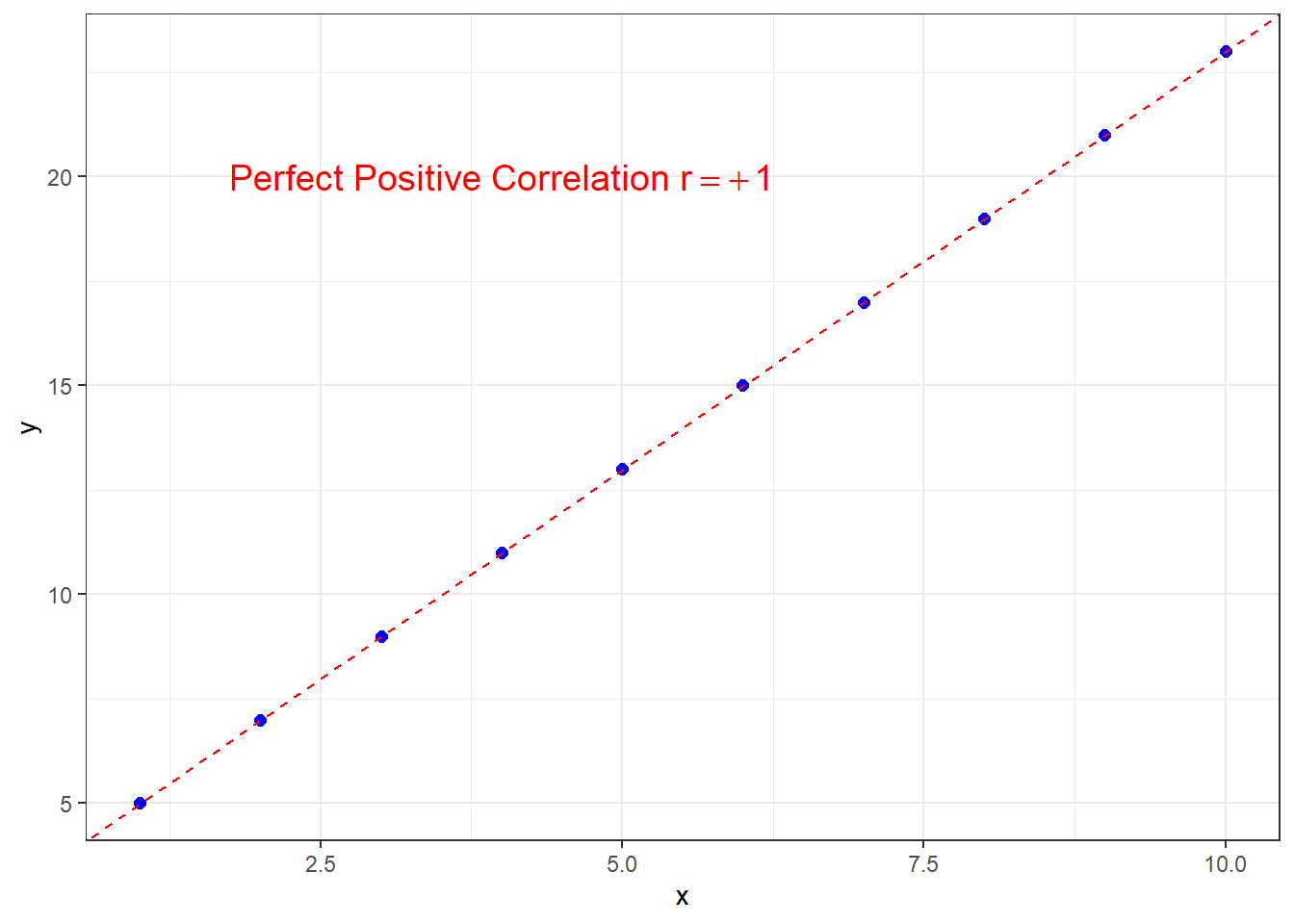
The correlation coefficient has the property that it will always take on a numerical value between \(-1\) and \(+1\). \[-1 \leq r \leq +1\]
\(\pagebreak\)
If the correlation is \(r=+1\), this is perfect positive correlation and all points lie exactly on a straight line with positive slope.
\(\pagebreak\)
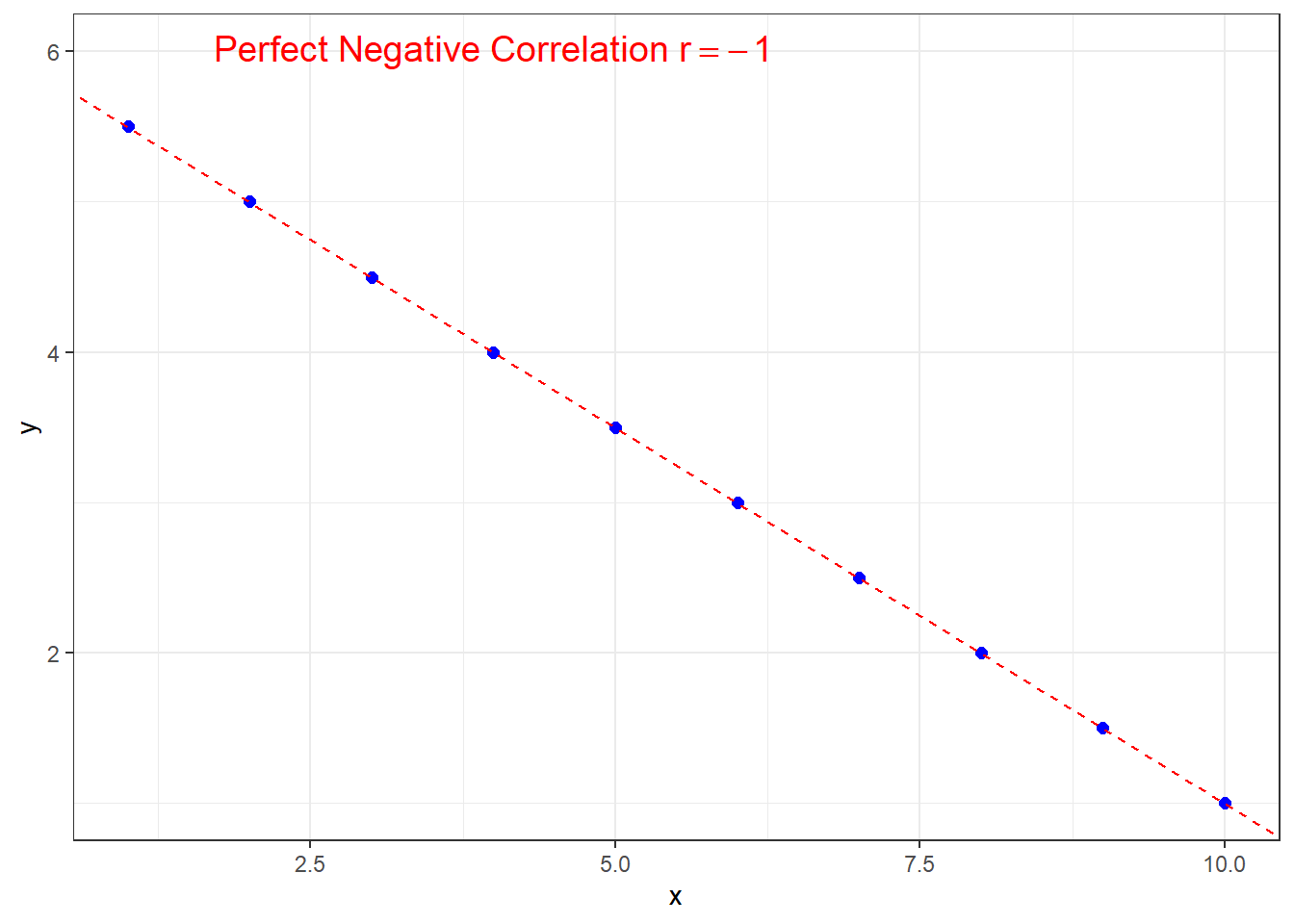
Similarly for \(r=-1\), except the line will have negative slope in order to have perfect negative correlation.
\(\pagebreak\)
For the correlation to be exactly zero, there must be no linear relationship between the two variables. On the plot, you wouldn’t even be able to tell if the “line of best fit” would have a positive or negative slope.
Note that this does not preclude that there is some nonlinear relationship, such as in this graph with \(r=0\).
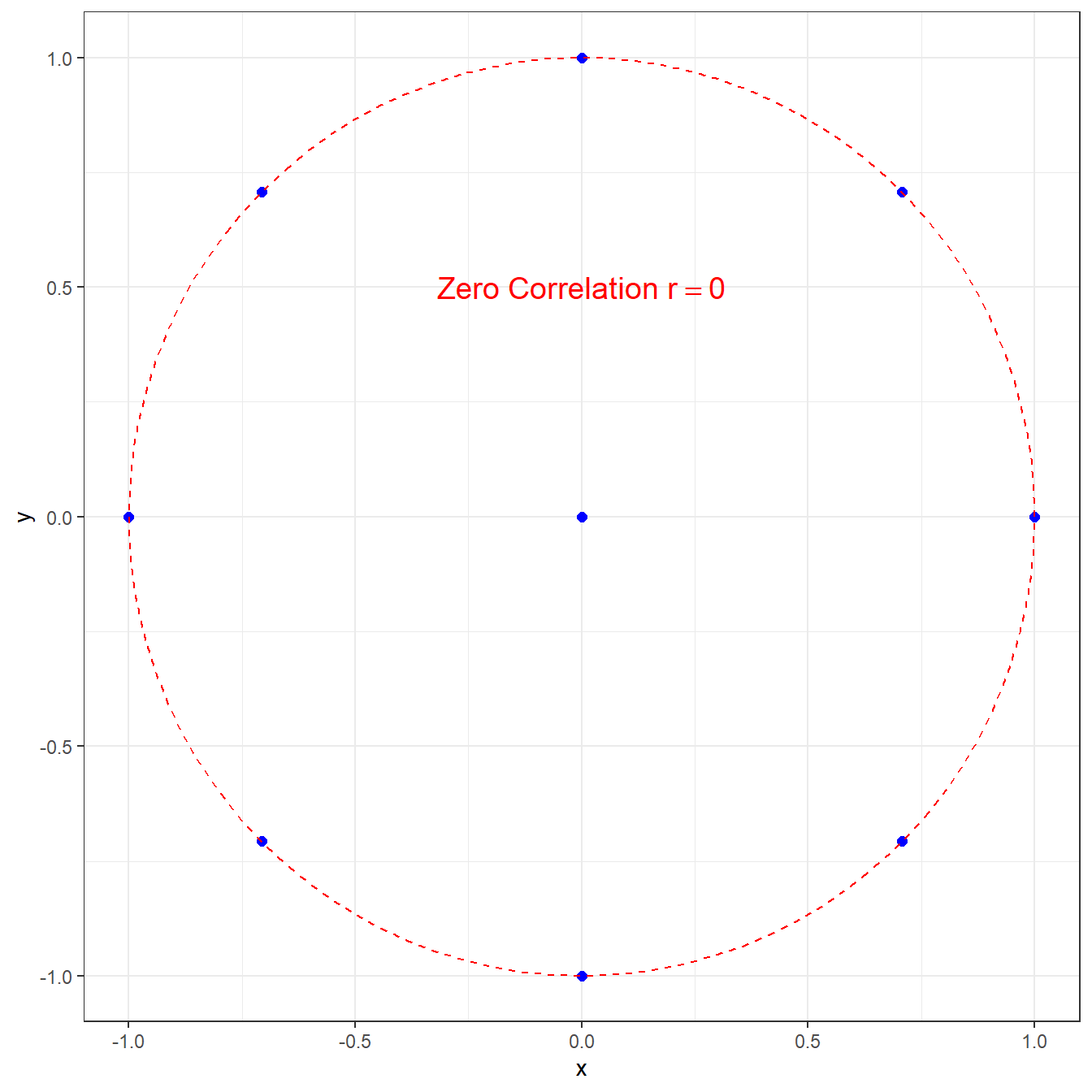
Most data sets of interest will have a correlation that is not exactly \(\pm 1\) or \(0\). Generally, we are interested in the magnitude and the direction of a correlation. I will demonstrate some examples from some data sets built into my statistical software package \(R\).
The data set faithful has data from Old Faithful Geyser in Yellowstone National Park. The park rangers use a linear regression model to predict the waiting time until the next eruption, using the length of the previous eruption. The scatterplot below is for \(n=272\) eruptions of this geyser.
If you would like to see a livestream of the geyser (along with a prediction of the next eruption), go to https://www.nps.gov/yell/learn/photosmultimedia/webcams.htm .
\(\pagebreak\)
The correlation is strong and positive, \(r=+0.901\).
## eruptions waiting
## 41 4.350 80
## 57 3.717 71
## 220 4.150 76
## 245 4.583 85
## 256 3.817 80## [1] "Length of Eruption (minutes)"## mean sd n
## 3.487783 1.141371 272## [1] "Waiting Time until next eruprtion (minutes)"## mean sd n
## 70.89706 13.59497 272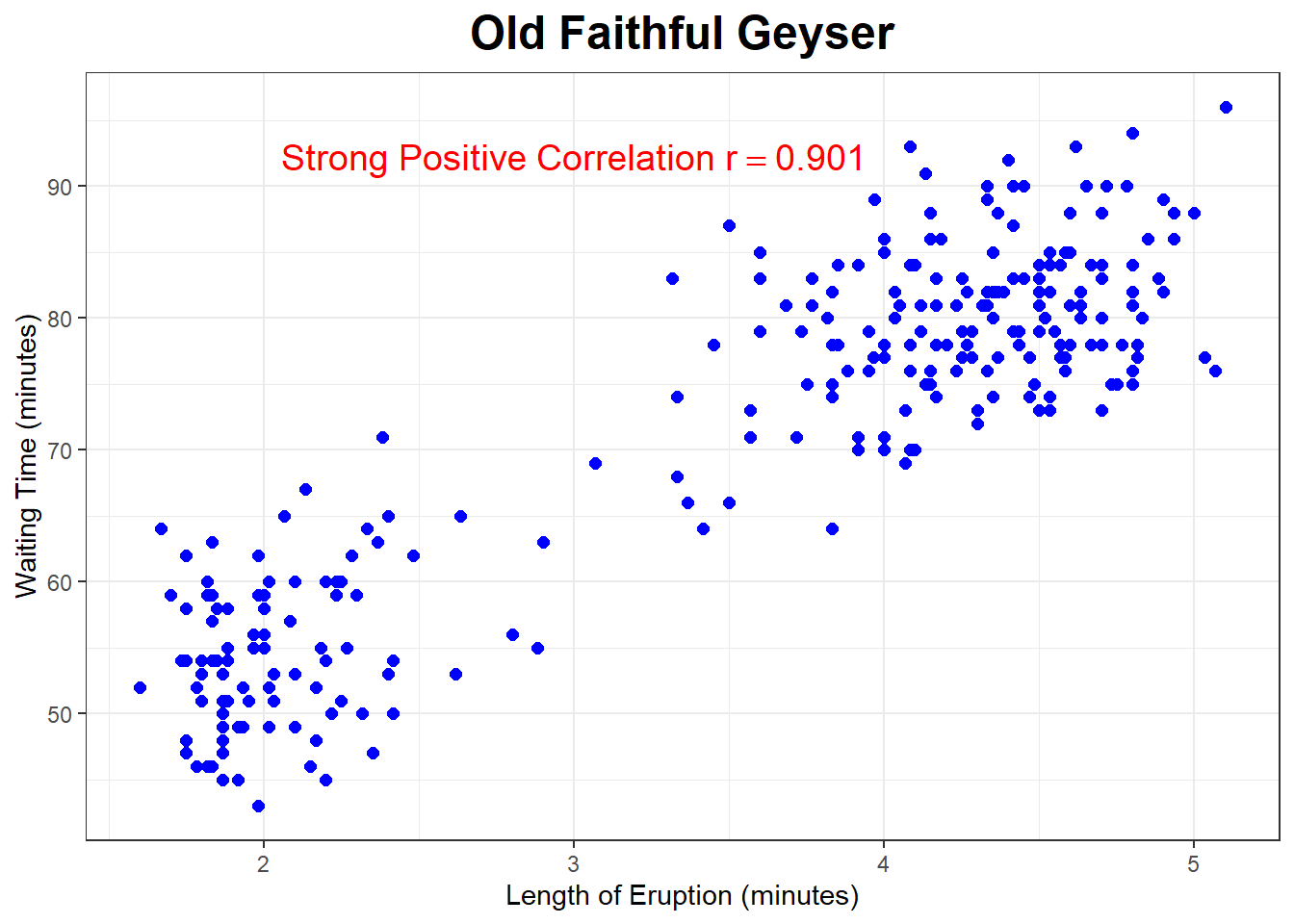
Using data from Motor Trend magazine, below is the scatterplot looking at the relationship between the weight of the vehicle (measured in thousands of pounds) and the gas mileage (measured in miles per gallon) for a sample of \(n=32\) cars.
What sort of correlation do you expect?
\(\pagebreak\)
## mpg cyl disp hp drat wt qsec vs am gear carb
## Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2
## Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2
## Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4
## Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1
## Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4## [1] "Weight of Vehicle (thousands of pounds"## mean sd n
## 3.21725 0.9784574 32## [1] "Gas Mileage (miles per gallon)"## mean sd n
## 20.09062 6.026948 32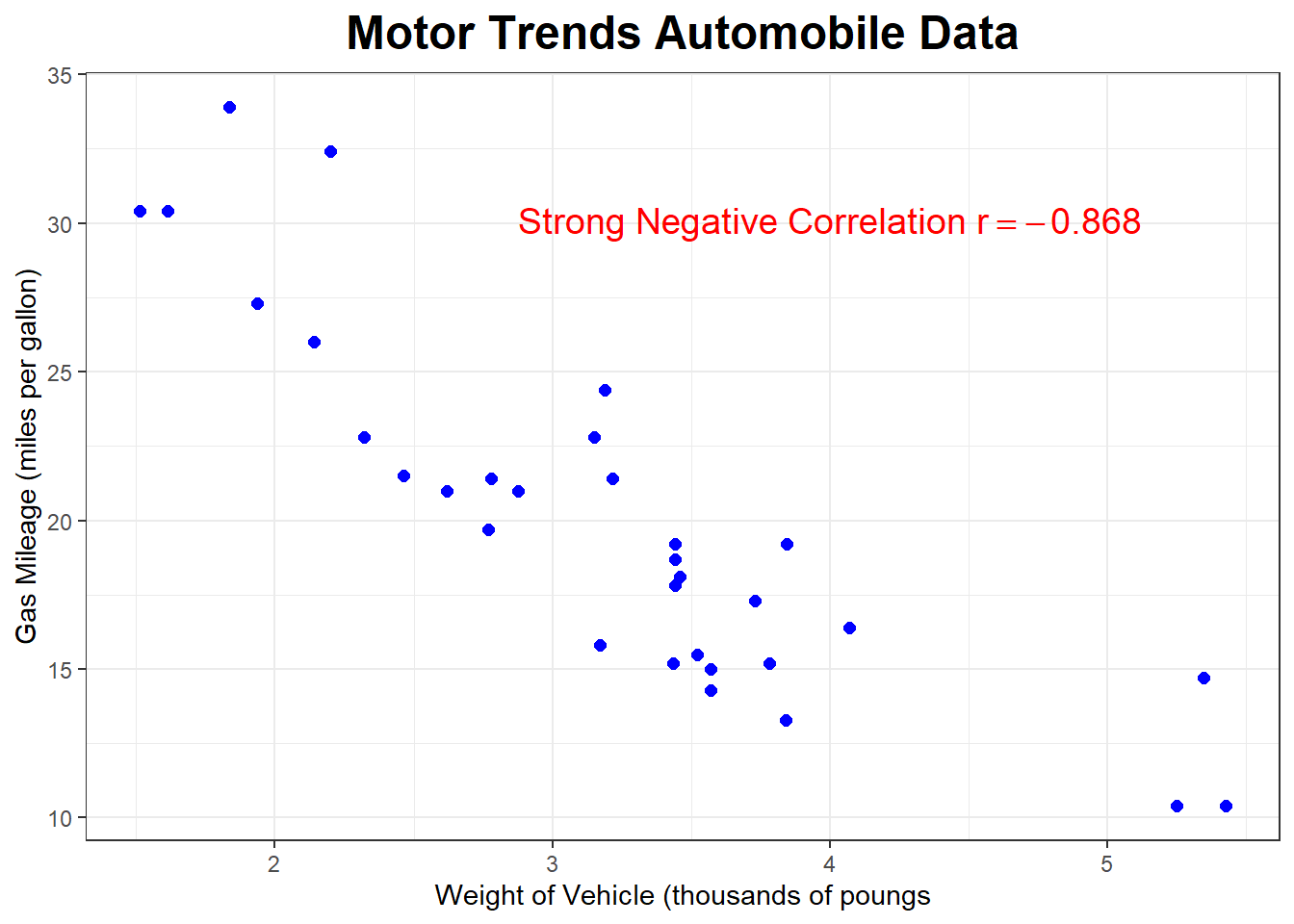
The correlation is negative and strong, with \(r=-0.868\).
The scatterplot below shows the relationship between wind speed (miles per hour) and ozone level in the air (parts per billion) in New York City.
What sort of correlation do you expect? (probably harder to answer without looking at the graph unless you know a lot about the science of ozone levels)
\(\pagebreak\)
## Ozone Solar.R Wind Temp Month Day
## 15 18 65 13.2 58 5 15
## 51 13 137 10.3 76 6 20
## 76 7 48 14.3 80 7 15
## 85 80 294 8.6 86 7 24
## 108 22 71 10.3 77 8 16## [1] "Wind Speed (miles per hour)"## mean sd n
## 9.93964 3.557713 111## [1] "Ozone Level (parts per billion)"## mean sd n
## 42.0991 33.27597 111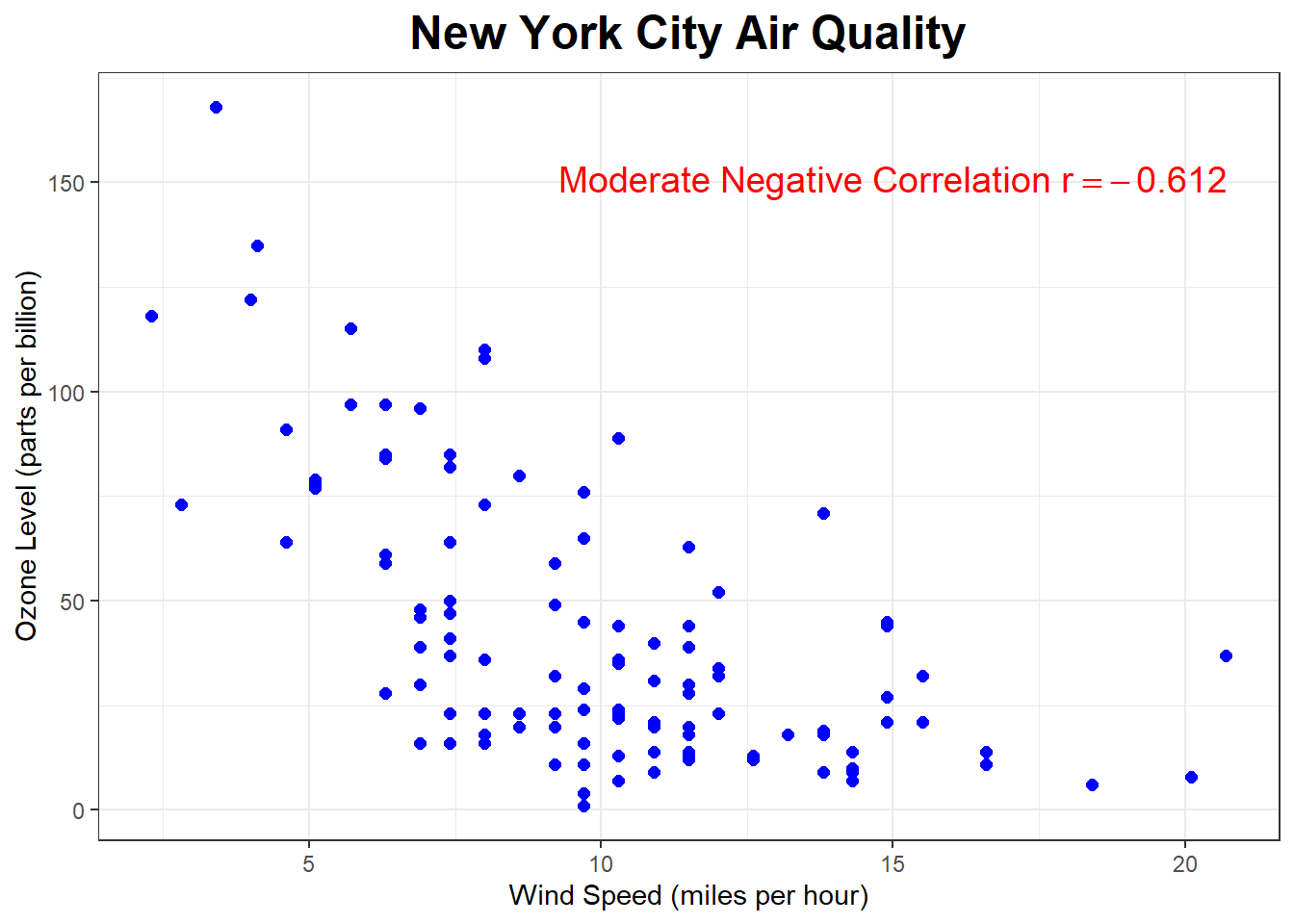
What about the correlation between Ozone and Temperature?
\(\pagebreak\)
## [1] "Temperature (degrees Fahrenheit)"## mean sd n
## 77.79279 9.529969 111## [1] "Ozone Level (parts per billion)"## mean sd n
## 42.0991 33.27597 111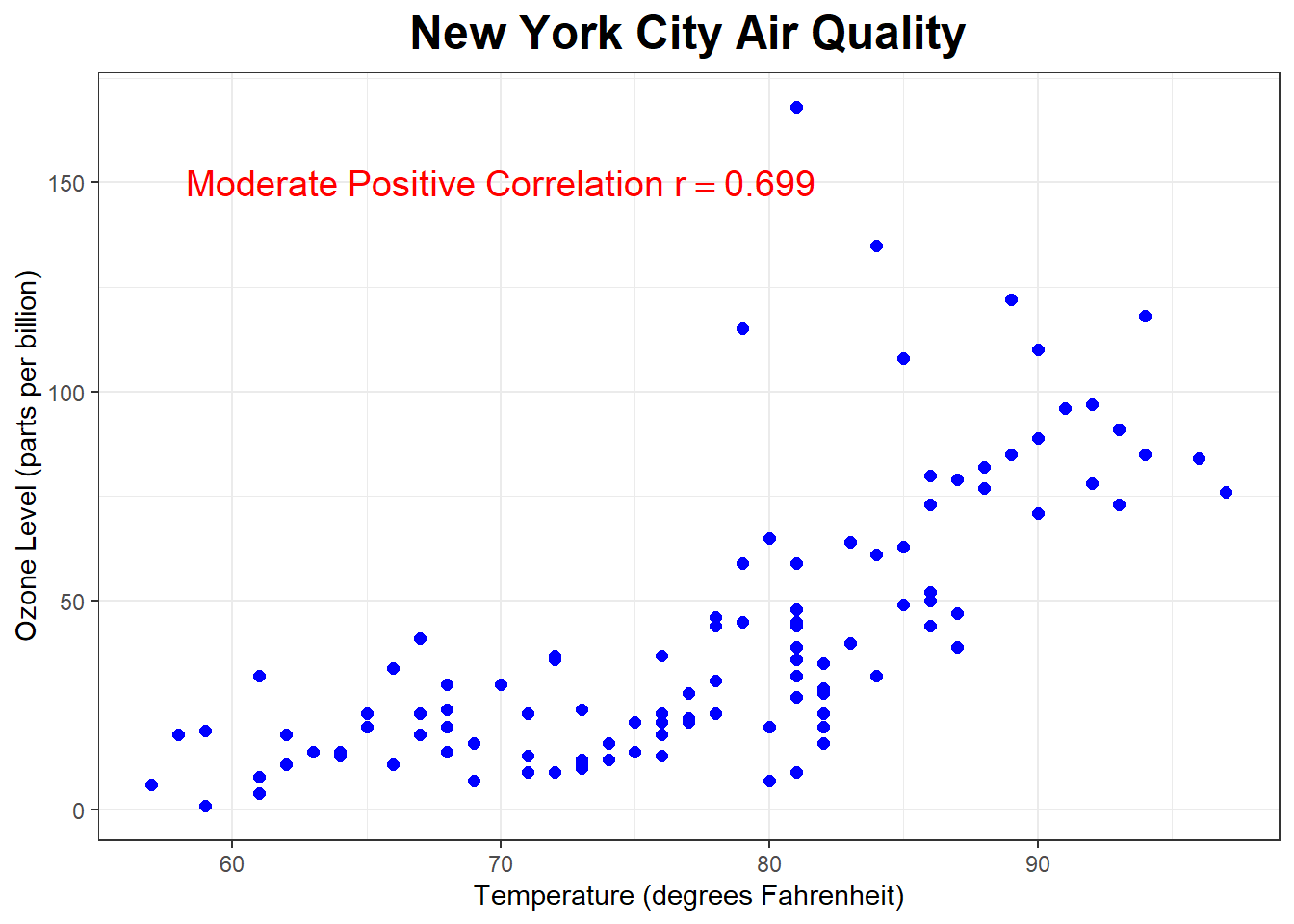
What about the relationship between the weight of a college student’s backpack to their bodyweight ?
\(\pagebreak\)
## BackpackWeight BodyWeight Ratio BackProblems Major Year Sex
## 1 9 125 0.0720000 1 Bio 3 Female
## 2 8 195 0.0410256 0 Philosophy 5 Male
## 33 9 135 0.0666667 0 LS 6 Female
## 42 13 135 0.0962963 1 SOCS 3 Female
## 100 15 170 0.0882353 0 History 5 Male## [1] "Weight of Backpack (pounds)"## mean sd n
## 11.66 5.765134 100## [1] "Body Weight (pounds)"## mean sd n
## 153.05 29.39744 100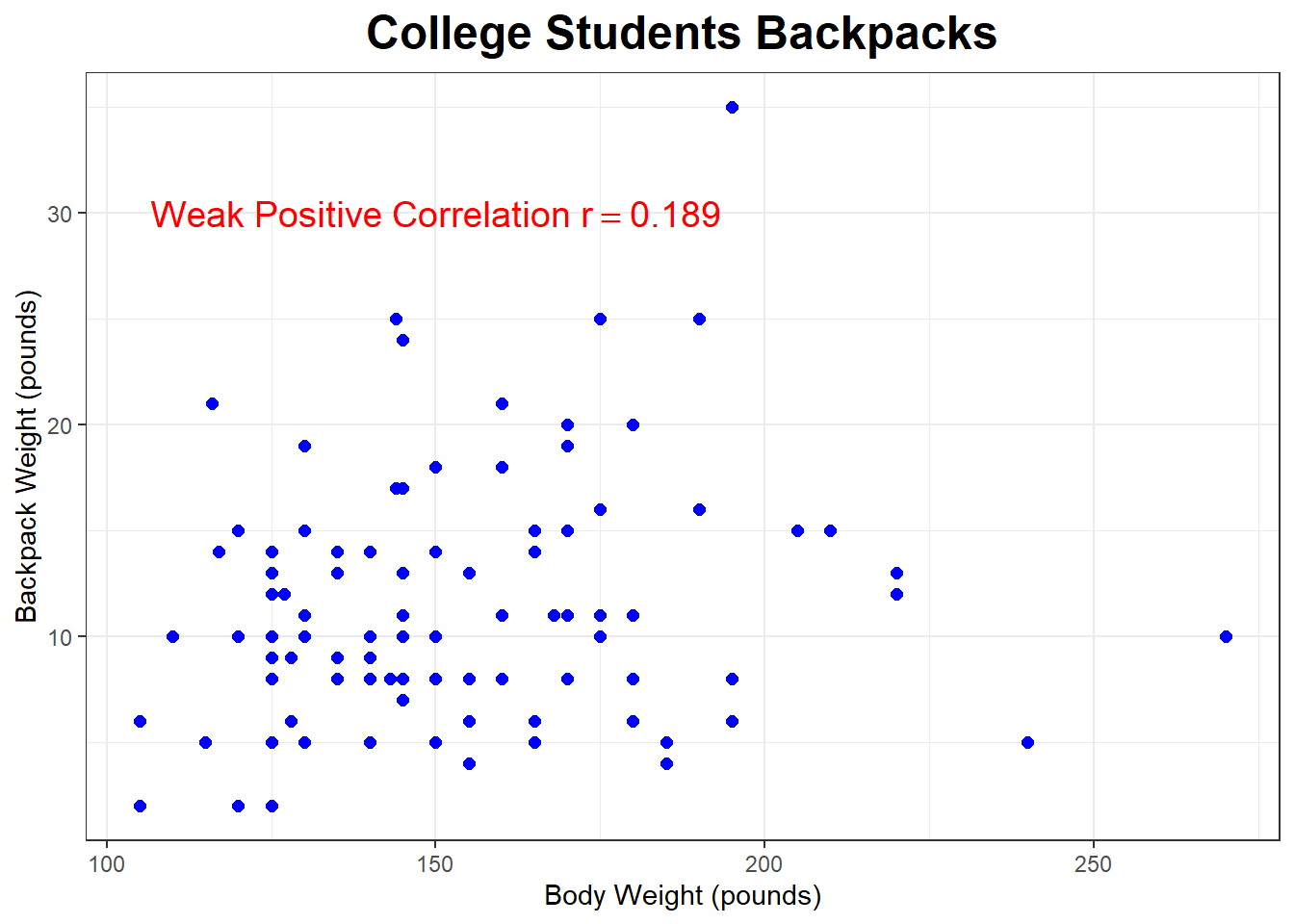
Using my class data, do you think there is a strong, moderate, or weak correlation between Texts and Height? Try to guess the correlation.
$
## Gender Color Texts Chocolate HSAlgebra Pizza Sushi Tacos Temp Height
## 1 F yellow 3 10 8 3 1 2 85 62
## 3 M orange 21 9 3 3 1 2 88 66
## 5 M blue 0 7 5 1 3 2 80 74
## 13 M green 0 6 4 3 1 2 85 72
## 18 M purple 0 7 9 2 1 3 87 71
## 27 F blue 31 8 6 1 3 2 80 65
## 31 F blue 3 8 3 1 3 2 89 64
## 33 F coral 6 7 1 2 3 1 88 64
## 40 F pink 10 5 8 1 3 2 87 67
## 42 F purple 11 9 8 1 3 2 80 66## [1] "Number of Text Messages"## mean sd n
## 12.59091 18.51878 44## [1] "Height (inches)"## mean sd n
## 67.22727 4.192261 44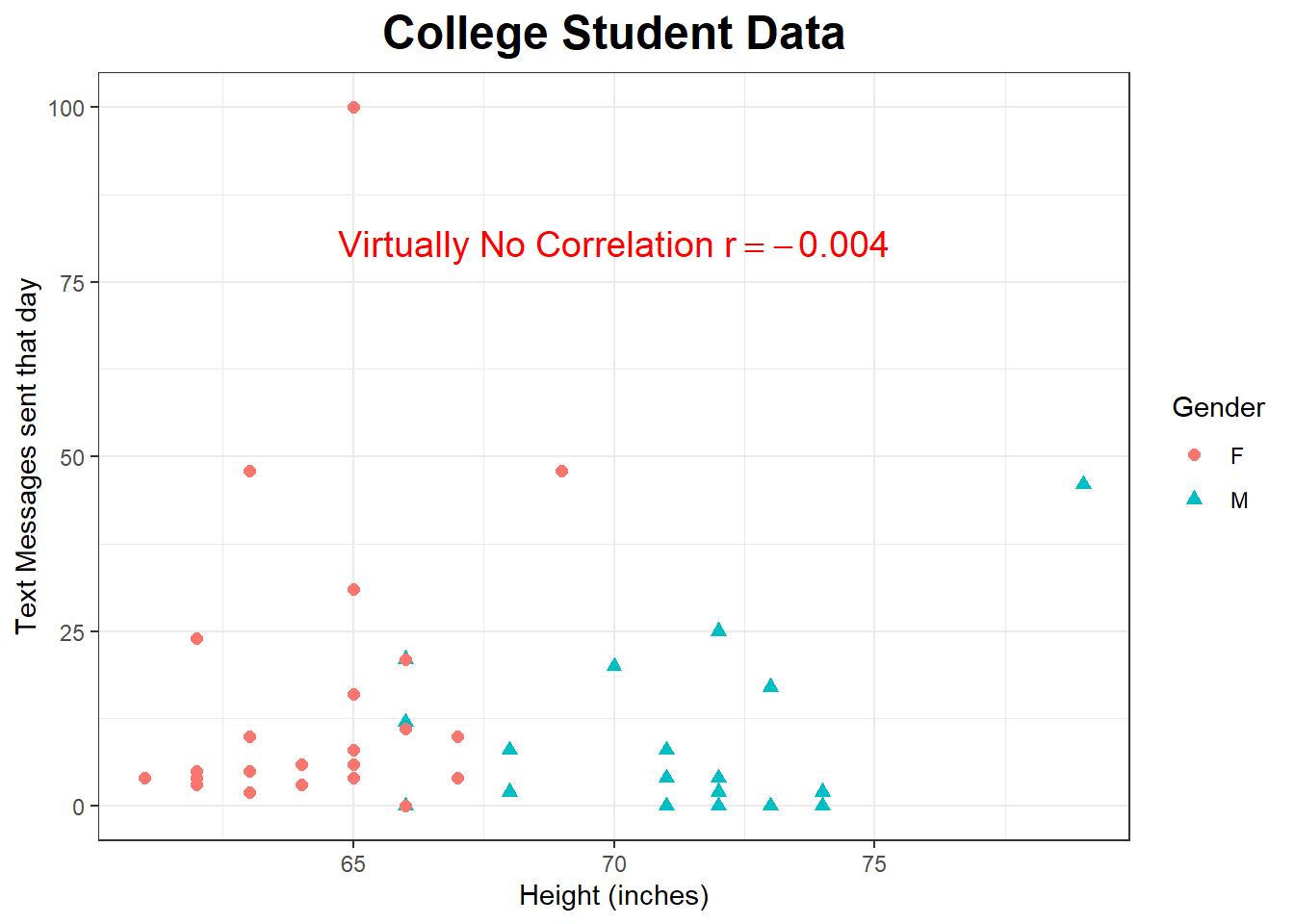
\(\pagebreak\)
10.4 Correlation does not imply causation
As we have discussed before, just because there is a an association or relationship between two measurement variables, as indicated by looking at a scatterplot or by computing the correlation coefficient \(r\), does not mean that there is a causal relationship. There are many situations where a strong correlation between variables \(X\) and \(Y\) is found when \(X\) does not cause \(Y\) (or vice versa).
Shark attacks vs ice cream sales
Number of churches vs number of liquor stores
Coffee consumption vs heart attacks
What are the confounding (or lurking) variables in the above examples?
10.5 Calculating the correlation coefficient
\[\Large{r=\frac{1}{n-1} \sum_{i=1}^n [\frac{(x_i-\bar{x})}{s_x}] [\frac{(y_i-\bar{y})}{s_y}]}\]
This estimates the population correlation coefficient \(\rho\) (the Greek letter “rho”). A different, but algebraically equivalent version of this formula is in your book. In reality, you would use software or a statistical calculator to compute \(r\).
Let’s go back to our sample of \(n=10\).
| \(X\) | \(Y\) |
|---|---|
| 32 | 4.0 |
| 28 | 3.5 |
| 26 | 1.2 |
| 24 | 3.3 |
| 22 | 3.0 |
| 21 | 2.8 |
| 20 | 2.6 |
| 20 | 2.1 |
| 19 | 3.5 |
| 18 | 2.4 |
We computed: \[\Large{\bar{x}=23, s_x=4.472136, \bar{y}=2.84, s_y=0.8126773}\]
Our formula could be written:
\[\Large{r=\frac{1}{n-1} \sum_{i=1}^n Z_X \times Z_Y}\]
If you were working this by hand, you would find the following (a spreadsheet would be nice here):
\[\Large{Z_X = \frac{x_i-\bar{x}}{s_x}}\]
\[\Large{Z_Y = \frac{y_i-\bar{y}}{s_y}}\]
\(\pagebreak\)
## X Y Z_X Z_Y Z_X.Z_Y
## [1,] 32 4.0 2.012 1.427 2.873
## [2,] 28 3.5 1.118 0.812 0.908
## [3,] 26 1.2 0.671 -2.018 -1.354
## [4,] 24 3.3 0.224 0.566 0.127
## [5,] 22 3.0 -0.224 0.197 -0.044
## [6,] 21 2.8 -0.447 -0.049 0.022
## [7,] 20 2.6 -0.671 -0.295 0.198
## [8,] 20 2.1 -0.671 -0.911 0.611
## [9,] 19 3.5 -0.894 0.812 -0.726
## [10,] 18 2.4 -1.118 -0.541 0.605The summation part of the formula is the sum of List L5.
\[\Large{r=\frac{1}{10-1}(3.218)=+0.358}\]
We have a moderate to weak positive correlation between ACT score and freshman GPA.
Let’s look at our plot again. Notice the dashed lines are drawn at \(\bar{x}=23\) and \(\bar{y=2.84}\) and serve to divide our graph into four “quadrants”. What is true about the points (the students) in the upper right hand quadrant?
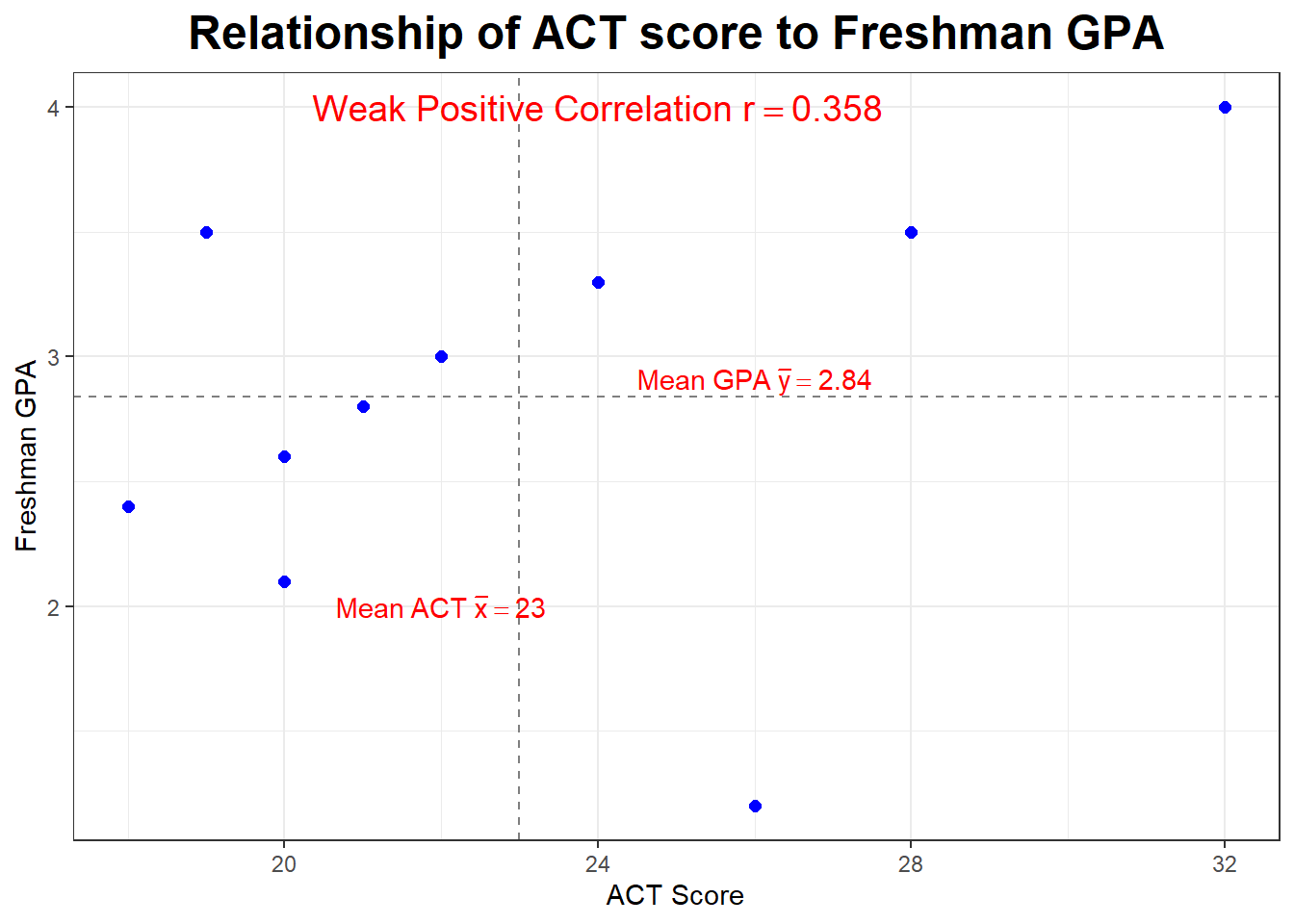
What if we deleted the outlier or influential point (the student with the ususually low GPA)? What would happen to the correlation?
\(\pagebreak\)