Chapter 21 Confidence Intervals for Means
21.1 Confidence Interval Based On the \(z\) distribution
We will cover how to construct a confidence interval when the parameter in question is the mean \(\mu\) of a single sample, rather than a proportion.
Suppose we want a \(100(1-\alpha)\%\) confidence interval for a mean. If we assume \(X \sim N(\mu, \sigma)\) where the value of \(\sigma\) is known, then \(\bar{X} \sim N(\mu, \sigma/\sqrt{n})\). So the formula will be:
\[\bar{x} \pm z^* \times \frac{\sigma}{\sqrt{n}}\]
This is basically identical to our formula for the CI of a proportion, substituting \(\bar{x}\) for \(\hat{p}\) as the point estimte and \(\frac{\sigma}{\sqrt{n}}\) for \(\sqrt{\frac{\hat{p} \hat{q}}{n}}\) as the standard error.
For 95% confidence, we can use \(z^* \approx 2\) as the approximate multiplier, or the more exact \(z^*=1.96\) critical value.
21.2 What if We Don’t Know \(\sigma\)?
It might have struck you as strange that we would know the true standard deviation \(\sigma\) of a distribution in a situation where we did not know the true mean \(\mu\) and felt it necessary to estimate \(\mu\) with a point estimate \(\bar{x}\) and a confidence interval.
In most situations, we would not know the true value for \(\sigma\). The sample standard deviation \(s\) seems like a natural choice to use in place of \(\sigma\) in our confidence interval formulas.
However, the distribution of the quantity \(\frac{\bar{x}-\mu}{s/\sqrt{n}}\) does not precisely follow a normal distribution, especially when \(n\) is small. The sampling distribution in this case follows the \(t\)-distribution, discovered by William Gosset.
21.3 The \(t\)-distribution
The \(t\)-distribution is similar to the standard normal distribution in that it is:
- Bell-shaped
- Symmetric
- Has \(\mu=0\)
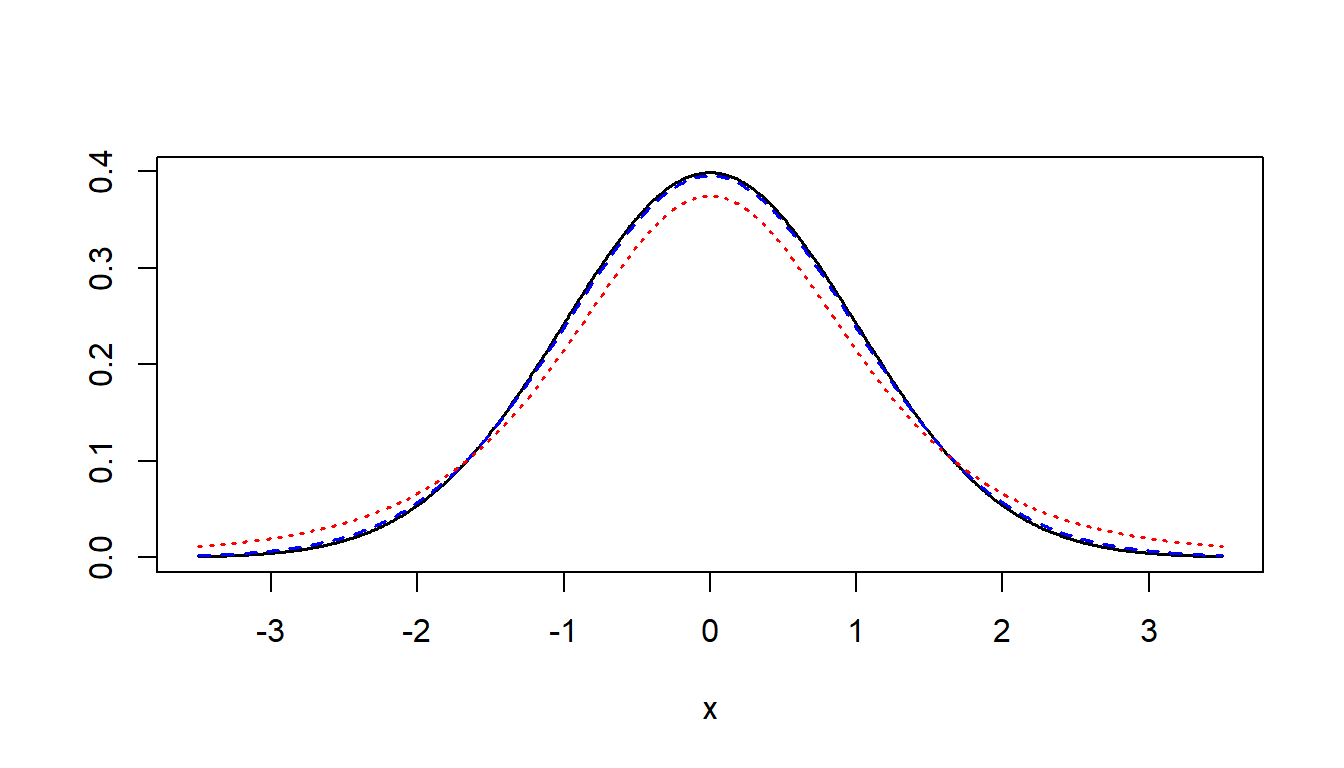
However, the \(t\)-distribution has ‘heavier tails’ (i.e. a higher variance) than the standard normal distribution. Visually, it is shorter and flatter than the standard normal curve, as seen on the next slide. Also, each \(t\) distribuiton is dscribed by a parameter called degrees of freedom, where \(df=n-1\). As \(n \rightarrow \infty\), the \(t\)-curve approaches the \(z\)-curve.
Comparing the Standard Normal and t distribution
The black line is standard normal, the blue line (very close to the black) is \(t\) with 30 df, and the red line (further from the black) is \(t\) with 4 df.
21.4 Confidence Interval Based On the \(t\) distribution
The formula for the confidence interval for a mean is changed slightly when we do not know \(\sigma\). We still need to assume \(X\) follows a normal distribution, or that we have a large sample size (\(n>30\)).
\[\bar{x} \pm t^* \times \frac{s}{\sqrt{n}}\]
We need to know both \(n\) and \(\alpha\) to find the critical value or t-muliplier \(t^*\). The degrees of freedom are \(df=n-1\) and the critical value will change for each sample size.
If \(df=15\) and a 95% confidence level (\(\alpha=.05\)), then we can use a \(t\)-distribution table. Use the row with \(df=15\) and the column with a confidence level of 95% (read from the bottom of the table). The critical value is \(t^*=\pm 2.131\).
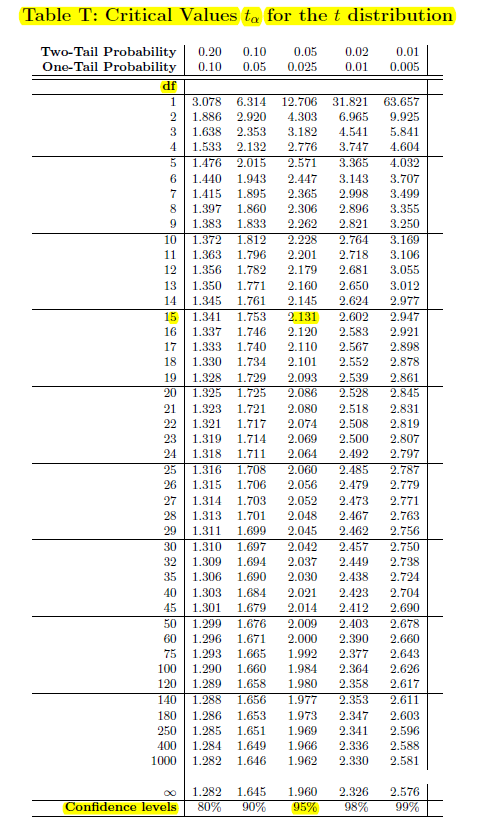
If \(n=16\) (so \(df=15\)), \(\bar{x}=192.4\) and \(s=26.5\), then the 95% confidence interval for \(\mu\) is:
\[192.4 \pm 2.131 \times \frac{26.5}{\sqrt{16}}\]
\[192.4 \pm 14.12\]
21.5 Some example of confidence intervals from the scientific literature
From the article “The Epidemiology of Social Isolation: National Health and Aging Trends Study” by Cudjoe, et al. (2018, The Journal of Gerontology)
https://academic.oup.com/psychsocgerontology/advance-article/doi/10.1093/geronb/gby037/4953727
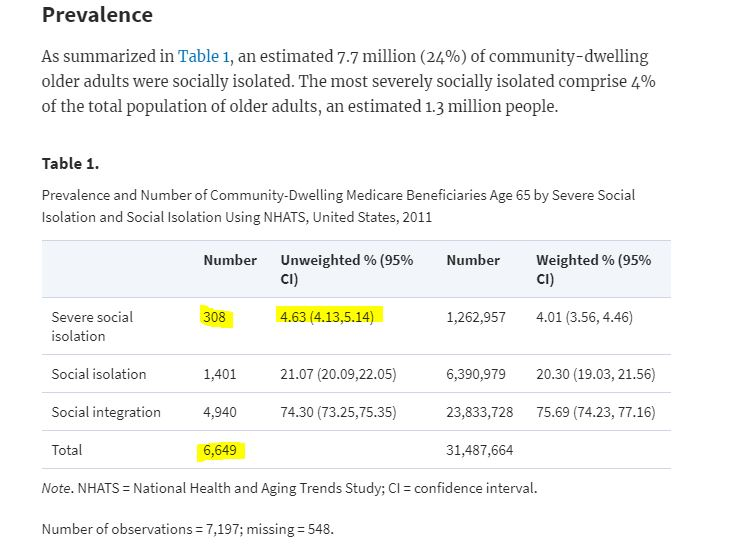
Note: The column labeled “Unweighted) is calculating confidence intervals for proportions as we have learned, multiplying the final result by 100 to give the answers as percentages rather than proportions.
For example, the confidence interval for “Severe Social Isolation” was computed using \[\hat{p}=\frac{308}{6649}\]
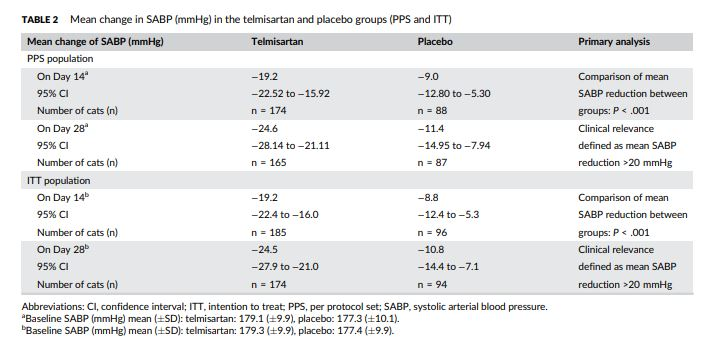
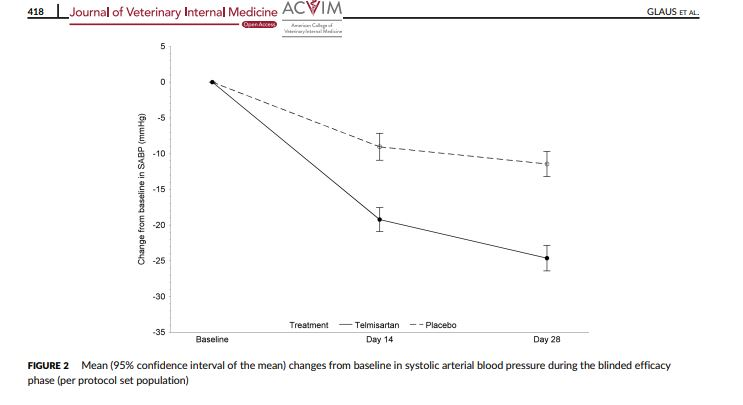
From the article “Efficacy of long-term oral telmisartan treatment in cats with hypertension: Results of a prospective European clinical trial” by Glaus, et al. (2018, Journal of Veterinary Internal Medicine)
https://onlinelibrary.wiley.com/doi/pdf/10.1111/jvim.15394