Chapter 7 Analysis of continuous outcomes

Effect size estimates quantify clinical relevance, confidence intervals (CIs) indicate the (im)precision of the effect size estimates as population values and $P$ -values quantify statistical significance, i.e. evidence against the null hypothesis. All three should be reported for each outcome of an RCT where the reported $p$ -value should be compatible with the type of confidence interval. While this chapter is about continuous outcomes, these reporting guidelines are true for all outcomes and elaborated on in Section 7.1. Throughout this chapter, the RCT in Example 7.1 will be used repeatedly for illustration. Binary outcomes are discussed in the next chapter.

7.1 The CONSORT Statement

The CONSORT Statement (Schulz, Altman, and Moher 2010,consortEE),

CONSolidated Standards Of Reporting Trials, (http://www.consort-statement.org/)

is an evidence-based minimum set of recommendations for reporting RCTs. It encompasses various initiatives developed by the CONSORT Group to alleviate the problems arising from inadequate reporting of RCTs. It offers a standard way for authors to prepare reports of trial findings, facilitating their complete and transparent reporting, and aiding their critical appraisal and interpretation. The CONSORT Statement comprises a 25-item checklist and a flow diagram, see Figures 7.1 and 7.2.

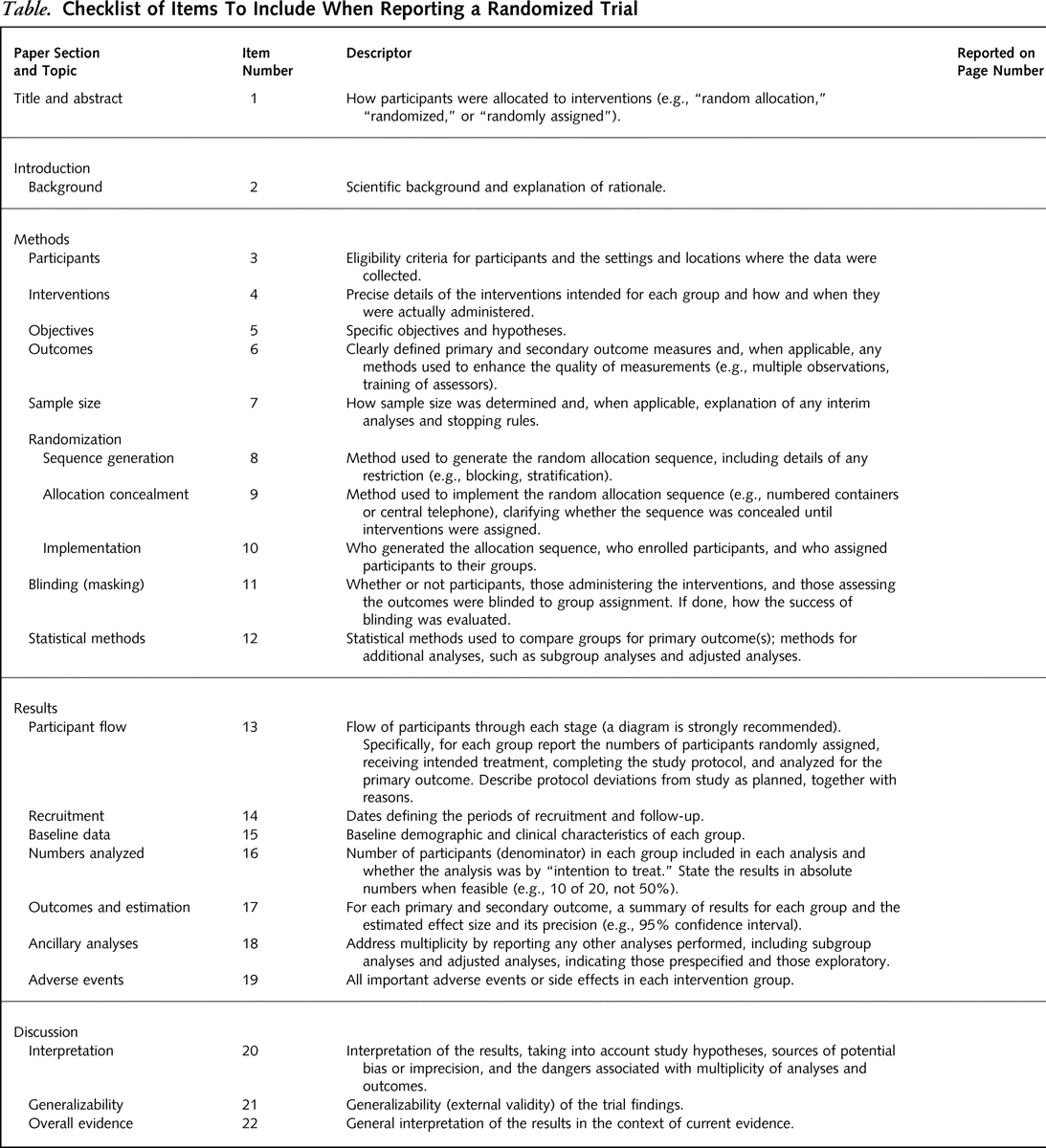
Figure 7.1: The CONSORT checklist.

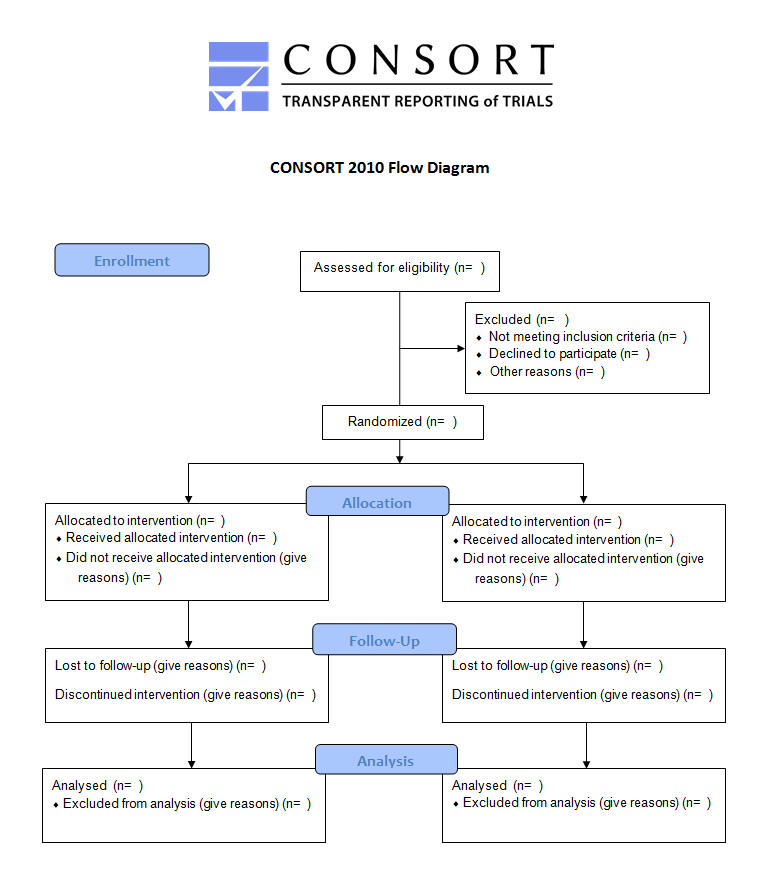
Figure 7.2: The CONSORT flow diagram.

7.1.1 Reporting results

Results from a statistical analysis should be reported as follows:

The recommended format for CIs is “from $a$ to $b$ ” or “ $a$ to $b$ ”, not “ $(a,b)$ ”, “ $[a,b]$ ” or “ $a-b$ ”.
Round $P$ -values to two significant digits, e.g. $p=0.43$ or $p=0.057$ . Round to one significant digit if $0.001 < p < 0.0001$ , e.g. $p=0.0004$ . Report very small $P$ -values with “ $p < 0.0001$ ”.
Do not report $P$ -values as $p<0.1$ or $p<0.05$ etc., as important information about the actual $P$ -value is lost.

An example from the Didgeridoo Study is (see Example 7.1):

“The difference in means at follow-up was 2.28 units (95% CI: $-1.34$ to $5.90$ , $p=0.21$ ).”

Example 7.1 The Didgeridoo Study (Puhan et al. 2005) is a randomized controlled trial with simple randomization, see the abstract in Figure 7.3.

Figure 7.3: Abstract of publication of the Didgeridoo Study.

Patients with moderate obstructive sleep apnoea syndrome are divided in two groups as follows:

table(treatment)

## treatment
##    Control Didgeridoo 
##         11         14

Treatment group: 4 months Didgeridoo practice ( $m=14$ )
Control group: 4 months waiting list ( $n=11$ )

The primary endpoint is the Epworth scale (integers from 0-24). This scale is ordinal but for the analysis, it is considered as continuous due to the large number of possible values. Measurements are taken at the start of the study (Baseline) and after four months (Follow-up). Figure 7.4 compares the follow-up measurements of the treatment and control group for the primary endpoint. When we want to analyze the difference of these follow-up measurements between the two groups, regression analysis gives equivalent results as a $t$ -test:

\begin{figure}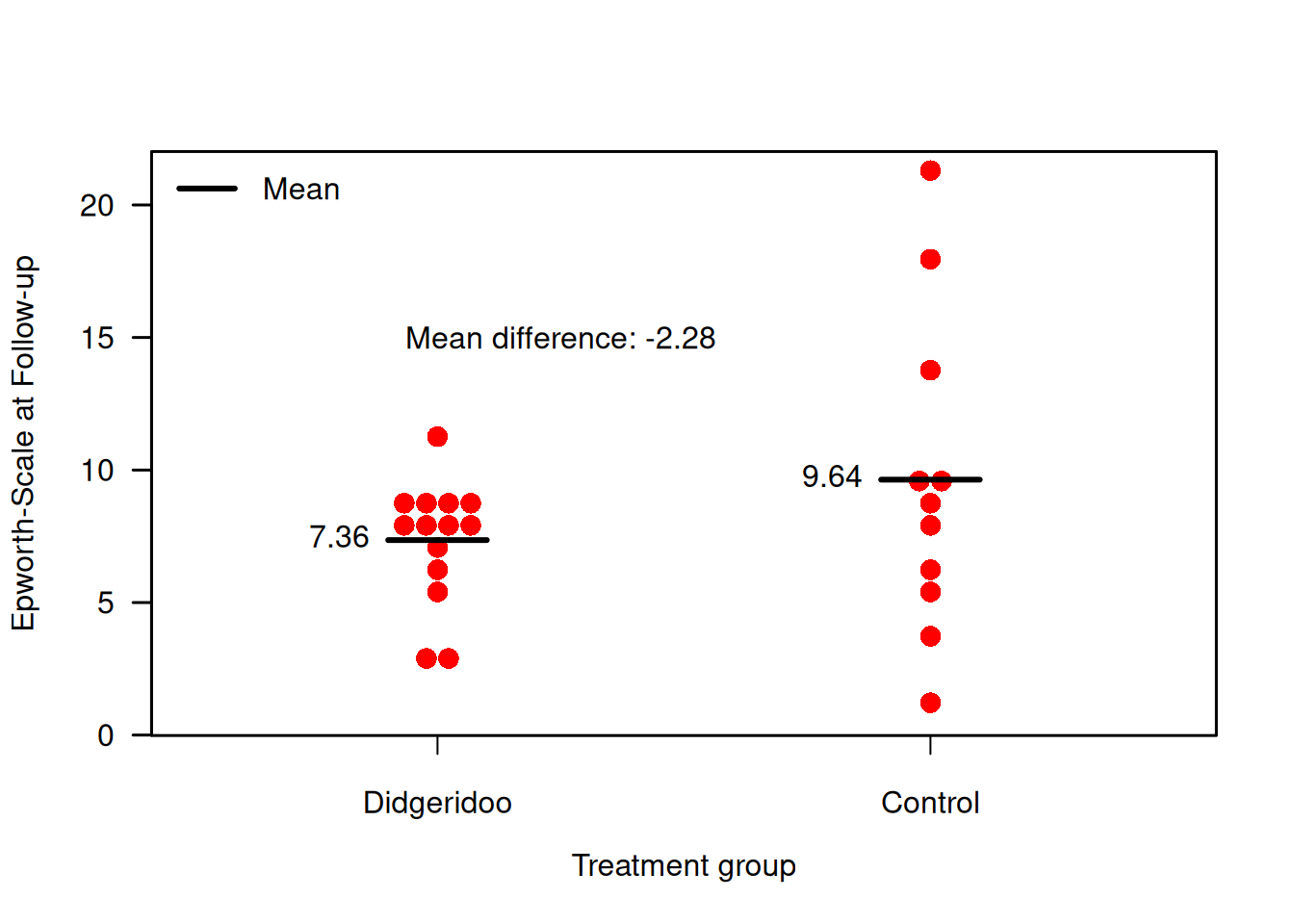

Figure 7.4: Follow-up measurements of primary endpoint in the Didgeridoo Study.

# t-test
print(res <- t.test(f.up ~ treatment, var.equal=TRUE))

## 
##  Two Sample t-test
## 
## data:  f.up by treatment
## t = 1.3026, df = 23, p-value = 0.2056
## alternative hypothesis: true difference in means between group Control and group Didgeridoo is not equal to 0
## 95 percent confidence interval:
##  -1.340366  5.898807
## sample estimates:
##    mean in group Control mean in group Didgeridoo 
##                 9.636364                 7.357143

(DifferenceInMeans <- mean(res$conf.int))

## [1] 2.279221

# regression analysis
library(biostatUZH)
m1 <- lm(f.up ~ treatment)
knitr::kable(tableRegression(m1, intercept=FALSE, latex = FALSE))

% latex table generated in R 4.4.1 by xtable 1.8-4 package % Fri Oct 4 10:19:09 2024

	Coefficient	95%-confidence interval	$p$ -value
treatmentDidgeridoo	-2.28	from -5.90 to 1.34	0.21

7.2 Comparison of two groups

We can compare the follow-up measurements in two groups

with a $t$ -test in case of equal variances,
with Welch’s-test or Behrens test in case of unequal variances.

The $t$ -test is explained in Appendix B (and also the $z$ -test). Alternative methods that adjust for baseline values are discussed in Section 7.3.

7.2.1 Equal variances

The $t$ -test assumes independent measurements in two groups that are normally distributed with equal variances. The null hypothesis is that the mean difference $\Delta$ between the two groups is $0$ . Assuming $H_0$ is true, the test statistic

$T = \frac{\widehat \Delta}{\mbox{se}(\widehat \Delta)}.$

follows a $t$ -distribution with $m+n-2$ degrees of freedom’’ (df).

For large df’s, the $t$ -distribution is close to a standard normal distribution as illustrated in Figure 7.5.

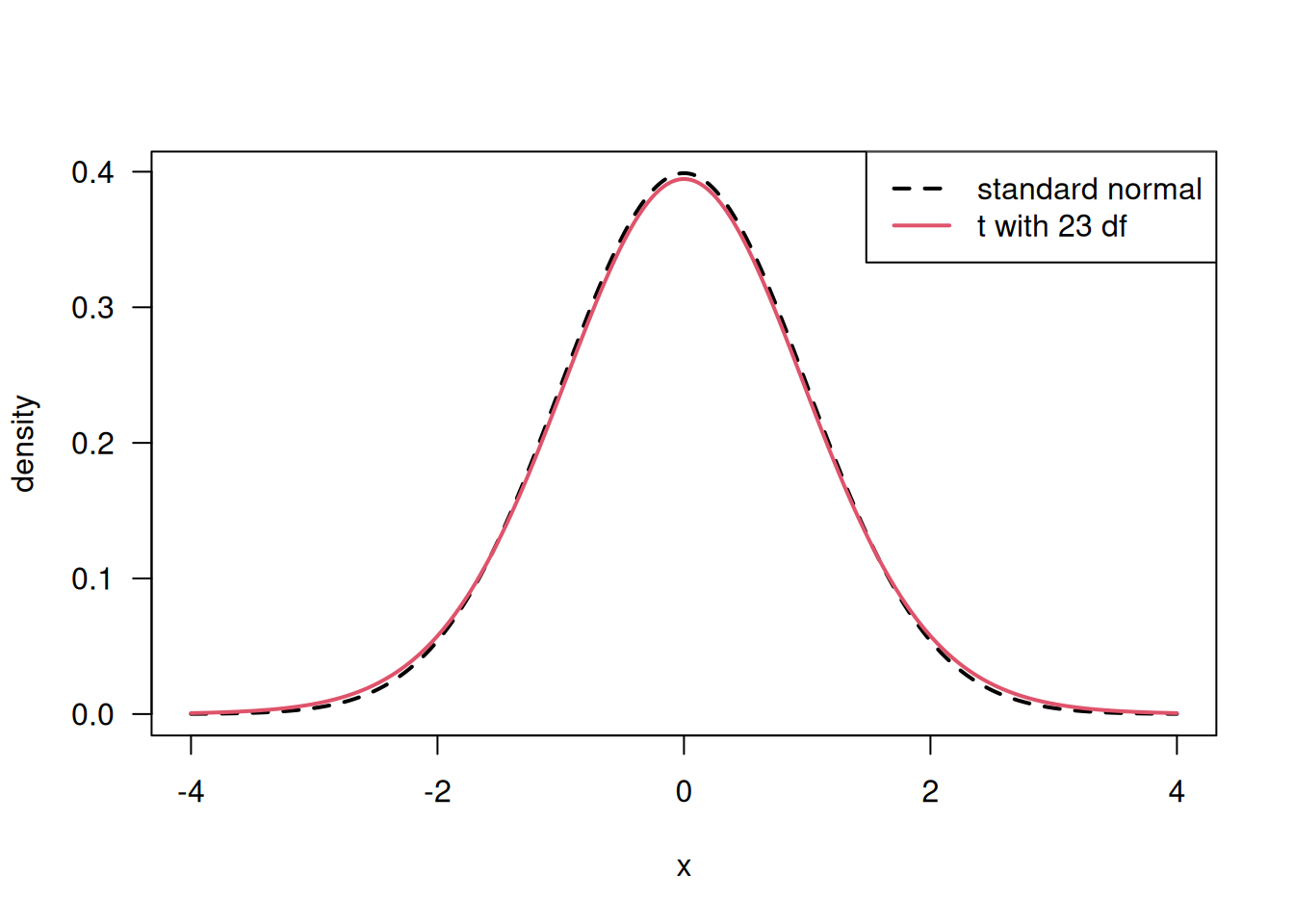
Figure 7.5: Comparison of $t$ -distribution (with large degree of freedom) to a standard normal distribution.

Here is a comparison of the two-sided $P$ -value $p = \operatorname{\mathsf{Pr}}(\left\lvert T\right\rvert \geq \left\lvert t\right\rvert)$ using the exact $t$ -distribution and the approximate normal distribution:

print(res$statistic)

##        t 
## 1.302615

## exact p-value based on t-distribution
unname(2*(1-pt(abs(res$statistic), df=23)))

## [1] 0.2055989

## normal approximation
unname(2*(1-pnorm(abs(res$statistic))))

## [1] 0.1927063

Here we compare the factor used to compute the limits of exact and approximate 95% confidence intervals ${\widehat \Delta} \pm t % t_{(1+\gamma)/2}%(m+n-2) \cdot \SE(\widehat \Delta)$ resp. ${\widehat \Delta} \pm z % t_{(1+\gamma)/2}%(m+n-2) \cdot \SE(\widehat \Delta)$ .

gamma <- 0.95
## Exact factor t based on t-distribution
(t <- qt((1+gamma)/2, df=23))

## [1] 2.068658

## Approximate factor z based on normal distribution
(z <- qnorm((1+gamma)/2))

## [1] 1.959964

7.2.2 Unequal variances

In case of unequal variances, $\sigma_T^2$ and $\sigma^2_C$ are assumed to be different and the standard error then is

$\begin{equation*} \mbox{se}(\widehat \Delta) = \sqrt{\frac{s_T^2}{m} + \frac{s_C^2}{n}}, \end{equation*}$ where $s_T^2$ and $s_C^2$ are estimates of the variances $\sigma_T^2$ and $\sigma_C^2$ in the two groups. In this case, the exact null distribution of $T=\widehat \Delta/{\mbox{se}(\widehat \Delta)}$ is unknown. Approximate solutions are:

Standard normal, which is fine for large $m$ and $n$ .
Welch’s Test, which uses a $t$ -distribution with (non-integer) degrees of freedom $\nu$ where $\nu$ is the solution of $\frac{(s_T^2/m+s_C^2/n)^2}{\nu} = \frac{(s_T^2/m)^2}{m-1} + \frac{(s_C^2/n)^2}{n-1}$
Behrens Test is another option that can be derived with Bayesian arguments .
The Mann-Whitney Test gives a $p$ -value, which is not compatible with the CI for the mean difference. Instead, it provides a CI for the median of the difference between a sample from X and a sample from Y.

In R

## Welch Test
print(res2 <- t.test(f.up ~ treatment, var.equal=FALSE))

## 
##  Welch Two Sample t-test
## 
## data:  f.up by treatment
## t = 1.187, df = 12.381, p-value = 0.2575
## alternative hypothesis: true difference in means between group Control and group Didgeridoo is not equal to 0
## 95 percent confidence interval:
##  -1.890289  6.448731
## sample estimates:
##    mean in group Control mean in group Didgeridoo 
##                 9.636364                 7.357143

print(DifferenceInMeans <- mean(res2$conf.int))

## [1] 2.279221

## Behrens Test
library(biostatUZH)
behrens.test(f.up ~ treatment)

## 
##  Behrens' t-test
## 
## data:  f.up by treatment
## t = 1.173, df = 11.361, p-value = 0.2648
## alternative hypothesis: true difference in means between group Control and group Didgeridoo is not equal to 0
## 95 percent confidence interval:
##  -1.980971  6.539413
## sample estimates:
##    mean in group Control mean in group Didgeridoo 
##                 9.636364                 7.357143

## Mann-Whitney Test
wilcox.test(f.up ~ treatment, conf.int=TRUE)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  f.up by treatment
## W = 94, p-value = 0.3623
## alternative hypothesis: true location shift is not equal to 0
## 95 percent confidence interval:
##  -2.000003  5.999959
## sample estimates:
## difference in location 
##               1.000079

7.3 Adjusting for baseline

7.3.1 Change scores

Baseline values may be imbalanced between treatment groups just as any other prognostic factor. To analyse change from baseline, we use change scores:

Definition 7.1 The change score is the change from baseline defined as: $\mbox{change score} = \mbox{follow-up} - \mbox{baseline}.$

Example 7.2 Figure 7.6 shows the combinations of baseline and follow-up measurements for each individual. It is visible that the change from baseline to follow-up is larger in the treatment group than in the control group. Figure 7.7 now directly compares the change scores.

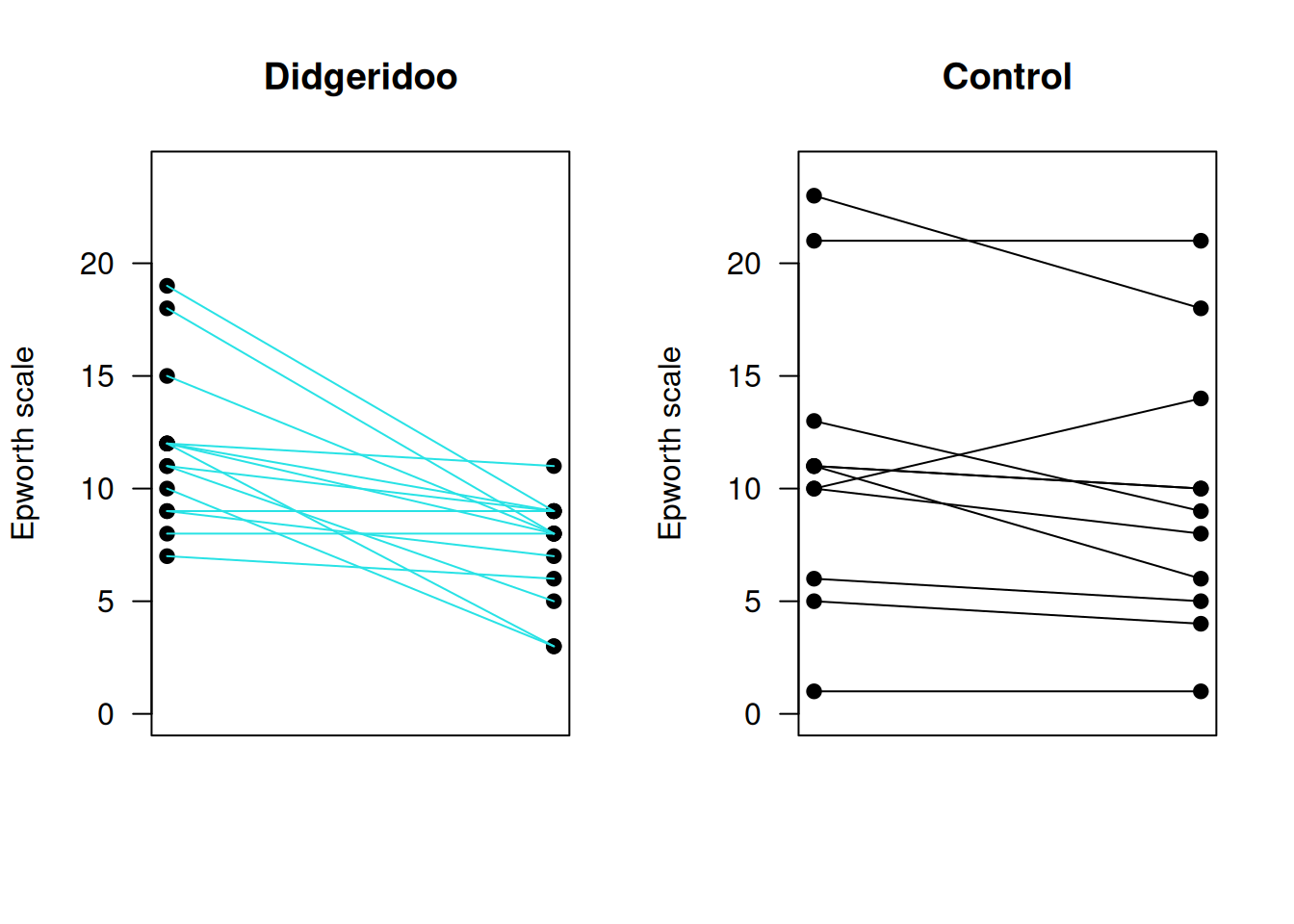
Figure 7.6: Individual baseline and follow-up measurements in the Didgeridoo Study by treatment group.

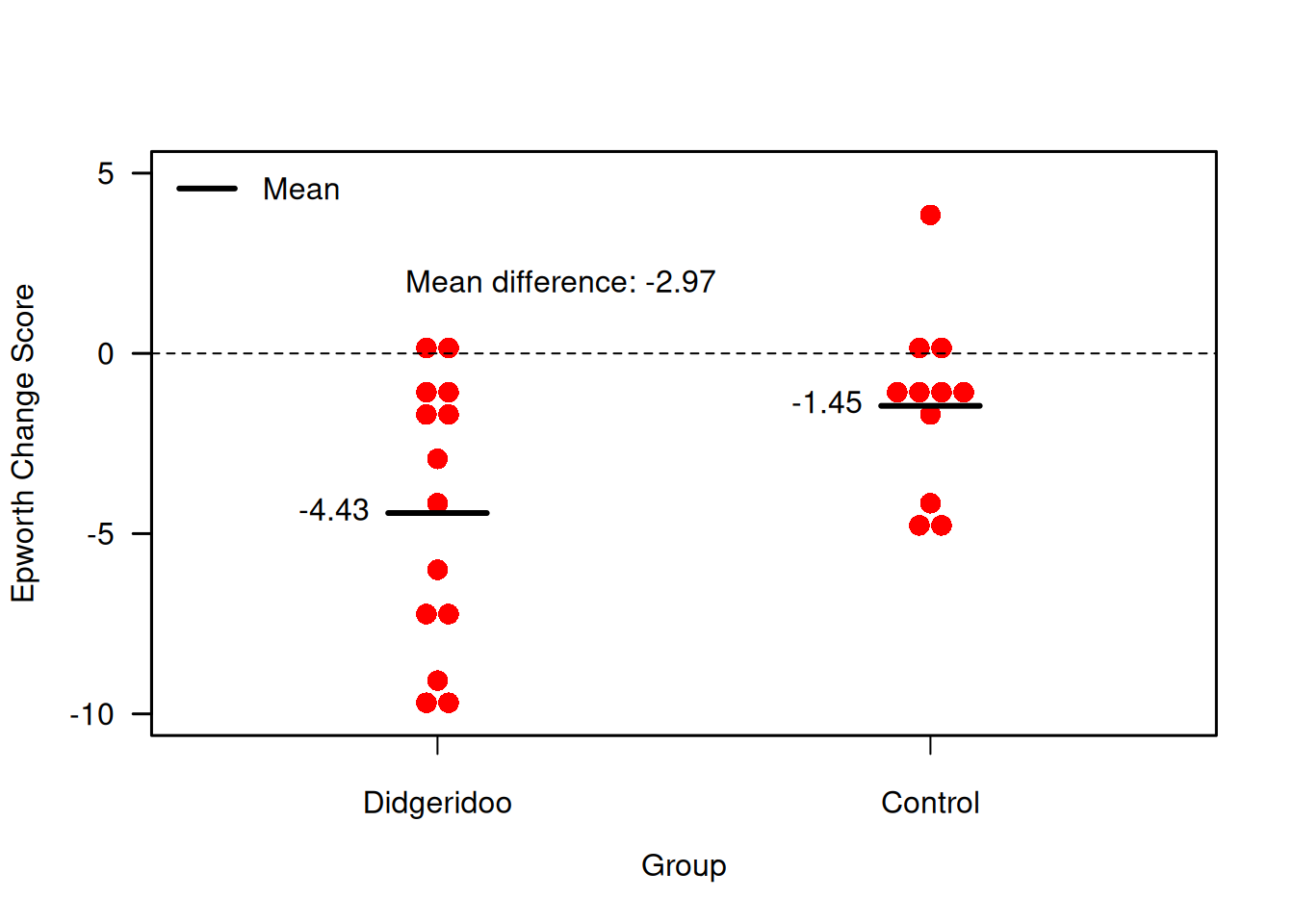
Figure 7.7: Change scores for primary endpoint in the Didgeridoo Study.

A change score analysis in for the Didgeridoo Study yields:

change.score <- f.up - baseline
print(res3 <- t.test(change.score ~ treatment, var.equal=TRUE))

## 
##  Two Sample t-test
## 
## data:  change.score by treatment
## t = 2.2748, df = 23, p-value = 0.03256
## alternative hypothesis: true difference in means between group Control and group Didgeridoo is not equal to 0
## 95 percent confidence interval:
##  0.2695582 5.6784938
## sample estimates:
##    mean in group Control mean in group Didgeridoo 
##                -1.454545                -4.428571

(DifferenceInMeans <- mean(res3$conf.int))

## [1] 2.974026

This result can also be found in an extract of the reported results in Figure 7.8.

Figure 7.8: Reported results of the Didgeridoo Study.

7.3.2 Analysis of covariance (ANCOVA)

Analysis of covariance (ANCOVA) is an extension of the change score analysis. First note that the change score analysis can also be done with regression, see model m2 in Example 7.2. Here, the command fixes the coefficient of at 1. It is therefore natural to extend this regression model to the ANCOVA model as it is done in model m3 of the example. Now the coefficient $\beta$ is estimated. The ANCOVA model reduces

to the analysis of follow-up for $\beta=0$ ,
to the analysis of change scores for $\beta=1$ .

Denote the different outcome means as $\mu_B$ at baseline (in both groups), $\mu$ at follow-up in the control group, $\mu + \Delta$ at follow-up in the treatment group. The mean difference $\Delta$ is of primary interest. Let $\sigma^2$ be the common variance of all measurements and $\rho$ the correlation between baseline and follow-up measurements. Assume there are $n$ observations in each group.

The ANCOVA model estimates $\beta$ and the mean difference $\Delta$ jointly with multiple regression. With ${\sigma_B^2}$ and ${\sigma_F^2}$ being the variances of baseline and follow-up, it holds that $\beta = \rho \, \frac{\sigma_F}{\sigma_B},$ which simplifies to $\rho$ if the variance does not change from baseline to follow-up, if $\sigma_B^2 = \sigma_F^2$ .

Example 7.3 Comparing the three different analysis methods in the Didgeridoo Study:

# Follow-up analysis
m1 <- lm(f.up ~ treatment)
knitr::kable(tableRegression(m1, intercept=FALSE, latex = FALSE))

% latex table generated in R 4.4.1 by xtable 1.8-4 package % Fri Oct 4 10:19:10 2024

	Coefficient	95%-confidence interval	$p$ -value
treatmentDidgeridoo	-2.28	from -5.90 to 1.34	0.21

# Change score analysis
m2 <- lm(f.up ~ treatment + offset(baseline))
knitr::kable(tableRegression(m2, intercept=FALSE, latex = FALSE))

% latex table generated in R 4.4.1 by xtable 1.8-4 package % Fri Oct 4 10:19:10 2024

	Coefficient	95%-confidence interval	$p$ -value
treatmentDidgeridoo	-2.97	from -5.68 to -0.27	0.033

# ANCOVA
m3 <- lm(f.up ~ treatment + baseline)
knitr::kable(tableRegression(m3, intercept = FALSE, latex = FALSE))

% latex table generated in R 4.4.1 by xtable 1.8-4 package % Fri Oct 4 10:19:10 2024

	Coefficient	95%-confidence interval	$p$ -value
treatmentDidgeridoo	-2.74	from -5.14 to -0.35	0.027
baseline	0.67	from 0.42 to 0.92	< 0.0001

7.3.2.1 Comparison of effect estimates

Let $\bar F_T$ and $\bar F_C$ be the mean follow-up values and $\bar B_T$ and $\bar B_C$ the mean baseline values in the treatment and control group, respectively. Then,

$\begin{eqnarray*} \widehat \Delta_1 & = & \bar F_T - \bar F_C, \\ \widehat \Delta_2 & = & (\bar F_T - \bar B_T) - (\bar F_C - \bar B_C). \end{eqnarray*}$

Now, let $\bar {b}_T$ and $\bar {b}_C$ denote the observed mean baseline values in the current trial. Conditioning on these baseline values, we have (the proof is part of the exercises):

$\begin{eqnarray*} \mathop{\mathrm{\mathsf{E}}}(\widehat \Delta_1 \;|\; \bar b_T, \bar b_C) & = & \Delta + \rho \cdot (\bar b_T - \bar b_C) \\ \mathop{\mathrm{\mathsf{E}}}(\widehat \Delta_2 \;|\; \bar b_T, \bar b_C) & = & \Delta + (\rho - 1) \cdot (\bar b_T - \bar b_C) \end{eqnarray*}$

Hence, given the mean baseline values $\bar {b}_T$ and $\bar {b}_C$ , $\widehat \Delta_1$ and $\widehat \Delta_2$ are unbiased if there is baseline balance ( $\bar {b}_T=\bar {b}_C$ ). However, they are both biased whenever the following two conditions hold:

There is (positive) correlation $0 < \rho < 1$ , between baseline and follow-up measurements.
There is baseline imbalance ( $\bar b_T \neq \bar b_C$ ):

In the Didgeridoo Study, , there is baseline imbalance: $\bar {b}_T=11.1$ , $\bar {b}_C=11.8$ .

The ANCOVA estimate

$\begin{equation*} \widehat \Delta_3 = \bar F_T - \bar F_C - \rho \cdot (\bar b_T - \bar b_C) \end{equation*}$

on the other hand is an unbiased estimate of the mean difference $\Delta$ (see proof in the exercises).

The variances of the effect estimates in the three models can be compared by the corresponding variance factors (derived in the exercises):

$\mathop{\mathrm{Var}}(\widehat \Delta) = \color{red}{\mbox{variance factor}} \cdot \sigma^2 /n$

$\begin{aligned} \mathop{\mathrm{Var}}(\widehat \Delta_1) &= \color{red}{2} \cdot \sigma^2 /n \\ \mathop{\mathrm{Var}}(\widehat \Delta_2) &= \color{red}{4 (1-\rho)} \cdot \sigma^2 /n \\ \mathop{\mathrm{Var}}(\widehat \Delta_3) &= \color{red}{2 (1-\rho^2)} \cdot \sigma^2/n \end{aligned}$

Figure 7.9 compares the variance factors of the three models for varying correlations $\rho$ . The variance of $\widehat \Delta_3$ is always smaller than the variances of $\widehat \Delta_1$ and $\widehat \Delta_2$ . Hence, the required sample size for ANCOVA reduces by the factor $(1-\rho^2)$ compared to the standard comparison of two groups without baseline adjustments. For $\rho > 1/2$ , $\widehat \Delta_2$ will have smaller variance than $\widehat \Delta_1$ , so will produce narrower CIs and more powerful tests. In the Didgeridoo Study we obtain $\hat \rho=0.72$ .

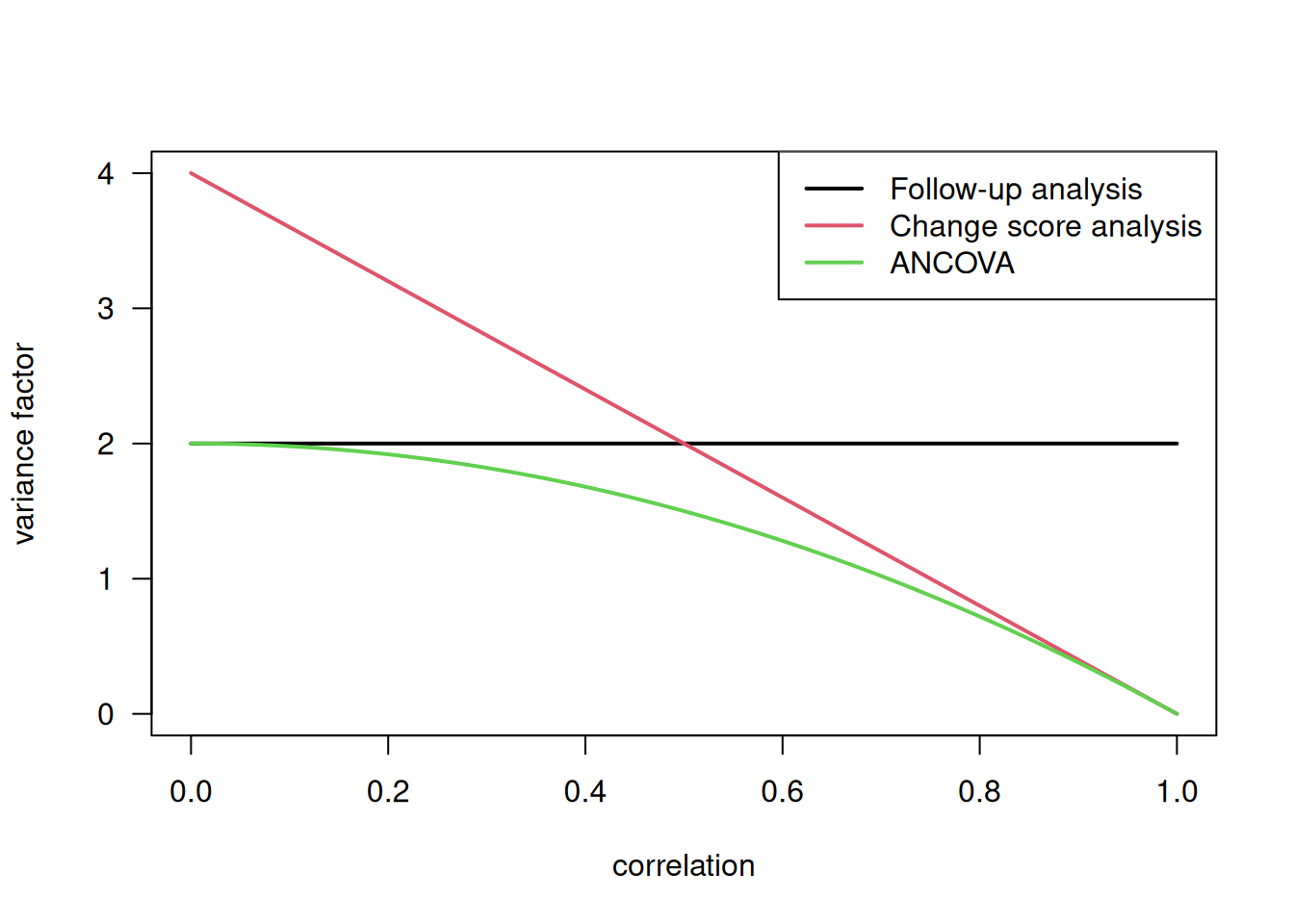
Figure 7.9: Comparison of variance factors

7.3.2.2 Adjusting for other variables

ANCOVA allows a wide range of variables measured at baseline to be used to adjust the mean difference. The safest approach to selecting these variables is to decide this before the trial starts (in the study protocol). Prognostic variables used to stratify the allocation should always be included as covariates.

Example 7.4 In the Didgeridoo Study, the mean difference has been adjusted for severity of the disease () and for weight change during the study period (). The same results as in Figure 7.8 can be obtained with the following regression model.

m4 <- lm(f.up ~ treatment + baseline + weight.change + base.apnoea)
knitr::kable(tableRegression(m4, intercept = FALSE, latex = FALSE))

% latex table generated in R 4.4.1 by xtable 1.8-4 package % Fri Oct 4 10:19:10 2024

	Coefficient	95%-confidence interval	$p$ -value
treatmentDidgeridoo	-2.75	from -5.35 to -0.15	0.039
baseline	0.67	from 0.41 to 0.93	< 0.0001
weight.change	-0.17	from -0.92 to 0.57	0.63
base.apnoea	0.023	from -0.25 to 0.29	0.86

7.4 Additional references

Relevant references are Chapter 10 “Comparing the Means of Small Samples” and Chapter 15 “Multifactorial Methods” in M. Bland (2015) as well as Chapter 6 “Analysis of Results” in J. N. S. Matthews (2006). Analysing controlled trials with baseline and follow up measurements is discussed in the Statistics Note Vickers and Altman (2001). Studies where the methods from this chapter are used in practice are for example Ravaud et al. (2009),porto,james.

References

Bland, Martin. 2015. An Introduction to Medical Statistics. Fourth. Oxford University Press.

Matthews, John N. S. 2006. Introduction to Randomized Controlled Clinical Trials. Second. Chapman & Hall/CRC.

Puhan, Milo A, Alex Suarez, Christian Lo Cascio, Alfred Zahn, Markus Heitz, and Otto Braendli. 2005. “Didgeridoo playing as alternative treatment for obstructive sleep apnoea syndrome: randomised controlled trial.” BMJ 332: 1–5.

Ravaud, P, RM Flipo, I Boutron, C Roy, A Mahmoudi, B Giraudeau, and T Pham. 2009. “ARTIST (osteoarthritis intervention standardized) study of standardised consultation versus usual care for patients with osteoarthritis of the knee in primary care in France: pragmatic randomised controlled trial.” BMJ 338.

Schulz, KF, DG Altman, and D for the CONSORT Group Moher. 2010. “CONSORT 2010 Statement: updated guidelines for reporting parallel group randomised trials.” BMJ 340.

Vickers, Andrew J, and Douglas G Altman. 2001. “Statistics Notes: Analysing controlled trials with baseline and follow up measurements.” BMJ 323 (7321): 1123–24.