第 73 章 生存數據中的回歸模型
73.1 生存數據的似然方程
\[ L = \prod_i f(t_i)^{\delta_i}S(t_i)^{1-\delta_i} \]
- \(i = 1, \cdots, n\) 是患者的編號
- \(t_i\) 是 \(i\) 號患者的生存/刪失時間
- \(\delta_i\) 是表示 \(i\) 號患者的生存/刪失狀態的啞變量 (indicator/dummy variable)
- \(f(t_i)\) 是生存數據(死亡/事件發生患者的)的概率密度方程 probablity density function
- \(S(t_i)\) 是生存數據(生存/刪失患者的)生存概率方程 survivor function
73.2 如何加入解釋變量
先考慮一個二分類變量 (binary explanatory variable \(X = 0 \text{ or } 1\)),可以是治療組對照組等簡單的二分類變量。可以認爲其中一組 \((X=1)\) 患者在時間點 \(t\) 時的風險度 (hazard) \(h_1(t)\) 和另一個被看作是對照的基準組 (baseline group \(X=0\)) 的風險度 \(h_0(t)\) 之間的關系是相乘的話:
\[ h_1(t) = \psi h_0 (t) \]
那麼這裏的 \(\psi\) 就是我們關心的參數。注意這裏兩組患者的風險度,等式左右兩邊都必須是大於零的,因此 \(psi\) 的取值要被限制在 \(>0\) 範圍。所以,我們常常直接寫成:
\[ h_1(t) = e^\beta h_0(t) \]
那麼參數 \(\beta\) 就沒有了取值的限制。這就是大名鼎鼎的比例風險度模型 (proportional hazard model)。\(e^\beta\) 就是風險度比 (Hazard ratio):
\[ \frac{h_1(t)}{h_0(t)} = e^\beta \]
\(\beta\) 是對數風險度比 (log-hazard ratio),這個風險度比,不隨着時間推進而變化。所以在生存分析的參數模型中,前提條件–比例風險度 (proportional hazard assumption),是必須被滿足的假設。當你認爲治療組對照組之間的療效差 (treatment effect) 會隨着時間發生變化的話,這個前提條件就被違反了。用於生存分析的這些參數模型,都需要比例風險度這一重要的前提條件被滿足。
73.3 指數模型 exponential model
指數模型是最簡單的生存時間分析參數模型。
風險度方程 hazard function:
\[ h(t) = \lim_{\delta\rightarrow0}\frac{1}{\delta}\text{Pr}(t\leqslant T <t + \delta | T>t) = \lambda \]
生存概率方程 survivor function:
\[ S(t) = \text{Pr}(T>t) = \exp\{-\lambda t\} \]
概率密度方程 probability density function:
\[ f(t) = \lambda \exp\{ - \lambda t\} \]
在指數分布時,風險度本身 (而不是比例) 保持不變。這也意味着事件發生的率 (rate of the event) 不隨時間發生變化 (constant over time)。
在指數分布模型下加入解釋變量:
\[ \left\{ \begin{array}{ll} h(t;0) = \lambda & X=0 \\ h(t;1) = \lambda e^\beta & X=1 \end{array} \right. \]
這個聯立方程等價於:
\[ h(t;x) = \lambda e^{\beta x} \]
類似地,風險度方程已知了的話,概率密度方程和生存方程可以寫作:
\[ f(t;x) = \lambda e^{\beta x} \exp({-\lambda t^{\beta x}}); \\ S(t;x) = \exp(-\lambda t^{\beta x}) \]
此時的似然方程就是
\[ L = \prod_{i = 1}^n\{\lambda e^{\beta x} \exp({-\lambda t^{\beta x}}) \}^{\delta_i}\{ \exp(-\lambda t^{\beta x})\}^{1-\delta_i} \]
此時,似然方程中兩個參數 \(\lambda, \beta\) 可以利用自己似然函數的方法分別對其中一個求導數獲得 MLE,然後用 Fisher information matrix 計算各自的標準誤,從而計算 95% 信賴區間。這裏的 \(\beta\) 回歸系數,可以做是否爲零 (等價於比較 \(e^\beta = 1\)) 的 Wald 檢驗:
\[ \frac{\hat\beta}{SE(\hat\beta)} \sim N(0,1) \]
\[ \begin{aligned} L & = \prod_{i = 1}^n\{\lambda e^{\beta x} \exp({-\lambda t^{\beta x}}) \}^{\delta_i}\{ \exp(-\lambda t^{\beta x})\}^{1-\delta_i} \\ & = \prod_{i = 1}^n\{\lambda e^{\beta x}\}^{\delta_i}\exp(-\lambda t^{\beta x}) \\ \Rightarrow \ell & = \log(\lambda)\sum_{i=1}^n \delta_i + \beta \sum_{i = 1}^n(x_i\delta_i) - \lambda\sum_{i = 1}^n t_ie^{\beta x_i} \\ \text{Let} & \sum_{i = 1}^n = n_1 \text{(numer of events)}; \\ &\sum_{i=1}^n(x_i\delta_i) = n_{11} \text{(number of events in } x=1); \\ &\sum_{x_i=1}^n t_i = T_1 \text{(sum of survival/censors T in } x=1);\\ &\sum_{x_i=0}^n t_i = T_0 \text{(sum of survival/censors T in } x=0);\\ \Rightarrow \ell & =n_1 \log(\lambda) + n_{11}\beta - \lambda(T_0 + T_1e^\beta) \end{aligned} \]
接下來求 MLE 就等同於解下面的聯立方程組:
\[ \left\{\begin{array}{l} \frac{\text{d}\ell}{\text{d}\lambda} = \frac{n_1}{\lambda} - (T_0 +T_1e^\beta) =0 \\ \frac{\text{d}\ell}{\text{d}\beta} = n_{11} = T_1\lambda e^\beta = 0 \end{array} \right. \\ \hat\lambda = \frac{n_1 - n_{11}}{T_0} \\ \hat\beta = \log\frac{T_0n_{11}}{T_1(n_1 - n_{11})} \]
73.4 Weibull 分布
指數分布的模型只能用於擬合數據滿足事件發生率恆定不變這一十分強的假設的前提下。Weibull 分布放鬆了這個假設前提,不再要求時間發生率恆定不變,但是它的前提條件是時間發生率隨着時間的變化是單調的 (遞增或者遞減,二者只能選一)。且 Weibull 分布是指數分布的一般化形式,或者說指數分布是 Weibull 分布的特殊形式。
Weibull 分布的風險度方程:
\[ h(t) = \kappa \lambda t^{\kappa - 1} \]
生存概率方程
\[ S(t;x) = \exp\{ -\lambda t^\kappa \} \]
概率密度方程
\[ f(t) = \kappa \lambda t^{\kappa - 1} \exp\{ -\lambda t^\kappa \} \]
那麼加入了一個二分類解釋變量 \(x\) 的 Weibull 比例風險度方程就是:
\[ h(t;x) = \kappa \lambda t^{\kappa - 1}e^{\beta x} \]
其生存概率方程就是:
\[ S(t;x) = \exp\{ -\lambda t^\kappa e^{\beta x}\} \]
概率密度方程是二者的乘積,那麼所有的生存數據的似然方程就是:
\[ L = \prod_{i=1}^n \{\kappa \lambda t^{\kappa - 1}e^{\beta x}\exp\{ -\lambda t^\kappa e^{\beta x}\} \}^{\delta_i}\{ \exp\{ -\lambda t^\kappa e^{\beta x}\}\}^{1-\delta_i} \]
但是,比較悲劇的是,在 Weibull 分布的生存模型中,沒有辦法簡單的獲得參數 \(\kappa, \lambda. \beta\) 的MLE。只能使用迭代法 (iterative numerical methods are required)。
73.5 Weibull 和 指數模型的比較
73.5.1 繪圖法
在指數分布模型中,累積風險度 cumulative hazard 是和時間呈正比的: \[ H(t;x) = -\log S(t;x) = \lambda t e^{\beta x} \]
在 Weibull 分布模型中,累積風險度 cumulative hazard,取了對數以後:
\[ \log H(t;x) = \log\{ -\log S(t;x) \} = \log \lambda + \kappa \log t + \beta x \]
所以,累積風險度如果取了對數,那麼這個值和時間的對數 \(\log t\) 是呈線性關系的,且當這個直線的坡度爲 1 的話 \(\kappa = 1\),就說明數據符合指數模型。如果,\(x\) 只是一個二分類解釋變量的話,你會看到對數累積風險度和對數時間呈現爲兩條平行線。
73.5.2 統計檢驗法
很簡單, Wald test:
\[ \frac{\log \hat\kappa}{SE(\log \hat\kappa)} \sim N(0,1) \]
當然你也可以使用似然比檢驗 likelihood ratio test,因爲指數分布模型是 Weibull 分布模型在 \(\kappa = 1\) 時的特殊形態,二者擬合的統計模型也會是嵌套式模型:
\[ -2(\ell_{\text{exponential}} - \ell_{\text{Weibull}}) \sim \chi_1^2 \]
服從的卡方分布的自由度是兩個模型的參數數量的差。
73.6 多於 1 個解釋變量的參數模型
當然可以在生存分析參數模型中加入多於一個變量,而且可以是分類型,連續型變量:
\[ h(t;x) = h_0 (t)e^{\beta^Tx} \]
- \(h_0(t)\) 是基線組的風險度 (baseline hazard);
- \(\mathbf{\beta} = (\beta_1, \beta_2, \cdots, \beta_p)^T\) 是一組解釋變量的回歸系數;
- \(\beta_k\) 是當保持所有其他變量不變時,解釋變量 \(X_k\) 在增加/減少一個單位對應的對數風險度比 (log-hazard ratio)。
73.7 Practical Survival 03
whitehall <- read_dta("backupfiles/whitehall.dta")
whitehall <- whitehall %>%
mutate(timein = as.numeric(timein),
timeout = as.numeric(timeout),
timebth = as.numeric(timebth)) %>%
mutate(time = (timeout - timein)/365.25)
with(whitehall, tabpct(grade, chd, graph = FALSE))##
## Original table
## chd
## grade 0 1 Total
## 1 1104 90 1194
## 2 419 64 483
## Total 1523 154 1677
##
## Row percent
## chd
## grade 0 1 Total
## 1 1104 90 1194
## (92.5) (7.5) (100)
## 2 419 64 483
## (86.7) (13.3) (100)
##
## Column percent
## chd
## grade 0 % 1 %
## 1 1104 (72.5) 90 (58.4)
## 2 419 (27.5) 64 (41.6)
## Total 1523 (100) 154 (100)#### median time
Median_t <- ddply(whitehall,c("grade","chd"),summarise,Median=median(time))
Median_t## grade chd Median
## 1 1 0 18.1779175
## 2 1 1 11.9110102
## 3 2 0 17.8726806
## 4 2 1 8.7679441whl.km <- survfit(Surv(time = time, event = chd) ~ as.factor(grade), data = whitehall)
plot(whl.km, conf.int = T, col = c("blue", "red"), mark.time = F, xlab = "Time", ylab = "Survivor function", ylim = c(0.8, 1))
legend(1, 0.85, c("Grade 1", "Grade 2"), col = c("blue", "red"), lty = 1)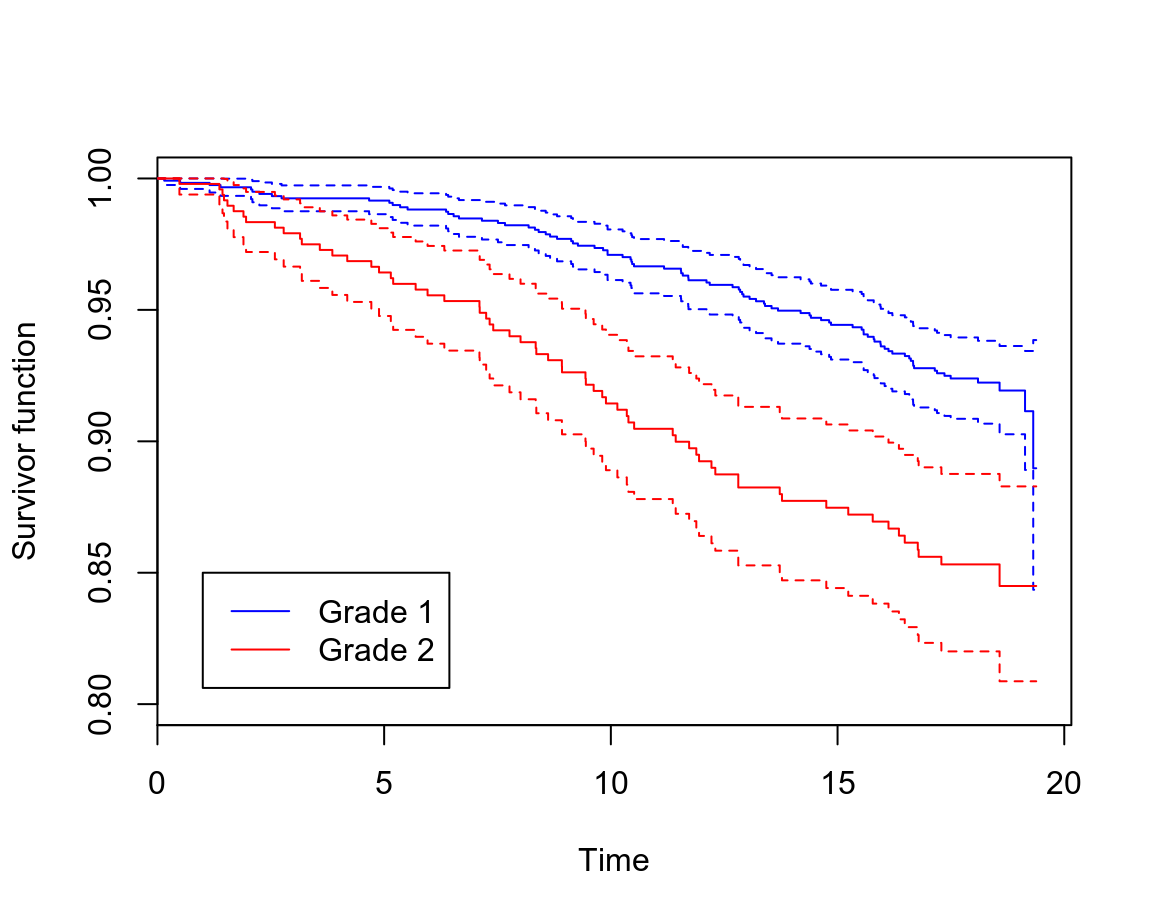
圖 73.1: Rplots of the Kaplan-Meier survivor functions
“Grade 1” 患者的生存概率明顯好於 “Grade 2”。而且,95% 信賴區間沒有重疊,提示這兩組之間的生存概率曲線應該有統計學上的顯著不同。
# How many individuals survived 5, 10, 15 years of follow-up in each job grade?
summary(whl.km, times = c(5, 10, 15))## Call: survfit(formula = Surv(time = time, event = chd) ~ as.factor(grade),
## data = whitehall)
##
## as.factor(grade)=1
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 5 1169 10 0.9916 0.002648 0.9864 0.9968
## 10 1114 24 0.9709 0.004913 0.9613 0.9806
## 15 1045 30 0.9443 0.006772 0.9311 0.9577
##
## as.factor(grade)=2
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 5 445 17 0.9642 0.008521 0.9477 0.9811
## 10 383 22 0.9144 0.013135 0.8890 0.9405
## 15 334 16 0.8747 0.015876 0.8442 0.9064# Log rank test to compare the estimated survivor functions in the two job grades
survdiff(Surv(time=time, event = chd) ~ as.factor(grade), data = whitehall)## Call:
## survdiff(formula = Surv(time = time, event = chd) ~ as.factor(grade),
## data = whitehall)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## as.factor(grade)=1 1194 90 114.19 5.123 19.85
## as.factor(grade)=2 483 64 39.81 14.692 19.85
##
## Chisq= 19.8 on 1 degrees of freedom, p= 8.393e-06# Fit an exponential model
whl.exp <- survreg(Surv(time, chd) ~ as.factor(grade), dist = "exponential", data = whitehall)
summary(whl.exp)##
## Call:
## survreg(formula = Surv(time, chd) ~ as.factor(grade), data = whitehall,
## dist = "exponential")
## Value Std. Error z p
## (Intercept) 5.4205 0.1054 51.424 0.00000000
## as.factor(grade)2 -0.6885 0.1635 -4.211 0.00002545
##
## Scale fixed at 1
##
## Exponential distribution
## Loglik(model)= -944.7 Loglik(intercept only)= -953.1
## Chisq= 16.76 on 1 degrees of freedom, p= 0.000042
## Number of Newton-Raphson Iterations: 6
## n= 1677這裏 R 的輸出結果和 STATA 的結果略有不同:
. streg i.grade, d(exp) nohr
failure _d: chd
analysis time _t: (timeout-origin)/365.25
origin: time timein
Iteration 0: log likelihood = -627.95275
Iteration 1: log likelihood = -620.09818
Iteration 2: log likelihood = -619.57374
Iteration 3: log likelihood = -619.57209
Iteration 4: log likelihood = -619.57209
Exponential PH regression
No. of subjects = 1,677 Number of obs = 1,677
No. of failures = 154
Time at risk = 27605.37066
LR chi2(1) = 16.76
Log likelihood = -619.57209 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
2.grade | .6885037 .1635118 4.21 0.000 .3680264 1.008981
_cons | -5.420525 .1054093 -51.42 0.000 -5.627123 -5.213926
------------------------------------------------------------------------------在 R 裏面,指數分布模型的回歸系數中,常數項 (Intercept) 等同於 STATA 裏的 _cons,但是,它在 R 裏估計的是 \(-\log \lambda\)。grade 的回歸系數 \(\beta\) 也一樣,在 R 裏它估計的是 \(-\beta\)。所以你會發現 R 的輸出結果和 STATA 的結果符號相反,但是殊途同歸。
# Change the time scale to age time and fit the models again
#The survreg function does not allow delayed entry times, so we can't use it with age as the time scale and entry at 'timein'
#But we can fit the same model using an alternative function called 'weibreg' which is in the 'eha' package. You will need to install this package.
# install.packages("eha") # install and loading this package by uncomment these two lines
# library(eha)
whl.exp2<-weibreg(Surv(timein/365.25, timeout/365.25,event=chd,origin=timebth/365.25)~as.factor(grade), data = whitehall,
shape = 1)
summary(whl.exp2)## Call:
## weibreg(formula = Surv(timein/365.25, timeout/365.25, event = chd,
## origin = timebth/365.25) ~ as.factor(grade), data = whitehall,
## shape = 1)
##
## Covariate Mean Coef Exp(Coef) se(Coef) Wald p
## as.factor(grade)
## 1 0.737 0 1 (reference)
## 2 0.263 0.689 1.991 0.164 0.000
##
## log(scale) 5.421 225.998 0.105 0.000
##
## Shape is fixed at 1
##
## Events 154
## Total time at risk 27605
## Max. log. likelihood -944.7
## LR test statistic 16.76
## Degrees of freedom 1
## Overall p-value 0.0000423884#Another alternative is the flexsurv package
# install.packages("flexsurv") # install and loading this package by uncomment these two lines
# library(flexsurv)
whl.exp3<-flexsurvreg(Surv(timein/365.25, timeout/365.25,event=chd,origin=timebth/365.25)~as.factor(grade), data = whitehall,dist = "exponential",inits = rep(0.1,2))## Warning in (function (q, rate = 1, lower.tail = TRUE, log.p = FALSE) : NaNs producedwhl.exp3## Call:
## flexsurvreg(formula = Surv(timein/365.25, timeout/365.25, event = chd,
## origin = timebth/365.25) ~ as.factor(grade), data = whitehall,
## dist = "exponential", inits = rep(0.1, 2))
##
## Estimates:
## data mean est L95% U95% se exp(est) L95% U95%
## rate NA 0.004425 0.003599 0.005440 0.000466 NA NA NA
## as.factor(grade)2 0.288014 0.688359 0.367869 1.008848 0.163518 1.990446 1.444653 2.742439
##
## N = 1677, Events: 154, Censored: 1523
## Total time at risk: 27605.371
## Log-likelihood = -944.69654, df = 2
## AIC = 1893.3931在指數分布模型下,我們默認事件發生率不會隨着時間變化,所以,改變了時間尺度,對生存分析估計的參數結果沒有影響。
whitehall <- whitehall %>%
mutate(agecat = cut(agein, breaks = c(40, 50, 55, 60, 65, 70),right = F, labels = F))
whl.exp <- survreg(Surv(time, chd) ~ as.factor(grade) + as.factor(agecat), dist = "exponential", data = whitehall)
summary(whl.exp)##
## Call:
## survreg(formula = Surv(time, chd) ~ as.factor(grade) + as.factor(agecat),
## data = whitehall, dist = "exponential")
## Value Std. Error z p
## (Intercept) 6.2076 0.1956 31.729 6.200e-221
## as.factor(grade)2 -0.2681 0.1755 -1.527 1.267e-01
## as.factor(agecat)2 -0.9559 0.2582 -3.703 2.133e-04
## as.factor(agecat)3 -1.4462 0.2416 -5.985 2.160e-09
## as.factor(agecat)4 -1.4832 0.2707 -5.480 4.258e-08
## as.factor(agecat)5 -2.4060 0.3749 -6.418 1.377e-10
##
## Scale fixed at 1
##
## Exponential distribution
## Loglik(model)= -914.1 Loglik(intercept only)= -953.1
## Chisq= 78.01 on 5 degrees of freedom, p= 2.2e-15
## Number of Newton-Raphson Iterations: 6
## n= 1677# Fit the Weibull model in R, keep job grade and age category
whl.weibull <- survreg(Surv(time, chd) ~ as.factor(grade) + as.factor(agecat), dist = "weibull", data = whitehall)
summary(whl.weibull)##
## Call:
## survreg(formula = Surv(time, chd) ~ as.factor(grade) + as.factor(agecat),
## data = whitehall, dist = "weibull")
## Value Std. Error z p
## (Intercept) 5.2390 0.22680 23.100 4.626e-118
## as.factor(grade)2 -0.2019 0.12469 -1.619 1.054e-01
## as.factor(agecat)2 -0.6855 0.18946 -3.618 2.966e-04
## as.factor(agecat)3 -1.0427 0.18683 -5.581 2.394e-08
## as.factor(agecat)4 -1.0783 0.20598 -5.235 1.648e-07
## as.factor(agecat)5 -1.8011 0.28840 -6.245 4.232e-10
## Log(scale) -0.3462 0.07678 -4.509 6.509e-06
##
## Scale= 0.7074
##
## Weibull distribution
## Loglik(model)= -905.1 Loglik(intercept only)= -946.7
## Chisq= 83.21 on 5 degrees of freedom, p= 2.2e-16
## Number of Newton-Raphson Iterations: 10
## n= 1677這個結果和 STATA 的結果也有些許不同:
streg i.grade i.agecat, d(weib) nohr
failure _d: chd
analysis time _t: (timeout-origin)/365.25
origin: time timein
Fitting constant-only model:
Iteration 0: log likelihood = -627.95275
Iteration 1: log likelihood = -621.65709
Iteration 2: log likelihood = -621.54148
Iteration 3: log likelihood = -621.54144
Fitting full model:
Iteration 0: log likelihood = -621.54144
Iteration 1: log likelihood = -591.43979
Iteration 2: log likelihood = -580.27283
Iteration 3: log likelihood = -579.9356
Iteration 4: log likelihood = -579.93477
Iteration 5: log likelihood = -579.93477
Weibull PH regression
No. of subjects = 1,677 Number of obs = 1,677
No. of failures = 154
Time at risk = 27605.37066
LR chi2(5) = 83.21
Log likelihood = -579.93477 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
2.grade | .285431 .1753856 1.63 0.104 -.0583184 .6291805
|
agecat |
2 | .9690825 .2581668 3.75 0.000 .463085 1.47508
3 | 1.47402 .2416534 6.10 0.000 1.000388 1.947652
4 | 1.524436 .2707669 5.63 0.000 .9937422 2.055129
5 | 2.546185 .3759036 6.77 0.000 1.809428 3.282943
|
_cons | -7.406372 .3705694 -19.99 0.000 -8.132675 -6.680069
-------------+----------------------------------------------------------------
/ln_p | .3462011 .0767777 4.51 0.000 .1957195 .4966827
-------------+----------------------------------------------------------------
p | 1.413687 .1085397 1.216186 1.643261
1/p | .7073702 .0543103 .6085461 .8222428
------------------------------------------------------------------------------- STATA裏的
ln_p(就是\(\kappa\)形狀參數 shape parameter),在 R 裏的名字是-log(scale)。 - STATA報告對數風險度比
2.grade |.285431,R 裏面的回歸系數as.factor(grade)2 -0.2019其實是對數風險度比除以形狀參數之後變更符號,所以 \(-\frac{0.2854}{\exp(0.346)} = 0.202\) - 所以在 R 中實際上輸出的結果是: \(-\log\kappa, -\frac{\beta}{\kappa}\)。
whl.km.agecat1 <- survfit(Surv(time=time,event=chd)~grade,data=subset(whitehall,agecat==1))
plot(whl.km.agecat1,conf.int=T,col=c("red","black"),mark.time=F,xlab="log time", ylab="log(-log S(t))",fun="cloglog")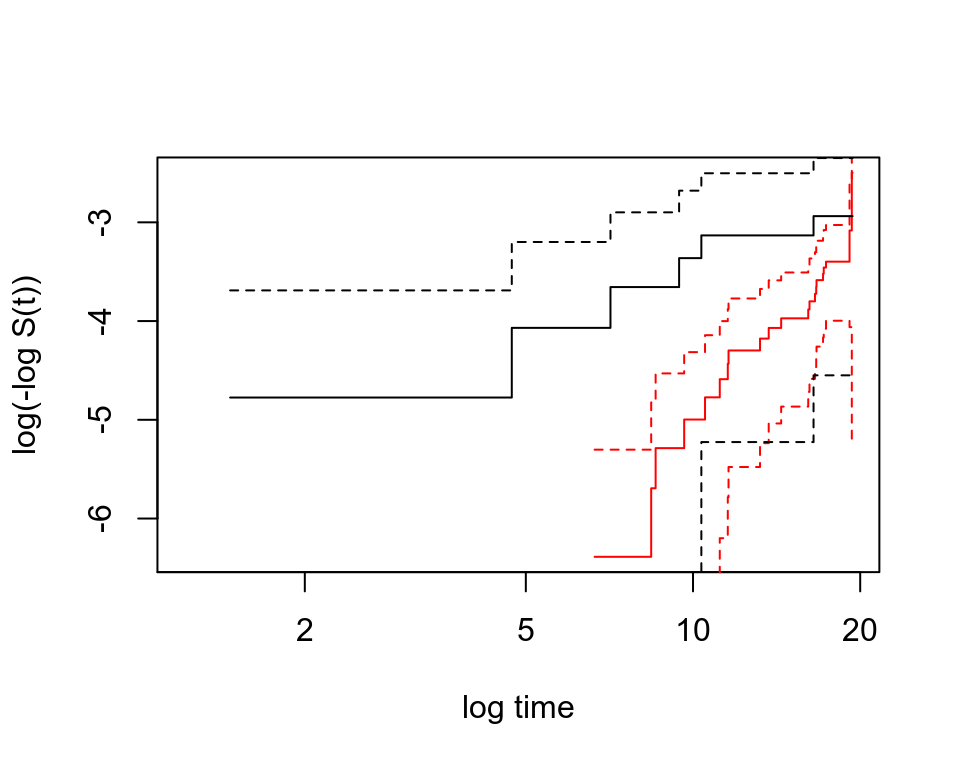
圖 73.2: Non-paramatric plot to investigate whether the Weibull model fit the data appropriate
用 Weibull 分布模型的結果,繪制兩個 job grade 在 5 個不同年齡層次的估計生存概率曲線:
whl.weibull <- survreg(Surv(time, chd) ~ as.factor(grade) + as.factor(agecat), dist = "weibull", data = whitehall)
plot(predict(whl.weibull, newdata = list(grade = 1, agecat = 1), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, col = "red",
xlab = "Time", ylab = "Survivor function: S(t)", xlim = c(0,20), ylim = c(0.5, 1))
lines(predict(whl.weibull, newdata = list(grade = 2, agecat = 1), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 2, col = "red")
lines(predict(whl.weibull, newdata = list(grade = 1, agecat = 2), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 1, col = "green")
lines(predict(whl.weibull, newdata = list(grade = 2, agecat = 2), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 2, col = "green")
lines(predict(whl.weibull, newdata = list(grade = 1, agecat = 3), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 1, col = "black")
lines(predict(whl.weibull, newdata = list(grade = 2, agecat = 3), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 2, col = "black")
lines(predict(whl.weibull, newdata = list(grade = 1, agecat = 4), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 1, col = "orange")
lines(predict(whl.weibull, newdata = list(grade = 2, agecat = 4), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 2, col = "orange")
lines(predict(whl.weibull, newdata = list(grade = 1, agecat = 5), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 1, col = "blue")
lines(predict(whl.weibull, newdata = list(grade = 2, agecat = 5), type = "quantile", p = seq(0.01, 0.99, by = 0.01)), seq(0.99, 0.01, by = -0.01), type = "l", lwd = 2, lty = 2, col = "blue")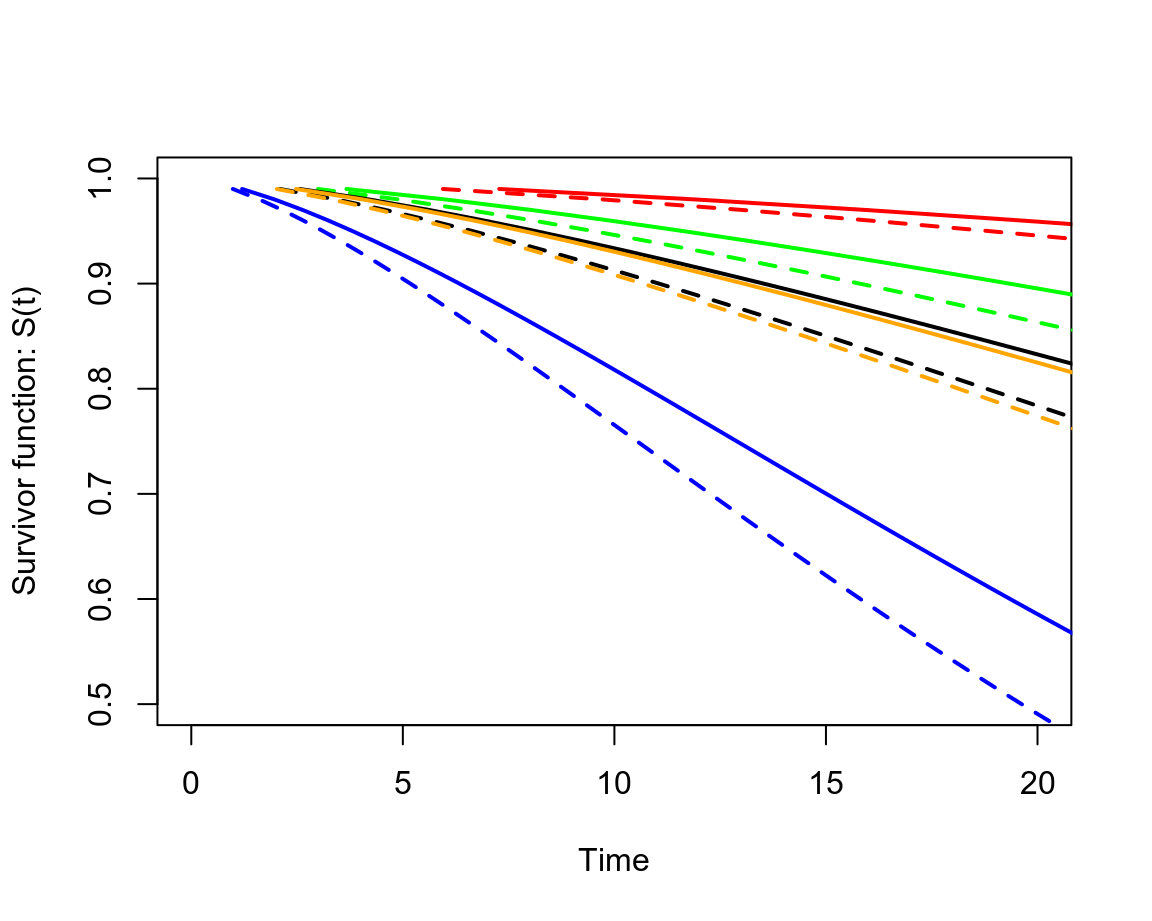
圖 73.3: The estimated survivor curves from the Weibull model in each job and age-at-entry category
下面把隨訪時間按照 5 到 20 年每間隔五年的方法把所有患者的追蹤時間截斷成4個部分。然後用指數分布回歸模型擬合數據,這也是一種放鬆恆定事件發生率這一前提條件的方法:
whl.split <- survSplit(Surv(time, chd) ~ ., whitehall, cut = c(0, 5, 10, 15, 20), start = "time0", episode = "fuband")
with(whitehall, whitehall[id == 5038,])## # A tibble: 1 x 16
## id all chd sbp chol grade4 smok agein grade cholgrp sbpgrp timein timeout timebth
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 5038 0 0 147 295 2 3 51.4 1 4 3 -840. 6239. -19630.
## # ... with 2 more variables: time <dbl>, agecat <int>with(whl.split, whl.split[id == 5038,])## id all sbp chol grade4 smok agein grade cholgrp sbpgrp timein timeout timebth
## 9 5038 0 147 295 2 3 51.444218 1 4 3 -840.01318 6238.9795 -19630.013
## 10 5038 0 147 295 2 3 51.444218 1 4 3 -840.01318 6238.9795 -19630.013
## 11 5038 0 147 295 2 3 51.444218 1 4 3 -840.01318 6238.9795 -19630.013
## 12 5038 0 147 295 2 3 51.444218 1 4 3 -840.01318 6238.9795 -19630.013
## agecat time0 time chd fuband
## 9 2 0 5.000000 0 2
## 10 2 5 10.000000 0 3
## 11 2 10 15.000000 0 4
## 12 2 15 19.381226 0 5whl.split.exp <- flexsurvreg(Surv(time0, time, chd) ~ as.factor(grade) + as.factor(agecat) +
as.factor(fuband), dist = "exponential", data = whl.split)
whl.split.exp## Call:
## flexsurvreg(formula = Surv(time0, time, chd) ~ as.factor(grade) +
## as.factor(agecat) + as.factor(fuband), data = whl.split,
## dist = "exponential")
##
## Estimates:
## data mean est L95% U95% se exp(est) L95%
## rate NA 0.001059 0.000627 0.001787 0.000283 NA NA
## as.factor(grade)2 0.266742 0.285903 -0.057834 0.629640 0.175379 1.330963 0.943806
## as.factor(agecat)2 0.218258 0.970764 0.464748 1.476781 0.258176 2.639961 1.591612
## as.factor(agecat)3 0.194422 1.477604 1.003895 1.951312 0.241692 4.382431 2.728891
## as.factor(agecat)4 0.114967 1.529979 0.999165 2.060792 0.270828 4.618078 2.716013
## as.factor(agecat)5 0.016053 2.562341 1.824347 3.300335 0.376535 12.966134 6.198745
## as.factor(fuband)3 0.261716 0.629043 0.153690 1.104397 0.242532 1.875815 1.166129
## as.factor(fuband)4 0.242744 0.784077 0.307457 1.260697 0.243178 2.190385 1.359963
## as.factor(fuband)5 0.223610 1.074577 0.569303 1.579852 0.257798 2.928755 1.767035
## U95%
## rate NA
## as.factor(grade)2 1.876935
## as.factor(agecat)2 4.378826
## as.factor(agecat)3 7.037915
## as.factor(agecat)4 7.852188
## as.factor(agecat)5 27.121721
## as.factor(fuband)3 3.017405
## as.factor(fuband)4 3.527880
## as.factor(fuband)5 4.854236
##
## N = 6167, Events: 154, Censored: 6013
## Total time at risk: 27605.371
## Log-likelihood = -904.07754, df = 9
## AIC = 1826.1551我們用指數分布回歸擬合的生存時間模型,其實還可以用泊鬆回歸模型來做,結果也是一樣的:
whl.poi <- glm(chd ~ as.factor(grade), family = poisson(link = log), offset = log(time), data = whitehall)
summary(whl.poi)##
## Call:
## glm(formula = chd ~ as.factor(grade), family = poisson(link = log),
## data = whitehall, offset = log(time))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.58433 -0.41268 -0.40212 -0.39440 3.55361
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.42052 0.10541 -51.4238 < 2.2e-16 ***
## as.factor(grade)2 0.68850 0.16351 4.2108 0.00002545 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 947.906 on 1676 degrees of freedom
## Residual deviance: 931.144 on 1675 degrees of freedom
## AIC: 1243.14
##
## Number of Fisher Scoring iterations: 6你可以回頭去和指數分布回歸的模型結果做個比較,他們的回歸系數估計和標準誤完全是一樣的。