第 30 章 多元模型分析：矩陣標記與其意義

在線性回歸目前為止介紹的內容中，我們最多只談到了預測變量為兩個的情況。本章，我們要把這些概念推廣到三個或者三個以上預測變量的情況。同時，多重線性回歸時採用的假設檢驗也會被談及。其實最常見的就是 \(F\) 檢驗。而且我們也見識過了，當預測變量只有一個的時候，\(F\) 檢驗和 \(t\) 檢驗是等價的。

重要的概念我們都已經介紹完畢。前一章的多重回歸模型中也強調了，我們之所以希望把多個預測變量放進模型，最大的目的就是想了解這些預測變量之間的相互關係，當他們得到調整 (adjustment) 之後，彼此之間的關係是怎樣的。這樣的關係我們稱之為條件關係 (conditional relationships)。當我們使用條件關係的稱呼時，需要同時指明我們說的是哪個變量，在那個變量不變的條件下，與因變量的關係是如何如何。

本章節最後的部分將會著重關注共線性 (collinearity) 的問題。

30.1 線性回歸模型的矩陣/非矩陣標記法

30.1.1 模型標記：

假如，因變量用 \(Y\) 表示，預測變量有 \(p\) 個之多 \((X_1,\cdots, X_p)\)。該模型的非矩陣標記法如下： \[ \begin{equation} y_i = \alpha + \beta_1 x_{1i}+ \beta_2 x_{2i} + \cdots + \beta_p x_{pi} + \varepsilon_i \text{ with } \varepsilon_i \sim \text{NID}(0, \sigma^2) \end{equation} \tag{30.1} \] 其中，

• \(y_i =\) 第 \(i\) 名觀察對象的因變量數據；
• \(x_{pi} =\) 第 \(i\) 名觀察對象的第 \(p\) 個預測變量的觀察數據。

上面的非矩陣標記法，等同於如下的矩陣標記法： \[ \begin{equation} \textbf{Y} = \textbf{X}\beta+\varepsilon, \text{ where } \varepsilon \sim N(0, \textbf{I}\sigma^2) \\ \left( \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array} \right) = \left( \begin{array}{c} 1& x_{11} & \cdots & x_{p1} \\ 1& x_{12} & \cdots & x_{p2} \\ \vdots & \vdots& \vdots & \vdots \\ 1& x_{1n}& \cdots &x_{pn} \\ \end{array} \right)\left( \begin{array}{c} \alpha \\ \beta_1\\ \beta_2 \\ \vdots \\ \beta_p \end{array} \right)+\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n\\ \end{array} \right) \end{equation} \tag{30.2} \] 此公式 (30.2) 中

• \(\textbf{X}\) 是一個 \(n\times(p+1)\) 的矩陣；
• \(\textbf{Y}\) 和 \(\varepsilon\) 分別是長度為 \(n\) 的列向量；
• \(\beta\) 是長度為 \(p+1\) 的列向量，且第一個元素是 \(\alpha\)，偶爾被人誤寫成 \(\beta_0\)。

殘差被認為服從多元正態分佈 (multivariate normal distribution)，這個多元正態分佈的方差協方差矩陣等於 \(\sigma^2\) 與單位矩陣相乘獲得的矩陣。這其實等價於認為殘差服從獨立正態且方差為 \(\sigma^2\) 的分佈，

30.2 解讀參數

模型中的參數的涵義為：

• \(\alpha\) 是截距，所有的預測變量都是零的時候，因變量 \(Y\) 的期待值大小；
• \(\beta_j\) 是預測變量 \(X_j\) 升高一個單位，且其他變量保持不變的同時，因變量 \(Y\) 的期待值的變化；
• \(\beta_j\) 都是偏回歸係數，每個偏回歸係數，測量的都是該預測變量調整了其他預測變量之後對於因變量期待值的影響。

30.2.1 最小二乘估計

還是同之前一樣，我們對殘差的平方和最小化，來獲取我們關心的預測變量的回歸變量。

\[ \begin{aligned} SS_{RES} & = \sum_{i=1}^n \hat\varepsilon_i^2 = \sum_{i=1}^n(y_i-\hat{y})^2 \\ & = \sum_{i=1}^n (y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i}-\cdots-\hat\beta_px_{pi})^2 \end{aligned} \tag{30.3} \]

下面用矩陣標記法計算 \(\hat\beta\)：

\[ \begin{aligned} \text{Because } \mathbf{Y} & = \mathbf{X\hat\beta + \varepsilon} \\ \Rightarrow \mathbf{\varepsilon} & = \mathbf{Y - X\hat\beta}\\ \Rightarrow \mathbf{SS_{RES}} & = \varepsilon_1\times \varepsilon_1 + \varepsilon_2\times \varepsilon_2 + \cdots + \varepsilon_n\times \varepsilon_n \\ & = (\varepsilon_1, \varepsilon_2, \cdots, \varepsilon_n)\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n \end{array} \right) \\ & = \mathbf{\varepsilon^\prime} \mathbf{\varepsilon} \\ & = \mathbf{(Y-X\hat\beta)^\prime(Y-X\hat\beta)} \\ & = \mathbf{Y^\prime Y - X^\prime\hat\beta^\prime Y - Y^\prime X\hat\beta + X^\prime\hat\beta^\prime X \hat\beta} \\ \text{Because} &\text{ transpose of a scalar is a scalar:} \\ \mathbf{Y^\prime X\hat\beta} & = \mathbf{(Y^\prime X\hat\beta)^\prime = X^\prime\hat\beta^\prime Y} \\ \Rightarrow \mathbf{SS_{RES}} & = \mathbf{Y^\prime Y - 2X^\prime\hat\beta^\prime Y + X^\prime\hat\beta^\prime X \hat\beta}\\ \Rightarrow \mathbf{\frac{\partial SS_{RES}}{\partial \hat\beta}} & = \mathbf{-2X^\prime Y + 2 X^\prime X \hat\beta} = 0 \\ \Rightarrow \mathbf{\hat\beta} & = \mathbf{(X^\prime X)^{-1}X^\prime Y} \end{aligned} \tag{30.4} \]

公式 (30.4) 是參數矩陣 \(\mathbf{\beta}\) 的無偏估計，且服從方差協方差矩陣爲 \(\mathbf{(X^\prime X)^{-1}\sigma^2}\) 的多元正態分佈：

\[ \begin{equation} \mathbf{\hat\beta} \sim N(\mathbf{\beta, (X^\prime X)^{-1}\sigma^2}) \end{equation} \tag{30.5} \]

另外可以被證明的是，多元線性迴歸模型的殘差方差的估計量計算公式爲：

\[ \begin{aligned} \hat\sigma^2 & = \sum^n_{i=1}\frac{\hat\varepsilon^2_i}{[n-(p+1)]} \\ & = \sum^n_{i=1}\frac{\sum_{i=1}^n (y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i}-\cdots-\hat\beta_px_{pi})^2}{[n-(p+1)]} \\ \text{Where } & p \text{ is the number of predictors} \end{aligned} \tag{30.6} \]

30.2.2 因變量的期待值 \(\mathbf{\hat Y}\)

因變量的期待值矩陣 \(\mathbf{\hat Y}\) 根據公式 (30.4) 推導：

\[ \begin{aligned} \mathbf{\hat Y} & = \mathbf{X\hat\beta} \\ & = \mathbf{X(X^\prime X)^{-1}X^\prime Y}= \mathbf{PY} \\ \text{Where } \mathbf{P} &= \mathbf{X(X^\prime X)^{-1}X^\prime} \end{aligned} \tag{30.7} \]

這裏的 \(n\times n\) 的正方形矩陣 \(\mathbf{P}\) 在多元線性迴歸中是一個極爲重要的矩陣。

• 它常被叫做“帽子/映射 (hat/projection)”矩陣，因爲它把觀察值 \(\mathbf{Y}\) 和觀察值的擬合值一一映射；
• 帽子矩陣的第 \(i\) 個對角元素，是第 \(i\) 名觀察值的影響值 (leverage)，會用在下章節的模型診斷中；
• 擬合值矩陣的方差協方差矩陣被定義爲：

\[ \begin{equation} \text{Var}(\mathbf{\hat Y}) = \mathbf{P}\sigma^2 \end{equation} \tag{30.8} \]

30.2.3 殘差

殘差的觀察值 \(\mathbf{\hat\varepsilon}\) 被定義爲觀察值和擬合值的差。根據前節 (30.8) 推導：

\[ \begin{equation} \mathbf{\hat\varepsilon} = \mathbf{Y - \hat Y} = \mathbf{Y - PY} = \mathbf{(I - P)Y} \end{equation} \tag{30.9} \]

這個觀察殘差的方差被定義爲：

\[ \begin{equation} \text{Var}(\mathbf{\hat\varepsilon}) = \mathbf{(I - P)}\sigma^2 \end{equation} \tag{30.10} \]

• 一般地，\(\mathbf{P}\) 不是一個對角矩陣，意思是觀察殘差之間無法保證是獨立的；
• \(\mathbf{P}\) 的對角元素也不全都相等，意思是觀察殘差的方差無法保證是恆定不變的。

30.3 方差分析一般化和 \(F\) 檢驗

30.3.1 多元線性迴歸時的決定係數和殘差方差

和簡單線性迴歸一樣，因變量的校正平方和可以被分割成兩部分：迴歸模型能夠解釋的平方和；模型無法解釋的殘差平方和。類比方差分析章節 (Section 28) 的公式 (28.1)：

\[ \begin{aligned} \sum_{i=1}^n(y_i-\bar{y})^2 & = \sum_{i=1}^n(\hat{y}_i - \bar{y})^2 + \sum_{i=1}^n(y_i - \hat{y}_i)^2 \\ SS_{yy} & = SS_{REG} + SS_{RES} \end{aligned} \tag{30.11} \]

和簡單線性迴歸也一樣，多元線性迴歸時的模型決定係數 (coefficient of determination) 的定義爲：

\[ \begin{aligned} R^2 & = \frac{SS_{yy}-SS_{RES}}{SS_{yy}} = 1- \frac{SS_{RES}}{SS_{yy}} \\ & = 1 - \frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\sum_{i=1}^n(y_i - \bar{y})^2} \end{aligned} \tag{30.12} \]

這裏的 \(R^2\) 也一樣可以被解釋爲模型能夠解釋的因變量變動部分的百分比 (proportion of the variability in the dependent variable explained by the model)。值得注意的是，當模型中預測變量不減少，每加入一個新的預測變量，決定係數也會增加，相反殘差平方和卻絕不會增加。

30.3.2 方差分析表格

下表和簡單線性迴歸的方差分析表格很類似，也可以用來作假設檢驗 (迴歸方程的顯著性檢驗 Global \(F-\text{test}\)，和偏 \(F\) 檢驗 Partial \(F-\text{test}\))。

表 30.1: Analysis of Variance table for a liear regression model with \(p\) predictor variables

Source of Variation	Sum of Squares	Degrees of Freedom	Mean Sum of Squares
Regression (model)	\(SS_{REG}\)	\(p\)	\(MS_{REG} = \frac{SS_{REG}}{p}\)
Residual	\(SS_{RES}\)	\(n-(p+1)\)	\(MS_{RES} = \frac{SS_{RES}}{[n-(p+1)]}\)
Total	\(SS_{yy}\)	\(n-1\)	\(\frac{SS_{yy}}{(n-1)}\)

30.3.3 迴歸方程的顯著性檢驗

整個方程的顯著性檢驗，檢驗的是所有的迴歸係數都等於零的零假設，其對應的替代假設則是：“迴歸係數不全爲零”。就是至少有一個不等於零。

在零假設條件下，檢驗統計量的計算公式爲：

\[ \begin{equation} F = \frac{MS_{REG}}{MS_{RES}} \sim F_{p, [n-(p+1)]} \end{equation} \tag{30.13} \]

在零假設條件下，\(F\) 的期望值接近 \(1\)，而替代假設條件下的 \(F\) 總是會大於此，所以和 \(F\) 分佈比較特徵值時只需要比較單側的 (右側的) 值，即可獲得雙側 \(p\) 值。

在 R 裏面，迴歸方程的結果的最底下會出現統計量 \(F\) 的大小，但是 \(MS_{REG}, MS_{RES}\) 要用 anova() 代碼獲得：

growgam1 <- read_dta("backupfiles/growgam1.dta")
growgam1$sex <- as.factor(growgam1$sex)

Model1 <- lm(wt ~ age + len, data=growgam1)
print(summary(Model1), digits = 5)

## 
## Call:
## lm(formula = wt ~ age + len, data = growgam1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.20525 -0.64402 -0.00303  0.55967  2.86277 
## 
## Coefficients:
##              Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -8.351244   1.259968 -6.6281 3.531e-10 ***
## age         -0.011260   0.016751 -0.6722    0.5023    
## len          0.237129   0.019516 12.1502 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9546 on 187 degrees of freedom
## Multiple R-squared:  0.74337,    Adjusted R-squared:  0.74063 
## F-statistic: 270.84 on 2 and 187 DF,  p-value: < 2.22e-16

print(anova(Model1), digits = 5)

## Analysis of Variance Table
## 
## Response: wt
##            Df Sum Sq Mean Sq F value    Pr(>F)    
## age         1 359.06  359.06  394.06 < 2.2e-16 ***
## len         1 134.52  134.52  147.63 < 2.2e-16 ***
## Residuals 187 170.39    0.91                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

可以看到 summary() 輸出結果的最後一行是關於迴歸方程整體的 \(F\) 檢驗結果 F-statistic: 270.84 on 2 and 187 DF, p-value: < 2.22e-16，從 anova() 結果中可以獲得 \(MS_{REG} = \frac{359.0632 + 134.5153}{2} = 246.7892\)。\(F_{2,187} = \frac{246.7892}{0.9111833} = 270.84\)。這個檢驗結果證明了，兩個預測變量 “體重” 和 “身長” 至少有一個的迴歸係數不等於零。

30.3.4 \(\text{partial }F\) 檢驗

如果我們建立兩個模型，一個稍微複雜一些 \((B)\)，比起略簡單的模型 \((A)\)，增加了 \(k\) 個預測變量。兩個模型放在一起的方差分析表格可以歸納成：

表 30.2: Analysis of Variance table comparing the fit of a model \((B)\) with \(p\) predictor variables with that of one (model \(A\)) with \(p-k\) predictor variables

Source of Variation	Sum of Squares	Degrees of Freedom	Mean Sum of Squares
Explained by model \(A\)	\(SS_{REG_A}\)	\(p-k\)	\(MS_{REG_A} = \frac{SS_{REG_A}}{p-k}\)
Extra Explained by model \(B\)	\(SS_{REG_B}-SS_{REG_A}\)	\(k\)	\(\frac{SS_{REG_B}-SS_{REG_A}}{k}\)
Residual from model \(B\)	\(SS_{RES_B}\)	\(n-(p+1)\)	\(MS_{RES_B} = \frac{SS_{RES_B}}{[n-(p+1)]}\)
Total	\(SS_{yy}\)	\(n-1\)	\(\frac{SS_{yy}}{(n-1)}\)

那麼偏 \(F\) 檢驗的零假設就是：\(B\) 模型中包含，\(A\) 模型中不包含的 \(k\) 個預測變量的迴歸係數都等於零。

\[ \begin{equation} F=\frac{(SS_{REG-B}-SS_{REG-A})/k}{MS_{RES-B}} \sim F_{k, [n-(p+1)]} \end{equation} \tag{30.14} \]

在 R 裏建立兩個模型：

Model1 <- lm(wt ~ len, data=growgam1)
print(summary(Model1), digits = 5)

## 
## Call:
## lm(formula = wt ~ len, data = growgam1)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -3.155217 -0.629239  0.014555  0.544783  2.928738 
## 
## Coefficients:
##               Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -7.6694406  0.7463556 -10.276 < 2.2e-16 ***
## len          0.2257467  0.0096893  23.299 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9532 on 188 degrees of freedom
## Multiple R-squared:  0.74275,    Adjusted R-squared:  0.74139 
## F-statistic: 542.82 on 1 and 188 DF,  p-value: < 2.22e-16

print(anova(Model1), digits = 5)

## Analysis of Variance Table
## 
## Response: wt
##            Df Sum Sq Mean Sq F value    Pr(>F)    
## len         1 493.17  493.17  542.82 < 2.2e-16 ***
## Residuals 188 170.80    0.91                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model2 <- lm(wt ~ len + age + sex, data = growgam1)
print(summary(Model2), digits = 5)

## 
## Call:
## lm(formula = wt ~ len + age + sex, data = growgam1)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -3.110422 -0.648401  0.026103  0.560621  2.768583 
## 
## Coefficients:
##               Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -7.8906758  1.3003091 -6.0683 7.091e-09 ***
## len          0.2317997  0.0198470 11.6793 < 2.2e-16 ***
## age         -0.0077959  0.0168974 -0.4614    0.6451    
## sex2        -0.1964758  0.1421171 -1.3825    0.1685    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9522 on 186 degrees of freedom
## Multiple R-squared:  0.74599,    Adjusted R-squared:  0.74189 
## F-statistic: 182.08 on 3 and 186 DF,  p-value: < 2.22e-16

print(anova(Model2), digits = 5)

## Analysis of Variance Table
## 
## Response: wt
##            Df Sum Sq Mean Sq  F value Pr(>F)    
## len         1 493.17  493.17 543.8753 <2e-16 ***
## age         1   0.41    0.41   0.4540 0.5013    
## sex         1   1.73    1.73   1.9113 0.1685    
## Residuals 186 168.66    0.91                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

根據公式 (30.14)，\(F=\frac{0.4116944+1.7330862}{2\times0.9067645} = 1.18\)。\(p\) 值可以在 R 裏面這樣計算：

1 - pf(df1 = 2,df2 = 186,q = (0.4116944+1.7330862)/(2*0.9067645))

## [1] 0.3088

更方便的是直接用 anova() 進行偏 \(F\) 檢驗：

print(anova(Model1, Model2), digits = 5)

## Analysis of Variance Table
## 
## Model 1: wt ~ len
## Model 2: wt ~ len + age + sex
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1    188 170.80                           
## 2    186 168.66  2    2.1448 1.1827 0.3088

30.4 添加新變量對迴歸模型的影響

當你決定給建立的模型 \(\mathbf{A}\) 增加新的預測變量時，輸出的結果改變的有：

1. 模型 \(\mathbf{A}\) 原先的預測變量的偏迴歸係數會改變；
2. 模型 \(\mathbf{A}\) 原先的預測變量的偏迴歸係數的方差會改變；
3. 模型 \(\mathbf{A}\) 原先的預測變量的偏迴歸係數的檢驗結果會改變；
4. 模型 \(\mathbf{A}\) 原先的 擬合值 (predicted values/fitted values)會改變；
5. 決定係數 \(R^2\) 會改變。

30.4.1 偏迴歸係數方差的改變

偏迴歸係數矩陣 \(\mathbf{\hat\beta}\) 的方差 \(\mathbf{(X^\prime X)^{-1}\sigma^2}\) (30.5)，取決於

1. 殘差方差 (residual variance) \(\sigma^2\)；
2. 樣本量大小 (sample size) \(n\)；
3. 預測變量之間的協方差 (covariance between the predictor variable in question and the others)。

在簡單線性迴歸中，預測變量的變化性 (variability，用方差或標準差衡量) 越大，迴歸係數的估計就越精確。類似地，多元線性迴歸中，預測變量之間的協方差之所以重要，因爲它決定了其他預測變量保持不變時，該預測變量的變化性。如果某兩個預測變量之間高度相關 (high covariance)，那麼當一個預測變量保持不變時，另一個的變化性就很小。

所以當給一個模型加入新的預測變量時，可能觀察的現象是原先模型中已有的預測變量的偏迴歸係數的方差可能升高，也可能降低。

• 如果新加入的變量能解釋很大比例的殘差方差，那麼其他原有變量的偏迴歸係數會降低 (變精確)；
• 如果新加入的變量和原模型中的某個變量高度相關，那麼加入新變量後，原模型中與之高度相關的預測變量的方差會升高 (不精確)，這個現象會在共線性 (collinearity) 中繼續討論。

30.4.2 偏迴歸係數檢驗結果的改變

加入新預測變量時，原有的偏迴歸係數的檢驗結果發生的改變可以歸類成兩種情況：

1. 估計的偏迴歸係數本身發生了改變；
2. 偏迴歸係數的方差改變，導致了檢驗結果發生變化。

30.4.3 擬合值的改變

很明顯，當模型中加入新的變量，觀察對象的擬合值會發生改變，但是通常這樣的影響要遠遠小於對偏迴歸係數估計 (和其方差) 的影響。

30.4.4 決定係數的改變

模型中增加新的預測變量，那麼模型的決定係數不會減少，只會增加。

30.4.5 共線性 collinearity

當預測變量 \(X_1\) 和另一個預測變量 \(X_2\) 之間呈高度線性關係時被定義爲共線性現象。如果這兩個變量的關係是完全線性 (exact linear)，那麼多元迴歸其實是無法進行的，因爲這兩個變量中的一個隨着另一個改變，無法像我們設想的那樣把其中一個變量保持不變，從而估計另一個變量的迴歸係數。用矩陣表示多元預測變量時 \(\mathbf{X}\) 是奇異矩陣 singular matrix，\(\mathbf{(X^\prime X)^{-1}}\) 是不存在的。

完全線性的最佳例子是我們在對分類變量使用啞變量的情況下。每個啞變量之間都是完全線性的關係，因而我們只能用 \(0,1\) 來編碼啞變量，當某個啞變量存在時，其餘的啞變量取 \(0\) 從模型中消失。否則模型將無法擬合。

如果某兩個變量之間高度相關，那麼他們的預測變量矩陣接近 奇異矩陣，把這兩個變量同時作爲預測變量放入模型中會引起共線性現象，表現出來的形式有：

1. 偏迴歸係數的方差變得很大；
2. 偏迴歸係數本身的絕對值變得異常大；
3. 某些已知的重要預測變量的偏迴歸係數變得過小且不再有意義；
4. 雖然會有 1-3 描述的異常現象出現，但是擬合值的變化卻可能微不足道。

所以擬合多元線性迴歸模型時，極爲重要的一點是要避免共線性。如果有些變量高度相關，必須考慮改變他們放入模型的形式：

1. 收縮期血壓，舒張期血壓兩個變量是高度相關的，不能一起放入模型中。如果需要同時考慮兩個變量，可以用其中一個，另一個預測變量用二者之差；
2. 身高，體重常常是高度相關的，儘量不要一起放入模型中，可以使用他們的結合形式體質指數 (BMI, \(\text{kg/m}^2\))；
3. 當使用二次方程進行模型擬合的時候，用 \((x_i - \bar{x})^2\) 取代 \(x_i^2\)。

30.5 實戰演習

30.5.1 血清維生素 C 濃度的預測變量

數據來自與某個橫斷面研究，其目的是找出與血清維生素 C 濃度相關的預測變量。

數據中個變量含義如下表所示。

表 30.3: Data set of serum vitamin C level explained

Variable name	content
serial	Patient identifier
age	Age of subjects in years
height	Height in metres
cigs	Smoking status (0=non-smoker; 1=smoker)
weight	Weight in kg
sex	Gender (0=men; 1=women)
seruvitc	Serum Vitamin C level (\(\mu\text{mol/L}\))
ctakers	Vitamin C supplements taken (1=yes, 0=no)

1. 在 R 裏讀入數據，並對數據內容總結，對維生素C濃度和其他連續性變量作散點圖，對分類變量如性別，吸菸狀況，和維生素C補充劑服用與否之間的維生素 C 濃度作初步的分析表格。

library(haven)
vitC <- read_dta("backupfiles/vitC.dta")

##########################################
# Recoding the categorical variables     #
##########################################

vitC$sex[vitC$sex == 0] <- "Men"
vitC$sex[vitC$sex == 1] <- "Women"
vitC$sex <- as.factor(vitC$sex)
vitC$cigs[vitC$cigs == 0] <- "Non-smoker"
vitC$cigs[vitC$cigs == 1] <- "Smoker"
vitC$cigs <- as.factor(vitC$cigs)
vitC$ctakers[vitC$ctakers == 0] <- "No"
vitC$ctakers[vitC$ctakers == 1] <- "Yes"
vitC$ctakers <- as.factor(vitC$ctakers)

############################################
# End of recoding the categorical variables#
############################################

summary(vitC) #Basic summary without any package

##      serial           age           height             cigs        weight         sex    
##  Min.   :  1.0   Min.   :65.0   Min.   :1.48   Non-smoker:80   Min.   : 44.0   Men  :44  
##  1st Qu.: 23.8   1st Qu.:67.0   1st Qu.:1.58   Smoker    :12   1st Qu.: 57.8   Women:48  
##  Median : 49.0   Median :69.0   Median :1.64                   Median : 67.0             
##  Mean   : 49.2   Mean   :69.3   Mean   :1.65                   Mean   : 68.6             
##  3rd Qu.: 73.2   3rd Qu.:71.0   3rd Qu.:1.72                   3rd Qu.: 76.5             
##  Max.   :100.0   Max.   :74.0   Max.   :1.89                   Max.   :103.0             
##                                 NA's   :1                      NA's   :1                 
##     seruvitc     ctakers 
##  Min.   :  8.0   No :73  
##  1st Qu.: 34.8   Yes:19  
##  Median : 58.0           
##  Mean   : 53.2           
##  3rd Qu.: 71.0           
##  Max.   :100.0           
## 

head(vitC) #See the first 6 observations

## # A tibble: 6 x 8
##   serial   age height cigs       weight sex   seruvitc ctakers
##    <dbl> <dbl>  <dbl> <fct>       <dbl> <fct>    <dbl> <fct>  
## 1      1    71   1.72 Smoker       68.8 Men          9 No     
## 2      2    70   1.63 Non-smoker   58.2 Women       19 No     
## 3      3    69   1.65 Non-smoker   94.3 Women       69 Yes    
## 4      4    67   1.62 Non-smoker   87.6 Women       71 No     
## 5      5    68   1.53 Non-smoker   66.3 Women       87 Yes    
## 6      6    71   1.64 Non-smoker   72.2 Women       96 Yes

library(psych) #some detailed summary function from this package
describe(vitC)

## vitC 
## 
##  8  Variables      92  Observations
## ----------------------------------------------------------------------------------------------------
## serial : subject number  Format:%3.0f 
##        n  missing distinct     Info     Mean      Gmd      .05      .10      .25      .50      .75 
##       92        0       92        1    49.25    33.74     5.55    10.10    23.75    49.00    73.25 
##      .90      .95 
##    88.90    95.45 
## 
## lowest :   1   2   3   4   5, highest:  96  97  98  99 100
## ----------------------------------------------------------------------------------------------------
## age : age on study entry  Format:%2.0f 
##        n  missing distinct     Info     Mean      Gmd      .05      .10      .25      .50      .75 
##       92        0       10    0.988    69.32    3.353     65.0     65.1     67.0     69.0     71.0 
##      .90      .95 
##     74.0     74.0 
##                                                                       
## Value         65    66    67    68    69    70    71    72    73    74
## Frequency     10     9    12     8    10    10    11     3     8    11
## Proportion 0.109 0.098 0.130 0.087 0.109 0.109 0.120 0.033 0.087 0.120
## ----------------------------------------------------------------------------------------------------
## height  Format:%4.1f 
##        n  missing distinct     Info     Mean      Gmd      .05      .10      .25      .50      .75 
##       91        1       34    0.999    1.647   0.1128     1.50     1.52     1.58     1.64     1.72 
##      .90      .95 
##     1.79     1.81 
## 
## lowest : 1.48 1.49 1.51 1.52 1.53, highest: 1.80 1.81 1.82 1.86 1.89
## ----------------------------------------------------------------------------------------------------
## cigs 
##        n  missing distinct 
##       92        0        2 
##                                 
## Value      Non-smoker     Smoker
## Frequency          80         12
## Proportion       0.87       0.13
## ----------------------------------------------------------------------------------------------------
## weight : Clothed weight  Format:%5.1f 
##        n  missing distinct     Info     Mean      Gmd      .05      .10      .25      .50      .75 
##       91        1       79        1    68.57    15.35    48.85    50.40    57.80    67.00    76.55 
##      .90      .95 
##    88.30    91.60 
## 
## lowest :  44.0  46.7  48.1  48.4  48.5, highest:  92.0  94.3  97.5 102.4 103.0
## ----------------------------------------------------------------------------------------------------
## sex 
##        n  missing distinct 
##       92        0        2 
##                       
## Value        Men Women
## Frequency     44    48
## Proportion 0.478 0.522
## ----------------------------------------------------------------------------------------------------
## seruvitc : Serum ascorbate  Format:%3.0f 
##        n  missing distinct     Info     Mean      Gmd      .05      .10      .25      .50      .75 
##       92        0       60        1    53.21    27.12    11.55    17.00    34.75    58.00    71.00 
##      .90      .95 
##    80.90    84.45 
## 
## lowest :   8   9  10  11  12, highest:  85  86  87  96 100
## ----------------------------------------------------------------------------------------------------
## ctakers 
##        n  missing distinct 
##       92        0        2 
##                       
## Value         No   Yes
## Frequency     73    19
## Proportion 0.793 0.207
## ----------------------------------------------------------------------------------------------------

library(epiDisplay) #some STATA-like simple summary function
summ(vitC)

## 
## No. of observations = 92
## 
##   Var. name obs. mean   median  s.d.   min.   max.  
## 1 serial    92   49.25  49      29.07  1      100   
## 2 age       92   69.32  69      2.91   65     74    
## 3 height    91   1.65   1.64    0.1    1.48   1.89  
## 4 cigs                                              
## 5 weight    91   68.57  67      13.48  44     103   
## 6 sex                                               
## 7 seruvitc  92   53.21  58      23.83  8      100   
## 8 ctakers

vitC$serial[which(is.na(vitC$height))]

## [1] 24

vitC$serial[which(is.na(vitC$weight))]

## [1] 24

從初步的熟悉數據結構和歸納結果可以看出，身高體重兩個數據有出現缺損值 (編號 24 的患者)。

summ(vitC$seruvitc, by=vitC$sex, graph = FALSE) # From package "epiDisplay"

## For vitC$sex = Men 
##  obs. mean   median  s.d.   min.   max.  
##  44   46.091 52.5    24.877 8      100   
## 
## For vitC$sex = Women 
##  obs. mean   median  s.d.   min.   max.  
##  48   59.729 66.5    21.043 15     96

summ(vitC$seruvitc, by=vitC$cigs, graph = FALSE)

## For vitC$cigs = Non-smoker 
##  obs. mean   median  s.d.   min.   max.  
##  80   55.138 58      23.323 8      100   
## 
## For vitC$cigs = Smoker 
##  obs. mean   median  s.d.   min.   max.  
##  12   40.333 49.5    24.186 9      68

summ(vitC$seruvitc, by=vitC$ctakers, graph = FALSE)

## For vitC$ctakers = No 
##  obs. mean   median  s.d.   min.   max.  
##  73   48.644 55      22.795 8      84    
## 
## For vitC$ctakers = Yes 
##  obs. mean   median  s.d.   min.   max.  
##  19   70.737 72      19.612 13     100

# You can also get similar detailed descriptive statistics by groups from package "psych"
describeBy(vitC$seruvitc, group = vitC$sex)

## 
##  Descriptive statistics by group 
## group: Men
##    vars  n  mean    sd median trimmed   mad min max range  skew kurtosis   se
## X1    1 44 46.09 24.88   52.5   45.61 25.95   8 100    92 -0.06    -1.12 3.75
## --------------------------------------------------------------------------- 
## group: Women
##    vars  n  mean    sd median trimmed   mad min max range  skew kurtosis   se
## X1    1 48 59.73 21.04   66.5   61.15 15.57  15  96    81 -0.65    -0.62 3.04

describeBy(vitC$seruvitc, group = vitC$cigs)

## 
##  Descriptive statistics by group 
## group: Non-smoker
##    vars  n  mean    sd median trimmed   mad min max range  skew kurtosis   se
## X1    1 80 55.14 23.32     58    56.3 22.24   8 100    92 -0.43    -0.85 2.61
## --------------------------------------------------------------------------- 
## group: Smoker
##    vars  n  mean    sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 12 40.33 24.19   49.5    40.7 25.2   9  68    59 -0.19    -1.93 6.98

describeBy(vitC$seruvitc, group = vitC$ctakers)

## 
##  Descriptive statistics by group 
## group: No
##    vars  n  mean    sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 73 48.64 22.79     55   49.47 25.2   8  84    76 -0.33    -1.24 2.67
## --------------------------------------------------------------------------- 
## group: Yes
##    vars  n  mean    sd median trimmed   mad min max range  skew kurtosis  se
## X1    1 19 70.74 19.61     72   72.41 19.27  13 100    87 -1.07     1.52 4.5

所以，血清維生素水平在女性，非吸菸者，和服用補充劑(廢話) 的人中較高。

par(mfrow=c(2,2))
plot(vitC$age, vitC$seruvitc, pch = 20, xlab = "age on study entry", ylab = "Serum ascorbate")
plot(vitC$weight, vitC$seruvitc, pch = 20, xlab = "Clothed weight", ylab = "Serum ascorbate")
plot(vitC$height, vitC$seruvitc, pch = 20, xlab = "Height", ylab = "Serum ascorbate")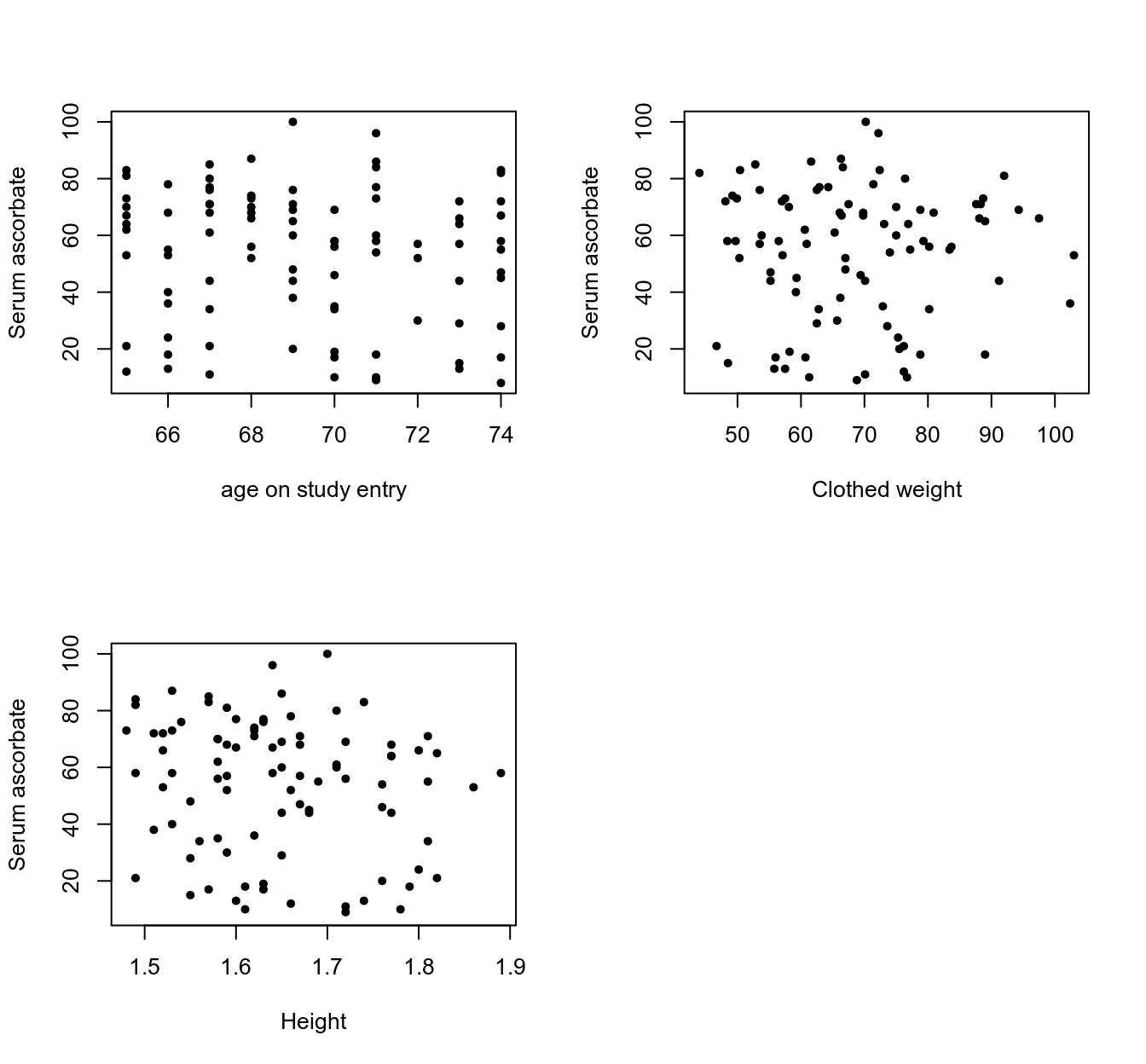

圖 30.1: Scatter plots between serum ascorbate and age/weight/height

散點圖似乎沒有證據提示血清維生素 C 濃度和連續型變量，年齡，身高，體重之間有什麼相關性。

2. 建立維生素 C 和其他預測變量的簡單線性迴歸模型，你有什麼結論？

summary(lm(seruvitc ~ age, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ age, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -44.94 -18.98   5.82  16.67  46.52 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)  113.104     59.511    1.90    0.061 .
## age           -0.864      0.858   -1.01    0.316  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23.8 on 90 degrees of freedom
## Multiple R-squared:  0.0111, Adjusted R-squared:  0.000163 
## F-statistic: 1.01 on 1 and 90 DF,  p-value: 0.316

confint(lm(seruvitc ~ age, data = vitC))

##              2.5 %   97.5 %
## (Intercept) -5.125 231.3335
## age         -2.568   0.8401

血清維生素 C 濃度隨着年齡增加遞減，但是迴歸係數不具有統計學意義 (\(p=0.32\))。年齡每增加 1 歲，血清維生素平均下降 \(0.864 \:\mu\text{mol/L， 95% CI:} (-2.57, 0.840)\)，

summary(lm(seruvitc ~ height, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ height, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -45.11 -19.81   5.76  17.94  48.29 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)    115.9       41.2    2.81    0.006 **
## height         -37.8       25.0   -1.51    0.134   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23.3 on 89 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.0251, Adjusted R-squared:  0.0141 
## F-statistic: 2.29 on 1 and 89 DF,  p-value: 0.134

confint(lm(seruvitc ~ height, data = vitC))

##              2.5 % 97.5 %
## (Intercept)  34.05 197.75
## height      -87.37  11.84

血清維生素 C 濃度隨着身高增加遞減，但是迴歸係數不具有統計學意義 (\(p=0.134\))。身高每增加 1cm，血清維生素平均下降 \(0.378 \:\mu\text{mol/L， 95% CI:} (-0.874, 0.118)\)，

summary(lm(seruvitc ~ cigs, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ cigs, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -47.14 -19.53   3.26  17.86  44.86 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    55.14       2.62   21.05   <2e-16 ***
## cigsSmoker    -14.80       7.25   -2.04    0.044 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23.4 on 90 degrees of freedom
## Multiple R-squared:  0.0442, Adjusted R-squared:  0.0336 
## F-statistic: 4.17 on 1 and 90 DF,  p-value: 0.0442

confint(lm(seruvitc ~ cigs, data = vitC))

##              2.5 %  97.5 %
## (Intercept)  49.93 60.3417
## cigsSmoker  -29.21 -0.3945

血清維生素 C 濃度與在吸菸人羣中較低，與不吸菸人羣相比，吸菸人羣的血清維生素 C 濃度平均低 \(14.8 \:\mu\text{mol/L， 95% CI:} (0.394, 29.2)\)，這個濃度差具有臨界統計學意義 \((p=0.044)\)。

summary(lm(seruvitc ~ weight, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ weight, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -44.71 -18.39   4.41  17.21  46.28 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 53.04017   12.90016    4.11  8.7e-05 ***
## weight       0.00967    0.18463    0.05     0.96    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23.6 on 89 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  3.08e-05,   Adjusted R-squared:  -0.0112 
## F-statistic: 0.00274 on 1 and 89 DF,  p-value: 0.958

confint(lm(seruvitc ~ weight, data = vitC))

##               2.5 %  97.5 %
## (Intercept) 27.4078 78.6725
## weight      -0.3572  0.3765

維生素濃度和體重關係幾乎可以忽略 \((p=0.96)\)。

summary(lm(seruvitc ~ sex, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ sex, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -44.73 -20.23   6.59  17.27  53.91 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    46.09       3.46   13.32   <2e-16 ***
## sexWomen       13.64       4.79    2.85   0.0055 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 23 on 90 degrees of freedom
## Multiple R-squared:  0.0826, Adjusted R-squared:  0.0724 
## F-statistic:  8.1 on 1 and 90 DF,  p-value: 0.00547

confint(lm(seruvitc ~ sex, data = vitC))

##             2.5 % 97.5 %
## (Intercept) 39.22  52.97
## sexWomen     4.12  23.16

血清維生素 C 濃度與在女性中較高，與男性相比，女性的血清維生素 C 濃度平均高 \(13.6 \:\mu\text{mol/L， 95% CI:} (4.12, 23.2)\)，這個濃度差具有顯著統計學意義 \((p=0.005)\)。

summary(lm(seruvitc ~ ctakers, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ ctakers, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -57.74 -15.42   5.81  18.61  35.36 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    48.64       2.60   18.73  < 2e-16 ***
## ctakersYes     22.09       5.72    3.87  0.00021 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 22.2 on 90 degrees of freedom
## Multiple R-squared:  0.142,  Adjusted R-squared:  0.133 
## F-statistic: 14.9 on 1 and 90 DF,  p-value: 0.000209

confint(lm(seruvitc ~ ctakers, data = vitC))

##             2.5 % 97.5 %
## (Intercept) 43.48  53.80
## ctakersYes  10.74  33.45

血清維生素 C 濃度與在服用補充劑的人中較高，與不服用補充劑的人相比，服用者的血清維生素 C 濃度平均高 \(22.1 \:\mu\text{mol/L， 95% CI:} (10.7, 33.4)\)，這個濃度差具有顯著統計學意義 \((p=0.00021)\)。

3. 擬合一個多元線性迴歸模型，因變量爲血清維生素 C 濃度，預測變量使用 性別，吸菸狀態，和 是否服用維生素補充劑。解釋輸出結果的數字的含義。跟這些預測變量單獨和血清維生素 C 濃度建立的簡單線性迴歸模型作比較。說明哪些結果發生了改變，爲什麼。

summary(lm(seruvitc ~ sex + cigs + ctakers, data = vitC))

## 
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers, data = vitC)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -40.66 -19.07   2.24  17.62  38.03 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    44.97       3.55   12.69  < 2e-16 ***
## sexWomen       10.66       4.51    2.36  0.02044 *  
## cigsSmoker    -11.57       6.66   -1.74  0.08586 .  
## ctakersYes     20.25       5.51    3.67  0.00041 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21.3 on 88 degrees of freedom
## Multiple R-squared:  0.23,   Adjusted R-squared:  0.203 
## F-statistic: 8.74 on 3 and 88 DF,  p-value: 3.88e-05

print(anova(lm(seruvitc ~ sex + cigs + ctakers, data = vitC)), digits = 5)

## Analysis of Variance Table
## 
## Response: seruvitc
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## sex        1   4270  4270.0  9.4354 0.0028320 ** 
## cigs       1   1497  1497.0  3.3080 0.0723454 .  
## ctakers    1   6102  6101.8 13.4831 0.0004125 ***
## Residuals 88  39824   452.5                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

confint(lm(seruvitc ~ sex + cigs + ctakers, data = vitC))

##               2.5 % 97.5 %
## (Intercept)  37.927 52.017
## sexWomen      1.687 19.630
## cigsSmoker  -24.799  1.666
## ctakersYes    9.291 31.211

從這個多元線性迴歸的輸出報告來看，血清維生素 C 濃度

• 在吸菸者中較低 \(-11.6 \:\mu\text{mol/L， 95% CI:} (-24.8, +1.67), p = 0.086\)；
• 在女性中較高 \(+10.7 \:\mu\text{mol/L， 95% CI:} (1.69, 19.6), p = 0.020\)；
• 在服用維生素補充劑的人中較高 \(+20.3 \:\mu\text{mol/L， 95% CI:} (9.29, 31.2), p = 0.0004\)。

故，本次數據告訴我們，服用維生素補充劑是最強的預測變量。在多元線性迴歸模型的結果中可以看到：

• 性別之間維生素 C 濃度差變小了 (\(+13.6 \rightarrow +10.7\))
  這是因爲女性中有較多人服用維生素補充劑。即便如此，性別差在多元線性迴歸模型中仍然是有意義的。

a <- Epi::stat.table(list("Vitamin C taker"=ctakers, "Gender" = sex), list(count(),percent(ctakers)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))

##  ---------------------------------- 
##           ---------Gender---------- 
##  Vitamin       Men   Women   Total  
##  C taker                            
##  ---------------------------------- 
##  No             37      36      73  
##              84.09   75.00   79.35  
##                                     
##  Yes             7      12      19  
##              15.91   25.00   20.65  
##                                     
##                                     
##  Total          44      48      92  
##             100.00  100.00  100.00  
##  ----------------------------------

• 吸菸與非吸菸者之間的維生素 C 濃度差也變小了 (\(-14.8 \rightarrow -11.6\))，因爲儘管吸菸與非吸菸者的維生素補充劑服用比例差不不大，但是吸菸者中大部分是男性。(詳見下表)
  吸菸者和非吸菸者之間維生素 C 濃度差經過多元線性迴歸調整後變得不再有統計學意義 \((p=0.086)\)。

a <- Epi::stat.table(list("Vitamin C taker"=ctakers, "Smoker" = cigs), list(count(),percent(ctakers)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))

##  ------------------------------------- 
##           -----------Smoker----------- 
##  Vitamin   Non-smoker  Smoker   Total  
##  C taker                               
##  ------------------------------------- 
##  No                63      10      73  
##                 78.75   83.33   79.35  
##                                        
##  Yes               17       2      19  
##                 21.25   16.67   20.65  
##                                        
##                                        
##  Total             80      12      92  
##                100.00  100.00  100.00  
##  -------------------------------------

a <- Epi::stat.table(list("Gender" = sex, "Smoker" = cigs), list(count(),percent(sex)), data = vitC, margins = TRUE)
print(a, digits = c(percent = 2))

##  ------------------------------------ 
##          -----------Smoker----------- 
##  Gender   Non-smoker  Smoker   Total  
##  ------------------------------------ 
##  Men              36       8      44  
##                45.00   66.67   47.83  
##                                       
##  Women            44       4      48  
##                55.00   33.33   52.17  
##                                       
##                                       
##  Total            80      12      92  
##               100.00  100.00  100.00  
##  ------------------------------------

4. 在前一個模型中加入年齡，身高，體重作爲新的預測變量。先解釋新的模型中報告的個數值的意義，利用方差分析表格比較兩個模型的差別 (先手計算，再用 R 計算確認你的答案)。

由於身高體重有缺損值(serial=24)，所以要比較預測變量增加前後的模型，需要先把之前的模型中 serial=24 的觀察對象刪除掉才公平。

Model1 <- lm(seruvitc ~ sex + cigs + ctakers, data = vitC[-24,])
summary(Model1);anova(Model1)

## 
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers, data = vitC[-24, 
##     ])
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -40.79 -18.21   2.21  17.59  36.97 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    46.03       3.55   12.96  < 2e-16 ***
## sexWomen        9.76       4.49    2.18  0.03228 *  
## cigsSmoker    -12.26       6.59   -1.86  0.06627 .  
## ctakersYes     19.83       5.45    3.64  0.00047 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21 on 87 degrees of freedom
## Multiple R-squared:  0.226,  Adjusted R-squared:  0.199 
## F-statistic: 8.46 on 3 and 87 DF,  p-value: 5.39e-05

## Analysis of Variance Table
## 
## Response: seruvitc
##           Df Sum Sq Mean Sq F value  Pr(>F)    
## sex        1   3689    3689    8.35 0.00486 ** 
## cigs       1   1679    1679    3.80 0.05440 .  
## ctakers    1   5841    5841   13.23 0.00047 ***
## Residuals 87  38418     442                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model2 <- lm(seruvitc ~ sex + cigs + ctakers + age + weight + height, data = vitC[-24,])
summary(Model2);anova(Model2)

## 
## Call:
## lm(formula = seruvitc ~ sex + cigs + ctakers + age + weight + 
##     height, data = vitC[-24, ])
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -40.56 -17.72   4.23  18.75  35.58 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   65.352     89.482    0.73  0.46722    
## sexWomen      10.367      7.285    1.42  0.15843    
## cigsSmoker   -11.800      6.757   -1.75  0.08444 .  
## ctakersYes    19.859      5.547    3.58  0.00057 ***
## age           -0.353      0.840   -0.42  0.67499    
## weight         0.107      0.223    0.48  0.63174    
## height        -1.573     42.259   -0.04  0.97040    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21.3 on 84 degrees of freedom
## Multiple R-squared:  0.233,  Adjusted R-squared:  0.178 
## F-statistic: 4.25 on 6 and 84 DF,  p-value: 0.00088

## Analysis of Variance Table
## 
## Response: seruvitc
##           Df Sum Sq Mean Sq F value  Pr(>F)    
## sex        1   3689    3689    8.14 0.00546 ** 
## cigs       1   1679    1679    3.70 0.05767 .  
## ctakers    1   5841    5841   12.88 0.00056 ***
## age        1    205     205    0.45 0.50283    
## weight     1    133     133    0.29 0.58951    
## height     1      1       1    0.00 0.97040    
## Residuals 84  38079     453                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

利用偏 \(F\) 檢驗的公式

\[ F=\frac{(205.2889295+132.9899543+0.6280691)/3}{38079.42/84} = 0.2492713 \]

anova(Model1, Model2)

## Analysis of Variance Table
## 
## Model 1: seruvitc ~ sex + cigs + ctakers
## Model 2: seruvitc ~ sex + cigs + ctakers + age + weight + height
##   Res.Df   RSS Df Sum of Sq    F Pr(>F)
## 1     87 38418                         
## 2     84 38079  3       339 0.25   0.86

所以檢驗統計量對應的 \(p=0.86\) 告訴我們沒有證明據證明調整了性別，吸菸狀況，服用補充劑與否之後，增加的年齡，體重，身高作爲預測變量和觀察對象的血清維生素 C 濃度有關係。模型 2 比模型 1 不能解釋更多的模型殘差 (不比模型 1 更加擬合數據)。

30.5.2 紅細胞容積與血紅蛋白

表 30.4: Data set of haemoglobin and PCV explained

Variable name	content
hb	Haemoglobin (gm/dl)
pcv	Pack cell volume %
age	Age (years)

5. 把數據導入 R，並且建立因變量爲血紅蛋白，預測變量爲 PCV 和 年齡的多元線性迴歸模型

library(haven)
haem <- read_dta("backupfiles/haem.dta")
psych::describe(haem)

##     vars  n  mean   sd median trimmed   mad  min  max range  skew kurtosis   se
## hb     1 12 12.53 1.70   12.8   12.56  1.70  9.6 15.1   5.5 -0.26    -1.39 0.49
## pcv    2 12 38.58 8.14   37.5   38.80 11.12 25.0 50.0  25.0 -0.10    -1.59 2.35
## age    3 12 32.75 8.98   31.5   32.40  9.64 20.0 49.0  29.0  0.31    -1.20 2.59

Model3 <- lm(hb ~ pcv + age, data = haem)
summary(Model3)

## 
## Call:
## lm(formula = hb ~ pcv + age, data = haem)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -1.413 -1.002  0.302  0.662  1.867 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)   5.0606     1.9680    2.57    0.030 *
## pcv           0.1056     0.0429    2.46    0.036 *
## age           0.1036     0.0389    2.66    0.026 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.15 on 9 degrees of freedom
## Multiple R-squared:  0.63,   Adjusted R-squared:  0.548 
## F-statistic: 7.65 on 2 and 9 DF,  p-value: 0.0114

haem$e_hat <- Model3$residuals
haem$y_hat <- Model3$fitted.values
print(haem)

## # A tibble: 12 x 5
##       hb   pcv   age  e_hat y_hat
##    <dbl> <dbl> <dbl>  <dbl> <dbl>
##  1  11.1    35    20  0.274  10.8
##  2  10.7    45    22 -1.39   12.1
##  3  12.4    47    25 -0.211  12.6
##  4  14      50    28  0.762  13.2
##  5  13.1    31    28  1.87   11.2
##  6  10.5    30    31 -0.938  11.4
##  7   9.6    25    32 -1.41   11.0
##  8  12.5    33    35  0.331  12.2
##  9  13.5    35    38  0.810  12.7
## 10  13.9    40    40  0.475  13.4
## 11  15.1    45    45  0.629  14.5
## 12  13.9    47    49 -1.20   15.1

6. 利用 R 的矩陣計算重現迴歸模型的計算結果

• 計算因變量和兩個預測變量各自的和

sumy <- sum(haem$hb)
sumx1 <- sum(haem$pcv)
sumx2 <- sum(haem$age)

• 計算因變量和兩個預測變量各自的平方和

sumy2 <- sum((haem$hb)^2)
sumx1y <- sum(haem$hb*haem$pcv)
sumx2y <- sum(haem$hb*haem$age)
sumx12 <- sum((haem$pcv)^2)
sumx22 <- sum((haem$age)^2)
sumx1x2 <- sum(haem$pcv*haem$age)

• 生成一個數值爲 1 的變量，名爲 one

one <- rep(1,12)

• 用 matrix() 命令生成矩陣

Rownames <- NULL
for(i in 1:12) {
  a <- paste("row", i, sep = "")
  Rownames <- c(Rownames,a); rm(a)
  }

Y <- matrix(haem$hb ,dimnames = list(Rownames, "hb"))
Y

##         hb
## row1  11.1
## row2  10.7
## row3  12.4
## row4  14.0
## row5  13.1
## row6  10.5
## row7   9.6
## row8  12.5
## row9  13.5
## row10 13.9
## row11 15.1
## row12 13.9

X <- matrix(c(one, haem$pcv, haem$age), nrow = 12, dimnames = list(Rownames, c("one", "pcv", "age")))
X

##       one pcv age
## row1    1  35  20
## row2    1  45  22
## row3    1  47  25
## row4    1  50  28
## row5    1  31  28
## row6    1  30  31
## row7    1  25  32
## row8    1  33  35
## row9    1  35  38
## row10   1  40  40
## row11   1  45  45
## row12   1  47  49

• 用公式 (30.4) 計算估計 \(\mathbf{\hat\beta}\) 矩陣

XX <- t(X) %*% X # these are the sum of squares of each variable and the sum of the cross products of the pairs of variables
XX

##     one   pcv   age
## one  12   463   393
## pcv 463 18593 15276
## age 393 15276 13757

(data.frame(sumx1,sumx12,sumx2,sumx22, sumx1x2))

##   sumx1 sumx12 sumx2 sumx22 sumx1x2
## 1   463  18593   393  13757   15276

XY <- t(X) %*% Y # this is the cross-product matrix of predictors against outcome
XY

##         hb
## one  150.3
## pcv 5887.7
## age 5026.0

(data.frame(sumy, sumx1y, sumx2y))

##    sumy sumx1y sumx2y
## 1 150.3   5888   5026

betahat <- solve( t(X) %*% X ) %*% t(X) %*% Y
betahat

##         hb
## one 5.0606
## pcv 0.1056
## age 0.1036

###or equivalently you can use
betahat <- solve( crossprod(X) ) %*% crossprod( X, Y )
betahat

##         hb
## one 5.0606
## pcv 0.1056
## age 0.1036

可以看到 betahat 的結果和多元迴歸模型輸出的迴歸係數估計是一致的。

• 計算擬合值

Fitted <- X%*%betahat
Fitted

##          hb
## row1  10.83
## row2  12.09
## row3  12.61
## row4  13.24
## row5  11.23
## row6  11.44
## row7  11.01
## row8  12.17
## row9  12.69
## row10 13.43
## row11 14.47
## row12 15.10

• 估計迴歸係數的方差協方差矩陣

e_hat <- Y-Fitted # residuals
e_hat

##            hb
## row1   0.2736
## row2  -1.3892
## row3  -0.2110
## row4   0.7616
## row5   1.8674
## row6  -0.9377
## row7  -1.4134
## row8   0.3314
## row9   0.8096
## row10  0.4747
## row11  0.6291
## row12 -1.1962

SSres <- t(e_hat) %*% e_hat # residual sum of squares
SSres

##       hb
## hb 11.81

Sigma2 <- SSres %*% (1/(12-(2+1))) # residual variance
Sigma2

##     [,1]
## hb 1.312

# multiply the inverse of the cross-product matrix for the predictors
# by the residual variance to get the variance-covariance matrix of
# the coefficients
V <- solve( crossprod(X) ) * as.numeric(Sigma2)
V

##          one        pcv        age
## one  3.87296 -0.0632072 -0.0404537
## pcv -0.06321  0.0018365 -0.0002336
## age -0.04045 -0.0002336  0.0015105

# the square root of the diagonal terms in the above matrix are the standard errors shown in the regression output
sqrt(diag(V))

##     one     pcv     age 
## 1.96798 0.04285 0.03887