第 21 章 信賴區間 confidence intervals

21.1 定義

信賴區間的定義，曾經在統計推斷中介紹過 (Section 10.1)。信賴區間 (CI)，提供了一種對參數估計精確度的度量。CI，也是一種統計量，有自己的樣本分佈，它總是成對成對地出現的。L，表示下限，U，表示上限。顯著性水平 (confidence level) 下的下限和上限之間的間距大小，是由信賴區間本身的樣本分佈決定的。

一般地，對於一個總體參數 \(\mu\)，它的 \(100(1-\alpha)\%\text{CI}\) 信賴區間的含義爲：

\[ \begin{equation} \text{Prob}\{\mu\in (\text{L}, \text{U}) | \mu\} = (1-\alpha) \end{equation} \tag{21.1} \]

所以，一個總體參數 \(\mu\)，的 \(95\%\text{CI}\) 信賴區間爲：

\[ \begin{equation} \text{Prob}\{ \mu \in (\text{L, U}) | \mu\} =0.95 \end{equation} \tag{21.2} \]

用公式 (21.2) 來解釋就是，區間 \(\text{(L, U)}\) 內包含了總體參數 \(\mu\) 的概率爲 \(95\%\)。本文以下部分從公式中省略 \(|\mu\) 部分。但是必須要記住，概率論環境下的信賴區間 (或者其他統計學參數估計) 都是總體參數的條件概率。在概率論語境下，信賴區間一般是左右對稱的。所以 \(100(1-\alpha)\%\text{CI}\) 的含義可以解讀爲：

\[ \begin{equation} \text{Prob} \{ \mu \leqslant \text{L} \} = \text{Prob} \{ \mu \geqslant \text{U} \} = \frac{\alpha}{2} \end{equation} \tag{21.3} \]

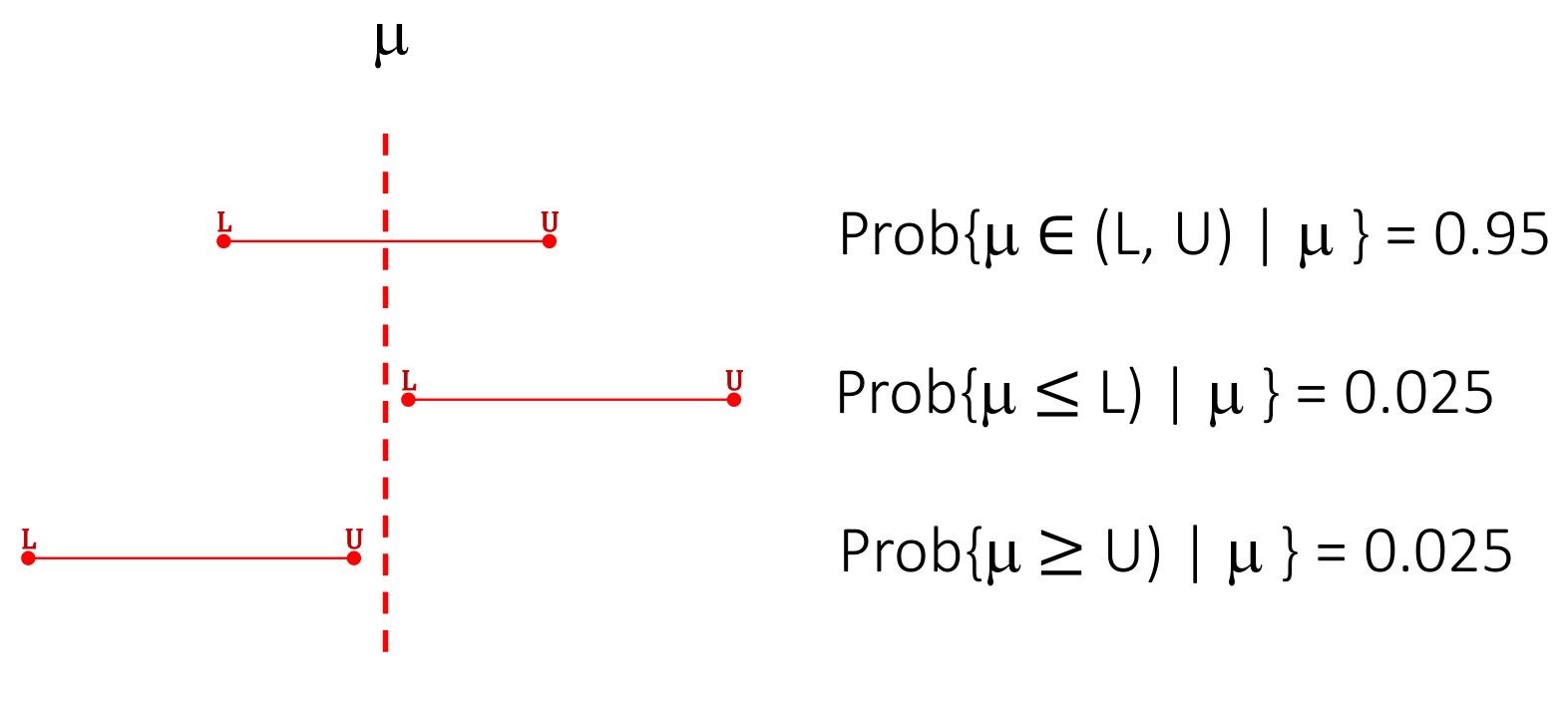
General definition of a CI for a 95% CI

圖 21.1: General definition of a CI for a 95% CI

21.2 利用總體參數的樣本分佈求信賴區間

總體參數的樣本分佈是求其信賴區間的關鍵。假設 \(\hat\mu\) 是總體參數 \(\mu\) 的估計量。且已知存在兩個單調遞增函數 \(A(\mu), B(\mu)\) 來描述該總體參數 \(\mu\) ：

\[ \begin{equation} \text{Prob} \{ \hat\mu \leqslant A(\mu) \} = \text{Prob} \{ \hat\mu \geqslant B(\mu) \} = \frac{\alpha}{2} \end{equation} \tag{21.4} \]

所以，

\[ \begin{equation} \text{Prob} \{ A^{-1} (\hat\mu) \leqslant \mu \} = \text{Prob} \{ B^{-1}(\hat\mu) \geqslant \mu \} = \frac{\alpha}{2} \end{equation} \tag{21.5} \]

因此，\(A^{-1}(\hat\mu), B^{-1}(\hat\mu)\) 就是我們想要找的公式 (21.3) 參數的估計信賴區間的下限 \(\text{L}\)，和上限 \(\text{U}\)。所以，關鍵的任務就在於，每一次尋找計算參數樣本分佈的方程 \(A, B\) 。

21.3 情況1：已知方差的正態分佈數據均值的信賴區間

從已知正態分佈且方差爲 \(\sigma^2\) 的人羣中抽取樣本量爲 \(n\) 的相互獨立觀察數據 \(Y_i (i=1,2,\cdots,n)\)。該樣本均值的估計量 \(\hat\mu=\bar{Y}\)，也服從方差已知的 \((\frac{\sigma^2}{n})\) 正態分佈：

\[ \begin{equation} \bar{Y}\sim N(\mu, \frac{\sigma^2}{n}) \Leftrightarrow Z=\frac{\bar{Y}-\mu}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0,1) \end{equation} \tag{21.6} \]

所以利用標準正態分佈，往公式 (21.3) 儘可能靠：\(\text{Prob}\{ Z \leqslant z_{\alpha/2}\} = \text{Prob}\{ Z \geqslant z_{1-\alpha/2}\} = \frac{\alpha}{2}\) 。

把式子 (21.6) 代入以後：

\[ \begin{equation} \text{Prob}\{ \bar{Y} \leqslant \mu+z_{\alpha/2}\frac{\alpha}{\sqrt{n}} \} = \text{Prob}\{ \bar{Y} \geqslant \mu+z_{1-\alpha/2}\frac{\alpha}{\sqrt{n}} \} = \frac{\alpha}{2} \end{equation} \tag{21.7} \]

至此，我們找到了描述總體均值的單調函數：

\[ \begin{aligned} A(\mu) &= \mu + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \\ B(\mu) &= \mu + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{aligned} \]

由於標準正態分佈左右對稱，所以 \(z_{\alpha/2}=-z_{1-\alpha/2}\) ，因而，\(A(\mu) = \mu - z_{1-\alpha/2}\frac{\sigma}{n}\)。

此時，求信賴區間上限和下限的方法應該已經一目瞭然：

\[ \begin{equation} \text{U} =A^{-1}(\bar{Y})=\bar{Y} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ \text{L} = B^{-1}(\bar{Y})=\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{equation} \tag{21.8} \]

我們也常將它簡寫成爲：\(\text{CI} = \bar{Y} \pm z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\)。

它的意義是：

\[ \begin{equation} \text{Prob} \{ \bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \bar{Y} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \} = 1-\alpha \end{equation} \tag{21.9} \]

所以區間 \((\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}, \bar{Y} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}})\) 包含了總體參數均值 \((\mu)\) 的概率是 \(1-\alpha\)。我們把這個區間叫做總體均值 \(\mu\) 的 \(100(1-\alpha)\%\) 信賴區間。常說的 \(95\%\) 信賴區間我們使用的 \(z_{0.975} = 1.96\)。其他置信水平的 \(z\) 值舉例如下：

\[ \begin{array}{lr} z_{0.90} = 1.28 & \text{for } 80\% \text{ level} \\ z_{0.95} = 1.645 & \text{for } 90\% \text{ level} \\ z_{0.995} = 2.58 & \text{for } 99\% \text{ level} \\ z_{0.9995} = 3.29 & \text{for } 99.9\% \text{ level} \\ \end{array} \]

所以，根據上面羅列的不同置信水平下 \(z\) 值的大小，我們不難判斷 \(\text{CI} = \bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\) 範圍隨着標準差增大而變寬 (不精確)，隨着樣本量增加而變窄 (精確)。

這裏補充另一個容易混淆的概念，參數估計的信賴區間公式 \(\text{CI} = \bar{Y} \pm z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\) ，和參考值範圍 (reference range) 是不同的概念。後者的公式爲 \(\bar{Y}\pm z_{1-\alpha/2} \sigma\)。參考值範圍的意義是， \(95\%\) 的樣本數據包含在這個區間內。信賴區間，給出的是這個樣本對總體均值的估計的精確度。

21.4 信賴區間的意義

當 \(\alpha = 0.05\) 時，我們說\((\bar{Y} - z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}, \bar{Y} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}})\) 包含了總體參數均值 \((\mu)\) 的概率是 \(95\%\)。但是要記住，千萬不能說：總體參數 \(\mu\) 有 \(95\%\) 的概率落在這個信賴區間內。因爲總體參數不是隨機變量，它不會隨我們的樣本變化而變化，它是恆定不變的。我們每一次實驗，每一次採樣，獲得的樣本數據，計算出一個新的信賴區間，這樣的區間都是在估計這個未知位置的總體參數。所以，從長遠來說，相同的實驗，重複20次，其中19次計算獲得的信賴區間，會包含真實的總體參數。

21.5 情況2：未知方差，但是已知服從正態分佈數據均值的信賴區間

多數情況下，總體的方差我們無從知曉。它也必須通過實驗數據來估計 \(\hat\sigma^2\)。那麼，下面的公式計算的統計量 \(T\) 服從自由度爲 \(n-1\) 的 \(t\) 分佈：

\[ T=\frac{\bar{Y}-\mu}{\sqrt{\hat\sigma^2/n}} \sim t_{n-1} \]

用跟前面類似的辦法，用統計量 \(T\) 取代 \(Z\)，我們可以求未知方差時正態分佈數據均值的信賴區間 (類比 (21.8))：

\[ \begin{aligned} &\text{U} = \bar{Y} + t_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ &\text{L} = \bar{Y} - z_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \\ &\text{Or, equivalently :} \\ &\text{CI } = \bar{Y} \pm t_{n-1, 1-\alpha/2}\frac{\sigma}{\sqrt{n}} \end{aligned} \tag{21.10} \]

21.6 情況3：服從正態分佈的隨機變量方差的信賴區間

用 \(Y_i (i=1,2,\cdots,n)\) 標記樣本量爲 \(n\) 的獨立觀察數據。已知該數據來自的人羣服從正態分佈，但是方差未知。那麼從統計推斷第二章 (Section 10.4) 推導過的內容，我們知道：

\[ \begin{aligned} &\text{Sample variance is defined as: } \\ &\hat\sigma^2 = \frac{\sum_{i=1}^n(Y_i-\bar{Y})^2}{n-1} \\ &\text{and } \\ &\frac{(n-1)\hat\sigma^2}{\sigma^2} \sim \chi^2_{n-1} \\ &\text{It follows that we want } \\ &\text{Prob}\{ \hat\sigma^2 \leqslant \frac{\sigma^2}{n-1}\chi^2_{n-1, \alpha/2} \} = \text{Prob}\{ \hat\sigma^2 \geqslant \frac{\sigma^2}{n-1}\chi^2_{n-1, 1-\alpha/2} \} = \frac{\alpha}{2} \\ & \Rightarrow \text{U} = \frac{(n-1)\hat\sigma^2}{\chi^2_{n-1, \alpha/2}} \; \text{L} = \frac{(n-1)\hat\sigma^2}{\chi^2_{n-1, 1-\alpha/2}} \\ \end{aligned} \]

21.7 當樣本量足夠大時

根據中心極限定理，當樣本量足夠大時，樣本均數服從正態分佈，即使樣本數據並不服從正態分佈。這就意味着，樣本足夠大，章節 21.4 中用到的均值信賴區間公式，也可適用於樣本數據不服從正態分佈的情況下。我們常使用這個定理，和章節 21.4 中的公式去計算許多總體均數以外的參數的 \(95\%\) 信賴區間，通過正態分佈近似法計算獲得的信賴區間，被叫做近似信賴區間。

21.8 情況4：求人羣百分比的信賴區間

21.8.1 一般原則

用 \(R\) 表示 \(n\) 次實驗中成功的次數。如果滿足實驗相互獨立的條件，那麼 \(R\sim \text{Binomial}(n,\pi)\)。那麼樣本比例 \(P=\frac{R}{n}\) 是人羣比例 \(\pi\) 的無偏估計。如果想要求 \(\pi\) 的 \(95\%\) 信賴區間 \((\pi_L, \pi_U)\)，我們可能自然而讓想到用成功次數 \(R\) 來計算。然而，由於 \(R\) 本身是離散型變量 (只能取大於等於零的整數)，恰好加起來概率等於 \(95\%\) 的 \(\pi\) 的區間是幾乎不可能計算的。我們處理比例的信賴區間的問題時，要計算的兩個下限值和上限值要滿足的條件：

  1. 尋找最小的 \(\pi_L\) 滿足 \(\text{Prob}(\pi_L>\pi) \leqslant 0.025\)
  2. 尋找最大的 \(\pi_U\) 滿足 \(\text{Prob}(\pi_U<\pi) \leqslant 0.025\)

有兩種方案可供選擇：

  1. 利用樣本分佈服從二項分佈 \(R \sim \text{Binomial}(n, \pi)\) 的原則來“精確”計算；
  2. 正態近似法計算。

第一種方法被叫做精確法，並不是因爲它能夠精確計算恰好概率和等於 \(95\%\) 的所有的 \(\pi\)，而是因爲它利用的是樣本分佈的二項分佈屬性進行計算。然而隨着樣本量的增加，兩種方法計算的信賴區間結果越來越接近概率和 \(95\%\)。

21.8.2 二項分佈的“精確法”計算信賴區間

例：樣本量 \(n=20\), 成功次數 \(r=5\) 時，你可以用查水錶的辦法，也可以利用 R 進行精確計算

binom.test(5, 20, conf.level = 0.95)
## 
##  Exact binomial test
## 
## data:  5 and 20
## number of successes = 5, number of trials = 20, p-value = 0.04
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.08657 0.49105
## sample estimates:
## probability of success 
##                   0.25

下面兩個圖分別展示了當 \(\pi\) 等於精確法計算的下限和上限時的概率分佈。可以看出 \(\pi=0.0866\) 時，\(\text{Prob}\{R \geqslant 5\} \leqslant 0.025\)。同時，當 \(\pi = 0.4910\) 時， \(\text{Prob}\{ R\leqslant 5 \} \leqslant 0.025\)

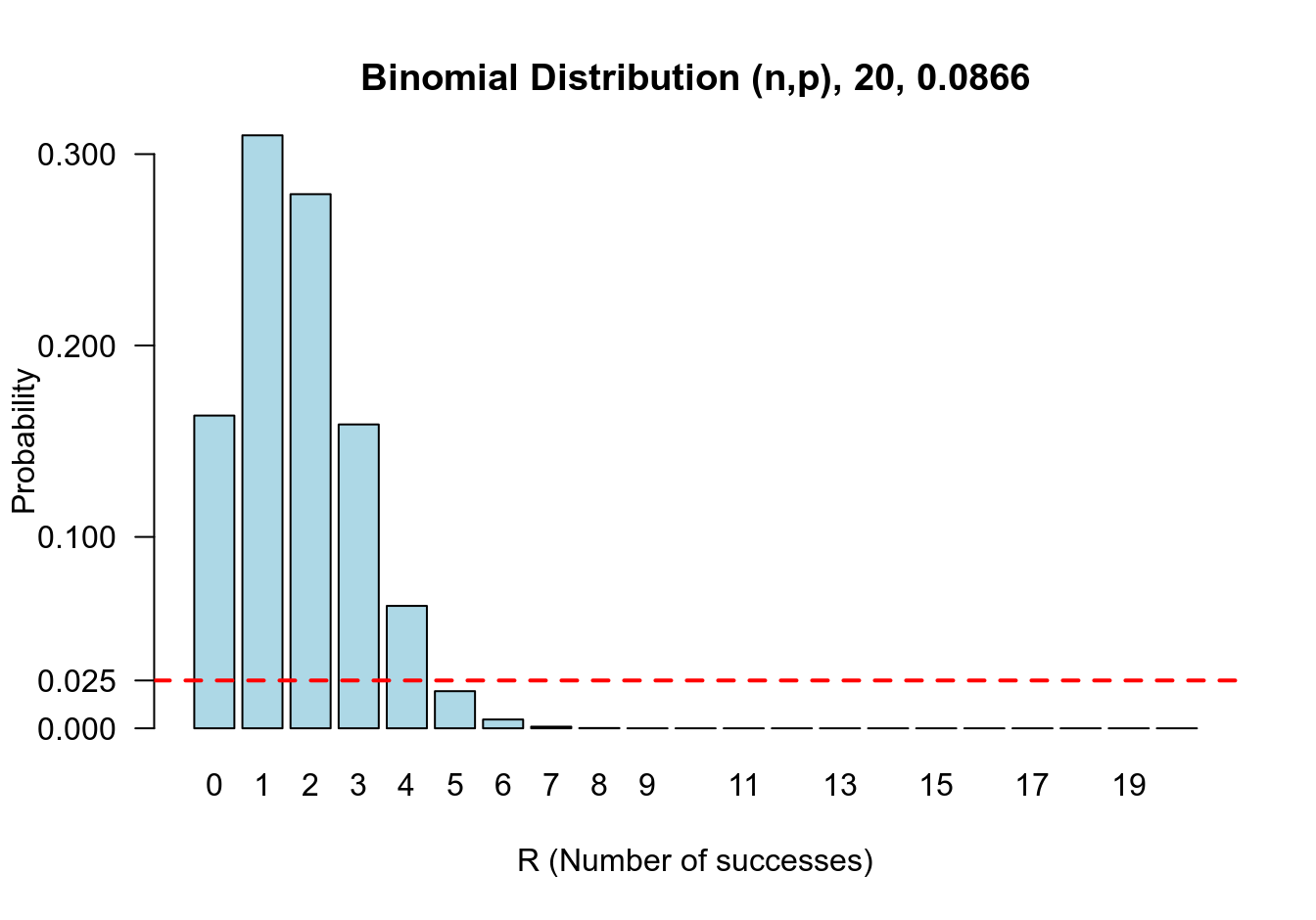
Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.0866

圖 21.2: Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.0866

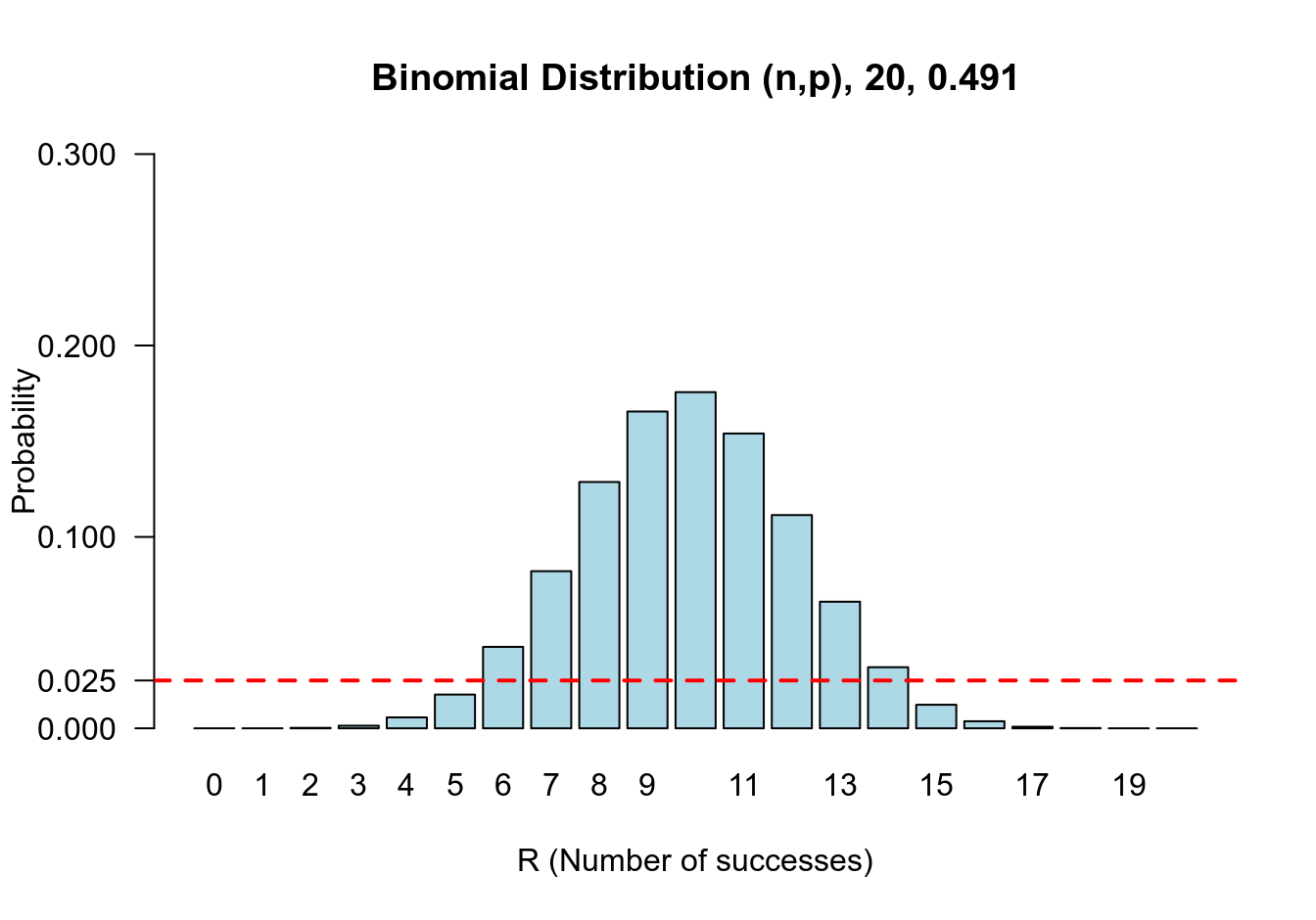
Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.4910

圖 21.3: Sampling distribution of number of successes out of 20 (R) conditional on the probability of success being 0.4910

21.8.3 二項分佈的近似法計算信賴區間

當 \(n\) 較大時，百分比 \(P\) 分佈 可以用正態分佈來近似：

\[ P\sim N(\pi, \sigma^2) \text{ where } \sigma^2 = \frac{\pi(1-\pi)}{n} \]

總體均值用樣本百分比 \(p\) 替代，方差用樣本方差 \(\hat\sigma^2 = \frac{p(1-p)}{n}\)，因此，當樣本量較大時二項分佈的近似正態分佈特徵可以描述爲：

\[ P \sim N(p, \hat\sigma^2) \text{ where } \hat\sigma^2 = \frac{p(1-p)}{n} \]

接下去對與百分比的信賴區間的計算就可以套用章節 21.4 中用到的均值信賴區間公式：

\[ \begin{aligned} & P\pm z_{1-\alpha/2}\sqrt{\frac{P(1-P)}{n}} \\ & \text{ where } z_{1-\alpha/2} = 1.96 \text{ for } 95\% \text{CI} \end{aligned} \tag{21.11} \]

正態近似法的好處是簡單，但是代價就是樣本量小時不準確。

例如：

  1. \(n=10, r=4, p=0.4\) 時
    • 精確法 \(95\%\) 信賴區間：0.1216, 0.7376
    • 正態近似法 \(95\%\) 信賴區間：\(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{10}} =\) 0.0964, 0.7036
  2. \(n=50, r=20, p=0.4\) 時
    • 精確法 \(95\%\) 信賴區間：0.2641, 0.5482
    • 正態近似法 \(95\%\) 信賴區間： \(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{50}} =\) 0.2642, 0.5358
  3. \(n=1000, r=400, p=0.4\) 時
    • 精確法 \(95\%\) 信賴區間：0.3695, 0.4311
    • 正態近似法 \(95\%\) 信賴區間： \(0.4\pm1.96\sqrt{\frac{0.4\times0.6}{1000}} =\) 0.3696, 0.4304

可以明顯看到隨着樣本量增加，信賴區間本身的範圍在不斷變小 (精確)。且正態近似法計算的信賴區間也越來越接近“精確法”。“Statistical Methods in Medical Research” (Armitage, Berry, and Matthews 2008) 書中建議，滿足 \(n\pi \geqslant 10 \text{ or } n(1-\pi) \geqslant 10\) 時，正態近似法可以給出較爲滿意的百分比的信賴區間估計。

21.9 率的信賴區間

21.9.1 利用泊松分佈精確計算

假設在一段時間 \(t\) 內某事件發生的次數記爲 \(Y\)。如果每個相同事件的發生相互獨立那麼 \(Y \sim \text{Poisson}(\mu t)\)。樣本率 \(R=\frac{Y}{t}\)，是人羣事件發生概率 \(\mu\) 的無偏估計。

\[ \text{The probability that } Y=y \text{ is given by } \frac{(\mu t)^y e^{-\mu t}}{y!} \text{ for } y= 0,1,2,\cdots,\infty \]

與前一節百分比的精確計算信賴區間相類似 (Section 21.8.2)，我們可以使用泊松分佈的性質進行計算：

  1. 尋找最小的 \(\mu_L\) 滿足 \(\text{Prob}(\mu_L>\mu) \leqslant 0.025\)
  2. 尋找最大的 \(\mu_U\) 滿足 \(\text{Prob}(\mu_U<\mu) \leqslant 0.025\)

例：某核電站附近的村莊從1968年起的10年內，發生了 6 人死於白血病。平均死亡率爲 0.6/年。計算死亡率的95%信賴區間。

可以利用 R 的精確計算發病率的代碼 poission.test 來獲得精確法率的信賴區間：

poisson.test(6, 10)
## 
##  Exact Poisson test
## 
## data:  6 time base: 10
## number of events = 6, time base = 10, p-value = 0.3
## alternative hypothesis: true event rate is not equal to 1
## 95 percent confidence interval:
##  0.2202 1.3059
## sample estimates:
## event rate 
##        0.6

21.9.2 利用正態近似法計算

當樣本量較大時，發生事件次數 \(Y\) 近似服從正態分佈，其均值和方差均等於 \(\mu t\) (參考 Section 6 推導)：

\[ Y \sim N(\mu t, \sigma^2) \text{ where } \sigma^2=\mu t \]

所以事件發生率 \(\mu\) 的信賴區間公式爲 \(\frac{Y\pm 1.96\sqrt{Y}}{t}\)。

References

Armitage, Peter, Geoffrey Berry, and John Nigel Scott Matthews. 2008. Statistical Methods in Medical Research. John Wiley & Sons.