第 10 章 估計和精確度 Estimation and Precision
10.1 估計量和他們的樣本分佈
例子: 最大呼氣量 (Forced Expoiratory Volume in one second, FEV1) 用於測量一個人的肺功能,它的測量值是連續的。我們從前來門診的人中隨機抽取 \(n\) 人作爲樣本,用這個樣本的 FEV1 平均值來估計這個診所的患者的平均肺功能。
模型假設: 在這個例子中,我們的假設有如下:每個隨機抽取的 FEV1 測量值都是從同一個總體 (人羣) 中抽取,每一個觀察值 \(Y_i\) 都互相獨立互不影響。我們用縮寫 iid 表示這些隨機抽取的樣本是服從獨立同分佈 (independent and identically distributed)。另外,總體的分佈也假定爲正態分佈,且總體均值爲 \(\mu\),總體方差爲 \(\sigma^2\)。那麼這個模型可以簡單的被寫成:
\[Y_i \stackrel{i.i.d}{\sim} N(\mu, \sigma^2), i=1,2,\dots,n\]
總體均值 \(\mu\) 的估計量: 顯然算術平均值: \(\bar{Y}=\frac{1}{n}\sum_{i=1}^ny_i\) 是我們用於估計總體均值的估計量。
估計量的樣本分佈: \[\bar{Y}\stackrel{i.i.d}{\sim}N(\mu, \frac{\sigma^2}{n})\]
證明
\[ \begin{aligned} E(\bar{Y}) &= E(\frac{1}{n}\sum Y_i) \\ &= \frac{1}{n}E(\sum Y_i) \\ &= \frac{1}{n}\sum E(Y_i) \\ &= \frac{1}{n}n\mu = \mu \\ Var(\bar{Y}) &= Var(\frac{1}{n}\sum Y_i) \\ \because Y_i \;\text{are} &\; \text{independent} \\ &= \frac{1}{n^2}\sum Var(Y_i) \\ &= \frac{1}{n^2} n Var(Y_i) \\ &= \frac{\sigma^2}{n} \end{aligned} \]
證明當 \(Z=\frac{\bar{Y}-\mu}{\sqrt{Var(\bar{Y})}}\) 時, \(Z\sim N(0,1)\):
由式子可知, \(Z\) 只是由一組服從正態分佈的數據 \(\bar{Y}\) 線性轉換 (linear transformation) 而來,所以 \(Z\) 本身也服從正態分佈
\[ \begin{aligned} E(Z) &= \frac{1}{\sqrt{Var(\bar{Y})}}E[\bar{Y}-\mu] \\ &= \frac{1}{\sqrt{Var(\bar{Y})}}[\mu-\mu] = 0 \\ Var(Z) &= \frac{1}{Var(\bar{Y})}Var[\bar{Y}-\mu] \\ &= \frac{1}{Var(\bar{Y})}Var(\bar{Y}) =1 \\ \therefore Z \;&\sim N(0,1) \end{aligned} \]
均值 \(\mu\) 的信賴區間: 上節說道,
信賴區間通常是成對成對的出現的,即有上限和下限。這樣的一對從樣本數據中計算得來的統計量,同樣也是有樣本分佈的。每次我們重新從總體或人羣中抽樣,計算獲得的信賴區間都不同,這些信賴區間就組成了信賴區間的樣本分佈。總體和人羣的參數落在這些信賴區間範圍內的概率,就是我們常說的信賴區間的水平(\(95\%\)) 。 常用的這個概率值就是 \(95\%, 90\%, 99\%\)。
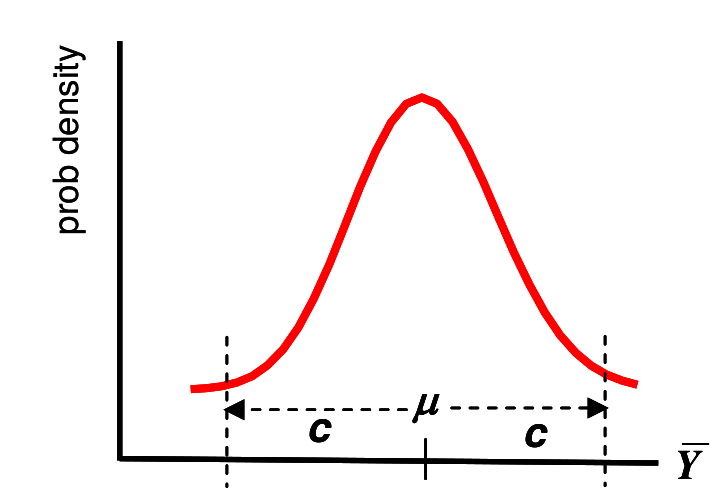
假定我們用 \(95\%\) 作爲信賴區間的水平。那麼下面我們嘗試推導一下信賴區間的計算公式。從長遠來說 (也就是假設我們從總體中抽樣無數次,每次都進行信賴區間的計算,也獲得無數個信賴區間) ,這些信賴區間中有 \(95\%\) 是包含了總體的真實均值 (但是卻是未知) 的,而且這些信賴區間由於是從一個服從正態分佈的數據而來,它們也服從正態分佈 (對真實均值左右對稱) 。所以我們有理由相信,可以找到一個數值 \(c\):
\[Prob(\bar{Y} > \mu+c) = 0.025 \\ Prob(\bar{Y} < \mu-c) = 0.025\]
因此,我們可以定義 \(95\%\) 信賴區間的上限和下限分別是:
\[L=\bar{Y}-c \Rightarrow Prob(L>\mu)=0.025 \\ U=\bar{Y}+c \Rightarrow Prob(U<\mu)=0.025\]
接下來就是推倒 (故意的) \(c\) 的過程啦:
\[ \begin{aligned} Prob(\bar{Y}>\mu+c)=Prob(\bar{Y}-\mu>c) \;&= 0.025 \\ \Rightarrow Prob(\frac{\bar{Y}-\mu}{\sqrt{Var(\bar{Y})}} > \frac{c}{\sqrt{Var(\bar{Y})}}) \;&= 0.025 \\ \Rightarrow Prob(Z>\frac{c}{\sqrt{Var(\bar{Y})}}) \;&= 0.025 \\ we\;have\;proved\; Z\sim N(0,1) \\ we\;also\;know\; Prob(Z>1.96) \;&= 0.025 \\ so\;let\; \frac{c}{\sqrt{Var(\bar{Y})}} =1.96 \\ \Rightarrow c=1.96\sqrt{Var(\bar{Y})} \\ the\;95\%\;confidence\;interval \;of\; &the\;population\;mean\;is\\ \mu = \bar{Y}\pm1.96\sqrt{Var(\bar{Y})}=\bar{Y}\pm & 1.96\frac{\sigma}{\sqrt{n}} \end{aligned} \]
其中,\(\sqrt{Var(\bar{Y})}\) 就是我們熟知的估計量 \(\bar{Y}\) 的標準誤。
10.2 估計量的特質
考慮以下的問題:
- 什麼因素決定了一個估計量 (estimator) 的好壞,是否實用?
- 如果有其他的可選擇估計量,該如何取捨呢?
- 當情況複雜的時候,我們該如何尋找合適的估計量?
10.2.1 偏倚
假設 \(T\) 是我們估計總體參數 \(\theta\) 的一個估計量。一般來說我們希望估計量的樣本分佈可以在 “正確的位置” 左右均勻分佈。換句話說我們希望:
\[E(T)=\theta\]
如果實現了這個條件,我們說這樣的估計量是無偏的 (unbiased)。然而,天下哪有這等好事,我們叫真實值和估計量之間的差距爲偏倚:
\[bias(T) = E(T)-\theta\]
其實偏倚完全等於零並不是最重要,許多常見的估計量都是有偏倚的。重要的是,這個偏倚會隨着樣本量的增加而逐漸趨近於零。所以我們就可以認爲這樣的估計量是漸進無偏的 (asymptotically unbiased):
\[T\;is\;an\;\textbf{unbiased}\;estimator\;for\;\theta\;if\;\\E(T)=\theta\\ T\;is\;an\;\textbf{asymptotically unbiased}\;estimator\;for\;\theta\;if\;\\lim_{n\rightarrow\infty}E(T)=\theta\]
10.2.2 估計量的效能 Efficiency
通常,我們希望一個估計量 (estimator) 的偏倚要小,同時,它的樣本分佈也希望能儘可能的不要波動太大。換句話說,我們還希望估計量的方差越小越好。
如果說,兩個估計量有相同的偏倚,均可以選擇來推斷總體,我們說,其中樣本分佈的方差小的那個 (波動幅度小) 的那個估計量是相對更好的。因爲樣本分佈方差越小,說明可以更加精確的估計總體參數。這兩個估計量的方差之比:\(Var(S)/Var(T)\) 被叫做這兩個估計量的相對效能 (relative efficiency)。所以我們用估計量去推斷總體時,需要選用效能最高,精確度最好的估計量 (the minimum variance unbiased estimator/an efficient estimator)。
10.2.3 均值和中位數的相對效能
在一個服從 \(N(\mu,\sigma^2)\) 正態分佈的數據中,中位數和均值是一樣的,也都同時等於總體均值參數 \(\mu\)。而且,樣本均數 \(\bar{Y}\) 和樣本中位數 \(\dot{Y}\) 都是對總體均值的無偏估計量。那麼應該選用中位數還是平均值呢?
之前證明過當 \(Y_i \sim N(\mu,\sigma^2)\) 時, \(Var(\bar{Y})=\sigma^2/n\)。然而,當 \(n\) 較大的時候,可以證明的是:
\[Var(\dot{Y})=\frac{\pi}{2}\frac{\sigma^2}{n}\approx1.571\frac{\sigma^2}{n}\]
因此,這兩個估計量的相對效能就是:
\[\frac{Var(\dot{Y})}{Var(\bar{Y})}\approx1.571\]
所以總體是正態分佈時,平均值就是較中位數更適合用來估計總體的估計量。
10.2.4 均方差 mean square error (MSE)
兩個估計量的偏倚不同時,可以比較他們和總體參數之間的差距,這被叫做均方差, Mean Square Error (MSE)。
\[MSE(T)=E[(T-\theta)^2]\]
這裏用一個數學技巧,將式子中的估計量和總體參數之間的差,分成兩個部分:一是估計量本身的方差 (\(T-E(T)\)),一是估計量的偏倚 (\(E(T)-\theta\))。
\[ \begin{aligned} MSE(T) &= E[(T-\theta)^2] \\ &= E\{[T-E(T)+E(T)-\theta]^2\} \\ &= E\{[T-E(T)]^2+[E(T)-\theta]^2 \\ & \;\;\;\;\; \;\;+2[T-E(T)][E(T)-\theta]\} \\ &= E\{[T-E(T)]^2\}+E\{[E(T)-\theta]^2\} + 0\\ &= Var(T) + [bias(T)^2] \end{aligned} \]
10.3 總體方差的估計,自由度
如果 \(Y_i \sim (\mu, \sigma^2)\),並不需要默認或者假定它服從正態分佈或者任何分佈。那麼它的方差我們會用:
\[V_{\mu}=\frac{1}{n}\sum_{i=1}^n(Y_i-\mu)^2\]
證明 \(V_{\mu}\) 是 \(\sigma^2\) 的無偏估計:
\[ \begin{aligned} V_{\mu} &= \frac{1}{n}\sum_{i=1}^n(Y_i-\mu)^2 \\ we\;need\;to\;prove &E(V_{\mu}) = \sigma^2 \\ \Rightarrow E(V_{\mu}) &= \frac{1}{n}\sum_{i=1}^nE(Y_i-\mu)^2 \\ &= \frac{1}{n}\sum_{i=1}^nVar(Y_i) \\ &= \frac{1}{n}\sum_{i=1}^n\sigma^2 \\ &= \sigma^2 \end{aligned} \]
然而通常情況下,我們並不知道總體的均值 \(\mu\)。因此,只好用樣本的均值 \(\bar{Y}\) 來估計 \(\mu\)。所以上面的方程就變成了:
\[V_{\mu}=\frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2\]
你如果仔細觀察認真思考,就會發現,上面這個式子是有問題的。這個大問題就在於,\(Y_i-\bar{Y}\) 中我們忽略掉了樣本均值 \(\bar{Y}\) 和總體均值 \(\mu\) 之間的差 (\(\bar{Y}-\mu\))。因此上面的計算式來估計總體方差時,很顯然是會低估平均平方差,從而低估了總體方差。
這裏需要引入自由度 (degree of freedom) 在參數估計中的概念。
字面上可以理解爲:自由度是估計過程中使用了多少互相獨立的信息。所以在上面第一個公式中:\(V_{\mu}=\frac{1}{n}\sum_{i=1}^n(Y_i-\mu)^2\)。所有的 \(n\) 個觀察值互相獨立,不僅如此,他們還對總體均值獨立。然而在第二個我們用 \(\bar{Y}\) 取代了 \(\mu\) 的公式中,樣本均數則與觀察值不互相獨立。因爲樣本均數必然總是落在觀察值的中間。然而總體均數並不一定就會落在觀察值中間。總體均數,和觀察值之間是自由,獨立的。因此,當我們觀察到 \(n-1\) 個觀察值時,剩下的最後一個觀察值,決定了樣本均值的大小。所以說,樣本均值的自由度,是 \(n-1\)。
所以,加入了自由度的討論,我們可以相信,用樣本估計總體的方差時,使用下面的公式將會是總體方差的無偏估計:
\[V_{n-1}=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\bar{Y})=\frac{n}{n-1}V_n\]
證明
利用上面也用到過的證明方法 – 把樣本和總體均值之間的差分成兩部分:
\[ \begin{aligned} V_{\mu} &= \frac{1}{n}\sum_{i=1}^n(Y_i-\mu)^2 \\ &= \frac{1}{n}\sum_{i=1}^n[(Y_i-\bar{Y})+(\bar{Y}-\mu)]^2 \\ &= \frac{1}{n}\sum_{i=1}^n[(Y_i-\bar{Y})^2+(\bar{Y}-\mu)^2\\ &\;\;\;\;\;\;\;\;\;\;\;\;+2(Y_i-\bar{Y})(\bar{Y}-\mu)]\\ &=\frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2+\frac{1}{n}\sum_{i=1}^n(\bar{Y}-\mu)^2\\ &\;\;\;\;\;\;\;\;\;\;\;\;+\frac{2}{n}(\bar{Y}-\mu)\sum_{i=1}^n(Y_i-\bar{Y}) \\ &= V_n+(\bar{Y}-\mu)^2 \\ &\;\;\;\;\;\;\;\;\;\;\;\;(\text{note that}\;\sum_{i=1}^n(Y_i-\bar{Y})=0) \\ \Rightarrow V_n &= V_{\mu}-(\bar{Y}-\mu)^2 \\ \therefore E(V_n)&= E(V_{\mu}) - E[(\bar{Y}-\mu)^2] \\ &= Var(Y)-Var(\bar{Y}) \\ &= \sigma^2-\frac{\sigma^2}{n} \\ &= \sigma^2(\frac{n-1}{n}) \end{aligned} \]
因此,我們看見 \(V_n\) 正如上面討論的那樣,是低估了總體方差的。雖然當 \(n\rightarrow\infty\) 時無限接近 \(\sigma^2\) 但是依然是低估了的。所以,我們可以對之進行修正:
\[ \begin{aligned} E[\frac{n}{n-1}V_n] &= \frac{n}{n-1}E[V_n] =\sigma^2 \\ \Rightarrow E[V_{n-1}] &= \sigma^2 \end{aligned} \]
10.4 樣本方差的樣本分佈
\(S^2\) 常用來標記樣本方差,取代上面我們用到的 \(V_{n-1}\):
\[S^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\bar{Y})^2\]
而且上面也證明了,\(E(S^2)=\sigma^2\) 是總體方差的無偏估計。然而,要注意的是,樣本標準差 \(\sqrt{S^2}\) 卻不是總體標準差 \(\sigma\) 的無偏估計(因爲並不是線性變換,而是開了根號) 。
證明樣本標準差 \(S\) 不是總體標準差 \(\sigma\) 的無偏估計
\[ \begin{aligned} Var(S) &=E(S^2)-[E(S)]^2 \\ \Rightarrow [E(S)]^2 &=E(S^2)-Var(S) \\ \because E(S^2) &=\sigma^2 \\ \therefore [E(S)]^2 &=\sigma^2-Var(S) \\ E(S) &=\sqrt{\sigma^2-Var(S)} \\ \end{aligned}\]
可見樣本標準差是低估了總體標準差的。
另外可以被證明的是:
\[\frac{n-1}{\sigma^2}S^2\sim \mathcal{X}_{n-1}^2\\ Var(S^2)=\frac{2\sigma^4}{n-1}\]
\(\mathcal{X}^2_m\): 自由度爲 \(m\) 的卡方分佈 (Section 11)。是在圖形上向右歪曲的分佈。當自由度增加時,會越來越接近正態分佈。