第 29 章 多元模型分析 Multivariable Models
簡單線性迴歸描述的是一個連續型的因變量 \((y)\)，和一個單一的預測變量 \((x)\) 之間的關係。我們考慮把這個模型擴展成包含多個預測變量，單一因變量的模型。例如，我們可以考慮建立一個模型使用生活習慣 (包括“年齡，性別，運動，飲食習慣等”) 來預測收縮期血壓。此時多重迴歸的思想就可以幫我們理解一些我們更加關心的因子，與因變量之間的關係，同時控制或者叫調整了其他的混雜因子 (control or adjust confounders)。有時候這樣的模型也可以直接應用到生活中去，比如上面的例子，我們可以通過瞭解一個人的生活習慣，用建立好的模型來估計這個人的收縮期血壓。
建立模型之前，必須明確研究的目的是什麼。例如我們關心一個新發現的因子可能與高血壓有關係，那麼模型中我們放進去調整的其他因子 (如年齡，性別，運動) 等和因變量 (血壓) 之間的關係就變得不那麼重要。
多重線性迴歸，或者叫多元模型分析 (multiple linear regression or multivariable linear regression) 是研究一個連續型因變量和多個預測變量之間關係的重要模型。本章還會着重討論混雜 (confounding)的概念。
29.1 兩個預測變量的線性迴歸模型
29.1.1 數學標記法和解釋
這裏假設我們研究一個因變量 \(Y\)，和兩個預測變量 \((X_1,X_2)\) 的模型。那麼此時兩個預測變量的線性迴歸模型可以記爲：
\[ \begin{equation} y_i = \alpha + \beta_1 x_{1i} + \beta_2 x_{2i} + \varepsilon_i, \text{ where } \varepsilon_i \sim \text {NID}(0, \sigma^2) \end{equation} \tag{29.1} \]
其中，
- \(y_i\) 是第 \(i\) 名研究對象的因變量數據 (例如體重)；
- \(x_{1i}\) 是第 \(i\) 名研究對象的第一個預測變量數據 (例如年齡)， \(X_1\)；
- \(x_{2i}\) 是第 \(i\) 名研究對象的第二個預測變量數據 (例如身高)， \(X_1\)；
- \(\alpha\) 的涵義是，當兩個預測變量均爲 \(0\) 時，因變量的期望值；
- \(\beta_1\) 的涵義是，當 \(X_2\) 不變時，\(X_1\) 每升高一個單位，因變量的期望值；
- \(\beta_2\) 的涵義是，當 \(X_1\) 不變時，\(X_2\) 每升高一個單位，因變量的期望值。
\(\beta_1, \beta_2\) 叫做偏迴歸係數 (partial regression coefficient)。它們測量的是兩個預測變量中，當一個被控制 (保持不變) 時，另一個對因變量的影響。
這個模型也可以用矩陣的形式來表示：
\[ \begin{equation} \textbf{Y} = \textbf{X}\beta+\varepsilon, \text{ where } \varepsilon \sim N(0, \textbf{I}\sigma^2) \\ \left( \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array} \right) = \left( \begin{array}{c} 1& x_{11} & x_{21} \\ 1& x_{12} & x_{22} \\ \vdots & \vdots& \vdots \\ 1& x_{1n}& x_{2n} \\ \end{array} \right)\left( \begin{array}{c} \alpha \\ \beta_1\\ \beta_2 \end{array} \right)+\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n\\ \end{array} \right) \end{equation} \tag{29.2} \]
此時上面的表達式中，\(\textbf{X}\) 是一個矩陣，\(\textbf{Y, \beta, \varepsilon}\) 均為向量。殘差被認為服從多變量正態分佈 (Multivariate normal distribution) ，這個多變量正態分佈的協方差矩陣為 \(\sigma^2\) 和單位矩陣 \(\textbf{I}\) 的乘積來描述。這等價於假設殘差是獨立同分佈且方差 \(\sigma^2\) 不變。
29.1.2 最小平方和估計 Least Squares Estimation
跟簡單線性回歸相似地，我們需要通過對殘差平方和最小化，來獲得此時多重線性回歸的各項參數估計：
\[ \begin{equation} SS_{RES} = \sum_{i=1}^n \hat\varepsilon_{i}^2 = \sum_{i=1}^n(y_i-\hat{y})^2=\sum_{i=1}^n(y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i})^2 \end{equation} \tag{29.3} \]
求能讓這個殘差平方和取最小值的參數估計 \(\hat\alpha,\hat\beta_1,\hat\beta_2\) 我們會在下一章用矩陣標記法來解釋。此處要強調的是，這些估計量都是無偏估計量，且可以被證明的是殘差方差可以用下面的式子來定義：
\[ \begin{equation} \hat\sigma^2=\sum_{i=1}^n\frac{\hat\varepsilon_i^2}{(n-3)}=\frac{\sum_{i=1}^n(y_i-\hat\alpha-\hat\beta_1x_{1i}-\hat\beta_2x_{2i})^2}{(n-3)} \end{equation} \tag{29.4} \]
29.2 線性回歸模型中使用分組變量
之前我們已展示過，分組變量可以使用啞變量來表示。分組變量多於兩組時，可用多個啞變量來同時表示。現在假設變量 \(X\) 有三個分組分別用 \(1,2,3\) 來表示。那麼用啞變量來描述含有這個分組變量的數學方法可以標記為：
\[ \begin{equation} y_i = \alpha+\beta_1u_{1i}+\beta_2u_{2i}+\varepsilon_i, \text{ where } \varepsilon_i \sim \text{NID} (0,\sigma^2) \end{equation} \tag{29.5} \]
其中
\[ \begin{aligned} u_{1i}=\left\{ \begin{array}{ll} 1 \text{ if } x_i=2 \\ 0 \text{ if } x_i\neq2 \\ \end{array} \right. ; u_{2i}=\left\{ \begin{array}{ll} 1 \text{ if } x_i=3 \\ 0 \text{ if } x_i\neq3 \\ \end{array} \right. \end{aligned} \]
其實如果你願意，你也可以把公式 (29.5) 寫成下面這樣：
\[ \begin{aligned} \begin{array}{ll} y_i = \alpha + \varepsilon_i & \text{if } x_i=1 \\ y_i = \alpha +\beta_1+ \varepsilon_i & \text{if } x_i=2 \\ y_i = \alpha +\beta_2+ \varepsilon_i & \text{if } x_i=3 \\ \end{array} \end{aligned} \] 所以，
- \(\alpha\) 是 \(X=1\) 時因變量的期待值；
- \(\alpha+\beta_1\) 是 \(X=2\) 時因變量的期待值，所以 \(\beta_1\) 是分組變量 \(X\) 前兩組之間因變量的期待值的差；
- \(\alpha+\beta_2\) 是 \(X=3\) 時因變量的期待值，所以 \(\beta_2\) 是分組變量 \(X\) 前兩組之間因變量的期待值的差。
此時的 \(X=1\) 這個組通常被當作是分組變量中的基準組，也就是參照組 (reference group)。實際情況下你可能可以改變這個參照組為其他組的任意一個。
29.3 協方差分析模型 the Analysis of Covariance (ANCOVA) Model
協方差分析模型用來分析一個連續型的因變量 \(Y\) ，與一個連續型的預測變量 \((X_1)\)和一個二分類的預測變量 \((X_2= 1,2)\)，模型被標記為：
\[ \begin{equation} y_i=\alpha+\beta_1x_{1i}+\beta_2u_{2i}+\varepsilon_i, \text{ where } \varepsilon_i \sim \text{NID}(0,\sigma^2) \end{equation} \tag{29.6} \] 其中，
- \(y_{i}\) 為第 \(i\) 名研究對象的因變量數據 (連續型)；
- \(x_{1i}\) 為第 \(i\) 名研究對象的第一個預測變量 (也是連續型)；
- \(u_i =\left\{ \begin{array}{ll} 1 \text{ if } x_{2i}=2 \\ 0 \text{ if } x_{2i}=1 \\ \end{array}\right.\)
此模型中用到的參數有：
- \(\alpha\) 是截距，意為當 \(X_1=0\) 且 \(X_2=1 \; (u=0)\) 時的因變量期待值；
- \(\beta_1\) 是當 \(X_2\) 保持不變時，\(X_1\) 每升高一個單位時，因變量 \(Y\) 的期待值；
- \(\beta_2\) 是當 \(X_1\) 保持不變時，分組變量 \(X_2\) 的兩組之間因變量 \(Y\) 的期待值差異大小。
所以理解了上面的解釋之後，就可以將表達式 (29.6) 描述為：
\[ \begin{array}{ll} y_i=\alpha+\beta_1x_{1i}+\varepsilon_i & \text{ if } x_{2i}=1 \\ y_i=\alpha+\beta_2+\beta_1x_{1i}+\varepsilon_i & \text{ if } x_{2i} = 2 \end{array} \]
所以，在一個二維圖形中繪製這兩條回歸直線，你會發現他們之間是平行的。因為他們之間相差的只有截距，決定直線斜率的回歸係數，都是 \(\beta_1\)。再用之前用過的數據，兒童的體重和年齡，如果此時考慮了性別因素的話，多重線性回歸的輸出結果和圖形分別應該是：
growgam1 <- read_dta("backupfiles/growgam1.dta")
growgam1$sex <- as.factor(growgam1$sex)
Model1 <- lm(wt ~ age + sex, data=growgam1)
print(summary(Model1), digits = 5)##
## Call:
## lm(formula = wt ~ age + sex, data = growgam1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.19236 -0.76268 -0.00696 0.75675 3.79163
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.152414 0.234254 30.5327 < 2.2e-16 ***
## age 0.163998 0.010919 15.0189 < 2.2e-16 ***
## sex2 -0.518854 0.183053 -2.8344 0.005095 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.25 on 187 degrees of freedom
## Multiple R-squared: 0.5597, Adjusted R-squared: 0.55499
## F-statistic: 118.85 on 2 and 187 DF, p-value: < 2.22e-16print(anova(Model1), digits = 5)## Analysis of Variance Table
##
## Response: wt
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 359.06 359.06 229.6755 < 2.2e-16 ***
## sex 1 12.56 12.56 8.0341 0.005095 **
## Residuals 187 292.35 1.56
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1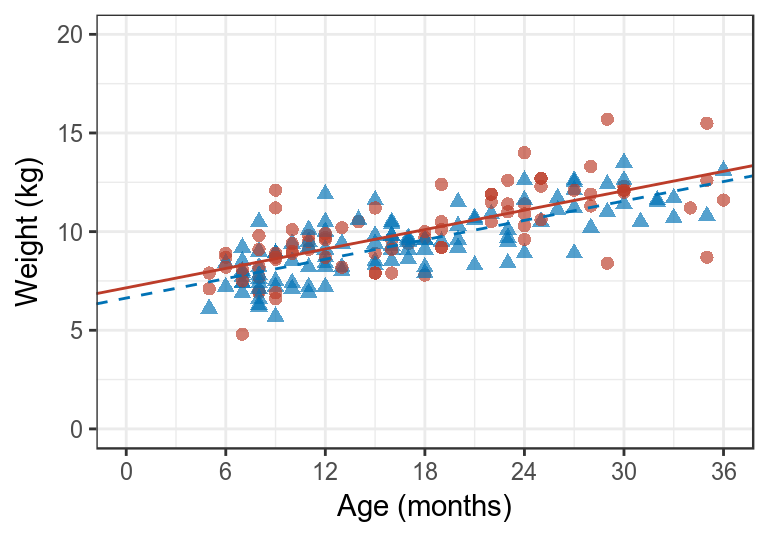
圖 29.1: Data and fitted values from a regression model relating age and gender to data from a cross-sectional survey. For male children data points shown as circles and fitted values linked by a solid line. For female children data points shown as triangles and fitted values linked by a dashed line.
29.4 偏回歸係數的變化
在增加不同的預測變量進入線性回歸模型中時，原先在方程中的預測變量的偏回歸係數發生了怎樣的變化？
我們先從最簡單的開始入手。先只考慮一個簡單先行回歸模型的情況。當我們新加入一個預測變量，模型發生了什麼變化？
\[ \begin{aligned} & \text{Model 1: } y_i = \alpha^*+\beta_1^*x_{1i}+\varepsilon^*_i \\ & \text{Model 2: } y_i = \alpha + \beta_1x_{1i} + \beta_2 x_{2i}+\varepsilon_i \end{aligned} \] \(\beta_1, \beta_1^*\) 表示的其實是完全不同的含義。\(\beta_1^*\) 被稱為粗回歸係數 (crude coefficient)，或者叫做調整前回歸係數，\(\beta_1\) 被稱為調整後回歸係數 (adjusted coefficient)。二者之間的差異，其實是可以通過對這兩個變量進行簡單線性回歸來度量的：
\[ \text{Model 3: } x_{2i} = \gamma+\delta_1x_{1i}+\omega_i \] 將 Model 2 中的 \(x_{2i}\) 用 Model 3 來替換掉： \[ \begin{aligned} \text{Model 2: }y_i &= \alpha + \beta_1 x_{1i} + \beta_2(\gamma + \delta_1x_{1i}+\omega_i) +\varepsilon_i \\ &= \alpha + \beta_2\gamma+(\beta_1+\beta_2\delta_1)x_{1i}+\beta_2\omega_i + \varepsilon_i \end{aligned} \] 比較 Model 1 和變形過後的 Model 2 中 \(x_{1i}\) 的係數就不難發現：
\[ \beta_1^* = \beta_1 + \beta_2\delta_1 \] 由此可見，調整前後 \(x_{1i}\) 的回歸係數的變化 \(\beta_1^*, \beta_1\) 之間的差異，取決於兩個部分的大小：
- \(\beta_2\) 的大小和它的符號；
- \(X_1, X_2\) 這兩個預測變量之間有多大關聯，用 Model 3 的 \(\delta_1\) 來度量。
所以，當調整後的 \(\beta_1 > 0\) 時，要分三種情況來討論
29.4.1 情況1： \(\beta_1 > \beta_1^*\)
此時，\(\beta_2\delta_1<0\) 所以，二者之間一正一負。如下圖所示：
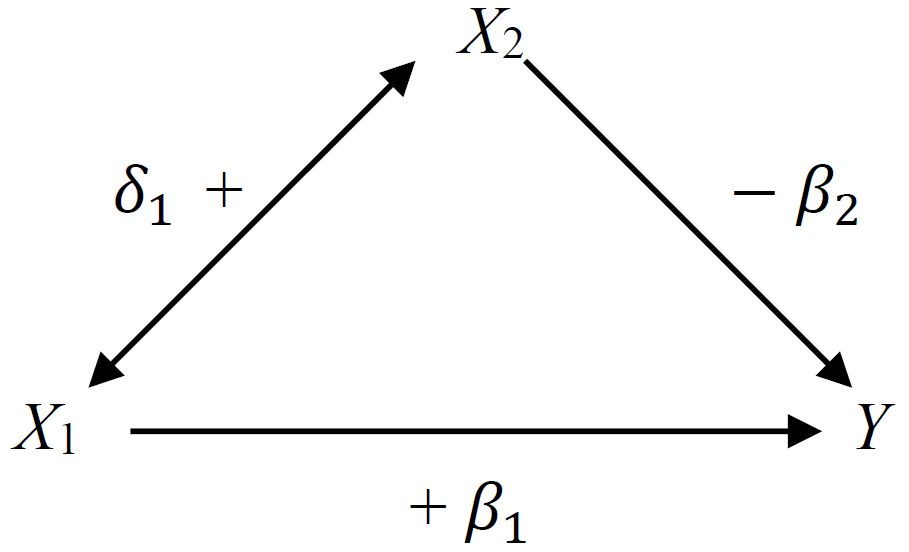按圖所示，當 \(X_2\) 保持不變，\(X_1\) 與因變量 \(Y\) 正相關 (\(\beta_1>0\))。但是，兩個預測變量之間 \(X_1, X_2\) 也呈正相關關係 \(\delta_1 >0\)。而同時，\(X_2\) 的升高會導致因變量 \(Y\) 的下降 ($_2 <0 $)。這種情況就意味著，如果，我們不調整 \(X_2\) (使之保持不變)，那麼 \(X_1\) 每升高一個單位，\(Y\) 的變化會低於調整 \(X_2\) 時，\(X_1\) 的變化所引起的 \(Y\) 的變化。如果這時候 \(\beta_2,\delta_1\) 較大，那麼對於 \(X_1\) 來說，調整 \(X_2\) 前後，回歸係數的變化較大，如果大到一定程度，甚至調整前後的回歸係數的方向 (正負) 都會發生變化。
29.4.2 情況2：\(\beta_1<\beta_1^*\)
本情況下，\(\beta_2\delta_1>0\) 是正的。所以二者要麼同時爲正，要麼同時爲負。如下圖所示：
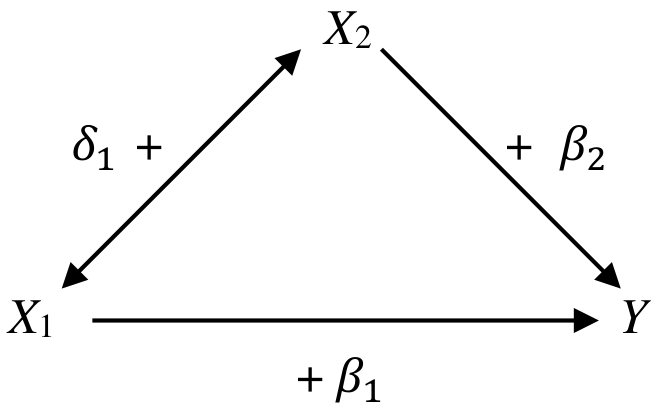
當 \(X_2\) 保持不變時， \(X_1\) 同 \(Y\) 呈正關係。但是，\(X_1\) 的升高也會引起 \(X_2\) 的升高，同時通過 \(X_2\) 和 \(Y\) 之間的正關係升高 \(Y\)。所以假設在模型裏我們不對 \(X_2\) 進行控制 (controld or adjust)，那麼 \(X_1\) 和 \(Y\) 之間的關係就被誇大了。
所以，當 \(X_1\rightarrow X_2\rightarrow Y\) 的這條通路大大超過 \(X_1\rightarrow Y\) 的話，調整後的迴歸係數 \(\beta_1\) 就會變得很小。
29.4.3 情況3： \(\beta_1 = \beta_1^*\)
這種情況只有當 \(\beta_2\delta_1=0\) 時才會出現。所以，二者至少有一個是 \(0\)。 如下圖所示：
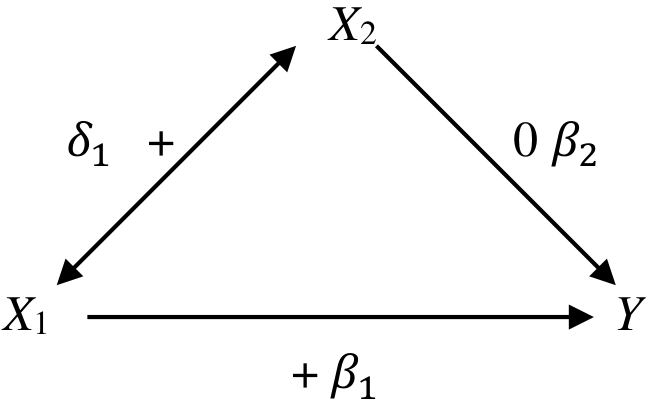
\(X_1\) 與 \(Y\) 呈正關係，\(X_1\) 與 \(X_2\) 呈正關係。但是 \(X_2\) 與 \(Y\) 無關聯。所以此時無論模型是否調整了 \(X_2\) 都不會影響 \(X_1\) 和 \(Y\) 之間關係的計算。
29.5 混雜 confounding
流行病學家最喜歡的詞彙恐怕要屬混雜 (confounding) 了 (interaction, 交互作用也要算一個 (Section 32，(笑))。他們常用混雜來解釋爲什麼調整其他因子前後迴歸係數發生了變化。當有其他因子 (測量了或者甚至是未知的) 對我們關心的預測變量和因變量之間的關係產生了影響 (加強或是減弱) 時，就叫做發生了混雜。
對於一個預測變量是否夠格被叫做混雜因子，它必須滿足下面的條件：
- 與關心的預測變量相關 (i.e. \(\delta_1 \neq 0\))；
- 與因變量相關 (當關心的預測變量不變時，\(\beta_2\neq0\) )；
- 不在預測變量和因變量的因果關係 (如果有的話) 中作媒介。Not be on the causal pathway between the predictor of interest and the dependent variable.
有時，判斷一個因子是否對我們關心的預測變量和因變量之間的關係構成了混雜並不容易，也不直觀。所以，有太多太多的情況下，我們無法準確地 100% 地確定我們關心的關係是否被別的因子混雜。所以，莫要用 “混雜” 一詞簡單糊弄人。
29.5.1 作為媒介 mediation effect
多數情況下，我們也無法從數據判斷一個變量是否在我們關心的預測變量和因變量之間關係的通路上。此時要做的是離開你的電腦，去學習他們之間的生物學知識，看是否真的有關係。
但是有些例子就很簡單啦。比如說，服用降血壓藥物可以預防發生中風。那麼此時血壓的降低，就處在了這二者因果關係的通路上。因爲藥物通過降低了血壓，從而預防了中風的發生。這一關係中，我們不能說血壓是混雜因子，它是一個媒介 (mediator)。但是多數的橫斷面研究 (cross-sectional study) 中我們無法是很難下結論的。
29.5.2 兩個預測變量之間的關係
如果另一個變量不是媒介，且它和我們關心的預測變量，因變量之間如果都有相關關係，那它的確有可能成為混雜因子。但是僅僅通過統計學模型來考察混雜是絕對不夠的。例如樣本量較小的數據中，我們可能無法檢驗出一個變量對模型的混雜影響是不是有統計學意義的，但是這不能提供證據否認它不是混雜因子。同樣的，更多的混雜因子是我們沒有測量沒有觀察到收集到的未知因素。所以，任何數據都無法提供完全去除混雜因子影響的模型。
29.5.3 RCT臨床實驗是個特例
因為隨機對照臨床實驗，在設計階段就已經把治療組對照組之間的差異最小化了，理想的隨機對照實驗，其治療組和對照組之間理論上除了治療藥物的差別之外完全相同。當然這是理想狀況，且所有的臨床實驗都必須向這個方向努力設計和實施。偶然出現的治療組和對照組在某些特徵上的不平衡，不能被認為是混雜因子。只能說這樣的臨床實驗是不理想的，提供的證據水平也就較弱。