第 20 章 探索數據和簡單描述
Happy families are all alike, every unhappy family is unhappy in its own way.
—- Leo Tolstoy
Tidy datasets are all alike, but every messy dataset is messy in its own way.
—- Hadley Wickham
20.1 數據分析的流程
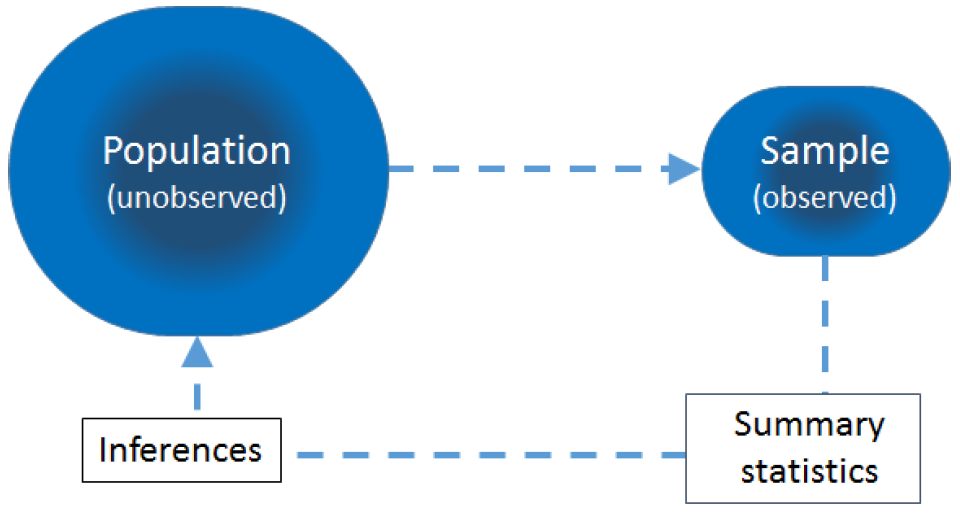
圖 20.1: Population, sample and statistical inference
統計推斷的目的,是通過從人群中取樣本,經過對樣本特徵的 (描述) 統計分析 (summary statistic),去推斷人群的相應特徵。
所以,無論什麼數據,到手以後我們一定要做的第一件事情,就是對其進行總結和描述,其過程又要盡可能地簡單明了。
在絕大多數的科學研究中數據分析都很重要,然而現實是,它多數情況下只出現在研究的第三部分:
- 研究設計
- 實施研究,收集數據
- 數據分析
- 結果報告
20.1.1 研究設計和實施
正確的統計推斷需要獲得具有代表性可以值得分析的數據,這必須建立在實驗研究設計良好,實施過程縝密的基礎上。設計糟糕,執行效率低下或者漏洞百出的實驗,給出的實驗數據必然是不可靠的,分析它也沒有意義。但是,不是說設計和實施階段就不需要統計學家的參與了。相反地,統計學家必須在研究實施過程中盡可能早的階段 (實驗設計) 參與進來。因為理解了實驗的目的,統計學家才能真正決定這個實驗要收集怎樣的數據,多大的樣本量,實施怎樣的分析方法。這些決定,注定了一項實驗研究的成敗。
20.1.2 數據分析
然而現實很殘酷,多數情況下實驗設計階段好像沒有統計學家什麼事,等到了數據分析階段,某些人才拍腦袋想讓統計學家來拯救他們收集的垃圾數據。通常都太晚了 (too late!)。
假設理想狀態下,我們收集到了想要分析的數據,可是接下來的工作流程的第一步,又常常被太多人忽略。許多 “科學家” 興奮地把數據輸入軟件,立刻就開始著手建立數學模型,進行假設檢驗,卻對數據的特徵一無所知!要知道,建立怎樣的模型,做怎樣的推斷,選用什麼樣的分析手段,都必須建立在你對數據內容完全熟悉的前提下,才能正確地實施。
數據分析第一步:數據清理, data cleaning。
這一步的目的很簡單,把收集來的粗糙的,充滿了缺失值和數據類型註解等等無法直接分析的數據,整理打扮成可以建模的數據庫。這個過程中,你可能需要對某些變量進行分類,可能兩三個實驗的結果需要被合併協調,可能在這個過程中你會發現數據錄入出現了一些錯誤導致數據庫裡有一些異常值,甚至是重複錄入。所以,各位小伙伴當你拿到一個數據準備分析的第一步,你必須要先了解你的數據。常用的手段包括簡單作圖,對感興趣的變量做概括分析 (summary your data!)。除此之外,由於沒有人能保證實驗中能收集到所有對象的完整數據,我們還需要分析缺失數據的特徵,思考他們為什麼會變成缺失數據。
20.2 數據類型
不同類型的數據,使用的初步描述手段各不相同。因此區分定性數據和定量數據,連續型數據,離散型數據,分類型數據顯得十分必要。
- 連續型變量,continuous data
連續型數據多來自實驗中對某些特徵的測量,例如身高,體重等,它們本質上是一組連續型的數據。現實生活中接觸到的許多數據也都是連續型的,例如:時間,距離,骨骼密度,藥物濃度等等。所謂連續型變量是由於它理論上可以取某段數值區間內的任何值。當然我們還會被測量尺度的精確度所局限。 - 離散型變量,discrete data
許多數據,是通過計數來收集的。離散型變量的本質上也是屬於數值型數據 (numeric),特徵是這種數值型數據總是取正整數或者零。例如,醫院中發生感染的次數,一個家庭中兄弟姐妹的人數,術後患者存活天數等等。 - 分類型變量,categorical data
分類型變量的數據,其每一個觀察值都歸類於一種類別 (或者屬性)。分類型數據和離散型數據最大的不同是,它從本質上說就不屬於數值型數據。例如,頭髮的顏色 (紅色,黃色,黑色),職業類型 (裝修工人,教師,總統)。儘管分類型數據本質上不是數值,分析過程中我們常常會給它們賦予一定的數值以便於計算。- 二分類型數據,binary:十分常見,例如,生存/死亡,有效/無效,成功/失敗;
- 名義型數據,nominal:數據本身沒有高低順序之分,例如,種族,血型等;
- 排序型數據,ordinal:每個分類是包函了順序含義的數據,例如,回答某些問卷問題時用的 “十分同意,同意,不同意,十分不同意”,某些癌症使用的分級診斷 “一級,二級,三級,終級”,對一些結果的評價時使用的 “優,良,中,差”。
其實,對於連續型變量我們還常常會將它們轉化成分類型變量,使用一些特定的或者事先定義好的閾值 (cutoff values) 把連續型數據分組,分級,分層等等。最常見的例子就是體重指數 (BMI),它本身是一個連續型的變量,但是又可以根據定義好的閾值把它分類成低體重 (\(< 18.5 \; kg/m^2\)),正常體重 (\(18.5 - 24.9 \; kg/m^2\)),超重 (\(25-29.9 \; kg/m^2\)),肥胖 (\(\geqslant 30 \; kg/m^2\))。另一個例子是血紅蛋白 (haemoglobin, \(g/l\)),它本身是一個連續型變量,但是我們利用它的閾值 (女性,\(<120 \; g/l\);男性,\(< 130 \; g/l\)),作為診斷是否患有貧血症的依據。
把連續型變量進行分類處理的代價是信息的丟失。如果一個人的體重指數是 \(25\),他/她的數據被和體重指數為 \(29.9\) 的人當作相同數值來對待是否合理是我們需要考慮的問題。而且許多情況下閾值的定義並不能達成共識,即使達成共識的閾值又是十分人為且恣意的,它可能導致一些相關關係被“強化”,或者反過來被“弱化”。所以,如果要對連續型數值進行分組,現在的要求是,在實驗設計階段就必須明確分組的閾值之定義,而不能在看到數據以後進行人為地劃分。更加不推薦的是直接使用四分位或者五分位來對數據分組。
20.3 如何總結並展示數據
光觀察原始數據很難真正明白數據的分佈特徵和形式,所以使用表格,或者用散點圖,柱狀圖等形式來描述數據就成為了常用的手段。前一節所描述的數據類型,決定了一組數據該如何被描述。
20.3.1 離散型分類型數據的描述 - 頻數分佈表 frequency table
下面的表格就是使用頻數分佈表來描述 cars 這個數據包中不同車速 (mph) 的分佈。汽車車速本身應該是一個連續型變量,但是這是1920年的數據當時的記錄只精確到整數,因此人為地造成了一組離散型變量的情況。下面的第二個表格使用的是繪圖瑞士軍刀包 ggplot2 裡自帶的鑽石數據。其中 cut 是對於鑽石切割水平的評價,所以是一個帶有排序性質的分組型變量。
data("cars")
epiDisplay::tab1(cars$speed, graph = FALSE)## cars$speed :
## Frequency Percent Cum. percent
## 4 2 4 4
## 7 2 4 8
## 8 1 2 10
## 9 1 2 12
## 10 3 6 18
## 11 2 4 22
## 12 4 8 30
## 13 4 8 38
## 14 4 8 46
## 15 3 6 52
## 16 2 4 56
## 17 3 6 62
## 18 4 8 70
## 19 3 6 76
## 20 5 10 86
## 22 1 2 88
## 23 1 2 90
## 24 4 8 98
## 25 1 2 100
## Total 50 100 100data("diamonds")
epiDisplay::tab1(diamonds$cut, graph = FALSE)## diamonds$cut :
## Frequency Percent Cum. percent
## Fair 1610 3.0 3.0
## Good 4906 9.1 12.1
## Very Good 12082 22.4 34.5
## Premium 13791 25.6 60.0
## Ideal 21551 40.0 100.0
## Total 53940 100.0 100.0離散型變量和分類型變量的描述還可以使用柱狀圖的形式來展示如下:
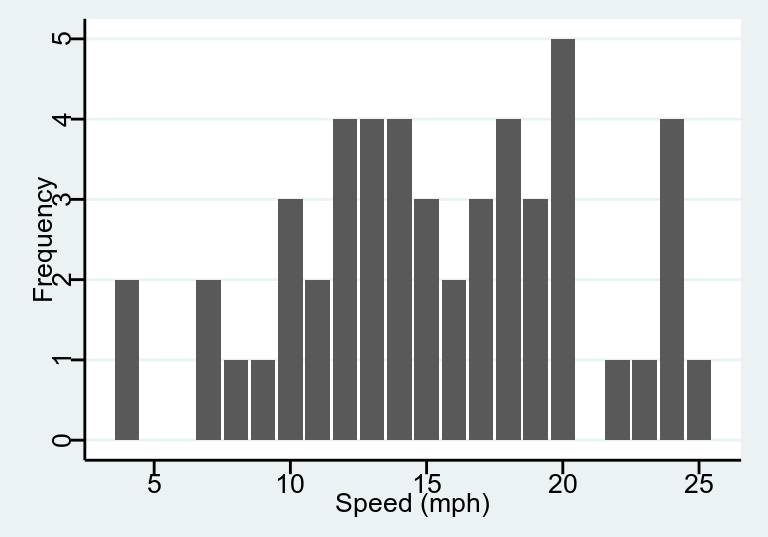
圖 20.2: Bar chart displaying the speed of cars
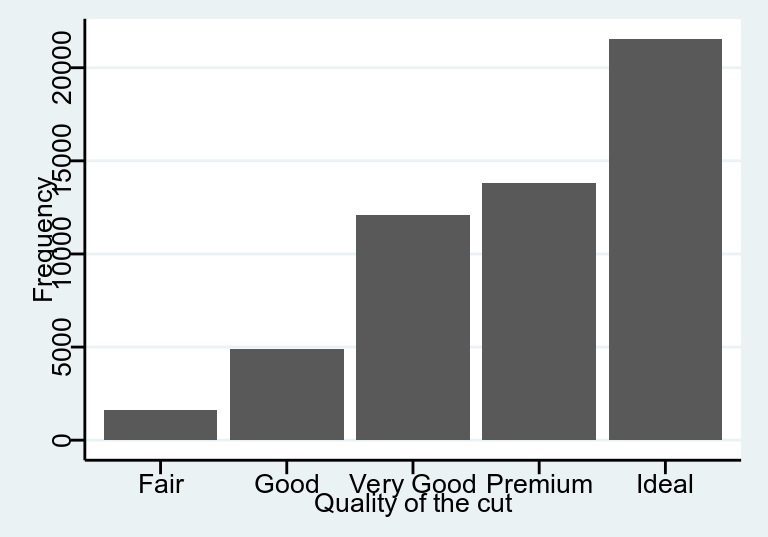
圖 20.3: Bar chart displaying distribution of evaluation of diamonds cut
上面這兩圖的 y 軸都用的是頻率,當然還可以使用百分比。不同組間分類型變量的分佈比較的話更常使用百分比作為 y 軸。如下面的表格及百分比條形圖所示。
diamonds$clarity2g <- "Good"
diamonds$clarity2g[(diamonds$clarity=="I1")|
(diamonds$clarity=="SI2")|
(diamonds$clarity=="SI1")|
(diamonds$clarity=="VS2")] <- "Poor"
tab <- stat.table(index=list(Cut=cut,Clarity=clarity2g),
contents=list(count(),percent(cut)), data=diamonds, margins=T)
print(tab, digits = 2)## ---------------------------------------
## ----------Clarity-----------
## Cut Good Poor Total
## ---------------------------------------
## Fair 265.00 1345.00 1610.00
## 1.42 3.81 2.98
##
## Good 1191.00 3715.00 4906.00
## 6.38 10.54 9.10
##
## Very Good 4067.00 8015.00 12082.00
## 21.77 22.73 22.40
##
## Premium 3705.00 10086.00 13791.00
## 19.83 28.61 25.57
##
## Ideal 9454.00 12097.00 21551.00
## 50.60 34.31 39.95
##
##
## Total 18682.00 35258.00 53940.00
## 100.00 100.00 100.00
## ---------------------------------------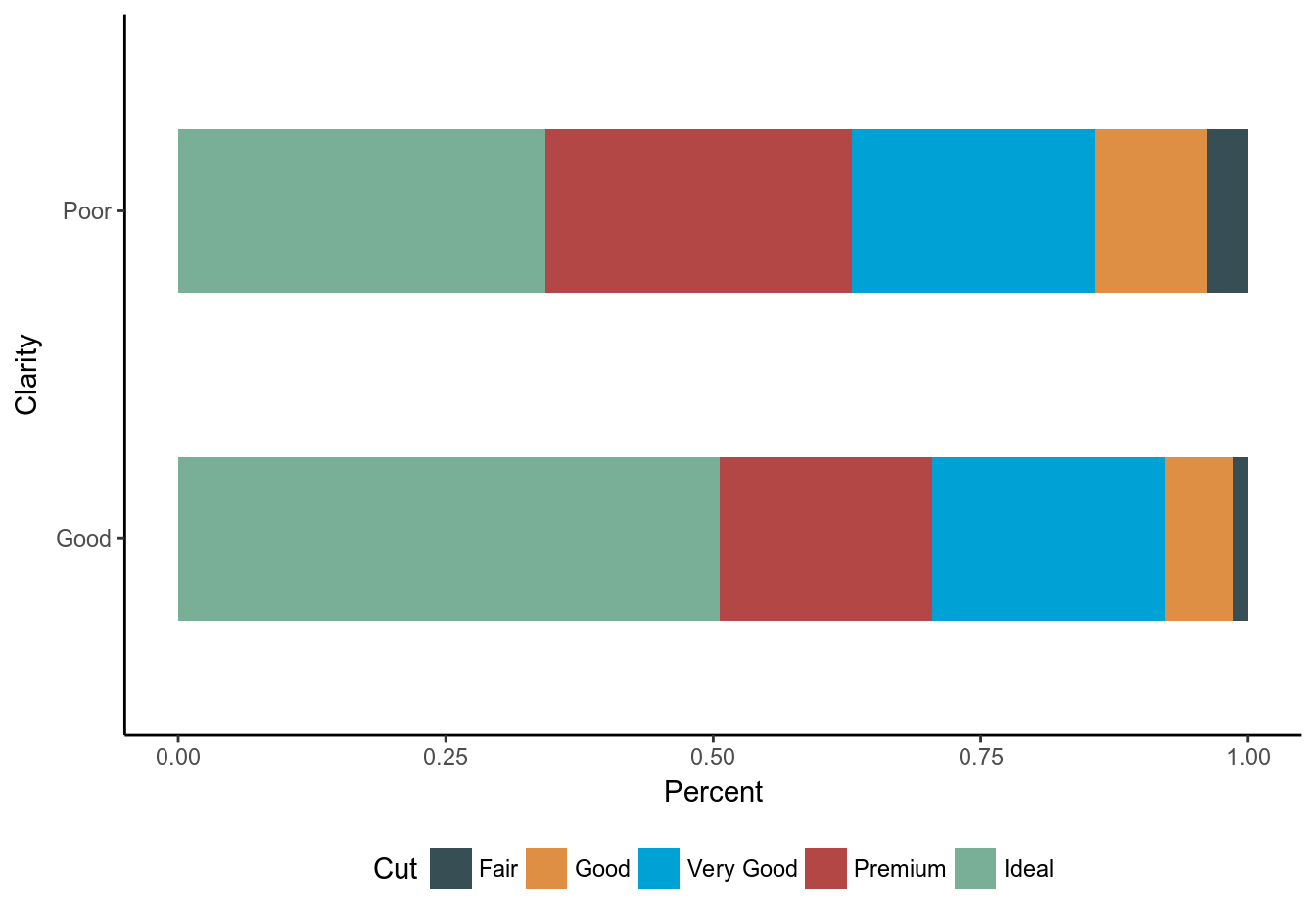
圖 20.4: Bar chart displaying distribution of evaluation of diamonds cut by clarity
20.3.2 連續型變量
連續型變量如果做頻數分佈表一般提供的信息量就較小。常用來描述連續型變量的手段是柱狀圖,histogram,和箱形圖,boxplot。柱狀圖應該不必過多解釋。箱形圖,展示的是連續型變量的中位數,四分位,範圍值,以及異常值。一個典型的箱形圖,中間的方形區域包括了該數據的四分位距,interquartile range (即中間 50% 的數據, IQR)。
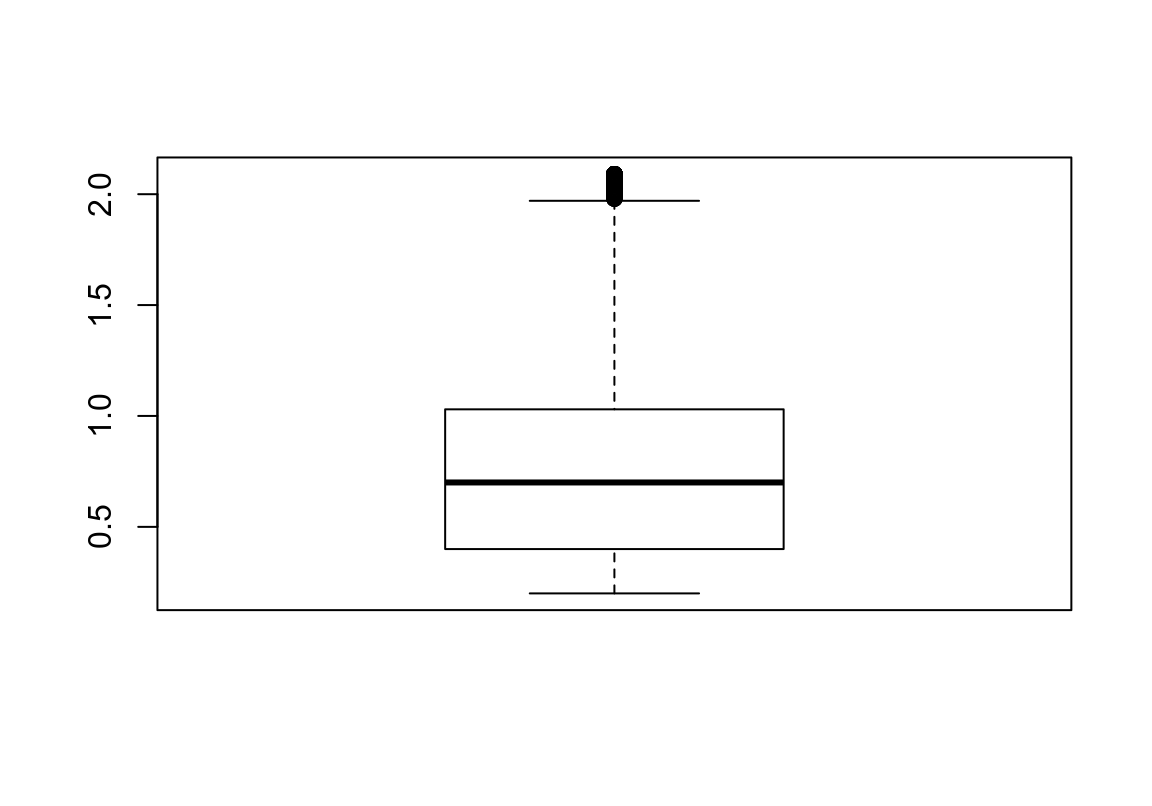
圖 20.5: Boxplot of the diamond carat data
R作出的箱形圖如 20.5 所示,箱子以上的橫線,意為最高值為75%分位值加上1.5倍的IQR;箱子以下橫線,意為最低值為25%分位值減去1.5倍的IQR。其他的觀察值如果不在這個上下限範圍之內的,會用黑點標記出來。這些值被認為是異常值 (outliers)。
20.4 數據總結方案:位置,分散,偏度,和峰度
20.4.1 位置
描述一組連續型變量的位置,location,此處的位置指的是數據分佈的中心位置,常用的數值是眾數 (mode),中位數 (median),均值 (mean)。
- 眾數 mode,的定義是,一組數據中出現最多次的數值大小;
- 中位數 median,的定義是,一組數據中從小到大/或者從大到小排序後50%位置的數值大小,如果觀察值有偶數個,中位數的定義是中間兩個數值的平均值大小;
- 算術平均值 arithmetic mean 的大小受異常值影響較大,通常簡略為均值,其定義可以用下面的表達式:\[\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i\]
- 幾何平均值 geometrix mean,常用在正偏態分佈數據 (positively skewed data),其定義為: \[\sqrt[n]{\prod_{i=1}^n X_i}=exp[\frac{1}{n}\sum_{i=1}^n log_e(X_i)]\]
- 調和平均值 harmonic mean,是所有觀察值的倒數和的倒數,定義為:\[\frac{1}{\frac{1}{n}\sum_{i=1}^n\frac{1}{X_i}}\]
20.4.2 分散
數據的分散程度,dispersion,也就是數據的波動大小 variation。同樣均值的數據,他們的分散可能差別很大:
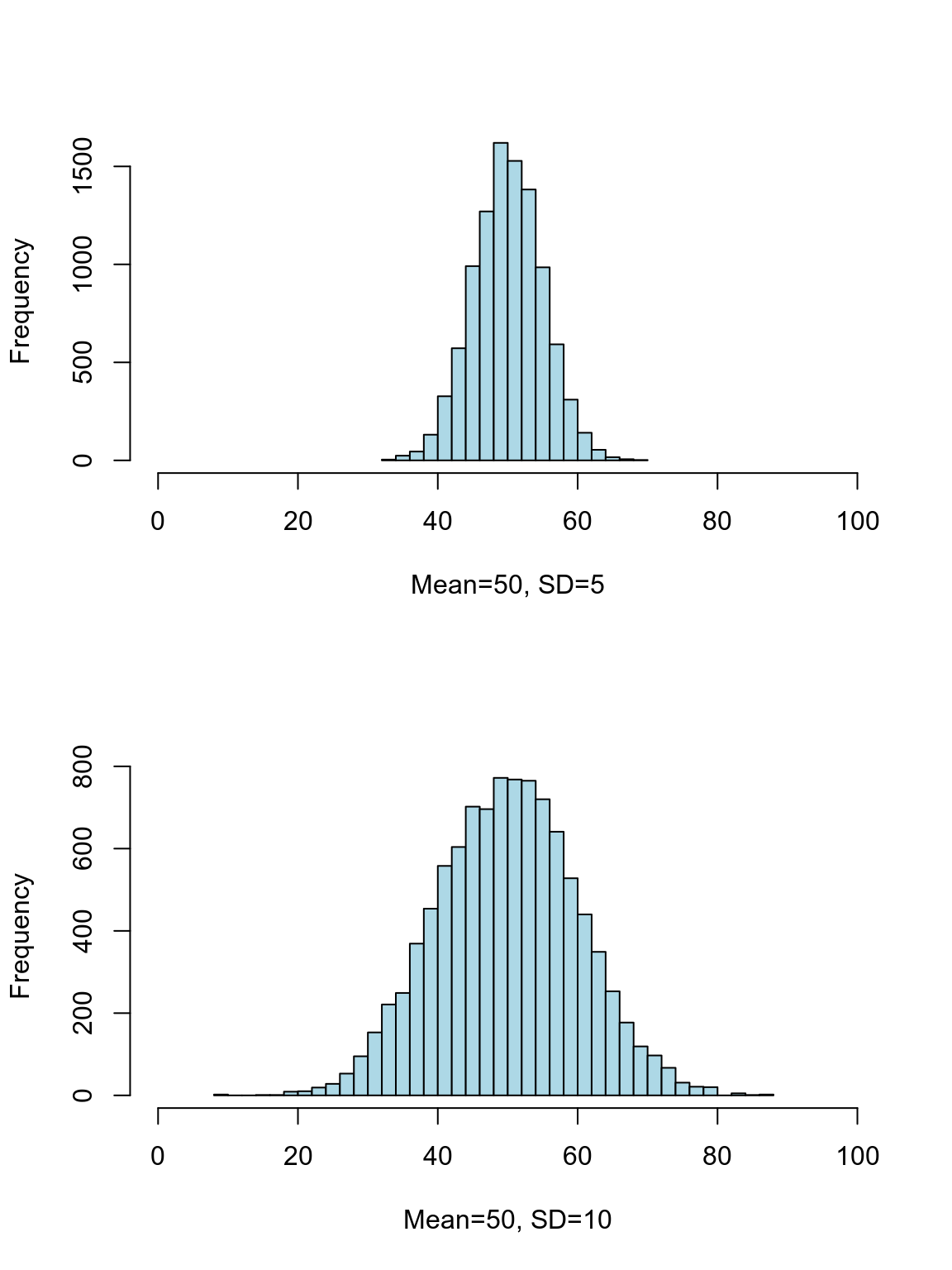
圖 20.6: Distributions with similar central location but different dispersion
分散程度的描述方法花樣不少,我們這裡先考慮範圍 (range),四分位差 (interquartile range),方差 (variance),標準差 (standard deviation)。
20.4.2.1 範圍 range
定義:最大值和最小值的差。
缺點:受樣本量大小,以及異常值影響較大。
在表格,論文中需要同時報告最大值和最小值。
20.4.2.2 四分位差 interquartile range (IQR)
定義:四分位差是包含了數據中間 50% 數值的範圍。即,75%分位數-25%分位數的差值。
當觀察值數量為奇數個時,計算方法為:去掉中位數,計算大於中位數和小於兩個部分數值的中位數,求其差,例如:\(5,10,12,14,16,19,22\) 這組數字,25%分位數為10,75%分位數為19,所以IQR等於9。
當觀察值數量為偶數個時,計算方法為:計算較小的50%數值的中位數,和較大50%數值的中位數,求其差,例如:\(5,10,12,14,16,19,22,38\) 這組數字,上下兩半部分的中位數分別是 \(Q_L=\frac{10+12}{2}=11;\;Q_U=\frac{19+22}{2}=20.5\),所以,其IQR等於9.5.
在表格,論文中需要同時報告25%,75%分位數兩個數值,例:[11,20.5]。
20.4.2.3 方差和標準差 variance and standard deviation
先定義每一個觀察值和均值之間的差為 \(D_i = X_i - \bar{X}\)。
根據定義,\(\frac{1}{n}\sum_{i=1}^n D_i=0\)。
樣本方差 Variance 被定義為 \(\frac{1}{n-1}\sum_{i=1}^n D_i^2\)。
樣本方差的平方根,被定義為標準差 standard deviation,\(\text{SD}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n D_i^2}\)
更常見的表達式為:
\[ \begin{aligned} \text{Var} &= \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 \\ &= \frac{1}{n-1}[(\sum_{i=1}^nX_i^2)-n\bar{X}^2] \end{aligned} \]
此處分母為 \(n-1\) 而不是 \(n\) 的原因,需要參考推斷部分的解釋 (Section 10.3)。
- 方差標準差受異常值影響較大。例如,下面的數據:
\[ 5, 9, 12, 14, 14, 15, 16, 19, 22\;\;\; \text{Var}=25.5\\ 5, 9, 12, 14, 14, 15, 16, 19, 58\;\; \text{Var}=241.5 \]
20.4.3 偏度 skewness
使用柱狀圖來描述數據時,如果柱狀圖左右基本對稱 (中位數和均值基本一致),偏度為零,正態分佈數據都是左右對稱的。如果柱狀圖右側的尾巴較長,偏度為正;如果左側的尾巴較長,偏度為負。偏度計算公式為:
\[ \frac{\frac{1}{n}\sum_{i=1}^n D_i^3}{(\frac{1}{n}\sum_{i=1}^n D_i^2)^{\frac{3}{2}}} \]
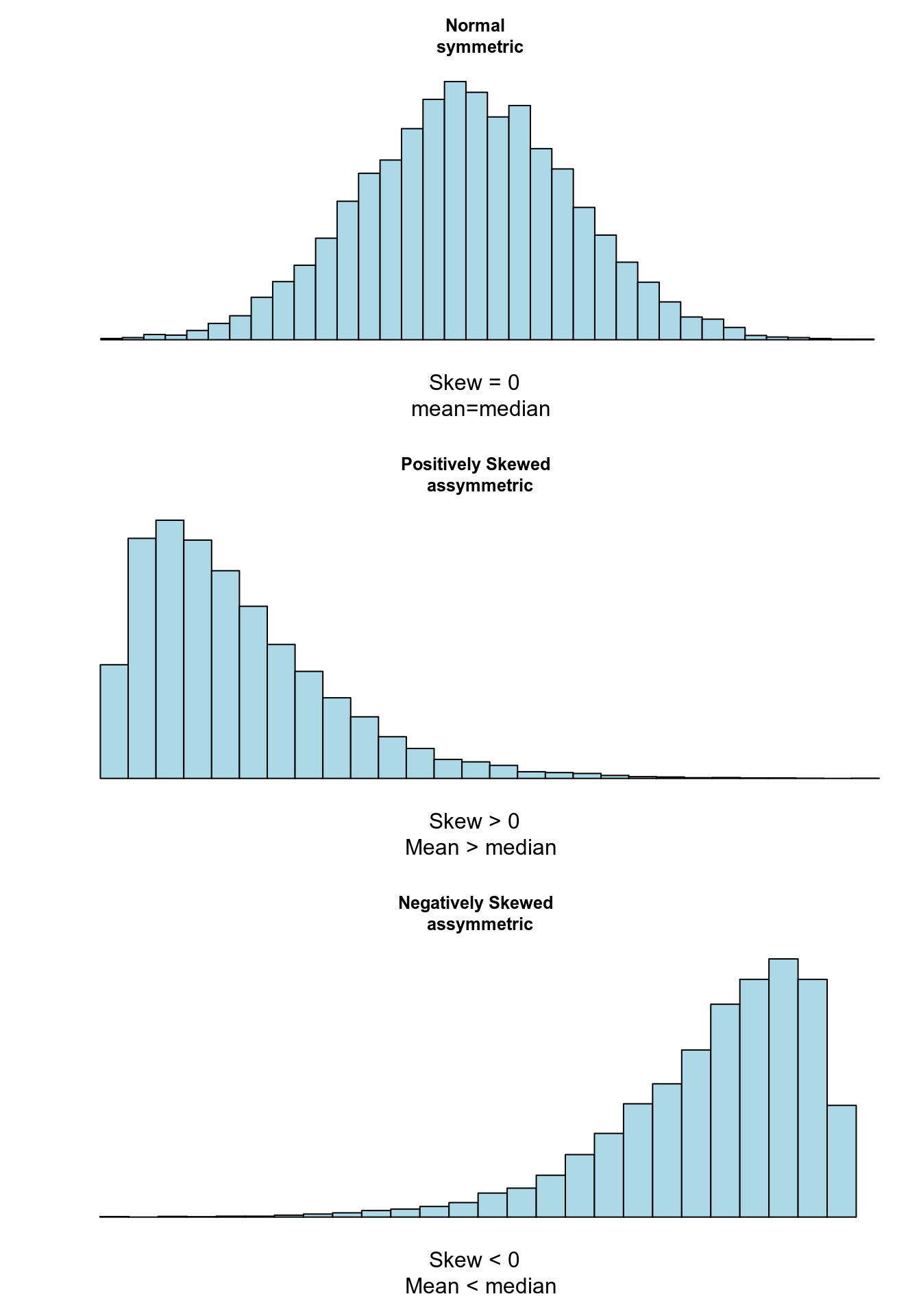
圖 20.7: Relationship between skew and measures of location
20.4.4 峯度 kurtosis
峯度是描述數據分佈的最後一個指標。峯度衡量的是一組數據分佈的尾部的厚度。一個正態分佈數據,大約 5% 的數據分佈在左右兩邊的尾部 (2.5% 低於 \(\mu-2\sigma\),2.5% 高於 \(\mu +2\sigma\))。峯度測量的是一組數據尾部數據的分佈和正態分佈兩側尾部數據之間的差距。
峯度的計算公式爲: \[ \frac{\frac{1}{n}\sum_{i=1}^nD_i^4}{(\frac{1}{n}\sum_{i=1}^nD_i^2)^2} \] 一個正態分佈數據,峯度值爲 3。當左右兩段的數值佔比低於正態分佈預期時,峯度值小於 3。反之,峯度大於 3。尾部較厚 (峯度較大) 的典型分佈之一是 \(t\) 分佈 (圖 20.8)
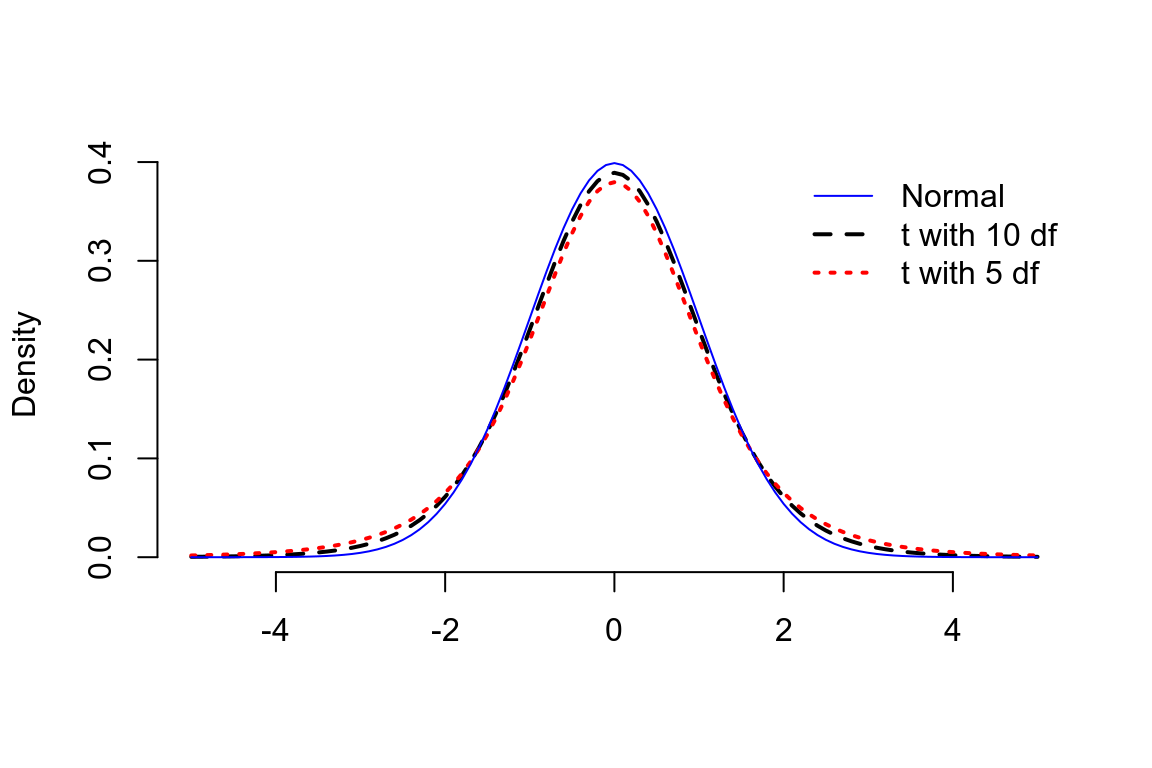
圖 20.8: t distributions with 5 and 10 degrees of freedom compared with a standard normal distribution