第 49 章混雜的調整，交互作用，和模型的可壓縮性

臨牀醫學，流行病學研究的許多問題，需要我們通過數據來評估某些結果變量 (outcome) 和某些預測變量 (predictors/exposures) 之間的關係 (甚至是因果關係)。這些問題的最佳解決方法應該說是隨機臨牀試驗 (ramdomized clinical trial, RCT)。但是有更多的時候 (由於違反醫學倫理，或者現狀所困，甚至是知識有限) 我們無法設計 RCT 來解決這些問題，就只能藉助於觀察性研究 (observational study)。觀察性研究最大的侷限性在於無法像 RCT 那樣從實驗設計階段把混雜因素排除或者降到最低，所以觀察數據在分析的時候，混雜 (confounding) 是必須要加以考慮的一大要因。在簡單線性迴歸章節 (Section 29.5)，詳細討論過混雜因素的定義及條件：

對於一個預測變量是否夠格被叫做混雜因子，它必須滿足下面的條件：

與關心的預測變量相關 (i.e. \(\delta_1 \neq 0\))；

與因變量相關 (當關心的預測變量不變時，\(\beta_2\neq0\) )；

不在預測變量和因變量的因果關係 (如果有的話) 中作媒介。Not be on the causal pathway between the predictor of interest and the dependent variable.

下面的統計數據來自一個比較手術和超聲碎石術對於腎結石治療結果的評價。已知大多數醫生都公認，腎結石的直徑小於 2 公分時治療成功的概率較高。

表 49.1: Lithotripsy
	< 2cm Diameter		>= 2cm Diameter
Group	Surgery	Lithotripsy	Surgery	Lithotripsy
Success	81.00	234	192.00	55
Failure	6.00	36	71.00	25
Total	87.00	270	263.00	80
Odds Ratios	2.08	NA	1.23	NA

表 49.1: Lithotripsy data
	\(<2\) cm Diameter		\(\geqslant2\) cm Diameter
Group	Surgery	Lithotripsy	Surgery	Lithotripsy
Success	81	234	192	55
Failure	6	36	71	25
Total	87	270	263	80
Odds Ratios	2.08		1.23

可以看到，在上面的分組表格中，左右兩邊的四格表分別統計了腎結石尺寸小於 2 cm 和大於 2 cm 時，手術摘除腎結石的成功/失敗次數，以及超聲碎石術的成功/失敗次數。這個表格告訴我們，無論腎結石的尺寸是大於還是小於 2 cm，手術的成功的比值比都大於超聲碎石術。但是如果我們沒有把數據按照腎結石尺寸區分時，數據就被壓縮 (collapsed) 成了下面表格總結的樣子：

表 49.2: Lithotripsy collapsed
Outcome	Surgery	Lithotripsy
Success	273 (78%)	289 (83%)
Failure	77	61
Total	350	350
Odds ratio	0.75

表 49.2: Lithotripsy data collapsed
Outcome	Surgery	Lithotripsy
Success	273 (78%)	289 (83%)
Failure	77	61
Total	350	350
Odds ratio	0.75

當腎結石尺寸被忽略時，數據卻顯示超聲碎石術的成功比值比要高於手術，和之前的結果是矛盾的，你會信哪個？

不要慌，數據不會撒謊，撒謊的永遠是人類。我們來把手術次數，超聲碎石術次數，以及腎結石尺寸之間的關係再列個表格：

表 49.3: Association between treatment and the size of the stone.
Size of the Stone	Surgery	Lithotripsy
\(< 2\) cm	87 (33%)	270 (77%)
\(\geqslant 2\) cm	263	80
Total	350	350

可見醫生也都不是傻子，明明腎結石尺寸很大還要用超聲碎石術的人很少，有 77% 的腎結石尺寸小的患者選擇了超聲碎石術。然後我們再列一個表格來看看腎結石的尺寸大小和超聲碎石術成功與否有沒有關係：

表 49.4: Among the **lithotripsy patients** higher percentage of success was observed when stones were small.
Outcome	\(< 2\) cm	\(\geqslant 2\) cm
Success	234 (87%)	55 (69%)
Failure	36	25
Total	370	80

可見結石尺寸較大時，超聲碎石術的成功率 (69%)，明顯低於尺寸小的時候的成功率 (87%)。在選擇做外科手術的患者中，大多數人的結石尺寸大於 2 cm，成功率仍然達到了 73%。

表 49.5: Among the **surgery patients** higher percentage of success in both stones compared with lithotripsy
Outcome	\(< 2\) cm	\(\geqslant 2\) cm
Success	81 (93%)	192 (73%)
Failure	6	71
Total	87	263

看到這裏，你是否也發現了，腎結石尺寸大小，同時和手術類型的選擇有關 (尺寸小的傾向於選擇超聲碎石術)，尺寸大小，同樣也和手術結果的成功與否，高度相關 (結石小的人成功率高)。所以，分析手術類型和結石手術的成功率的關係的時候，患者體內結石尺寸的大小，對這個關係是產生了混雜效應的。他們三者之間的關係，可以用下面的圖 49.1 來理解：

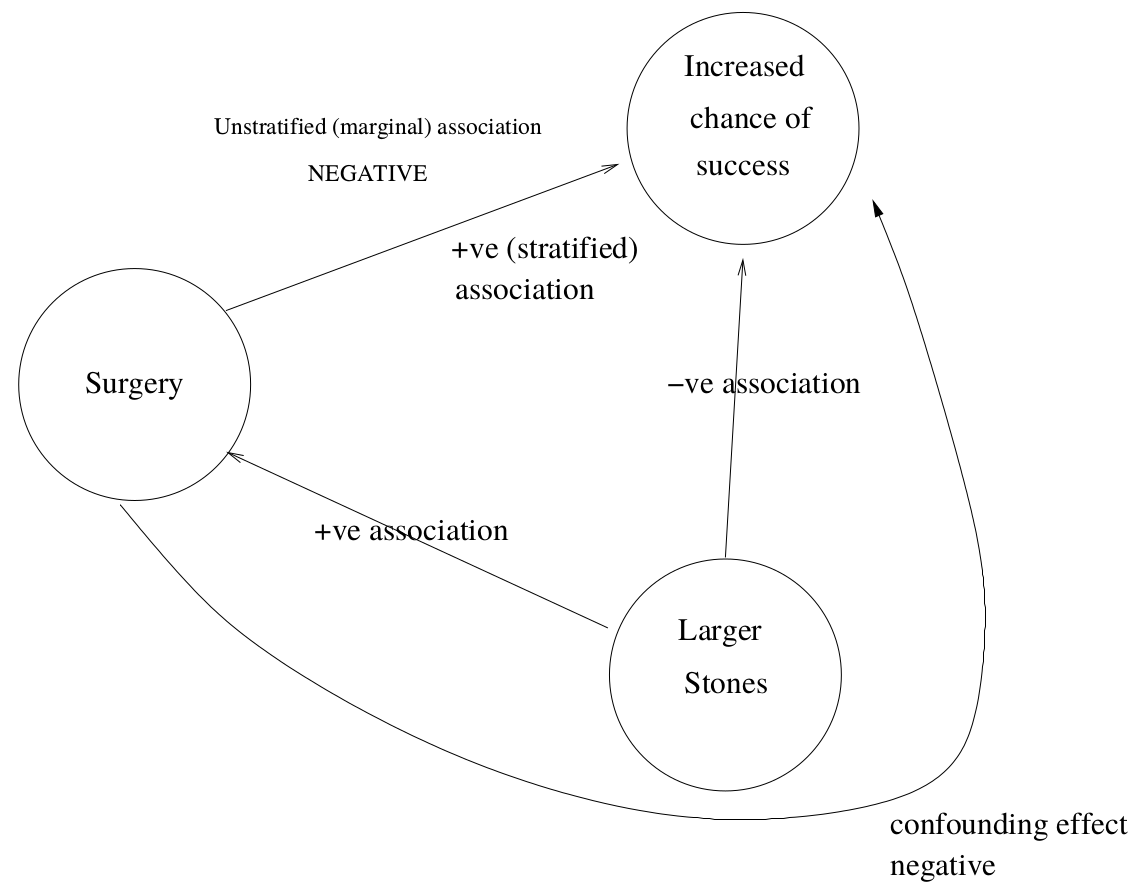
圖 49.1: Confounding in kidney stones example

當數據被壓縮 (忽略了腎結石尺寸時)，比較兩種手術類型的成功率的時候，接受外科手術患者的尺寸大多數都較大的事實被“人爲的掩蓋住了”，但是當數據按照結石大小分層以後，你會看見外科手術不論是對付大的結石，還是小的結石，成功率都高於超聲碎石術。這個例子是混雜效應直接逆轉真實相關關係的極佳的實例。同時也提示我們，總體的比值比 (overall odds ratio) 不能通過簡單地把分層表格直接壓縮 (collapsed table) 獲得的數字來計算。

49.1 混雜因素的調整

在前面的腎結石手術的例子中，我們利用已有的背景知識 (小尺寸結石的成功率高)，和初步的統計分析 (變量之間兩兩列表分析其內在關係) 發現了混雜因素 (結石尺寸)，並且其結果也讓我們認定了要暴露因素和結果變量之間的關係，混雜因素必須被調整 (adjusted)。

如腎結石數據這樣簡單的情境下 (被認爲是混雜因素的變量和預測變量/暴露變量都只是一個二分類變量)，我們可以把變量兩兩捉對列表分析其相互關係，確定了混雜效應以後把暴露變量和結果變量按照混雜因素的有無列表之後，就可以求得混雜因素被調整後的分層的比值比。這些分層比值比，在暴露變量與結果變量的關係保持混雜因素的層之間保持不變的前提下，可以被“平均化”(簡單地說)以後求得總體/合併的比值比 (overall/pooled odds ratio)。這就是 Mantel-Haenszel 法或者 Woolf 法的合併比值比的思想出發點。我們來回顧一下 Woolf 法的全部計算過程：

現在假設我們關心的是某種疾病的患病與否 (是/否)，和某個暴露變量 (是/否) 之間的關係，但是同時想要調整另一個具有 \(k\) 個分層的混雜因素變量。

表 49.6: Woolf Method for estimating the stratified and pooled odds ratio
		Group
		\(X=0\)	\(X=1\)
\(D=0\)	\(X=0\)	\(n_{00}\)	\(n_{10}\)
	\(X=1\)	\(n_{01}\)	\(n_{10}\)

49.1.1 Woolf 法估算合併比值比

對想要調整的一個 \(k\) 組的混雜因素，把數據按照它的分組分層整理以後，可以得到上面的 \(k\) 個四格表 (每個分層四格表都是暴露變量和結果變量結合的四個觀察值 \(a_i, b_i, c_i, d_i, i=1,\cdots, k\))。每個分層四格表的觀測比值比爲 \(\hat\Psi_i = \frac{a_id_i}{c_ib_i}\)，且可以證明方差爲

\[ \text{Var}(\text{log}\hat\Psi_i) \approx \frac{1}{a_i} + \frac{1}{b_i} + \frac{1}{c_i} + \frac{1}{d_i} = \frac{1}{w_i} \]

合併比值比的對數 \(\text{log}\hat\Psi_w\) 的 Woolf 的計算方法就是

\[ \text{log}\hat\Psi_w = \frac{\sum w_i\text{log}\hat\Psi_i}{\sum w_i} \]

所以，每個分層的對數比值比乘以自己的方差的倒數 (權重 weights) 之後求和，再除以所有權重之和，獲得的是合併後的對數比值比，然後再逆運算回來就是 Woolf 法計算合併比值比的原理是。

這個合併比值比的對數的方差是

\[ \text{Var}(\text{log}\hat\Psi_w) = \frac{1}{\sum w_i} \]

有了加權後的合併比值比，和方差，就可以求加權後的合併比值比的信賴區間了。值得注意的是，分層之後每個分層四格表中的四個數字 (四個樣本量) 都不能太小。腎結石手術數據滿足這些條件，那麼不妨跟我一起手算一下結石尺寸調整後的手術與超聲碎石術成功與否的比值比：

\[ \begin{aligned} \hat\Psi_1 = 2.08 ;&\; \hat\Psi_2 = 1.23 \\ \text{Var}(\text{log}\hat\Psi_1) = \frac{1}{81} & + \frac{1}{234} + \frac{1}{6} + \frac{1}{36} = 0.2111 \\ \text{Var}(\text{log}\hat\Psi_2) = \frac{1}{192} & + \frac{1}{55} + \frac{1}{71} + \frac{1}{25} = 0.0775 \\ w_1 = \frac{1}{\text{Var}(\text{log}\hat\Psi_1)} = 4.74 ; \;& w_2 = \frac{1}{\text{Var}(\text{log}\hat\Psi_2)} = 12.91 \\ \text{log}\hat\Psi_w = & \frac{4.74\times\text{log(2.08)} + 12.91\times\text{log(1.23)}}{4.74 + 12.91} \\ = & 0.3481 \\ \Rightarrow \hat\Psi_w =& e^{0.3481} = 1.42\\ \text{Var}(\hat\Psi_w) =& \frac{1}{4.74+12.91} = 0.0567 \\ \Rightarrow 95\% \text{ CI} = & e^{0.3481 \pm 1.96\times\sqrt{0.0567}} \\ = & (0.89, 2.26) \end{aligned} \]

Woolf 的計算調整後的合併比值比的方法是在線性迴歸和廣義線性迴歸被發現之前誕生的，但是其想法之精妙，確實令人感嘆。可惜其最大的缺陷是無法用這樣的方法進行連續型變量的調整，也很難同時進行多個變量的調整，所以現在這一算法已經逐漸被淘汰。現在我們有了廣義線性迴歸模型這一更強大的工具，只要把變量加入廣義線性模型進行調整就可以計算曾經難以計算和擴展的調整後的合併比值比。從下面的代碼計算獲得的調整後比值比 \(1.43 (0.91, 2.34)\) 也可以看出，Woolf 方法的計算結果也是足夠令人滿意的。

size <- c("< 2cm", "< 2cm", ">= 2cm", ">= 2cm")
treatment <- c("Surgery","Lithotripsy","Surgery","Lithotripsy")
n <- c(87, 270, 263, 80)
Success <- c(81, 234, 192, 55)
Stone <- data.frame(size, treatment, n, Success)
ModelStone <- glm(cbind(Success, n - Success) ~ treatment + size, family = binomial(link = logit), data = Stone)
summary(ModelStone)

## 
## Call:
## glm(formula = cbind(Success, n - Success) ~ treatment + size, 
##     family = binomial(link = logit), data = Stone)
## 
## Deviance Residuals: 
##        1         2         3         4  
##  0.76357  -0.35881  -0.27563   0.46948  
## 
## Coefficients:
##                  Estimate Std. Error z value  Pr(>|z|)    
## (Intercept)       1.93655    0.17045 11.3614 < 2.2e-16 ***
## treatmentSurgery  0.35723    0.22908  1.5594    0.1189    
## size>= 2cm       -1.26057    0.23900 -5.2742 1.333e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 33.12395  on 3  degrees of freedom
## Residual deviance:  1.00816  on 1  degrees of freedom
## AIC: 26.3554
## 
## Number of Fisher Scoring iterations: 3

epiDisplay::logistic.display(ModelStone)

## 
## Logistic regression predicting cbind(Success, n - Success) 
##  
##                                   crude OR(95%CI)   adj. OR(95%CI)    P(Wald's test) P(LR-test)
## treatment: Surgery vs Lithotripsy 0.75 (0.51,1.09)  1.43 (0.91,2.24)  0.119          < 0.001   
##                                                                                                
## size: >= 2cm vs < 2cm             0.34 (0.23,0.51)  0.28 (0.18,0.45)  < 0.001        < 0.001   
##                                                                                                
## Log-likelihood = -10.1777
## No. of observations = 4
## AIC value = 26.3554

所以，此次分析的結論是，在 5% 的顯著性水平下，數據無法提供有效證據證明，當調整了結石尺寸之後，外科手術和超聲碎石術治療腎結石有差別。 We can conclude that there is no evidence at the 5% level for an effect of surgery, adjusted for stone size.

49.2 交互作用

我們決定調整一個混雜因素的時候，其實同時包含了 “在不同混雜因素的程度下，暴露變量和結果變量之間的關係不變/This implicitly assumes that the effect of the exposure is the same irrespective of the levels of the confounder.” 的假設。但是，一個混雜因素，它可能同時還扮演了改變暴露變量和結果變量之間關係的角色 (effect modifier/交互作用效應)。另外還有的情況下，某變量可能改變了暴露變量和結果變量之間的關係，卻不一定是一個混雜因素。此時我們說這個起到改變關係的變量和暴露變量之間發生了交互作用。

如果暴露變量在某個分組變量的不同層 (strata) 之間是不同質的 (hetergeneous, not constant)，我們建議要分析且報告不同層各自的比值比。惟一的例外是 RCT 臨牀試驗的時候，我們更加關心調整後合併比值比。因爲一項治療藥物對不同的 “個體” 有不同的療效是必然的，但是，RCT 的目的是要評價的其實是這個藥物或者新療法在整個人羣中的療效是怎樣的。

我們給腎結石數據加上治療方案和結石尺寸大小的交互作用項，結果如下：

ModelStone2 <- glm(cbind(Success, n - Success) ~ treatment*size, family = binomial(link = logit), data = Stone)
summary(ModelStone2)

## 
## Call:
## glm(formula = cbind(Success, n - Success) ~ treatment * size, 
##     family = binomial(link = logit), data = Stone)
## 
## Deviance Residuals: 
## [1]  0  0  0  0
## 
## Coefficients:
##                             Estimate Std. Error z value  Pr(>|z|)    
## (Intercept)                  1.87180    0.17903 10.4553 < 2.2e-16 ***
## treatmentSurgery             0.73089    0.45942  1.5909 0.1116310    
## size>= 2cm                  -1.08334    0.30039 -3.6065 0.0003104 ***
## treatmentSurgery:size>= 2cm -0.52453    0.53716 -0.9765 0.3288211    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3.31239e+01  on 3  degrees of freedom
## Residual deviance: 3.66374e-14  on 0  degrees of freedom
## AIC: 27.3472
## 
## Number of Fisher Scoring iterations: 3

epiDisplay::logistic.display(ModelStone2)

## 
## Logistic regression predicting cbind(Success, n - Success) 
##  
##                                   crude OR(95%CI)   adj. OR(95%CI)    P(Wald's test) P(LR-test)
## treatment: Surgery vs Lithotripsy 0.75 (0.51,1.09)  2.08 (0.84,5.11)  0.112          < 0.001   
##                                                                                                
## size: >= 2cm vs < 2cm             0.34 (0.23,0.51)  0.34 (0.19,0.61)  < 0.001        < 0.001   
##                                                                                                
## treatmentSurgery:size>= 2cm       -                 0.59 (0.21,1.7)   0.329          < 0.001   
##                                                                                                
## Log-likelihood = -9.6736
## No. of observations = 4
## AIC value = 27.3472

交互作用項的迴歸係數是否爲零的檢驗結果是 \(p = 0.329\)，提示數據無法提供足夠的證據證明結石尺寸對治療方案和手術成功與否之間的關係造成有意義的交互作用 (There is no evidence of an interaction between stone size and surgery)。所以此次的數據分析我們可以報告結石尺寸調整後的手術成功比值比就可以了。其中，交互作用項的迴歸係數 \(-0.5245 = \text{log}(0.59)\)，的含義是當結石尺寸 \(\geqslant 2 \text{cm}\) 時，外科手術和超聲碎石術成功比值比的對數的差。我們可以看到一開始我們計算的分層比值比的比值 \(\frac{1.23}{2.08} = 0.59\)。還注意到這已經是一個飽和模型 (模型偏差爲零)，模型的擬合值和我們的觀測值是完全相同的。

另外一點不得不提的是，交互作用項的迴歸係數的點估計 \(0.59\) 其實低於零假設時的 \(1\) 挺多的，它的 \(95\%\) 信賴區間也相當的寬 \((0.21,1.70)\)，所以其實這裏我們沒有獲得足夠的證據證明替代假設 (有交互作用)，很難說不是因爲樣本量不足導致的統計效能較低，所以我們沒有辦法從這個數據完全排除結石尺寸對治療方案的選擇和手術成功的關係之間的交互作用。(We really cannot be sure that there is no interaction in truth - the data are consistent with quite large interactions between size and surgery effect.) 因此，有些統計學家可能會傾向於報告分層的比值比，因爲我們沒有辦法從這個樣本數據排除有較強交互作用存在的可能性。

49.3 可壓縮性 collapsibility

模型可壓縮性的概念可以這樣來理解：

當我們把一個 我們認爲很重要的混雜因子 加到模型中去時，自然而然我們會期待其對結果變量的 效果估計 (effect estimate) (迴歸係數)在調整前後發生變化。如果是反過來，當我們把一個 我們認爲不重要的非混雜因子 加到模型中去時，我們也會自然而然地期待其對結果變量的 效果估計 (effect estimate) 在調整前後不會發生改變才是。不幸的是，我們這種理想中的想當然，僅僅在某些情境下成立，其中之一是簡單線性迴歸 (Section 26)。

49.3.1 線性迴歸的可壓縮性

證明

令 \(Y\) 標記結果變量，\(X\) 標記暴露變量，\(Z\) 則標記我們想要調整的莫個混雜因子：

\[ Y = \alpha + \beta_X X + \beta_Z Z + \varepsilon, \text{ where } \varepsilon \sim N(0, \sigma^2) \]

然後把等式兩邊同時取以暴露變量 \(X\) 爲條件的期待值：

\[ E(Y | X) = \alpha + \beta_X X + \beta_Z E(Z|X) \]

如果 \(Z\) 和 \(X\) 是相互獨立的 (即，不是 \(X, Y\) 之間關係的混淆因子)，那麼 \(E(Z|X) = E(Z) = \mu_Z\)，因爲 \(X\) 不能提供任何 \(Z\) 的有效信息。所以，等式就變爲：

\[ E(Y|X) = \alpha + \beta_Z \mu_Z + \beta_X X \]

所以，當我們用簡單線性迴歸來擬合 \(X,Y\) 之間的關係時，如果 \(Z,X\) 是相互獨立的，模型中增加了 \(Z\)，不會影響 \(X\) 的迴歸係數。線性迴歸的這個性質被定義爲模型的可壓縮性 (linear regression models are collapsible)。

49.3.2 邏輯鏈接方程時的不可壓縮性

使用對數鏈接方程 (\(\text{log link}\)) 的迴歸模型，同樣具有和線性迴歸類似的可壓縮性。但是，邏輯鏈接方程 (\(\text{logit link}\)) 的迴歸模型則不具有可壓縮性。下面舉例的分層表格和壓縮表格，證明了邏輯鏈接方程不具有可壓縮性：

表 49.7: **Non-collapsibility** of logit link in GLM **(stratified data)**
	Strata 1		Strata 2
Outcome	Exposure \(+\)	Exposure \(-\)	Exposure \(+\)	Exposure \(-\)
Success	90	50	50	10
Failure	10	50	50	90
Total	100	100	100	100
Odds Ratios	9		9

從表格的數據計算可知，要被調整的分組變量的兩層數據中，暴露變量和結果變量的關係相同，比值比都是 \(9\)，沒有交互作用，也沒有混雜效應 (每一層中暴露與非暴露均佔相同的 \(50\%\))。但是，你如果把這個觀測數據合併：

表 49.8: **Non-collapsibility** of logit link in GLM **(collapsed data)**
Outcome	Exposure \(+\)	Exposure \(-\)
Success	140	60
Failure	60	140
Total	200	200
Odds ratio	5.4

既然已知我們拿來分層的變量對暴露和結果的關係既沒有交互作用，也沒有混雜效應，那麼壓縮數據以後的合併比值比應該和分層比值比一樣才說的通，可惜我們獲得了截然不同的合併比值比 (非調整的)。所以在應用邏輯鏈接方程建立廣義線性迴歸模型的時候，一定不能忘記其不可壓縮性的特徵。所以，即使加入一個非混淆因子，暴露變量的邏輯迴歸的效應估計 (係數) 也會發生改變。調整了 \(Z\) 以後的比值比被叫做條件 (或直接使用分層) 比值比。如同表格中實例所示，條件比值比會比邊緣比值比 (非調整) 看起來要大一些。

邏輯迴歸的不可壓縮性給我們的啓示是，加入某個變量進入邏輯迴歸模型前後，其他預測變量的迴歸係數發生的變化可能僅僅是由於模型的不可壓縮性導致的變化，而非由於新加入的變量對原先變量與結果之間的關係起到了交互作用或者混雜效應。所以，擬合迴歸模型的時候，如果你要考慮對莫個因素進行調整，必須做的一件事是，先分析它和其他模型中已有的預測變量之間的關係，從而有助於分析，當把要調整的變量放進模型前後的迴歸係數變化是否是真的來自於交互作用或者混雜效應。

49.4 交互作用對尺度的依賴性

GLM 模型中的交互作用檢驗，對選用的尺度 (比值比 OR，還是危險度比 RR) 依賴性極高。用模型可壓縮性的數據例子也可以說明交互作用對尺度的依賴性。上文書說到，兩個分層中的比值比都是 9，該分層變量既沒有交互作用，也不是混淆因子 (當使用比值比的時候)。如果我們改用危險度比 (risk ratio, RR)，在分類變量的第一層 (Strata 1) 中，暴露的危險度比是 \(\frac{90/100}{50/100} = 1.8\)；分類變量的第二層 (Strata 2) 中，暴露的危險度比是 \(\frac{50/100}{10/100} = 5\)。所以使用危險度比作爲評價指標的時候，被調整的分類變量就突然搖身一變變成了有交互作用的因子。這裏，我們用數據，證明了交互作用的存在與否，對尺度的選用依賴性極高。這就導致我們在描述一個變量是否對我們關心的暴露和結果之間的關係有交互作用時，必須明確指出所使用的是比值比，還是危險度比進行的交互作用評價。

第 49 章 混雜的調整，交互作用，和模型的可壓縮性