第 23 章 相關 association

23.1 背景介紹

兩個變量如果相關 (associated)，那麼它們二者中的一個的分佈是依賴另一個的分佈的 the distribution of one is dependent on the value taken by the other and vice-versa。統計學中如何描述兩個變量之間的相關關係取決於兩個變量的性質 (連續型還是分類型，continuous or categorical variables)。本章討論不同情形下兩個變量相關關係及統計學上的假設檢驗方法。

兩個變量之間的關係除了可以用相關來描述，還可以利用迴歸的手段來分析。但是迴歸分析，和本章討論的相關性分析的本質區別在於，相關分析着重討論兩個變量的聯合分佈 (joint distribution)，而迴歸分析則是要探索一個變量在另一個變量的條件下的條件分佈 (conditional distribution)。因此，相關分析從某種意義上來說是對稱的 (X 與 Y 的相關性等同於 Y 與 X 的相關性)，迴歸分析則不然 (Y 對 X 的迴歸不等同與 X 對 Y 的迴歸)。

另外一個要點是，相關分析絕不討論因果關係。

23.2 兩個連續型變量的相關分析

23.2.1 相關係數的定義

在概率論 (Section 8.2) 中也已經介紹過相關係數 \(\rho\) 的定義：

\[ \begin{equation} \rho=\frac{E[(X-E(X))(Y-E(Y))]}{\sqrt{E(X-E(X))^2E(Y-E(Y))^2}} = \frac{\text{Cov}(X,Y)}{\sqrt{V(X)V(Y)}} \end{equation} \tag{23.1} \]

用 \(\textbf{x}=\{x_1, x_2, \cdots, x_n \}\) 和 \(\textbf{y}=\{ y_1, y_2, \cdots, y_n \}\) 表示對 \(n\) 個隨機研究對象測量的兩個變量。那麼這兩個變量的相關關係 \(r\) 的計算式爲：

\[ \begin{equation} r = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2\sum(y_i-\bar{y})^2}} = \frac{S_{xy}}{S_xS_y} \end{equation} \tag{23.2} \]

\(S_{xy}\) 代表樣本數據的協方差 (Section 8.1)，\(S_x\) 是變量 \(X\) 的樣本標準差 (有時會記爲 \(\hat\rho_x\))，\(S_y\) 是變量 \(Y\) 的樣本標準差。\(r\) 被命名爲相關係數 \(\rho\) 的 Pearson 积矩估計 (Pearson Product-Moment estimator)。

23.2.2 相關係數的性質

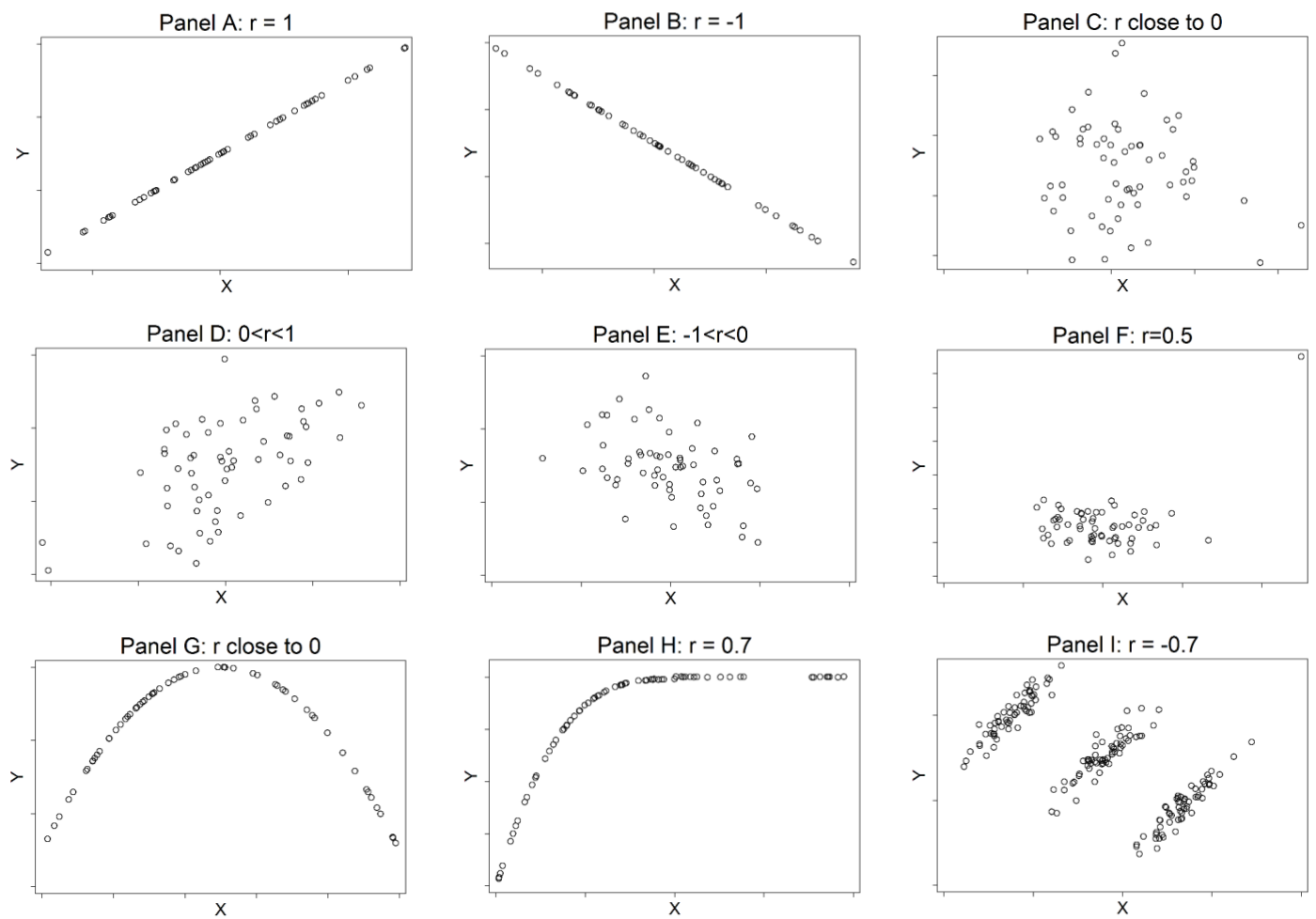
Examples of Peason correlation coefficients

圖 23.1: Examples of Peason correlation coefficients

上圖 23.1 描述了9種不同設定時的相關係數 \(r\)。\(r\) 的主要性質可以總結爲：

  1. \(r\) 的取值範圍是 \(-1\sim1\text{, i.e. } -1\leqslant r \leqslant 1\)；
  2. \(r>0\) 時，二者呈正相關， \(r<0\) 時，二者呈負相關；
  3. 當且僅當兩個變量的散點圖呈現圖 23.1 中 A，B 顯示的直線時才有 \(|r|=1\)，然而直線的坡度卻與相關係數無關；
  4. 如果兩個變量之間沒有直線的 linear相關關係，那麼相關係數 \(r\) 會接近於零；
  5. 求 X 和 Y 的相關係數，等同於求 Y 和 X 的相關係數 (與迴歸不同)；
  6. 相關係數 \(r\) 沒有單位，並且位置不會發生改變 (location invariant)，如果兩個變量乘以或者除以，加上或者減去任意常數，不會改變相關係數的大小 (與迴歸不同)。

圖 23.1 中 F 顯示的相關關係可以看出，\(r\) 受異常值的影響很大，如果將右上角的異常值從數據中去除掉的話，該圖中的相關係數會變小到幾乎爲零。G 和 H 則表示非線性相關時，Pearson 相關係數不適用。I 則告訴我們如果不熟悉數據本身的分佈的話，如果只看總體的相關是多麼的危險 (總體爲負相關，但是在不同的分層數據中卻是呈正相關的)。

23.2.3 對相關係數是否爲零進行假設檢驗

在線性迴歸 (Section 27.6) 中會討論和證明 Pearson 相關係數和統計量 \(t\) 之間的關係，該公式也被用於檢驗相關係數是否爲零：

\[ \begin{equation} T=r\sqrt{\frac{n-2}{1-r^2}} \sim t_{n-2} \end{equation} \tag{23.3} \]

23.2.4 相關係數的 \(95\%\) 信賴區間

如果要計算相關係數 \(r\) 的信賴區間，我們需要知道兩個變量 \(X,Y\) 之間的聯合分佈 (joint distribution)。\(X,Y\) 如果服從二元正態分佈，可以利用 Fisher’s Z-transformation 計算相關係數的信賴區間。圖 23.2 完美展示了兩個服從二元正態分佈的三維立體概率密度分布圖。可以用鼠標拖動下面那個三維圖，就能理解什麼叫做二元正態分佈。就是無論是在 X 軸看 Y，還是在 Y 軸看 X，每一個切面都呈現正態分佈。因此二元正態分佈的概率密度方程繪製出來是成爲一個完美的鍾罩形狀。很美吧！

\[ X|Y \sim N(\mu_x, \sigma_x^2) \text{ AND } Y|X \sim N(\mu_y, \sigma_y^2) \]

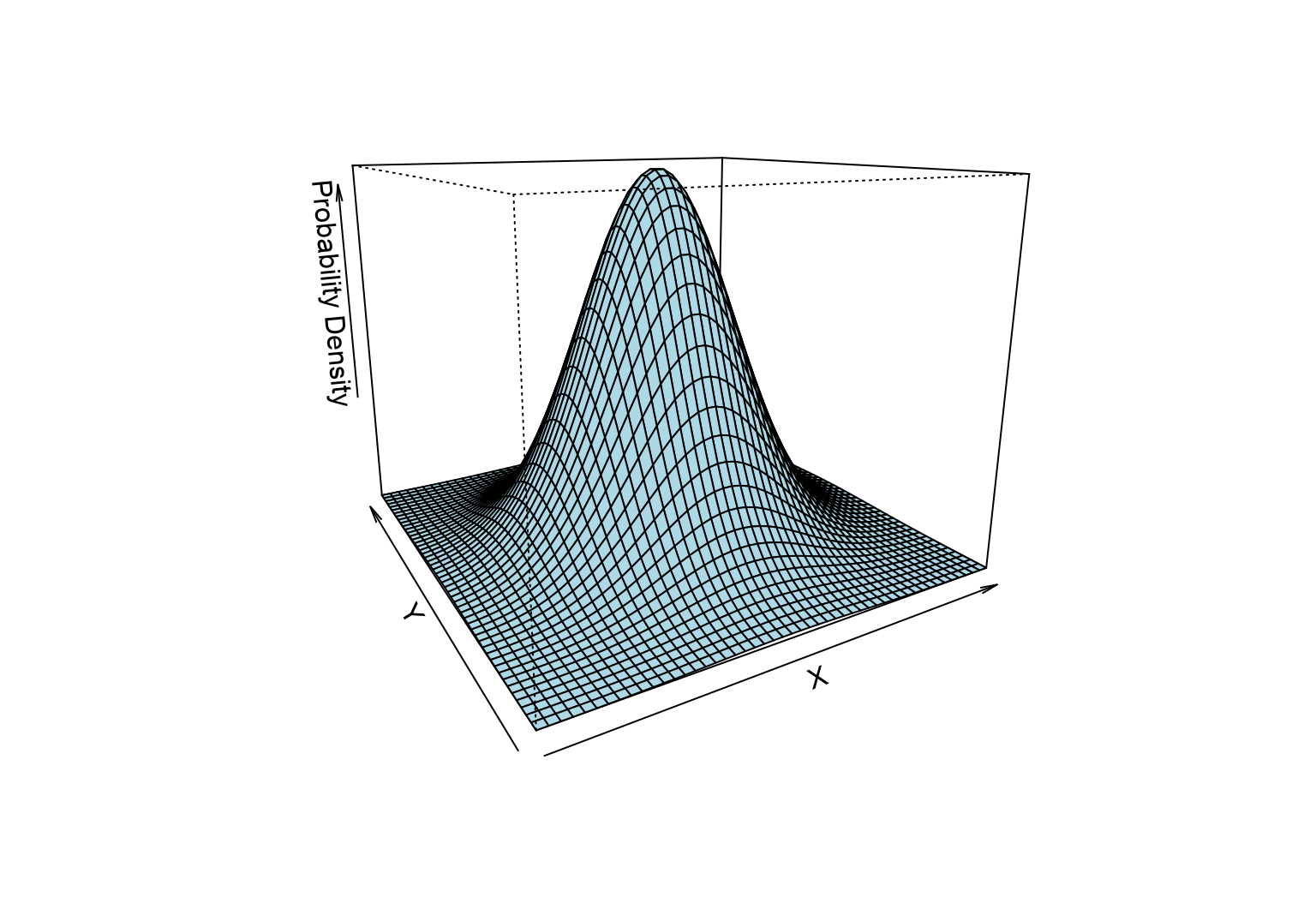
Bivariate normal distribution of X and Y

圖 23.2: Bivariate normal distribution of X and Y

如果 \(\rho\neq0\)，相關係數的樣本分佈雖然不是正態分佈，但是只要 \(X,Y\) 服從上面的圖形顯示的二元正態分佈，就可以利用Fisher’s Z-transformation 公式計算統計量 \(Z_r\)：

\[ \begin{equation} Z_r = \frac{1}{2}\text{log}_e(\frac{1+r}{1-r}) = \text{tanh}^{-1} (r) \end{equation} \tag{23.4} \]

\(Z_r\)，近似服從正態分佈：

\[ \begin{equation} Z_r \sim N(\frac{1}{2}\text{log}_e(\frac{1+\rho}{1-\rho}), \frac{1}{n-3}) \end{equation} \tag{23.5} \]

利用這個性質，我們可以計算 \(Z_\rho\) 的信賴區間，然後再通過逆運算轉換之後獲得 \(\rho\) 的信賴區間：

\[ \begin{equation} \rho = \frac{exp(2Z_\rho)-1}{exp(2Z_\rho)+1} = \text{tanh}(Z_\rho) \end{equation} \tag{23.6} \]

23.2.5 比較兩個相關係數是否相等

假設需要比較兩個相關係數，可以繼續使用 Fisher’s Z-transformation 計算相關係數之差的統計量，它服從標準正態分佈 \(N(0,1)\)。很少會碰到比較兩個相關係數，但是偶爾碰到的實例有這樣的：要比較男性和女性之間，食鹽攝入量和血壓的相關關係是否相同。

\[ \text{Test statistics} = \frac{Z_{r_2}-Z_{r_1}}{\sqrt{\frac{1}{n_2-3}+\frac{1}{n_1-3}}} \sim N(0,1) \]

在實際應用中，其實相關係數的比較意義並不是很大。更常見的是使用迴歸分析的手段比較兩個人羣 (男性女性) 中血壓和食鹽攝入量的迴歸係數 (即，性別對實驗和血壓的關係是否產生了交互作用，interaction)。

23.2.6 相關係數那些事兒

醫學文獻中你會碰見非常多的人使用相關係數，但是相信我，許多人都用錯了。其實比起相關係數，能提供更多信息的手段是進行迴歸分析。下面羅列一些常見的錯誤使用相關係數的例子：

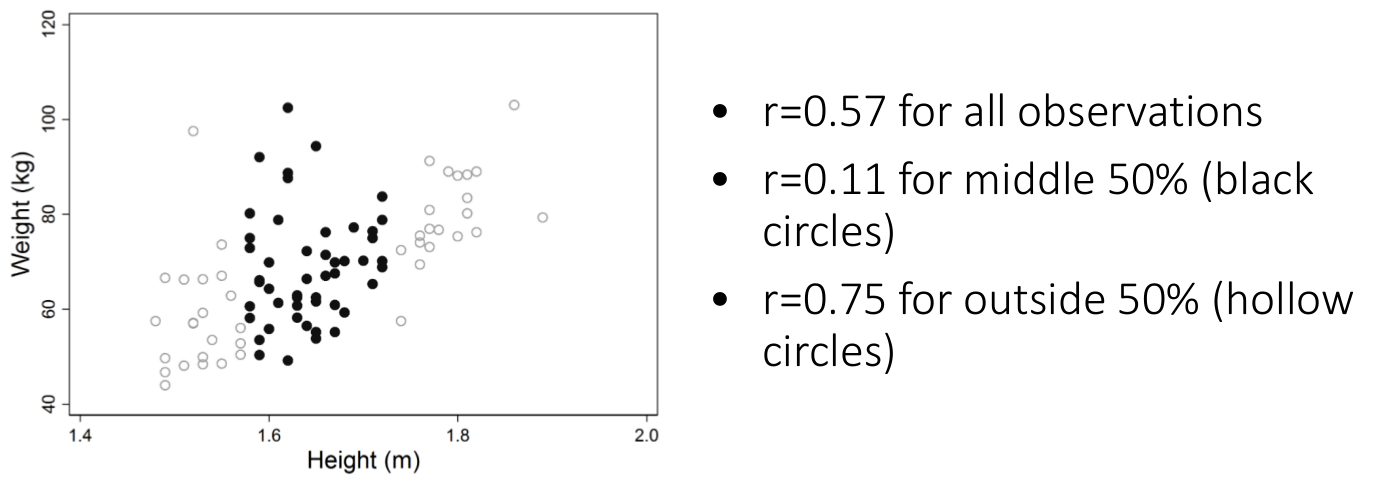
Effect of data restrictions on the Pearson correlation coefficient

圖 23.3: Effect of data restrictions on the Pearson correlation coefficient

  1. 圖 23.3 展示了同樣的一組數據，如果只是斷章取義，其相關係數可能發生極大的變化。所以，想用相關係數作合理的統計推斷，必須保證數據的完整性，否則就有玩弄數據之嫌。然而，如果你用的是線性迴歸的方法，受數據限制 (data restriction) 的影響就幾乎可以忽略不計。
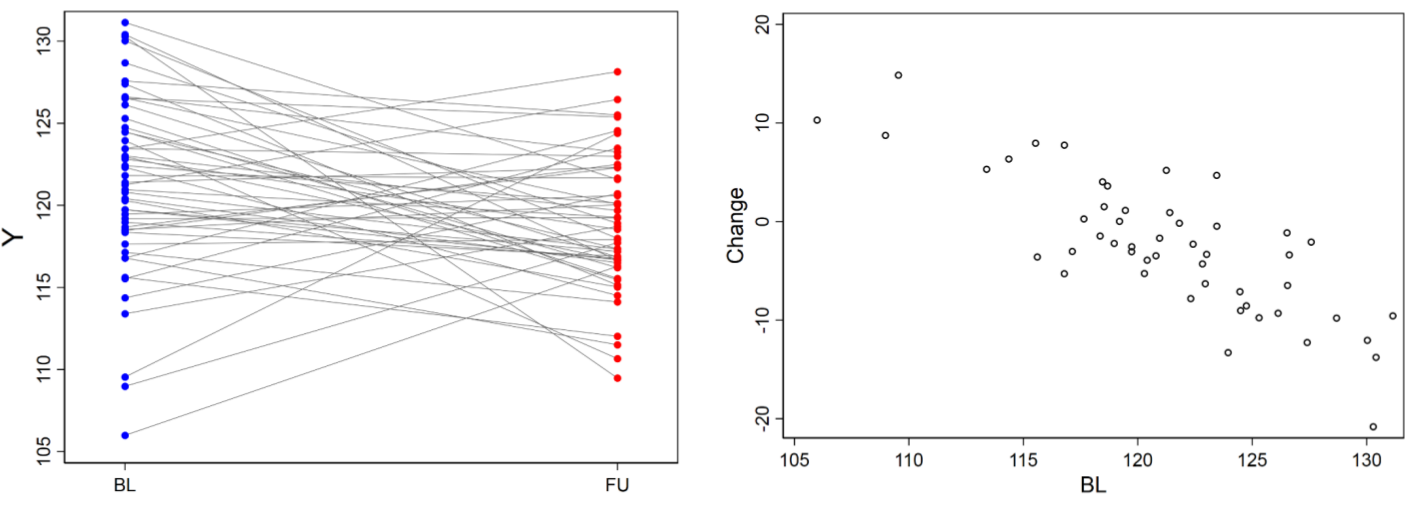
Effect of regression to the mean

圖 23.4: Effect of regression to the mean

  1. 均數迴歸現象，regression to the mean phenomenon，是指在進行重複測量時，前次測量中獲得的極高或極低分數會在後期測量時傾向於向平均值偏移，即隨着時間的推移，高分者成績下降，低分者成績升高的一種自然迴歸效應。所以在一些臨牀實驗中宣稱自己發現的測量值的變化和基線值之間的相關關係 (correlation between initial measurement and a change in that measurement)，其實是一種自然現象而不是真的存在什麼相關關係，如圖 23.4。要避免這樣的低級失誤，可以計算測量值的變化 (\(X_2-X_1\)) 和前後兩次測量值的均值 (\((X_2+X_1)/2\)) 之間的相關關係。

  2. 有些科學家聲稱自己用迴歸係數來衡量兩個變量之間的一致性 (assess agreement between variables)，這當然是完全錯誤的。兩個變量之間高度相關，和他們高度一致是完全不同的概念 (單位，測量方法，可能都不一樣怎麼可能一致呢)。你完全可以將同一個變量乘以2以後和它原來的值作相關分析，就會發現二者相關係數等於 1，但是二者數值上相差兩倍。

一般來說，迴歸模型 (regression models) 顯得比 Pearson 相關係數更加實用，能提供更多的信息用於推斷 (甚至是用一個值的變化預測另一個變量的大小)，也能避免上面舉例的錯誤使用。

23.2.7 在 R 裏面計算相關係數

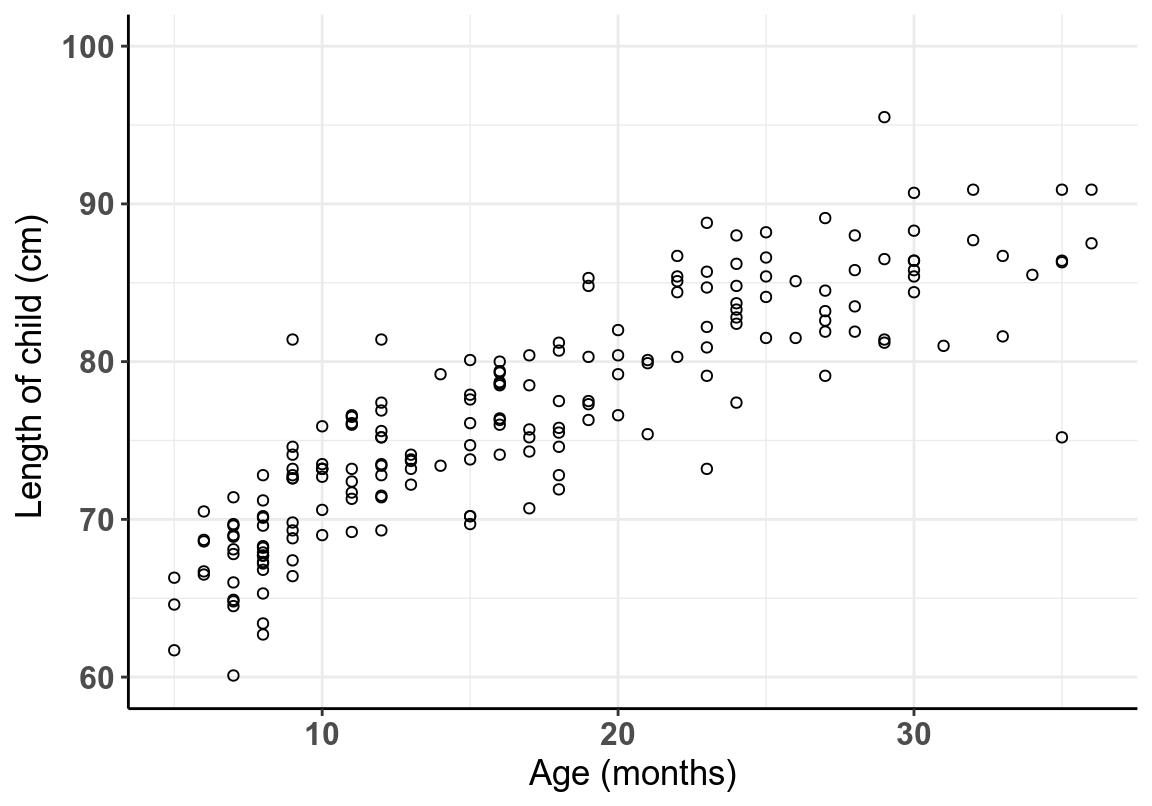
Association between age and height in children aged 6-36 months

圖 23.5: Association between age and height in children aged 6-36 months

在 R 裏面用 cor() 可以簡單的獲得兩個變量之間的相關係數，cor.test() 可以用於獲得相關係數的信賴區間和是否爲零的假設檢驗結果：

cor(growgam1$age, growgam1$len)
## [1] 0.8676
cor.test(growgam1$age, growgam1$len)
## 
##  Pearson's product-moment correlation
## 
## data:  growgam1$age and growgam1$len
## t = 24, df = 190, p-value <2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.8275 0.8990
## sample estimates:
##    cor 
## 0.8676

23.3 二元變量之間的相關性 association between pairs of binary variables

兩個二元變量之間的相關性常用比值比 Odds Ratio (OR) 來衡量。跟連續型變量的 Pearson 相關係數一樣，二元變量之間的比值比也是一種對稱的特徵值。所以，X 對於 Y 的 OR，和 Y 對於 X 的 OR 是一樣的。令 \(\pi_{ij}\) 表示 \(X=i, Y=j\) 時的概率。

表23.1： Population parameters in a \(2\times2\) contingency table
\(Y = 0\) \(Y = 1\) Total
\(X = 0\) \(\pi_{00}\) \(\pi_{01}\) \(\pi_{0\cdot}\)
\(X = 1\) \(\pi_{10}\) \(\pi_{11}\) \(\pi_{1\cdot}\)
Total \(\pi_{\cdot 0}\) \(\pi_{\cdot 1}\) 1

利用表格可以看出，求 Y 對 X 的 OR 計算式爲 (horizontal)：

\[ \Psi = \frac{\pi_{00}/\pi_{01}}{\pi_{10}/\pi_{11}} = \frac{\pi_{00}\times\pi_{11}}{\pi_{10}\times\pi_{01}} \]

求 X 對 Y 的 OR 計算式爲 (vertical)：

\[ \Psi = \frac{\pi_{00}/\pi_{10}}{\pi_{01}/\pi_{11}} = \frac{\pi_{00}\times\pi_{11}}{\pi_{10}\times\pi_{01}} \]

可見兩個計算 OR (parameter) 值關係的計算式是完全等價的。

表23.2： Observed data in a \(2\times2\) contingency table
\(Y = 0\) \(Y = 1\) Total
\(X = 0\) \(O_{00}\) \(O_{01}\) \(O_{0\cdot}\)
\(X = 1\) \(O_{10}\) \(O_{11}\) \(O_{1\cdot}\)
Total \(O_{\cdot 0}\) \(O_{\cdot 1}\) 1

所以用觀察數據 (Observed data, all “O”s in the table) 替代掉 OR 計算式中的 \(\pi\) 可得觀察數據的 OR 估計值 (estimator) 的計算公式：

\[ \begin{equation} \hat\Psi = \frac{\hat\pi_{00}\times\hat\pi_{11}}{\hat\pi_{10}\times\hat\pi_{01}} = \frac{O_{00}\times O_{11}}{O_{10}\times O_{01}} \end{equation} \tag{23.7} \]

23.3.1 OR 的信賴區間

由於 OR 是乘法計算的結果，我們習慣上使用對數轉換 OR 以後 \((\text{log}(\hat\Psi))\) 計算完對稱的 95% 信賴區間，然後再通過對數的反函數獲得 OR 的 95% 信賴區間。

樣本量足夠大時， \(\text{log}(\hat\Psi)\) 的分佈是正態分佈，標準誤 (standard error) 是：

\[ \begin{equation} \sqrt{\frac{1}{N\pi_{00}}+\frac{1}{N\pi_{01}}+\frac{1}{N\pi_{10}}+\frac{1}{N\pi_{11}}} \end{equation} \tag{23.8} \]

其中 \(N\pi_{ij}\) 表示的是 \(2\times2\) 表格中四個觀察數據的觀察樣本量 (sample size in the contingency table)。

所以一個 OR 的信賴區間的計算流程如下：

  1. 計算 OR 值 \(\hat\Psi\) (用公式 (23.7))；
  2. 取對數 \(\text{log}\Psi\)；
  3. 求 \(\text{SE}(\text{log}\Psi)\) (用公式 (23.8))；
  4. 計算 \(\text{log}\Psi\) 的 \(95\%\) 信賴區間：\(\text{log}\Psi \pm 1.96\text{SE}(\text{log}\Psi)\)；
  5. 求獲得的 \(\text{log}\Psi\) 的 \(95\%\) 信賴區間的下限上限的對數的反函數 (自然底數的指數函數) 作爲 OR \(\hat\Psi\) 值的信賴區間。

23.3.2 比值比的假設檢驗

比值比 OR 假設檢驗時的零假設爲，二者不相關，比值比 \(\Psi=1\)。所以：\(\text{H}_0: \Psi = 1 \text{ or log}_e(\Psi) = 0\)。

這個零假設可以用計算信賴區間時的性質進行：

\[ z=\frac{\text{log}(\hat\Psi)}{SE(\text{log}_e(\Psi))} \sim N(0,1) \]

另外更加常用的檢驗 OR 值是否等於 1 的檢驗方法有下面兩種：

  1. 樣本量大時：\(\chi^2\) 的擬合優度檢驗 goodness of fit test；
  2. 小樣本時：Fisher 的精確檢驗法 Fisher’s exact test。

23.3.3 兩個百分比的卡方檢驗

檢驗統計量如下：

\[ \begin{aligned} \chi^2 &= \sum_i\sum_i(\frac{(O_{ij}-E_{ij})^2}{E_{ij}}) \\ \text{Where } &E_{ij} = \frac{O_{i\cdot}\times O_{\cdot j}}{O_{\cdot\cdot}} \end{aligned} \tag{23.9} \]

計算獲得了卡方值之後和自由度爲 1 的卡方分佈相比較獲得雙側 \(p\) 值。

優化版本 用連續性校正法：

\[ \begin{aligned} \chi^2 &= \sum_i\sum_i(\frac{(|O_{ij}-E_{ij}| - 0.5)^2}{E_{ij}}) \\ \text{Where } &E_{ij} = \frac{O_{i\cdot}\times O_{\cdot j}}{O_{\cdot\cdot}} \end{aligned} \tag{23.10} \]

23.3.4 確切檢驗法 Fisher’s “exact” test

如果 \(2\times2\) 表格中的四個數字的 期待值 均大於 5，那麼用上面的卡方檢驗沒有問題，如果期待值都很小，就建議要使用精確檢驗法。 確切檢驗法的思想理論是超幾何分佈 (Section 5.2)，在四個表格邊緣合計固定不變的條件下，利用下面公式 (23.11) 直接計算表內四個格子數據的各種組合的概率，然後計算單側或者雙側累計概率，與顯著性水平 \(\alpha\) 比較。

\[ \begin{aligned} P_{O_{00}} & = \text{Prob}(O_{00},O_{01},O_{10},O_{11}|O_{0\cdot},O_{1\cdot},O_{\cdot0},O_{\cdot1}) \\ & = \frac{O_{0\cdot}!O_{1\cdot}!O_{\cdot0}!O_{\cdot1}!}{O_{\cdot\cdot}!O_{00}!O_{01}!O_{10}!O_{11}!} \end{aligned} \tag{23.11} \]

在 R 裏可以用 fisher.test 對四格表內容進行確切檢驗。

x3 <- matrix(c(7,5,3,8), ncol = 2, byrow = TRUE)
addmargins(x3)
##           Sum
##      7  5  12
##      3  8  11
## Sum 10 13  23
fisher.test(x3)
## 
##  Fisher's Exact Test for Count Data
## 
## data:  x3
## p-value = 0.2
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##   0.4942 31.9433
## sample estimates:
## odds ratio 
##      3.513

23.4 多分類 (無排序) 的情況 \(M\times N\) 表格

卡方檢驗可以推廣到兩個多分類變量之間的相關分析。

\[ \begin{aligned} & \chi^2 = \sum_i\sum_j(\frac{(O_{ij}-E_{ij})^2}{E_{ij}}) \\ & \text{Where } E_{ij} = \frac{O_{i\cdot}O_{\cdot j}}{O_{\cdot\cdot}} \\ & \text{Under H}_0: \chi^2 \sim \chi^2_{(m-1)\times(n-1)} \end{aligned} \]

表23.3： Observed data in a \(M\times N\) contingency table
\(Y = 1\) \(Y = 2\) \(\cdots\) \(Y = n\) Total
\(X = 1\) \(O_{11}\) \(O_{12}\) \(\cdots\) \(O_{1n}\) \(O_{1\cdot}\)
\(X = 2\) \(O_{21}\) \(O_{22}\) \(\cdots\) \(O_{2n}\) \(O_{2\cdot}\)
\(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\)
\(X = m\) \(O_{m1}\) \(O_{m2}\) \(\cdots\) \(O_{mn}\) \(O_{m\cdot}\)
Total \(O_{\cdot 1}\) \(O_{\cdot 2}\) \(\cdots\) \(O_{\cdot n}\) \(O_{\cdot\cdot}\)