第 31 章 線性迴歸的模型診斷

和其他的統計學模型一樣，線性迴歸也有自己的前提條件，而且從模型結果作出的各種推斷都依賴這些前提條件的成立。所以，我們需要有一些統計學的手段來檢查線性迴歸模型中這些前提是否得到滿足。然而理想總是很豐滿，現實通常又太骨感。你不大可能找到一組真實的數據能夠 100% 完美的滿足所需要的前提條件。當然不是說不能滿足模型的前提條件，我們就無法進行統計推斷了。而且我們也有不少結果穩健 (robust) 的統計學手段，讓我們可以不必考慮太多前提條件。檢查數據，瞭解數據內容，理解數據本身的結構永遠都是有助於數據分析的。

還要記得一點就是，根據中心極限定理，(即使有一些前提假設不能成立) 大型數據分析結果的穩健性/可靠性，要高於小型數據的分析。

31.1 線性迴歸模型的前提條件

  1. 因變量和各個預測變量之間的關係都是線性 linear relationship 的；
  2. 因變量之間相互獨立；
  3. 真實 true 殘差的方差是恆定不變的 constant。這裏的含義是在真實迴歸直線上下散佈的因變量的點，在任意一個預測變量值的位置的方差 (分散) 要保持恆定不變。這個特性被描述成方差齊性 homoscedasticity (殘差方差的一致性 homogeneity of the residual variance)，與之相對的定義是異方差性 heteroscedasticity (殘差方差的不同質性，heterogeneity of the residual variance)。
  4. 真實殘差服從正態分佈。(儘管你發現統計忍者包裏丟入隨便什麼數據都能給你個線性迴歸的報告來，但是，如果你真想用其結果做統計推斷，p CI 的話，這條前提必須滿足。)

本章着重討論第 1，3，4 前提條件的診斷法。因爲觀測數據之間是否獨立性 (第 2 條) 並不是你光盯着數據看就能知道的。你要去問給你數據的 (沒良心的) 人。

31.2 用圖形來視覺診斷

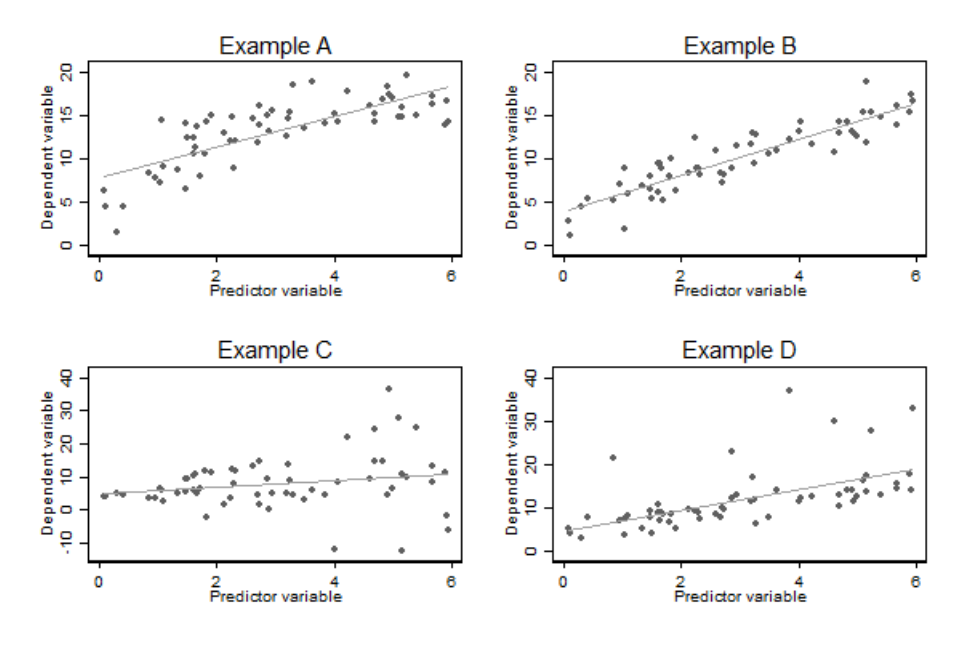
Illustration the usefullness of scatter plots of the dependent variable against the predictor variable in simple linear regression

圖 31.1: Illustration the usefullness of scatter plots of the dependent variable against the predictor variable in simple linear regression

圖 31.1 中展示了四種實例。把預測變量和因變量做散點圖，這常常是甄別出異方差性 (Example C)，非線性 (Example A)，異常值 (Example D) 的最好方法。其中右上角的 Example B 是良好的迴歸模型的散點圖應該有的樣子。

建議進行視覺判斷的時候把擬合曲線去掉再作一次，看看有迴歸直線和沒有迴歸直線前後的散點圖差別，更容易看出數據的分佈特徵。但是光看散點圖作判斷的方法，在多元線性迴歸模型中只能看看能否找到一些異常值，對輔助判斷方差齊性和線性關係就沒有太大的用處。殘差點圖就更加實用。

31.3 殘差圖

如果線性迴歸模型的前提條件能夠得到滿足，那麼擬合模型後的殘差，一定會服從正態分佈且方差均勻一致。所以另一個診斷異方差性的辦法可以通過作觀察殘差和擬合值之間的散點圖來輔助判斷。下圖 31.2 是各個簡單線性迴歸擬合後的殘差和擬合值之間的散點圖。可以看出左下角的 Example C 的異方差性展現得更加明顯了。同樣此圖也能幫助判斷線性關係，如左上角的 Example A 所示，如果預測變量和因變量之間不是線性關係，那麼殘差就不可能均勻的分佈在 \(0\) 的兩側。

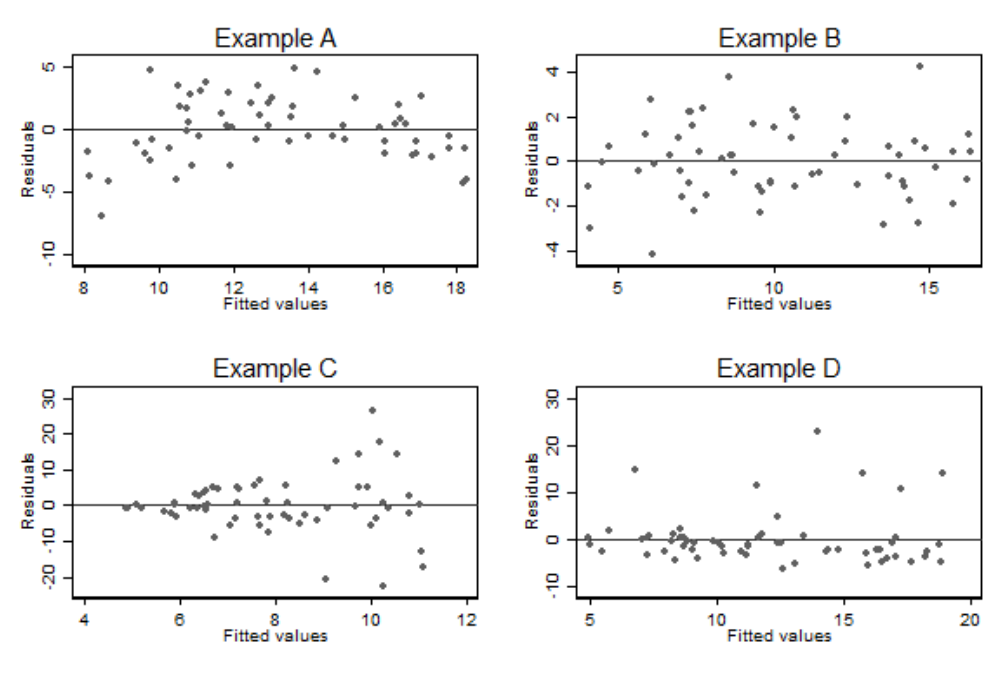
Plots of residuals agianst fitted values for the examples in the previous figure

圖 31.2: Plots of residuals agianst fitted values for the examples in the previous figure

對於一個簡單線性迴歸模型來說，擬合值僅僅只是預測變量的一個線性數學轉換，所以上面圖中的殘差和擬合值的散點圖，其實等價於殘差和預測變量的散點圖。所以圖 31.1 和圖 31.2 兩圖展現的信息量此時是一樣的。

但是，多元線性迴歸時，殘差和擬合值的散點圖會比殘差和預測變量散點圖更適合判斷異方差性，和線性關係的假設。

31.4 殘差正態圖 normal plot of residuals

正態圖在分析技巧的章節也有介紹 (Section 25.2.1)。這是最佳的判斷數據是否服從正態分佈的視覺圖。所以用它來繪製線性迴歸擬合後的殘差，是個很好的辦法。可惜的是殘差正態圖無法用於判斷異方差性，和線性關係兩個假設。

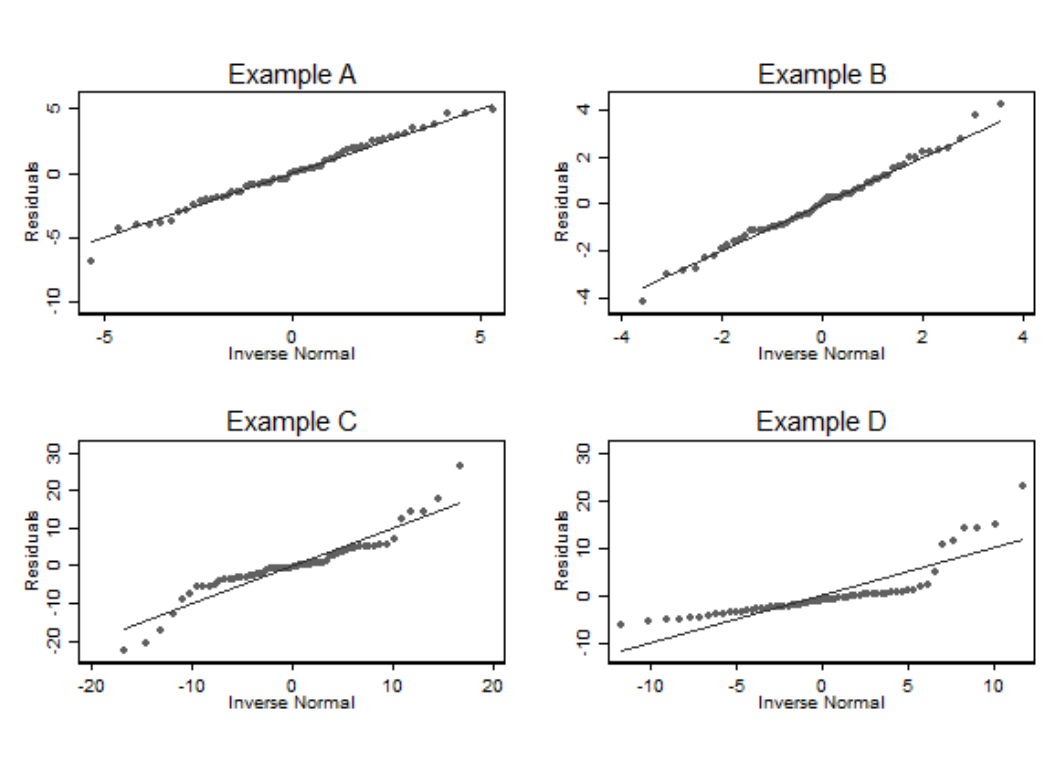
Normal plots of residuals for the examples in the previous figure

圖 31.3: Normal plots of residuals for the examples in the previous figure

有時後觀察殘差 (observed residuals) 可能不能滿足齊方差性質而真實殘差 (true residuals) 反而滿足。所以一些統計學家建議把計算的殘差標準化 (standardised residuals) 以後再作正態圖。

31.4.1 模型診斷實例

前面建立過的兒童體重和年齡，身長之間的多元迴歸模型的診斷 (Section 30.3.3) 見下圖。所有四個圖都沒有證據證明非線性關係和異方差性。看不見顯著的異常值。正態圖看出殘差有那麼一點點不太正態分佈，但是不嚴重到讓人懷疑模型給出的推斷是否受到重大影響。

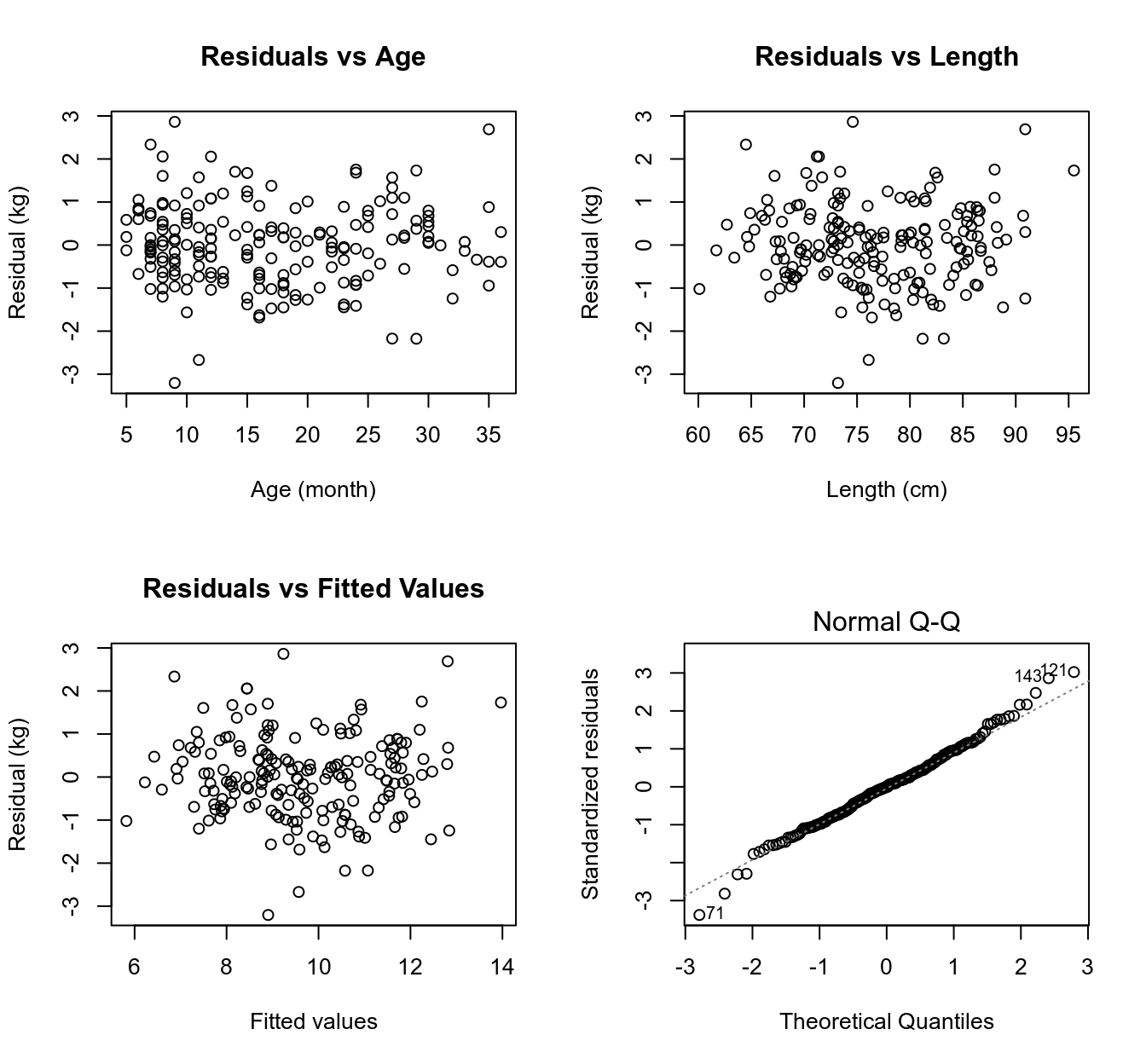
Residual plots for the linear regression relating a child's weight to their age and length

圖 31.4: Residual plots for the linear regression relating a child’s weight to their age and length

31.5 前提條件的統計學檢驗

31.5.1 二次方程迴歸法檢驗非線性

二次方程迴歸法是一種多元迴歸模型，它包含了兩個預測變量，一個是另一個的平方。數學模型可以標記成爲：

\[ \begin{aligned} y_i & = \alpha + \beta_1 x_i + \beta_2 x_i^2 + \varepsilon_i \\ \text{Where } & \varepsilon_i \sim \text{NID}(0, \sigma^2) \end{aligned} \tag{31.1} \]

儘管你看到了二次方程在這裏，但是這仍然是一個線性迴歸模型。但是二次方程的迴歸模型描述的是 \(Y, X\) 兩個變量之間的非線性關係。如果你把方程 \(\hat{y}_i = \hat\alpha + \hat\beta_1x_i + \hat\beta_2x^2_i\) 對 \(x_i\) 求微分，你會得到 \(\hat\beta_1+2\hat\beta_2 x_i\)。這是二次方程的曲率方程。所以如果結果中報告 \(\hat\beta_2\) 是有統計學意義的，就等於是有證據證明這兩個變量之間的關係不是線性的。

growgam1$age2 <- (growgam1$age)^2
Model2 <- lm(wt ~ len + age + age2, data=growgam1)
print(summary(Model1), digits = 5)
## 
## Call:
## lm(formula = wt ~ age + len, data = growgam1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.20525 -0.64402 -0.00303  0.55967  2.86277 
## 
## Coefficients:
##              Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -8.351244   1.259968 -6.6281 3.531e-10 ***
## age         -0.011260   0.016751 -0.6722    0.5023    
## len          0.237129   0.019516 12.1502 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9546 on 187 degrees of freedom
## Multiple R-squared:  0.74337,    Adjusted R-squared:  0.74063 
## F-statistic: 270.84 on 2 and 187 DF,  p-value: < 2.22e-16
print(summary(Model2), digits = 5)
## 
## Call:
## lm(formula = wt ~ len + age + age2, data = growgam1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.30561 -0.64811 -0.01615  0.54829  2.74233 
## 
## Coefficients:
##               Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) -8.5918429  1.2537775 -6.8528 1.031e-10 ***
## len          0.2514685  0.0205039 12.2644 < 2.2e-16 ***
## age         -0.1110198  0.0502050 -2.2113   0.02823 *  
## age2         0.0023351  0.0011091  2.1055   0.03659 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9459 on 186 degrees of freedom
## Multiple R-squared:  0.74935,    Adjusted R-squared:  0.74531 
## F-statistic: 185.36 on 3 and 186 DF,  p-value: < 2.22e-16

正如上面的二次方程模型輸出結果所示，年齡和體重之間，當調整了身高以後，有證據 (但是較弱) 證明不呈現線性關係 \((p=0.037)\)。

31.5.2 非線性關係模型

二次方程的迴歸模型的應用在非線性模型中的應用其實有許許多多的缺陷。例如二次方程迴歸只能默認有一個極致點。也就是在二次方程模型中，預測變量和因變量的關係要麼是先下降後升高，要麼是先升高再下降。不光如此，二次方程迴歸還默認二者之間的關係在極致點是左右對稱的。這無論如何在現實中都很難有成這樣關係的兩個變量。所以，假如你使用二次方程模型迴歸之後發現非線性的證據是有意義的，那麼更好的辦法是接下來擬合一個更加符合實際情況的非線性模型-多項式曲線迴歸模型。

二次方程回顧模型是多項式曲線迴歸模型的最簡單形式，其次是三次方程模型 (其實就是在公式 (31.1) 裏面加一個 \(+\beta_3 x_i^3\))。另一種更加靈活的模型是擬合一個精確的分段式多項式模型，即允許在不同範圍 (被描述爲 “結點 knots”) 的預測變量 \(X\) 內擬合不同的模型。其中一種叫做 限制性立方曲線模型 restricted cubic spline model (點這裏看我用了這種方法的論文)：

  1. 默認第一個節點之前和最後一個節點以後爲直線模型；
  2. 其餘節點之間默認用三次方迴歸模型擬合數據；
  3. 在節點處的兩個方程之間用平滑的曲線連接 (強制兩個方程的一階二階導數相等即可 constraining the first and second derivatives of adjacent functions to agree when they meet at the knot point)

31.6 異常值，槓桿值，和庫克距離

觀測值中的異常值很顯然對模型的擬合會有較大的影響。如果某個觀測值對應的擬合值是異常值的話，那麼這樣的值被認爲槓桿值很大。庫克距離 (Cook’s Distance) 是另一種用來衡量異常值的手段。

31.6.1 異常值和標準化殘差

異常值指的是那些通過模型擬合過後，觀測值和擬合值差異很大的那些觀察對象。這些值需要被甄別出來因爲它們

  1. 可能是數據錄入階段造成的人爲失誤，或者是有什麼別的原因導致的系統性異常需要讓輸入數據的人員進行進一步的調查；
  2. 異常值可能較大的影響迴歸係數的方差估計，造成不精確甚至錯誤的結果；
  3. 異常值也會影響迴歸係數本身的估計。

觀測值和擬合值之間的差，被命名爲觀測殘差 (observed residuals)。線性迴歸模型的前提之一是 真實殘差 獨立且方差維持恆定不變。但是觀測殘差卻無可能做到獨立且方差恆定不變。

之所以說觀測殘差不是獨立的，可以這樣來理解：假如擬合某個線性迴歸模型，預測變量是二分類的，且其中一個分類只有兩個觀測值，那麼擬合的直線會通過這兩個觀測值的中心點 (均值)，那麼這兩個觀測值的觀測殘差就恰好分佈在迴歸直線的兩側 (相加之和爲零，呈完美負相關)，它們是相關的！！！

觀測殘差的方差不可能恆定的理由，可以這樣來理解：同樣假如擬合某個預測變量是二分類的線性迴歸模型，其中一個分類只有一個觀測值，那麼迴歸直線在這個觀測值處的殘差方差是零。

標準化殘差 (standardized residuals) \((r_i)\)，被定義爲每個觀測值的殘差和模型估計的殘差標準誤相除獲得的數據。所以符合前提條件的線性模型擬合後，計算的標準化殘差會服從標準正態分佈。從標準正態分佈的知識你也應該知道，\(95\%\) 的觀測值的標準化殘差必須分佈在數值 \(-2, 2\) 範圍內。另外一種標準化殘差的方法叫做內學生化殘差 (studentised residual)。內學生化殘差是把觀測值的殘差除以每一個觀測值各自的估計標準誤。在 R 裏面可以通過 rstandard() 命令計算迴歸模型每個觀測值的內學生化殘差。內學生化殘差也是服從標準正態分佈的。

31.6.2 槓桿值 Leverage

如果一個觀測值的擬合值十分極端，那麼該觀測值本身可能對迴歸模型的參數估計影響很大。這個影響程度大小用槓桿值衡量。簡單線性迴歸時，每個觀測值的槓桿值計算公式爲：

\[ \begin{aligned} l_i = \frac{1}{n} + \frac{x_i-\bar{x}}{SS_{xx}} \end{aligned} \tag{31.2} \]

槓桿值的範圍是 \(\frac{1}{n}, 1\) 之間。槓杆值方程提示這是一個單調函數，它是評價預測變量本身到該變量均值之間距離的指標。槓桿值越大，該觀測值就有越大的可能性對模型擬合造成影響。如果槓桿值大到等於 \(1\)，那麼槓桿效應造成的影響極大，觀測值和擬合值就完全一致。意味着在這個觀測值附近，只有它自己，沒有其他觀測值。

(2018-05-14 嘗試過去試題 2014 Paper 2-Q2 時發現槓杆值的問題，在此繼續增加關於多元現行回歸中槓杆值的性質。)

多元線性迴歸時的槓桿值計算公式和 (30.7) 中的帽子矩陣 \(\mathbf{P}\) 有關：

\[ \begin{aligned} & l_i = \mathbf{P}_{ii} \text{ The } i\text{ th diagonal element of } \\ & \mathbf{X(X^\prime X)^{-1}X^\prime} \end{aligned} \tag{31.3} \]

In multiple regression, leverage measures “distance” from the centre of the joint distribution of the predecitor variables, but with distance scaled by the directional degree of dispersion. Notice that the point with largest leverage would not have particularly high leverage in either simple linear regression models including only one of the two (or more) predictor variables. Further this point would not be readily identified in plots of each of the predictor variables against the dependent variable. The value of measures such as the leverage is greatest in complex multiple regression models where it can be difficult to identify points with an atypical (非典型) combination of predictor variables using more simple graphical techniques.

31.6.3 庫克距離 Cook’s Distance

當通過計算觀測值的槓桿值之後，發現具有較大槓桿值的那些觀測點，應該被視爲對模型的穩定性有“潛在威脅”。此時就輪到庫克距離的登場。庫克距離可以用來衡量一個觀測值對模型的影響大小 (比較把觀測值移除出模型前後的模型變化)。

對於一個有 \(p\) 個預測變量的迴歸模型來說，如果殘差方差的估計值爲 \(\hat\sigma^2\)，那麼第 \(i\) 個觀測值的庫克距離的計算過程就是把該觀測值移除，重新擬合相同的模型，計算獲得該點做的新的擬合值 \(\hat y_{j(i)}\)：

\[ \begin{aligned} D_i = \frac{\sum^n_{j=1}(\hat y_{j(i)} - \hat y_j)^2}{(p+1)\hat\sigma^2} \end{aligned} \tag{31.4} \]

可以被證明的是，庫克距離其實是結合標準化殘差值 \((r_i)\)，和槓桿值 \((l_i)\) 的一個綜合量：

\[ \begin{aligned} D_i & = \frac{\sum^n_{j=1}(\hat y_{j(i)} - \hat y_j)^2}{(p+1)\hat\sigma^2} \\ & = \frac{r^2_il_i}{(p+1)(1-l_i)} \end{aligned} \tag{31.5} \]

所以從庫克距離和標準化殘差，以及槓桿值之間的關係公式 (31.5) 也可以看出，當槓桿值大同時標準化殘差值的絕對值也大的觀測值，庫克距離就會很大。用線性迴歸時，把每個觀測值得庫克距離和擬合值作散點圖，或者把槓桿值和標準化殘差作散點圖是常用的判斷異常值的手段。

31.7 在統計忍者包裏面對模型診斷作圖

擬合好了一個線性迴歸模型以後，plot(Modelname) 即可看到四個診斷圖 (Section 26.8.5)。