5.4 DICA Analysis
#DICA
resDICA <- tepDICA(bin_data,
DESIGN = wk0$Product,
graphs = TRUE,
make_data_nominal = TRUE)
# Inferences -----
nIter <- 1000
resDICA.inf <- tepDICA.inference.battery(
bin_data,
make_data_nominal = FALSE,
DESIGN = wk0$Product,
make_design_nominal = TRUE,
symmetric = TRUE, graphs = TRUE, k = 0
)## [1] "It is estimated that your iterations will take 0.04 minutes."
## [1] "R is not in interactive() mode. Resample-based tests will be conducted. Please take note of the progress bar."
## ================================================================================5.4.1 Scree Plot
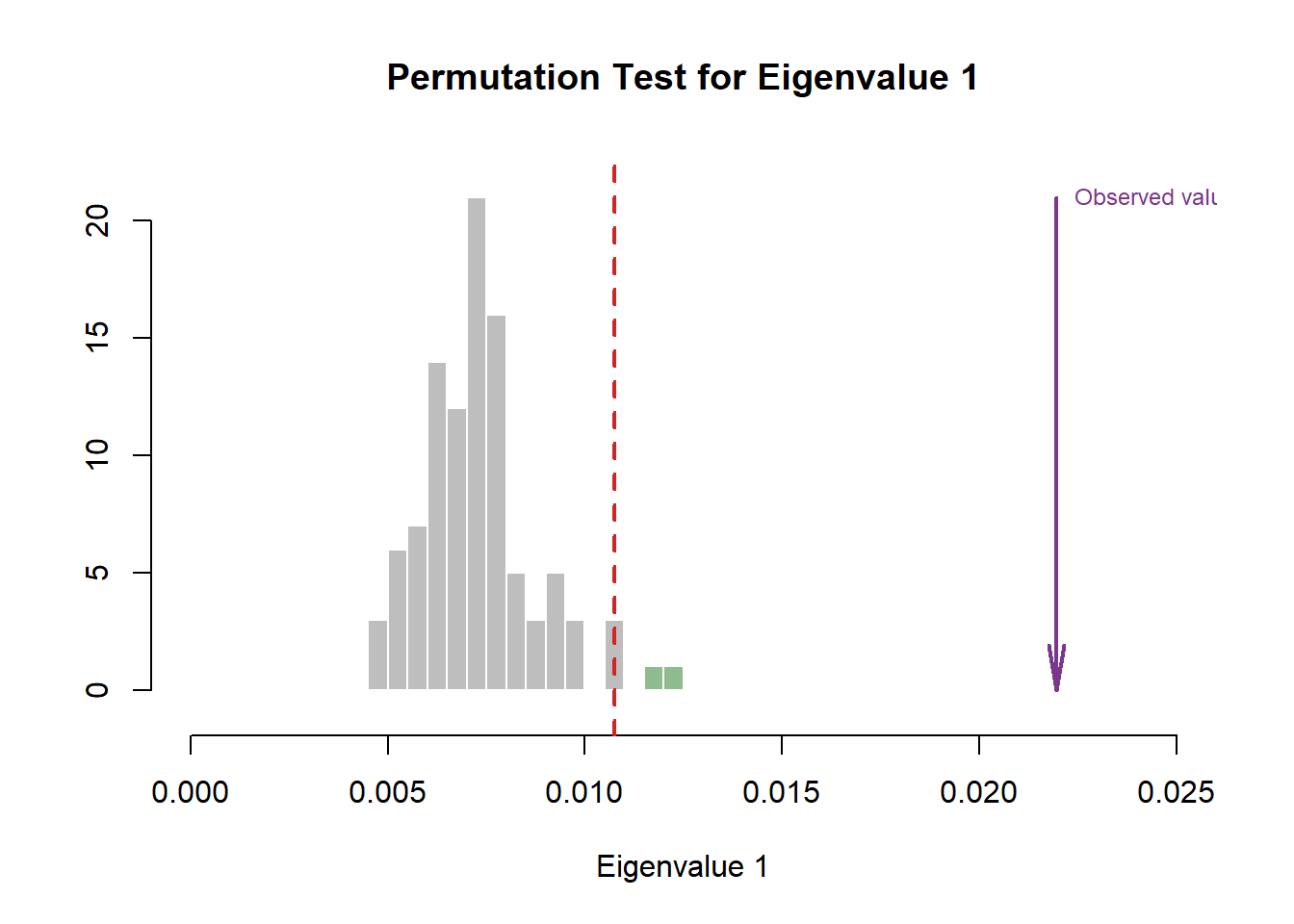
Compare to the Scree Plot yielded from MCA, this time it also looks like there is quite a bit of over-estimation in Components Significance. We will also double check this effect by performing eigen value tests on Component 1 and 2. From these test, we can see that there is indeed an effect of over-estimation in Components Significance when using DiCA. Ideally, we should also test Component 3 and 4.
# Scree
inf.scree <- PlotScree(ev = resDICA.inf$Fixed.Data$TExPosition.Data$eigs,
p.ev = resDICA.inf$Inference.Data$components$p.vals,
plotKaiser = TRUE,
title = "DICA: Explained Variance per Dimension")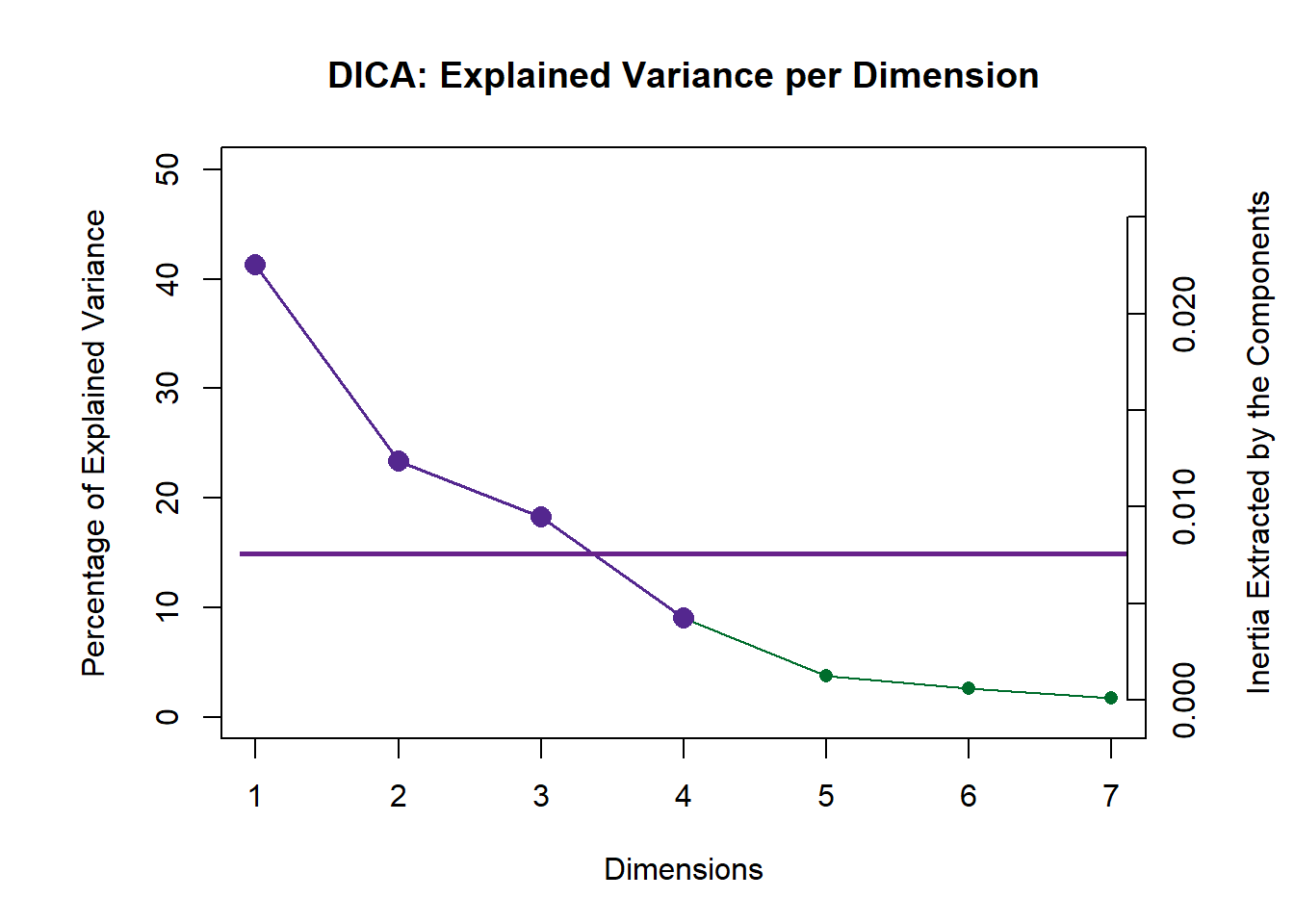
EIGEN TESTS
#eigen plot 1
zeDim = 1
pH1 <- prettyHist(
distribution = resDICA.inf$Inference.Data$components$eigs.perm[,zeDim],
observed = resDICA.inf$Fixed.Data$TExPosition.Data$eigs[zeDim],
xlim = c(0, 0.025), # needs to be set by hand
breaks = 20,
border = "white",
main = paste0("Permutation Test for Eigenvalue ",zeDim),
xlab = paste0("Eigenvalue ",zeDim),
ylab = "",
counts = FALSE,
cutoffs = c( 0.975)
)
eigs1 <- recordPlot()
eigs1
#eigen plot 2
zeDim = 2
pH2 <- pH1 <- prettyHist(
distribution = resDICA.inf$Inference.Data$components$eigs.perm[,zeDim],
observed = resDICA.inf$Fixed.Data$TExPosition.Data$eigs[zeDim],
xlim = c(0, 0.015), # needs to be set by hand
breaks = 20,
border = "white",
main = paste0("Permutation Test for Eigenvalue ",zeDim),
xlab = paste0("Eigenvalue ",zeDim),
ylab = "",
counts = FALSE,
cutoffs = c(0.975))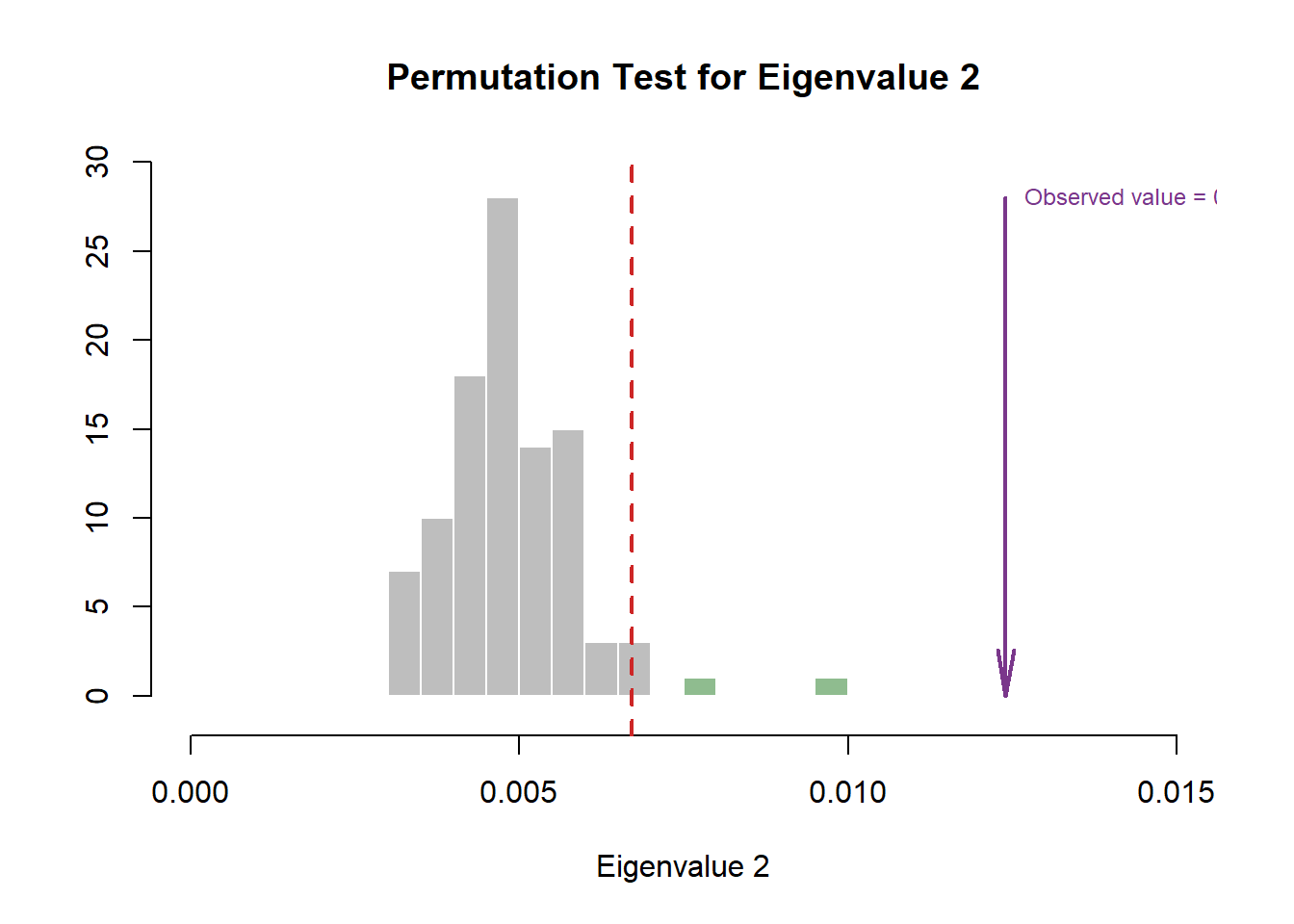
5.4.2 Row Factor Scores
5.4.3 All Observations and Their Maps
# Main Map for Observations ----
Imap <- PTCA4CATA::createFactorMap(
resDICA$TExPosition.Data$fii,
col.points = prod.color.type,
col.labels = prod.color.type,
alpha.points = .5
)
# Labels -------
label4Map <- createxyLabels.gen(1,2,
lambda = resDICA$TExPosition.Data$eigs,
tau = resDICA$TExPosition.Data$t)5.4.4 Group Means and Their Maps
#Factor map with Product as grouping
sausageMeans2 <- PTCA4CATA::getMeans(
resDICA$TExPosition.Data$fii,
wk0$Product)
#Color
prod.color.type.mean <- dplyr::recode(wk6$Product,
'SALCHICHA DE PAVO CHIMEX' = 'green3',
'Salchicha de pavo FUD' = 'green3',
'Salchicha de Pavo Nutrideli' = 'green3',
'Salchicha pavo CHERO' = 'green3',
'SALCHICHA VIENA CHIMEX' = 'orange',
'Salchicha viena FUD' = 'orange',
'Salchicha Viena Nutrideli' = 'orange',
'Salchicha VIENA VIVA' = 'orange')
#Map by Grouping under Sausage Types
MapGroup2 <- PTCA4CATA::createFactorMap(sausageMeans2,
# use the constraint from the main map
constraints = Imap$constraints,
col.points = prod.color.type.mean,
cex = 7, # size of the dot (bigger)
col.labels = prod.color.type.mean,
text.cex = 4,
pch = 17)5.4.5 Make Tolerance Intervals
Notes on Row Factor Scores Map with TI:
1. The Triangle data points are the Group Means (Barycenters) by Products.
2. The Tolerance Intervals are made by polygon of all observations per according Product Groups. As expected, we see that the Group Means data points stays in the relative “Center” of the polygon hull.
3. The coloring option here depicts Product Groups as their sausage type. We chose this coloring scheme because we found that this grouping makes the most sense from PCA.
4. Most notably, when compared to BADA, we see that the arrangement of the hulls compared to each others and the components differ significantly. This might mean that the analysis is dissecting new insights about our dataset. Perhaps, we should re-color out observation and decipher a new narrative.
#Make TI Layer Map:
TIplot.type2 <- MakeToleranceIntervals(resDICA$TExPosition.Data$fii,
design = as.factor(wk0$Product),
# line below is needed
names.of.factors = c("Dim1","Dim2"), # needed
col = prod.color.type.mean,
line.size = .50,
line.type = 3,
alpha.ellipse = .2,
alpha.line = .4,
p.level = .95)
#Compile Maps:
row.full.4TI <- Imap$zeMap_background +
TIplot.type2 + label4Map+
MapGroup2$zeMap_dots + MapGroup2$zeMap_text +
ggtitle('DICA: Group Centers with Hulls and Observations')
row.full.4TI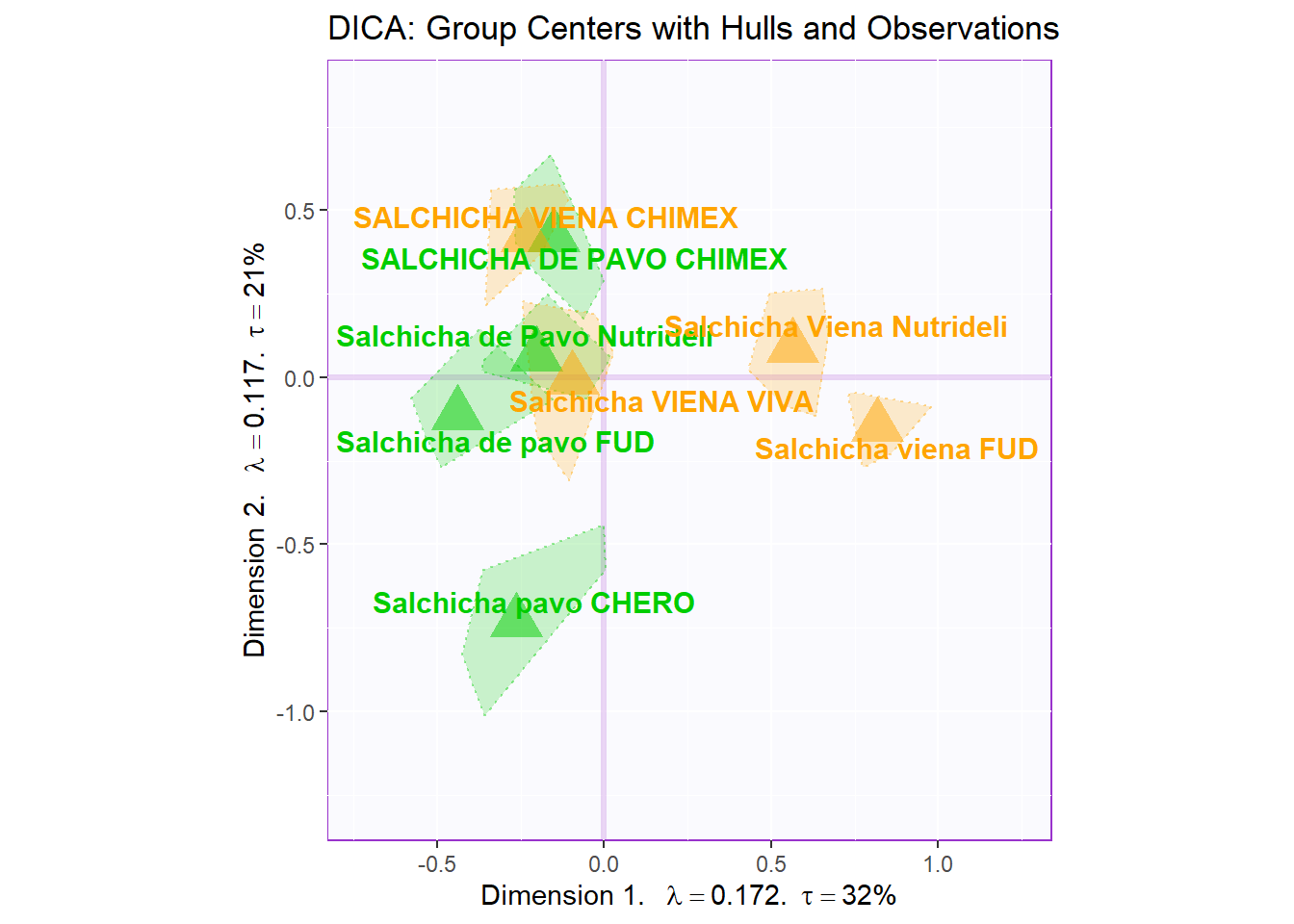
5.4.6 Make Boostrap Intervals
Notes on Row Factor Scores Map with BI:
1. The Triangle data points are the Group Means (Barycenters) by Products.
2. The Bootstrap Intervals are made by Esclipse of all observations per according Product Groups. As expected, we see that the Group Means data points stays in the relative “Center” of the polygon hull.
3. The coloring option here follow the coloring scheme for variables used in PCA - for consistency.
4. Most notably, when compared to BADA, we see that the arrangement of the Eclipses compared to each others and the components differ significantly. This might mean that the analysis is dissecting new insights about our dataset. Perhaps, we should re-color out observation and decipher a new narrative.
#Make BI Layer Map:
bootCI4mean.type <- MakeCIEllipses(resDICA.inf$Inference.Data$boot.data$fi.boot.data$boots,
col = prod.color.type.mean)
#Map by Grouping under Sausage Types
MapGroup3 <- PTCA4CATA::createFactorMap(resDICA.inf$Fixed.Data$TExPosition.Data$fi,
# use the constraint from the main map
constraints = Imap$constraints,
col.points = prod.color.type.mean,
cex = 7, # size of the dot (bigger)
col.labels = prod.color.type.mean,
text.cex = 4,
pch = 17)
#Compile Maps:
row.full.4BI <- Imap$zeMap_background +
bootCI4mean.type +
MapGroup3$zeMap_dots +
MapGroup3$zeMap_text + label4Map +
ggtitle('DICA: Group Centers with CI and Observations')
row.full.4BI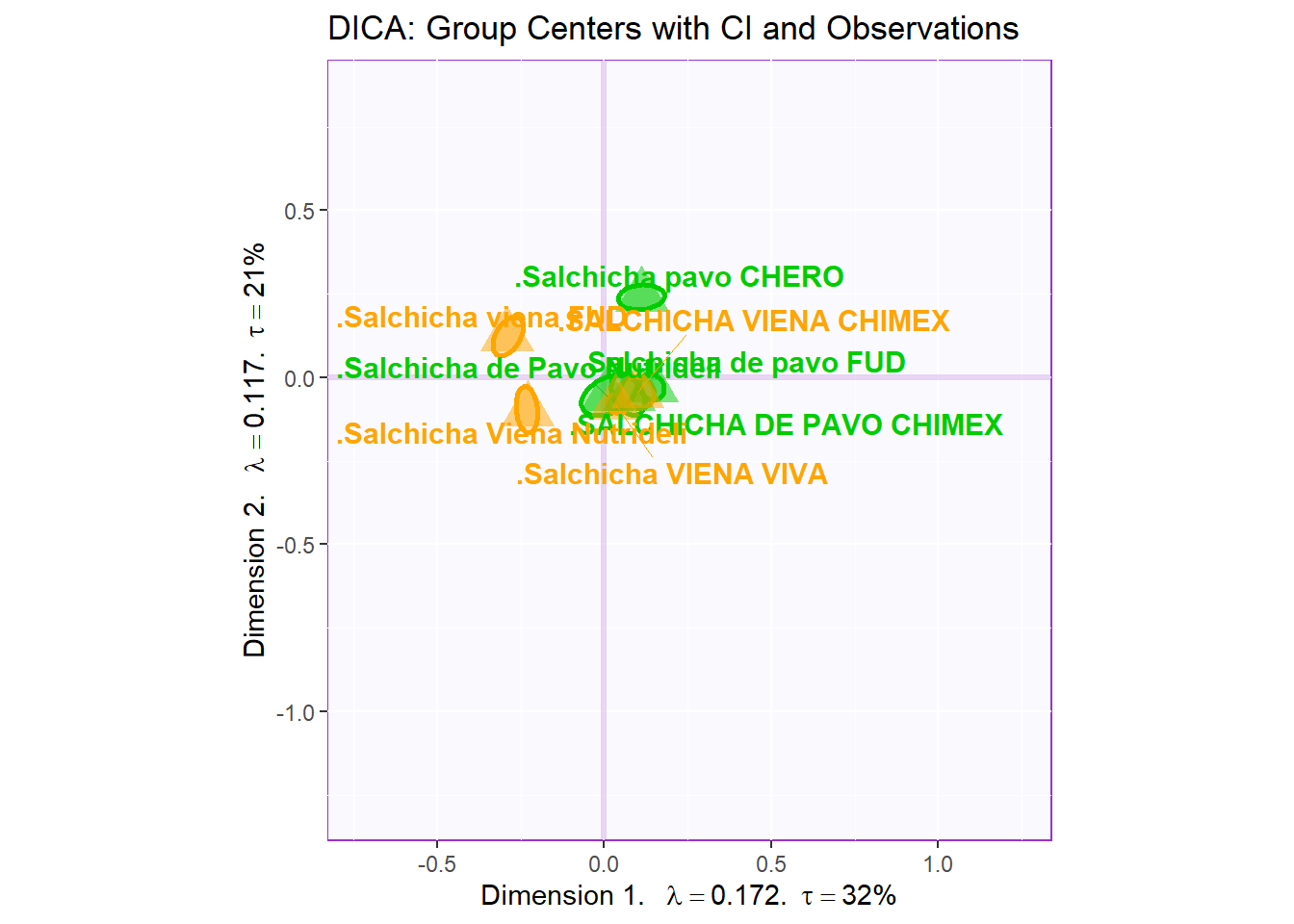
5.4.7 Columns Factor Scores
Notes on Column Factor Scores Map:
1. We see that the overall relationships between variables are relatively similar to MCA.
2. Their relationships with each component 1 and 2 also don’t differ from MCA, in term of Cosine.
3. Note that the way to interpret this plot is similar to when we interpret PCA in which we will assess the Cosine between arrows to see how similar they are to each other: small angle present they are more similar wile large (180) presents opposite relationship.
4. Most notably, when compared to BADA, we see that more variables are close to Component 1. This might means that Component 1 is is being explained by more attributes.
5.4.7.1 Loadings:
# variables fs----------
var <- colnames(sausage.processed)
var.color <- prettyGraphsColorSelection(n.colors = ncol(sausage.processed))
col4Levels <- coloringLevels(
rownames(resDICA$TExPosition.Data$fj), var.color)
#too many var to assign color manually so we use prettyGraphsColorSelection() to automatically assign colors
#Column Factor Scores----
Fj <- resDICA$TExPosition.Data$fj
baseMap.j <- PTCA4CATA::createFactorMap(Fj,
col.points = col4Levels$color4Levels,
alpha.points = .3,
col.labels = col4Levels$color4Levels)
# arrows
zeArrows <- addLines4MCA(Fj, col4Var = col4Levels$color4Levels)
# A graph for the J-set
b001.aggMap.j <- baseMap.j$zeMap_background + # background
baseMap.j$zeMap_dots + # dots
baseMap.j$zeMap_text + # names
label4Map # lables for the axes
b002.aggMap.j <- b001.aggMap.j + zeArrows
b003.aggMap.j <- baseMap.j$zeMap_background + # background
baseMap.j$zeMap_text + # names
zeArrows + label4Map +
ggtitle('DICA: Col Factor Scores - All Levels')
b003.aggMap.j 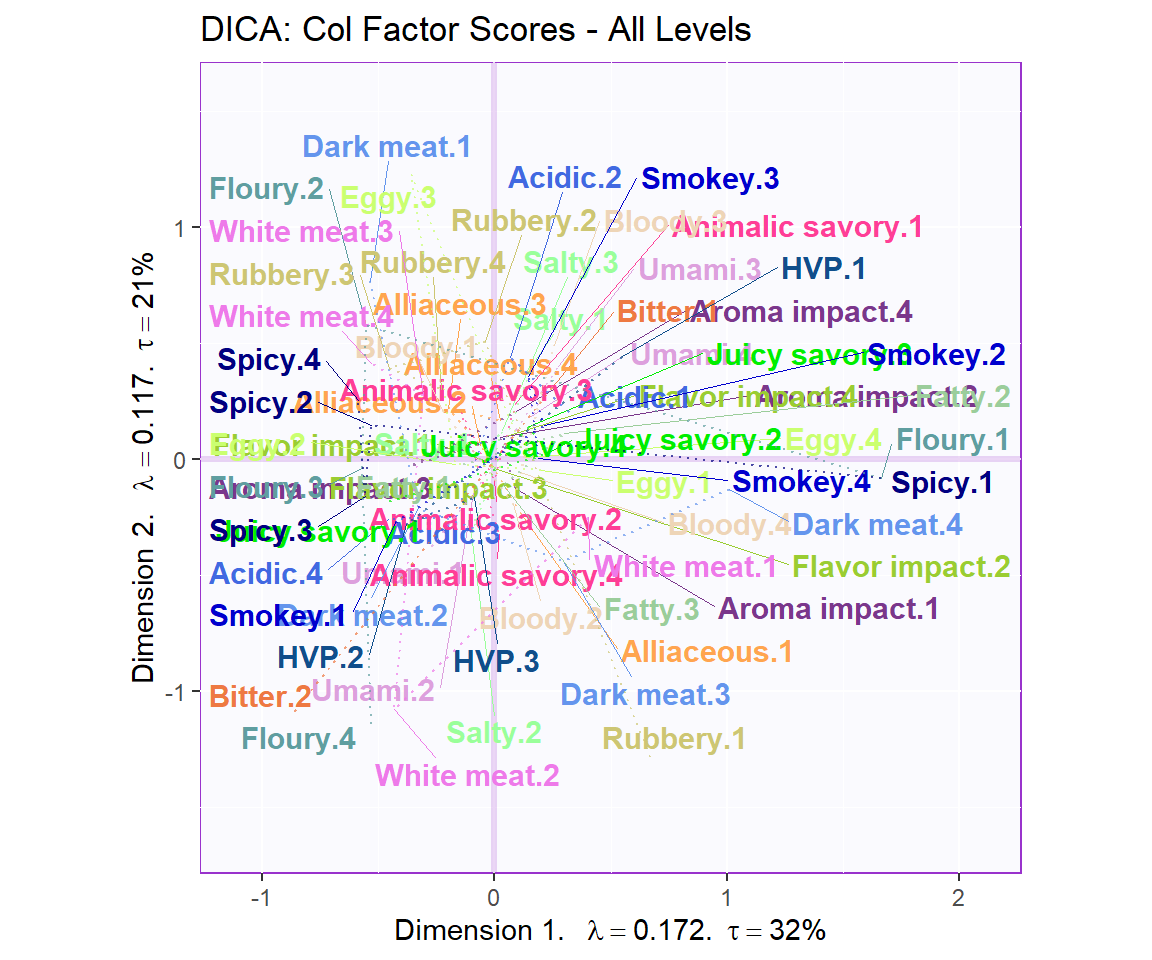
5.4.7.2 Loadings based on Important Variables:
#Color for Sigificant Vars
t.color <- as.data.frame(col4Levels$color4Levels)
rownames(t.color) <- rownames(Fj)
t.color.sig <- t.color[c("Bitter.2", "Floury.2", "Floury.3", "Dark meat.1",
"Dark meat.4", "Dark meat.3", "HVP.1", "HVP.2",
"Juicy savory.1", "Rubbery.2", "White meat.2",
"Rubbery.3", "Rubbery.1", "Smokey.1", "Spicy.3",
"Spicy.2", "Spicy.1", "White meat.1", "Salty.2",
"Salty.1", "Umami.1", "Umami.3", "Bitter.1",
"Floury.1", "Floury.4"
),]
#Column Factor Scores----
Fj <- resDICA$TExPosition.Data$fj
baseMap.j <- PTCA4CATA::createFactorMap(Fj [c("Bitter.2", "Floury.2", "Floury.3", "Dark meat.1",
"Dark meat.4", "Dark meat.3", "HVP.1", "HVP.2",
"Juicy savory.1", "Rubbery.2", "White meat.2",
"Rubbery.3", "Rubbery.1", "Smokey.1", "Spicy.3",
"Spicy.2", "Spicy.1", "White meat.1", "Salty.2",
"Salty.1", "Umami.1", "Umami.3", "Bitter.1",
"Floury.1", "Floury.4"
),],
col.points = t.color.sig,
alpha.points = .3,
col.labels = t.color.sig)
# arrows
zeArrows <- addLines4MCA(Fj, col4Var = t.color.sig, size = 0.5)
# A graph for the J-set
b001.aggMap.j <- baseMap.j$zeMap_background + # background
baseMap.j$zeMap_dots + # dots
baseMap.j$zeMap_text + # names
label4Map # lables for the axes
b002.aggMap.j <- b001.aggMap.j + zeArrows
b004.aggMap.j <- baseMap.j$zeMap_background + # background
baseMap.j$zeMap_text + # names
zeArrows + label4Map +
ggtitle('DICA: Col Factor Scores - Important Levels Only')
b004.aggMap.j 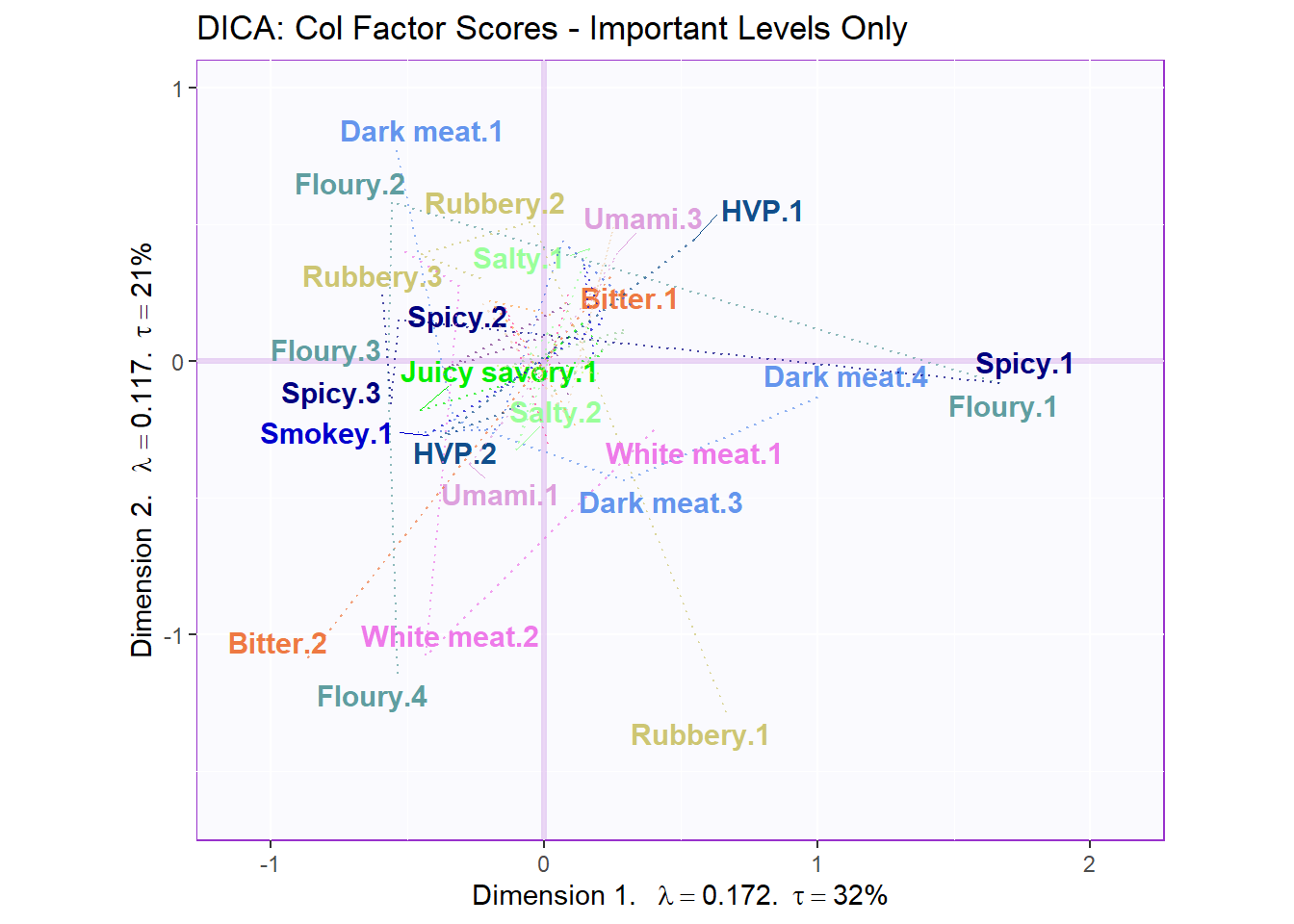
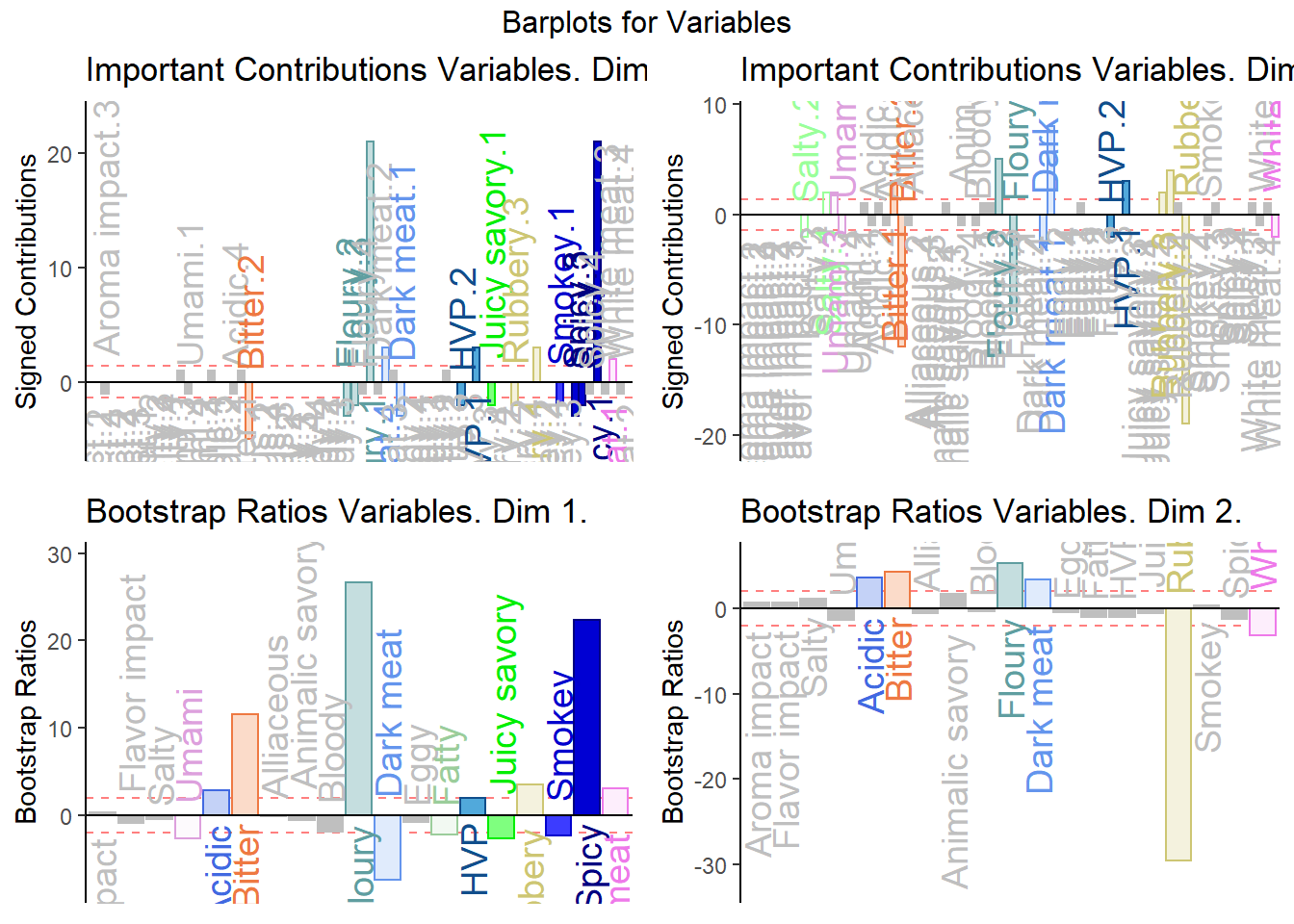
5.4.8 Contributions and Bootstrap Ratios
5.4.8.1 Contributions
#Contributions
ctrj <- resDICA$TExPosition.Data$cj
signed.ctrj <- ctrj * sign(resDICA$TExPosition.Data$fj)
# Contrib 1
c001.plotCtrj.1 <- PrettyBarPlot2(
bootratio = round(100*signed.ctrj[,1]),
threshold = 100 / nrow(signed.ctrj),
ylim = NULL,
color4bar = gplots::col2hex(col4Levels$color4Levels),
color4ns = "gray75",
plotnames = TRUE,
main = 'Important Contributions Variables. Dim 1.',
ylab = "Signed Contributions",
font.size = 5)
print(c001.plotCtrj.1)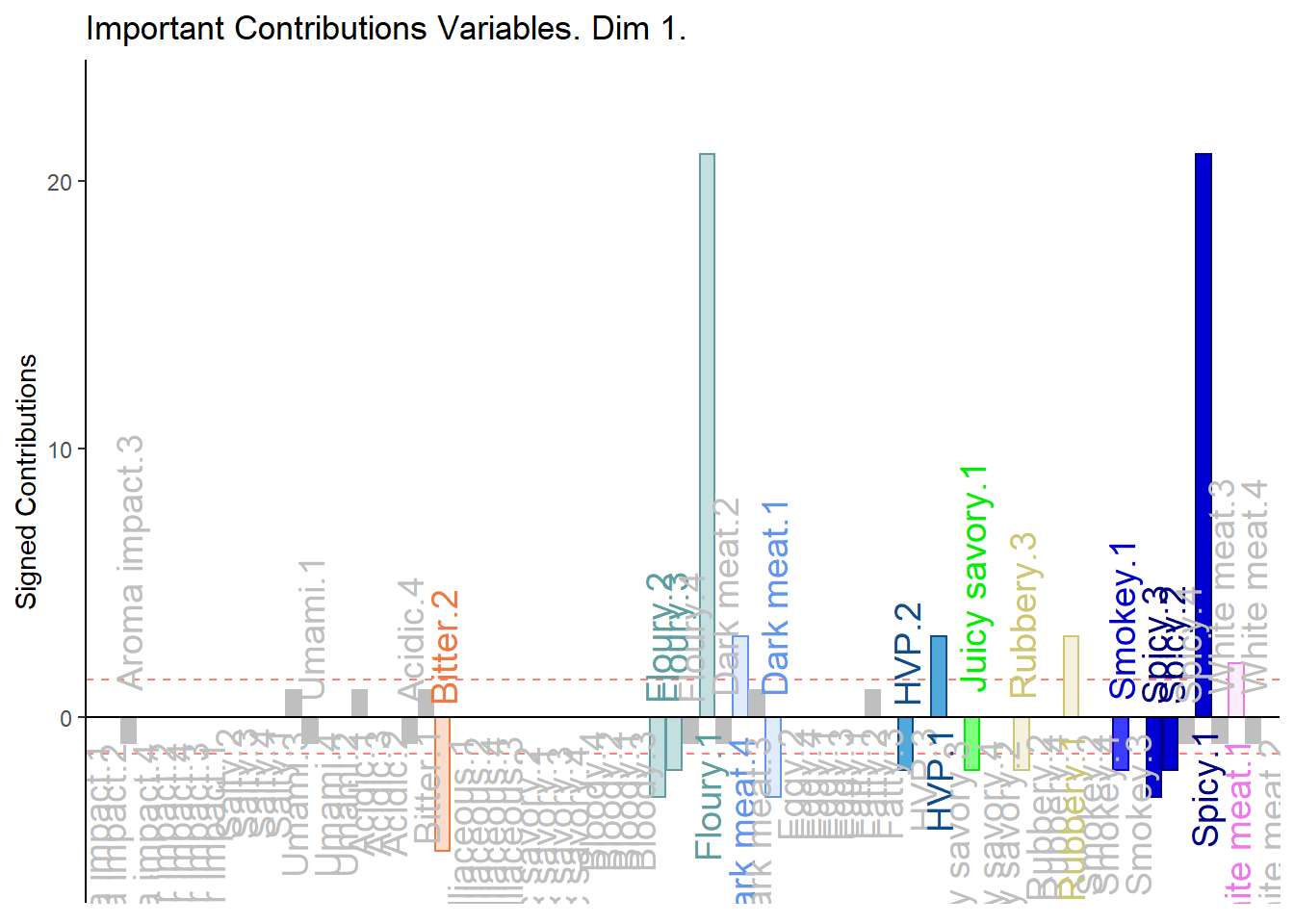
# Contrib 2
c002.plotCtrj.2 <- PrettyBarPlot2(
bootratio = round(100*signed.ctrj[,2]),
threshold = 100 / nrow(signed.ctrj),
ylim = NULL,
color4bar = gplots::col2hex(col4Levels$color4Levels),
color4ns = "gray75",
plotnames = TRUE,
main = 'Important Contributions Variables. Dim 2.',
ylab = "Signed Contributions",
font.size = 5)
print(c002.plotCtrj.2)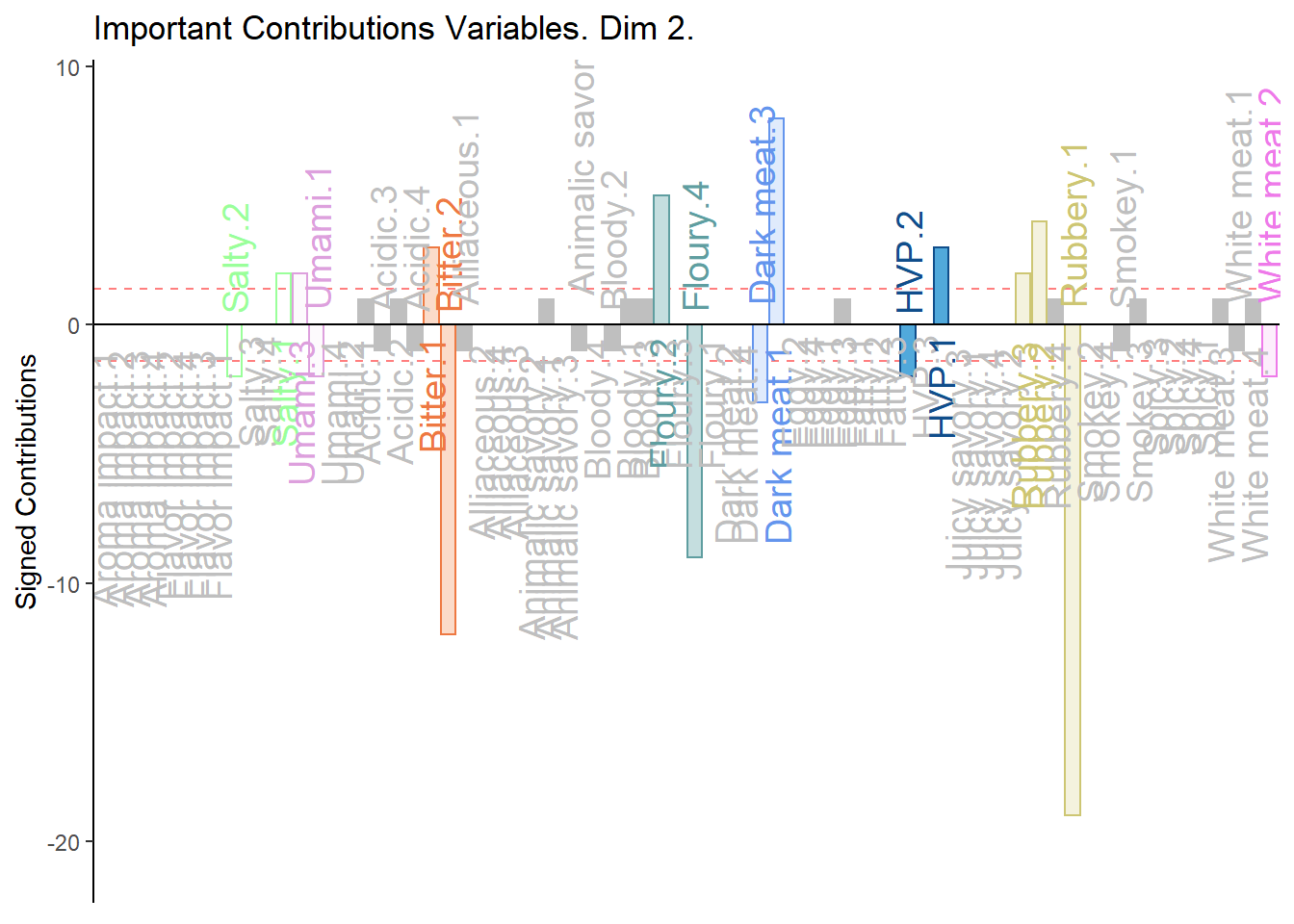
5.4.8.2 BOOTSTRAP RATIOS
# Bootstrap ratios
BRj <- resDICA.inf$Inference.Data$boot.data$fj.boot.data$tests$boot.ratios
# BR1
d001.plotBRj.1 <- PrettyBarPlot2(
bootratio = BRj[,1],
threshold = 2,
ylim = NULL,
color4bar = gplots::col2hex(var.color),
color4ns = "gray75",
plotnames = TRUE,
main = 'Bootstrap Ratios Variables. Dim 1.',
ylab = "Bootstrap Ratios",
font.size = 5)
print(d001.plotBRj.1)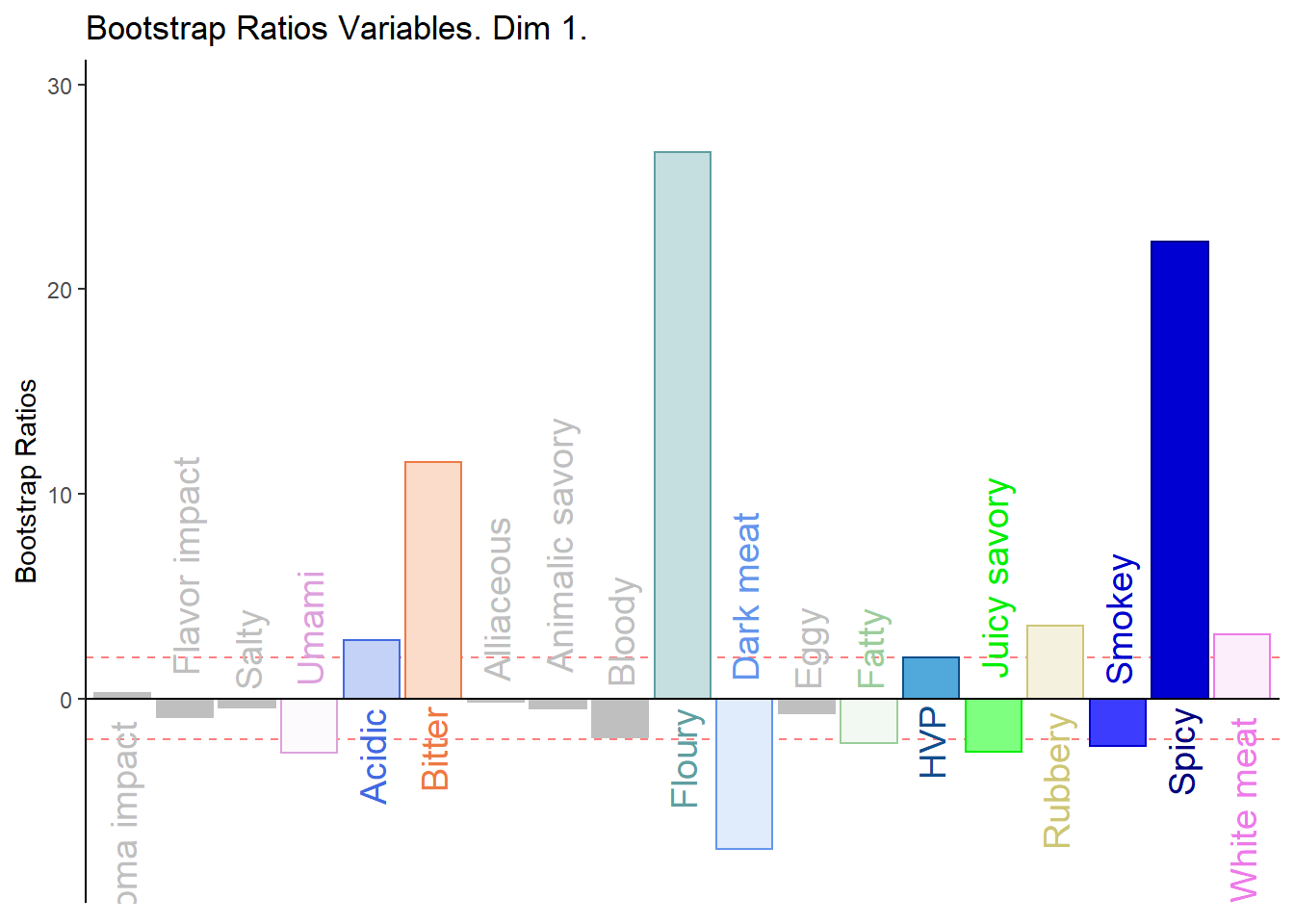
#BR. 2
d003.plotBRj.2 <- PrettyBarPlot2(
bootratio = BRj[,2],
threshold = 2,
ylim = NULL,
color4bar = gplots::col2hex(var.color),
color4ns = "gray75",
plotnames = TRUE,
main = 'Bootstrap Ratios Variables. Dim 2.',
ylab = "Bootstrap Ratios",
font.size = 5)
print(d003.plotBRj.2)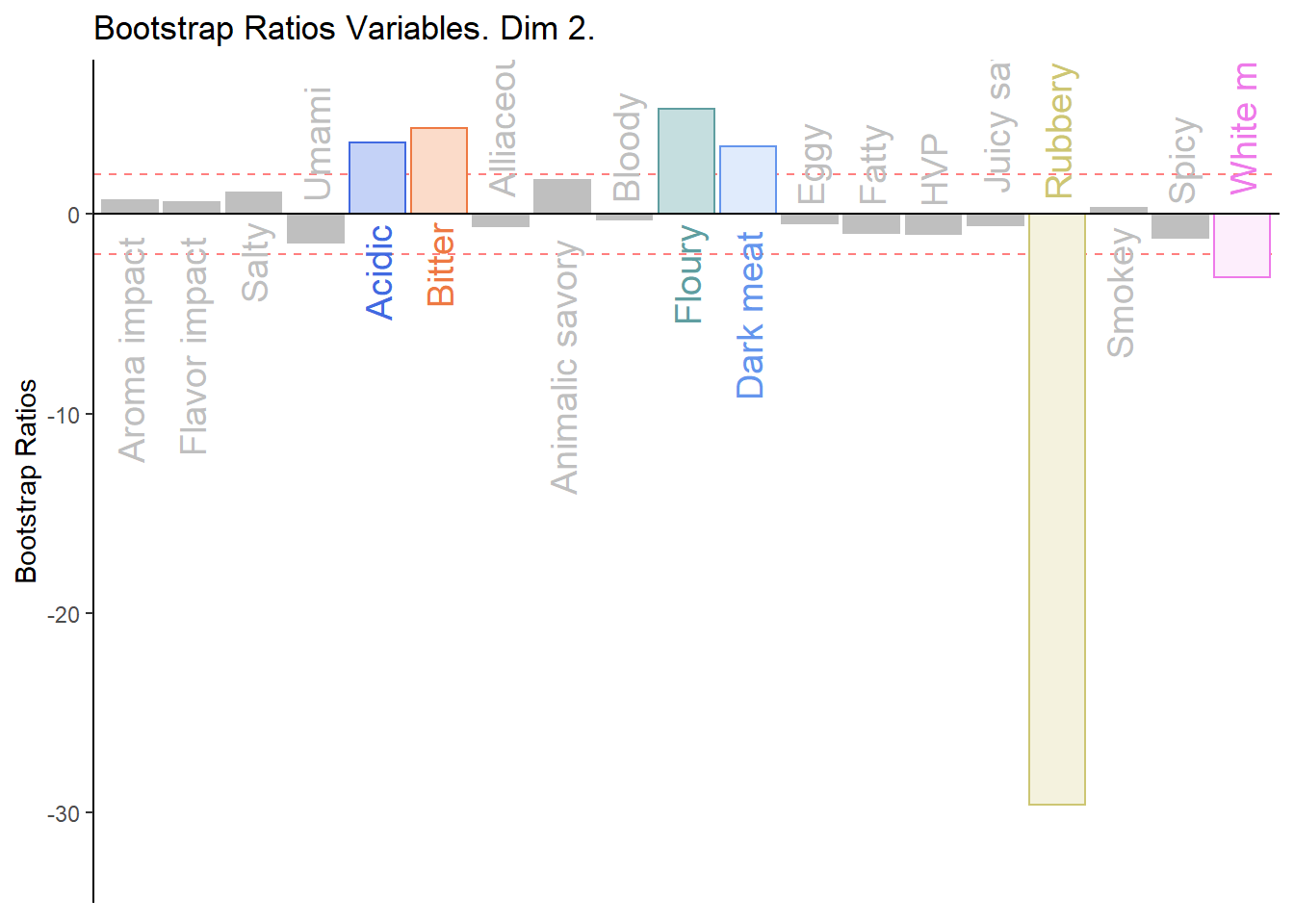
5.4.8.3 Combine All Barplots:
Notes on Barplots:
1. We see that the overall relationships between variables, compared to average contribustion are exactly similar to MCA.
2. We do notice a few variables show a more pronounce contribution (either positive or negativce) compared to MCA.
3. When compared to BADA, we see that there are fewer variables with contribution level higher than average. Other than the ones found in BADA, we notice some returning variables like White Meat, Dark Meat, Acidic, Spicy, FLoury, Smokey and Rubbery.
#We then use the next line of code to put two figures side to side:
final.output.barplots <- grid.arrange(
c001.plotCtrj.1,
c002.plotCtrj.2,
d001.plotBRj.1,
d003.plotBRj.2,
ncol = 2,nrow = 2,
top = "Barplots for Variables"
)