C Szablony
Uwagi
Arkusze Google są oczywiście udostępnione tylko do odczytu. Aby skorzystać z szablonów, należy zalogować się na konto Google, a następnie wybrać z menu Plik > Utwórz kopię.
W arkuszach starałem się zachować następującą konwencję, jeżeli chodzi o kolory:
Zielony kolor oznacza miejsca, które należy zmienić (np. wprowadzić dane).
Żółtym kolorem zaznaczono najważniejsze wyniki, nie powinno się zmieniać formuł w tych polach ani nic wpisywać.
Niektóre komórki mogą zawierać obliczenia, mimo że wyglądają na puste. Należy zachować ostrożność i nie nadpisywać tych komórek.
Szablony w Excel mogą nie działać w Excelu 2007 ze względu na ograniczoną dostępność funkcji statystycznych w tej wersji Excela. Użytkowników Excela 2007 proszę o zgłaszanie, które arkusze nie działają – być może uda się znaleźć obejście.
C.1 Wzór Bayesa
Wzór Bayesa — arkusz Google
Wzór Bayesa — szablon w Excelu: Bayes.xlsx
# Oznaczenia hipotez (opcjonalnie)
hipotezy <- c("Choroba", "Brak choroby")
# Zaczątek (rozkład a priori, ang. prior)
prior <- c(.001, .999)
# Zdarzalność (prawdopodobieństwa warunkowe danych, ang. likelihood)
likelihood <- c(.95, .01)
# Wyznaczenie wyniku (rozkładu a posteriori, ang. posterior)
posterior <- prior*likelihood
posterior <- posterior/sum(posterior)
# Sprawdzenie
if(length(prior)!=length(likelihood))
{print("Liczebność wektorów prior (zaczątek) i likelihood (zdarzalność) powinna być równa. ")}
if(sum(prior)!=1){
print("Suma prawdopodobieństw w rozkładzie zaczątkowym (prior) powinna być równa 1.")}
if (!exists("hipotezy") || length(hipotezy)!=length(prior)) {
hipotezy <- paste0('H', 1:length(prior))
}
# Wynik w formie ramki danych:
print(data.frame(
Hipotezy = hipotezy, `Zaczątek` = prior, `Zdarzalność` = likelihood, `Wynik` = posterior
))## Hipotezy Zaczątek Zdarzalność Wynik
## 1 Choroba 0.001 0.95 0.08683729
## 2 Brak choroby 0.999 0.01 0.91316271# Wykres
library(ggplot2)
hipotezy<-factor(hipotezy, levels=hipotezy)
df <- data.frame(Hipotezy = c(hipotezy, hipotezy),
`Rozkład` = factor(c(rep("zaczątek", length(prior)), rep("wynik", length(posterior))),
levels=c("zaczątek", "wynik")
),
`Prawdopodobieństwo` = c(prior, posterior)
)
ggplot(data=df, aes(x=Hipotezy, y=`Prawdopodobieństwo`, fill=`Rozkład`)) +
geom_bar(stat="identity", position=position_dodge())+
geom_text(aes(label = format(round(`Prawdopodobieństwo`,4), nsmall=4), group=`Rozkład`),
position = position_dodge(width = .9), vjust = -0.2)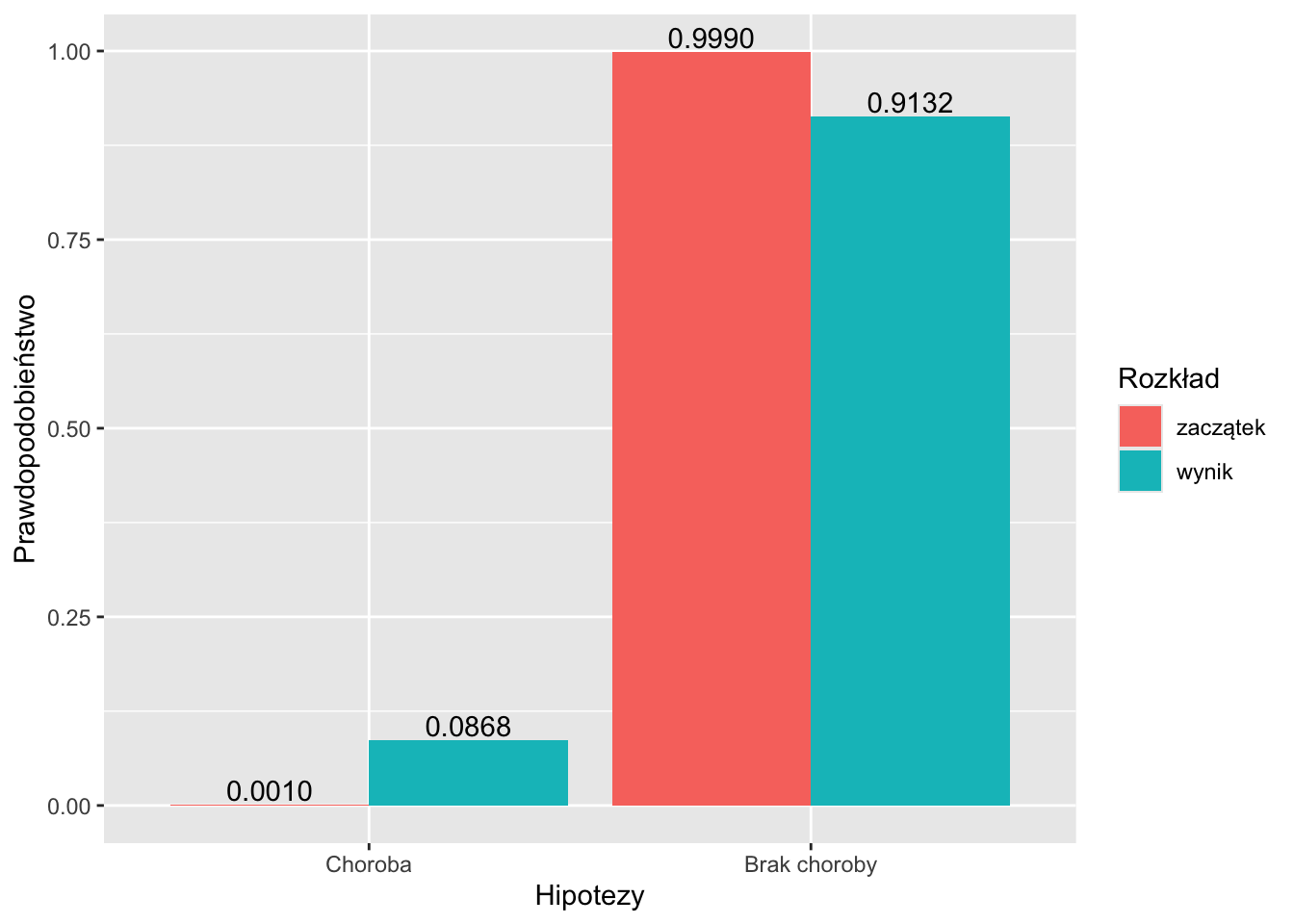
# Oznaczenia hipotez (opcjonalnie)
hipotezy = ["Choroba", "Brak choroby"]
# Zaczątek (rozkład a priori, ang. prior)
prior = [.001, .999]
# Zdarzalność (prawdopodobieństwa warunkowe danych, ang. likelihood)
likelihood = [.95, .01]
# Wyznaczenie wyniku (rozkładu a posteriori, ang. posterior)
posterior = [a*b for a, b in zip(prior, likelihood)]
posterior = [p/sum(posterior) for p in posterior]
# Sprawdzenie
if len(prior) != len(likelihood):
print("Liczebność wektorów prior (zaczątek) i likelihood (zdarzalność) powinna być równa.")
if sum(prior) != 1:
print("Suma prawdopodobieństw w rozkładzie zaczątkowym (prior) powinna być równa 1.")
if not "hipotezy" in locals() or len(hipotezy) != len(prior):
hipotezy = ["H" + str(i) for i in range(1, len(prior)+1)]
# Wynik w formie ramki danych:
import pandas as pd
df = pd.DataFrame({
"Hipotezy": hipotezy,
"Zaczątek": prior,
"Zdarzalność": likelihood,
"Wynik": posterior
})
print(df)## Hipotezy Zaczątek Zdarzalność Wynik
## 0 Choroba 0.001 0.95 0.086837
## 1 Brak choroby 0.999 0.01 0.913163import numpy as np
import matplotlib.pyplot as plt
x = np.arange(len(hipotezy))
width = 0.375
fig, ax = plt.subplots(layout='constrained')
rects = ax.bar(x-width/2, np.round(prior, 4), width, label = 'zaczątek')
ax.bar_label(rects, padding=3)
rects = ax.bar(x+width/2, np.round(posterior, 4), width, label = 'wynik')
ax.bar_label(rects, padding=3)
ax.set_ylabel('prawdopodobieństwo')
ax.set_xlabel('hipotezy')
ax.set_xticks(x, hipotezy)
ax.legend(loc='upper left', ncols=2)
#ax.set_ylim(0, np.max([prior, posterior])*1.2)
plt.show()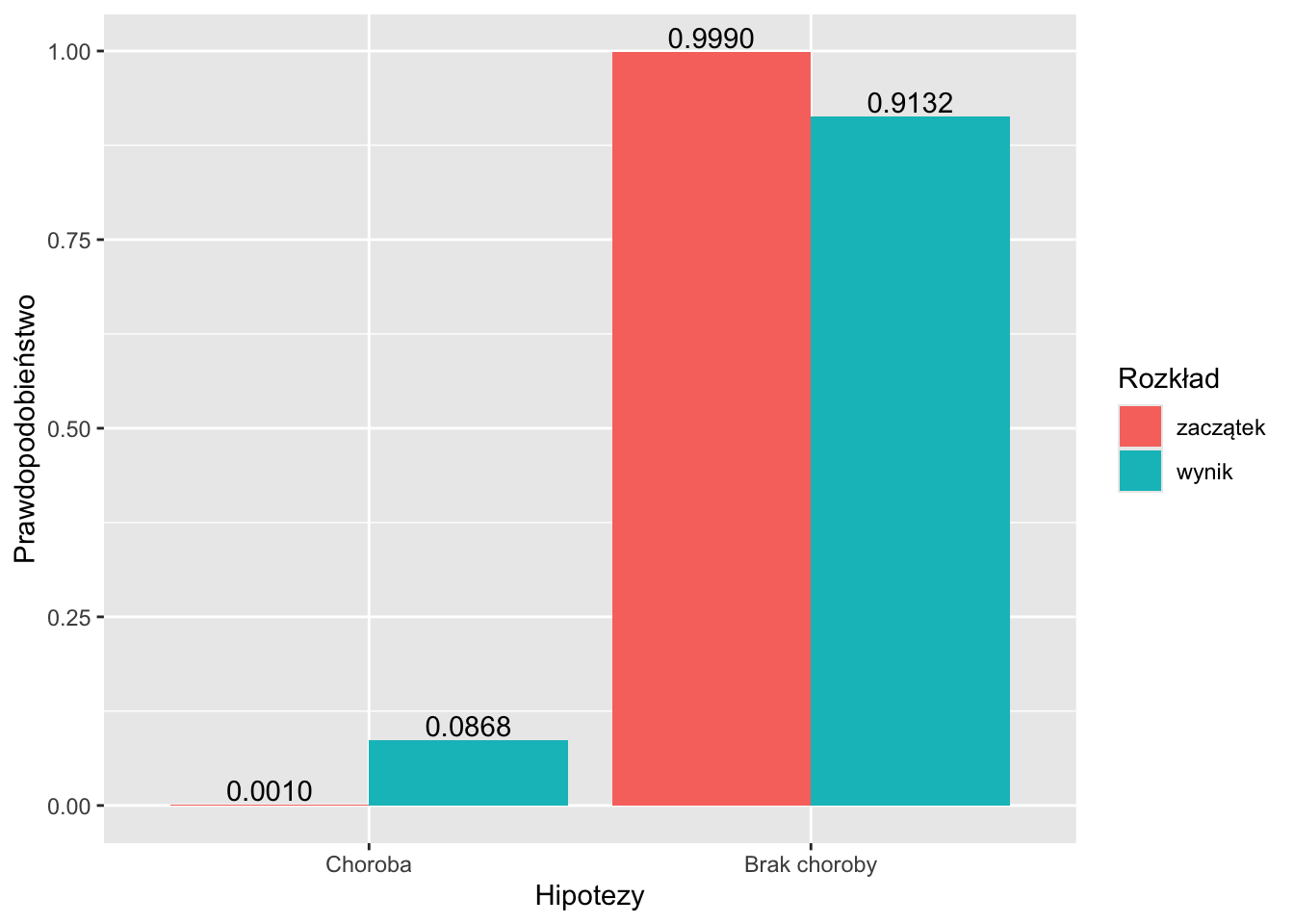
C.2 Rozkłady
C.2.1 Dyskretna zmienna losowa
Dyskretna zmienna losowa – kalkulator — arkusz Google
Dyskretna zmienna losowa – kalkulator — szablon w Excelu
# Rozkład dyskretny jednej zmiennej
x <- c(0, 1, 4)
Px <- c(1/3, 1/3, 1/3)
# Sprawdzenie
if(length(x)!=length(Px))
{print("Oba wektory powinny być równej długości.")}
if(!sum(Px)==1)
{print("Prawdopodobieństwa powinny sumować się do 1. ")}
if(any(Px<0))
{print("Prawdopodobieństwa nie mogą być ujemne. ")}
# Obliczenia
EX <- sum(x*Px)
VarX <- sum((x-EX)^2*Px)
SDX <- sqrt(VarX)
SkX <- sum((x-EX)^3*Px)/SDX^3
KurtX <- sum((x-EX)^4*Px)/SDX^4 - 3
print(c('Wartość oczekiwana' = EX,
'Wariancja' = VarX,
'Odchylenie standardowe' = SDX,
'Skośność' = SkX,
'(Nadwyżkowa) kurtoza' = KurtX))## Wartość oczekiwana Wariancja Odchylenie standardowe
## 1.666667 2.888889 1.699673
## Skośność (Nadwyżkowa) kurtoza
## 0.528005 -1.500000# Rozkład dyskretny dwóch zmiennych
x <- c(2, -1, -1)
y <- c(-1, 1, -1)
Pxy <- c(1/2, 1/3, 1-1/2-1/3) #sum(c(1/2, 1/3, 1/6))==1 zwraca czasem FALSE z powodów numerycznych
# Sprawdzenie
if(length(x)!=length(y) || length(x)!=length(Pxy))
{print("Wektory powinny być równej długości. ")}
if(!sum(Pxy)==1)
{print("Prawdopodobieństwa powinny sumować się do 1. ")}
if(any(Pxy<0))
{print("Prawdopodobieństwa nie mogą być ujemne. ")}
EX <- sum(x*Pxy)
VarX <- sum((x-EX)^2*Pxy)
SDX <- sqrt(VarX)
SkX <- sum((x-EX)^3*Pxy)/SDX^3
KurtX <- sum((x-EX)^4*Pxy)/SDX^4 - 3
EY <- sum(y*Pxy)
VarY <- sum((y-EY)^2*Pxy)
SDY <- sqrt(VarY)
SkY <- sum((y-EY)^3*Pxy)/SDY^3
KurtY <- sum((y-EY)^4*Pxy)/SDY^4 - 3
CovXY <- sum((x-EX)*(y-EY)*Pxy)
CorXY <- CovXY/(SDX*SDY)
print(c('Wartość oczekiwana X' = EX,
'Wariancja X' = VarX,
'Odchylenie standardowe X' = SDX,
'Skośność X' = SkX,
'(Nadwyżkowa) kurtoza X' = KurtX,
'Wartość oczekiwana Y' = EY,
'Wariancja Y' = VarY,
'Odchylenie standardowe Y' = SDY,
'Skośność Y' = SkY,
'(Nadwyżkowa) kurtoza Y' = KurtY,
'Kowariancja X i Y' = CovXY,
'Korelacja X i Y' = CorXY
))## Wartość oczekiwana X Wariancja X Odchylenie standardowe X
## 5.000000e-01 2.250000e+00 1.500000e+00
## Skośność X (Nadwyżkowa) kurtoza X Wartość oczekiwana Y
## -3.289550e-17 -2.000000e+00 -3.333333e-01
## Wariancja Y Odchylenie standardowe Y Skośność Y
## 8.888889e-01 9.428090e-01 7.071068e-01
## (Nadwyżkowa) kurtoza Y Kowariancja X i Y Korelacja X i Y
## -1.500000e+00 -1.000000e+00 -7.071068e-01# Rozkład dyskretny jednej zmiennej
x = [0, 1, 4]
Px = [1/3, 1/3, 1/3]
# Sprawdzenie
if len(x) != len(Px):
print("Oba wektory powinny być równej długości.")
if sum(Px) != 1:
print("Prawdopodobieństwa powinny sumować się do 1. ")
if any(p < 0 for p in Px):
print("Prawdopodobieństwa nie mogą być ujemne. ")
# Obliczenia
EX = sum([a*b for a, b in zip(x, Px)])
VarX = sum([(a-EX)**2*b for a, b in zip(x, Px)])
SDX = VarX**0.5
SkX = sum([(a-EX)**3*b for a, b in zip(x, Px)]) / SDX**3
KurtX = sum([(a-EX)**4*b for a, b in zip(x, Px)]) / SDX**4 - 3
# Wyniki
print({'Wartość oczekiwana': EX,
'Wariancja': VarX,
'Odchylenie standardowe': SDX,
'Skośność': SkX,
'(Nadwyżkowa) kurtoza': KurtX})## {'Wartość oczekiwana': 1.6666666666666665, 'Wariancja': 2.888888888888889, 'Odchylenie standardowe': 1.699673171197595, 'Skośność': 0.5280049792181879, '(Nadwyżkowa) kurtoza': -1.5000000000000002}# Rozkład dyskretny dwóch zmiennych
x = [2, -1, -1]
y = [-1, 1, -1]
Pxy = [1/2, 1/3, 1-1/2-1/3]
# Sprawdzenie
if len(x) != len(y) or len(x) != len(Pxy):
print("Wektory powinny być równej długości. ")
if sum(Pxy) != 1:
print("Prawdopodobieństwa powinny sumować się do 1. ")
if any(p < 0 for p in Pxy):
print("Prawdopodobieństwa nie mogą być ujemne. ")
# Obliczenia
EX = sum([a*b for a, b in zip(x, Pxy)])
VarX = sum([(a-EX)**2*b for a, b in zip(x, Pxy)])
SDX = VarX**0.5
SkX = sum([(a-EX)**3*b for a, b in zip(x, Pxy)]) / SDX**3
KurtX = sum([(a-EX)**4*b for a, b in zip(x, Pxy)]) / SDX**4 - 3
EY = sum([a*b for a, b in zip(y, Pxy)])
VarY = sum([(a-EY)**2*b for a, b in zip(y, Pxy)])
SDY = VarY**0.5
SkY = sum([(a-EY)**3*b for a, b in zip(y, Pxy)]) / SDY**3
KurtY = sum([(a-EY)**4*b for a, b in zip(y, Pxy)]) / SDY**4 - 3
CovXY = sum([(a-EX)*(b-EY)*c for a, b, c in zip(x, y, Pxy)])
CorXY = CovXY / (SDX*SDY)
# Wyniki
print({'Wartość oczekiwana X': EX,
'Wariancja X': VarX,
'Odchylenie standardowe X': SDX,
'Skośność X': SkX,
'(Nadwyżkowa) kurtoza X': KurtX,
'Wartość oczekiwana Y': EY,
'Wariancja Y': VarY,
'Odchylenie standardowe Y': SDY,
'Skośność Y': SkY,
'(Nadwyżkowa) kurtoza Y': KurtY,
'Kowariancja X i Y': CovXY,
'Korelacja X i Y': CorXY
})## {'Wartość oczekiwana X': 0.5, 'Wariancja X': 2.25, 'Odchylenie standardowe X': 1.5, 'Skośność X': -3.289549702593056e-17, '(Nadwyżkowa) kurtoza X': -2.0, 'Wartość oczekiwana Y': -0.33333333333333337, 'Wariancja Y': 0.888888888888889, 'Odchylenie standardowe Y': 0.9428090415820634, 'Skośność Y': 0.7071067811865478, '(Nadwyżkowa) kurtoza Y': -1.4999999999999991, 'Kowariancja X i Y': -1.0, 'Korelacja X i Y': -0.7071067811865476}C.2.2 Sparametryzowane rozkłady dyskretne
Kalkulator dla rozkładów dyskretnych — arkusz Google
Kalkulator dla rozkładów dyskretnych — szablon w Excelu: Rozkłady_dyskretne.xlsx
# Rozkład dwumianowy
n <- 18
p <- 0.6
from <- 12
to <- 14
result <- pbinom(to, n, p)-pbinom(from-1, n, p)
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
} else {
p=paste0("P(", from, " <= X <= ", to, ")")
print(p)
print(result)
}## [1] "P(12 <= X <= 14)"
## [1] 0.3414956# Rozkład Poissona
lambda <- 5/3
from <- 2
to <- Inf
result <- ppois(to, lambda)-ppois(from-1, lambda)
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
} else {
p=paste0("P(", from, " <= X <= ", to, ")")
print(p)
print(result)
}## [1] "P(2 <= X <= Inf)"
## [1] 0.4963317# Rozkład hipergeometryczny
N <- 49
r <- 6
n <- 6
from <- 3
to <- 6
result <- phyper(to, r, N-r, n)-phyper(from-1, r, N-r, n)
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
} else {
p=paste0("P(", from, " <= X <= ", to, ")")
print(p)
print(result)
}## [1] "P(3 <= X <= 6)"
## [1] 0.01863755from scipy.stats import binom, poisson, hypergeom
# Rozkład dwumianowy
n = 18
p = 0.6
_from = 12
_to = 14
result = binom.cdf(_to, n, p) - binom.cdf(_from-1, n, p)
if _from > _to:
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
else:
p = "P(" + str(_from) + " <= X <= " + str(_to) + ")"
print(p)
print(result)## P(12 <= X <= 14)
## 0.34149556326865305
# Rozkład Poissona
lambda_val = 5/3
from_val = 2
to_val = float('inf')
result = poisson.cdf(to_val, lambda_val) - poisson.cdf(from_val-1, lambda_val)
if from_val > to_val:
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
else:
p = "P(" + str(from_val) + " <= X <= " + str(to_val) + ")"
print(p)
print(result)## P(2 <= X <= inf)
## 0.49633172576650164
# Rozkład hipergeometryczny
N = 49
r = 6
n = 6
_from = 3
_to = 6
result = hypergeom.cdf(_to, N, r, n) - hypergeom.cdf(_from-1, N, r, n)
if _from > _to:
print("!!! Wartość 'od' nie może być większa od wartości 'do' !!!")
else:
p = "P(" + str(_from) + " <= X <= " + str(_to) + ")"
print(p)
print(result) ## P(3 <= X <= 6)
## 0.018637545002022304C.2.3 Rozkłady ciągłe
Kalkulator dla rozkładu normalnego — arkusz Google
Kalkulator dla rozkładu normalnego — szablon w Excelu: Kalkulator_rozkladu_normalnego.xlsx
##### 1. Pole pod krzywą #####
# Parametry rozkładu Gaussa:
# średnia:
m <- 0
# odchylenie standardowe:
sd <- 2
# Będziemy obliczać pole pod krzywą gęstości rozkładu Gaussa
# od
# *można wpisać from <- -Inf, co oznacza minus nieskończoność
from <- -Inf
# do
# *można wpisać to <- Inf, co oznacza (plus) nieskończoność
to <- 2
# Sprawdzenie danych, obliczenie pola pod krzywą
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
} else {
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", from, ")")
} else if (from==-Inf) {
p=paste0("P(X<", to, ")")
} else {
p=paste0("P(", from, "<X<", to, ")")
}
print(p)
# Obliczenie prawdopodobieństwa, czyli pole pod wycinkiem krzywej:
result<-pnorm(to, m, sd)-pnorm(from, m, sd)
print(result)
}## [1] "P(X<2)"
## [1] 0.8413447# Rysunek
library(ggplot2)
x1=if(from==-Inf){min(-4*sd+m, to-2*sd)} else {min(from-2*sd, -4*sd+m)}
x2=if(to==Inf){max(4*sd+m, from+2*sd)} else {max(to+2*sd, 4*sd+m)}
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dnorm(x, m, sd)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dnorm(x, m, sd)}, col = "blue", lty=2, lwd=1) +
scale_x_continuous(breaks=c(m, m-sd, m-2*sd, m+sd, m+2*sd, m-3*sd, m+3*sd, m-4*sd, m+4*sd)) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("M = ", m, "\nSD = ", sd, "\n", p, " = ", signif(result,6)),
x = x1, y = dnorm(m, m, sd)*1.2, size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))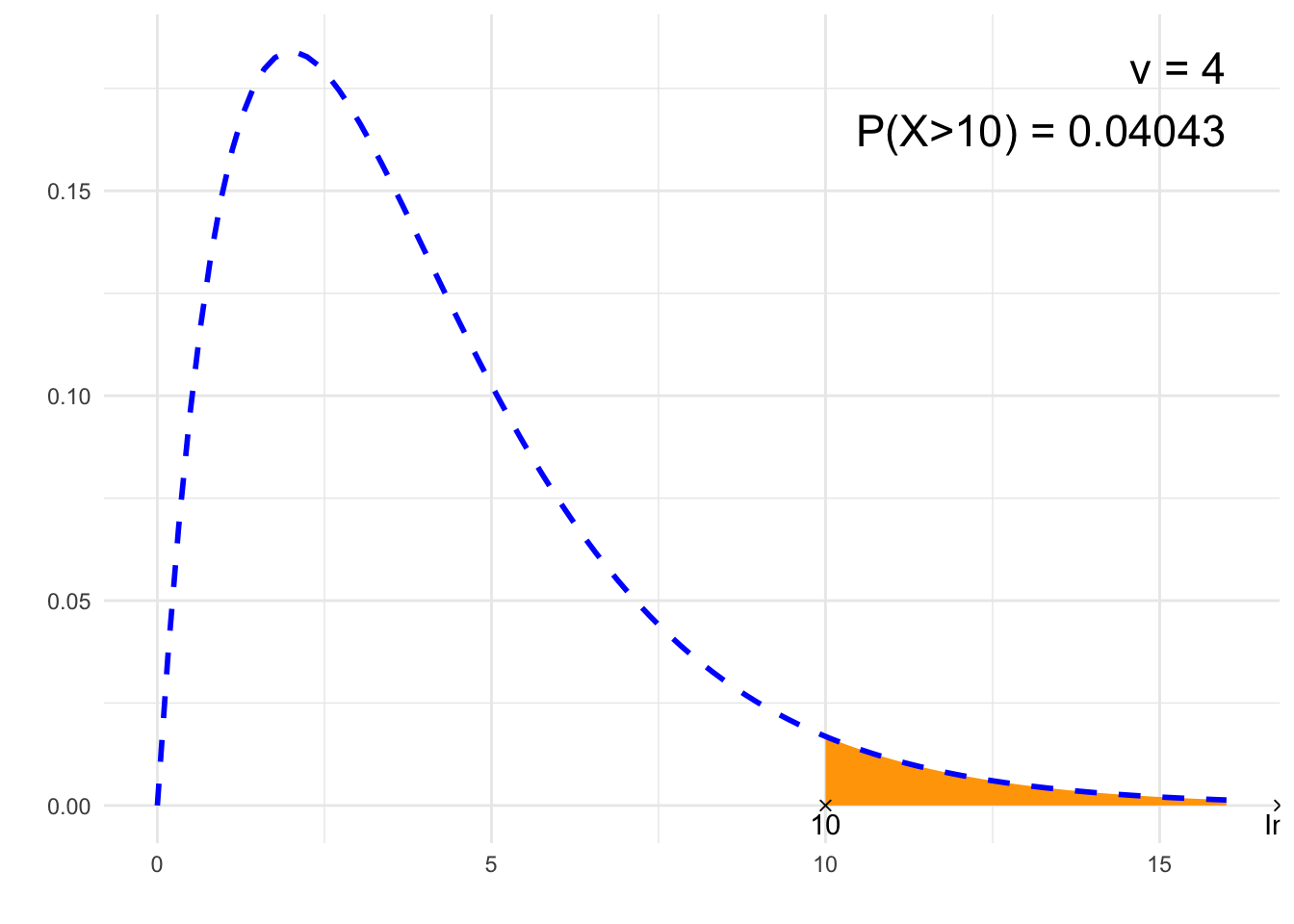
##### 2. Szukaj x #####
# Parametry rozkładu Gaussa:
# średnia:
m <- 1
# odchylenie standardowe:
sd <- 3
# Zadane pole pod krzywą:
P <- 0.95
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ <- 'L'
# Obliczenia
from <- -qnorm(if(typ=='L'){1} else if(typ=='P'){P} else {1-(1-P)/2})*sd+m
to <- qnorm(if(typ=='L'){P} else if(typ=='P'){1} else {1-(1-P)/2})*sd+m
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", signif(from, 6), ")")
} else if (from==-Inf) {
p=paste0("P(X<", signif(to, 6), ")")
} else {
p=paste0("P(", signif(from, 6), " < X < ", signif(to, 6), ")")
}
print(paste0(p, " = ", P))## [1] "P(X<5.93456) = 0.95"# Rysunek
library(ggplot2)
x1=if(from==-Inf){min(-4*sd+m, to-2*sd)} else {min(from-2*sd, -4*sd+m)}
x2=if(to==Inf){max(4*sd+m, from+2*sd)} else {max(to+2*sd, 4*sd+m)}
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dnorm(x, m, sd)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dnorm(x, m, sd)}, col = "blue", lty=2, lwd=1) +
scale_x_continuous(breaks=c(m, m-sd, m-2*sd, m+sd, m+2*sd, m-3*sd, m+3*sd, m-4*sd, m+4*sd)) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("M = ", m, "\nSD = ", sd, "\n", p, " = ", P),
x = x1, y = dnorm(m, m, sd)*1.2, size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))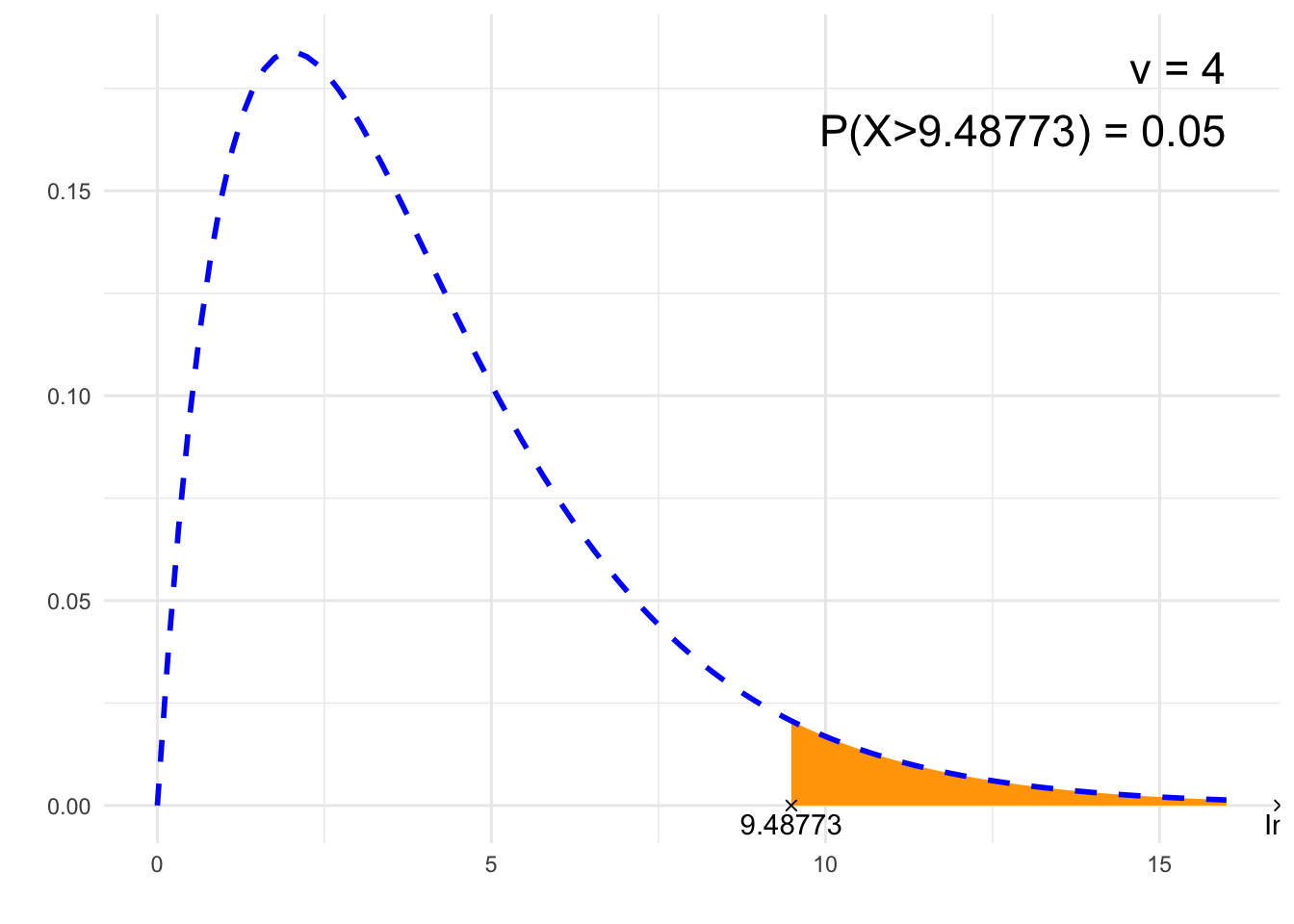
from scipy.stats import norm
##### 1. Pole pod krzywą #####
# Parametry rozkładu Gaussa:
# średnia:
m = 0
# odchylenie standardowe:
sd = 2
# Będziemy obliczać pole pod krzywą gęstości rozkładu Gaussa
# od
# *można wpisać _from = float('-inf'), co oznacza minus nieskończoność
_from = float('-inf')
# to
_to = 2
if _from > _to:
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
else:
if _to == float('inf'):
p = "P(X>" + str(_from) + ")"
elif _from == float('-inf'):
p = "P(X<" + str(_to) + ")"
else:
p = "P(" + str(_from) + "<X<" + str(_to) + ")"
print(p)
result = norm.cdf(_to, m, sd) - norm.cdf(_from, m, sd)
print(result)## P(X<2)
## 0.8413447460685429##### 2. Szukaj x #####
import numpy as np
from scipy.stats import norm
# Parametry rozkładu Gaussa:
# średnia:
m = 1
# odchylenie standardowe:
sd = 3
# Zadane pole pod krzywą:
P = 0.95
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ = 'L'
# Obliczenia
if typ == 'L':
_from = -norm.ppf(1) * sd + m
_to = norm.ppf(P) * sd + m
elif typ == 'P':
_from = -norm.ppf(P) * sd + m
_to = norm.ppf(1) * sd + m
else:
_from = -norm.ppf(1-(1-P)/2) * sd + m
_to = norm.ppf(1-(1-P)/2) * sd + m
# Zapis prawdopodobieństwa
if np.isinf(_to):
p = f"P(X>{np.round(_from, 6)})"
elif np.isinf(_from):
p = f"P(X<{np.round(_to, 6)})"
else:
p = f"P({np.round(_from, 6)} < X < {np.round(_to, 6)})"
print(f"{p} = {P}")## P(X<5.934561) = 0.95Kalkulator dla rozkładu t-Studenta — arkusz Google
Kalkulator dla rozkładu t-Studenta — szablon w Excelu: Kalkulator_rozkładu_t.xlsx
##### 1. Pole pod krzywą #####
# Parametr rozkładu t:
# liczba stopni swobody:
nu <- 23
# Będziemy obliczać pole pod krzywą gęstości rozkładu t-Studenta
# od
# *można wpisać from <- -Inf, co oznacza minus nieskończoność
from <- 1
# do
# *można wpisać to <- Inf, co oznacza (plus) nieskończoność
to <- Inf
# Sprawdzenie danych, obliczenie pola pod krzywą
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
} else {
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", from, ")")
} else if (from==-Inf) {
p=paste0("P(X<", to, ")")
} else {
p=paste0("P(", from, "<X<", to, ")")
}
print(p)
# Obliczenie prawdopodobieństwa, czyli pole pod wycinkiem krzywej:
result<-pt(to, nu)-pt(from, nu)
print(result)
}## [1] "P(X>1)"
## [1] 0.1638579# Rysunek
library(ggplot2)
x1=-5
x2=5
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dt(x, nu)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dt(x, nu)}, col = "blue", lty=2, lwd=1) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν = ", nu, "\n", p, " = ", signif(result,6)),
x = x1, y = dt(0, nu)*1.2, size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))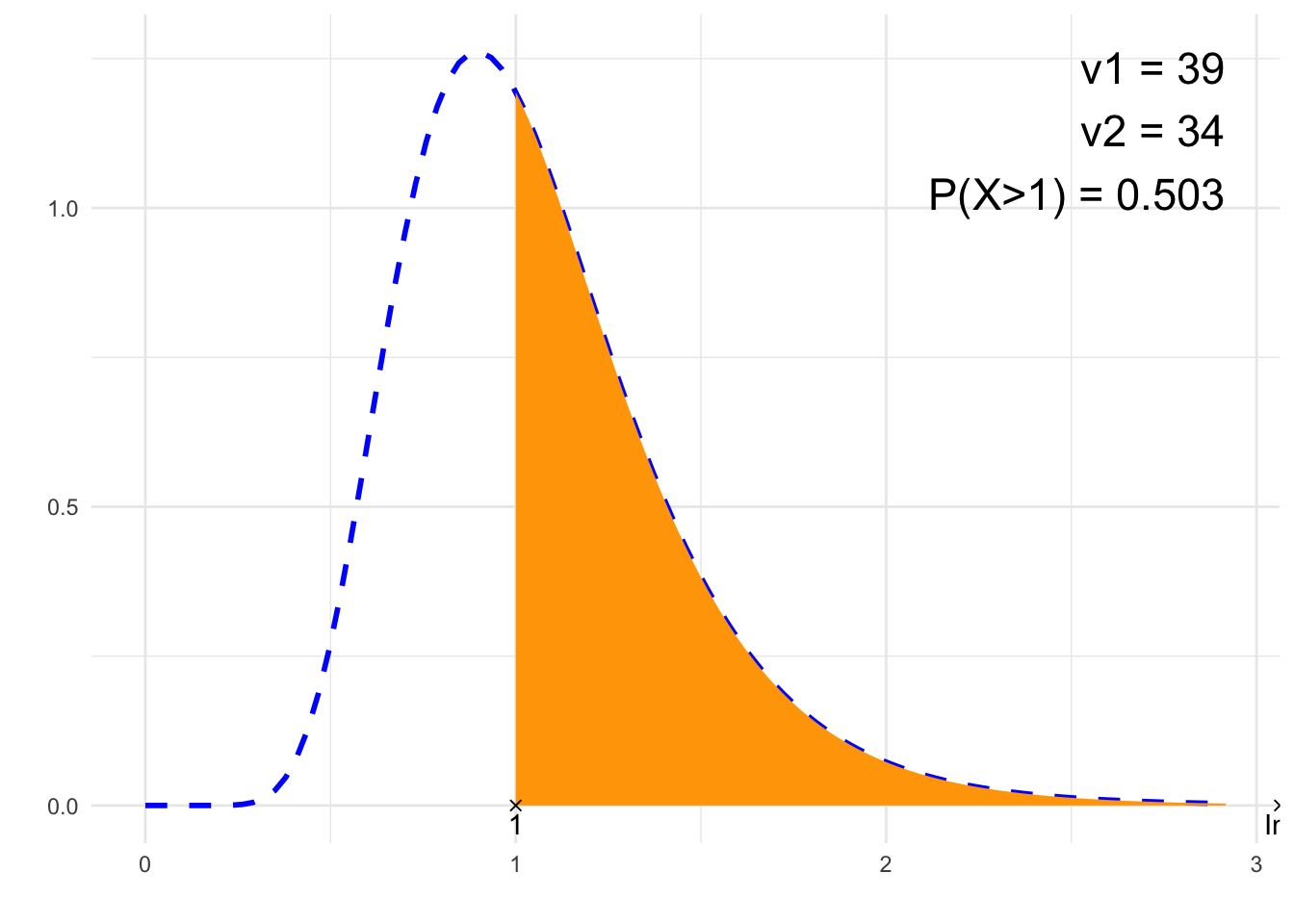
##### 2. Szukaj x #####
# Parametr rozkładu t:
# liczba stopni swobody:
nu <- 23
# Zadane pole pod krzywą:
P <- 0.95
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ <- 'S'
# Obliczenia
from <- -qt(if(typ=='L'){1} else if(typ=='P'){P} else {1-(1-P)/2}, nu)
to <- qt(if(typ=='L'){P} else if(typ=='P'){1} else {1-(1-P)/2}, nu)
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", signif(from, 6), ")")
} else if (from==-Inf) {
p=paste0("P(X<", signif(to, 6), ")")
} else {
p=paste0("P(", signif(from, 6), " < X < ", signif(to, 6), ")")
}
print(paste0(p, " = ", P))## [1] "P(-2.06866 < X < 2.06866) = 0.95"# Rysunek
library(ggplot2)
x1=-5
x2=5
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dt(x, nu)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dt(x, nu)}, col = "blue", lty=2, lwd=1) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν = ", nu, "\n", p, " = ", P),
x = x1, y = dt(0, nu)*1.2, size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))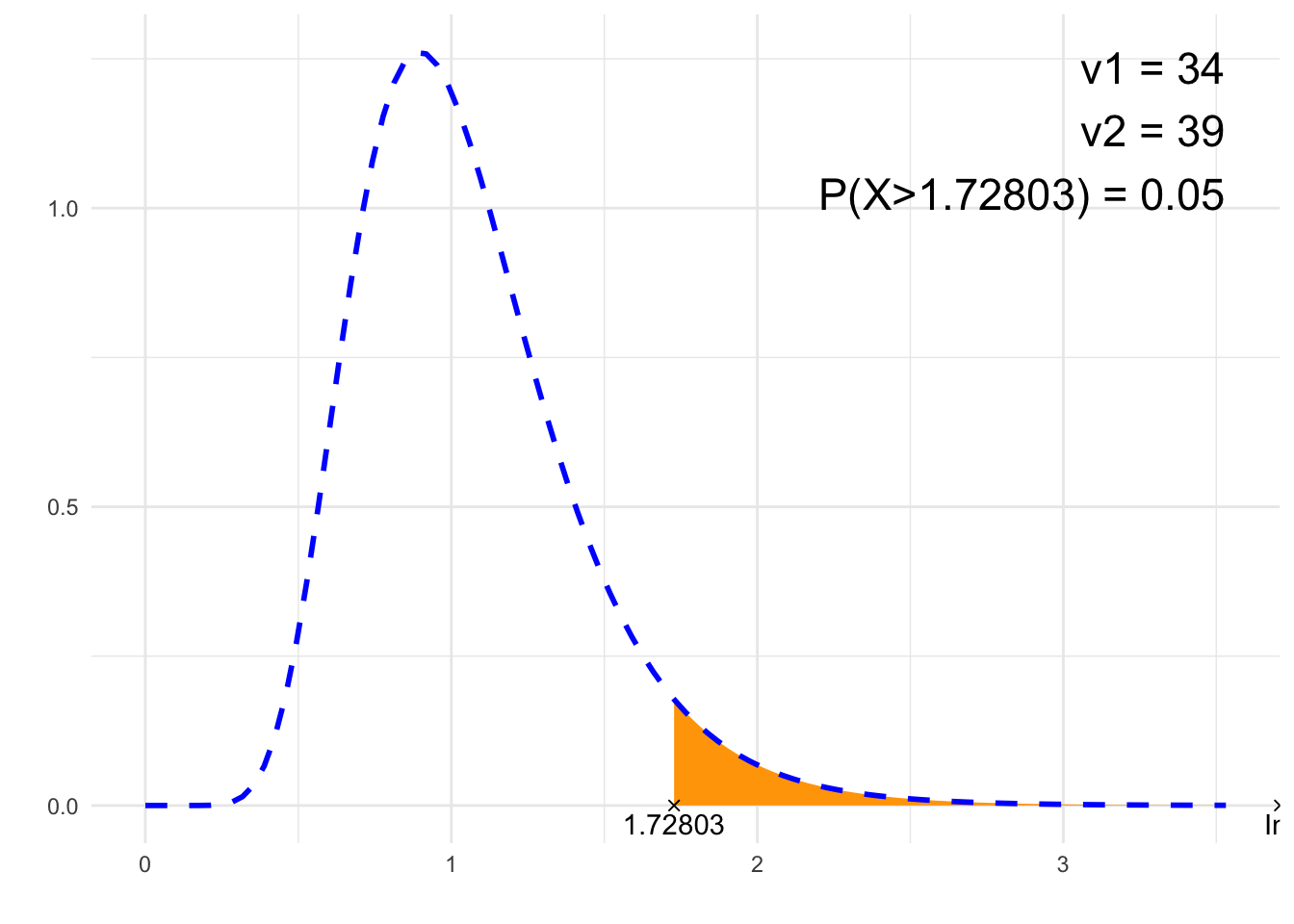
from scipy.stats import t
##### 1. Pole pod krzywą #####
# Parametr rozkładu t-Studenta:
# Liczba stopni swobody:
nu = 23
# Będziemy obliczać pole pod krzywą gęstości rozkładu t
# od
# *można wpisać _from = float('-inf'), co oznacza minus nieskończoność
_from = 1
# to
# *można wpisać _from = float('inf'), co oznacza plus nieskończoność
_to = float('inf')
if _from > _to:
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
else:
if _to == float('inf'):
p = "P(X>" + str(_from) + ")"
elif _from == float('-inf'):
p = "P(X<" + str(_to) + ")"
else:
p = "P(" + str(_from) + "<X<" + str(_to) + ")"
print(p)
result = t.cdf(_to, nu) - t.cdf(_from, nu)
print(result)## P(X>1)
## 0.16385790307142933
##### 2. Szukaj x #####
import numpy as np
from scipy.stats import t
# Parametr rozkładu t-Studenta:
# Liczba stopni swobody:
nu = 23
# Zadane pole pod krzywą:
P = 0.95
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ = 'S'
# Obliczenia
if typ == 'L':
_from = -t.ppf(1, nu)
_to = t.ppf(P, nu)
elif typ == 'P':
_from = -t.ppf(P, nu)
_to = t.ppf(1)
else:
_from = -t.ppf(1-(1-P)/2, nu)
_to = t.ppf(1-(1-P)/2, nu)
# Zapis prawdopodobieństwa
if np.isinf(_to):
p = f"P(X>{np.round(_from, 6)})"
elif np.isinf(_from):
p = f"P(X<{np.round(_to, 6)})"
else:
p = f"P({np.round(_from, 6)} < X < {np.round(_to, 6)})"
print(f"{p} = {P}")## P(-2.068658 < X < 2.068658) = 0.95Kalkulator dla rozkładu chi-kwadrat — arkusz Google
##### 1. Pole pod krzywą #####
# Parametr rozkładu chi-kwadrat:
# liczba stopni swobody:
nu <- 4
# Będziemy obliczać pole pod krzywą gęstości rozkładu chi-kwadrat
# od
# *można wpisać from <- -Inf, co oznacza minus nieskończoność
from <- 10
# do
# *można wpisać to <- Inf, co oznacza (plus) nieskończoność
to <- Inf
# Sprawdzenie danych, obliczenie pola pod krzywą
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
} else {
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", from, ")")
} else if (from==-Inf) {
p=paste0("P(X<", to, ")")
} else {
p=paste0("P(", from, "<X<", to, ")")
}
print(p)
# Obliczenie prawdopodobieństwa, czyli pole pod wycinkiem krzywej:
result<-pchisq(to, nu)-pchisq(from, nu)
print(result)
}## [1] "P(X>10)"
## [1] 0.04042768# Rysunek
library(ggplot2)
x1=0
x2=nu*4
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dchisq(x, nu)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dchisq(x, nu)}, col = "blue", lty=2, lwd=1) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν = ", nu, "\n", p, " = ", signif(result,4)),
x = 4*nu, y = dchisq(max(nu-2,0), nu), size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))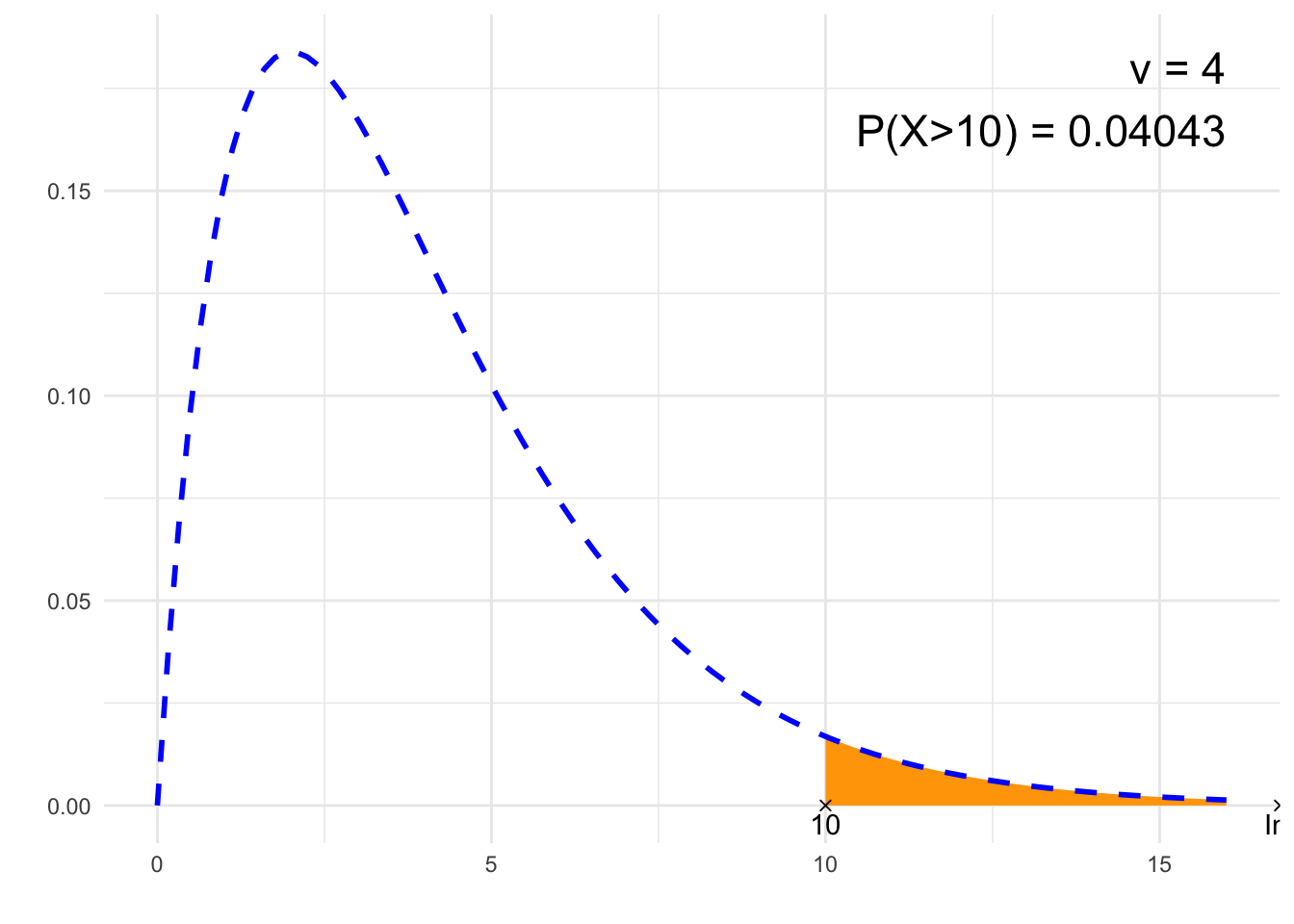
##### 2. Szukaj x #####
# Parametr rozkładu chi-kwadrat:
# liczba stopni swobody:
nu <- 4
# Zadane pole pod krzywą:
P <- 0.05
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ <- 'P'
# Obliczenia
from <- qchisq(if(typ=='L'){0} else if(typ=='P'){1-P} else {(1-P)/2}, nu)
to <- qchisq(if(typ=='L'){P} else if(typ=='P'){1} else {1-(1-P)/2}, nu)
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", signif(from, 6), ")")
} else if (from==-Inf) {
p=paste0("P(X<", signif(to, 6), ")")
} else {
p=paste0("P(", signif(from, 6), " < X < ", signif(to, 6), ")")
}
print(paste0(p, " = ", P))## [1] "P(X>9.48773) = 0.05"# Rysunek
library(ggplot2)
x1=0
x2=nu*4
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){dchisq(x, nu)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){dchisq(x, nu)}, col = "blue", lty=2, lwd=1) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν = ", nu, "\n", p, " = ", P),
x = 4*nu, y = dchisq(max(nu-2,0), nu), size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))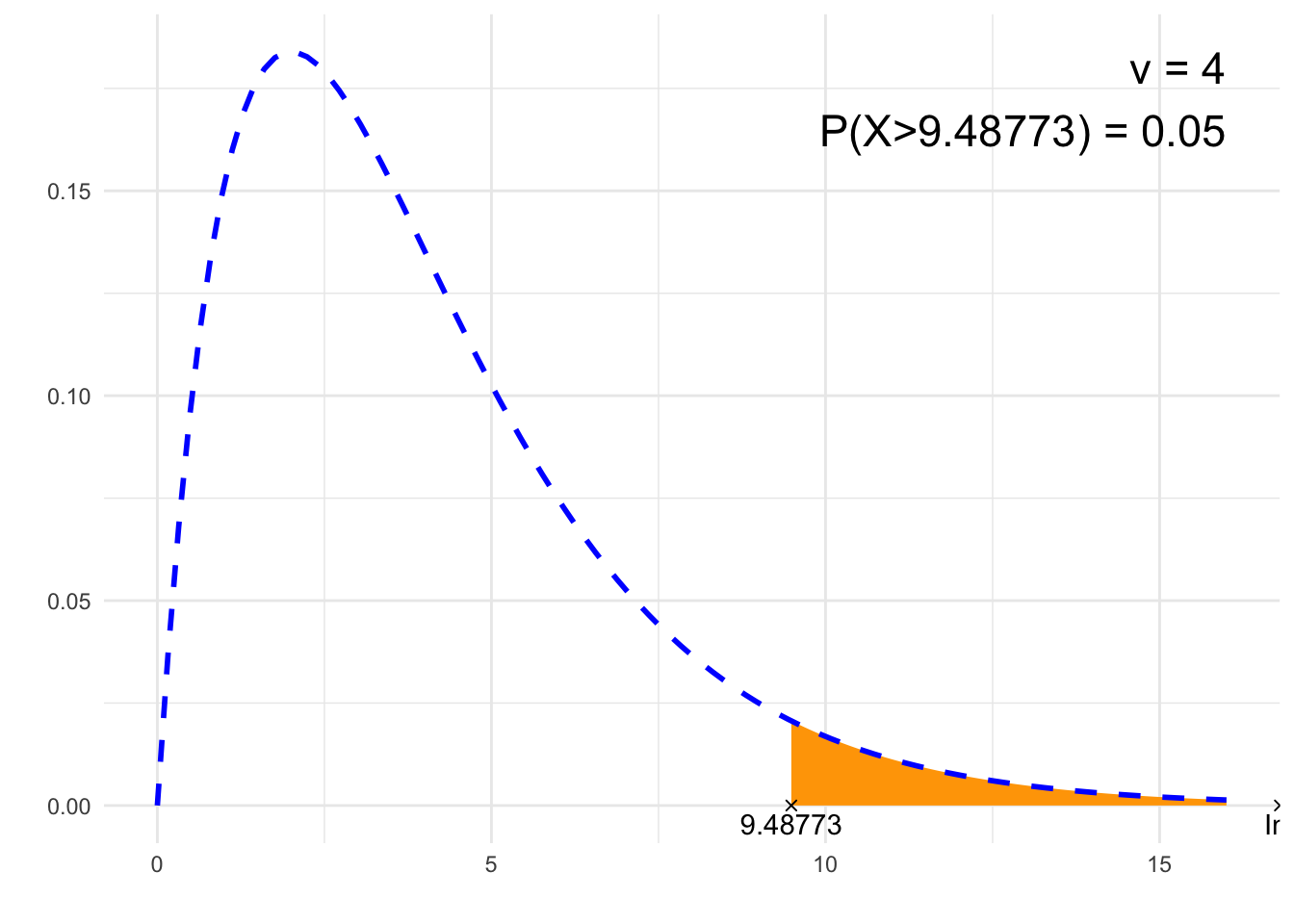
from scipy.stats import chi2
##### 1. Pole pod krzywą #####
# Parametr rozkładu chi-kwadrat:
# Liczba stopni swobody:
nu = 4
# Będziemy obliczać pole pod krzywą gęstości rozkładu chi-kwadrat:
# od
# *można wpisać _from = float('-inf'), co oznacza minus nieskończoność
_from = 10
# to
# *można wpisać _from = float('inf'), co oznacza plus nieskończoność
_to = float('inf')
if _from > _to:
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
else:
if _to == float('inf'):
p = "P(X>" + str(_from) + ")"
elif _from == float('-inf'):
p = "P(X<" + str(_to) + ")"
else:
p = "P(" + str(_from) + "<X<" + str(_to) + ")"
print(p)
result = chi2.cdf(_to, nu) - chi2.cdf(_from, nu)
print(result)## P(X>10)
## 0.04042768199451274
##### 2. Szukaj x #####
import numpy as np
from scipy.stats import chi
# Parametr rozkładu chi-kwadrat:
# Liczba stopni swobody:
nu = 4
# Zadane pole pod krzywą:
P = 0.05
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ = 'P'
# Obliczenia
if typ == 'L':
_from = chi2.ppf(0, nu)
_to = chi2.ppf(P, nu)
elif typ == 'P':
_from = chi2.ppf(1-P, nu)
_to = chi2.ppf(1, nu)
else:
_from = chi2.ppf((1-P)/2, nu)
_to = chi2.ppf(1-(1-P)/2, nu)
# Zapis prawdopodobieństwa
if np.isinf(_to):
p = f"P(X>{np.round(_from, 6)})"
elif np.isinf(_from):
p = f"P(X<{np.round(_to, 6)})"
else:
p = f"P({np.round(_from, 6)} < X < {np.round(_to, 6)})"
print(f"{p} = {P}")## P(X>9.487729) = 0.05Kalkulator rozkładu F — arkusz Google
##### 1. Pole pod krzywą #####
# Parametry rozkładu F:
# liczba stopni swobody 1:
nu1 <- 39
nu2 <- 34
# Będziemy obliczać pole pod krzywą gęstości rozkładu chi-kwadrat
# od
# *można wpisać from <- -Inf, co oznacza minus nieskończoność
from <- 1
# do
# *można wpisać to <- Inf, co oznacza (plus) nieskończoność
to <- Inf
# Sprawdzenie danych, obliczenie pola pod krzywą
if (from > to) {
# błąd od > do
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
} else {
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", from, ")")
} else if (from==-Inf) {
p=paste0("P(X<", to, ")")
} else {
p=paste0("P(", from, "<X<", to, ")")
}
print(p)
# Obliczenie prawdopodobieństwa, czyli pole pod wycinkiem krzywej:
result<-pf(to, nu1, nu2)-pf(from, nu1, nu2)
print(result)
}## [1] "P(X>1)"
## [1] 0.5030343# Rysunek
library(ggplot2)
x1=0
x2=qf(.999, nu1, nu2)
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_line(stat = "function", fun = function(x){df(x, nu1, nu2)}, col = "blue", lty=2, lwd=1) +
geom_area(stat = "function",
fun = function(x){df(x, nu1, nu2)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν1 = ", nu1, "\n", "ν2 = ", nu2, "\n", p, " = ", signif(result,4)),
x = x2, y = df(max((nu1-2)/nu1*nu2/(nu2+2),0), nu1, nu2), size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))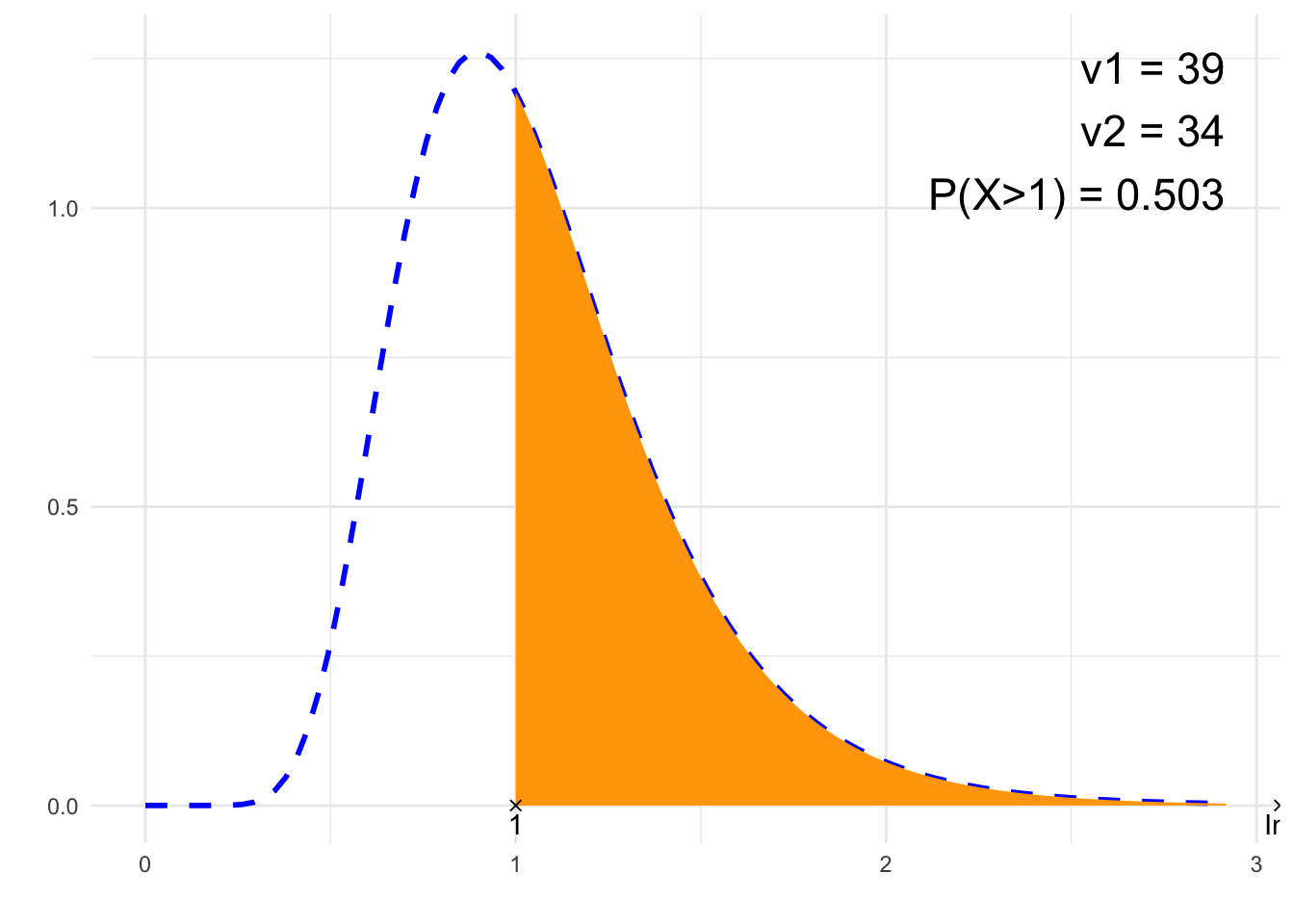
##### 2. Szukaj x #####
# Parametr rozkładu chi-kwadrat:
# liczba stopni swobody:
nu1 <- 34
nu2 <- 39
# Zadane pole pod krzywą:
P <- 0.05
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ <- 'P'
# Obliczenia
from <- qf(if(typ=='L'){0} else if(typ=='P'){1-P} else {(1-P)/2}, nu1, nu2)
to <- qf(if(typ=='L'){P} else if(typ=='P'){1} else {1-(1-P)/2}, nu1, nu2)
# Zapis prawdopodobieństwa
if (to==Inf) {
p=paste0("P(X>", signif(from, 6), ")")
} else if (from==-Inf) {
p=paste0("P(X<", signif(to, 6), ")")
} else {
p=paste0("P(", signif(from, 6), " < X < ", signif(to, 6), ")")
}
print(paste0(p, " = ", P))## [1] "P(X>1.72803) = 0.05"# Rysunek
library(ggplot2)
x1=0
x2=qf(.9999, nu1, nu2)
df<-data.frame(y=c(0, 0),
x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))
plt<-ggplot(NULL, aes(c(x1, x2))) +
theme_minimal() +
xlab('') +
ylab('') +
geom_area(stat = "function",
fun = function(x){stats::df(x, nu1, nu2)},
fill = "orange",
xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
geom_line(stat = "function", fun = function(x){stats::df(x, nu1, nu2)}, col = "blue", lty=2, lwd=1) +
geom_point(data = df, aes(x=x, y=y), shape=4) +
geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
annotate("text", label = paste0("ν1 = ", nu1, "\nν2 = ", nu2, "\n", p, " = ", P),
x = x2, y = df(max((nu1-2)/nu1*nu2/(nu2+2),0), nu1, nu2), size = 6, hjust="inward", vjust = "inward")
suppressWarnings(print(plt))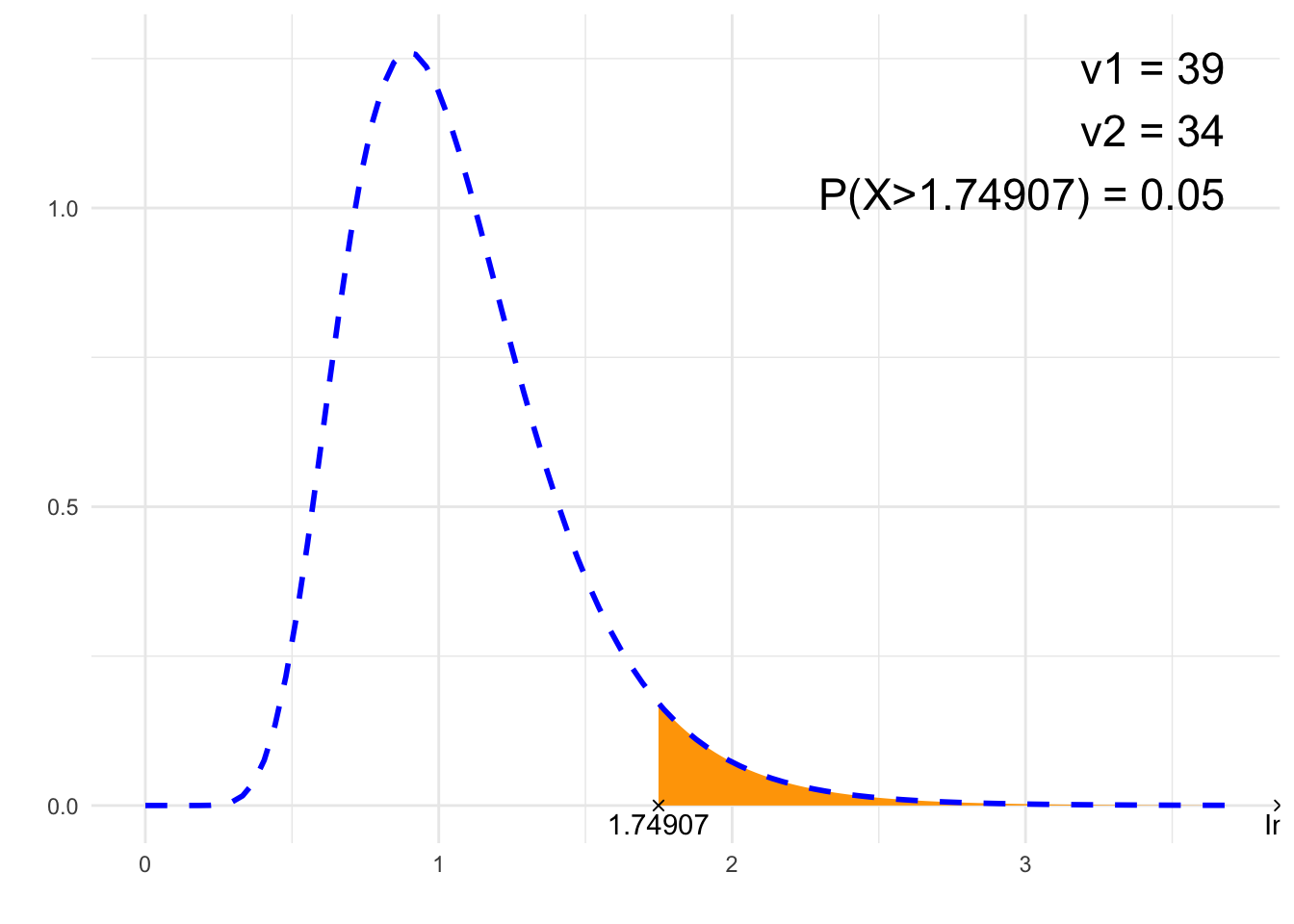
from scipy.stats import f
##### 1. Pole pod krzywą #####
# Parametr rozkładu chi-kwadrat:
# Liczba stopni swobody:
nu1 = 39
nu2 = 34
# Będziemy obliczać pole pod krzywą gęstości rozkładu chi-kwadrat:
# od
# *można wpisać _from = float('-inf'), co oznacza minus nieskończoność
_from = 1
# to
# *można wpisać _from = float('inf'), co oznacza plus nieskończoność
_to = float('inf')
if _from > _to:
print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
else:
if _to == float('inf'):
p = "P(X>" + str(_from) + ")"
elif _from == float('-inf'):
p = "P(X<" + str(_to) + ")"
else:
p = "P(" + str(_from) + "<X<" + str(_to) + ")"
print(p)
result = f.cdf(_to, nu1, nu2) - f.cdf(_from, nu1, nu2)
print(result)## P(X>1)
## 0.5030343220915879
##### 2. Szukaj x #####
import numpy as np
from scipy.stats import chi
# Parametr rozkładu chi-kwadrat:
# Liczba stopni swobody:
nu1 = 34
nu2 = 39
# Zadane pole pod krzywą:
P = 0.05
# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ = 'P'
# Obliczenia
if typ == 'L':
_from = f.ppf(0, nu1, nu2)
_to = f.ppf(P, nu1, nu2)
elif typ == 'P':
_from = f.ppf(1-P, nu1, nu2)
_to = f.ppf(1, nu1, nu2)
else:
_from = f.ppf((1-P)/2, nu1, nu2)
_to = f.ppf(1-(1-P)/2, nu1, nu2)
# Zapis prawdopodobieństwa
if np.isinf(_to):
p = f"P(X>{np.round(_from, 6)})"
elif np.isinf(_from):
p = f"P(X<{np.round(_to, 6)})"
else:
p = f"P({np.round(_from, 6)} < X < {np.round(_to, 6)})"
print(f"{p} = {P}")## P(X>1.72803) = 0.05C.3 Przedziały ufności
Przedział ufności dla proporcji — arkusz Google
Przedział ufności dla proporcji — szablon w Excelu
# Przedział ufności dla proporcji
# Dane:
# Liczba wszystkich obserwacji:
n <- 160
# Liczba obserwacji sprzyjających:
x <- 15
# Proporcja w próbie:
p <- x/n
# Poziom ufności:
conf <- 0.95
# Prosty wzór:
alpha <- 1 - conf
resa <- p + c(-qnorm(1-alpha/2), qnorm(1-alpha/2)) * sqrt((1/n)*p*(1-p))
# Wilson score:
resw <- prop.test(x, n, conf.level = 1-alpha, correct = FALSE)$conf.int
print(paste(
list(
"Przedział ufności - prosty wzór:",
resa,
"Przedział ufności - Wilson score:",
resw)))## [1] "Przedział ufności - prosty wzór:"
## [2] "c(0.0485854437380776, 0.138914556261922)"
## [3] "Przedział ufności - Wilson score:"
## [4] "c(0.0576380069455474, 0.148912026631301)"# Przedział ufności dla proporcji
# Dane:
# Liczba wszystkich obserwacji:
n = 160
# Liczba obserwacji sprzyjających:
x = 15
# Proporcja w próbie:
p = x/n
# Poziom ufności:
conf = 0.95
from statsmodels.stats.proportion import proportion_confint
# Prosty wzór:
resa = proportion_confint(x, n, alpha=1-conf, method='normal')
# Wilson score:
resw = proportion_confint(x, n, alpha=1-conf, method='wilson')
print("Przedział ufności - prosty wzór:", resa,
"\nPrzedział ufności - Wilson score:", resw)## Przedział ufności - prosty wzór: (0.048585443738077556, 0.13891455626192245)
## Przedział ufności - Wilson score: (0.05763800694554742, 0.14891202663130057)Przedział ufności dla średniej — arkusz Google
Przedział ufności dla średniej — szablon w Excelu
# Przedział ufności dla średniej
# Dane:
# Wielkość próby:
n <- 24
# Średnia w próbie:
xbar <- 183
# Odchylenie standardowe w populacji lub w próbie:
s <- 5.19
# Poziom ufności:
conf <- 0.95
alpha <- 1 - conf
# z:
ci_z <- xbar + c(-qnorm(1-alpha/2), qnorm(1-alpha/2)) * s/sqrt(n)
# t:
df<- n-1
ci_t <- xbar + c(-qt(1-alpha/2, df), qt(1-alpha/2, df)) * s/sqrt(n)
print(paste(
list(
"Przedział ufności - z:",
ci_z,
"Przedział ufności - t:",
ci_t)))## [1] "Przedział ufności - z:" "c(180.923605699976, 185.076394300024)"
## [3] "Przedział ufności - t:" "c(180.808455203843, 185.191544796157)"# Na podstawie danych:
dane <- c(34.1, 35.6, 34.2, 33.9, 25.1)
test_result<-t.test(dane, conf.level = 0.99)
print(test_result$conf.int)## [1] 23.85964 41.30036
## attr(,"conf.level")
## [1] 0.99import math
import scipy.stats as stats
n = 24
xbar = 183
s = 5.19
conf = 0.95
alpha = 1 - conf
ci_z = [xbar + (-stats.norm.ppf(1-alpha/2)) * s/math.sqrt(n), xbar + (stats.norm.ppf(1-alpha/2)) * s/math.sqrt(n)]
df = n-1
ci_t = [xbar + (-stats.t.ppf(1-alpha/2, df)) * s/math.sqrt(n), xbar + (stats.t.ppf(1-alpha/2, df)) * s/math.sqrt(n)]
print("Przedział ufności - z:", ci_z,
"\nPrzedział ufności - t:", ci_t)## Przedział ufności - z: [180.92360569997632, 185.07639430002368]
## Przedział ufności - t: [180.80845520384258, 185.19154479615742]# Wersja 2
print(stats.norm.interval(confidence=conf, loc=xbar, scale=s/math.sqrt(n)), "\n",
stats.t.interval(confidence=conf, df=df, loc=xbar, scale=s/math.sqrt(n)))## (180.92360569997632, 185.07639430002368)
## (180.80845520384258, 185.19154479615742)# Na podstawie danych:
import numpy as np
from scipy import stats
dane = np.array([34.1, 35.6, 34.2, 33.9, 25.1])
test_result = stats.ttest_1samp(dane, popmean=np.mean(dane))
conf_int = test_result.confidence_interval(0.99)
print(conf_int)## ConfidenceInterval(low=23.85964498330358, high=41.300355016696415)C.4 Testy dla średnich i proporcji
C.4.1 Testy dla 1 średniej i proporcji
Testowanie 1 populacji (średnia i proporcja) — arkusz Google
Testowanie 1 populacji (średnia i proporcja) — szablon w Excelu
# Test dla jednej średniej
# Wielkość próby:
n <- 38
# Średnia w próbie:
xbar <- 184.21
# Odchylenie standardowe w populacji lub w próbie:
s <- 6.1034
# Poziom istotności:
alpha <- 0.05
# Wartość null w hipotezie zerowej:
mu0 <- 179
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- ">"
# Obliczenia:
# stopnie swobody:
df <- n-1
# Wartość krytyczna (test t):
crit_t <- if (alt == "<") {qt(alpha, df)} else if (alt == ">") {qt(1-alpha, df)} else {qt(1-alpha/2, df)}
# Statystyka testowa t/z:
test_tz <- (xbar-mu0)/(s/sqrt(n))
# Wartość p (test t):
p.value = if(alt == ">"){1-pt(test_tz, df)} else if (alt == ">") {pt(test_tz, df)} else {2*(1-pt(abs(test_tz),df))}
# Wartość krytyczna (test z):
crit_z <- if (alt == "<") {qnorm(alpha)} else if (alt == ">") {qnorm(1-alpha)} else {qnorm(1-alpha/2)}
# Wartość p (test z):
p.value.z = if(alt == ">"){1-pnorm(test_tz)} else if (alt == ">") {pnorm(test_tz)} else {2*(1-pnorm(abs(test_tz)))}
print(c('Średnia' = xbar,
'Odchylenie st.' = s,
'Liczebność' = n,
'Hipoteza zerowa' = paste0('mu = ', mu0),
'Hipoteza alt.' = paste0('mu ', alt, ' ', mu0),
'Statystyka testowa t/z' = test_tz,
'Wartość krytyczna t' = crit_t,
'Wartość p (test t)' = p.value,
'Wartość krytyczna z' = crit_z,
'Wartość p (test z)' = p.value.z
))## Średnia Odchylenie st. Liczebność
## "184.21" "6.1034" "38"
## Hipoteza zerowa Hipoteza alt. Statystyka testowa t/z
## "mu = 179" "mu > 179" "5.26208293008297"
## Wartość krytyczna t Wartość p (test t) Wartość krytyczna z
## "1.68709361959626" "3.1304551380007e-06" "1.64485362695147"
## Wartość p (test z)
## "7.12162456784071e-08"# Na podstawie danych (test t):
# Wektor z danymi
data <- c(176.5267, 195.5237, 184.9741, 179.5349, 188.2120, 190.7425, 178.7593, 196.2744, 186.6965, 187.8559, 183.1323, 176.2569, 191.4752, 186.5975, 180.2120, 184.3434, 178.1691, 184.8852, 187.7973, 178.5013, 172.7343, 176.8545, 184.2068, 181.2395, 186.1983, 173.6317, 181.9529, 185.9135, 188.6081, 183.0285, 183.3375, 188.5512, 184.6348, 186.9657, 183.9622, 200.9014, 183.5353, 177.2538)
# Zapisanie wyników testu do obiektu
# Należy wybrać wartość parametru alternative: "two-sided" (domyślnie), "less" lub "greater" oraz wartość zerową (ang. null value), która domyślnie wynosi 0
test_result <- t.test(data, alternative = "greater", mu = 179)
# Wyświetlanie wyników testu. Można wyświetlać tylko poszczególne składowe wyniku (np. test_result$statistic)
print(test_result)##
## One Sample t-test
##
## data: data
## t = 5.2621, df = 37, p-value = 3.13e-06
## alternative hypothesis: true mean is greater than 179
## 95 percent confidence interval:
## 182.5396 Inf
## sample estimates:
## mean of x
## 184.21# Test dla jednej średniej
from scipy.stats import t, norm
from math import sqrt
# Wielkość próby:
n = 38
# Średnia w próbie:
xbar = 184.21
# Odchylenie standardowe w populacji lub w próbie:
s = 6.1034
# Poziom istotności:
alpha = 0.05
# Wartość null w hipotezie zerowej
mu0 = 179
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt = ">"
# Obliczenia:
# stopnie swobody:
df = n - 1
# Wartość krytyczna (test t):
if alt == "<":
crit_t = t.ppf(alpha, df)
elif alt == ">":
crit_t = t.ppf(1 - alpha, df)
else:
crit_t = t.ppf(1 - alpha / 2, df)
# Statystyka testowa t/z:
test_tz = (xbar - mu0) / (s / sqrt(n))
# Wartość p (test t):
if alt == ">":
p_value_t = 1 - t.cdf(test_tz, df)
elif alt == "<":
p_value_t = t.cdf(test_tz, df)
else:
p_value_t = 2 * (1 - t.cdf(abs(test_tz), df))
# Wartość krytyczna (test z):
if alt == "<":
crit_z = norm.ppf(alpha)
elif alt == ">":
crit_z = norm.ppf(1 - alpha)
else:
crit_z = norm.ppf(1 - alpha / 2)
# Wartość p (test z):
if alt == ">":
p_value_z = 1 - norm.cdf(test_tz)
elif alt == "<":
p_value_z = norm.cdf(test_tz)
else:
p_value_z = 2 * (1 - norm.cdf(abs(test_tz)))
results = {
'Średnia': xbar,
'Odchylenie st.': s,
'Liczebność': n,
'Hipoteza zerowa': f'mu = {mu0}',
'Hipoteza alt.': f'mu {alt} {mu0}',
'Statystyka testowa t/z': test_tz,
'Wartość krytyczna t': crit_t,
'Wartość p (test t)': p_value_t,
'Wartość krytyczna z': crit_z,
'Wartość p (test z)': p_value_z
}
for key, value in results.items():
print(f"{key}: {value}")## Średnia: 184.21
## Odchylenie st.: 6.1034
## Liczebność: 38
## Hipoteza zerowa: mu = 179
## Hipoteza alt.: mu > 179
## Statystyka testowa t/z: 5.262082930082973
## Wartość krytyczna t: 1.6870936167109873
## Wartość p (test t): 3.1304551380006984e-06
## Wartość krytyczna z: 1.6448536269514722
## Wartość p (test z): 7.121624567840712e-08# Na podstawie danych (test t):
import scipy.stats as stats
data = [176.5267, 195.5237, 184.9741, 179.5349, 188.2120, 190.7425, 178.7593, 196.2744, 186.6965, 187.8559, 183.1323, 176.2569, 191.4752, 186.5975, 180.2120, 184.3434, 178.1691, 184.8852, 187.7973, 178.5013, 172.7343, 176.8545, 184.2068, 181.2395, 186.1983, 173.6317, 181.9529, 185.9135, 188.6081, 183.0285, 183.3375, 188.5512, 184.6348, 186.9657, 183.9622, 200.9014, 183.5353, 177.2538]
test_result = stats.ttest_1samp(data, popmean=179, alternative='greater')
print(test_result)## TtestResult(statistic=5.262096550537936, pvalue=3.1303226590428976e-06, df=37)# Przedział ufności dla proporcji
# Liczba wszystkich obserwacji:
n <- 200
# Liczba obserwacji sprzyjających:
x <- 90
# Proporcja w próbie:
p <- x/n
# Poziom istotności:
alpha <- 0.1
# Proporcja wartość zerowa:
p0 <- 0.5
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- "≠"
alttext <- if(alt==">") {"greater"} else if(alt=="<") {"less"} else {"two.sided"}
test <- prop.test(x, n, p0, alternative=alttext, correct=FALSE)
test_z <- unname(sign(test$estimate-test$null.value)*sqrt(test$statistic))
crit_z <- if(test$alternative=="less") {qnorm(alpha)} else if(test$alternative=="greater") {qnorm(1-alpha)} else {qnorm(1-alpha/2)}
print(c('Proporcja w próbie' = test$estimate,
'Liczebność' = n,
'Hipoteza zerowa' = paste0('p = ', test$null.value),
'Hipoteza alt.' = paste0('p ', alt, ' ', test$null.value),
'Stat. testowa z' = test_z,
'Stat. testowa chi^2' = unname(test$statistic),
'Wartość krytyczna z' = crit_z,
'Wartość p' = test$p.value
))## Proporcja w próbie.p Liczebność Hipoteza zerowa Hipoteza alt.
## "0.45" "200" "p = 0.5" "p ≠ 0.5"
## Stat. testowa z Stat. testowa chi^2 Wartość krytyczna z Wartość p
## "-1.4142135623731" "2" "1.64485362695147" "0.157299207050284"# Przedział ufności dla proporcji
from statsmodels.stats.proportion import proportions_ztest
# Liczba wszystkich obserwacji:
n = 200
# Liczba obserwacji sprzyjających:
x = 90
# Proporcja w próbie:
p = x/n
# Poziom istotności:
alpha = 0.1
# Proporcja wartość zerowa:
p0 = 0.5
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt = "≠"
if alt == ">":
alttext = "larger"
elif alt == "<":
alttext = "smaller"
else:
alttext = "two-sided"
test_result = proportions_ztest(count = x, nobs = n, value = p0, alternative = alttext, prop_var=p0)
print("Statystyka testowa z:", test_result[0], "\np-value:", test_result[1])## Statystyka testowa z: -1.4142135623730947
## p-value: 0.15729920705028533C.4.2 Testy i przedziały ufności dla 2 średnich
Test i przedziały dla 2 średnich — arkusz Google
Test i przedziały dla 2 średnich — szablon w Excelu
# Test z dla dwóch średnich
# Wielkość próby 1:
n1 <- 100
# Średnia w próbie 1:
xbar1 <- 76.5
# Odchylenie standardowe w próbie 1:
s1 <- 38.0
# Wielkość próby 2:
n2 <- 100
# Średnia w próbie 2:
xbar2 <- 88.1
# Odchylenie standardowe w próbie 2:
s2 <- 40.0
# Poziom istotności:
alpha <- 0.05
# Wartość null w hipotezie zerowej (zwykle 0):
mu0 <- 0
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- "<"
# Obliczenia:
# Statystyka testowa z:
test_z <- (xbar1-xbar2-mu0)/sqrt(s1^2/n1+s2^2/n2)
# Wartość krytyczna (test z):
crit_z <- if (alt == "<") {qnorm(alpha)} else if (alt == ">") {qnorm(1-alpha)} else {qnorm(1-alpha/2)}
# Wartość p (test z):
p.value.z = if(alt == ">"){1-pnorm(test_z)} else if (alt == "<") {pnorm(test_z)} else {2*(1-pnorm(abs(test_z)))}
print(c('Średnia 1' = xbar1,
'Odchylenie st. 1' = s1,
'Liczebność 1' = n1,
'Średnia 2' = xbar2,
'Odchylenie st. 2' = s2,
'Liczebność 2' = n2,
'Hipoteza zerowa' = paste0('mu1-mu2 = ', mu0),
'Hipoteza alt.' = paste0('mu1-mu2 ', alt, ' ', mu0),
'Statystyka testowa z' = test_z,
'Wartość krytyczna z' = crit_z,
'Wartość p (test z)' = p.value.z
))## Średnia 1 Odchylenie st. 1 Liczebność 1 Średnia 2
## "76.5" "38" "100" "88.1"
## Odchylenie st. 2 Liczebność 2 Hipoteza zerowa Hipoteza alt.
## "40" "100" "mu1-mu2 = 0" "mu1-mu2 < 0"
## Statystyka testowa z Wartość krytyczna z Wartość p (test z)
## "-2.1024983574238" "-1.64485362695147" "0.0177548216928505"# Test t dla dwóch średnich
# Wielkość próby 1:
n1 <- 14
# Średnia w próbie 1:
xbar1 <- 185.2142
# Odchylenie standardowe w próbie 1:
s1 <- 7.5261
# Wielkość próby 2:
n2 <- 19
# Średnia w próbie 2:
xbar2 <- 184.8421
# Odchylenie standardowe w próbie 2:
s2 <- 5.0471
# Poziom istotności:
alpha <- 0.05
# Wartość null w hipotezie zerowej (zwykle 0):
mu0 <- 0
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- "≠"
# Założenie o równości wariancji (TRUE/FALSE):
eqvar <- FALSE
# Obliczenia
# Zbiorcze odchylenie standardowe:
sp <- sqrt(((n1-1)*s1^2+(n2-1)*s2^2)/(n1+n2-2))
# Statystyka testowa t:
test_t <- if(eqvar) {(xbar1-xbar2-mu0)/sqrt(sp^2*(1/n1+1/n2))} else {(xbar1-xbar2-mu0)/sqrt(s1^2/n1+s2^2/n2)}
# Liczba stopni swobody:
df<-if(eqvar) {n1+n2-2} else {(s1^2/n1+s2^2/n2)^2/((s1^2/n1)^2/(n1-1)+(s2^2/n2)^2/(n2-1))}
# Wartość krytyczna (test t):
crit_t <- if (alt == "<") {qt(alpha, df)} else if (alt == ">") {qt(1-alpha, df)} else {qt(1-alpha/2, df)}
# Wartość p (test t):
p.value.t = if(alt == ">"){1-pt(test_t, df)} else if (alt == ">") {pt(test_t, df)} else {2*(1-pt(abs(test_t),df))}
print(c('Średnia 1' = xbar1,
'Odchylenie st. 1' = s1,
'Liczebność 1' = n1,
'Średnia 2' = xbar2,
'Odchylenie st. 2' = s2,
'Liczebność 2' = n2,
'Hipoteza zerowa' = paste0('mu1-mu2 = ', mu0),
'Hipoteza alt.' = paste0('mu1-mu2 ', alt, ' ', mu0),
'Statystyka testowa t' = test_t,
'Wartość krytyczna t' = crit_t,
'Wartość p (test t)' = p.value.t
))## Średnia 1 Odchylenie st. 1 Liczebność 1 Średnia 2
## "185.2142" "7.5261" "14" "184.8421"
## Odchylenie st. 2 Liczebność 2 Hipoteza zerowa Hipoteza alt.
## "5.0471" "19" "mu1-mu2 = 0" "mu1-mu2 ≠ 0"
## Statystyka testowa t Wartość krytyczna t Wartość p (test t)
## "0.160325899672522" "2.07753969816904" "0.874131604618"# Na podstawie danych (test t)
# Dwa wektory z danymi:
data1 <- c(1.2, 3.1, 1.7, 2.8, 3.0)
data2 <- c(4.2, 2.7, 3.6, 3.9)
# Zapisanie wyników testu do obiektu
# Należy wybrać wartość parametru alternative: "two.sided" (domyślnie), "less" lub "greater" oraz założenie odnośnie do równości wariancji (domyślnie FALSE)
test_result <- t.test(data1, data2, alternative="two.sided", var.equal = TRUE)
# Wyświetlanie wyników testu. Można wyświetlać tylko poszczególne składowe wyniku (np. test_result$statistic)
print(test_result)##
## Two Sample t-test
##
## data: data1 and data2
## t = -2.3887, df = 7, p-value = 0.04826
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.46752406 -0.01247594
## sample estimates:
## mean of x mean of y
## 2.36 3.60import math
from scipy.stats import norm
# Test z dla dwóch średnich
# Wielkość próby 1:
n1 = 100
# Średnia w próbie 1:
xbar1 = 76.5
# Odchylenie standardowe w próbie 1:
s1 = 38.0
# Wielkość próby 2:
n2 = 100
# Średnia w próbie 2:
xbar2 = 88.1
# Odchylenie standardowe w próbie 2:
s2 = 40.0
# Poziom istotności:
alpha = 0.05
# Wartość null w hipotezie zerowej (zwykle 0):
mu0 = 0
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt = "<"
# Obliczenia:
# Statystyka testowa z:
test_z = (xbar1 - xbar2 - mu0) / math.sqrt(s1**2 / n1 + s2**2 / n2)
# Wartość krytyczna (test z):
if alt == "<":
crit_z = norm.ppf(alpha)
elif alt == ">":
crit_z = norm.ppf(1 - alpha)
else:
crit_z = norm.ppf(1 - alpha / 2)
# Wartość p (test z):
if alt == ">":
p_value_z = 1 - norm.cdf(test_z)
elif alt == "<":
p_value_z = norm.cdf(test_z)
else:
p_value_z = 2 * (1 - norm.cdf(abs(test_z)))
results = {
'Średnia 1': xbar1,
'Odchylenie st. 1': s1,
'Liczebność 1': n1,
'Średnia 2': xbar2,
'Odchylenie st. 2': s2,
'Liczebność 2': n2,
'Hipoteza zerowa': f'mu1-mu2 = {mu0}',
'Hipoteza alt.': f'mu1-mu2 {alt} {mu0}',
'Statystyka testowa z': test_z,
'Wartość krytyczna z': crit_z,
'Wartość p (test z)': p_value_z
}
for key, value in results.items():
print(f"{key}: {value}")## Średnia 1: 76.5
## Odchylenie st. 1: 38.0
## Liczebność 1: 100
## Średnia 2: 88.1
## Odchylenie st. 2: 40.0
## Liczebność 2: 100
## Hipoteza zerowa: mu1-mu2 = 0
## Hipoteza alt.: mu1-mu2 < 0
## Statystyka testowa z: -2.102498357423799
## Wartość krytyczna z: -1.6448536269514729
## Wartość p (test z): 0.017754821692850486# Test t dla dwóch średnich
from scipy.stats import t
# Wielkość próby 1:
n1 = 14
# Średnia w próbie 1:
xbar1 = 185.2142
# Odchylenie standardowe w próbie 1:
s1 = 7.5261
# Wielkość próby 2:
n2 = 19
# Średnia w próbie 2:
xbar2 = 184.8421
# Odchylenie standardowe w próbie 2:
s2 = 5.0471
# Poziom istotności:
alpha = 0.05
# Wartość null w hipotezie zerowej (zwykle 0):
mu0 = 0
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt = "≠"
# Założenie o równości wariancji (True/False)
eqvar = False
# Obliczenia:
# Zbiorcze odchylenie standardowe:
sp = math.sqrt(((n1 - 1) * s1**2 + (n2 - 1) * s2**2) / (n1 + n2 - 2))
# Statystyka testowa t i liczba stopni swobody:
if eqvar:
test_t = (xbar1 - xbar2 - mu0) / math.sqrt(sp**2 * (1/n1 + 1/n2))
df = n1 + n2 - 2
else:
test_t = (xbar1 - xbar2 - mu0) / math.sqrt(s1**2 / n1 + s2**2 / n2)
df = (s1**2 / n1 + s2**2 / n2)**2 / ((s1**2 / n1)**2 / (n1 - 1) + (s2**2 / n2)**2 / (n2 - 1))
# Wartość krytyczna (test t):
if alt == "<":
crit_t = t.ppf(alpha, df)
elif alt == ">":
crit_t = t.ppf(1 - alpha, df)
else:
crit_t = t.ppf(1 - alpha / 2, df)
# Wartość p (test t)
if alt == ">":
p_value_t = 1 - t.cdf(test_t, df)
elif alt == "<":
p_value_t = t.cdf(test_t, df)
else:
p_value_t = 2 * (1 - t.cdf(abs(test_t), df))
results = {
'Średnia 1': xbar1,
'Odchylenie st. 1': s1,
'Liczebność 1': n1,
'Średnia 2': xbar2,
'Odchylenie st. 2': s2,
'Liczebność 2': n2,
'Hipoteza zerowa': f'mu1-mu2 = {mu0}',
'Hipoteza alt.': f'mu1-mu2 {alt} {mu0}',
'Statystyka testowa t': test_t,
'Wartość krytyczna t': crit_t,
'Wartość p (test t)': p_value_t
}
for key, value in results.items():
print(f"{key}: {value}")## Średnia 1: 185.2142
## Odchylenie st. 1: 7.5261
## Liczebność 1: 14
## Średnia 2: 184.8421
## Odchylenie st. 2: 5.0471
## Liczebność 2: 19
## Hipoteza zerowa: mu1-mu2 = 0
## Hipoteza alt.: mu1-mu2 ≠ 0
## Statystyka testowa t: 0.16032589967252212
## Wartość krytyczna t: 2.0775396981690264
## Wartość p (test t): 0.8741316046180003
# Na podstawie danych (test t)
from scipy.stats import ttest_ind, t
# Dwa wektory z danymi:
data1 = [1.2, 3.1, 1.7, 2.8, 3.0]
data2 = [4.2, 2.7, 3.6, 3.9]
# Zapisanie wyników testu do obiektu
# Należy wybrać wartość parametru alternative: "two.sided" (domyślnie), "less" lub "greater" oraz założenie odnośnie do równości wariancji (domyślnie FALSE)
test_result = ttest_ind(data1, data2, alternative='two-sided', equal_var=True)
print(test_result)## TtestResult(statistic=-2.3886571085065054, pvalue=0.04826397365151946, df=7.0)C.4.3 Testy i przedziały ufności dla 2 proporcji
Test i przedziały dla 2 proporcji — arkusz Google
Test i przedziały dla 2 proporcji — szablon w Excelu
# Test dla dwóch proporcji
# Liczba wszystkich obserwacji w próbie 1:
n1 <- 24
# Liczba obserwacji sprzyjających w próbie 1:
x1 <- 21
# Proporcja w próbie 1:
phat1 <- x1/n1
# Liczba wszystkich obserwacji w próbie 2:
n2 <- 24
# Liczba obserwacji sprzyjających w próbie 2:
x2 <- 14
# Proporcja w próbie 2:
phat2 <- x2/n2
# Poziom istotności:
alpha <- 0.05
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- ">"
alttext <- if(alt==">") {"greater"} else if(alt=="<") {"less"} else {"two.sided"}
test <- prop.test(c(x1, x2), c(n1, n2), alternative=alttext, correct=FALSE)
test_z <- unname(-sign(diff(test$estimate))*sqrt(test$statistic))
crit_z <- if(test$alternative=="less") {qnorm(alpha)} else if(test$alternative=="greater") {qnorm(1-alpha)} else {qnorm(1-alpha/2)}
print(c('Proporcje w próbach ' = test$estimate,
'Liczebność ' = c(n1, n2),
'Hipoteza zerowa' = paste0('p1-p2 = ', 0),
'Hipoteza alt.' = paste0('p1-p2 ', alt, ' ', 0),
'Stat. testowa z' = test_z,
'Stat. testowa chi^2' = unname(test$statistic),
'Wartość krytyczna z' = crit_z,
'Wartość krytyczna chi^2' = crit_z^2,
'Wartość p' = test$p.value
))## Proporcje w próbach .prop 1 Proporcje w próbach .prop 2 Liczebność 1
## "0.875" "0.583333333333333" "24"
## Liczebność 2 Hipoteza zerowa Hipoteza alt.
## "24" "p1-p2 = 0" "p1-p2 > 0"
## Stat. testowa z Stat. testowa chi^2 Wartość krytyczna z
## "2.27359424023522" "5.16923076923077" "1.64485362695147"
## Wartość krytyczna chi^2 Wartość p
## "2.70554345409541" "0.0114951970462325"from statsmodels.stats.proportion import proportions_ztest
from scipy.stats import norm, chi2_contingency
import numpy as np
n1 = 24
x1 = 21
phat1 = x1 / n1
n2 = 24
x2 = 14
phat2 = x2 / n2
alpha = 0.05
alt = ">"
if alt == ">":
alttext = "larger"
elif alt == "<":
alttext = "smaller"
else:
alttext = "two-sided"
test_result = proportions_ztest(count = np.array([x1, x2]), nobs = np.array([n1, n2]), alternative = alttext)
print("Statystyka testowa z:", test_result[0],
"\np-value:", test_result[1])## Statystyka testowa z: 2.2735942402352203
## p-value: 0.011495197046232447C.5 Testy chi-kwadrat
Test chi-kwadrat — arkusz Google
Test chi-kwadrat — szablon w Excelu
# Test niezależności/jednorodności chi-kwadrat
# Macierz z danymi (wektor wejściowy)
m <- c(
21, 14,
3, 10
)
# Liczba wierszy w macierzy
nrow <- 2
# Poziom istotności
alpha <- 0.05
# Przekształcenie wektora w macierz
m <- matrix(data=m, nrow=nrow, byrow=TRUE)
# Test chi-kwadrat bez poprawki Yatesa
test_chi <- chisq.test(m, correct=FALSE)
# Test chi-kwadrat z poprawką Yatesa w przypadku tabel 2x2
test_chi_corrected <- chisq.test(m)
# Test G
test_g <- AMR::g.test(m)
# Dokładny test Fishera
exact_fisher<-fisher.test(m)
print(c('Liczba stopni swobody' = test_chi$parameter,
'Wartość krytyczna' = qchisq(1-alpha, test_chi$parameter),
'Statystyka chi^2' = unname(test_chi$statistic),
'Wartość p (test chi-kwadrat)' = test_chi$p.value,
'V Cramera' = unname(sqrt(test_chi$statistic/sum(m)/min(dim(m)-1))),
'Współczynnik fi (dla tabel 2x2)' = if(all(dim(m)==2)) {psych::phi(m, digits=10)},
'Statystyka chi^2 z poprawką Yatesa' = unname(test_chi_corrected$statistic),
'Wartość p (test chi^2 z poprawką Yatesa)' = test_chi_corrected$p.value,
'Statystyka G' = unname(test_g$statistic),
'Wartość p (test G)' = test_g$p.value,
'Wartość p (test dokładny Fishera)' = exact_fisher$p.value
))## Liczba stopni swobody.df Wartość krytyczna
## 1.00000000 3.84145882
## Statystyka chi^2 Wartość p (test chi-kwadrat)
## 5.16923077 0.02299039
## V Cramera Współczynnik fi (dla tabel 2x2)
## 0.32816506 0.32816506
## Statystyka chi^2 z poprawką Yatesa Wartość p (test chi^2 z poprawką Yatesa)
## 3.79780220 0.05131990
## Statystyka G Wartość p (test G)
## 5.38600494 0.02029889
## Wartość p (test dokładny Fishera)
## 0.04899141# Test zgodności chi-kwadrat
# Liczebności rzeczywiste:
observed <- c(70, 10, 20)
# Liczebności oczekiwane:
expected <- c(80, 10, 10)
# Ewentualna korekta liczebności oczekiwanych, żeby ich suma była na pewno równa sumie rzeczywistych:
expected <- expected / sum(expected) * sum(observed)
# Poziom istotności
alpha <- 0.05
test_chi <- chisq.test(x = observed, p = expected, rescale.p = TRUE)
test_g <- AMR::g.test(x = observed, p = expected, rescale.p = TRUE)
print(c('Liczba stopni swobody' = test_chi$parameter,
'Wartość krytyczna' = qchisq(1-alpha, test_chi$parameter),
'Statystyka chi^2' = unname(test_chi$statistic),
'Wartość p (test chi-kwadrat)' = test_chi$p.value,
'Statystyka G' = unname(test_g$statistic),
'Wartość p (test G)' = test_g$p.value
))## Liczba stopni swobody.df Wartość krytyczna
## 2.000000000 5.991464547
## Statystyka chi^2 Wartość p (test chi-kwadrat)
## 11.250000000 0.003606563
## Statystyka G Wartość p (test G)
## 9.031492255 0.010935443# Test niezależności/jednorodności chi-kwadrat
import numpy as np
import scipy.stats as stats
from scipy.stats import chi2
from statsmodels.stats.contingency_tables import Table2x2
# Dane (macierz):
m = np.array([
[21, 14],
[3, 10]
])
alpha = 0.05
# Test chi-kwadrat bez poprawki Yatesa:
test_chi = stats.chi2_contingency(m, correction=False)
# Test chi-kwadrat z poprawką Yatesa:
test_chi_corrected = stats.chi2_contingency(m)
# Test G:
g, p, dof, expected = stats.chi2_contingency(m, lambda_="log-likelihood")
# Dokładny test Fishera:
exact_fisher = stats.fisher_exact(m)
# V Cramera:
cramers_v = np.sqrt(test_chi[0] / m.sum() / min(m.shape[0]-1, m.shape[1]-1))
# Współczynnik fi dla tabeli 2x2:
phi_coefficient = None
if m.shape == (2, 2):
phi_coefficient = cramers_v*np.sign(np.diagonal(m).prod()-np.diagonal(np.fliplr(m)).prod())
# Wyniki
results = {
'Liczba stopni swobody': test_chi[2],
'Wartość krytyczna': chi2.ppf(1-alpha, test_chi[2]),
'Statystyka chi-kwadrat': test_chi[0],
'p-value (test chi-kwadrat)': test_chi[1],
"V Cramera": cramers_v,
'Współczynnik fi (dla tabeli 2x2)': phi_coefficient,
'Statystyka chi-kwadrat z poprawką Yatesa': test_chi_corrected[0],
'p-value (test chi-kwadrat z poprawką Yatesa)': test_chi_corrected[1],
'Statystyka G': g,
'p-value (test G)': p,
'p-value (dokładny test Fishera)': exact_fisher[1]
}
for key, value in results.items():
print(f"{key}: {value}")## Liczba stopni swobody: 1
## Wartość krytyczna: 3.841458820694124
## Statystyka chi-kwadrat: 5.169230769230769
## p-value (test chi-kwadrat): 0.022990394092464842
## V Cramera: 0.3281650616569468
## Współczynnik fi (dla tabeli 2x2): 0.3281650616569468
## Statystyka chi-kwadrat z poprawką Yatesa: 3.7978021978021976
## p-value (test chi-kwadrat z poprawką Yatesa): 0.05131990358807137
## Statystyka G: 3.9106978537750194
## p-value (test G): 0.04797967015430134
## p-value (dokładny test Fishera): 0.048991413058947844# Test zgodności chi-kwadrat
from scipy.stats import chisquare, chi2
import numpy as np
# Liczebności rzeczywiste:
observed = np.array([70, 10, 20])
# Liczebności oczekiwane:
expected = np.array([80, 10, 10])
# Ewentualna korekta liczebności oczekiwanych, żeby ich suma była na pewno równa sumie rzeczywistych:
expected = expected / expected.sum() * observed.sum()
# Test chi-kwadrat:
chi_stat, chi_p = chisquare(f_obs=observed, f_exp=expected)
# Liczba stopni swobody:
df = len(observed) - 1
# Poziom istotności:
alpha = 0.05
# Wartość krytyczna:
critical_value = chi2.ppf(1 - alpha, df)
# Test G:
from scipy.stats import power_divergence
g_stat, g_p = power_divergence(f_obs=observed, f_exp=expected, lambda_="log-likelihood")
# Wyniki
results = {
'Liczba stopni swobody': df,
'Wartość krytyczna': critical_value,
'Statystyka chi^2': chi_stat,
'Wartość p (test chi-kwadrat)': chi_p,
'Statystyka G': g_stat,
'Wartość p (test G)': g_p
}
for key, value in results.items():
print(f"{key}: {value}")## Liczba stopni swobody: 2
## Wartość krytyczna: 5.991464547107979
## Statystyka chi^2: 11.25
## Wartość p (test chi-kwadrat): 0.0036065631360157305
## Statystyka G: 9.031492254964643
## Wartość p (test G): 0.010935442847719828C.6 ANOVA i test Levene'a
ANOVA — arkusz Google
ANOVA — szablon w Excelu
# Przykładowe dane
group <- as.factor(c(rep("A",7), rep("B",7), rep("C",7), rep("D",7)))
result <- c(51, 87, 50, 48, 79, 61, 53, 82, 91, 92, 80, 52, 79, 73,
79, 84, 74, 98, 63, 83, 85, 85, 80, 65, 71, 67, 51, 80)
data<-data.frame(group, result)
#Aby obejrzeć dane, można uruchomić: View(data)
#Aby zapisać dane do pliku tekstowego, można uruchomić: write.csv2(data, "data.csv")
#Aby wczytać dane z pliku tekstowego, można uruchomić: read.csv2("data.csv")
# Tabela z podsumowaniem
library(dplyr)
data %>%
group_by(group) %>%
summarize(n=n(), suma = sum(result), srednia = mean(result), odch_st=sd(result), mediana = median(result)) %>%
data.frame() -> summary_table
# Tabela ANOVA
model<-aov(result~group, data=data)
anova_summary<-summary(model)
# Test Levene'a (Browna-Forsythe'a)
levene_result<-car::leveneTest(result~group, data=data)
# Procedura Tukeya
tukey_result<-TukeyHSD(x=model, conf.level=0.95)
print(list(`Podsumowanie` = summary_table, `Tabela ANOVA` = anova_summary, `Test Levene'a` = levene_result,
`HSD Tukeya` = tukey_result))## $Podsumowanie
## group n suma srednia odch_st mediana
## 1 A 7 429 61.28571 15.56400 53
## 2 B 7 549 78.42857 13.45185 80
## 3 C 7 566 80.85714 10.76148 83
## 4 D 7 499 71.28571 11.61485 71
##
## $`Tabela ANOVA`
## Df Sum Sq Mean Sq F value Pr(>F)
## group 3 1620 539.8 3.204 0.0412 *
## Residuals 24 4043 168.5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## $`Test Levene'a`
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 3 0.1898 0.9023
## 24
##
## $`HSD Tukeya`
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = result ~ group, data = data)
##
## $group
## diff lwr upr p adj
## B-A 17.142857 -1.996412 36.282127 0.0905494
## C-A 19.571429 0.432159 38.710698 0.0437429
## D-A 10.000000 -9.139270 29.139270 0.4870470
## C-B 2.428571 -16.710698 21.567841 0.9849136
## D-B -7.142857 -26.282127 11.996412 0.7340659
## D-C -9.571429 -28.710698 9.567841 0.5237024import pandas as pd
import numpy as np
from scipy import stats
import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from statsmodels.stats.anova import anova_lm
# Ramka danych
group = ['A']*7 + ['B']*7 + ['C']*7 + ['D']*7
result = [51, 87, 50, 48, 79, 61, 53,
82, 91, 92, 80, 52, 79, 73,
79, 84, 74, 98, 63, 83, 85,
85, 80, 65, 71, 67, 51, 80]
data = pd.DataFrame({'group': group, 'result': result})
# Tabela z podsumowaniem danych
summary_table = data.groupby('group')['result'].agg(['count', 'sum', 'mean', 'std', 'median']).reset_index()
summary_table.columns = ['group', 'n', 'suma', 'srednia', 'odch_st', 'mediana']
# ANOVA
model = ols('result ~ group', data=data).fit()
anova_summary = anova_lm(model, typ=2)
# Test Levene'a (Browna-Forsythe'a)
levene_result = stats.levene(data['result'][data['group'] == 'A'],
data['result'][data['group'] == 'B'],
data['result'][data['group'] == 'C'],
data['result'][data['group'] == 'D'])
# Procedura HSD Tukeya
tukey_result = pairwise_tukeyhsd(endog=data['result'], groups=data['group'], alpha=0.05)
print('Podsumowanie:\n\n', summary_table, '\n\nTabela ANOVA:\n\n', anova_summary, '\n\nTest Levene\'a:\n\n', levene_result,
'\n\nHSD Tukeya:\n\n', tukey_result)## Podsumowanie:
##
## group n suma srednia odch_st mediana
## 0 A 7 429 61.285714 15.564000 53.0
## 1 B 7 549 78.428571 13.451854 80.0
## 2 C 7 566 80.857143 10.761483 83.0
## 3 D 7 499 71.285714 11.614851 71.0
##
## Tabela ANOVA:
##
## sum_sq df F PR(>F)
## group 1619.535714 3.0 3.204282 0.041204
## Residual 4043.428571 24.0 NaN NaN
##
## Test Levene'a:
##
## LeveneResult(statistic=0.18975139523084725, pvalue=0.9023335775328473)
##
## HSD Tukeya:
##
## Multiple Comparison of Means - Tukey HSD, FWER=0.05
## =====================================================
## group1 group2 meandiff p-adj lower upper reject
## -----------------------------------------------------
## A B 17.1429 0.0905 -1.9964 36.2821 False
## A C 19.5714 0.0437 0.4322 38.7107 True
## A D 10.0 0.487 -9.1393 29.1393 False
## B C 2.4286 0.9849 -16.7107 21.5678 False
## B D -7.1429 0.7341 -26.2821 11.9964 False
## C D -9.5714 0.5237 -28.7107 9.5678 False
## -----------------------------------------------------C.7 Najważniejsze testy nieparametryczne
C.7.1 Test Manna-Whitneya
Test Manna-Whitneya — arkusz Google
Test Manna-Whitneya — szablon w Excelu
C.7.2 Test Wilcoxona dla par obserwacji
Test Wilcoxona dla par obserwacji — arkusz Google
Test Wilcoxona dla par obserwacji — szablon w Excelu
C.7.3 Test Kruskalla-Wallisa
Test Kruskala-Wallisa — arkusz Google
Test Kruskala-Wallisa — szablon w Excelu
C.8 Inne testy
C.8.1 Regresja
Regresja prosta — arkusz Google
Regresja prosta — szablon w Excelu
Regresja wieloraka — arkusz Google
Regresja wieloraka — szablon w Excelu
C.8.2 Sprawdzanie normalności rozkładu
Sprawdzanie normalności — arkusz Google
Sprawdzanie normalności — szablon w Excelu
# Sprawdzenie normalności
# Dane
data<-c(76, 62, 55, 62, 56, 64, 44, 56, 94, 37, 72, 85, 72, 71, 60, 61, 64, 71, 69, 70, 64, 59, 71, 65, 84)
# Średnia
m<-mean(data)
# Odchylenie standardowe
s<-sd(data)
# Skośność
skew<-e1071::skewness(data, type=2)
# Kurtoza
kurt<-e1071::kurtosis(data, type=2)
# iloraz IQR do odchylenia standardowego
IQR_to_s<-IQR(data)/s
#udział obserwacji odległych o mniej niż 1 odchylenie standardowe od średniej
within1s<-mean(abs(data-m)<s)
#...o mniej niż 2 odchylenia...
within2s<-mean(abs(data-m)<2*s)
#...o mniej niż 3 odchylenia...
within3s<-mean(abs(data-m)<3*s)
# Test Shapiro-Wilka
SW_res<-shapiro.test(data)
# Test Jarque'a-Bery
JB_res<-tseries::jarque.bera.test(data)
# Test Andersona-Darlinga
AD_res<-nortest::ad.test(data)
# Test Kołmogorowa-Smirnowa
KS_res <- ks.test(data, function(x){pnorm(x, mean(data), sd(data))})
# Wyniki
print(c('Średnia' = m,
'Odchylenie st.' = s,
'Liczebność' = length(data),
'Skośność (~=0?)' = skew,
'Kurtoza (~=0?)' = kurt,
'IQR/s (~=1,3?)' = IQR_to_s,
'Reguła 68%' = within1s*100,
'Reguła 95%' = within2s*100,
'Reguła 100%' = within3s*100,
'Stat. test. - test SW' = SW_res$statistic,
'Wartość p - test SW' = SW_res$p.value,
'Stat. test. - test JB' = JB_res$statistic,
'Wartość p - test JB' = JB_res$p.value,
'Stat. test. - test AD' = AD_res$statistic,
'Wartość p - test AD' = AD_res$p.value,
'Stat. test. - test KS' = KS_res$statistic,
'Wartość p - test KS' = KS_res$p.value
))## Średnia Odchylenie st.
## 65.760000000 12.145918382
## Liczebność Skośność (~=0?)
## 25.000000000 -0.002892879
## Kurtoza (~=0?) IQR/s (~=1,3?)
## 1.121315636 0.905654036
## Reguła 68% Reguła 95%
## 80.000000000 92.000000000
## Reguła 100% Stat. test. - test SW.W
## 100.000000000 0.964892812
## Wartość p - test SW Stat. test. - test JB.X-squared
## 0.520206266 0.479578632
## Wartość p - test JB Stat. test. - test AD.A
## 0.786793609 0.445513641
## Wartość p - test AD Stat. test. - test KS.D
## 0.260454333 0.143712404
## Wartość p - test KS
## 0.680154210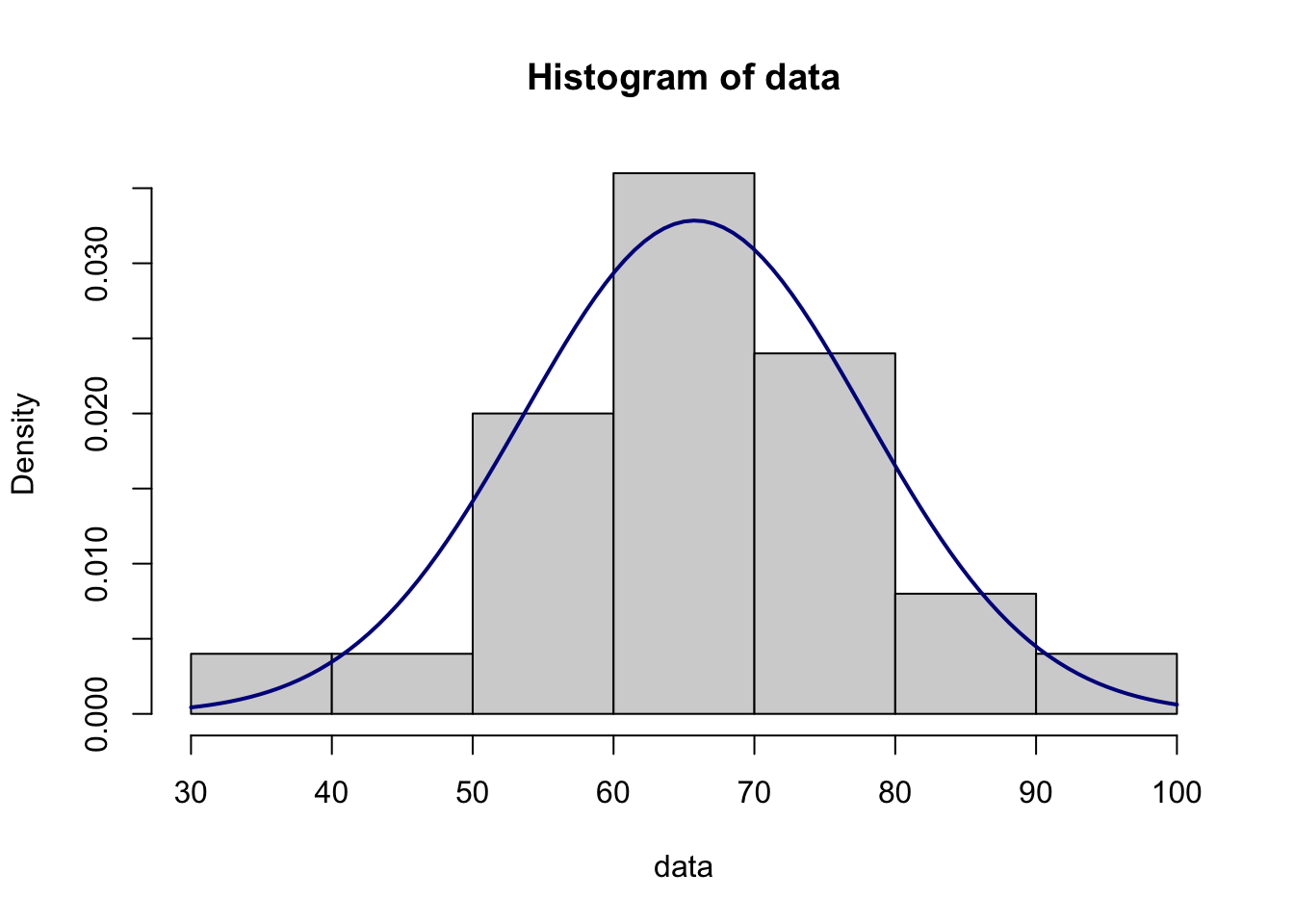
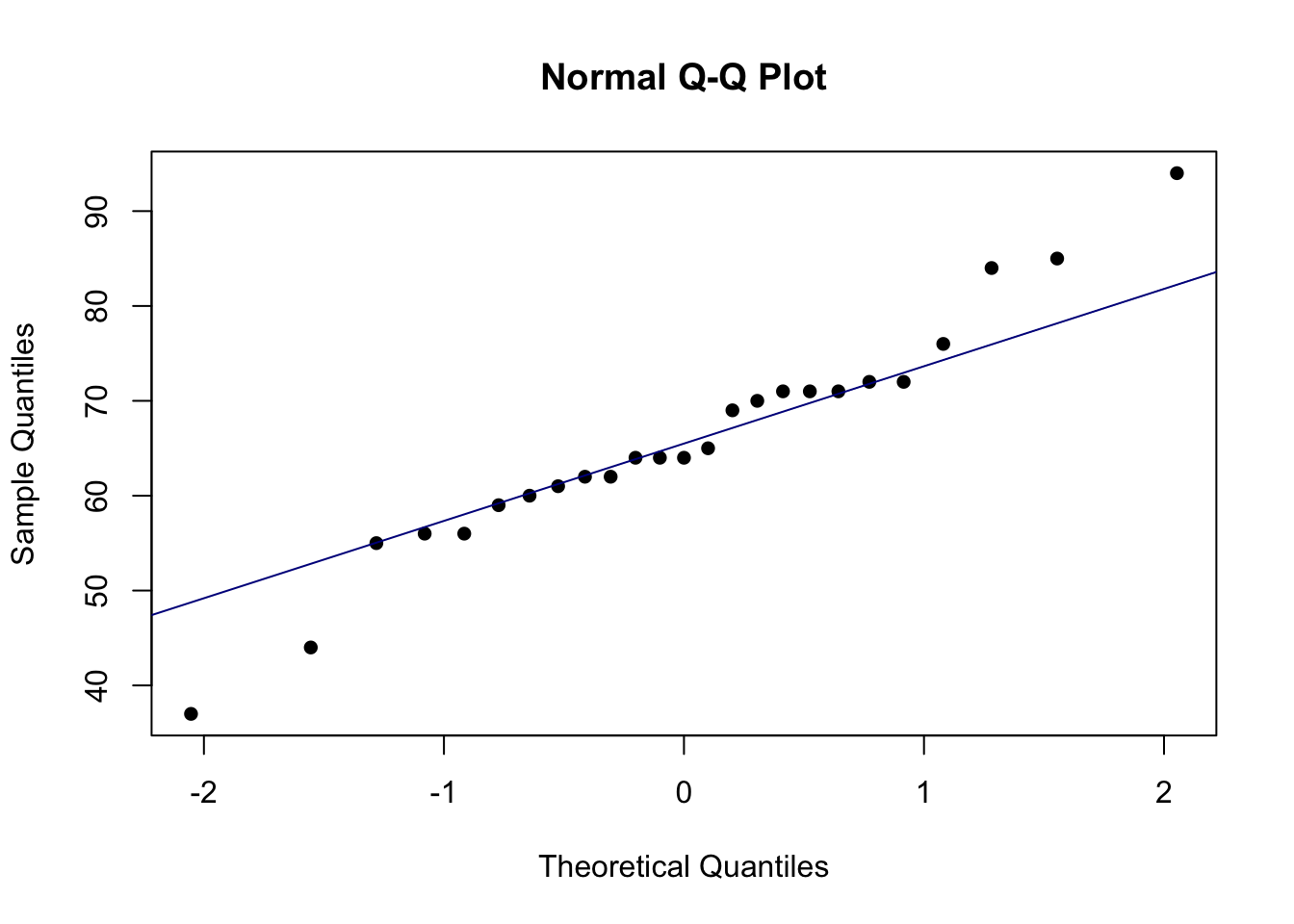
C.8.3 Współczynnik korelacji
Współczynnik korelacji – szablon — arkusz Google
Współczynnik korelacji – szablon — szablon w Excelu
#dane:
x <- c(4, 8, 6, 5, 3, 8, 6, 5, 5, 6, 3, 3, 3, 7, 3, 6, 4, 4, 8, 7)
y <- c(4, 6, 8, 3, 4, 6, 5, 8, 1, 4, 4, 3, 1, 6, 7, 5, 4, 4, 9, 5)
#test i przedział ufności:
cor.test(x, y, alternative = "two.sided", conf.level = 0.95)##
## Pearson's product-moment correlation
##
## data: x and y
## t = 2.56, df = 18, p-value = 0.01968
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.09607185 0.78067292
## sample estimates:
## cor
## 0.5166288