Rozdział 4 Prawdopodobieństwo

4.1 Aksjomaty

Matematyczne zasady działania prawdopodobieństwa jako funkcji przypisującej zdarzeniom wartość liczbową można zapisać za pomocą kilku aksjomatów. Fachowo jest to opisane np. tutaj (vide Aksjomatyka Kołomogorowa).

W uproszczeniu aksjomaty możemy sformułować na przykład tak:

1. Prawdopodobieństwo dowolnego zdarzenia A jest nieujemne.

\[\begin{equation} \mathbb{P}(A) \ge 0 \tag{4.1} \end{equation}\]

2. Jeżeli zdarzenia A i B wzajemnie się wykluczają (są rozłączne), to prawdopodobieństwo ich sumy równa się sumie prawdopodobieństw:

\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) \tag{4.2} \end{equation}\]

3. Prawdopodobieństwo zdarzenia pewnego \(\Omega\) wynosi 1.

\[\begin{equation} \mathbb{P}(\Omega) = 1 \tag{4.3} \end{equation}\]

4.2 Interpretacje prawdopodobieństwa:

1. Prawdopodobieństwo klasyczne

Jeżeli mamy skończoną liczbę równoprawdopodobnych zdarzeń elementarnych, to prawdopodobieństwo zdarzenia A jest udziałem zdarzeń elementarnych sprzyjających zdarzeniu A w łącznej liczbie zdarzeń elementarnych.

2. Częstościowa interpretacja prawdopodobieństwa

Prawdopodobieństwo jakiegoś zdarzenia to „względna częstość jego zachodzenia stwierdzona po powtórzeniu procesu wielką liczbę razy w podobnych warunkach” (von Mises).

Wizualizacja dla rzutu idealną monetą: https://seeing-theory.brown.edu/basic-probability/index.html

3. Subiektywna interpretacja prawdopodobieństwa

Według tej interpretacji prawdopodobieństwo to miara pewności, jaką można przypisać poszczególnym zdarzeniom.

4.3 Zdarzenia – podstawowe pojęcia

4.3.1 Zdarzenie elementarne

Zdarzenie elementarne to jeden z możliwych wyników doświadczenia losowego.

4.3.2 Zdarzenie złożone

Zdarzenie złożone to zbiór złożony z (niekoniecznie wszystkich) zdarzeń elementarnych. Zdarzenia elementarne wchodzące w skład zdarzenia złożonego, to zdarzenia elementarne sprzyjające zdarzeniu złożonemu.

4.3.3 Zbiór zdarzeń elementarnych (przestrzeń zdarzeń elementarnych)

Przestrzeń zdarzeń elementarnych to zbiór wszystkich zdarzeń elementarnych.

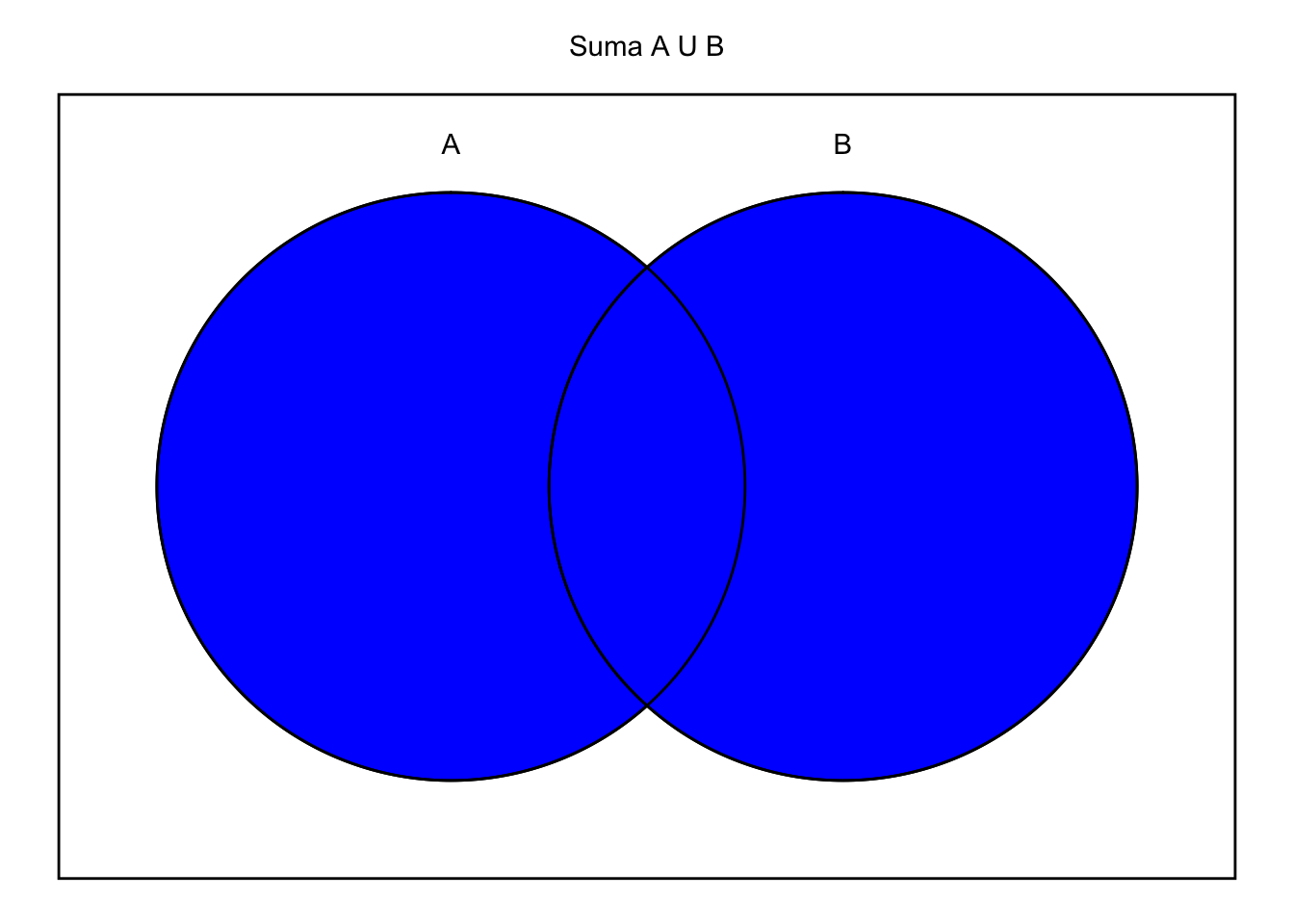
4.3.4 Suma zdarzeń

Suma zdarzeń A i B, nazywana też unią zdarzeń, to zdarzenie polegające na tym, że nastąpi zdarzenie A lub zdarzenie B. W celu uniknięcia nieporozumień warto zaznaczyć, że unia zdarzeń zawiera też część wspólną zdarzeń.

Sumę zdarzeń A i B możemy zapisywać jako \(A \cup B\) i czytać „A lub B”, „A suma B”. W niektórych podręcznikach sumę zdarzeń zapisuje się jako \(A + B\).

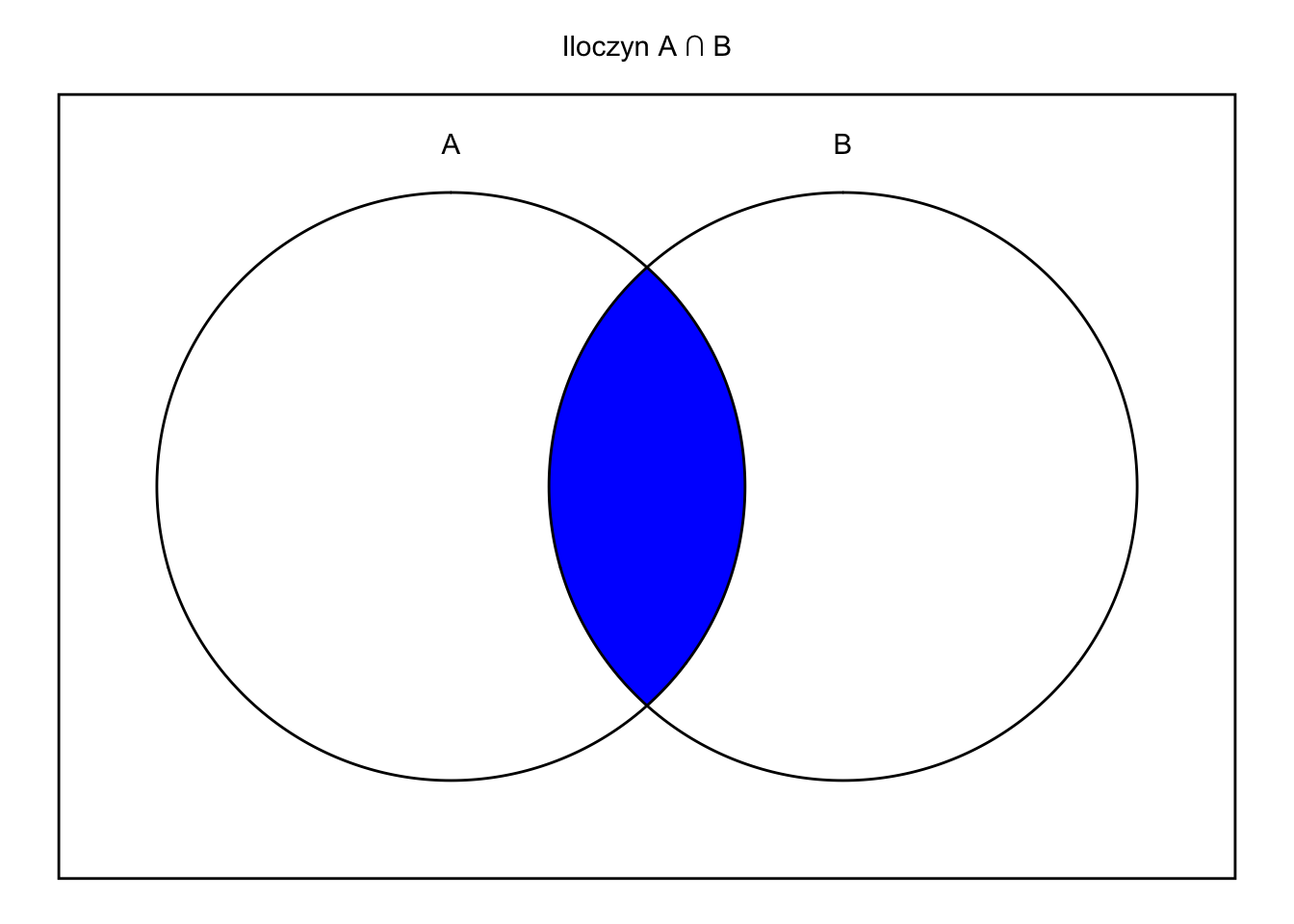
4.3.5 Iloczyn zdarzeń

Iloczyn zdarzeń (część wspólna, przekrój zdarzeń, przecięcie zdarzeń) to zdarzenie polegające na tym, że wystąpiło zarówno zdarzenie A, jak i zdarzenie B.

Iloczyn zdarzeń A i B możemy zapisywać jako \(A \cap B\) i czytać „A i B”, „A iloczyn B”. W niektórych podręcznikach iloczyn zdarzeń zapisuje się jako \(AB\), przez analogię do zwykłego iloczynu.

4.3.6 Zdarzenie przeciwne

Zdarzenie przeciwne do zdarzenia \(A\) to „nie \(A\)”. Zdarzenie przeciwne będziemy oznaczać symbolem „\({}^C\)” (od angielskiego complement – dopełnienie zbioru). Inne symbole stosowane w podręcznikach to: \(A'\), \(\bar{A}\), \(\neg A\).

https://pl.wikipedia.org/wiki/Zdarzenie_losowe_przeciwne

4.3.7 Prawdopodobieństwo warunkowe:

https://pl.wikipedia.org/wiki/Prawdopodobie%C5%84stwo_warunkowe

Wzór przy założeniu niezerowego \(\mathbb{P}(B)\):

\[\begin{equation} \mathbb{P}(A|B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \tag{4.4} \end{equation}\]

Prawdopodobieństwo warunkowe – wizualizacja

4.3.8 Zdarzenia wzajemnie wykluczające się (rozłączne)

Zdarzenia A i B wzajemnie się wykluczają, jeżeli nie mają części wspólnej (żadne ze zdarzeń elementarnych nie sprzyja jednocześnie zdarzeniu A i zdarzeniu B). Innymi słowy iloczyn A i B jest zdarzeniem niemożliwym (zbiorem pustym).

\[\begin{equation} \mathbb{P}(A\cap B) = \mathbb{P}(\emptyset) = 0 \tag{4.5} \end{equation}\]

4.3.9 Zdarzenia niezależne

Zdarzenia A i B są niezależne wtedy, kiedy prawdopodobieństwo ich iloczynu równa się iloczynowi ich prawdopodobieństw:

\[\begin{equation} \mathbb{P}(A\cap B) = \mathbb{P}(A)\mathbb{P}(B) \tag{4.6} \end{equation}\]

Jeżeli zdarzenia A i B są niezależne, to fakt, że zaszło zdarzenie A nie zmienia prawdopodobieństwa zdarzenia B i odwrotnie:

\[\begin{equation} \mathbb{P}(B|A) = \mathbb{P}(B) \tag{4.7} \end{equation}\]

\[\begin{equation} \mathbb{P}(A|B) = \mathbb{P}(A) \tag{4.8} \end{equation}\]

Zdarzenia, które nie są niezależne, nazywamy zdarzeniami zależnymi.

4.4 Prawdopodobieństwo – podstawowe reguły

Warto zapoznać się z wizualizacją 1 i wizualizacją 2, za pomocą których można sprawdzić niektóre z poniższych reguł.

4.4.1 Zasada dopełnień

Suma prawdopodobieństw zdarzeń dopełniających się (zdarzenia \(A\) i przeciwnego mu zdarzenia \(A^C\)) wynosi 1.

\[\begin{equation} \mathbb{P}(A) + \mathbb{P}(A^C) = 1 \tag{4.9} \end{equation}\]

4.4.2 Zasada dodawania

Prawdopodobieństwo sumy dwóch zdarzeń równa się sumie prawdopodobieństw tych zdarzeń pomniejszonej o prawdopodobieństwo iloczynu tych zdarzeń.

\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B) \tag{4.10} \end{equation}\]

Oczywiście, jeżeli zdarzenia A i B wzajemnie się wykluczają, wzór ten upraszcza się. W takiej sytuacji prawdopodobieństwo sumy zdarzeń jest równe sumie prawdopodobieństw tych zdarzeń

\[\begin{equation} \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) \tag{4.11} \end{equation}\]

Równanie (4.10) i (4.11) dotyczą dwóch zdarzeń. Wzory dla trzech zdarzeń można znaleźć w sekcji A.

4.4.3 Zasada mnożenia

Prawdopodobieństwo iloczynu zdarzeń A i B równa się iloczynowi prawdopodobieństwa zdarzenia A i zdarzenia B|A.

\[\begin{equation} \mathbb{P}(A \cap B) = \mathbb{P}(A) \mathbb{P}(B|A) \tag{4.12} \end{equation}\]

lub

\[\begin{equation} \mathbb{P}(A \cap B) = \mathbb{P}(B) \mathbb{P}(A|B) \tag{4.13} \end{equation}\]

Wzory upraszczają się dla zdarzeń niezależnych (vide wzór (4.6)).

Analogiczne wzory dla trzech zdarzeń można znaleźć w sekcji A.

4.5 Zadania

Zadanie 4.1 Przypuśćmy, że rzucamy dwiema monetami i obserwujemy co wypadło (orzeł/reszka).

  1. Wymień wszystkie zdarzenia elementarne tego eksperymentu.

  2. Przyporządkuj prawdopodobieństwo każdemu zdarzeniu elementarnemu. (Czy wszystkie zdarzenia elementarne są jednakowo prawdopodobne?)

  3. Niech A oznacza zdarzenie polegające na tym, że wypadł dokładnie jeden orzeł, zaś B niech oznacza, że wypadł przynajmniej jeden orzeł. Wymień wszystkie zdarzenia elementarne dla A i B.

  4. Na podstawie odpowiedzi z pytania (c), znajdź \(\mathbb{P}(A)\), \(\mathbb{P}(B)\), \(\mathbb{P}(A \cap B)\), \(\mathbb{P}(A \cup B)\), \(\mathbb{P}(A^C \cup B)\).

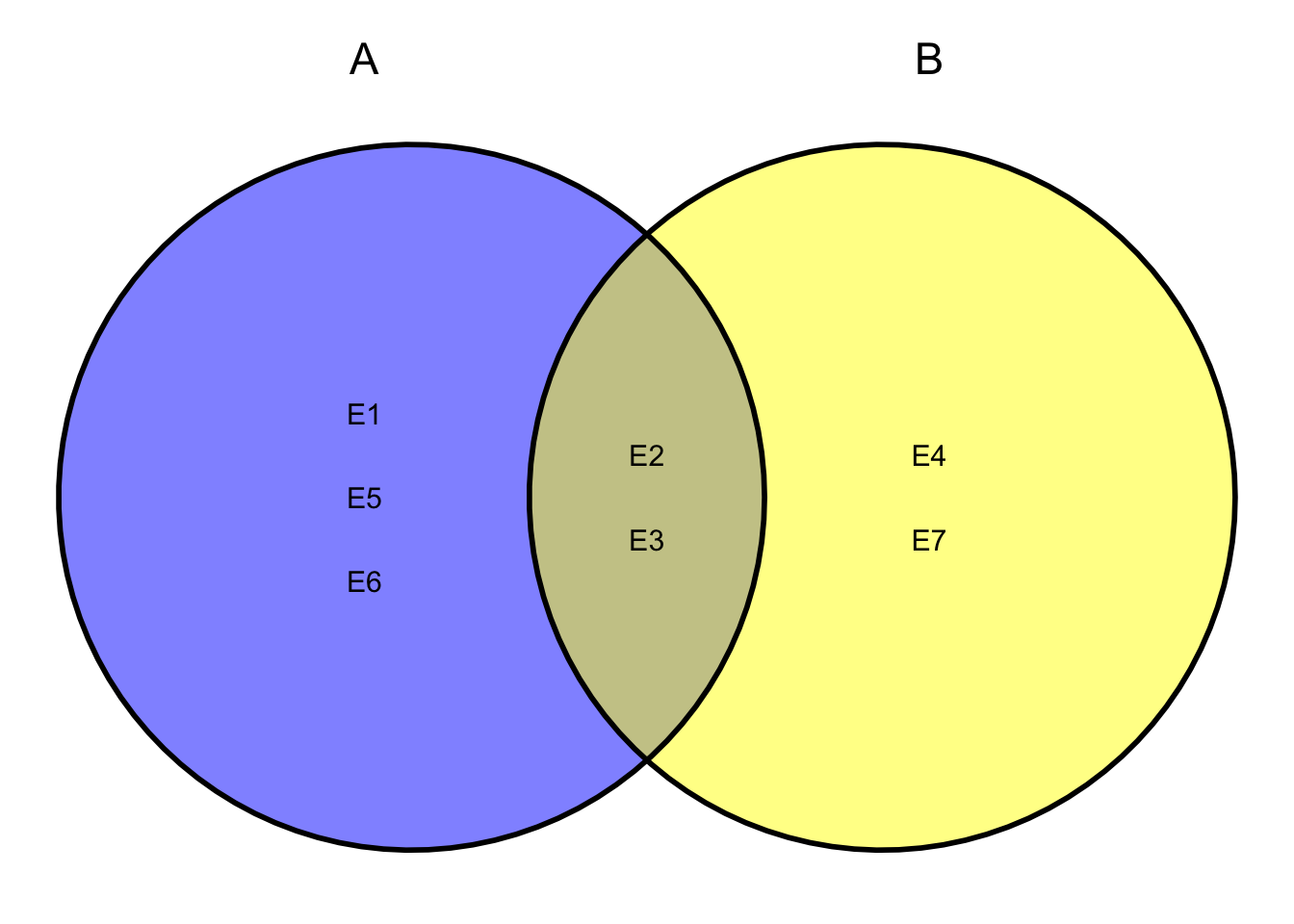
Zadanie 4.2 Przedstawione na poniższym diagramie Venna zdarzenia elementarne (jest ich siedem) mają następujące prawdopodobieństwa: \(\mathbb{P}(E_2)=\mathbb{P}(E_3)=\frac{1}{5}\), \(\mathbb{P}(E_4)=\mathbb{P}(E_5)=\frac{1}{20}\), \(\mathbb{P}(E_6)=\frac{1}{10}\), \(\mathbb{P}(E_7)=\frac{1}{5}\).

Znajdź prawdopodobieństwa następujących zdarzeń:

  1. \(\mathbb{P}(A)\)
  2. \(\mathbb{P}(B)\)
  3. \(\mathbb{P}(A\cup B)\)
  4. \(\mathbb{P}(A\cap B)\)
  5. \(\mathbb{P}(A^C)\)
  6. \(\mathbb{P}(B^C)\)
  7. \(\mathbb{P}(A^C \cup A)\)
  8. \(\mathbb{P}(A^C \cap B)\)

Zadanie 4.3 Losujemy dwie karty z talii. Jakie jest prawdopodobieństwo, że będą to dwa asy, jeżeli:

  1. losujemy ze zwracaniem,

  2. losujemy bez zwracania.

Zadanie 4.4 (Miller and Miller 2012) Losowo wybieramy dwa telefony komórkowe z dostawy liczącej 240 telefonów, z czego 15 jest wadliwych. Jakie jest prawdopodobieństwo, że oba będą wadliwe?

Zadanie 4.5 (Miller and Miller 2012) Przy pewnym wyjeździe z autostrady prawdopodobieństwa, że zatrzymana ciężarówka będzie miała uszkodzony układ hamulcowy lub nadmiernie zużyte opony, wynoszą odpowiednio 0,23 i 0,24. Prawdopodobieństwo, że zatrzymana ciężarówka będzie miała nadmiernie zużyte opony lub/i uszkodzony układ hamulcowy, wynosi 0,38. Jakie jest prawdopodobieństwo, że ciężarówka zatrzymana przy tym wyjeździe będzie miała zarówno nadmiernie zużyte opony, jak i uszkodzony układ hamulcowy?

Zadanie 4.6 (Aczel and Sounderpandian 2018) Urządzenie elektroniczne zostało zbudowane z dwóch komponentów A i B w taki sposób, że urządzenie może działać, kiedy przynajmniej jeden z tych komponentów działa. Prawdopodobieństwo uszkodzenia komponentu A w ciągu miesiąca to 0,02, zaś komponentu B – 0,1. Komponenty funkcjonują niezależnie od siebie. Jakie jest prawdopodobieństwo że urządzenie będzie działać przez cały miesiąc?

Zadanie 4.7 Nastąpią trzy rzuty monetą i mamy osiem równoprawdopodobnych możliwości: OOO, OOR, ORO, ROO, ORR, ROR, RRO i RRR. Przez A oznaczmy zdarzenie polegające na tym, że w pierwszych dwóch rzutach będą orły, B to zdarzenie, że w trzecim rzucie będzie reszka, zaś C to zdarzenie, że w trzech rzutach wystąpią dokładnie dwie reszki. Pokaż, że:

  1. Zdarzenia A i B są niezależne

  2. Zdarzenia B i C są zależne

Zadanie 4.8 (DeFusco et al. 2015) Przedsiębiorstwo wykorzystuje trzy kryteria, by dokonać wstępnej selekcji potencjalnych celów akwizycji z listy 500 przedsiębiorstw:

Kryterium 1. Kompatybilne linie produktowe – proporcja przedsiębiorstw spełniających kryterium: 0,20.

Kryterium 2. Połączone przedsiębiorstwa będą miały większy wskaźnik wzrostu przychodów – proporcja przedsiębiorstw spełniających kryterium: 0,45.

Kryterium 3. Zakup wykonalny z punktu widzenia zarządzania aktywami i pasywami – proporcja przedsiębiorstw spełniających kryterium: 0,78.

Jakiej liczby przedsiębiorstw należy się spodziewać po przefiltrowaniu listy 500, jeżeli założymy, że trzy kryteria działają niezależnie.

Zadanie 4.9 Weźmy pod uwagę wyniki podwójnego rzutu kostką. Narysuj diagram Venna dla tej przestrzeni zdarzeń elementarnych i wskaż zdarzenie „wynik drugiego rzutu jest wyższy od wyniku pierwszego rzutu”. Oblicz prawdopodobieństwo tego zdarzenia.

Zadanie 4.10 Biuro maklerskie obraca akcjami i obligacjami. Analityk biura chce oszacować prawdopodobieństwo, że osoba, która zasięga porady, będzie chciała nabyć akcje (zdarzenie S) lub obligacje (zdarzenie B). Zdefiniuj sumę i iloczyn obu tych zdarzeń.

Zadanie 4.11 Zdarzenia A, B i C są (wzajemnie) niezależne. \(\mathbb{P}(A)=0{,}6\); \(\mathbb{P}(B)=0{,}7\); \(\mathbb{P}(C)=0{,}8\). Jakie jest prawdopodobieństwo sumy zdarzeń A, B i C?

Zadanie 4.12 (Miller and Miller 2012) Wśród małżeństw żyjących w pewnym mieście prawdopodobieństwo, że mąż weźmie udział w wyborach do rady rodziców wynosi 0,21; prawdopodobieństwo wzięcia udziału w wyborach do rady przez żonę wynosi 0,28; zaś prawdopodobieństwo, że oboje zagłosują to 0,15. Jakie jest prawdopodobieństwo, że przynajmniej jedno z nich zagłosuje?

Zadanie 4.13 (Miller and Miller 2012) W grupie 200 studentów uniwersytetu 138 osób zapisało się na psychologię, 115 – na socjologię, a 91 zapisało się na oba przedmioty. Ilu studentów nie zapisało się na żaden z tych dwóch? (Wskazówka: można wykorzystać diagram Venna i wpisać liczby w odpowiadających obszarach).

Zadanie 4.14 (Maddala 2006) Cztery tak samo wykształcone osoby, dwie kobiety i dwóch mężczyzn, ubiegają się o pracę w Compact S.A. Przedsiębiorstwo wybierze dwie osoby, przy czym nie zwraca uwagi na płeć kandydata. Jeśli będzie wybierać w sposób losowy, to jakie jest prawdopodobieństwo, że obie osoby będą tej samej płci? Student odpowiedział na to pytanie w następujący sposób: są trzy możliwe wyniki – 2 kobiety, 2 mężczyzn oraz 1 kobieta i 1 mężczyzna. Liczba zdarzeń sprzyjających wynosi 2, zatem szukane prawdopodobieństwo wynosi 2/3. Czy miał rację?

Zadanie 4.15 (Maddala 2006) Pewne przedsiębiorstwo, podejmując próbę poszukiwania ropy, wykonało kolejno cztery różne niezależne od siebie odwierty. Prawdopodobieństwo znalezienia ropy w każdym z nich jest takie samo i wynosi \(p\). Rozważmy następujące zdarzenia:

  • zdarzenie \(A\): w dokładnie dwóch odwiertach jest ropa,

  • zdarzenie \(B\): w co najmniej trzech odwiertach jest ropa,

  • zdarzenie \(C\): w odwiercie trzecim jest ropa,

  • zdarzenie \(D\): w mniej niż trzech odwiertach jest ropa.

Wyprowadź następujące prawdopodobieństwa:

  1. \(\mathbb{P}(A)\)

  2. \(\mathbb{P}(B)\)

  3. \(\mathbb{P}(C)\)

  4. \(\mathbb{P}(D)\)

  5. \(\mathbb{P}(A\cap B)\)

  6. \(\mathbb{P}(A \cup B)\)

  7. \(\mathbb{P}(B\cap C)\)

  8. \(\mathbb{P}(B \cup C)\)

  9. \(\mathbb{P}(B\cap D)\)

  10. \(\mathbb{P}(A|B)\)

  11. \(\mathbb{P}(B|C)\)

  12. \(\mathbb{P}(C|D)\)

  13. \(\mathbb{P}(D|C)\)

Zadanie 4.16 O zdarzeniach A i B wiemy tyle, że \(\mathbb{P}(A) = 1/3\) i \(\mathbb{P}(A\cap B) = 1/5\). Oblicz, o ile to możliwe, ile wynosi:

  1. \(\mathbb{P}(B|A)\)

  2. \(\mathbb{P}(A^C \cup B^C)\)

Literatura

Aczel, A. D., and J. Sounderpandian. 2018. Statystyka w Zarządzaniu. PWN. https://ksiegarnia.pwn.pl/Statystyka-w-zarzadzaniu,731934758,p.html.
DeFusco, Richard A., Dennis W. McLeavey, Jerald E. Pinto, David E. Runkle, and Mark J. P. Anson. 2015. Quantitative Investment Analysis. John Wiley & Sons.
Maddala, G. S. 2006. Ekonometria. Wydawnictwo Naukowe PWN.
Miller, Irwin, and Marylees Miller. 2012. John E. Freund’s Mathematical Statistics with Applications. 8th edition. Boston: Pearson.