G Jak korzystać z arkuszy kalkulacyjnych

G.1 Arkusze kalkulacyjne – typowe problemy

G.1.1 Ustawienia regionalne

G.1.2 Formuły tablicowe

G.1.3 Różnice między Excelem a Google sheets

G.2 Jak to zrobić w arkuszach kalkulacyjnych

G.2.1 Rozkłady prawdopodobieństwa

Podobnie jak w R (F.2.2), w arkuszach kalkulacyjnych można znaleźć funkcje umożliwiające podstawowe obliczenia związane z rozkładami prawdopodobieństwa.

Na przykładzie rozkładu normalnego:

• funkcję gęstości rozkładu normalnego uzyskamy za pomocą funkcji ROZKŁAD.NORMALNY (ang. NORMDIST– Excel, Google), jako czwarty argument wpisując FAŁSZ (lub 0); jest to odpowiednik funkcji dnorm w R:

=ROZKŁAD.NORMALNY(183,5; 180; 6; FAŁSZ) w arkuszu kalkulacyjnym to dnorm(183.5, 180, 6) w R

• dystrybuanta rozkładu normalnego powstaje z wykorzystaniem tej samej funkcji z argumentem PRAWDA albo 1

=ROZKŁAD.NORMALNY(183,5; 180; 6; 1) w arkuszu kalkulacyjnym to pnorm(183.5, 180, 6) w R

• odwrotną dystrybuantę rozkładu normalnego uzyskamy, używając funkcji ROZKŁAD.NORMALNY.ODW (ang. NORMINV– Excel, Google)

=ROZKŁAD.NORMALNY.ODW(0,72; 180; 6) w arkuszu kalkulacyjnym to qnorm(0.72, 180, 6) w R

• losowanie z rozkładu normalnego jest możliwe poprzez przekształcenie wartości wylosowanych z rozkładu jednostajnego przy użyciu odwrotnej dystrybuanty:

=ROZKŁAD.NORMALNY.ODW(LOS(); 180; 6) w arkuszu kalkulacyjnym to rnorm(1, 180, 6) w R

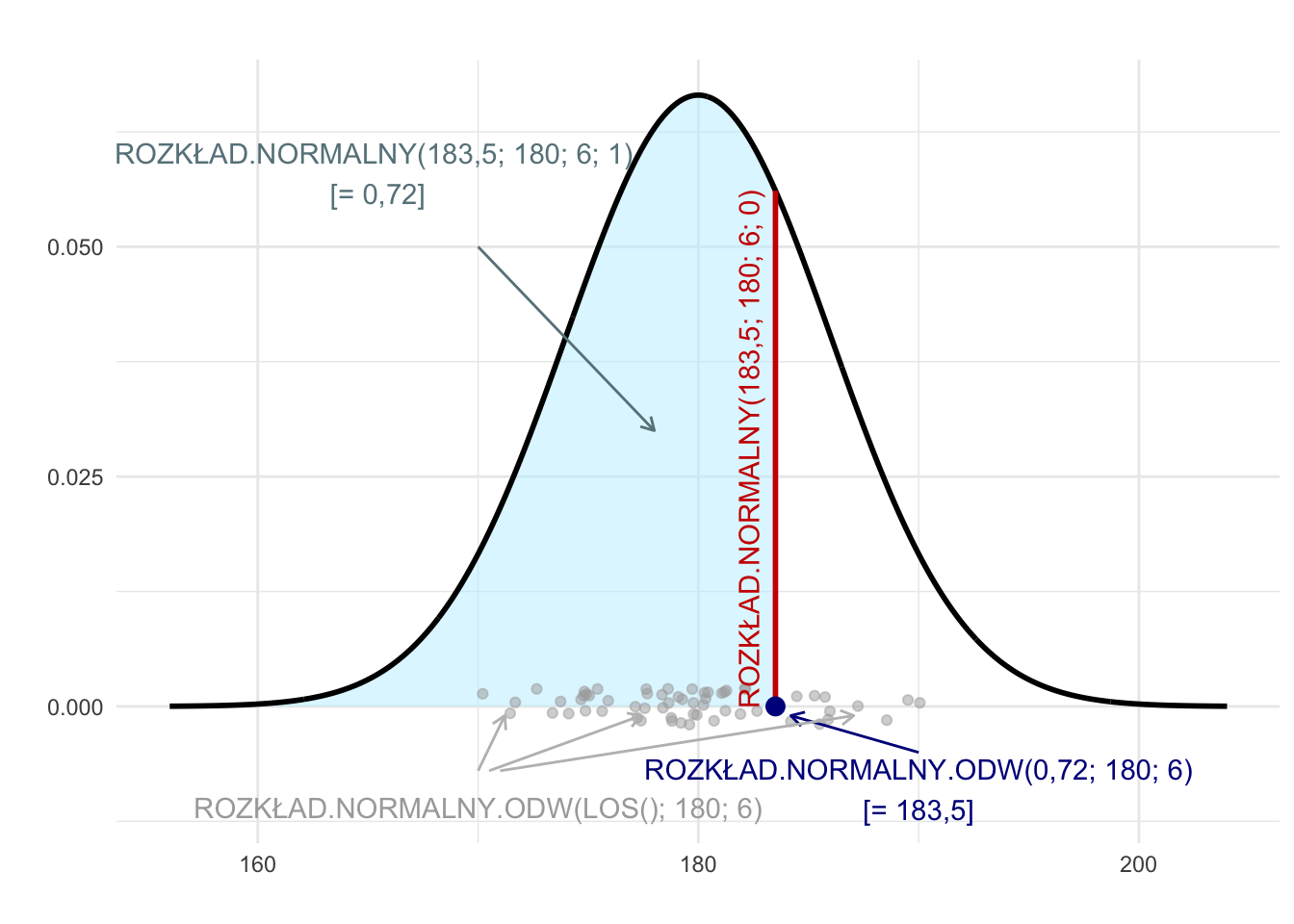
Rysunek G.1: Ilustracja zastosowania funkcji ROZKŁAD.NORMALNY i ROZKŁAD.NORMALNY.ODW dla rozkładu o średniej równej 180 i odchyleniu standardowym równym 6.