Rozdział 9 Ciągłe rozkłady prawdopodobieństwa

9.1 Funkcja gęstości

W przypadku zmiennych ciągłych zamiast funkcji masy prawdopodobieństwa mamy do czynienia z funkcją gęstości.

Funkcja gęstości prawdopodobieństwa (ang. PDF), najczęściej w statystyce oznaczana po prostu literą \(f\), spełnia dwa warunki:

1. Jest nieujemna

\[ f(x) \geqslant 0 \text{ dla wszystkich x,} \]

2. Pole pod krzywą gęstości wynosi 1 (prawdopodobieństwo zdarzenia pewnego).

\[ \int_{-\infty}^{\infty}f(x) dx = 1 \]

Prawdopodobieństwo odczytujemy, obliczając całkę (czyli określając pole powierzchni pod krzywą):

\[ \mathbb{P}(a < X < b) = \int_{a}^{b}f(x)dx \]

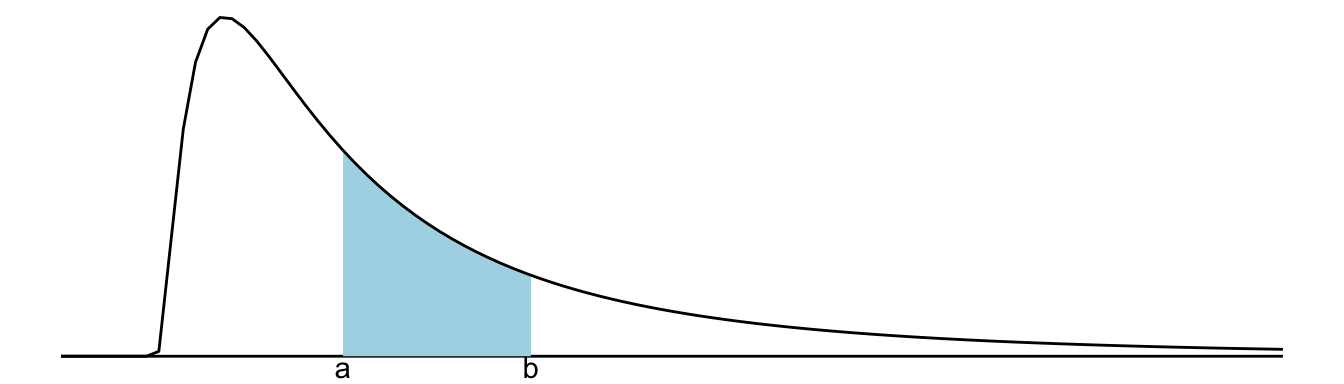
Rysunek 9.1: Dla zmiennej ciągłej prawdopodobieństwo, że zmienna przyjmie wartość między a i b jest równe polu powierzchni pod krzywą gęstości nad tym odcinkiem

Matematycznie patrząc, pole powierzchni nad pojedynczym punktem jest nieskończenie małe, zerowe. Oznacza to, że dla zmiennych ciągłych dla dowolnej pojedynczej wartości \(a\) zachodzi \(\mathbb{P}(X=a) = 0\). Może to być nieintuicyjne dla czytelnika, ale za to jest to logicznie spójne...

Stąd dla zmiennych ciągłych zachodzi następująca równość:

\[ \mathbb{P}(a< X < b) = \mathbb{P}(a\leqslant X \leqslant b) = \mathbb{P}(a\leqslant X < b) = \mathbb{P}(a < X \leqslant b)\]

Innymi słowy dla zmiennych ciągłych nie ma znaczenia, czy obliczając prawdopodobieństwo dla przedziału, uwzględniamy jego końce (przedział domknięty) czy nie (przedział otwarty). Generalnie liczenie prawdopodobieństw dla zmiennej losowej możliwe jest tylko dla przedziałów.

9.2 Rozkład jednostajny

Rozkład jednostajny ciągły to rozkład, dla którego gęstość w określonym przedziale (od \(c\) do \(d\)) jest równomierna.

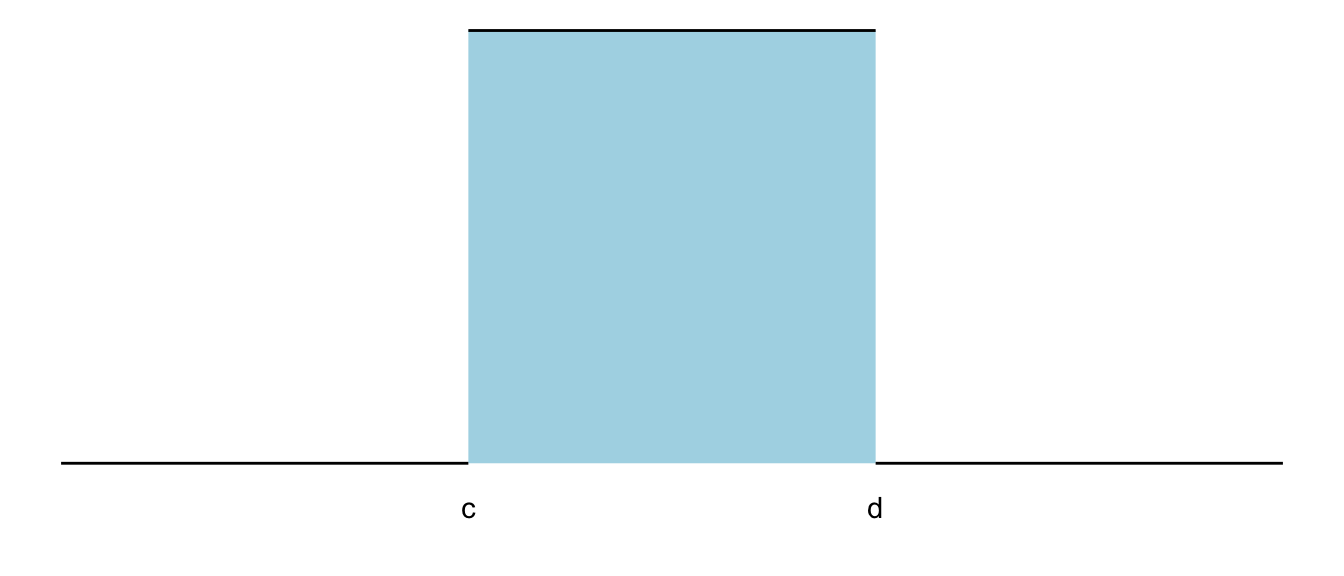
Rysunek 9.2: Funkcja gęstości rozkładu jednostajnego ciągłego

Ponieważ pole powierzchni pod wykresem funkcji gęstości powinno wynosić 1, wartość funkcji gęstości prawdopodobieństwa w przedziale (c,d) to \(f(x) = 1/(d-c)\).

Korzystając ze wzorów (7.9) i (7.12), można wykazać, że w rozkładzie jednostajnym średnia wynosi:

\[\begin{equation} \mu=\frac{c+d}{2}, \tag{9.1} \end{equation}\]

a wariancja:

\[\begin{equation} \sigma^2= \frac{(d-c)^2}{12} \tag{9.2} \end{equation}\]

9.3 Rozkład Gaussa

Rozkład Gaussa nazywany jest rozkładem normalnym. Nie oznacza to, że inne rozkłady są nienormalne – to po prostu nazwa¹.

Wzór na gęstość prawdopodobieństwa tego rozkładu (nie będziemy używać tego wzoru w sposób jawny, całkować go będzie komputer):

\[ f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}\:\:\:\:\:\:\: x \in \left(-\infty, \infty \right) \]

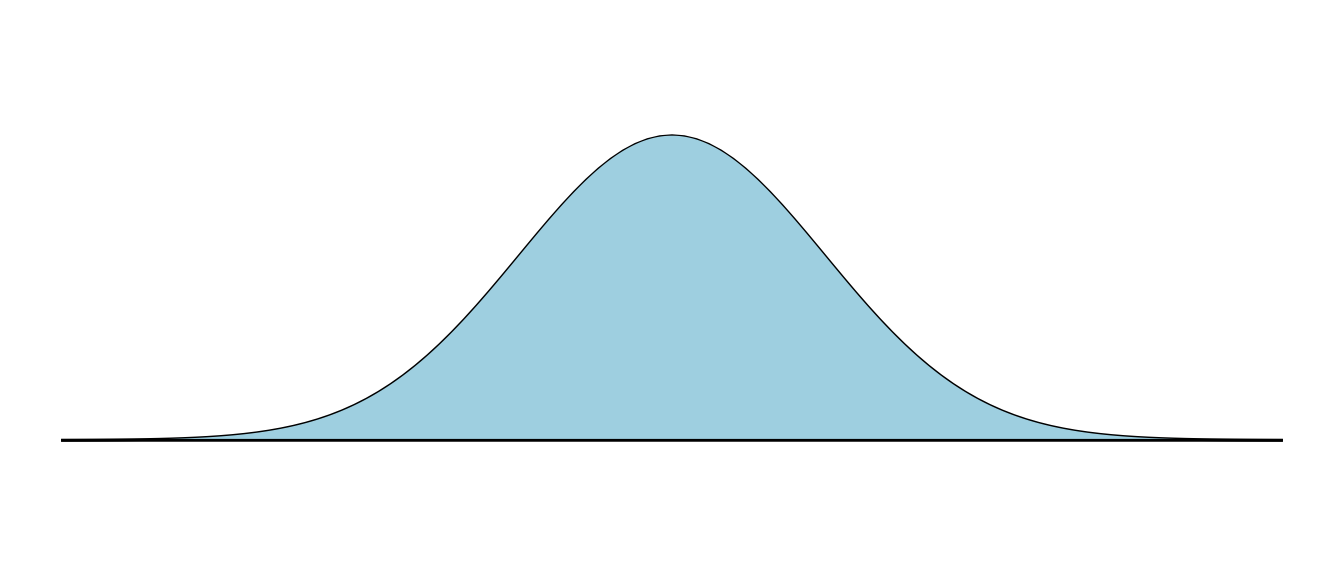
Rysunek 9.3: Kształt funkcji gęstości rozkładu normalnego

9.3.1 Standaryzowany rozkład normalny

Rozkład normalny ma generalnie dwa parametry: średnią (\(\mu\)) i odchylenie standardowe (\(\sigma\)). Jeżeli \(\mu=0\), a \(\sigma=1\), to zmienna taka ma standardowy (lub: standaryzowany) rozkład normalny. Zmienną charakteryzującą się standardyzowanym rozkładem Gaussa często oznaczamy literą \(Z\).

Zmienną \(X\) mającą rozkład normalny o wartości oczekiwanej \(\mu\) i odchyleniu standardowym \(\sigma\) możemy przekształcić (transformować) w zmienną standardową normalną \(Z\), odejmując od niej wartość oczekiwaną i dzieląc wynik przed odchylenie standardowe:

\[ Z = \frac{X - \mu}{\sigma} \]

Przy okazji warto wspomnieć, że standaryzować można dowolną zmienną lub listę danych. Standaryzacja (obliczanie wyniku standardowego z-score) polega na przekształceniu zmiennej lub listy zgodnie z powyższą zasadą (odejmujemy średnią, a uzyskaną różnicę dzielimy przez odchylenie standardowe). Oczywiście tak przeprowadzona standaryzacja nie zamieni zmiennej o rozkładzie innym niż normalny na zmienną o rozkładzie normalnym.

9.3.2 Suma i różnica zmiennych o rozkładzie normalnym

Jeżeli mamy dwie niezależne zmienne X i Y o rozkładzie normalnym o średnich odpowiednio \(\mu_X\) i \(\mu_Y\) oraz odchyleniach standardowych odpowiednio \(\sigma_X\) i \(\sigma_Y\), to

1. zmienna losowa X+Y ma rozkład normalny o średniej \(\mu_X+\mu_Y\) i odchyleniu standardowym \(\sqrt{\sigma^2_X+\sigma^2_Y}\),

2. zmienna losowa X-Y ma rozkład normalny o średniej \(\mu_X-\mu_Y\) i odchyleniu standardowym \(\sqrt{\sigma^2_X\:\mathbf{+}\:\sigma^2_Y}\).

Powyższe wzory można rozszerzyć na większą liczbą zmiennych.

9.3.3 Przybliżanie rozkładu dwumianowego rozkładem normalnym

Rozkład dwumianowy o parametrach \(n\) i \(p\) można przybliżyć za pomocą rozkładu normalnego o średniej \(np\) i odchyleniu standardowym \(\sqrt{np(1-p)}=\sqrt{npq}\). Czasem jest to wygodne i przydatne, a niekiedy może okazać się konieczne. Przybliżenie działa dość dobrze, jeżeli ogony rozkładu normalnego do trzech sigm mieszczą się pomiędzy wartościami \(0\) i \(n\), tzn:

\[ np - 3\sqrt{npq\vphantom{b}} > 0 \:\:\:\:\:\: \text{i} \:\:\:\:\:\: np + 3\sqrt{npq\vphantom{b}} < n\]

Kiedy przybliżamy rozkład dwumianowy za pomocą rozkładu normalnego, często korzystamy z tzw. poprawki na ciągłość, to znaczy przyjmujemy, że wartości zmiennej dwumianowej \(a\) odpowiada pole pod krzywą odpowiedniego rozkładu normalnego nad odcinkiem \((a-0{,}5; a+0{,}5)\) – zob. rysunek 9.4.

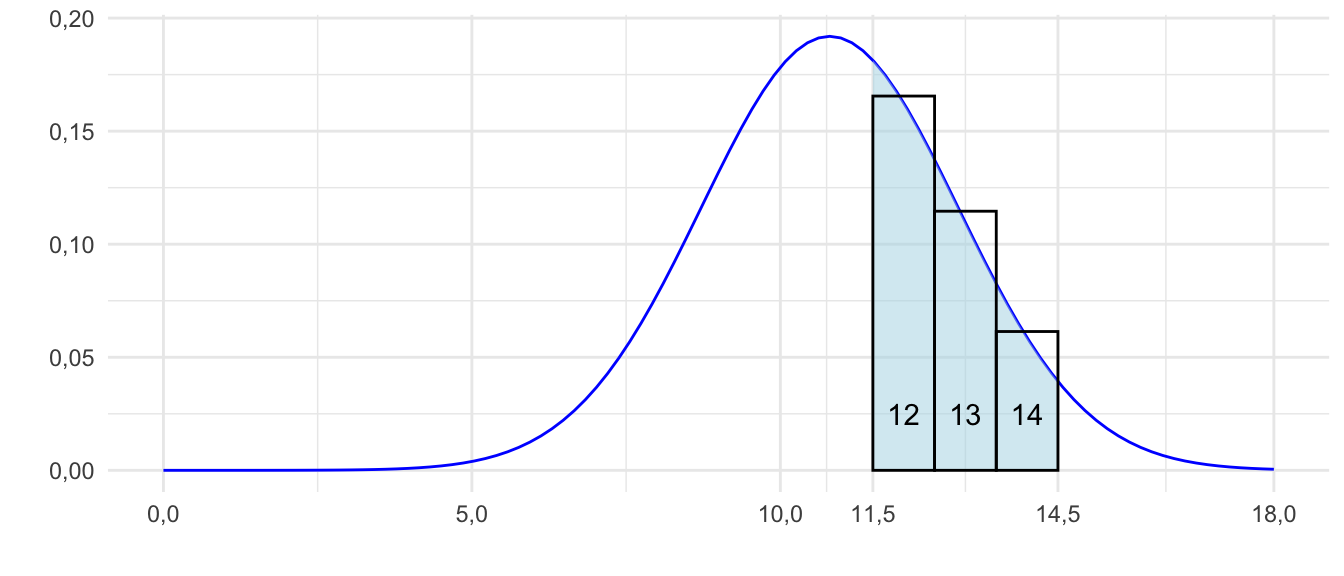
Rysunek 9.4: Rozkład zmiennej o rozkładzie dwumianowym można przybliżyć przez rozkład normalny o średniej \(np\) i odchyleniu standardowym \(\sqrt{npq}.\)

Wizualizacja przybliżenia rozkładu dwumianowego rozkładem normalnym: [https://college.cengage.com/nextbook/statistics/utts_13540/student/html/simulation8_4.html]

9.4 Szablony

Arkusze kalkulacyjne

Kalkulator dla rozkładu normalnego — arkusz Google

Kalkulator dla rozkładu normalnego — szablon w Excelu: Kalkulator_rozkladu_normalnego.xlsx

Kod w R

##### 1. Pole pod krzywą #####
# Parametry rozkładu Gaussa:
# średnia:
m <- 0
# odchylenie standardowe:
sd <- 2

# Będziemy obliczać pole pod krzywą gęstości rozkładu Gaussa
# od 
# *można wpisać from <- -Inf, co oznacza minus nieskończoność
from <- -Inf
# do
# *można wpisać to <- Inf, co oznacza (plus) nieskończoność
to <- 2

# Sprawdzenie danych, obliczenie pola pod krzywą
if (from > to) {
  # błąd od > do
  print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
} else {
  
  # Zapis prawdopodobieństwa
  
  if (to==Inf) {
    p=paste0("P(X>", from, ")")
  } else if (from==-Inf) {
    p=paste0("P(X<", to, ")")
  } else {
    p=paste0("P(", from, "<X<", to, ")")
  }
  print(p)
  
  # Obliczenie prawdopodobieństwa, czyli pole pod wycinkiem krzywej:
  result<-pnorm(to, m, sd)-pnorm(from, m, sd)
  print(result)
}

## [1] "P(X<2)"
## [1] 0.8413447

# Rysunek
library(ggplot2)

x1=if(from==-Inf){min(-4*sd+m, to-2*sd)} else {min(from-2*sd, -4*sd+m)}
x2=if(to==Inf){max(4*sd+m, from+2*sd)} else {max(to+2*sd, 4*sd+m)}

df<-data.frame(y=c(0, 0), 
               x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
               label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))

plt<-ggplot(NULL, aes(c(x1, x2))) +
  theme_minimal() +
  xlab('') +
  ylab('') +
  geom_area(stat = "function", 
            fun = function(x){dnorm(x, m, sd)}, 
            fill = "orange", 
            xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
  geom_line(stat = "function", fun = function(x){dnorm(x, m, sd)}, col = "blue", lty=2, lwd=1) +
  scale_x_continuous(breaks=c(m, m-sd, m-2*sd, m+sd, m+2*sd, m-3*sd, m+3*sd, m-4*sd, m+4*sd)) +
  geom_point(data = df, aes(x=x, y=y), shape=4) +
  geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
  annotate("text", label = paste0("M = ", m, "\nSD = ", sd, "\n", p, " = ", signif(result,6)), 
           x = x1, y = dnorm(m, m, sd)*1.2, size = 6, hjust="inward", vjust = "inward")

suppressWarnings(print(plt))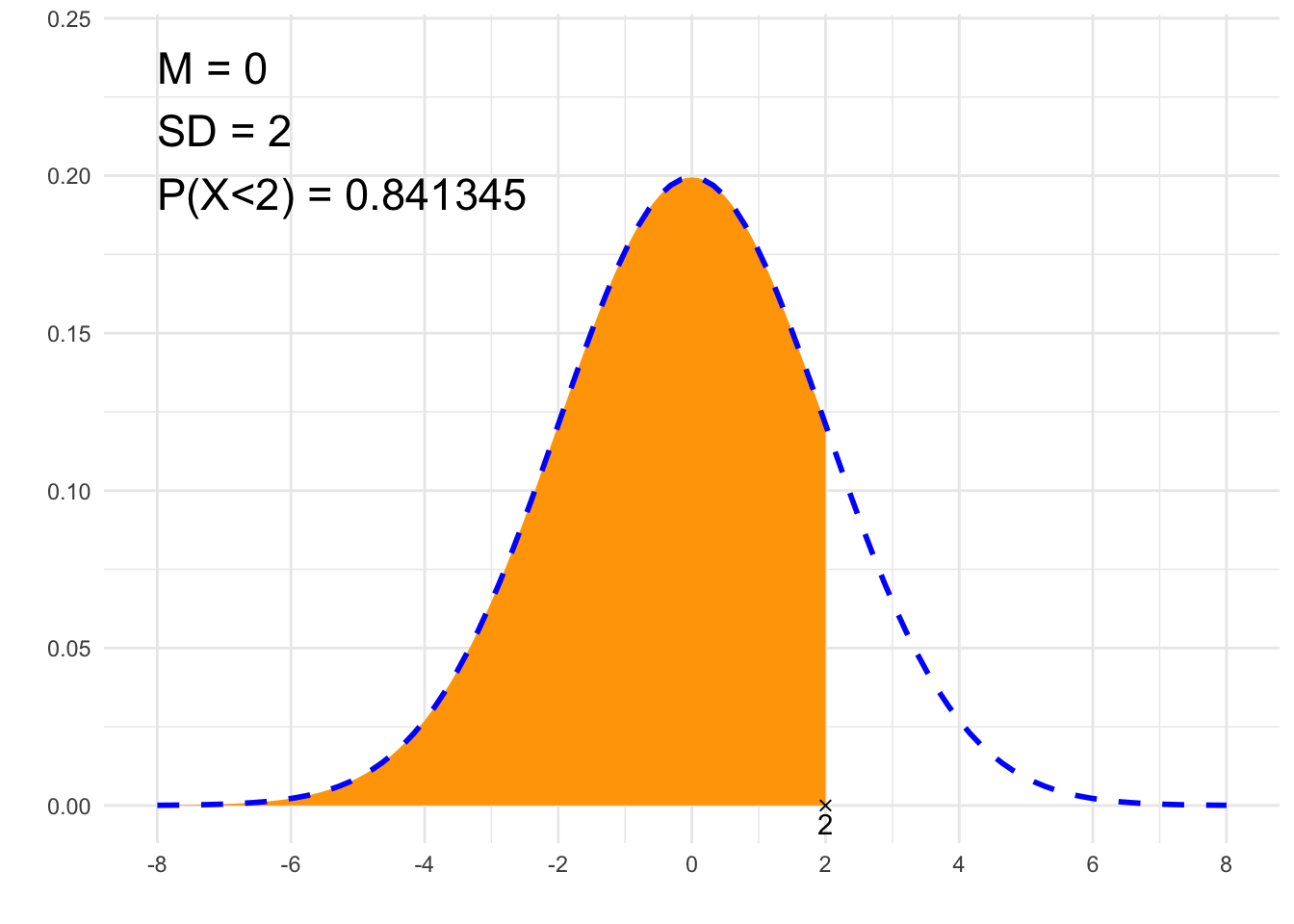

##### 2. Szukaj x #####
# Parametry rozkładu Gaussa:
# średnia:
m <- 1
# odchylenie standardowe:
sd <- 3

# Zadane pole pod krzywą:
P <- 0.95

# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ <- 'L'

# Obliczenia
from <- -qnorm(if(typ=='L'){1} else if(typ=='P'){P} else {1-(1-P)/2})*sd+m
to <- qnorm(if(typ=='L'){P} else if(typ=='P'){1} else {1-(1-P)/2})*sd+m

# Zapis prawdopodobieństwa
if (to==Inf) {
  p=paste0("P(X>", signif(from, 6), ")")
} else if (from==-Inf) {
  p=paste0("P(X<", signif(to, 6), ")")
} else {
  p=paste0("P(", signif(from, 6), " < X < ", signif(to, 6), ")")
}
print(paste0(p, " = ", P))

## [1] "P(X<5.93456) = 0.95"

# Rysunek
library(ggplot2)

x1=if(from==-Inf){min(-4*sd+m, to-2*sd)} else {min(from-2*sd, -4*sd+m)}
x2=if(to==Inf){max(4*sd+m, from+2*sd)} else {max(to+2*sd, 4*sd+m)}

df<-data.frame(y=c(0, 0), 
               x=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}),
               label=c(if(from==-Inf){NA}else{from}, if(to==-Inf){NA}else{to}))

plt<-ggplot(NULL, aes(c(x1, x2))) +
  theme_minimal() +
  xlab('') +
  ylab('') +
  geom_area(stat = "function", 
            fun = function(x){dnorm(x, m, sd)}, 
            fill = "orange", 
            xlim = c(if(from==-Inf){x1}else{from}, if(to==Inf){x2}else{to})) +
  geom_line(stat = "function", fun = function(x){dnorm(x, m, sd)}, col = "blue", lty=2, lwd=1) +
  scale_x_continuous(breaks=c(m, m-sd, m-2*sd, m+sd, m+2*sd, m-3*sd, m+3*sd, m-4*sd, m+4*sd)) +
  geom_point(data = df, aes(x=x, y=y), shape=4) +
  geom_text(data = df, aes(x=x, y=y, label=signif(label, 6)), vjust=1.4) +
  annotate("text", label = paste0("M = ", m, "\nSD = ", sd, "\n", p, " = ", P), 
           x = x1, y = dnorm(m, m, sd)*1.2, size = 6, hjust="inward", vjust = "inward")

suppressWarnings(print(plt))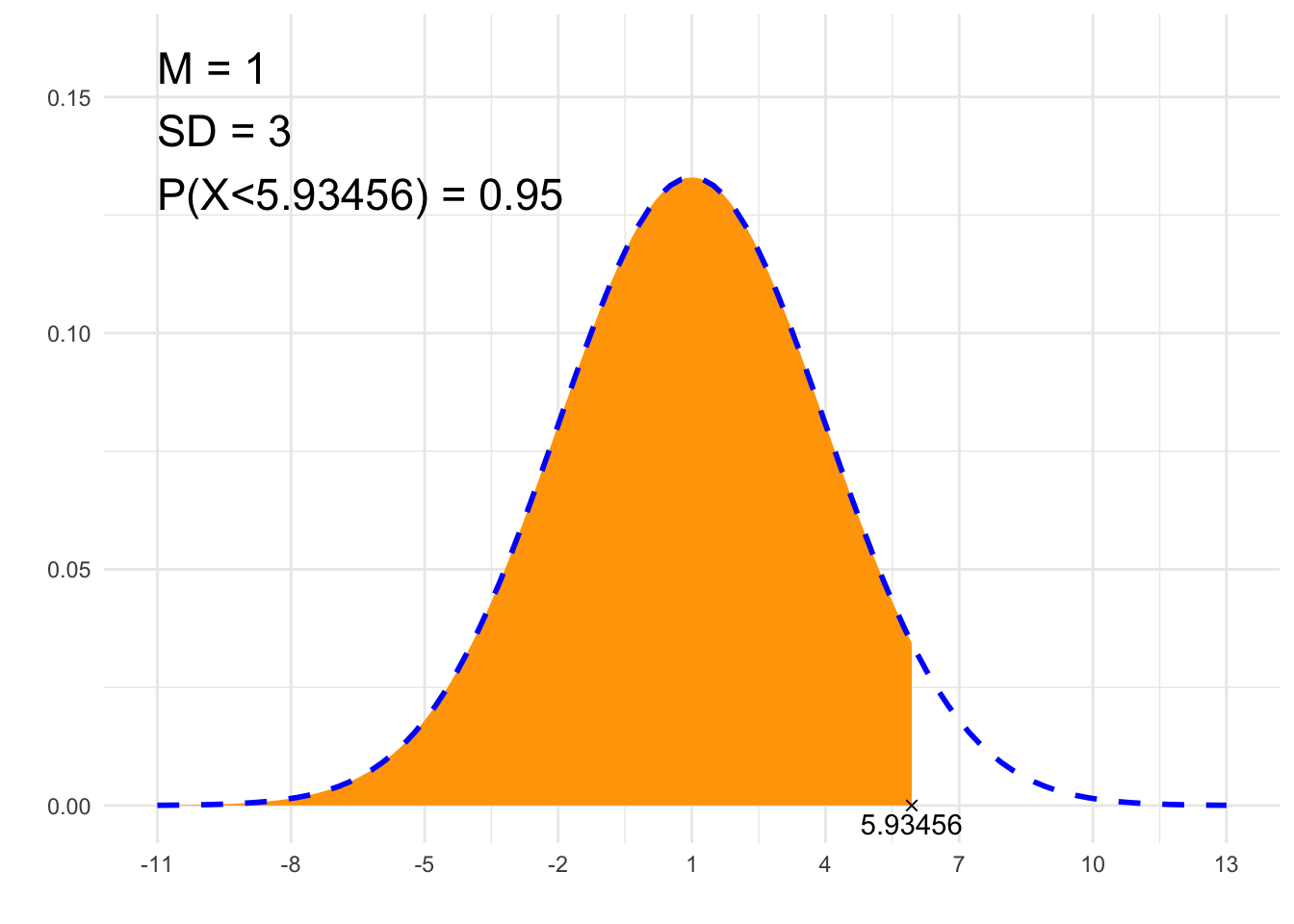

Kod w Pythonie

from scipy.stats import norm
##### 1. Pole pod krzywą #####
# Parametry rozkładu Gaussa:
# średnia:
m = 0
# odchylenie standardowe:
sd = 2
# Będziemy obliczać pole pod krzywą gęstości rozkładu Gaussa
# od 
# *można wpisać _from = float('-inf'), co oznacza minus nieskończoność
_from = float('-inf')
# to
_to = 2

if _from > _to:
    print("!!! Wartość 'od' powinna być niższa od wartości 'do' !!!")
else:
    if _to == float('inf'):
        p = "P(X>" + str(_from) + ")"
    elif _from == float('-inf'):
        p = "P(X<" + str(_to) + ")"
    else:
        p = "P(" + str(_from) + "<X<" + str(_to) + ")"
    print(p)

    result = norm.cdf(_to, m, sd) - norm.cdf(_from, m, sd)
    print(result)

## P(X<2)
## 0.8413447460685429

##### 2. Szukaj x #####

import numpy as np
from scipy.stats import norm

# Parametry rozkładu Gaussa:
# średnia:
m = 1
# odchylenie standardowe:
sd = 3

# Zadane pole pod krzywą:
P = 0.95

# 'L' - lewostronne, 'P' - prawostronne, 'S' - symetryczne
typ = 'L'

# Obliczenia
if typ == 'L':
    _from = -norm.ppf(1) * sd + m
    _to = norm.ppf(P) * sd + m
elif typ == 'P':
    _from = -norm.ppf(P) * sd + m
    _to = norm.ppf(1) * sd + m
else:
    _from = -norm.ppf(1-(1-P)/2) * sd + m
    _to = norm.ppf(1-(1-P)/2) * sd + m

# Zapis prawdopodobieństwa
if np.isinf(_to):
    p = f"P(X>{np.round(_from, 6)})"
elif np.isinf(_from):
    p = f"P(X<{np.round(_to, 6)})"
else:
    p = f"P({np.round(_from, 6)} < X < {np.round(_to, 6)})"
print(f"{p} = {P}")

## P(X<5.934561) = 0.95

9.5 Zadania

Zadanie 9.1 Czas potrzebny do wykonania pewnego zadania ma rozkład jednostajny w przedziale [4, 10] minut.

1. Zapisz funkcję gęstości tej zmiennej losowej.

2. Jakie jest prawdopodobieństwo, że zadanie będzie wykonane w co najwyżej 8 minut?

3. Jaki jest oczekiwany czas wykonania zadania?

Zadanie 9.2 Kevin właśnie wylądował na lotnisku i stoi w hali odbioru bagażu przed karuzelą bagażową, która własnie ruszyła. Załóżmy, że taśma będzie w ruchu przez 10 minut, bagaż wykładany jest równomiernie. Jakie jest prawdopodobieństwo, że walizka Kevina pojawi się na taśmie w ciągu pierwszych trzech minut?

Zadanie 9.3 Student jeździ na uczelnię metrem. Pociągi przyjeżdżają równo co 12 minut, ale czas ich przyjazdu jest losowy. Student, planując swój dzień, zakłada, maksymalnie 8 minut oczekiwania na metro, jeżeli będzie czekał dłużej – spóźni się na zajęcia.

1. Jaki jest oczekiwany czas czekania na metro? Ile wynosi wariancja?

2. Ile wynosi prawdopodobieństwo, że student będzie czekał na metro więcej niż cztery, ale nie dłużej niż sześć minut?

3. Ile wynosi prawdopodobieństwo, że student zdąży na zajęcia?

4. Jeśli student chce być pewny na 95%, że zjawi się punktualnie na zajęciach, ile czasu może maksymalnie czekać na metro?

Zadanie 9.4 Niech X ma następującą funkcję gęstości:

\[f(x) =\begin{cases} (x-5)/18 & \text{ dla } 5 \leqslant x \leqslant 11 \\ 0 & \text { dla pozostałych } \end{cases}\]

1. Naszkicuj wykres funkcji gęstości.

2. Pokaż, że f(x) jest funkcją gęstości.

3. Jakie jest prawdopodobieństwo, że X przyjmie wartość większą niż 7?

Zadanie 9.5 Kwantyle (mediana, kwartyle, percentyle) mają swoją definicję nie tylko dla danych rzeczywistych, ale również dla zmiennych losowych. Np. kwartyl 1 to taka wartość \(x_1\) zmiennej losowej \(X\), że \(\mathbb{P}(X<x_1)=0{,}25\). Znajdź medianę, kwartyl 1 i 3, rozstęp międzykwartylowy (IQR), piąty, dziesiąty, dziewięćdziesiąty i dziewięćdziesiąty piąty percentyl standaryzowanego rozkładu Gaussa.

Zadanie 9.6 (McClave and Sincich 2012) Czas pracy bez awarii pewnej drukarki (w godzinach) ma rozkład normalny ze średnią 549 i odchyleniem standardowym 68. Znajdź prawdopodobieństwo, że drukarka będzie działać bez awarii przynajmniej 500 godzin.

Zadanie 9.7 (Aczel and Sounderpandian 2018) Moc prądu wytwarzanego przez baterię słoneczną ma (w przybliżeniu) rozkład normalny ze średnią 15,6 kilowata i odchyleniem standardowym 4,1 kilowata. Ile co najmniej kilowatów wytworzy bateria z 95% pewnością?

Zadanie 9.8 Załóżmy, że rozkład wzrostu pacjentów jest w przybliżeniu normalny ze średnią 175,9 cm i odchyleniem 9,0 cm. Jaki rozmiar musi mieć łóżko, żeby zmieściło się w nim 99,5% pacjentów?

Zadanie 9.9

(Aczel and Sounderpandian 2018) Wyniki egzaminu GMAT studentów, którzy rozważają aplikowanie na uniwersytet, mają w przybliżeniu rozkład normalny z wartością oczekiwaną 487 punktów i odchyleniem standardowym 98 punktów.

1. Jaki procent studentów uzyska wynik powyżej 500?

2. Jaki procent studentów uzyska wynik między 600 a 700?

3. Jeśli uniwersytet chciałby umożliwić aplikowanie tylko 75% najlepszych, jaka powinna być graniczna, minimalna liczba punktów GMAT?

4. Znajdź najwęższy przedział, który będzie zawierał wyniki 75% studentów.

Zadanie 9.10

(McClave and Sincich 2012) Naukowcy ustalili, że długość skorupy zielonych żółwi morskich w jednej z lagun na wyspie Wielki Kajman ma (w przybliżeniu) rozkład normalny ze średnią 55,7 cm i odchyleniem standardowym 11,5 cm.

1. Tylko żółwie o skorupie dłuższej niż 40 cm i krótszej niż 60 cm mogą być przedmiotem legalnego połowu. Jakie jest prawdopodobieństwo schwytania żółwia, którego rozmiary są nielegalne?

2. Jaki jest maksymalny limit L, taki że po jego ustawieniu tylko 10% schwytanych żółwi będzie przekraczało ten limit?

Zadanie 9.11 Kilka lat temu bar z jedzeniem na wagę przy stacji Gdańsk Politechnika oferował darmowy obiad, jeżeli waga pokaże 777 \(\pm\) 3 gramy. Jakie było prawdopodobieństwo przypadkowego otrzymania darmowego posiłku, jeżeli rozkład masy porcji nakładanych sobie przez klientów był normalny ze średnią równą 620 g i odchyleniem standardowym 130 g?

Zadanie 9.12 (Utts and Heckard 2014) Meg często podróżuje i ostatnio zaczęła ryzykować, jeśli chodzi o zapewnienie sobie wystarczającej ilości czasu na dotarcie na lotnisko. Wychodzi z domu 45 minut przed ostatnim wezwaniem na lot. Jej czas podróży od drzwi mieszkania na parking lotniska ma rozkład normalny ze średnią 25 minut i odchyleniem standardowym wynoszącym 3 minuty. Z parkingu musi następnie wsiąść do autobusu wahadłowego do terminalu i przejść przez kontrolę bezpieczeństwa. Średni czas na wykonanie tego to 15 minut, a odchylenie standardowe to 2 minuty, i ten czas również ma rozkład normalny. Czas dojazdu i czas na lotnisku są od siebie niezależne. Jakie jest prawdopodobieństwo, że Meg spóźni się na lot, ponieważ jej całkowity czas na dotarcie na lotnisko przekroczy 45 minut?

Zadanie 9.13 (Utts and Heckard 2014) Czy Alison może wygrać z siostrą? Alison i jej siostra Julie pływają codziennie milę. Czasy Alison mają rozkład normalny ze średnią = 37 minut i odchyleniem standardowym = 1 minuta. Julie jest szybsza, ale jej czasy są mniej jednolite niż wyniki Alison: mają rozkład normalny ze średnią = 33 minuty i odchyleniem standardowym = 2 minuty. Każdego dnia ich wyniki są od siebie niezależne. Czy Alison kiedykolwiek pokona Julie? Jakie jest prawdopodobieństwo takiego zdarzenia?

Zadanie 9.14 Ile wynosi prawdopodobieństwo, że w 1000 rzutach „uczciwą” monetą uzyskamy orła więcej niż 550 razy? Odpowiedź należy podać, przybliżając rozkład dwumianowy za pomocą rozkładu normalnego.

Zadanie 9.15 Ile wynosi prawdopodobieństwo, że rzucając „uczciwą” monetą bilion razy², uzyskamy orła mniej niż 499999 milionów razy?

Zadanie 9.16 (Maddala 2006) Funkcja gęstości ciągłej zmiennej losowej X przyjmuje postać:

\[f(x) =\begin{cases} kx(2-x) & \text{ dla } 0 \leqslant x \leqslant 2 \\ 0 & \text { dla pozostałych } \end{cases}\]

1. Wyznacz \(k\).

2. Oblicz \(\mathbb{E}(X)\) i \(\mathbb{V}(X)\).

3. Jakie jest prawdopodobieństwo, że X będzie mniejsze od 0,5?

Zadanie 9.17 (Maddala 2006) Funkcja gęstości ciągłej zmiennej losowej X przyjmuje postać:

\[f(x) =\begin{cases} kx & \text{ dla } 0 \leqslant x \leqslant 1 \\ k(2-x) & \text{ dla } 1 < x \leqslant 2 \\ 0 & \text { dla pozostałych } \end{cases}\]

1. Wyznacz \(k\).

2. Oblicz \(\mathbb{E}(X)\) i \(\mathbb{V}(X)\).

3. Jakie jest prawdopodobieństwo, że X będzie mniejsze od 0,5?

Zadanie 9.18 Nauczyciel ocenił sprawdziany i zorientował się, że dwa sprawdziany (pierwszy oceniony na 80/100 i drugi oceniony na 45/100) nie są podpisane. Na podstawie listy obecności mógł stwierdzić, że należą one do Alka i Bolka. Na podstawie dotychczasowej pracy tych uczniów spodziewałby się, że wynik Alka powinien być w okolicach 75 plus/minus 12 punktów, zaś wynik Bolka powinien wynieść około 60 punktów plus/minus 20. Zakładając w obu przypadkach rozkłady normalne (dla Alka ze średnią 75 i odchyleniem standardowym 12 punktów, dla Bolka – ze średnią 60 i odchyleniem standardowym 20 punktów), podaj prawdopodobieństwo, że pierwszy sprawdzian jest Alka, a drugi Bolka.

Literatura

Aczel, A. D., and J. Sounderpandian. 2018. Statystyka w Zarządzaniu. PWN. https://ksiegarnia.pwn.pl/Statystyka-w-zarzadzaniu,731934758,p.html.

Maddala, G. S. 2006. Ekonometria. Wydawnictwo Naukowe PWN.

McClave, J. T., and T. T. Sincich. 2012. Statistics. Pearson Education. https://books.google.pl/books?id=gcYsAAAAQBAJ.

Utts, Jessica M., and Robert F. Heckard. 2014. Mind on Statistics - Standalone Book. 5th edition. Australia; United States: Brooks Cole.

---

1. Podobnie jak wartość oczekiwana niekoniecznie jest oczekiwana, a sukces w rozkładzie dwumianowym niekoniecznie jest sukcesem...↩︎

2. Proszę nie próbować rzucać tyle razy monetą. Google podaje, że „1 billion seconds is about 31.7 years”, ale jest jeszcze gorzej. „Billion” to miliard po angielsku. Po polsku 1 bilion sekund to 31 tysięcy lat.↩︎