Rozdział 21 Regresja liniowa
21.1 Model regresji liniowej – założenia
Modelem w statystyce często określamy założenie, że dane w próbce zostały wygenerowane przez proces probabilistyczny należący do określonej grupy procesów18.
Model regresji liniowej zakłada, że sposób, w jaki dane zostały wygenerowane, można opisać następującym równaniem:
\[y_i = \beta_0 + \beta_1 \cdot x_i + \varepsilon_i, \tag{21.1}\]
w przypadku regresji prostej (gdy jest tylko jedna zmienna objaśniająca)
lub następującym:
\[y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} + \varepsilon_i, \tag{21.2}\]
gdy zmiennych objaśniających jest \(k\) (więcej niż jedna, \(k>1\)) – regresja wieloraka.
Zakłada się więc, że relacja pomiędzy zmiennymi objaśniającymi (oznaczanymi literą X) i zmienną objaśnianą (oznaczaną literą Y) jest liniowa.
W równaniach modelu regresji pojawia się składnik losowy \(\varepsilon_i\), co do którego typowe założenia są następujące:
jego wartość oczekiwana wynosi zawsze zero: \(\mathbb{E}(\varepsilon_i)=0\),
jego wariancja jest stała (nie zależy od X ani od niczego innego) i wynosi \(\sigma_\varepsilon^2\) (założenie stałej wariancji w tym kontekście nazywa się homoskedastycznością19),
jego wartości są generowane bez autokorelacji (czyli wartość składnika losowego dla dowolnej obserwacji \(i\) nie jest skorelowana z wartością składnika losowego dla dowolnej innej obserwacji \(j\)),
jego wartości mają rozkład normalny.
W efekcie, klasyczny model regresji liniowej sprowadza się do tego, że rozkład warunkowy \(Y_i|\left(X_1=x_{i1}, X_2=x_{i2}, \dots X_k=x_{ik}\right)\) jest rozkładem Gaussa o wartości oczekiwanej równej
\[\mu_{y_i} = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} \tag{21.3}\]
i odchyleniu standardowym równym \(\sigma_\varepsilon\).
Rysunek 21.1: Model regresji to model warunkowego rozkładu zmiennej objaśnianej – przykład wykorzystujący symulowaną zależność między liczbą godzin nauki a wynikiem egzaminu
21.2 Model regresji liniowej – estymacja
Wartości \(\beta_0\), \(\beta_1\), ..., \(\beta_k\) oraz \(\sigma_\varepsilon\) są nieobserwowanymi wprost parametrami procesu generującego dane („populacji”), możemy je oszacować na podstawie próbki losowej.
W przypadku klasycznego modelu regresji liniowej współczynniki \(\beta\) szacuje się za pomocą estymatora najmniejszych kwadratów.
Dla regresji prostej estymator współczynnik nachylenia linii regresji (\(\beta_1\)) można przedstawić w następującej formie:
\[ \widehat{\beta}_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}, \tag{21.4} \]
zaś wzór na estymator wyrazu wolnego to:
\[ \widehat{\beta}_0 = \bar{y} - \widehat{\beta}_1 \bar{x}. \tag{21.5} \]
Dla regresji wielorakiej estymator najmniejszych kwadratów ma w zapisie macierzowym następującą formę:
\[\widehat{\boldsymbol{\beta}}=\left(\mathbf{X}^\top\mathbf{X}\right)^{-1}\mathbf{X}^\top \mathbf{y}, \tag{21.6} \]
gdzie \(\widehat{\boldsymbol{\beta}}\) to wektor kolumnowy oszacowań współczynników \(\beta_0, \dots, \beta_k\) (\(k\) to liczba zmiennych objaśniających), \(\mathbf{X}\) to macierz układu, czyli macierz z wierszami odpowiadającymi poszczególnym obserwacjom i z kolumnami odpowiadającymi poszczególnym zmiennym objaśniającym (z kolumną jedynek odpowiadającą wyrazowi wolnemu), a \(\mathbf{y}\) to wektor kolumnowy z wartościami zmiennej objaśnianej.
Parametr \(\sigma\) szacuje się natomiast za pomocą następującego wzoru:
\[ \widehat{\sigma}_\varepsilon = \sqrt{\widehat{\sigma}_\varepsilon^2} \tag{21.7} \]
\[ \widehat{\sigma}_\varepsilon^2 = \frac{\sum_i(y_i-\hat{y}_i)^2}{n-k-1} \tag{21.8} \]
Estymację przeprowadza się zwykle z wykorzystaniem oprogramowania.
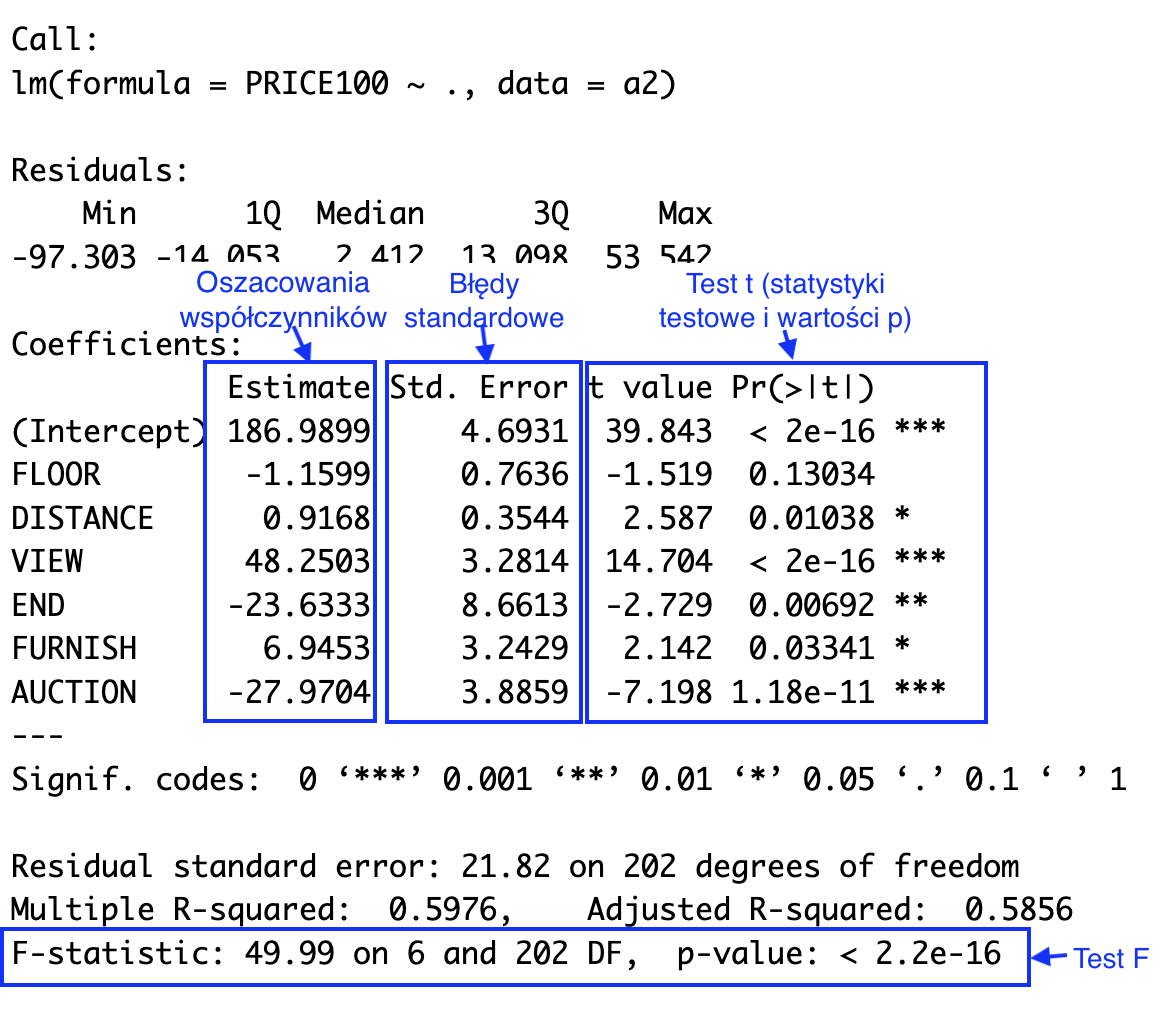
Rysunek 21.2: Typowe podsumowanie modelu regresji liniowej w R
21.2.1 Przedziały ufności dla współczynników modelu
Przedział ufności dla współczynnika modelu \(\beta_j\) (\(j = 1, 2, \dots, p\)) możemy wyznaczyć, korzystając z następującego wzoru.
\[\widehat{\beta}_j \pm t_{\alpha/2} \cdot \widehat{SE}(\widehat{\beta}_j), \tag{21.9}\]
gdzie \(\hat{\beta_j}\) to oszacowanie punktowe współczynnika \(\beta_j\), \(\widehat{SE}(\widehat{\beta}_j)\) to oszacowany błąd standardowy estymatora tego współczynnika, zaś wartość \(t_{\alpha/2}\) to odpowiedni kwantyl z rozkładu t-Studenta o \(n - p - 1\) stopniach swobody (\(n\) to liczba obserwacji w próbie, a \(p\) to liczba zmiennych objaśniających).
Wzory umożliwiające wyznaczenie błędu standardowego dla regresji prostej są następujące. Dla współczynnika nachylenia linii regresji (\(\beta_1\)):
\[ \widehat{SE}(\widehat{\beta}_1) = \frac{\widehat{\sigma}_\varepsilon}{\sqrt{\sum_i (x_i - \bar{x})^2}} \tag{21.10}\]
a dla wyrazu wolnego (punktu przecięcia):
\[ \widehat{SE}(\widehat{\beta}_0) = \widehat{\sigma}_\varepsilon \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum_i (x_i - \bar{x})^2}} \tag{21.11}\]
W przypadku regresji wielorakiej oszacowania błędów standardowych uzyskujemy dzięki następującego wzoru wykorzystującego algebrę macierzy.
\[\widehat{SE}(\widehat{\beta}_j) = \widehat{\sigma}_\varepsilon \sqrt{\left[\left( \mathbf{X}^\top\mathbf{X}\right)^{-1} \right]_{jj}}, \tag{21.12}\]
gdzie \(\mathbf{A}_{jj}\) oznacza element macierzy \(\mathbf{A}\) znajdujący się w \(j\)-tym wierszu w \(j\)-tej kolumnie.
W praktyce błędy standardowe są obliczane przez pakiety statystyczne.
21.2.2 Przedziały ufności dla wartości oczekiwanej zmiennej objaśnianej
Przedziały ufności dla warunkowej średniej (warunkowej wartości oczekiwanej) zmiennej objaśnianej przy ustalonych wartościach zmiennych objaśniających wyznaczamy na podstawie następującego wzoru:
\[\widehat{y}_h \pm t_{\alpha/2} \cdot \widehat{SE}(\widehat{y}_h), \tag{21.13}\]
gdzie \(x_{h1}, \dots, x_{hp}\) to ustalone wartości zmiennych objaśniających, z których można utworzyć wektor kolumnowy \(\mathbf{x}_h\), \(\hat{y}_h = \hat{\beta_0} + \hat{\beta_1} x_{h1} + \dots + \hat{\beta_k} x_{hk}\) to punktowe oszacowanie wartości oczekiwanej zmiennej \(Y\) w takiej sytuacji, zaś \(\widehat{SE}(\hat{y}_h)\) to szacunek jego błędu standardowego.
Dla regresji prostej:
\[ \widehat{SE}(\hat{y}_h) = \widehat{\sigma}_\varepsilon\sqrt{\frac{1}{n}+\frac{(x_h-\bar{x})^2}{\sum_i(x_i-\bar{x})^2}}, \tag{21.14} \]
zaś dla regresji wielorakiej:
\[\widehat{SE}(\hat{y}_h) = \widehat{\sigma}_\varepsilon\sqrt{\mathbf{x}_h^\top (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{x}_h}. \tag{21.15}\]
21.3 Przedziały predykcji
Zwykle jesteśmy zainteresowani nie tylko wartością oczekiwaną, ale również rozrzutem wokół tej wartości. Przedział predykcji uwzględnia obie te informacje, ponieważ stanowi oszacowanie zakresu wartości, w którym z ustalonym prawdopodobieństwem (równym \(1-\alpha\)) będzie się mieścić nowa pojedyncza obserwacja pochodząca z tej samej populacji (wygenerowana przez ten sam proces).
Dla regresji prostej przedział predykcji wyznaczamy za pomocą następującego wzoru:
\[ \hat{y}_h\pm t_{\alpha/2}\widehat{\sigma}_\varepsilon\sqrt{1+\frac{1}{n}+\frac{(x_h-\bar{x})^2}{\sum_i(x_i-\bar{x})^2}}, \tag{21.16} \]
gdzie \(\hat{y}_h\) to wartość oczekiwana zmiennej objaśnianej \(Y\) pod warunkiem, że zmienna objaśniająca X jest równa \(x_h\):
Dla regresji wielorakiej można zastosować następujący wzór macierzowy:
\[ \hat{y}_h\pm t_{\alpha/2}\widehat{\sigma}_\varepsilon\sqrt{1+\mathbf{x}_h^\top (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{x}_h} \tag{21.17} \]
21.4 Model regresji liniowej – test t i test F
Pakiety statystyczne (a nawet arkusze kalkulacyjne takie jak Excel) zwykle obliczają statystyki umożliwiające przeprowadzenie dwóch rodzajów testów dla regresji liniowej: testów istotności pojedynczych współczynników \(\beta_j\) („testów t”) oraz testu łącznej istotności modelu („testu F”).
21.4.1 Testy istotności współczynników
1. W teście t współczynnika \(\beta_j\) hipoteza zerowa zakłada, że jest on równy zero:
\[ H_0: \beta_j = 0 \] 2. Hipoteza alternatywna jest dwustronna:
\[ H_A: \beta_j \ne 0 \]
3. Statystykę testową t wyznacza się w następujący sposób:
\[t = \frac{\widehat{\beta}_j}{\widehat{SE}(\widehat{\beta}_j)} \tag{21.18} \]
Przy założeniu prawdziwości hipotezy zerowej statystyka testowa ma rozkład t z liczbą stopni swobody równą \(n-p-1\).
4. Obszar odrzucenia i p-value wyznacza się tak, jak w innych dwustronnych testach t.
21.4.2 Test F
1. W teście F hipoteza zerowa stwierdza, że wszystkie współczynniki przy zmiennych objaśniających są równe zero:
\[ H_0: \beta_1 = \dots = \beta_k = 0 \] Warto zauważyć, że hipoteza zerowa nie obejmuje wyrazu wolnego (\(\beta_0\)).
2. Hipoteza alternatywna stwierdza zaś, że przynajmniej jeden z nich jest różny od zera:
\[ H_A:\text {istnieje } j \in \{1, \dots, k\}\text{, takie że } \beta_j \ne 0 \]
3. Statystyka testowa ma rozkład F z liczbą stopni swobody w liczniku (\(df_1\)) równą \(k\) i liczbą stopni swobody w mianowniku (\(df_2\)) równą \(n - k - 1\).
\[ F_{(k,n-k-1)}=\frac{SSR/k}{SSE/(n-k-1)}=\frac{\sum_{i=1}^n\left(\widehat{y}_i-\bar{y}\right)^2/k}{\sum_{i=1}^n\left(y_i-\widehat{y}_i\right)^2/({n-k-1})} \tag{21.19} \]
21.5 Testy diagnostyczne modelu regresji
Należy pamiętać, że założenia modelu liniowego regresji w praktyce prawie zawsze są spełnione tylko w przybliżeniu. W związku z tym interesuje nas nie tyle odrzucenie hipotezy zerowej (o liniowości, normalności itp.), ile stwierdzenie czy stopień odstępstwa od założeń jest duży czy niewielki.
Testy istotności odpowadają jednak na inne pytanie: gdyby proces generujący dane spełniał idealnie założenia modelu, jak bardzo prawdopodobne byłoby uzyskanie otrzymanych lub bardziej skrajnych od otrzymanych wyników.
(...)
Testy diagnostyczne mogą pełnić więc jedynie rolę pomocniczą, rzadko będą mogły być jedynym kryterium, na podstawie podejmujemy decyzje.
21.6 Linki
Analiza regresji liniowej (Pogotowie statystyczne): https://pogotowiestatystyczne.pl/aploud/2023/04/2023-11-Regresja-liniowa.pdf
21.7 Szablony
Regresja prosta — arkusz Google
Regresja prosta — szablon w Excelu
Regresja wieloraka — arkusz Google
Regresja wieloraka — szablon w Excelu