Rozdział 15 Testowanie hipotez dla jednej proporcji
15.1 Test jednej proporcji oparty na statystyce \(z\)
- W teście jednej proporcji hipoteza zerowa brzmi, że proporcja w populacji, z której pobieramy próbę wynosi \(p_0\) (czyli przyjmuje pewną określoną w hipotezie wartość):
\[ H_0: p = p_0 \] 2. Hipotezę alternatywną musimy wybrać spośród trzech opcji. W teście dwustronnym:
\[H_A: p \ne p_0\] W teście lewostronnym: \[H_A: p < p_0 \]
W teście prawostronnym:
\[H_A: p > p_0 \]
- Statystyka testowa \(z\):
\[\begin{equation} z= \frac{\hat{p}-p_0}{\sqrt{p_0 q_0/n}} \tag{15.1} \end{equation}\]
gdzie \(\hat{p}\) to proporcja z próby, \(p_0\) to zakładana w hipotezie zerowej wartość proporcji w populacji (\(p\)), \(q_0=1-p_0\), a \(n\) to liczebność próbki.
Obszar odrzucenia zależy od hipotezy alternatywnej. Zasady jego ustalania są analogiczne do zasad testu \(z\) dla średniej (14.8).
Jak zwykle należy pamiętać, że próbka powinna być losowa i zostać pobrana z badanej populacji. Aby stosować test powinno się spełnić warunki minimalnej liczebności: \(np_0 \geqslant 15\) oraz \(nq_0 \geqslant 15\) (czasem obniża się ten wymóg z 15 do 5).
15.2 Wartość p (p-value)
Wartość p10 (p-value, prawdopodobieństwo testowe) to prawdopodobieństwo wystąpienia statystyki testowej o wartości równej zaobserwowanej lub bardziej ekstremalnej niż zaobserwowana, jeżeli założymy, że hipoteza zerowa jest prawdziwa. Na przykład, jeżeli statystyka testowa \(z\) w konkretnej próbie wynosi 2, to przy teście dwustronnym p-value wynosi \(\mathbb{P}(|Z|\geqslant2) \approx0,0455\), przy prawostronnym \(\mathbb{P}(Z\geqslant2)\approx0,0228\), zaś przy teście lewostronnym \(\mathbb{P}(Z\leqslant2) \approx 0,9772\).
Aby obliczyć p-value trzeba więc znać formę hipotezy alternatywnej, rozkład statystyki testowej i jej wartość w konkretnej próbie.
Bardzo często wartość p-value jest obliczana przez program komputerowy. Można wtedy ją wykorzystać do podejmowania decyzji, czy odrzucać \(H_0\) na podstawie wyników testu statystycznego.
Korzystamy z faktu, że statystyka testowa leży wewnątrz obszaru odrzucenia wtedy, i tylko wtedy, gdy p-value jest mniejsze niż \(\alpha\). Zamiast patrzeć na wartość krytyczną i sprawdzać, czy statystyka testowa wpadła do obszaru odrzucenia, możemy patrzeć na wartość p i sprawdzać, czy jest ona mniejsza niż \(\alpha\). Jeżeli p<\(\alpha\), odrzucamy hipotezę zerową.
Jest to o tyle wygodne, że statystyk testowych i obszarów krytycznych może być wiele, natomiast sposób postępowania z p-value jest zawsze taki sam. Można więc powiedzieć, że p-value sprowadza testy statystyczne do wspólnego mianownika.
Należy zwrócić uwagę, że p-value to nie jest prawdopodobieństwo, że hipoteza zerowa jest prawdziwa, albo że hipoteza zerowa jest fałszywa. Aby sobie to uświadomić, warto jeszcze raz przemyśleć zadanie 5.11.
15.3 Moc
Moc testu to (warunkowe) prawdopodobieństwo niepopełnienia błędu II rodzaju. Dokładniej rzecz ujmując, moc testu to prawdopodobieństwo odrzucenia hipotezy zerowej, jeżeli prawdziwa jest pewna konkretna punktowa hipoteza alternatywna.
Błąd II rodzaju oznaczamy literą \(\beta\), stąd moc testu oznaczamy najczęściej symbolem \(1-\beta\).
Aby wyznaczyć moc danego testu, należy:
określić liczebność próby,
sprecyzować poziom istotności \(\alpha\) testu, który wyznacza granicę obszaru odrzucenia hipotezy zerowej,
określić, czy obszar odrzucenia jest jednostronny czy dwustronny, i go wyznaczyć
wybrać pewną konkretną punktową hipotezę alternatywną (np. „prawdziwą wartość” proporcji \(H_1: p = 0{,}5\)).
Generalnie, przy testowaniu hipotez statystycznych, hipoteza alternatywna (oznaczana w tym skrypcie przez \(H_A\)) ma formę zakresu/przedziału. Natomiast moc testu wyznaczamy dla jednej konkretnej „punktowej” wartości.
15.4 Linki
Moc testu – ilustracja na przykładzie testowania 2 średnich: https://rpsychologist.com/d3/nhst/
Moc testu – ilustracja na przykładzie testowania 1 proporcji: https://istats.shinyapps.io/power/
15.5 Szablony
Arkusze kalkulacyjne
Testowanie 1 populacji (średnia i proporcja) — arkusz Google
Testowanie 1 populacji (średnia i proporcja) — szablon w Excelu
Kod w R
# Test dla jednej proporcji
# Liczba wszystkich obserwacji:
n <- 200
# Liczba obserwacji sprzyjających:
x <- 90
# Proporcja w próbie:
p <- x/n
# Poziom istotności:
alpha <- 0.1
# Proporcja wartość zerowa:
p0 <- 0.5
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt <- "≠"
alttext <- if(alt==">") {"greater"} else if(alt=="<") {"less"} else {"two.sided"}
test <- prop.test(x, n, p0, alternative=alttext, correct=FALSE)
test_z <- unname(sign(test$estimate-test$null.value)*sqrt(test$statistic))
crit_z <- if(test$alternative=="less") {qnorm(alpha)} else if(test$alternative=="greater") {qnorm(1-alpha)} else {qnorm(1-alpha/2)}
print(c('Proporcja w próbie' = test$estimate,
'Liczebność' = n,
'Hipoteza zerowa' = paste0('p = ', test$null.value),
'Hipoteza alt.' = paste0('p ', alt, ' ', test$null.value),
'Stat. testowa z' = test_z,
'Stat. testowa chi^2' = unname(test$statistic),
'Wartość krytyczna z' = crit_z,
'Wartość p' = test$p.value
))## Proporcja w próbie.p Liczebność Hipoteza zerowa Hipoteza alt. Stat. testowa z
## "0.45" "200" "p = 0.5" "p ≠ 0.5" "-1.4142135623731"
## Stat. testowa chi^2 Wartość krytyczna z Wartość p
## "2" "1.64485362695147" "0.157299207050284"Kod w Pythonie
# Test dla 1 proporcji
from statsmodels.stats.proportion import proportions_ztest
# Liczba wszystkich obserwacji:
n = 200
# Liczba obserwacji sprzyjających:
x = 90
# Proporcja w próbie:
p = x/n
# Poziom istotności:
alpha = 0.1
# Proporcja wartość zerowa:
p0 = 0.5
# Hipoteza alternatywna (znak): "<"; ">"; "<>"; "≠"
alt = "≠"
if alt == ">":
alttext = "larger"
elif alt == "<":
alttext = "smaller"
else:
alttext = "two-sided"
test_result = proportions_ztest(count = x, nobs = n, value = p0, alternative = alttext, prop_var=p0)
print("Statystyka testowa z:", test_result[0], "\np-value:", test_result[1])## Statystyka testowa z: -1.4142135623730947
## p-value: 0.1572992070502853315.6 Zadania
Zadanie 15.1 Pan Onur Güntürkün w artykule opublikowanym w Nature w 2003 (Güntürkün 2003) opisał, że obserwował pary w wieku 13-70 lat całujące się w miejscach publicznych (lotniska, dworce, parki i plaże) w USA, Turcji i w Niemczech i notował, w którą stronę przechylają głowę podczas pocałunku. Ze 124 par, które zaobserwował, 80 przechylała głowy w prawą stronę, pozostałe przechylały głowę w lewo. Czy na tej podstawie można stwierdzić, że prawdopodobieństwo, że całująca się losowo wybrana para przechyli głowę w prawą stronę jest istotnie większe niż 0,5? Jakich założeń wymaga w tym przypadku wykorzystanie testu?
Zadanie 15.2 Pewien analityk geopolityczny uważa, że 75% jego prognoz się spełnia. Weryfikator fake newsów twierdzi, że ten procent jest mniejszy niż 60%. Aby to sprawdzić, odnalazł 60 prognoz analityka i ustalił, że 28 z nich można uznać za spełnione. Zakładając, że te 60 prognoz to próba losowa, przeprowadź odpowiedni test, aby określić, czy uzyskane dane sugerują, że spełnialność prognoz jest istotnie niższa niż 75%? Niż 60%?
Zadanie 15.3 Pan Łukasz w pracy dyplomowej sprawdził, czy można było zarobić, inwestując w wybrane spółki rynku NASDAQ na podstawie formacji świecowej białe marubozu. Formacja białe marubozu w badanym okresie wystąpiła na tych spółkach 107 razy, z czego 60 razy dała zarobić (to znaczy postępowanie polegające na zakupie akcji po wystąpieniu formacji i ich sprzedaży po 10 dniach prowadziłoby do zysku). Zakładamy, że losowa inwestycja w te akcje w badanym okresie przyniosłaby zysk w 51% przypadków. Przeprowadź odpowiedni test, przyjmując istotność \(\alpha\)=0,1.
Zadanie 15.4 (Agresti and Kateri 2021) W pewnym eksperymencie wzięło udział 116 osób. Dla każdej z nich na podstawie daty urodzenia astrologowie przygotowali horoskop. Następnie w przypadku każdego z horoskopów astrologom przedstawiono kwestionariusz wypełniony przez tę osobę oraz dwa inne kwestionariusze. Zadaniem astrologa było odgadnąć, który z trzech kwestionariuszy został wypełniony przez osobę, dla której przygotowany był horoskop. Astrologowie potrafili wskazać właściwą osobę w 40 z 116 przypadków. Czy można odrzucić hipotezę zerową mówiącą o tym, że astrologowie odgadywali w sposób losowy? Przyjęto \(\alpha = 0{,}05\).
Jaka była moc testu, przy założeniu, że punktowa hipoteza alternatywna, pochodząca z Narodowej Rady Badań Geokosmicznych (zrzeszającej astrologów) brzmiała, że astrologom uda się odgadnąć właściwą osobę przynajmniej w połowie przypadków?
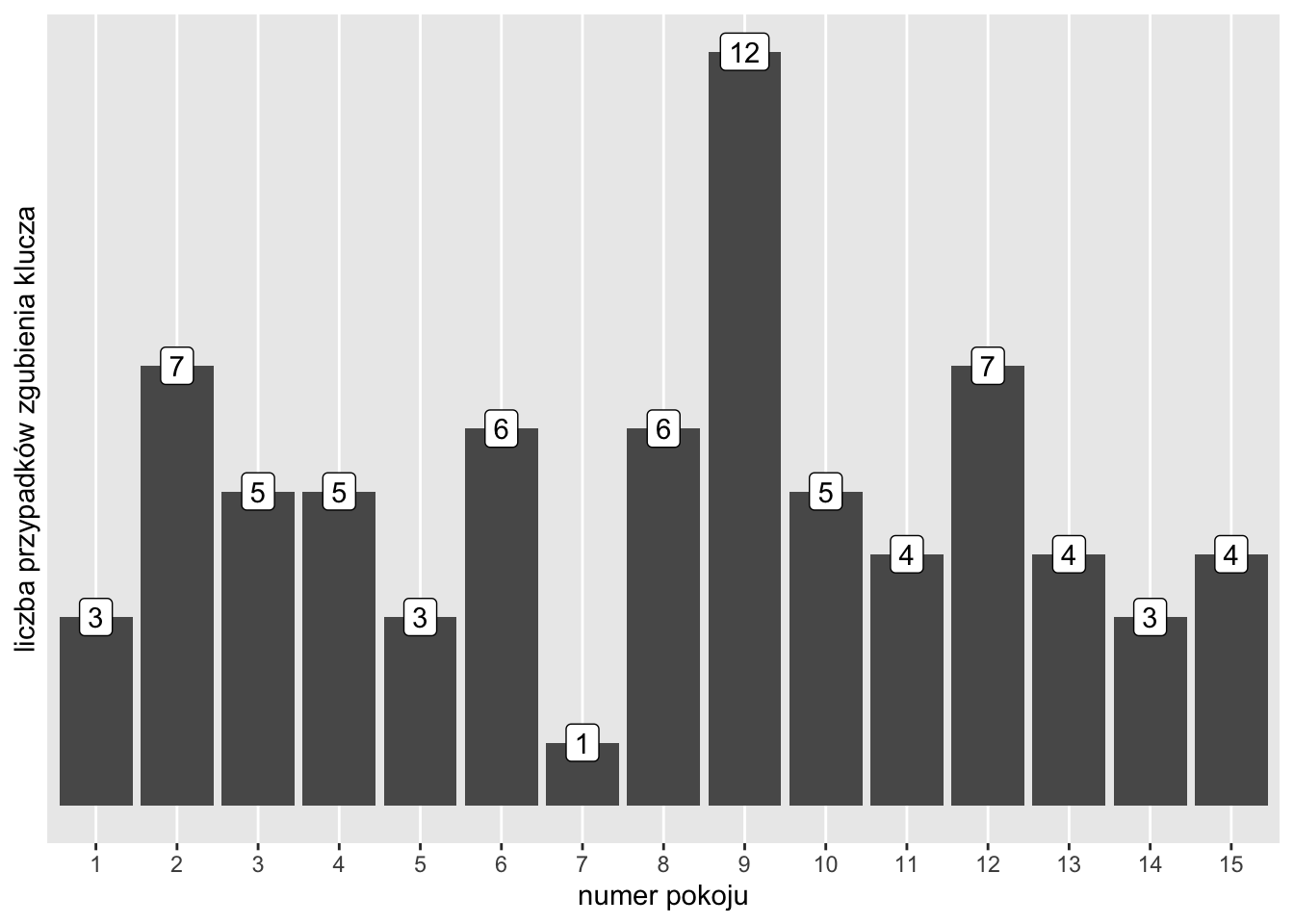
Zadanie 15.5 W opowiadaniu „Dziewięć” (stanowiącym fragment powieści „Bieguni”) Olga Tokarczuk opisuje hotel, w którym częściej niż inne klucze gubił się klucz numer dziewięć. Załóżmy, że uzyskaliśmy dane z tego hotelu, jest w nim 15 pokoi, liczba przypadków zgubienia klucza od czasu założenia hotelu wynosi 75, a w podziale na poszczególne pokoje wygląda tak, jak na poniższym wykresie.
Przetestuj, czy frakcja „dziewiątek” wśród zgubionych kluczy jest większa niż frakcja wynikająca z rozkładu równomiernego (1/15).
Uwaga! Wydaje się, że tak postawiona hipoteza jest nadużyciem testu statystycznego. Dlaczego? Jak wyglądałaby lepsza pod tym względem hipoteza? Test statystyczny umożliwiający przeprowadzenie odpowiedniego testu zostanie przedstawiony w jednym z kolejnych rozdziałów.
Zadanie 15.6 (Agresti, Franklin, and Klingenberg 2016) Sieć fast foodów chce porównać dwa sposoby promocji nowego burgera (burgera z indykiem). Jednym ze sposobów jest skorzystanie z kuponu dostępnego w sklepie. Drugi sposób polega na wywieszeniu plakatu na zewnątrz sklepu. Przed promocją dział marketingu dobrał 50 par sklepów. Każda para to dwa sklepy o porównywalnym wolumenie sprzedaży, podobne pod względem demografii klientów. Na podstawie losowania ustalono, który sklep z każdej pary będzie korzystał z kuponów. Po miesiącu porównano wzrosty sprzedaży burgera z indyka w każdej parze sklepów. W 28 przypadkach zanotowano większy wzrost sprzedaży w sklepach korzystających z kuponów, w 22 przypadkach przyrost sprzedaży był większy w sklepach korzystających z plakatu.
Czy jest to wystarczająco mocna przesłanka, żeby stosować podejście oparte na kuponach, czy też wynik ten można wytłumaczyć przypadkiem?
Literatura
Proszę zwrócić uwagę, że p-value to kolejna sytuacja, kiedy używamy litery p jako symbolu. Mieliśmy już \(\mathbb{P}\) jako funkcję prawdopodobieństwa zdarzenia (4), \(\textbf{p}\) jako funkcję masy prawdopdobieństwa zmiennej dyskretnej (7.1), \(p\) jako prawdopodobieństwo sukcesu w pojedynczej próbie w rozkładzie dwumianowym (8.2), \(p\) jako oznaczenie proporcji w populacji oraz \(\hat{p}\) jako oznaczenie proporcji w próbie (10). Teraz mamy p po raz kolejny, już chyba po raz ostatni.↩︎