Rozdział 5 Wzór Bayesa
Definicja na początek: Rozbiciem przestrzeni zdarzeń \(\Omega\) będziemy nazywali zestaw wzajemnie rozłącznych (\(B_i \cap B_j = \emptyset\)) zdarzeń \(B_1\), \(B_2\),..., \(B_k\), których suma stanowi całą przestrzeń (\(\Omega = B_1 \cup B_2 \cup ... \cup B_k\)).
5.1 Twierdzenie o prawdopodobieństwie całkowitym
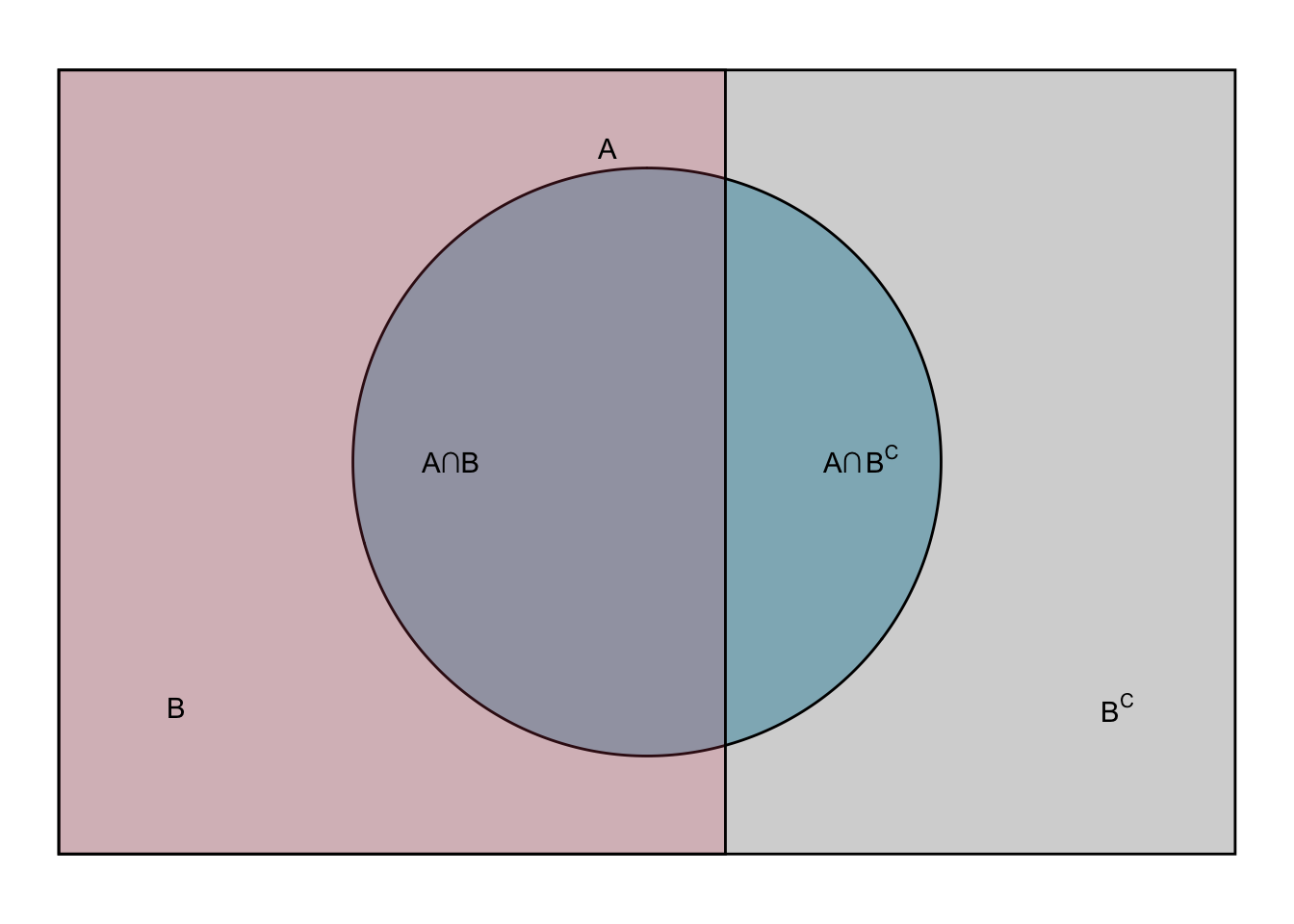
Rozbicie dwuczłonowe (\(B\) i \(B^C\)):
\[\begin{equation} \mathbb{P}(A) = \mathbb{P}(A \cap B) + \mathbb{P}(A \cap B^c) \tag{5.1} \end{equation}\]
\[\begin{equation} \mathbb{P}(A) = \mathbb{P}(A|B)\mathbb{P}(B) + \mathbb{P}(A|B^c)\mathbb{P}(B^c) \tag{5.2} \end{equation}\]
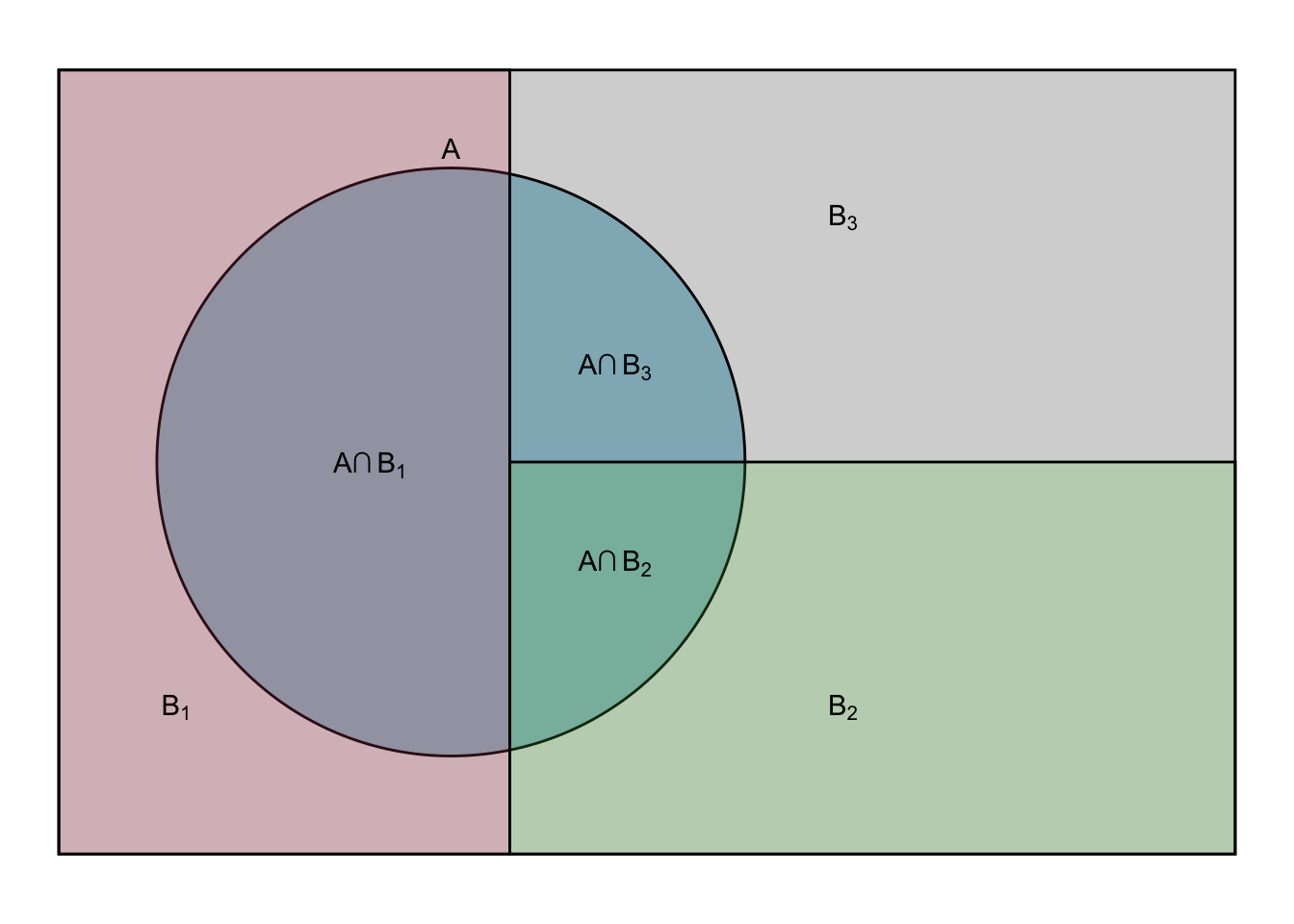
Rozbicie wieloczłonowe:
\[\begin{equation} \mathbb{P}(A)=\sum_i \mathbb{P}(A \cap B_i) \tag{5.3} \end{equation}\]
\[\begin{equation} \mathbb{P}(A)=\sum_i \mathbb{P}(A|B_i)\mathbb{P}(B_i) \tag{5.4} \end{equation}\]
5.2 Twierdzenie Bayesa
\[\begin{equation} \mathbb{P}(H|D) = \frac{\mathbb{P}(D|H)\cdot \mathbb{P}(H)}{\mathbb{P}(D)} = \frac{\mathbb{P}(D|H)\cdot \mathbb{P}(H)}{\mathbb{P}(D|H)\mathbb{P}(H) + \mathbb{P}(D|H^c)\mathbb{P}(H^c)} \tag{5.5} \end{equation}\]
Analogicznie, w przypadku rozbicia wieloczłonowego (\({H_i}\) to konkurujące rozłączne hipotezy wyczerpujące wszystkie możliwości):
\[\begin{equation} \mathbb{P}(H|D) = \frac{\mathbb{P}(D|H)\cdot \mathbb{P}(H)}{\mathbb{P}(D)} = \frac{\mathbb{P}(D|H)\cdot \mathbb{P}(H)}{\sum_i{\mathbb{P}(D|H_i)\mathbb{P}(H_i)}} \tag{5.6} \end{equation}\]
We wzorze, zamiast sztampowych \(A\) i \(B\) zastosowano oznaczenia \(H\) jak „hipoteza” i \(D\) jak „dane”, żeby uzmysłowić, jak może być (i jest) wykorzystywane twierdzenie Bayesa.
Zanim uzyskamy nowe dane, zakładamy, że prawdopodobieństwo naszej hipotezy to \(\mathbb{P}(H)\). Prawdopodobieństwo \(\mathbb{P}(H)\) nazywane jest prawdopodobieństwem zaczątkowym (apriorycznym, a priori, ang. prior).
Kiedy już uzyskamy nowe dane (\(D\)), otrzymujemy zmienione prawdopodobieństwo naszej hipotezy \(\mathbb{P}(H|D)\), prawdopodobieństwo wynikowe (a posteriori, ang. posterior).
Aby obliczyć prawdopodobieństwa a posteriori, uwzględniające nowe dane \(D\), wykorzystujemy \(\mathbb{P}(D|H)\) prawdopodobieństwo danych w świetle hipotezy (ang. likelihood). Nie ma dobrego tłumaczenia na polski słowa likelihood. Czasem tłumaczy się je jako „wiarygodność”, ale w tym kontekście takie tłumaczenie niekoniecznie pasuje. Gdybym miał wymyślić jakieś nowe słowo, napisałbym „zdarzalność”.
We wzorze wykorzystujemy również całkowite prawdopodobieństwo danych \(\mathbb{P}(D)\) wyznaczone najczęściej za pomocą wzorów na prawdopodobieństwo całkowite (5.1) – (5.4).
Twierdzenie Bayesa można zapamiętać w następujący sposób: wynik jest proporcjonalny do iloczynu zaczątku i zdarzalności:
\[Posterior \propto Prior \times Likelihood\]
5.3 Przykłady
Przykład 5.1 Załóżmy, że mamy do czynienia z względnie rzadką chorobą. W populacji choruje na nią jedna na 1000 osób. Mamy też niedoskonały test, którego zadaniem jest wykryć tę chorobę. Jego czułość (prawdopodobieństwo, że zwróci on wynik pozytywny – to znaczy wykryje chorobę – u osoby, która jest chora) to 0,95. Prawdopodobieństwo błędnego („fałszywego”) pozytywnego wyniku u zdrowej osoby wynosi 0,01.
Z populacji losujemy osobę i przeprowadzamy omawiany test. Zwraca on wynik pozytywny. Jakie jest prawdopodobieństwo, że ta osoba jest chora?
Mamy dwie hipotezy (rozbicie dwuczłonowe): \(H\) – wylosowana osoba jest chora i \(H^C\) – wylosowana osoba nie jest chora. Prawdopodobieństwa zaczątkowe to \(\mathbb{P}(H) = 0{,}001\) i \(\mathbb{P}(H^C) = 0{,}999\). Nasze dane \(D\) to pozytywny test. Zdarzalności, czyli prawdopodobieństwa otrzymania pozytywnego testu w sytuacji prawdziwości hipotez \(H\) i \(H^C\), wynoszą odpowiednio \(\mathbb{P}(D|H)=0{,}95\) i \(\mathbb{P}(D|H^C) = 0{,}01\). Poszukujemy prawdopodobieństwa, że osoba jest chora, gdy znamy już dane (pozytywny wynik testu): \(\mathbb{P}(H|D)\).
Korzystamy ze wzoru Bayesa:
\(\mathbb{P}(H|D) = \frac{\mathbb{P}(D|H)\cdot \mathbb{P}(H)}{\sum_i{\mathbb{P}(D|H_i)\mathbb{P}(H_i)}} = \frac{0{,}95\cdot 0{,}001}{0{,}95\cdot 0{,}001+0{,}01\cdot 0{,}999} \approx 0{,}0868\)
Prawdopodobieństwo, że wylosowana osoba, która otrzymała pozytywny wynik testu, jest chora wynosi około 8,68%.
5.4 Szablony
Arkusze kalkulacyjne
Wzór Bayesa — szablon w Google sheets
Wzór Bayesa – szablon w Excelu: Bayes.xlsx
Kod w R
# Oznaczenia hipotez (opcjonalnie)
hipotezy <- c("Choroba", "Brak choroby")
# Zaczątek (rozkład a priori, ang. prior)
prior <- c(.001, .999)
# Zdarzalność (prawdopodobieństwa warunkowe danych, ang. likelihood)
likelihood <- c(.95, .01)
# Wyznaczenie wyniku (rozkładu a posteriori, ang. posterior)
posterior <- prior*likelihood
posterior <- posterior/sum(posterior)
# Sprawdzenie
if(length(prior)!=length(likelihood))
{print("Liczebność wektorów prior (zaczątek) i likelihood (zdarzalność) powinna być równa. ")}
if(sum(prior)!=1){
print("Suma prawdopodobieństw w rozkładzie zaczątkowym (prior) powinna być równa 1.")}
if (!exists("hipotezy") || length(hipotezy)!=length(prior)) {
hipotezy <- paste0('H', 1:length(prior))
}
# Wynik w formie ramki danych:
print(data.frame(
Hipotezy = hipotezy, `Zaczątek` = prior, `Zdarzalność` = likelihood, `Wynik` = posterior
))## Hipotezy Zaczątek Zdarzalność Wynik
## 1 Choroba 0.001 0.95 0.08683729
## 2 Brak choroby 0.999 0.01 0.91316271# Wykres
library(ggplot2)
hipotezy<-factor(hipotezy, levels=hipotezy)
df <- data.frame(Hipotezy = c(hipotezy, hipotezy),
`Rozkład` = factor(c(rep("zaczątek", length(prior)), rep("wynik", length(posterior))),
levels=c("zaczątek", "wynik")
),
`Prawdopodobieństwo` = c(prior, posterior)
)
ggplot(data=df, aes(x=Hipotezy, y=`Prawdopodobieństwo`, fill=`Rozkład`)) +
geom_bar(stat="identity", position=position_dodge())+
geom_text(aes(label = format(round(`Prawdopodobieństwo`,4), nsmall=4), group=`Rozkład`),
position = position_dodge(width = .9), vjust = -0.2)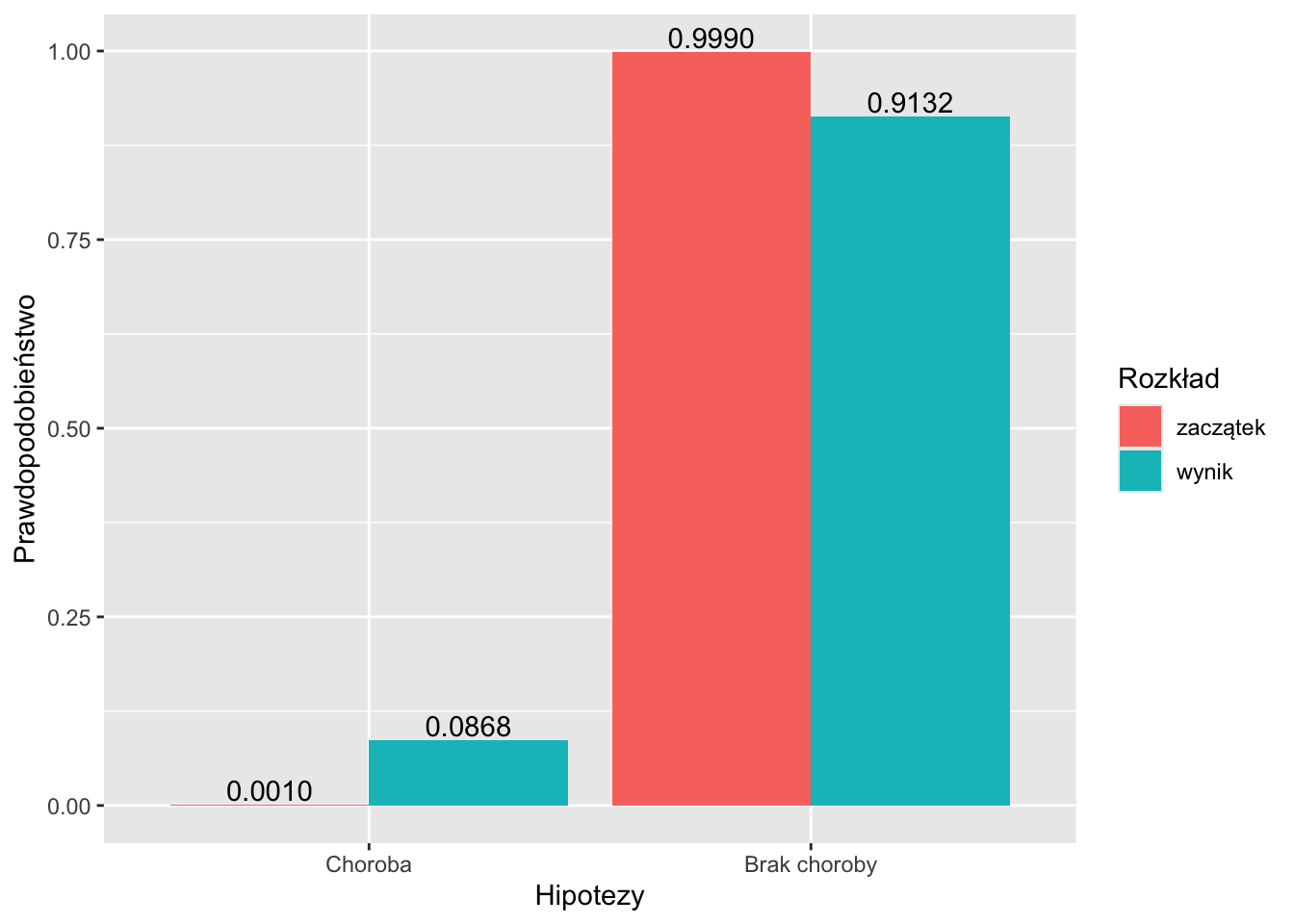
Kod w Pythonie
# Oznaczenia hipotez (opcjonalnie)
hipotezy = ["Choroba", "Brak choroby"]
# Zaczątek (rozkład a priori, ang. prior)
prior = [.001, .999]
# Zdarzalność (prawdopodobieństwa warunkowe danych, ang. likelihood)
likelihood = [.95, .01]
# Wyznaczenie wyniku (rozkładu a posteriori, ang. posterior)
posterior = [a*b for a, b in zip(prior, likelihood)]
posterior = [p/sum(posterior) for p in posterior]
# Sprawdzenie
if len(prior) != len(likelihood):
print("Liczebność wektorów prior (zaczątek) i likelihood (zdarzalność) powinna być równa.")
if sum(prior) != 1:
print("Suma prawdopodobieństw w rozkładzie zaczątkowym (prior) powinna być równa 1.")
if not "hipotezy" in locals() or len(hipotezy) != len(prior):
hipotezy = ["H" + str(i) for i in range(1, len(prior)+1)]
# Wynik w formie ramki danych:
import pandas as pd
df = pd.DataFrame({
"Hipotezy": hipotezy,
"Zaczątek": prior,
"Zdarzalność": likelihood,
"Wynik": posterior
})
print(df)## Hipotezy Zaczątek Zdarzalność Wynik
## 0 Choroba 0.001 0.95 0.086837
## 1 Brak choroby 0.999 0.01 0.913163import numpy as np
import matplotlib.pyplot as plt
x = np.arange(len(hipotezy))
width = 0.375
fig, ax = plt.subplots(layout='constrained')
rects = ax.bar(x-width/2, np.round(prior, 4), width, label = 'zaczątek')
ax.bar_label(rects, padding=3)
rects = ax.bar(x+width/2, np.round(posterior, 4), width, label = 'wynik')
ax.bar_label(rects, padding=3)
ax.set_ylabel('prawdopodobieństwo')
ax.set_xlabel('hipotezy')
ax.set_xticks(x, hipotezy)
ax.legend(loc='upper left', ncols=2)
#ax.set_ylim(0, np.max([prior, posterior])*1.2)
plt.show()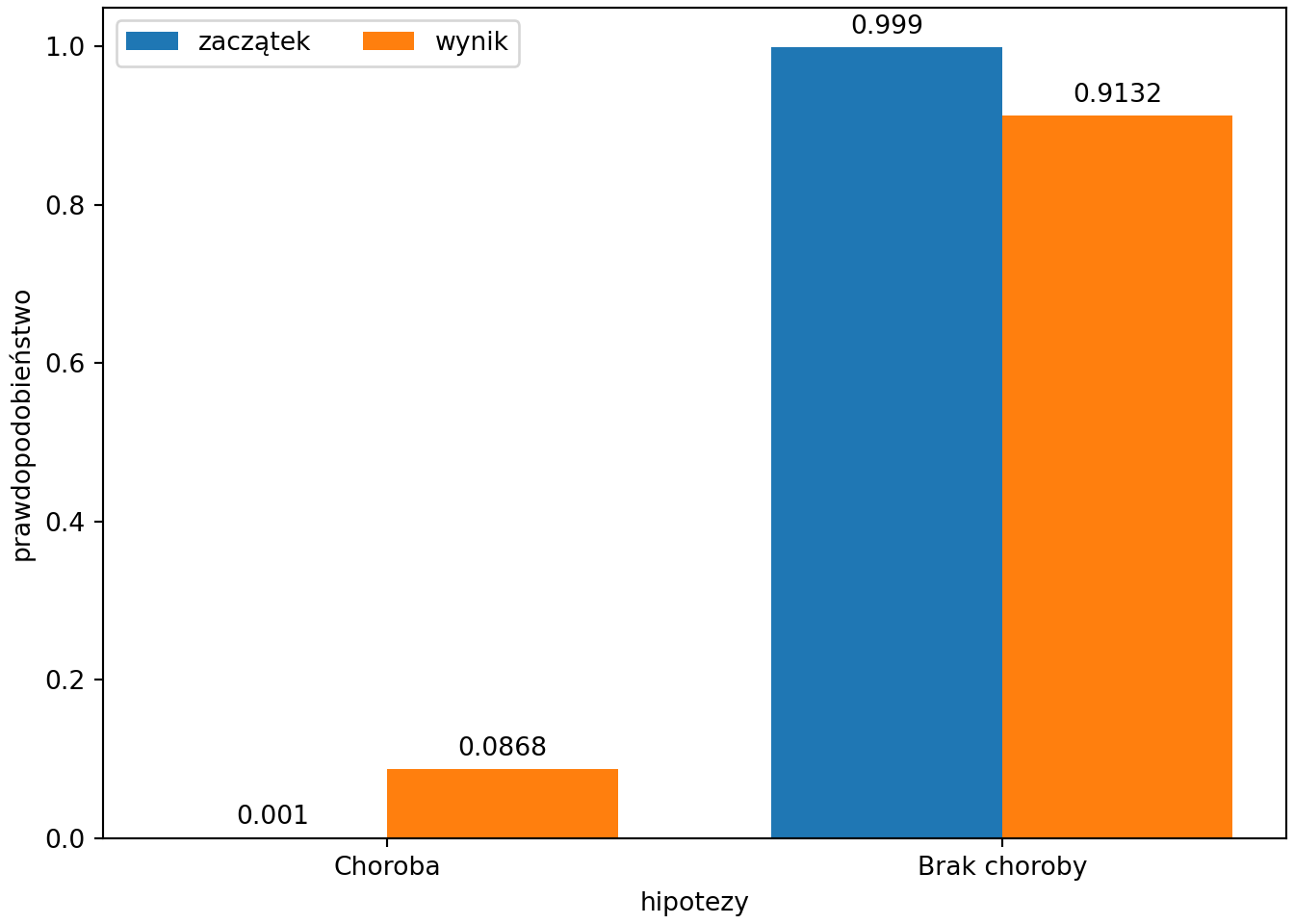
5.6 Zadania
Zadanie 5.1 W populacji 1 promil (0,1%) osób jest zarażony pewnym wirusem. Jeśli wirus jest w organizmie, test na obecność wirusa zwraca wynik pozytywny z prawdopodobieństwem 0,90, zaś negatywny z prawdopodobieństwem 0,10. W sytuacji, gdy wirusa w organizmie nie ma, test daje wynik negatywny z prawdopodobieństwem 0,99, a pozytywny (błędny) z prawdopodobieństwem 0,01. Jakie jest prawdopodobieństwo, że losowo wybrana i przetestowana osoba będzie miała pozytywny wynik testu na obecność wirusa?
Zadanie 5.2 (Aczel and Sounderpandian 2018) Zarząd holdingu dążącego do przejęcia pewnego przedsiębiorstwa ocenia prawdopodobieństwo przejęcia na 0,65, jeżeli zarząd przejmowanego przedsiębiorstwa ustąpi, oraz na 0,30, jeżeli zarząd przejmowanego przedsiębiorstwa nie ustąpi. Prawdopodobieństwo ustąpienia zarządu przejmowanego przedsiębiorstwa zarząd holdingu ocenia na 0,70. Jakie jest prawdopodobieństwo, że holdingowi uda się przejąć przedsiębiorstwo?
Zadanie 5.3 (McClave and Sincich 2012) 60% pasażerów małego lotniska podróżuje dużymi liniami lotniczymi, 30% podróżuje prywatnymi samolotami, pozostali podróżują samolotami komercyjnymi nienależącymi do dużych linii. Spośród podróżujących dużymi liniami, 50% podróżuje służbowo; procent podróżujących służbowo wśród podróżujących prywatnymi samolotami to 60%; wśród pozostałych – 90%. Wybieramy losowo jednego pasażera lotniska. Jakie jest prawdopodobieństwo, że osoba ta: (a) podróżuje służbowo? (b) podróżuje służbowo prywatnym samolotem? (c) podróżuje prywatnym samolotem, jeżeli wiemy, że podróżuje służbowo? (d) podróżuje służbowo, jeżeli wiemy, że przyleciała samolotem komercyjnym (nie-prywatnym)?
Zadanie 5.4 (Maddala 2006) Zadanie stanowi ilustrację techniki zrandomizowanej odpowiedzi (randomized response technique) – umożliwiającą otrzymywanie odpowiedzi, gdy nie jest się pewnym, czy zadało się pytanie.
Chcemy poznać frakcję studentów, którzy próbowali narkotyków. Na zadane wprost pytanie możemy nie otrzymać szczerych odpowiedzi. Zamiast tego wręczamy studentom pudełko zawierające 4 kule niebieskie, 3 czerwone i 4 białe. Każdy student jest proszony o wylosowanie (ze zwracaniem) kuli i postępowanie zgodnie z instrukcją, która mówi, że w przypadku wylosowania kuli:
- niebieskiej odpowiedz na pytanie „czy próbowałeś narkotyków”;
- czerwonej odpowiedz „tak”;
- białej odpowiedz „nie”.
Zadający pytanie nie widzi, którą kulę wylosował uczestnik, w związku z tym nie jest pewien, czy student odpowiada na pytanie, czy nie.
Jeżeli 40% odpowiedziało „tak”, to jaki jest szacowany odsetek studentów, którzy próbowali narkotyków?
Zadanie 5.5 (Aczel and Sounderpandian 2018) Ankieter chce przeprowadzić wywiad wśród małżeństw w sprawie przydatności pewnego produktu. Przychodzi on do bloku, w którym są trzy mieszkania. Z nazwisk umieszczonych na skrzynkach pocztowych na klatce schodowej orientuje się, że w jednym mieszkaniu mieszka małżeństwo, w drugim dwóch mężczyzn, a w trzecim dwie kobiety. Okazuje się jednak, że na drzwiach trzech mieszkań nie ma ani numerów, ani nazwisk lokatorów. Nie wiadomo więc, w którym z trzech mieszkań mieszka małżeństwo. Ankieter wybiera drzwi na chybił-trafił i dzwoni. Drzwi otwiera kobieta. Jakie, w świetle tych faktów, jest prawdopodobieństwo, że ankieter trafił do mieszkania zajętego przez małżeństwo? (Przyjmij założenie, że: jeżeli mieszkanie zajmują dwaj mężczyźni, to drzwi nie może otworzyć kobieta, jeżeli mieszkanie zajmują dwie kobiety, to tylko kobieta może otworzyć drzwi, jeśli mieszkanie zajmuje małżeństwo, to prawdopodobieństwo otwarcia drzwi przez kobietę jest równe 1/2. Przyjmij też, że a priori istnieje prawdopodobieństwo 1/3 trafienia do mieszkania zajętego przez małżeństwo).
Zadanie 5.6 W populacji 1 promil (0,1%) osób jest zarażony pewnym wirusem. Jeśli wirus jest w organizmie, test na obecność wirusa zwraca wynik pozytywny z prawdopodobieństwem 0,90, zaś negatywny z prawdopodobieństwem 0,10. W sytuacji, gdy wirusa w organizmie nie ma, test daje wynik negatywny z prawdopodobieństwem 0,99, a pozytywny (błędny) z prawdopodobieństwem 0,01. Jakie jest prawdopodobieństwo, że losowo wybrana i przetestowana osoba jest zarażona wirusem, jeżeli wiemy, że test dał wynik pozytywny?
Zadanie 5.7 (Lee 2018) Załóżmy, że 40% wszystkich e-maili to spam; 10% wiadomości e-mail będących spamem zawiera słowo „viagra”, podczas gdy tylko 0,5% wiadomości e-mail niebędących spamem zawiera słowo „viagra”. Jakie jest prawdopodobieństwo, że wiadomość e-mail jest spamem, jeśli zawiera słowo „viagra”?
Zadanie 5.8 Oszukańcze transakcje stanowią 0,035% wszystkich transakcji kartami płatniczymi. Wśród transakcji oszukańczych 19,3% to transakcje, które są wykonywane w lokalizacjach odległych geograficznie od miejsca zamieszkania klienta. Wśród zwykłych transakcji transakcje w odległych geograficznie miejscach stanowią jedynie 0,4%.
Ile wynosi udział transakcji odległych geograficznie we wszystkich transakcjach?
Wylosowano transakcję i stwierdzono, że została wykonana w miejscu geograficznie odległym od miejsca zamieszkania klienta. Jakie jest prawdopodobieństwo, że jest to transakcja oszukańcza?
Zadanie 5.9 Załóżmy, że testy PCR na COVID-19 miały czułość na poziomie 80% i swoistość na poziomie 98,5%. Załóżmy, że wśród osób z objawami przeziębienia w momencie badania 30% miało COVID, zaś w całej populacji w danym momencie zakażona COVID-em była co setna osoba.
Jaki było prawdopodobieństwo, że osoba wylosowana spośród osób z objawami przeziębienia miała rzeczywiście COVID, jeżeli jej test był pozytywny?
Jakie było prawdopodobieństwo, że osoba, która po wylosowaniu z całej populacji uzyskała pozytywny wynik testu, była rzeczywiście zakażona COVID?
Zadanie 5.10 (Na podstawie Mcelreath 2020) Załóżmy, że w pewnym układzie planetarnym są dwie planety: „Ziemia” i „Mars”. „Ziemia” jest pokryta w 70% wodą, w 30% lądem, zaś „Mars” jest w 100% lądowy. Lądujemy na jednej z planet (załóżmy, że wylądowanie na każdej z planet jest równie prawdopodobne), w losowym miejscu. Wylądowaliśmy na lądzie. Jakie jest prawdopodobieństwo, że to „Ziemia”?
Zadanie 5.11 Pewni psychologowie szukają zależności między różnymi zachowaniami za pomocą testów statystycznych. Tylko 1% hipotetycznych zależności to zależności prawdziwe. Jeżeli zależność jest nieprawdziwa, testy statystyczne w 5% przypadków wskazują, że jest ona istotna statystycznie. Jeżeli zależność jest prawdziwa, testy statystyczne wykrywają ją (wskazują ją jako istotną statystycznie) w 80% przypadków.
Zależność została zidentyfikowana jako istotna przez test statystyczny. Jakie jest prawdopodobieństwo, że jest prawdziwa?
Jakie jest prawdopodobieństwo, że jedna wylosowana i przetestowana hipotetyczna zależność będzie wskazana jako istotna przez test statystyczny?
Zadanie 5.12 Bogdan przyleciał z Gdańska do La Paz (z dwiema przesiadkami) i właśnie czeka na swoją walizkę. Wie, że raz na 1000 razy może się zdarzyć, że bagaż się zgubi. Bagaże wykładane są na taśmę równomiernie, przez 10 minut. Minęło już 8 minut, większość pasażerów odebrała swój bagaż, ale walizka Bogdana jeszcze się nie pojawiła. Jakie jest prawdopodobieństwo, że walizka została zgubiona?
Zadanie 5.13 (Na podstawie Mcelreath 2020) Załóżmy, że istnieją dwa gatunki pandy. Obydwa są równie powszechne na wolności i żyją w tych samych miejscach. Wyglądają i odżywiają się dokładnie tak samo, różnią się jednak częstotliwością porodów bliźniaczych. Gatunek A rodzi bliźnięta w 10% przypadków. Gatunek B rodzi bliźnięta w 20% przypadków. Załóżmy teraz, że obserwujesz pewną samicę pandy nieznanego gatunku, a ona właśnie urodziła bliźnięta.
Jakie jest prawdopodobieństwo, że jest to panda gatunku A?
Jakie jest prawdopodobieństwo, że przy następnym porodzie również będą bliźnięta?
W kolejnym porodzie ta sama panda urodziła pojedyncze dziecko. Jakie teraz jest prawdopodobieństwo, że jest to panda gatunku A?
Zadanie 5.14 (Na podstawie “Bayes’ Rule: Log-Odds Form,” n.d.) Janusz dość często podróżuje do Alicante, gdzie mieszkają jego przyjaciele Alejandro i Beatriz. Jedno z nich zawsze odbiera Janusza z lotniska. Załóżmy, że oboje równie często przyjeżdżają po Janusza. Mają oni dwa auta: czerwone i srebrne. Beatriz woli czerwone auto; korzysta z czerwonego auta w 60% przypadków. Alejandro używa srebrnego auta 4 razy częściej niż czerwonego. Alejandro częściej się spóźnia. Jeżeli Janusza odbiera Alejandro, prawdopodobieństwo, że będzie na czas, wynosi 0,4; Beatriz zdąży na czas z prawdopodobieństwem 0,8. Beatriz lubi używać klaksonu. Jeżeli zobaczy Janusza, zatrąbi w ośmiu przypadkach na 10. Alejandro też czasem używa klaksonu – prawdopodobieństwo, że zatrąbi, widząc Janusza, wynosi 0,2. Janusz właśnie wyszedł z hali przylotów i widzi, że czeka już na niego srebrne auto, a jego kierowca daje mu sygnał klaksonem. Jakie jest prawdopodobieństwo, że to Beatriz? Załóżmy, że używanie klaksonu, kolor auta i przybycie na czas bądź spóźnienie się są niezależne od siebie.