F Jak korzystać z R
F.2 Jak to zrobić w R
F.2.1 Wczytywanie danych
F.2.1.1 Wczytywanie danych w formacie csv
Dane w formacie csv mogą być wczytane do R za pomocą funkcji read.csv (lub read.csv2, gdy plik csv jest przygotowany w ramach polskich ustawień regionalnych).
Przykład F.1 W poniższym pliku zawarte dane o wzroście trzech osób. Wczytaj dane do R i oblicz średni wzrost tych osób.
F.2.1.2 Wczytywanie danych z arkuszy Google
Do integracji z arkuszami Google służy pakiet googlesheets4. W ramach tego pakietu można skorzystać z funkcji read_sheet, która umożliwia wczytanie danych do R. Aby nie było konieczne logowanie się, można użyć funkcji gs4_deauth.
Przykład F.2 Szablon regresji prostej znajduje się pod linkiem https://docs.google.com/spreadsheets/d/15NS-y-Lb0RvDIGti2oymg68cqnKYdu2lGWljJK9ggNw. Wczytaj dane z tego szablonu do R i oblicz odchylenie standardowe zmiennej Y.
F.2.2 Rozkłady prawdopodobieństwa
F.2.2.1 Rozkład normalny
Wiele popularnych rozkładów prawdopodobieństwa jest dostępnych w R w postaci czterech funkcji, które można przedstawić na przykładzie rozkładu normalnego (zobacz rysunek F.1):
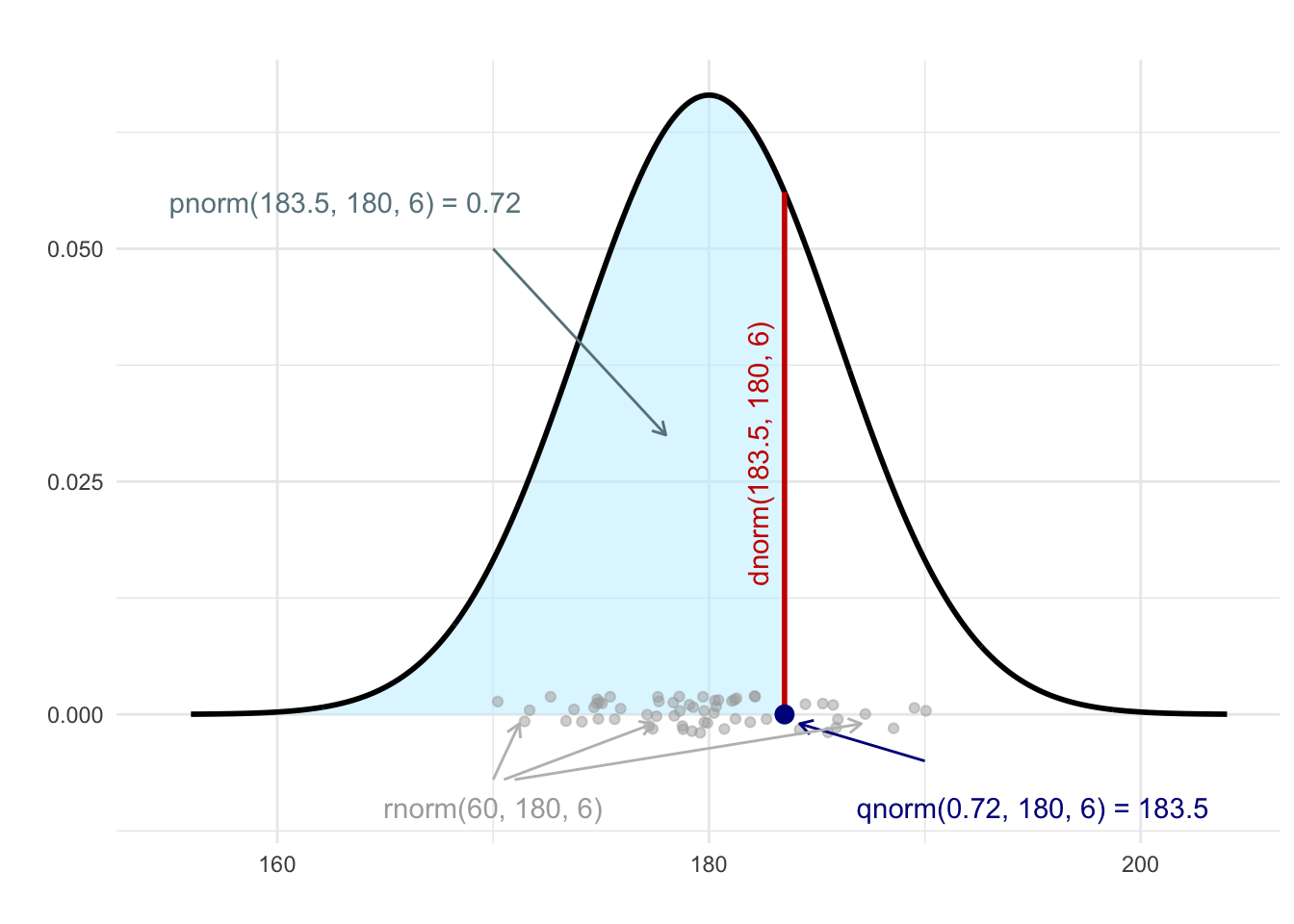
Rysunek F.1: Ilustracja zastosowania funkcji pnorm, qnorm, dnorm i rnorm dla rozkładu normalnego o średniej równej 180 i odchyleniu standardowym równym 6.
funkcja
dnorm(x, mean = mu, sd = sigma)to funkcja gęstości rozkładu normalnego (9.1) o średniejmui odchyleniu standardowymsigma,funkcja
pnorm(x, mu, sigma)to dystrybuanta (7.4) takiego rozkładu normalnego,funkcja
qnorm(a, mu, sigma)to funkcja odwrotna do dystrybuanty umożliwiająca np. wyznaczenie wartości krytycznych (granic obszaru odrzucenia),funkcja
rnorm(k, mu sigma)to funkcja umożliwiająca losowaniekwartości z tego rozkładu normalnego.
Przykład F.3 Zmienna losowa \(X\) ma rozkład normalny ze średnią 180 i odchyleniem standardowym 6. Wykorzystując dystrybuantę, należy za pomocą R obliczyć \(\mathbb{P}(178 < X < 183)\).
F.2.2.2 Rozkład dwumianowy
Analogicznie dla rozkładów dyskretnych na przykładzie rozkładu dwumianowego:
funkcja
dbinom(x, size = n, prob = p)to funkcja masy prawdopodobieństwa (7.1) rozkładu dwumianowego z parametraminip,funkcja
pbinom(x, n, p)to dystrybuanta tego rozkładu,funkcja
qbinom(a, n, p)to funkcja odwrotna do dystrybuanty,a funkcja
rbinom(k, n, p)umożliwia losowanie z tego rozkładu.
Przykład F.4 Wykorzystując R, należy obliczyć prawdopodobieństwo, że rzucając 20 razy symetryczną monetą, otrzymamy 15 lub więcej razy orła.
F.2.3 Symulacje z wykorzystaniem R
Przydatne funkcje w R służące do symulacji:
generowanie wartości losowych z rozkładów:
rnorm(rozkład normalny),runif(rozkład jednostajny) itp.sample,replicate.
Funkcje takie jak rnorm, runif i podobne służą do generowania zmiennych losowych z konkretnych rozkładów. Na przykład rnorm(100, 4, 2) wygeneruje 100 wartości z rozkładu normalnego o średniej 4 i odchyleniu standardowym 2.
Funkcja sample umożliwia losowe wybieranie wartości z danego zbioru, przetasowywanie (permutowanie) zbioru lub losowanie próbek z określonymi prawdopodobieństwami. Na przykład:
sample(1:200, 5)losuje pięć liczb całkowitych ze zbioru od 1 do 200,sample(0:9)przedstawia losową permutację (przetasowanie) liczb jednocyfrowych,opcja
replace=TRUEumożliwia losowanie z powótrzeniami, stąd 10 wyników rzutu kostką można wygenerować, piszącsample(1:6, 10, replace=TRUE),opcja
prob=umożliwia ustawienie prawdopodobieństw, stąd kodsample(c("O","R"), size=20, prob=c(0.6, 0.4), replace=TRUE)generuje 20 wyników rzutów niesymetryczną monetą, w przypadku której prawdopodobieństwo orła (O) wynosi 0,6.
Funkcja replicate pozwala na zapisanie wyników wielokrotnego powtarzania jakichś obliczeń zawierających element losowy. Na przykład za pomocą kodu wyniki <- replicate(1000, mean(rnorm(100, 180, 6))) można zapisać w wektorze wyniki 1000 średnich ze 100-elementowych prób pochodzących z rozkładu normalnego o średniej 180 i odchyleniu standardowym 6.