Rozdział 22 Inne testy statystyczne

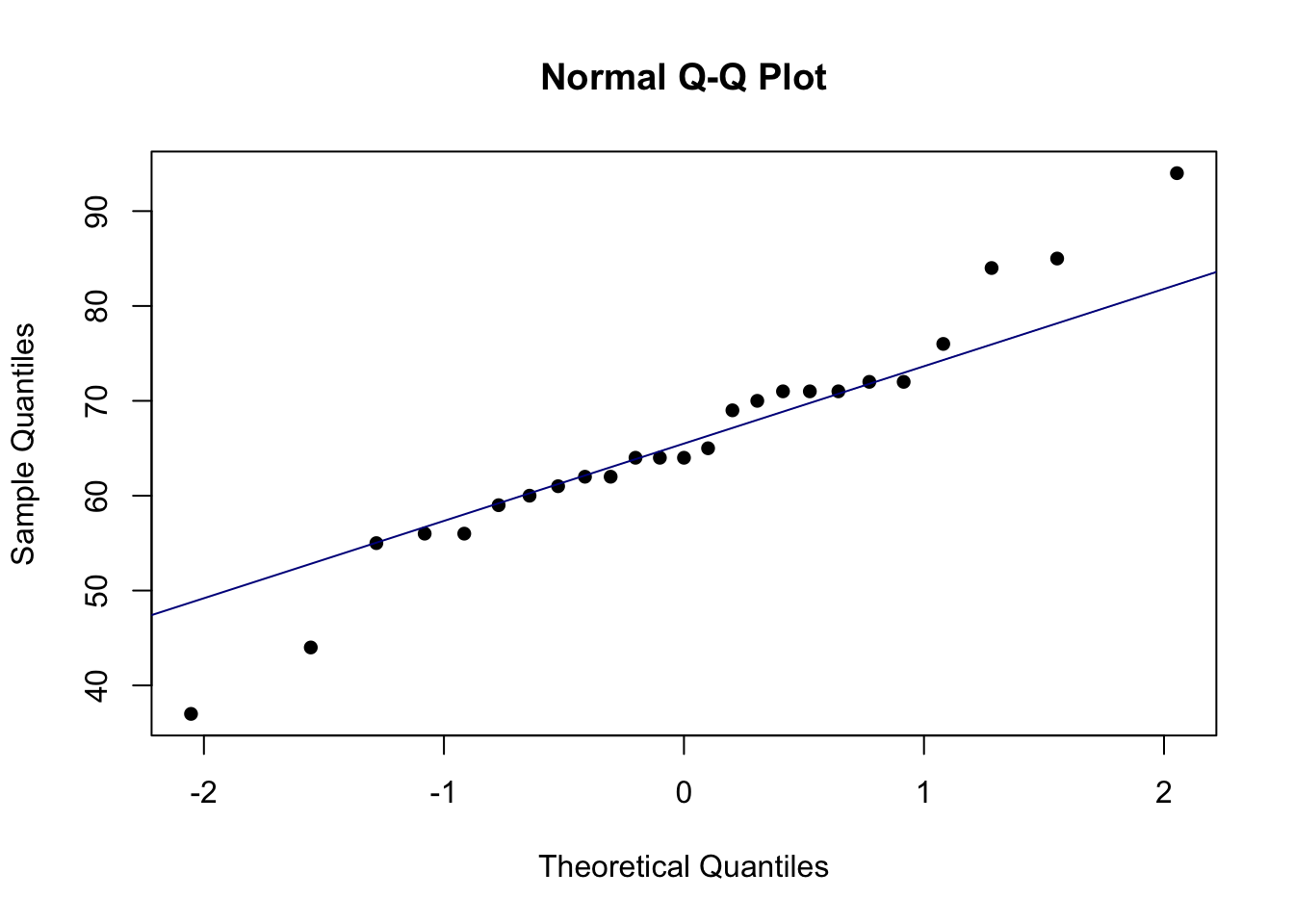
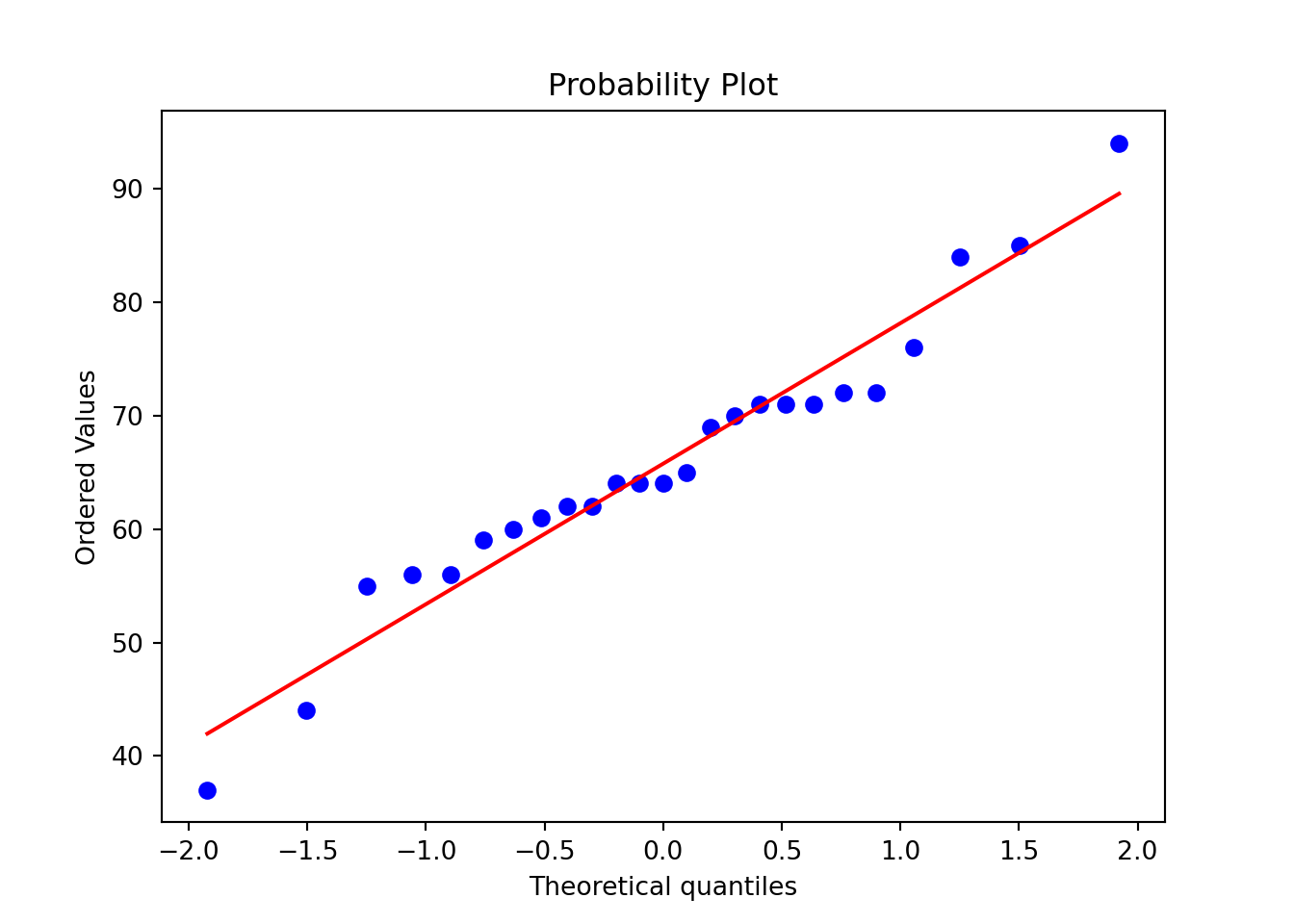
22.1 Sprawdzanie zgodności z rozkładem Gaussa

Do popularnych „testów normalności” należą test Kołmogorowa-Smirnowa, test Shapiro-Wilka-Roystona, test Jarque'a-Bery.

22.1.1 Test Kołmogorowa-Smirnowa

22.1.2 Test Shapira-Wilka-Roystona

22.1.3 Test Jarque'a-Bery

22.1.4 Test Andersona-Darlinga

22.2 Test i przedział ufności dla współczynnika korelacji Pearsona

Współczynnik korelacji bada powiązanie pomiędzy dwoma zmiennymi ilościowymi. Może być dodatni i ujemny, przyjmuje wartości między -1 a 1. Współczynnik korelacji z próby często oznaczamy symbolem \(r\), zaś współczynnik z populacji oznaczamy grecką literą \(\rho\) („ro”, ang. „rho”).

Popularnym testem współczynnika korelacji jest test t. Test ten zakłada, że wspólny rozkład prawdopodobieństwa dwóch zmiennych to rozkład dwuwymiarowy normalny.

Hipoteza zerowa w tym teście stwierdza, że zmienne w populacji nie są skorelowane liniowo:

\[ H_0: \rho = 0, \]

a hipoteza alternatywna (dwustronna), że są:

\[ H_A: \rho \ne 0 \]

Możliwe jest również zastosowanie hipotez jednostronnych: \(H_A: \rho > 0\) lub \(H_A: \rho < 0\).

Statystyka testowa jest oparta na rozkładzie \(t\) o \(n-2\) stopniach swobody i przyjmuje postać:

\[ t = r {\sqrt {\frac {n-2}{1-r^{2}}}}, \] gdzie \(n\) to liczebność próbki, a \(r\) to współczynnik korelacji w próbie.

Wzór na przedział ufności współczynnika Pearsona jest dość złożony. Dolny kraniec uzyskujemy w następujący sposób:

\[ \frac{\text{exp}\left(ln\frac{1+r}{1-r}-\frac{2}{\sqrt{n-3}}z_{\alpha/2}\right)-1}{\text{exp}\left(ln\frac{1+r}{1-r}-\frac{2}{\sqrt{n-3}}z_{\alpha/2}\right)+1} \]

zaś górny (prawy) kraniec w następujący:

\[ \frac{\text{exp}\left(ln\frac{1+r}{1-r}+\frac{2}{\sqrt{n-3}}z_{\alpha/2}\right)-1} {\text{exp}\left(ln\frac{1+r}{1-r}+\frac{2}{\sqrt{n-3}}z_{\alpha/2}\right)+1} \]

22.3 Lektura dodatkowa

https://danetyka.com/rozklad-normalny-czy-nienormalny/

22.4 Szablony

Sprawdzanie normalności — arkusz Google

Sprawdzanie normalności — szablon w Excelu

Współczynnik korelacji — szablon — arkusz Google

Współczynnik korelacji — szablon — szablon w Excelu

Kod w R

# Sprawdzenie normalności
# Dane
data<-c(76, 62, 55, 62, 56, 64, 44, 56, 94, 37, 72, 85, 72, 71, 60, 61, 64, 71, 69, 70, 64, 59, 71, 65, 84)
# Średnia
m<-mean(data)
# Odchylenie standardowe
s<-sd(data)
# Skośność
skew<-e1071::skewness(data, type=2)
# Kurtoza
kurt<-e1071::kurtosis(data, type=2)
# iloraz IQR do odchylenia standardowego
IQR_to_s<-IQR(data)/s
#udział obserwacji odległych o mniej niż 1 odchylenie standardowe od średniej
within1s<-mean(abs(data-m)<s)
#...o mniej niż 2 odchylenia...
within2s<-mean(abs(data-m)<2*s)
#...o mniej niż 3 odchylenia...
within3s<-mean(abs(data-m)<3*s)
# Test Shapiro-Wilka
SW_res<-shapiro.test(data)
# Test Jarque'a-Bery
JB_res<-tseries::jarque.bera.test(data)
# Test Andersona-Darlinga
AD_res<-nortest::ad.test(data)
# Test Kołmogorowa-Smirnowa
KS_res <- ks.test(data, function(x){pnorm(x, mean(data), sd(data))})

# Wyniki
print(c('Średnia' = m, 
        'Odchylenie st.' = s,
        'Liczebność' = length(data),
        'Skośność (~=0?)' = skew,
        'Kurtoza (~=0?)' = kurt,
        'IQR/s (~=1,3?)' = IQR_to_s,
        'Reguła 68%' = within1s*100,
        'Reguła 95%' = within2s*100,
        'Reguła 100%' = within3s*100,
        'Stat. test. - test SW' = SW_res$statistic,
        'Wartość p - test SW' = SW_res$p.value,
        'Stat. test. - test JB' = JB_res$statistic,
        'Wartość p - test JB' = JB_res$p.value,
        'Stat. test. - test AD' = AD_res$statistic,
        'Wartość p - test AD' = AD_res$p.value,
        'Stat. test. - test KS' = KS_res$statistic,
        'Wartość p - test KS' = KS_res$p.value
))

##                         Średnia                  Odchylenie st.                      Liczebność 
##                    65.760000000                    12.145918382                    25.000000000 
##                 Skośność (~=0?)                  Kurtoza (~=0?)                  IQR/s (~=1,3?) 
##                    -0.002892879                     1.121315636                     0.905654036 
##                      Reguła 68%                      Reguła 95%                     Reguła 100% 
##                    80.000000000                    92.000000000                   100.000000000 
##         Stat. test. - test SW.W             Wartość p - test SW Stat. test. - test JB.X-squared 
##                     0.964892812                     0.520206266                     0.479578632 
##             Wartość p - test JB         Stat. test. - test AD.A             Wartość p - test AD 
##                     0.786793609                     0.445513641                     0.260454333 
##         Stat. test. - test KS.D             Wartość p - test KS 
##                     0.143712404                     0.680154210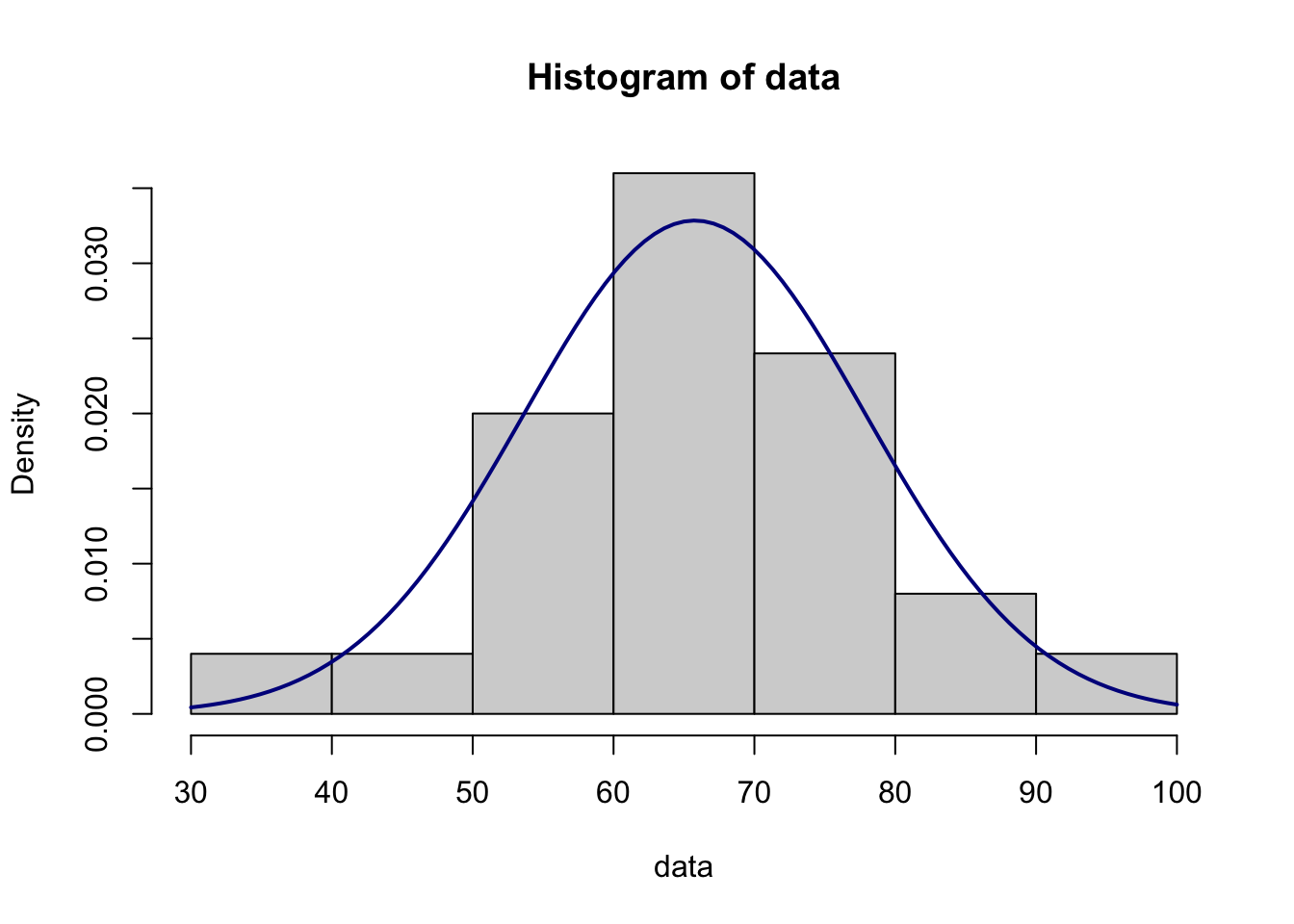

# Wykresy
hist(data, prob=TRUE)
curve(dnorm(x, m, s), col="darkblue", lwd=2, add=TRUE)

qqnorm(data, pch=16)
qqline(data, col='darkblue')

#dane:
x <- c(4, 8, 6, 5, 3, 8, 6, 5, 5, 6, 3, 3, 3, 7, 3, 6, 4, 4, 8, 7)
y <- c(4, 6, 8, 3, 4, 6, 5, 8, 1, 4, 4, 3, 1, 6, 7, 5, 4, 4, 9, 5)
#test i przedział ufności:
cor.test(x, y, alternative = "two.sided", conf.level = 0.95)

## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = 2.56, df = 18, p-value = 0.01968
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.09607185 0.78067292
## sample estimates:
##       cor 
## 0.5166288

Kod w Pythonie

import numpy as np
import math as math
from scipy import stats
from scipy.stats import skew, kurtosis, anderson, kstest, norm

data = [76, 62, 55, 62, 56, 64, 44, 56, 94, 37, 72, 85, 72, 71, 60, 61, 64, 71, 69, 70, 64, 59, 71, 65, 84]

m = np.mean(data)

s = np.std(data, ddof=1)

skew = skew(data, bias=False)

kurt = kurtosis(data, bias=False)

IQR_to_s = stats.iqr(data) / s

within1s = np.mean(np.abs(data - m) < s)

within2s = np.mean(np.abs(data - m) < 2 * s)

within3s = np.mean(np.abs(data - m) < 3 * s)

SW_res = stats.shapiro(data)

JB_res = stats.jarque_bera(data)

AD_res = stats.anderson(data)

AD2 = AD_res[0]*(1 + (.75/50) + 2.25/(50**2))

if AD2 >= .6:
    AD_p = math.exp(1.2937 - 5.709*AD2 - .0186*(AD2**2))
elif AD2 >=.34:
    AD_p = math.exp(.9177 - 4.279*AD2 - 1.38*(AD2**2))
elif AD2 >.2:
    AD_p = 1 - math.exp(-8.318 + 42.796*AD2 - 59.938*(AD2**2))
else:
    AD_p = 1 - math.exp(-13.436 + 101.14*AD2 - 223.73*(AD2**2))
    
KS_res = kstest(data, norm(loc=np.mean(data), scale=np.std(data)).cdf)

results = {
    'Średnia': m, 
    'Odchylenie st.': s,
    'Liczebność': len(data),
    'Skośność (~=0?)': skew,
    'Kurtoza nadwyżkowa (~=0?)': kurt,
    'IQR/s (~=1,3?)': IQR_to_s,
    'Reguła 68%': within1s * 100,
    'Reguła 95%': within2s * 100,
    'Reguła 100%': within3s * 100,
    'Stat. test. - test SW': SW_res[0],
    'Wartość p - test SW': SW_res[1],
    'Stat. test. - test JB': JB_res[0],
    'Wartość p - test JB': JB_res[1],
    'Stat. test. - test AD': AD_res[0],
    'Wartość p - test AD': AD_p,
    'Stat. test. - test KS': KS_res[0],
    'Wartość p - test KS': KS_res[1]
}


for key, value in results.items():
    print(f"{key}: {value}")

## Średnia: 65.76
## Odchylenie st.: 12.145918381634768
## Liczebność: 25
## Skośność (~=0?): -0.002892878582795321
## Kurtoza nadwyżkowa (~=0?): 1.121315636006976
## IQR/s (~=1,3?): 0.9056540357320815
## Reguła 68%: 80.0
## Reguła 95%: 92.0
## Reguła 100%: 100.0
## Stat. test. - test SW: 0.9648927450180054
## Wartość p - test SW: 0.5202044248580933
## Stat. test. - test JB: 0.47957863171421605
## Wartość p - test JB: 0.7867936085428064
## Stat. test. - test AD: 0.44551364110243696
## Wartość p - test AD: 0.27208274566708046
## Stat. test. - test KS: 0.14001867878746022
## Wartość p - test KS: 0.6601736174333425

import matplotlib.pyplot as plt

# Histogram
plt.hist(data, density=True)
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, m, s)
plt.plot(x, p, 'k', linewidth=2, color="darkblue")
plt.show()

# Q-Q plot
qq_data = stats.probplot(data, dist="norm", plot=plt)
plt.show()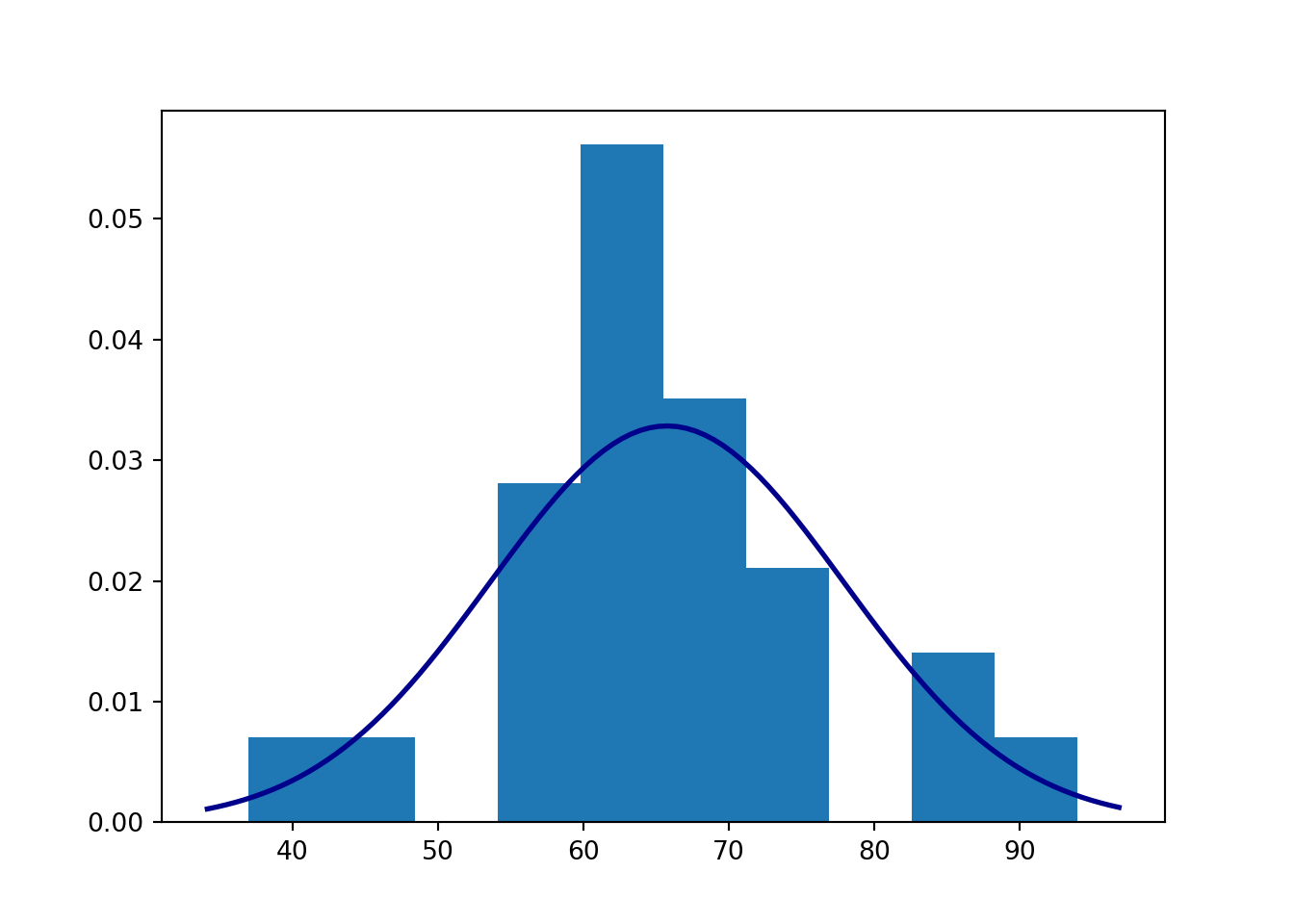

import scipy.stats as stats
import numpy as np

x = [4, 8, 6, 5, 3, 8, 6, 5, 5, 6, 3, 3, 3, 7, 3, 6, 4, 4, 8, 7]
y = [4, 6, 8, 3, 4, 6, 5, 8, 1, 4, 4, 3, 1, 6, 7, 5, 4, 4, 9, 5]

correlation_test = stats.pearsonr(x, y)

# Przedział ufności:
ci_tmp = stats.norm.interval(0.95, 
  loc=0.5*math.log((1+correlation_test[0])/(1-correlation_test[0])), 
  scale=1/((len(x)-3)**0.5))
confidence_interval = (np.exp(2*np.array(ci_tmp))-1)/(np.exp(2*np.array(ci_tmp))+1)

print('Test:\n\n', correlation_test, '\n\n Przedział ufności: \n\n', confidence_interval)

## Test:
## 
##  PearsonRResult(statistic=0.5166287822129882, pvalue=0.01968490591016886) 
## 
##  Przedział ufności: 
## 
##  [0.09607185 0.78067292]

22.5 Zadania

Zadanie 22.1 30 studentów próbowało odgadnąć wiek pewnej osoby na podstawie fotografii. Każdy student podawał swoje oszacowanie. Potraktujmy tych 30 studentów jak próbę losową z populacji, na temat której chcemy wnioskować. Czy należy odrzucić hipotezę zerową stwierdzającą, że rozkład liczb podawanych przez studentów jako oszacowanie wieku osoby na zdjęciu ma rozkład Gaussa? Oto liczby podane przez 30 studentów: 35, 35, 44, 36, 25, 27, 37, 35, 35, 39, 25, 34, 28, 37, 29, 39, 40, 38, 30, 32, 30, 40, 34, 27, 36, 27, 29, 34, 19, 39.

Zadanie 22.2 W poniższym pliku zamieszczono dane dotyczące wyników wyborczych kandydata partii rządzącej (partii urzędującego prezydenta) oraz stanu gospodarki mierzonego przeciętnym ważonym rocznym wzrostem dochodów osobistych w ciągu czterech lat poprzedzających wybory.

hibbs.csv

W kolejnych kolumnach umieszczono następujące informacje:

rok – rok wyborów,
wzrost_dochodow – średnia ważona roczna stopa wzrostu w czteroletnim okresie poprzedzającym wybory,
udzial_glosow – odsetek głosów oddanych na kandydata wystawionego przez partię rządzącą (partię urzędującego prezydenta, Demokratów albo Republikanów),
kand_partii_rzad – nazwisko kandydata partii rządzącej,
drugi_kand – nazwisko drugiego kandydata.

Dane pochodzą z książki Gelman, Hill, and Vehtari (2021).

Potraktuj dane jak wygenerowane niezależnie z losowego procesu (próbę losową z populacji). Czy można odrzucić hipotezę zerową o braku korelacji pomiędzy wzrostem dochodów a odsetkiem głosów na kandydata partii rządzącej?

Podaj przedział ufności dla współczynnika korelacji.

Literatura

Gelman, A., J. Hill, and A. Vehtari. 2021. Regression and Other Stories. Analytical Methods for Social Research. Cambridge University Press. https://books.google.pl/books?id=fILoDwAAQBAJ.