Rozdział 7 Zmienne losowe
Formalnie zmienna losowa to funkcja/mapowanie przypisujące wartości liczbowe zdarzeniom elementarnym (zobacz zadanie 7.1). Można powiedzieć, że jest to matematyczna formalizacja obiektu, który w losowy sposób może przyjąć różne wartości z określonymi prawdopodobieństwami.
Często wyróżnia się zmienne losowe dyskretne (skokowe) i ciągłe. Zmienne ciągłe mogą przyjmować dowolną wartość w określonym przedziale (na przykład od zera do nieskończoności), zaś zmienne skokowe mogą przyjmować wartości oddalone od siebie na osi liczbowej (na przykład tylko nieujemne liczby całkowite: 0, 1, 2, 3...) i nic pomiędzy.
Warto zaznaczyć, że zmienne ciągłe i dyskretne to przede wszystkim byty matematyczne, przydatne do modelowania. Fizyk może argumentować, że masa jest kwantowa (czyli dyskretna), a nie ciągła. Tak czy owak, czasem używa się zmiennych ciągłych do modelowania zmiennych, które w rzeczywistości w oczywisty sposób są dyskretne. Na przykład wynagrodzenie może przyjmować wartości w dolarach i centach (np. 2345,01 USD lub 2345,02 USD – połówki centa nie są możliwe), natomiast modeluje się je często za pomocą rozkładów ciągłych.
7.1 Rozkład prawdopodobieństwa
Rozkład prawdopodobieństwa umożliwia określenie prawdopodobieństw poszczególnych wartości zmiennej losowej. Rozkłady prawdopodobieństwa będziemy przedstawiali w postaci tabeli albo w postaci wzoru matematycznego. Forma tabelaryczna przydaje się, gdy zmienna losowa jest dyskretna i ma niewiele możliwych wartości. Zmienne dyskretne można przedstawiać również w postaci wzoru, który umożliwia obliczenie prawdopodobieństwa \(\textbf{p}(x_i)\) dla każdej możliwej wartości \(x_i\), którą może przyjąć zmienna \(X\). Funkcja \(\textbf{p}(x_i)\) dla zmiennej dyskretnej nazywana jest funkcją masy prawdopodobieństwa.
Funkcja masy prawdopodobieństwa ma następujące własności. Po pierwsze, przyjmuje tylko wartości nieujemne:
\[\begin{equation} \textbf{p}(x_i)\geqslant 0 \text{ dla wszystkich } x_i \text{, } \tag{7.1} \end{equation}\]
po drugie, suma wszystkich wartości jest równa 1:
\[\begin{equation} \sum_i \textbf{p}(x_i)=1 \text{. } \tag{7.2} \end{equation}\]
| \(x\) | \(\textbf{p}(x)\) |
|---|---|
| 0 | 0,25 |
| 1 | 0,50 |
| 2 | 0,25 |
Dla zmiennych ciągłych rozkład prawdopodobieństwa przedstawia się za pomocą funkcji gęstości prawdopodobieństwa \(f(x)\). Analogicznie do funkcji masy prawdopodobieństwa dla zmiennych dyskretnych (wzory (7.1)-(7.2)), funkcja \(f\) przyjmuje wartości nieujemne:
\[\begin{equation} f(x)\geqslant 0 \text{ dla wszystkich } x \text{, } \tag{7.3} \end{equation}\]
a pole powierzchni pomiędzy jej wykresem a osią x wynosi 1:
\[\begin{equation} \int_{-\infty}^{\infty} f(x) dx = 1{. } \tag{7.4} \end{equation}\]
Przykłady zmiennych ciągłych pojawią się w rozdziale 9.
7.2 Wartość oczekiwana
Wartość oczekiwana (ang. expected value) to średnia zmiennej losowej o danym rozkładzie prawdopodobieństwa. Zamiast terminu „wartość oczekiwana” używa się także (rzadko) pojęcia „nadzieja matematyczna”. Wartość oczekiwaną zmiennej \(X\) oznaczamy symbolem \(\mathbb{E}(X)\), \(\mu_X\) lub po prostu \(\mu\) (kiedy z kontekstu jasno wynika, której zmiennej dotyczy).
Dla zmiennej losowej dyskretnej o skończonej liczbie wartości \(m\) (indeksowanych od \(x_1\) do \(x_m\)) wartość oczekiwaną można wyznaczyć następującym wzorem:
\[\begin{equation} \mu=\mathbb{E}(X)=\sum_{i=1}^m x_i \textbf{p}(x_i) \tag{7.5} \end{equation}\]
Analogicznie, jeżeli liczba wartości przyjmowanych przez dyskretną zmienną losową jest nieskończona, wzór ma taką postać:
\[\begin{equation} \mu=\mathbb{E}(X)=\sum_{i=1}^\infty x_i \textbf{p}(x_i) \tag{7.6} \end{equation}\]
W uproszczeniu zapisujemy to w ten sposób:
\[\begin{equation} \mu=\mathbb{E}(X)=\sum x \textbf{p}(x) \tag{7.7} \end{equation}\]
Dla zmiennej losowej ciągłej wzór przyjmuje następującą postać:
\[\begin{equation} \mu=\mathbb{E}(X)=\int_{-\infty}^{\infty} x f(x) dx \tag{7.8} \end{equation}\]
W uproszczonym zapisie będziemy pomijać granice całkowania:
\[\begin{equation} \mu=\mathbb{E}(X)=\int x f(x) dx \tag{7.9} \end{equation}\]
7.3 Wariancja i odchylenie standardowe
Wariancję zmiennej losowej oznaczamy przez \(\mathbb{V}(X)\), \(Var(X)\), \(D^2(X)\) albo \(\sigma^2_X\) (lub po prostu \(\sigma^2\)) i wyznaczamy za pomocą wzoru2:
\[\begin{equation} \sigma^2=\mathbb{V}(X)=\mathbb{E}[(X-\mu)^2] \tag{7.10} \end{equation}\]
Dla zmiennych dyskretnych:
\[\begin{equation} \sigma^2=\mathbb{E}[(X-\mu)^2]=\sum (x-\mu)^2 \textbf{p}(x) = \sum x^2 \textbf{p}(x)-\mu^2 \tag{7.11} \end{equation}\]
Dla zmiennych ciągłych:
\[\begin{equation} \sigma^2=\mathbb{E}[(X-\mu)^2]=\int (x-\mu)^2 f(x) dx = \int x^2 f(x) dx-\mu^2 \tag{7.12} \end{equation}\]
Odchylenie standardowe zmiennej losowej to pierwiastek z wariancji:
\[\begin{equation} \sigma=\sqrt{\sigma^2} \tag{7.13} \end{equation}\]
7.4 Dystrybuanta zmiennej losowej
Często rozkład zmiennej losowej opisuje się poprzez jej dystrybuantę. Dotyczy to w szczególności zmiennych losowych ciągłych, ale dystrybuantę można wyznaczyć również dla zmiennych dyskretnych. Dystrybuantę po angielsku nazywamy skumulowaną funkcją rozkładu (skrót CDF - cumulative distribution function). Oznaczamy ją literą F, czasami zaznaczając za pomocą indeksu dolnego, której zmiennej dotyczy (na przykład \(F_X\)).
Dystrybuantę definiujemy następująco:
\[ F_X(x) = \mathbb{P}(X \leqslant x) \tag{7.14}\]
Dystrybuanta przyjmuje wartości od 0 do 1 (jej granicą w nieskończoności jest 1, a w minus nieskończoności 0). Jest funkcją niemalejącą.
Poniżej przedstawiono wykresy przykładowych dystrybuant. Rysunek 7.1 przedstawia dystrybuantę dyskretnej zmiennej X oznaczającej liczbę orłów w dwóch rzutach symetryczną monetą (zob. tabela 7.1), zaś na rysunku 7.2 przedstawiono dystrybuantę zmiennej ciągłej mającej rozkład normalny standaryzowany opisany w jednym z kolejnych rozdziałów (9.3.1).
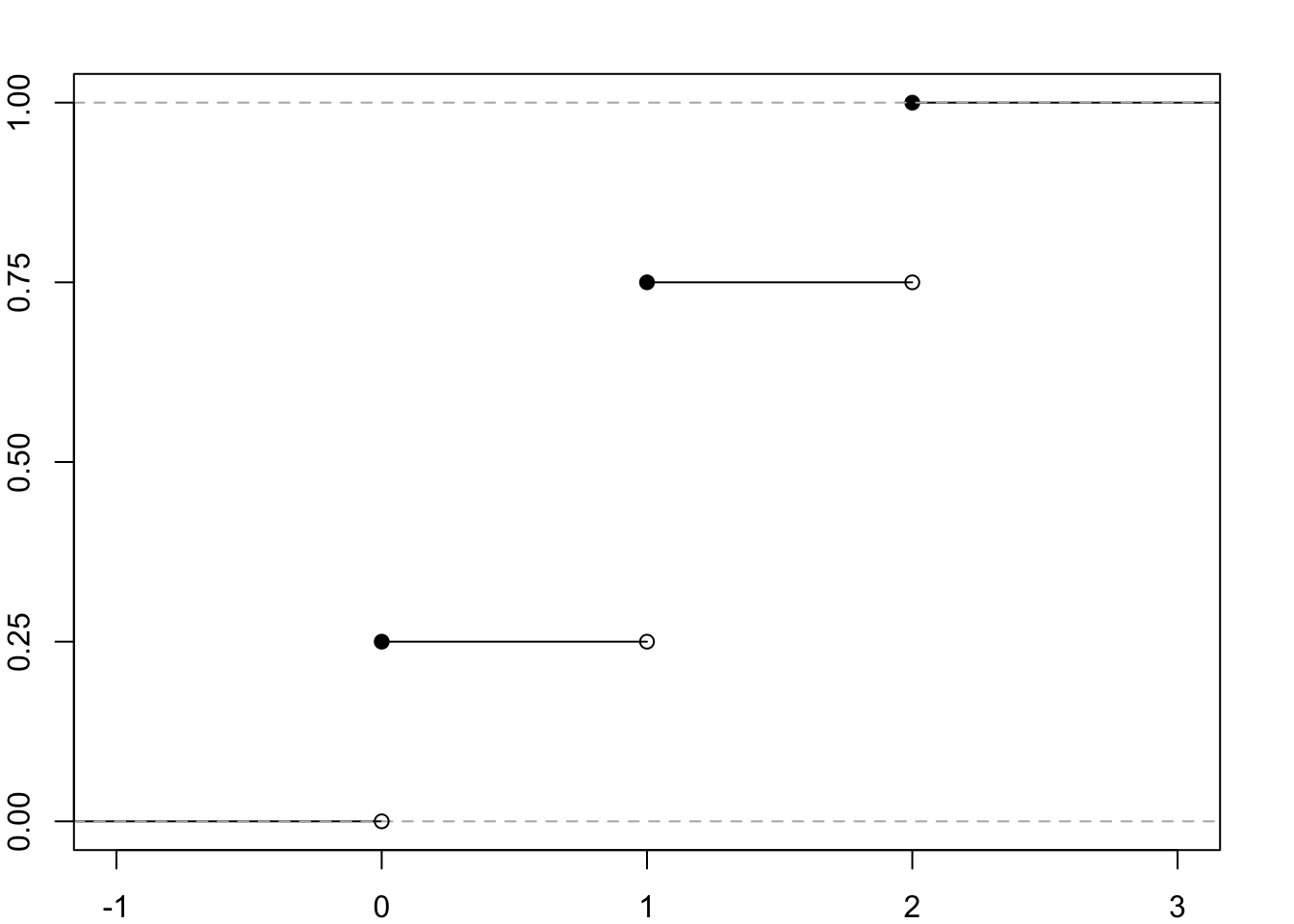
Rysunek 7.1: Dystrybuanta zmiennej losowej X oznaczającej liczbę orłów w dwóch rzutach symetryczną monetą.
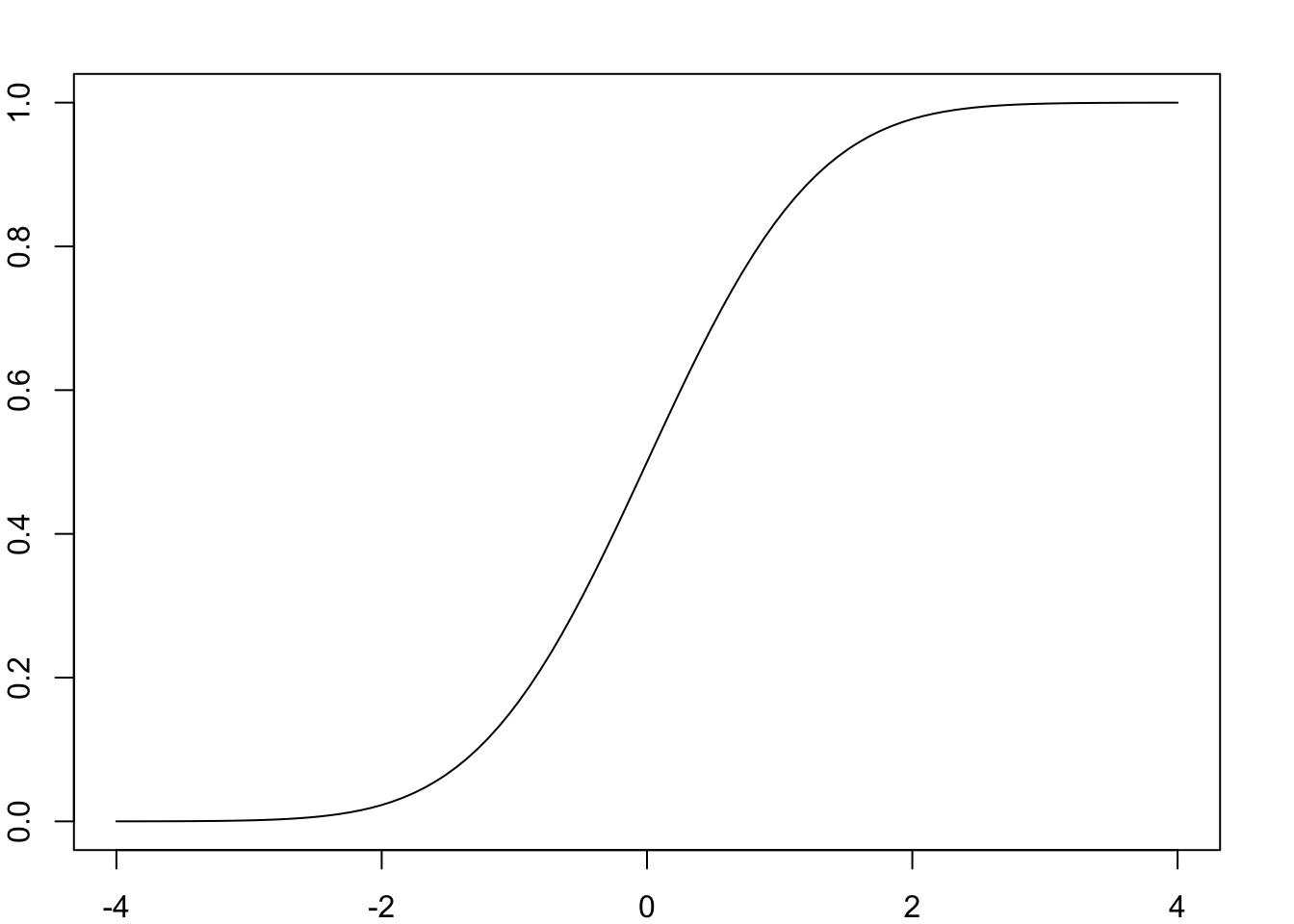
Rysunek 7.2: Dystrybuanta zmiennej losowej Z mającej standaryzowany rozkład Gaussa.
7.5 Przekształcenia zmiennych losowych
7.5.1 Dodawanie stałej do zmiennej
Jeżeli do zmiennej X dodamy stałą \(a\), to wartość oczekiwana odpowiednio się przesunie, a wariancja się nie zmieni:
\[\begin{equation} \mathbb{E}(X + a) = \mathbb{E}(X) + a \tag{7.15} \end{equation}\]
\[\begin{equation} \mathbb{V}(X + a) = \mathbb{V}(X) \tag{7.16} \end{equation}\]
7.5.2 Mnożenie zmiennych przez stałą
Jeżeli zmienną X przemnożymy przez stałą \(k\), to wartość oczekiwana będzie \(k\) razy większa, wariancja będzie \(k^2\) razy większa (odchylenie standardowe będzie \(k\) razy większe).
\[\begin{equation} \mathbb{E}(k\cdot X)=k \cdot \mathbb{E}(X) \tag{7.17} \end{equation}\]
\[\begin{equation} \mathbb{V}(k \cdot X) = k^2 \cdot \mathbb{V}(X) \tag{7.18} \end{equation}\]
7.5.3 Dodawanie zmiennych losowych
Jeżeli mamy dwie zmienne losowe X i Y, to wartość oczekiwana ich sumy (różnicy) będzie równa sumie (różnicy) ich wartości oczekiwanych.
\[\begin{equation} \begin{matrix} \mathbb{E}(X + Y)=\mathbb{E}(X) + \mathbb{E}(Y) \\ \mathbb{E}(X - Y)=\mathbb{E}(X) - \mathbb{E}(Y) \\ \end{matrix} \:\:\:\: \text{ nawet gdy X i Y są zależne} \tag{7.19} \end{equation}\]
Wariancja sumy zmiennych X i Y jest równa sumie ich wariancji, tylko gdy X i Y są niezależne. Wariancja różnicy zmiennych X i Y jest równa sumie (nie: różnicy) ich wariancji.
\[\begin{equation} \begin{matrix} \mathbb{V}(X + Y) = \mathbb{V}(X) + \mathbb{V}(Y) \\ \mathbb{V}(X - Y) = \mathbb{V}(X)\: \mathbf{+}\: \mathbb{V}(Y) \\ \end{matrix} \:\:\:\: \text{ tylko gdy X i Y są niezależne} \tag{7.20} \end{equation}\]
Szczególnym przypadkiem, dla którego stosujemy powyższe wzory, uwzględniając większą liczbę zmiennych, jest suma niezależnych zmiennych o jednakowym rozkładzie (i.i.d. - independent and identically distributed random variables).
Jeżeli mamy \(n\) takich (i.i.d.) zmiennych o średniej \(\mu\) i odchyleniu standardowym \(\sigma\) każda, to ich suma \(Y = X_1 + X_2 + ... + X_n\) ma średnią \(\mathbb{E}(Y) = \mathbb{E}(X_1) + \mathbb{E}(X_2) + ... + \mathbb{E}(X_n) = n\mu\), wariancję \(\mathbb{V}(Y)=n\sigma^2\), zaś odchylenie standardowe \(\sigma_Y = \sigma \sqrt{n}\).
7.6 Szablony
Arkusze kalkulacyjne
Dyskretna zmienna losowa - kalkulator — arkusz Google
Dyskretna zmienna losowa - kalkulator — szablon w Excelu
Kod w R
# Rozkład dyskretny jednej zmiennej
x <- c(0, 1, 4)
Px <- c(1/3, 1/3, 1/3)
# Sprawdzenie
if(length(x)!=length(Px))
{print("Oba wektory powinny być równej długości.")}
if(!sum(Px)==1)
{print("Prawdopodobieństwa powinny sumować się do 1. ")}
if(any(Px<0))
{print("Prawdopodobieństwa nie mogą być ujemne. ")}
# Obliczenia
EX <- sum(x*Px)
VarX <- sum((x-EX)^2*Px)
SDX <- sqrt(VarX)
SkX <- sum((x-EX)^3*Px)/SDX^3
KurtX <- sum((x-EX)^4*Px)/SDX^4 - 3
print(c('Wartość oczekiwana' = EX,
'Wariancja' = VarX,
'Odchylenie standardowe' = SDX,
'Skośność' = SkX,
'(Nadwyżkowa) kurtoza' = KurtX))## Wartość oczekiwana Wariancja Odchylenie standardowe Skośność
## 1.666667 2.888889 1.699673 0.528005
## (Nadwyżkowa) kurtoza
## -1.500000# Rozkład dyskretny dwóch zmiennych
x <- c(2, -1, -1)
y <- c(-1, 1, -1)
Pxy <- c(1/2, 1/3, 1-1/2-1/3) #sum(c(1/2, 1/3, 1/6))==1 zwraca czasem FALSE z powodów numerycznych
# Sprawdzenie
if(length(x)!=length(y) || length(x)!=length(Pxy))
{print("Wektory powinny być równej długości. ")}
if(!sum(Pxy)==1)
{print("Prawdopodobieństwa powinny sumować się do 1. ")}
if(any(Pxy<0))
{print("Prawdopodobieństwa nie mogą być ujemne. ")}
EX <- sum(x*Pxy)
VarX <- sum((x-EX)^2*Pxy)
SDX <- sqrt(VarX)
SkX <- sum((x-EX)^3*Pxy)/SDX^3
KurtX <- sum((x-EX)^4*Pxy)/SDX^4 - 3
EY <- sum(y*Pxy)
VarY <- sum((y-EY)^2*Pxy)
SDY <- sqrt(VarY)
SkY <- sum((y-EY)^3*Pxy)/SDY^3
KurtY <- sum((y-EY)^4*Pxy)/SDY^4 - 3
CovXY <- sum((x-EX)*(y-EY)*Pxy)
CorXY <- CovXY/(SDX*SDY)
print(c('Wartość oczekiwana X' = EX,
'Wariancja X' = VarX,
'Odchylenie standardowe X' = SDX,
'Skośność X' = SkX,
'(Nadwyżkowa) kurtoza X' = KurtX,
'Wartość oczekiwana Y' = EY,
'Wariancja Y' = VarY,
'Odchylenie standardowe Y' = SDY,
'Skośność Y' = SkY,
'(Nadwyżkowa) kurtoza Y' = KurtY,
'Kowariancja X i Y' = CovXY,
'Korelacja X i Y' = CorXY
))## Wartość oczekiwana X Wariancja X Odchylenie standardowe X Skośność X
## 5.000000e-01 2.250000e+00 1.500000e+00 -3.289550e-17
## (Nadwyżkowa) kurtoza X Wartość oczekiwana Y Wariancja Y Odchylenie standardowe Y
## -2.000000e+00 -3.333333e-01 8.888889e-01 9.428090e-01
## Skośność Y (Nadwyżkowa) kurtoza Y Kowariancja X i Y Korelacja X i Y
## 7.071068e-01 -1.500000e+00 -1.000000e+00 -7.071068e-01Kod w Pythonie
# Rozkład dyskretny jednej zmiennej
x = [0, 1, 4]
Px = [1/3, 1/3, 1/3]
# Sprawdzenie
if len(x) != len(Px):
print("Oba wektory powinny być równej długości.")
if sum(Px) != 1:
print("Prawdopodobieństwa powinny sumować się do 1. ")
if any(p < 0 for p in Px):
print("Prawdopodobieństwa nie mogą być ujemne. ")
# Obliczenia
EX = sum([a*b for a, b in zip(x, Px)])
VarX = sum([(a-EX)**2*b for a, b in zip(x, Px)])
SDX = VarX**0.5
SkX = sum([(a-EX)**3*b for a, b in zip(x, Px)]) / SDX**3
KurtX = sum([(a-EX)**4*b for a, b in zip(x, Px)]) / SDX**4 - 3
# Wyniki
print({'Wartość oczekiwana': EX,
'Wariancja': VarX,
'Odchylenie standardowe': SDX,
'Skośność': SkX,
'(Nadwyżkowa) kurtoza': KurtX})## {'Wartość oczekiwana': 1.6666666666666665, 'Wariancja': 2.888888888888889, 'Odchylenie standardowe': 1.699673171197595, 'Skośność': 0.5280049792181879, '(Nadwyżkowa) kurtoza': -1.5000000000000002}# Rozkład dyskretny dwóch zmiennych
x = [2, -1, -1]
y = [-1, 1, -1]
Pxy = [1/2, 1/3, 1-1/2-1/3]
# Sprawdzenie
if len(x) != len(y) or len(x) != len(Pxy):
print("Wektory powinny być równej długości. ")
if sum(Pxy) != 1:
print("Prawdopodobieństwa powinny sumować się do 1. ")
if any(p < 0 for p in Pxy):
print("Prawdopodobieństwa nie mogą być ujemne. ")
# Obliczenia
EX = sum([a*b for a, b in zip(x, Pxy)])
VarX = sum([(a-EX)**2*b for a, b in zip(x, Pxy)])
SDX = VarX**0.5
SkX = sum([(a-EX)**3*b for a, b in zip(x, Pxy)]) / SDX**3
KurtX = sum([(a-EX)**4*b for a, b in zip(x, Pxy)]) / SDX**4 - 3
EY = sum([a*b for a, b in zip(y, Pxy)])
VarY = sum([(a-EY)**2*b for a, b in zip(y, Pxy)])
SDY = VarY**0.5
SkY = sum([(a-EY)**3*b for a, b in zip(y, Pxy)]) / SDY**3
KurtY = sum([(a-EY)**4*b for a, b in zip(y, Pxy)]) / SDY**4 - 3
CovXY = sum([(a-EX)*(b-EY)*c for a, b, c in zip(x, y, Pxy)])
CorXY = CovXY / (SDX*SDY)
# Wyniki
print({'Wartość oczekiwana X': EX,
'Wariancja X': VarX,
'Odchylenie standardowe X': SDX,
'Skośność X': SkX,
'(Nadwyżkowa) kurtoza X': KurtX,
'Wartość oczekiwana Y': EY,
'Wariancja Y': VarY,
'Odchylenie standardowe Y': SDY,
'Skośność Y': SkY,
'(Nadwyżkowa) kurtoza Y': KurtY,
'Kowariancja X i Y': CovXY,
'Korelacja X i Y': CorXY
})## {'Wartość oczekiwana X': 0.5, 'Wariancja X': 2.25, 'Odchylenie standardowe X': 1.5, 'Skośność X': -3.289549702593056e-17, '(Nadwyżkowa) kurtoza X': -2.0, 'Wartość oczekiwana Y': -0.33333333333333337, 'Wariancja Y': 0.888888888888889, 'Odchylenie standardowe Y': 0.9428090415820634, 'Skośność Y': 0.7071067811865478, '(Nadwyżkowa) kurtoza Y': -1.4999999999999991, 'Kowariancja X i Y': -0.9999999999999998, 'Korelacja X i Y': -0.7071067811865475}7.7 Zadania
Zadanie 7.1 Rzucamy czterema rzetelnym monetami.
Wymień wszystkie równoprawdopodobne zdarzenia elementarne w przestrzeni prób. Ile ich jest?
Do każdego zdarzenia przypisz wartości zmiennej losowej X: liczba orłów.
Zapisz rozkład prawdopodobieństwa zmiennej X w formie tabeli.
Oblicz wartość oczekiwaną zmiennej X.
Oblicz wariancję i odchylenie standardowe zmiennej X.
Zadanie 7.2 Zmienna losowa ma następujący skokowy rozkład prawdopodobieństwa:
| \(x\) | \(\textbf{p}(x)\) |
|---|---|
| 10 | 0,2 |
| 11 | 0,3 |
| 12 | 0,2 |
| 13 | 0,1 |
| 14 | 0,2 |
Ponieważ wartości przyjmowane przez zmienną są zdarzeniami wzajemnie wykluczającymi się, zdarzenie \({ X \leqslant 12 }\) to suma trzech wzajemnie wykluczających się zdarzeń:
\[\{ X = 10 \} \cup \{ X = 11 \} \cup \{ X = 12 \}\]
Znajdź:
- \(\mathbb{P}(X \leqslant 12)\)
- \(\mathbb{P}(X > 12)\)
- \(\mathbb{P}(X \leqslant 14)\)
- \(\mathbb{P}(X = 14)\)
- \(\mathbb{P}(X \leqslant 11\:lub\:X > 12)\)
Zadanie 7.3 Dealer samochodowy rejestruje liczbę pojazdów sprzedanych każdego dnia. Dane zostały wykorzystane do wyznaczenia następującego rozkładu prawdopodobieństwa dziennej sprzedaży:
| \(x\) | \(\textbf{p}(x)\) |
|---|---|
| 0 | 0,1 |
| 1 | 0,1 |
| 2 | 0,2 |
| 3 | 0,2 |
| 4 | 0,3 |
| 5 | 0,1 |
Jakie jest prawdopodobieństwo, że liczba pojazdów sprzedanych jutro będzie pomiędzy 2 i 4 (w obu przypadkach włącznie)?
Znajdź dystrybuantę dziennej liczby sprzedanych aut.
Zadanie 7.4 W pewnej grze hazardowej uczestnik losuje jedną kartę ze zwykłej talii (52 karty). Jeżeli wylosowana karta to dama lub walet, uczestnikowi wypłacone jest 30 zł, jeżeli król lub as – wygrana wynosi 8 zł. W przypadku innej karty osoba płaci (traci) 5 zł. Ile wynosi oczekiwana wypłata? Ile wynosi odchylenie standardowe wypłaty?
Zadanie 7.5 Rzucamy jeden raz idealnie wyważoną kością do gry. Przez Y oznaczmy uzyskaną liczbę oczek. Jaka jest wartość oczekiwana i wariancja Y?
Zadanie 7.6 Pewien koszykarz, wykonując rzut za trzy punkty, trafia do kosza z prawdopodobieństwem 0,2. Załóżmy, że skuteczność w dwóch kolejnych rzutach jest od siebie niezależna, tzn. trafienie lub nie w pierwszym rzucie nie zmienia prawdopodobieństwa w drugim rzucie. Niech zmienna losowa X oznacza liczbę trafień w dwóch rzutach. Ile wynosi średnia i wariancja zmiennej X?
Zadanie 7.7 Dany jest następujący rozkład prawdopodobieństwa:
| \(x\) | \(\textbf{p}(x)\) |
|---|---|
| 1 | 0,2 |
| 2 | 0,4 |
| 5 | 0,3 |
| 10 | 0,1 |
Ile wynosi \(\mu = \mathbb{E}(X)\)?
Ile wynosi \(\sigma^2 = \mathbb{E}[ (X-\mu)^2]\)?
Ile wynosi \(\sigma\)?
Czy ta zmienna losowa kiedykolwiek przyjmie wartość \(\mu\)? Jak interpretować wartość oczekiwaną?
Podaj przykład zmiennej losowej, która może przyjąć wartość równą swojej wartości oczekiwanej.
Zadanie 7.8 Jaka jest wartość oczekiwana i odchylenie standardowe rozkładu zero-jedynkowego (w literaturze angielskojęzycznej nazywanego rozkładem Bernoulliego) z parametrem \(p\)?
| \(x\) | \(\textbf{p}(x)\) |
|---|---|
| 1 | \(p\) |
| 0 | \((1-p)\) |
Zadanie 7.9 Ile wynosi oczekiwany zysk (lub strata) w polskim Lotto przy następujących założeniach: jeden zakład kosztuje 3 złote, za trójkę otrzymujemy 24 złote, za czwórkę średnio 200 złotych, za piątkę 5000 złotych, zaś za szóstkę 9 milionów złotych?
Dodatkowo: ile minimalnie musielibyśmy otrzymać za szóstkę, żeby oczekiwany zysk był dodatni?
Zadanie 7.10 Skala staninowa (nazwa pochodzi od angielskiego „standarized nine”) powstaje, kiedy przekształcamy jakąś zmienną (np. wyniki egzaminu albo sumę punktów w teście psychometrycznym) w następujący sposób: 4% najniższych wyników trafia do klasy („kategorii staninowej”, „stanina”) 1, kolejnych 7% do klasy 2, 12% do klasy 3, 17% do klasy 4, 20% środkowych wyników do klasy 5, kolejnych 17% do klasy 6, 12% do 7, 7% do 8 i 4% najwyższych wyników do klasy 9. Potraktuj klasy staninowe jako nową zmienną przyjmującą wartości całkowite od 1 do 9. Oblicz, jaką średnią i odchylenie standardowe ma taka zmienna.
Zadanie 7.11 Podobny do skali staninowej jest system stenowy (od ang. „standarized ten”): 2,27% najniższych wyników trafia do klasy 1, 4,41% do klasy 2, 9,18% do klasy 3, 14,99% do klasy 4, 19,15% do klasy 5. Analogicznie powyżej mediany 19,15% wyników trafia do klasy 6, 14,99% – do 7, 9,18% do 8, 4,41% – do 9, zaś 2,27% najwyższych wyników – do 10. Oblicz średnią i odchylenie standardowe skali stenowej.
Zadanie 7.12 Oblicz wartość oczekiwaną zakładu, jeżeli w ruletce amerykańskiej postawimy na:
Straight Up, numer pojedynczy
Split, dwa numery
Street, trzy numery
Corner, cztery numery
Top Line (Five), 0 – 3
Six Line / Double Street, sześć numerów
Column, kolumnę
Dozen, tuziny: 1 – 12, 13 – 24, 25 – 36
Even, parzyste lub Odd, nieparzyste
Red, czerwone lub Black - czarne
1st 18, numery 1 – 18 lub 2nd 18, numery 19 – 36
Alternatywny równoważny wzór, często używany w praktyce to: \[\mathbb{V}(X) = \mathbb{E}(X^2) - \mu^2\]↩︎