Chapter 29 Review + Fun data sets if you need them

29.1 Review

You should be pretty comfortable with the ideas of

  • Parameters vs Estimates
  • Sampling and what can go wrong
  • Null hypothesis significance testing
  • Common test statistics
    • F
    • t
  • Calculating Sums of Squares
  • Interpreting stats output like that below
ToothGrowth <- mutate(ToothGrowth, dose = factor(dose))
tooth_lm <- lm(len ~ supp * dose, data = ToothGrowth)


summary(tooth_lm)   
## 
## Call:
## lm(formula = len ~ supp * dose, data = ToothGrowth)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -8.20  -2.72  -0.27   2.65   8.27 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    13.230      1.148  11.521 3.60e-16 ***
## suppVC         -5.250      1.624  -3.233  0.00209 ** 
## dose1           9.470      1.624   5.831 3.18e-07 ***
## dose2          12.830      1.624   7.900 1.43e-10 ***
## suppVC:dose1   -0.680      2.297  -0.296  0.76831    
## suppVC:dose2    5.330      2.297   2.321  0.02411 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.631 on 54 degrees of freedom
## Multiple R-squared:  0.7937, Adjusted R-squared:  0.7746 
## F-statistic: 41.56 on 5 and 54 DF,  p-value: < 2.2e-16
anova(tooth_lm)
## Analysis of Variance Table
## 
## Response: len
##           Df  Sum Sq Mean Sq F value    Pr(>F)    
## supp       1  205.35  205.35  15.572 0.0002312 ***
## dose       2 2426.43 1213.22  92.000 < 2.2e-16 ***
## supp:dose  2  108.32   54.16   4.107 0.0218603 *  
## Residuals 54  712.11   13.19                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova(tooth_lm, type = "II")   
## Anova Table (Type II tests)
## 
## Response: len
##            Sum Sq Df F value    Pr(>F)    
## supp       205.35  1  15.572 0.0002312 ***
## dose      2426.43  2  92.000 < 2.2e-16 ***
## supp:dose  108.32  2   4.107 0.0218603 *  
## Residuals  712.11 54                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

29.2 Quiz

Reflection questions on [canvas] ## Potential data sets

Spend the weekend pushing forward on your linear model project.

Recall that a major assumption of linear models is that errors are normally distributed.

Although linear models are robust to minor violations of these assumptions, they are not a good choice for a categorical response variable – so if your early analyses had categorical response variables you probably need a new data set. Here are some currated options.

Consequences of extinction

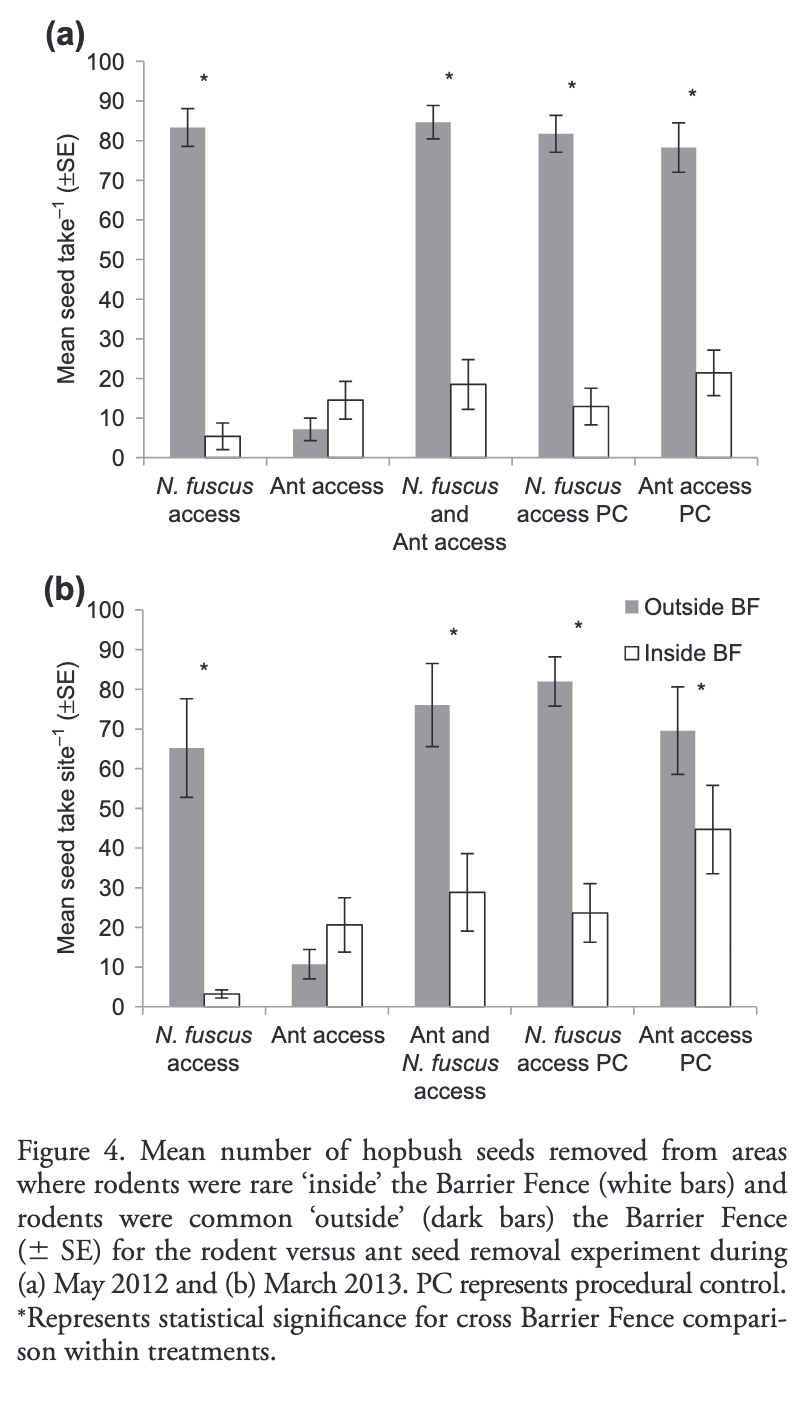
Functional extinction of a desert rodent: implications for seed fate and vegetation dynamics. Gordon and Letnic (2016) . data for project (.xlsx format), paper, full data on dryad.

Image from paper [dont try to recreate this]

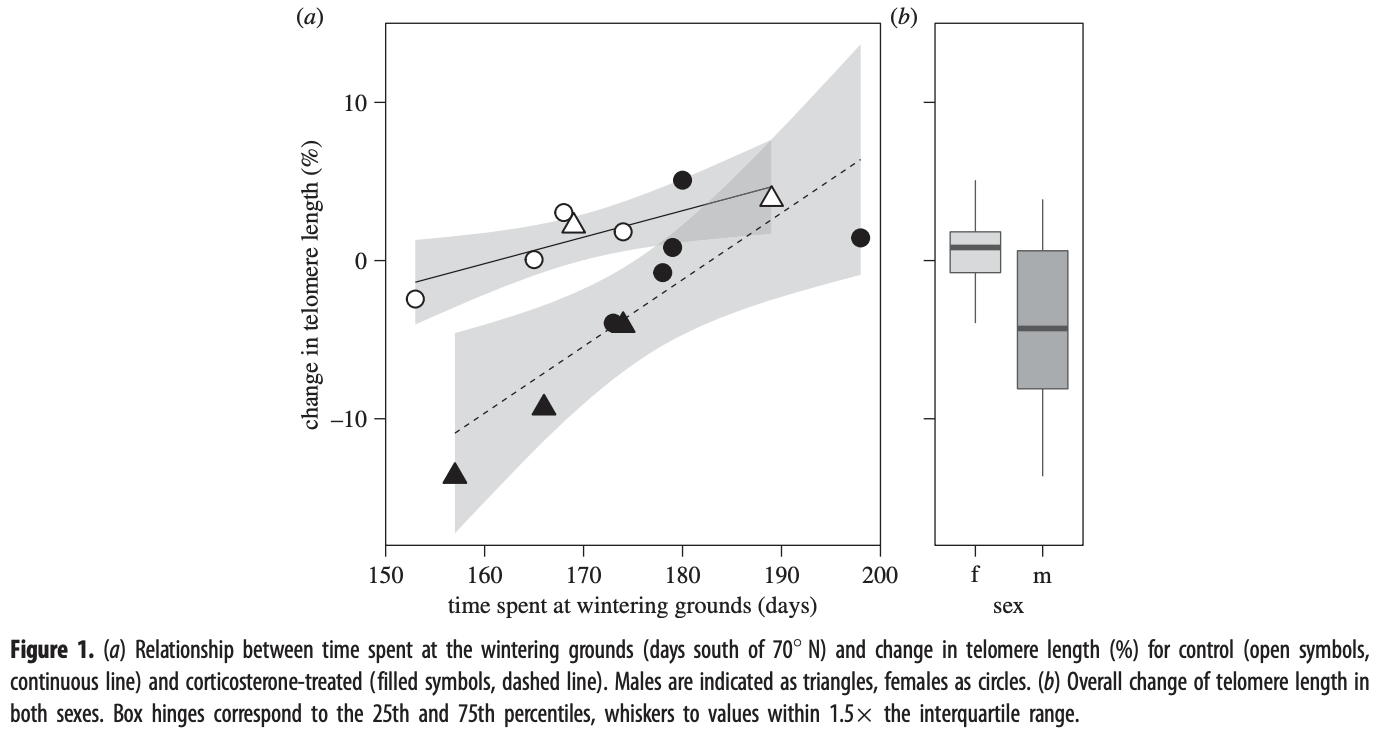
Moving and other stresses might shorten telomeres

Migration and stress during reproduction govern telomere dynamics in a seabird. Schultner et al. (2014). data for project (.xlsx format), paper.

Associations between neurons and IQ

Large and fast human pyramidal neurons associate with intelligence. Goriounova et al. (2018). data for project (.xlsx format), paper, dryad.

Inbreeding and fitness

A high-quality pedigree and genetic markers both reveal inbreeding depression for quality but not survival in a cooperative mammal. Wells et al. (2018). data for project annual reproduction (.csv format), yearling weight (.csv format). paper, dryad.

References

Gordon, Christopher E, and Mike Letnic. 2016. “Functional Extinction of a Desert Rodent: Implications for Seed Fate and Vegetation Dynamics.” Ecography 39 (9): 815–24.
Goriounova, Natalia A, Djai B Heyer, René Wilbers, Matthijs B Verhoog, Michele Giugliano, Christophe Verbist, Joshua Obermayer, et al. 2018. “Large and Fast Human Pyramidal Neurons Associate with Intelligence.” Edited by David Badre, Timothy E Behrens, and Christof Koch. eLife 7 (December): e41714. https://doi.org/10.7554/eLife.41714.
Schultner, Jannik, Børge Moe, Olivier Chastel, Claus Bech, and Alexander S Kitaysky. 2014. “Migration and Stress During Reproduction Govern Telomere Dynamics in a Seabird.” Biology Letters 10 (1): 20130889–89. https://doi.org/10.1098/rsbl.2013.0889.
Wells, David A., Michael A. Cant, Hazel J. Nichols, and Joseph I. Hoffman. 2018. “A High-Quality Pedigree and Genetic Markers Both Reveal Inbreeding Depression for Quality but Not Survival in a Cooperative Mammal.” Molecular Ecology 27 (9): 2271–88. https://doi.org/https://doi.org/10.1111/mec.14570.